6.2: Principios de Procesamiento Térmico de Alimentos Envasados
- Page ID
- 80928
Ricardo Simpson
Departamento de Ingeniería Química y Ambiental, Universidad Técnica Federico Santa María, Valparaíso, Chile
Centro Regional de Estudios en Alimentos y Salud (CREAS) Proyecto Conicyt-Regional GORE Valparaíso R17A10001, Curauma, Valparaíso, Chile
Helena Núñez
Departamento de Ingeniería Química y Ambiental, Universidad Técnica Federico Santa María, Valparaíso, Chile
Cristian Ramírez
Departamento de Ingeniería Química y Ambiental, Universidad Técnica Federico Santa María, Valparaíso, Chile
Centro Regional de Estudios en Alimentos y Salud (CREAS) Proyecto Conicyt-Regional GORE Valparaíso R17A10001, Curauma, Valparaíso, Chile
| Términos Clave |
| Transferencia de calor | Inactivación bacteriana | Esterilización de alimentos |
| Resistencia al calor de microorganismos | Tiempo de reducción decimal | Esterilización comercial |
Variables
Introducción
El procesamiento térmico de los alimentos, como la cocción, implica calor y alimentos. Sin embargo, el procesamiento térmico se aplica para garantizar la inocuidad de los alimentos y no necesariamente para cocinar los alimentos. El procesamiento térmico como medio de conservación de alimentos crudos fue inventado en Francia en 1795 por Nicholas Appert, un chef que estaba decidido a ganar el premio de 12 mil francos ofrecidos por Napoleón para una forma de evitar que los suministros de alimentos militares se echaran a perder. Appert trabajó con Peter Durand para conservar carnes y verduras encerradas en frascos o latas al vacío y selladas con brea y, para 1804, abrió su primera planta de envasado al vacío. Este secreto militar francés pronto se filtró, pero Louis Pasteur tardó más de 50 años en dar la explicación de la efectividad del método de Appert, cuando Pasteur pudo demostrar que el crecimiento de microorganismos era la causa del deterioro de los alimentos.
La conservación para almacenamiento mediante tratamiento térmico y remoción de atmósfera se conoce genéricamente como enlatado, independientemente de qué contenedor se utilice para almacenar los alimentos. Los principios básicos del enlatado no han cambiado drásticamente desde que Appert y Durand desarrollaron el proceso: aplicar suficiente calor a los alimentos para destruir o inactivar microorganismos, luego empacar los alimentos en recipientes sellados o “herméticos”, idealmente al vacío. Los alimentos enlatados tienen una vida útil de uno a cuatro años a temperaturas normales, lo que los hace convenientes, asequibles y fáciles de transportar.
Resultados
Después de leer este capítulo, deberías poder:
- • Identificar el papel de los conceptos de transferencia de calor en el procesamiento térmico de alimentos envasados
- • Describir los principios de esterilización comercial de alimentos
- • Describir las condiciones de inactivación necesarias para algunos microorganismos de ejemplo importantes para la inocuidad de los alimentos
- • Definir algunos criterios de esterilización para alimentos específicos
- • Aplicar, en forma simple, las principales técnicas de evaluación de procesamiento térmico de alimentos
Conceptos
Los principales conceptos utilizados en el procesamiento térmico de alimentos incluyen: (a) transferencia de calor; (b) resistencia al calor de microorganismos de interés; y (c) inactivación bacteriana.
Transferencia de Calor
Los principales mecanismos de transferencia de calor involucrados en el procesamiento térmico de los alimentos envasados son la convección y la conducción. La transferencia de calor por convección ocurre debido al movimiento y mezcla de flujos. El término convección natural se refiere al caso cuando el movimiento y la mezcla del flujo son causados por diferencias de densidad en diferentes ubicaciones debido a gradientes de temperatura. El término convección forzada se refiere al caso en el que el movimiento y la mezcla del flujo se producen por una fuerza exterior, por ejemplo, un ventilador. La transferencia de calor por conducción ocurre cuando los átomos y las moléculas chocan, transfiriendo energía cinética. Conceptualmente, los átomos están unidos a sus vecinos, y si se suministra energía a una parte del sólido, los átomos vibrarán y transferirán su energía a sus vecinos y así sucesivamente.
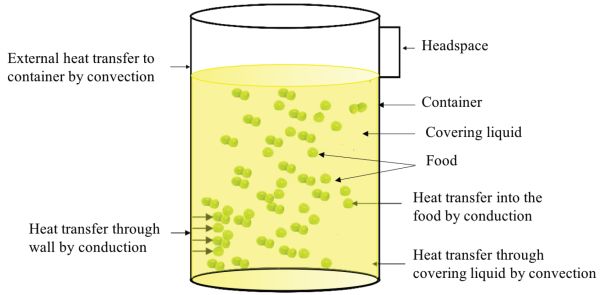
Los principales mecanismos de transferencia de calor involucrados en el procesamiento térmico de alimentos envasados se muestran en la Figura 6.2.1. Si bien la figura muestra una lata cilíndrica (un cilindro de diámetro y altura finitos), una situación similar surgirá cuando se procesen otros tipos de envases como envases de vidrio, bolsas retortables y recipientes de plástico rígidos y semirrígidos. En general, independientemente de la forma, los tamaños de los paquetes de alimentos varían de 0.1 L a 5 L (Holdsworth y Simpson, 2016).
El mecanismo principal de transferencia de calor desde el medio de calentamiento (por ejemplo, vapor o agua caliente) al recipiente o empaque es la convección. Luego el calor se transfiere por conducción a través de la pared del contenedor o paquete. Una vez dentro del contenedor, la transferencia de calor a través del líquido de cobertura se produce por convección, y en alimentos sólidos principalmente por conducción. En el caso de los alimentos líquidos, el mecanismo principal es la convección.
La tasa de transferencia de calor en los alimentos envasados depende de los factores del proceso, los factores del producto y los tipos de empaque. Los factores del proceso incluyen el perfil de temperatura de retorta, el tiempo de proceso, el medio de transferencia de calor y la agitación Los factores del producto incluyen la composición de los alimentos, la consistencia, la temperatura inicial, la carga inicial de esporas, la difusividad térmica y el pH. Los factores relacionados con el tipo de empaque son el material del contenedor, ya que la tasa de transferencia de calor depende de la conductividad térmica y el grosor del material, y la forma del contenedor, ya que el área superficial por unidad de volumen juega un papel en la tasa de penetración de calor.
Para los alimentos líquidos, la velocidad de calentamiento está determinada no sólo por la difusividad térmica α, sino también por la viscosidad. La difusividad térmica es una propiedad material que representa la rapidez con la que el calor se mueve a través de los alimentos y se determina como:
\[ a=K_{t}/(\rho\ C_{p}) \]
donde α = difusividad térmica (m 2 /s)
- K t = conductividad térmica (W/m-K)
- ρ = densidad (kg/m 3)
- C p = calor específico (W/s-kg-K)
Es extremadamente difícil desarrollar un modelo teórico para la predicción de un historial de tiempo-temperatura dentro del material de empaque. Por lo tanto, desde un punto de vista práctico, se suele determinar un proceso térmico satisfactorio (es decir, relación tiempo-temperatura) utilizando el punto de calentamiento más lento, el punto frío, dentro del contenedor.
Resistencia al calor de microorganismos de preocupación
El objetivo principal en el diseño de un proceso de esterilización de alimentos es la inactivación de los microorganismos que causan intoxicación alimentaria y deterioro. Para diseñar un proceso de esterilización seguro, se deben determinar las condiciones de operación adecuadas (tiempo y temperatura) para cumplir con el criterio de esterilización preestablecido. Para establecer este criterio, es necesario conocer la resistencia al calor de los microorganismos (algunos ejemplos se dan en el Cuadro 6.2.1), las propiedades térmicas de los alimentos y envases, y la forma y dimensiones del alimento envasado. A partir de estos, es posible determinar la temperatura de la retorta y el tiempo de retención (es decir, las condiciones para la inactivación), cuánto tiempo llevará alcanzar esa temperatura (el tiempo de subida) y cuánto tiempo llevará enfriarse a aproximadamente 40°C (el tiempo de enfriamiento) (Holdsworth y Simpson, 2016).
| Organismo | Condiciones para la inactivación |
|---|---|
|
Células vegetativas |
10 min a 80°C |
|
Ascosporas de levadura |
5 min a 60°C |
|
Hongos |
30—60 min a 88°C |
|
Organismos termófilos: |
|
|
Bacillus stearothermophilus |
4 min a 121.1°C |
|
Clostridium thermosaccharolyticum |
3—4 min a 121,1°C |
|
Organismos mesófilos: |
|
|
Esporas de Clostridium botulinum |
3 min a 121.1°C |
|
Toxinas Clostridium botulinum Tipos A y B |
0.1—1 min a 121.1°C |
|
Clostridium sporogenes |
1.5 min a 121.1°C |
|
Bacillus subtilis |
0.6 min a 121.1°C |
El pH del alimento es extremadamente relevante para la selección de los parámetros del proceso de esterilización, es decir, temperatura de retorta y tiempo de retención, debido a que los microorganismos crecen mejor en un ambiente menos ácido. Es por ello que el proceso de esterilización comercial estándar se basa en el microorganismo más resistente (Clostridium botulinum) en las condiciones del peor escenario (pH más alto) (Teixeira et al., 2006). La resistencia al calor de microorganismos es mayor en productos bajos en ácido (pH ≥ 4.5—4.6). Por otro lado, los alimentos medio-ácidos a ácidos requieren un tratamiento térmico mucho más suave (menor temperatura) para cumplir con el criterio de esterilización. En base a eso, los alimentos se clasifican en tres grupos:
- productos bajos en ácido: pH > 4.5—4.6 (por ejemplo, mariscos, carne, verduras, productos lácteos);
- productos medio-ácidos: 3.7 < pH < 4.6 (por ejemplo, pasta de tomate);
- productos ácidos: pH < 3.7 (e.g., la mayoría de los frutos).
Inactivación Bacteriana
La abundante literatura científica apoya la aplicación de cinéticas de primer orden para cuantificar la inactivación bacteriana (esporas) como (Esty y Meyer, 1922; Ball y Olson, 1957; Stumbo, 1973, Holdsworth y Simpson, 2016):
\[ (\dfrac{dN}{dt})_{I} = -kN \]
donde\(N\) = concentración bacteriana viable (microbiana) (microorganismos/g) después del tiempo de proceso t
- t = tiempo
- I = inactivación
- k = constante de la velocidad de inactivación bacteriana (1/tiempo)
En lugar de k, los tecnólogos de alimentos han utilizado el concepto de tiempo de reducción decimal, D, definido como el tiempo para reducir la concentración bacteriana en diez veces. Es decir, D es el tiempo requerido a una temperatura especificada para inactivar el 90% de la población del microorganismo. Se desarrolla una expresión matemática que relaciona la constante de velocidad, k, de la Ecuación 6.2.2 a D separando variables e integrando la concentración bacteriana de la concentración inicial, N 0, a N 0 /10 y a partir del tiempo 0 a D, obteniendo por lo tanto:
\[ k=\dfrac{ln\ 10}{D} = \dfrac{2.303}{D} \]
o
\[ D = \dfrac{ln\ 10}{k} = \dfrac{2.303}{k} \]
donde k = constante de velocidad de reacción (1/min)
D = tiempo de reducción decimal (min)
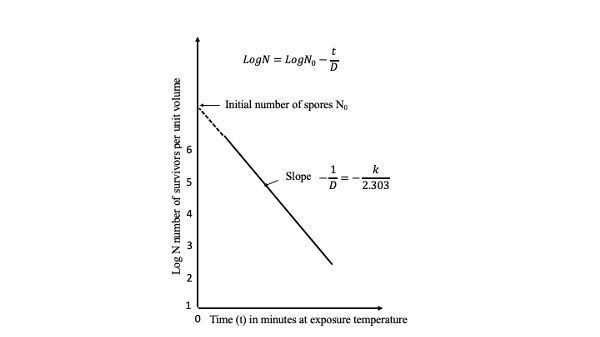
Una gráfica del log de los supervivientes (log N) contra D se denomina curva de sobreviviente (Figura 6.2.2). La pendiente de la línea a través de un ciclo logarítmico (reducción decimal) es −1/ D y
\[ log\ N = log\ N_{0} - \dfrac{t}{D} \]
donde N = número de supervivientes
N 0 = N en el tiempo cero, el inicio del proceso
Dependencia de Temperatura del Tiempo de Reducción Decimal, D
Cada proceso térmico de un producto alimenticio es función de la resistencia térmica del microorganismo en cuestión. Cuando el logaritmo del tiempo de reducción decimal, D, se grafica contra la temperatura, resulta una línea recta. Esta gráfica se denomina curva de tiempo de muerte térmica (TDT) (Figura 6.2.3). A partir de dicha gráfica, se puede determinar la sensibilidad térmica de un microorganismo, z, como el cambio de temperatura necesario para variar el TDT en un ciclo logarítmico.
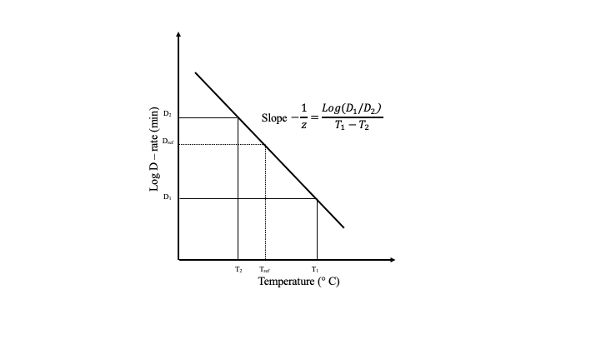
Bigelow y sus compañeros de trabajo (Bigelow y Esty, 1920; Bigelow, 1921) fueron los primeros en acuñar el término tasa de mortalidad térmica para relacionar la dependencia de la temperatura de D. Matemáticamente, se ha utilizado la siguiente expresión:
\[ log\ D = log\ D_{ref}-\dfrac{T-T_{ref}}{z} \]
o
\[ D = D_{ref}10^{\dfrac{T-T_{ref}}{z}} \]
donde D = tiempo de reducción decimal a temperatura T (min)
D ref = tiempo de reducción decimal a temperatura de referencia T ref (min)
z = cambio de temperatura necesario para variar la TDT en un ciclo logarítmico (°C), por ejemplo, normalmente z = 10°C para Clostridium botulinum
T = temperatura (°C)
T ref = temperatura de referencia (normalmente 121.1°C para esterilización)
El valor D está directamente relacionado con la resistencia térmica de un microorganismo dado. Cuanto más resistente sea el microorganismo al tratamiento térmico, mayor será el valor D. Por otro lado, el valor z representa la dependencia de la temperatura pero no tiene relación con la resistencia térmica del microorganismo diana. Entonces, cuanto mayor es el valor z, menos sensible es el microorganismo dado a los cambios de temperatura. Los valores de D se expresan como D T. Por ejemplo, D 140 significa el tiempo requerido para reducir la población microbiana en un ciclo logarítmico cuando el alimento se calienta a 140°C.
Criterio y cálculo de esterilización de alimentos
Esterilización significa la destrucción completa o inactivación de microorganismos. La comunidad de ciencias e ingeniería de los alimentos ha aceptado la utilización de una cinética de primer orden para la inactivación de Clostridium botulinum (Ecuación 6.2.2). Nuevamente, este patógeno es el microorganismo diana en procesos que utilizan el calor para esterilizar los alimentos. Teóricamente, el tiempo de inactivación necesario para inactivar completamente Clostridium botulinum es infinito. De acuerdo con las Ecuaciones 6.2.2 y 6.2.3 y asumiendo una temperatura de proceso constante y que k es constante, se obtiene la siguiente expresión:
\[ N_{f} = N_{0}e^{-kt} = N_{0}e^{-\dfrac{ln10}{D}t} \]
Esta ecuación muestra que la concentración final de Clostridium botulinum (N f) tiende a cero cuando el tiempo (t) tiende al infinito; por lo tanto, no es posible alcanzar una concentración final igual a cero para el microorganismo diana. Por lo tanto, es necesario definir un criterio de esterilización (o criterio de esterilización comercial) para diseñar un proceso que garantice un producto seguro dentro de un tiempo finito.
El nivel de inactivación microbiana, definido por el valor de letalidad microbiana o letalidad acumulativa, es la forma en que se cuantifica el proceso de esterilización. Específicamente, el valor de esterilización, denotado por F 0, es el tiempo requerido a 121.1°C para lograr 12 reducciones decimales (12 D). Es decir, F 0 es el tiempo requerido para reducir la concentración inicial de microorganismos de N 0 a N 0 /10 12 a la temperatura del proceso de 121.1°C.
El criterio de esterilización 12 D es un proceso extremo (es decir, exageración) diseñado para garantizar que no queden células de C. botulinum en los alimentos y, por lo tanto, prevenir enfermedades o muertes. De acuerdo con la FDA (1972), el tratamiento térmico mínimo para un alimento bajo en ácido debe alcanzar un valor mínimo de F 0 de 3 min (es decir, mayor de 12 D; D para C. botulinum a 121.1°C es 0.21 min, luego 12 × 0.21 = 2.52 min, que es menor a 3 min). Por lo tanto, un proceso térmico para la esterilización comercial de un producto alimenticio debe tener un valor F 0 mayor a 3 minutos.
El F 0 alcanzado para un alimento se puede calcular fácilmente cuando la temperatura en el centro del alimento durante el procesamiento térmico es conocida por:
\[ F_{0}=\int^{t}_{0}10^{\dfrac{T-T_{ref}}{z}}dt \]
donde F 0 = letalidad acumulada del proceso desde el tiempo 0 hasta el final del proceso (t)
T = temperatura medida en el punto frío de los alimentos, que es el lugar en el alimento que se calienta en último lugar
T ref = temperatura de referencia de microorganismos; para esterilización de alimentos bajos en ácido, T ref = 121.1°C para C. botulinum
z = cambio de temperatura necesario para reducir el valor D en diez veces; en el caso de esterilización de alimentos bajos en ácido, z = 10°C para C. botulinum
t = tiempo de proceso para alcanzar F 0
La ecuación 6.2.9 puede calcularse de acuerdo con el método general propuesto por Bigelow y sus compañeros de trabajo hace 100 años (Bigelow et al., 1920; Simpson et al., 2003).
Si el alimento se calienta instantáneamente a 121.1°C y se mantiene a esta temperatura por 3 min, entonces el valor F 0 para este proceso será de 3 min. De la Ecuación 6.2.9,
\(F_{0}=\int^{t}_{0}10^{\dfrac{121.1-121.1}{10}}dt=\int^{t}_{0}10^{0}dt=\int^{3}_{0}1dt \)
Dado que el intervalo de tiempo está entre 0 y 3 min, entonces la solución integral es de 3 min o\(\int^{3}_{0}1dt\) = 3 — 0 = 3. Sin embargo, en la práctica, debido a la resistencia de los alimentos a la transferencia de calor, el proceso de esterilización térmica requiere un tiempo más largo para obtener un F 0 ≥ 3 min, debido a que se necesita una parte significativa del tiempo de procesamiento para elevar la temperatura del punto frío del alimento y posteriormente para enfriar la comida.
Aplicaciones
Proceso de Esterilización Comercial
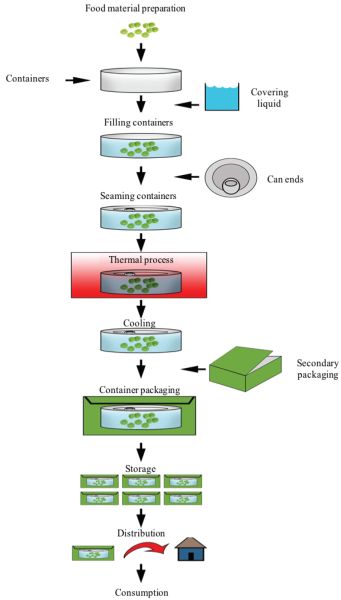
En la Figura 6.2.4 se presenta un diagrama de flujo general y simplificado para una fábrica de conservas comerciales típicas.
Etapa 1: Seleccionar y preparar los alimentos de la manera más limpia, rápida y precisa posible. Los alimentos que mantienen su color, sabor y textura deseables a través de la esterilización comercial incluyen brócoli, maíz, espinacas, guisantes, judías verdes, melocotones, cerezas, bayas, salsas, purés, mermeladas y jaleas, jugos de frutas y verduras, y algunas carnes (Featherstone, 2015). La preparación debe realizarse con mucho cuidado y con la menor cantidad de daños y pérdidas para minimizar el costo monetario de la operación. Si los alimentos no se manejan adecuadamente, la efectividad del tratamiento de esterilización se ve comprometida.
Etapa 2: Empaque el producto en recipientes herméticamente sellables (frascos, latas o bolsas) y sellando al vacío para eliminar el aire residual. Un enfoque menos común es esterilizar primero los alimentos y luego envasarlos asépticamente (procesamiento aséptico y envasado de alimentos).
Etapa 3: Estabilizar los alimentos esterilizándolos a través de un riguroso procesamiento térmico (es decir, alta temperatura para lograr el grado correcto de esterilización o la destrucción objetivo de los microorganismos presentes en el alimento), seguido de enfriamiento del producto a una temperatura baja (aproximadamente 40°C), en el que las reacciones enzimáticas y químicas comienzan a disminuir la velocidad.
Etapa 4: Almacenar a una temperatura inferior a 35°C, temperatura por debajo de la cual no pueden crecer los organismos que dañan los alimentos.
Etapa 5: Etiquetado, empaque secundario, distribución, comercialización y consumo. Aunque no forma parte del proceso térmico per se, esta etapa aborda los pasos requeridos para la comercialización de los alimentos tratados.
La etapa 3, procesamiento térmico, es el foco de este capítulo. El objetivo del proceso térmico es inactivar, por efecto del calor, esporas y microorganismos presentes en el producto no procesado. El proceso térmico se realiza en recipientes conocidos como retortas o autoclaves para lograr las altas temperaturas requeridas (generalmente superiores a 100°C).
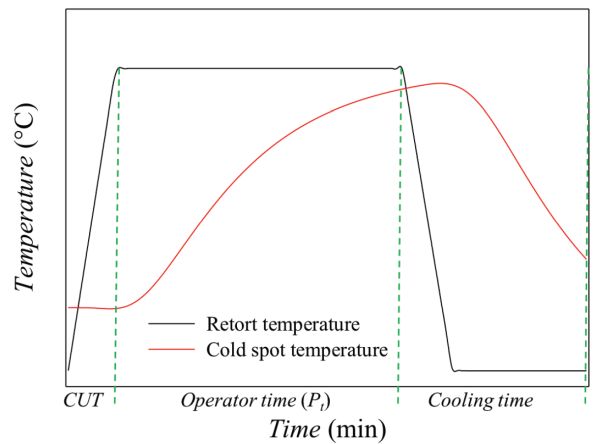
Como se muestra en la Figura 6.2.5, un proceso de esterilización típico tiene tres pasos principales: tiempo de llegada, tiempo de proceso del operador y enfriamiento. El primer paso, el tiempo de llegada (CUT), es el tiempo requerido para alcanzar la temperatura de retorta especificada (TRT), es decir, la temperatura objetivo en la retorta. El segundo paso es el tiempo de retención (P t), también llamado tiempo de proceso del operador, que es la cantidad de tiempo que se debe mantener la temperatura de retorta para asegurar el grado deseado de letalidad. Esto depende del microorganismo diana o de la contaminación microbiológica esperada. El paso final es el enfriamiento, cuando se disminuye la temperatura del producto introduciendo agua fría en la retorta. El propósito de enfriar los alimentos es minimizar el procesamiento excesivo (calor) de los alimentos, y evitar el riesgo de desarrollo de microorganismos termófilos. Durante el ciclo de enfriamiento, puede ser necesario inyectar aire estéril en el empaque de los alimentos para evitar caídas repentinas de presión interna y evitar la deformación del paquete.
Los conceptos descritos en este capítulo describen los principios clave para aplicar un proceso térmico a los alimentos envasados para lograr la letalidad requerida para la inocuidad de los alimentos. Estos conceptos se pueden utilizar para diseñar un proceso térmico que garantice el tiempo de procesamiento adecuado y la seguridad alimentaria, evitando al mismo tiempo el sobreprocesamiento de los alimentos envasados. Esto debería garantizar alimentos envasados seguros, sabrosos y nutritivos.
Ejemplos
Ejemplo\(\PageIndex{1}\)
Ejemplo 1: Cálculo del recuento microbiano después de un proceso térmico dado
Problema:
El valor D 120°C para un microorganismo es de 3 minutos. Si la contaminación microbiana inicial es de 10 12 células por gramo de producto, ¿cuántos microorganismos quedarán en la muestra después del tratamiento térmico a 120°C durante 18 minutos?
Solución
Calcular el número de celdas restantes usando la Ecuación 6.2.5 con N 0 = 10 12 celdas/g, t = 18 minutos, y D 120°C = 3 minutos.
De la Ecuación 6.2.5,
\( log\ N_{(t)} =log\ N_{0}-\dfrac{t}{D} \)
\( log\ N_{(18)} =log\ 10^{12}\dfrac{\text{cells}}{g}-\dfrac{18\text{ min}}{3\text{ min}} \)
Resolviendo para N (18) rendimientos:
\( N_{(18)} =10^{6}\text{ cells/g} \)
Discusión:
A partir de una concentración microbiana conocida (N 0), se puede calcular la concentración final de un microorganismo específico para un proceso térmico dado a temperatura constante si se conoce la resistencia térmica del microorganismo a una temperatura dada. En este caso, D 120°C = 3 min.
Ejemplo\(\PageIndex{2}\)
Ejemplo 2: Cálculo del valor z para un microorganismo particular
Problema:
D de una bacteria dada en la leche a 65°C es de 15 minutos. Cuando una muestra de alimento que tiene 10 10 células de la bacteria por gramo de alimento se calienta durante 10 minutos a 75°C, el número de supervivientes es de 2.15 × 10 3 células. Calcula z para esta bacteria.
Solución
Primero, calcule D a la temperatura del proceso de 75°C, D 75°C, usando la Ecuación 6.2.5. Después calcula z usando la Ecuación 6.2.6 con D 65°C = 15 minutos, N 0 = 10 10 celdas/g, y t = 10 minutos a T = 75°C.
\( log\ N_{(t)} = log\ N_{0} - \dfrac{t}{D} \)(Ecuación\(\PageIndex{5}\))
\( log\ 2.15\times10^{3} \text{ cells/g} = log\ 10^{10} \text{ cells/g}-\dfrac{10\text{ min}}{D_{75^\circ C}} \)
y D 75°C = 1.5 min.
Para calcular z, recuerde la Ecuación 6.2.6:
\( log\ D = log\ D_{ref} - \dfrac{T-T_{ref}}{z} \)
Resolviendo para z, la Ecuación 6.2.6 se puede expresar como:
\( z = \dfrac{\Delta T}{log(\dfrac{D_{1}}{D_{2}})} \)
con ∆T = (75 — 65) °C, D 1 = D 65°C y D 2 = D 75°C,
\( z = \dfrac{75-65}{log(\dfrac{15}{1.5})}=10 ^\circ C \)
Discusión:
Como se explicó anteriormente, el valor z representa el cambio en la temperatura del proceso requerido para reducir el valor D del microorganismo diana en diez veces. En este caso, el valor z es de 10°C y en consecuencia el valor D se redujo 10 veces, de 15 minutos a 1.5 minutos.
Ejemplo\(\PageIndex{3}\)
Ejemplo 3: Letalidad del procesamiento térmico de una lata de atún
Problema:
En el Cuadro 6.2.2 se presentan los valores de temperatura medidos en la retorta (TRT) y la temperatura medida en el punto frío de una lata de atún (T punto frío) durante un proceso térmico. El tiempo total del proceso fue de 63 min hasta que el producto estuvo lo suficientemente frío como para ser retirado de la retorta.
- (a) Determinar CUT (el tiempo requerido para llegar a TRT), el tiempo de proceso del operador P t y el tiempo de enfriamiento.
- b) Determinar el valor de letalidad (F 0) alcanzado para la lata de atún.
| Tiempo (min) | TRT (°C) | Punto frío T (°C) |
|---|---|---|
|
0.97 |
29.7 |
45.0 |
|
1.97 |
39.7 |
45.0 |
|
2.97 |
49.7 |
45.0 |
|
3.97 |
59.7 |
45.0 |
|
4.97 |
69.7 |
44.9 |
|
5.97 |
79.7 |
44.9 |
|
6.97 |
89.7 |
44.8 |
|
7.97 |
99.7 |
44.7 |
|
8.97 |
109.7 |
44.7 |
|
9.97 |
119.7 |
44.8 |
|
10.97 |
120.0 |
45.0 |
|
11.97 |
120.0 |
45.4 |
|
12.97 |
120.0 |
46.0 |
|
13.97 |
120.0 |
46.9 |
|
14.97 |
120.0 |
48.0 |
|
15.97 |
120.0 |
49.3 |
|
16.97 |
120.0 |
50.8 |
|
17.97 |
120.0 |
52.6 |
|
18.97 |
120.0 |
54.4 |
|
19.97 |
120.0 |
56.4 |
|
20.97 |
120.0 |
58.5 |
|
21.97 |
120.0 |
60.6 |
|
22.97 |
120.0 |
62.8 |
|
23.97 |
120.0 |
65.0 |
|
24.97 |
120.0 |
67.1 |
|
25.97 |
120.0 |
69.3 |
|
26.97 |
120.0 |
71.4 |
|
27.97 |
120.0 |
73.5 |
|
28.97 |
120.0 |
75.5 |
|
29.97 |
120.0 |
77.5 |
|
30.97 |
120.0 |
79.4 |
|
31.97 |
120.0 |
81.2 |
|
32.97 |
120.0 |
83.0 |
|
33.97 |
120.0 |
84.7 |
|
34.97 |
120.0 |
86.3 |
|
35.97 |
120.0 |
87.9 |
|
36.97 |
120.0 |
89.4 |
|
37.97 |
120.0 |
90.8 |
|
38.97 |
120.0 |
92.2 |
|
39.97 |
120.0 |
93.6 |
|
40.97 |
120.0 |
94.8 |
|
41.97 |
120.0 |
96.0 |
|
42.97 |
120.0 |
97.2 |
|
43.97 |
120.0 |
98.3 |
|
44.97 |
120.0 |
99.3 |
|
45.97 |
120.0 |
100.3 |
|
46.97 |
120.0 |
101.3 |
|
47.97 |
120.0 |
102.2 |
|
48.97 |
120.0 |
103.0 |
|
49.97 |
120.0 |
103.9 |
|
50.97 |
120.0 |
104.7 |
|
51.97 |
120.0 |
105.4 |
|
52.97 |
120.0 |
106.1 |
|
53.97 |
120.0 |
106.8 |
|
54.97 |
120.0 |
107.4 |
|
55.97 |
120.0 |
108.0 |
|
56.97 |
120.0 |
108.6 |
|
57.97 |
120.0 |
109.2 |
|
58.97 |
120.0 |
109.7 |
|
59.97 |
120.0 |
110.2 |
|
60.97 |
120.0 |
110.7 |
|
61.97 |
120.0 |
111.1 |
|
62.97 |
120.0 |
111.6 |
|
63.97 |
120.0 |
112.0 |
|
64.97 |
120.0 |
112.4 |
|
65.97 |
120.0 |
112.8 |
|
66.97 |
120.0 |
113.1 |
|
67.97 |
120.0 |
113.4 |
|
68.97 |
120.0 |
113.8 |
|
69.97 |
120.0 |
114.1 |
|
70.97 |
120.0 |
114.4 |
|
71.97 |
120.0 |
114.6 |
|
72.97 |
120.0 |
114.9 |
|
73.97 |
120.0 |
115.2 |
|
74.97 |
120.0 |
115.4 |
|
76 |
25.0 |
115.6 |
|
77 |
25.0 |
115.8 |
|
78 |
25.0 |
116.0 |
|
79 |
25.0 |
116.2 |
|
80 |
25.0 |
116.2 |
|
81 |
25.0 |
116.0 |
|
82 |
25.0 |
115.5 |
|
83 |
25.0 |
114.6 |
|
84 |
25.0 |
113.4 |
|
85 |
25.0 |
111.8 |
|
86 |
25.0 |
110.0 |
|
87 |
25.0 |
107.9 |
|
88 |
25.0 |
105.6 |
|
89 |
25.0 |
103.1 |
|
90 |
25.0 |
100.6 |
|
91 |
25.0 |
97.9 |
|
92 |
25.0 |
95.3 |
|
93 |
25.0 |
92.6 |
|
94 |
25.0 |
89.9 |
|
95 |
25.0 |
87.3 |
|
96 |
25.0 |
84.7 |
|
97 |
25.0 |
82.1 |
|
98 |
25.0 |
79.6 |
|
99 |
25.0 |
77.2 |
|
100 |
25.0 |
74.9 |
|
101 |
25.0 |
72.6 |
|
102 |
25.0 |
70.5 |
|
103 |
25.0 |
68.4 |
|
104 |
25.0 |
66.3 |
|
105 |
25.0 |
64.4 |
|
106 |
25.0 |
62.6 |
|
107 |
25.0 |
60.8 |
|
108 |
25 |
59.08 |
|
109 |
25 |
57.46 |
|
110 |
25 |
55.91 |
|
111 |
25 |
54.43 |
|
112 |
25 |
53.01 |
|
113 |
25 |
51.67 |
|
114 |
25 |
50.38 |
|
115 |
25 |
49.15 |
|
116 |
25 |
47.99 |
|
117 |
25 |
46.87 |
|
118 |
25 |
45.81 |
|
119 |
25 |
44.8 |
|
120 |
25 |
43.84 |
|
121 |
25 |
42.92 |
|
122 |
25 |
42.05 |
|
123 |
25 |
41.22 |
|
124 |
25 |
40.43 |
Solución
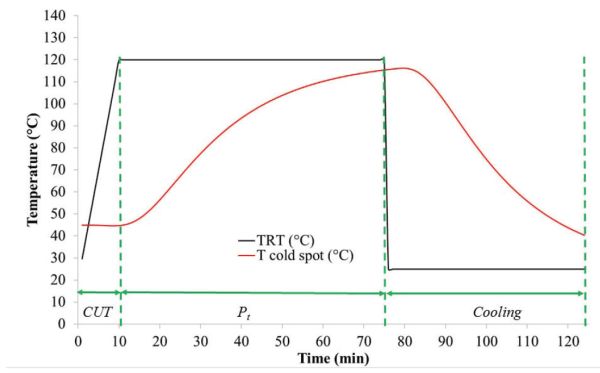
- (a) Para determinar CUT y P t, graficar TRT y T punto frío contra el tiempo, lo que produce los perfiles térmicos en la Figura 6.2.6.
La Figura 6.2.6 muestra que el CUT es aproximadamente de 10 min y P t, durante el cual la temperatura del proceso se mantiene constante a 120°C, es de aproximadamente 64 min.
- (b) El valor de letalidad, F 0, se puede obtener mediante la integración numérica de la Ecuación 6.2.9 utilizando la regla trapezoidal (Patashnik, 1953). Los cálculos se pueden completar de la siguiente manera o utilizando software como Excel.
Como se presenta en la Tabla 6.2.3, para cada vez, podemos evaluar la Ecuación 6.2.9:
-
\( F_{0}=\int^{t}_{0}10^{\dfrac{T-121.1}{10}}dt \)(Ecuación\(\PageIndex{9}\))
donde T = T punto frío y T ref y z valor para Clostridium botulinum son 121.1°C y 10°C, respectivamente.
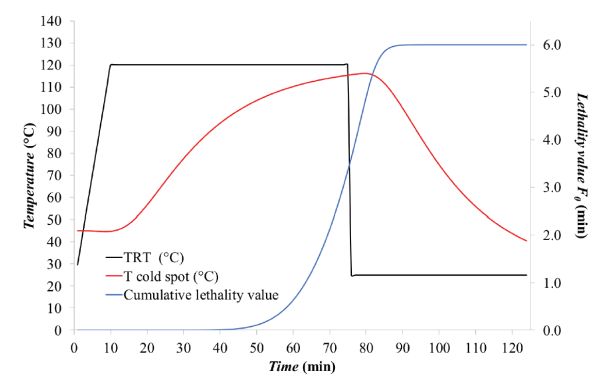
- Dado que F 0 corresponde a la integral de 10 [(Tcold spot −Tef) /z], esto se puede resolver numéricamente mediante el método de regla trapezoidal, es decir, determinando el área bajo la curva dividiendo el área en trapezoides, calculando el área de cada trapecio y sumando todos áreas trapezoidales para producir F 0. (En el apéndice se incluyen más detalles sobre la regla trapezoidal.) Los cálculos se resumen en la Tabla 6.2.3. En este caso particular, F 0 fue de aproximadamente 6.07 min. El cambio de F 0 a lo largo del proceso térmico se muestra como la línea azul en la Figura 6.2.7.
| Tiempo (min) | TRT (°C) | Punto frío T (°C) | (T punto frío − T ref)/z | 10 [(Punto Tfrío −Tef) /z] | Zona Trapezoidal | Suma de Áreas |
|---|---|---|---|---|---|---|
|
0.97 |
29.67 |
45 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
1.97 |
39.67 |
45 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
2.97 |
49.67 |
44.99 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
3.97 |
59.67 |
44.97 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
4.97 |
69.67 |
44.93 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
5.97 |
79.67 |
44.85 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
6.97 |
89.67 |
44.76 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
7.97 |
99.67 |
44.69 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
8.97 |
109.67 |
44.68 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
9.97 |
119.67 |
44.77 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
10.97 |
120 |
45 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
11.97 |
120 |
45.41 |
−7.6 |
0.000 |
0.000 |
0.000 |
|
12.97 |
120 |
46.03 |
−7.5 |
0.000 |
0.000 |
0.000 |
|
13.97 |
120 |
46.88 |
−7.4 |
0.000 |
0.000 |
0.000 |
|
14.97 |
120 |
47.97 |
−7.3 |
0.000 |
0.000 |
0.000 |
|
15.97 |
120 |
49.29 |
−7.2 |
0.000 |
0.000 |
0.000 |
|
16.97 |
120 |
50.83 |
−7.0 |
0.000 |
0.000 |
0.000 |
|
17.97 |
120 |
52.55 |
−6.9 |
0.000 |
0.000 |
0.000 |
|
18.97 |
120 |
54.42 |
−6.7 |
0.000 |
0.000 |
0.000 |
|
19.97 |
120 |
56.41 |
−6.5 |
0.000 |
0.000 |
0.000 |
|
20.97 |
120 |
58.49 |
−6.3 |
0.000 |
0.000 |
0.000 |
|
21.97 |
120 |
60.63 |
−6.0 |
0.000 |
0.000 |
0.000 |
|
22.97 |
120 |
62.79 |
−5.8 |
0.000 |
0.000 |
0.000 |
|
23.97 |
120 |
64.97 |
−5.6 |
0.000 |
0.000 |
0.000 |
|
24.97 |
120 |
67.14 |
−5.4 |
0.000 |
0.000 |
0.000 |
|
25.97 |
120 |
69.29 |
−5.2 |
0.000 |
0.000 |
0.000 |
|
26.97 |
120 |
71.41 |
−5.0 |
0.000 |
0.000 |
0.000 |
|
27.97 |
120 |
73.48 |
−4.8 |
0.000 |
0.000 |
0.000 |
|
28.97 |
120 |
75.5 |
−4.6 |
0.000 |
0.000 |
0.000 |
|
29.97 |
120 |
77.46 |
−4.4 |
0.000 |
0.000 |
0.000 |
|
30.97 |
120 |
79.36 |
−4.2 |
0.000 |
0.000 |
0.000 |
|
31.97 |
120 |
81.2 |
−4.0 |
0.000 |
0.000 |
0.000 |
|
32.97 |
120 |
82.97 |
−3.8 |
0.000 |
0.000 |
0.001 |
|
33.97 |
120 |
84.67 |
−3.6 |
0.000 |
0.000 |
0.001 |
|
34.97 |
120 |
86.31 |
−3.5 |
0.000 |
0.000 |
0.001 |
|
35.97 |
120 |
87.89 |
−3.3 |
0.000 |
0.001 |
0.002 |
|
36.97 |
120 |
89.4 |
−3.2 |
0.001 |
0.001 |
0.003 |
|
37.97 |
120 |
90.84 |
−3.0 |
0.001 |
0.001 |
0.004 |
|
38.97 |
120 |
92.22 |
−2.9 |
0.001 |
0.002 |
0.005 |
|
39.97 |
120 |
93.55 |
−2.8 |
0.002 |
0.002 |
0.007 |
|
40.97 |
120 |
94.81 |
−2.6 |
0.002 |
0.003 |
0.010 |
|
41.97 |
120 |
96.02 |
−2.5 |
0.003 |
0.004 |
0.014 |
|
42.97 |
120 |
97.17 |
−2.4 |
0.004 |
0.005 |
0.018 |
|
43.97 |
120 |
98.27 |
−2.3 |
0.005 |
0.006 |
0.024 |
|
44.97 |
120 |
99.31 |
−2.2 |
0.007 |
0.007 |
0.032 |
|
45.97 |
120 |
100.31 |
−2.1 |
0.008 |
0.009 |
0.041 |
|
46.97 |
120 |
101.27 |
−2.0 |
0.010 |
0.012 |
0.053 |
|
47.97 |
120 |
102.17 |
−1.9 |
0.013 |
0.014 |
0.067 |
|
48.97 |
120 |
103.04 |
−1.8 |
0.016 |
0.017 |
0.084 |
|
49.97 |
120 |
103.86 |
−1.7 |
0.019 |
0.021 |
0.105 |
|
50.97 |
120 |
104.65 |
−1.6 |
0.023 |
0.025 |
0.130 |
|
51.97 |
120 |
105.39 |
−1.6 |
0.027 |
0.029 |
0.159 |
|
52.97 |
120 |
106.1 |
−1.5 |
0.032 |
0.034 |
0.193 |
|
53.97 |
120 |
106.78 |
−1.4 |
0.037 |
0.040 |
0.233 |
|
54.97 |
120 |
107.42 |
−1.4 |
0.043 |
0.046 |
0.279 |
|
55.97 |
120 |
108.04 |
−1.3 |
0.049 |
0.053 |
0.332 |
|
56.97 |
120 |
108.62 |
−1.2 |
0.056 |
0.060 |
0.393 |
|
57.97 |
120 |
109.18 |
−1.2 |
0.064 |
0.068 |
0.461 |
|
58.97 |
120 |
109.7 |
−1.1 |
0.072 |
0.077 |
0.538 |
|
59.97 |
120 |
110.21 |
−1.1 |
0.081 |
0.086 |
0.624 |
|
60.97 |
120 |
110.69 |
−1.0 |
0.091 |
0.096 |
0.720 |
|
61.97 |
120 |
111.14 |
−1.0 |
0.101 |
0.106 |
0.826 |
|
62.97 |
120 |
111.57 |
−1.0 |
0.111 |
0.117 |
0.943 |
|
63.97 |
120 |
111.99 |
−0.9 |
0.123 |
0.129 |
1.072 |
|
64.97 |
120 |
112.38 |
−0.9 |
0.134 |
0.140 |
1.212 |
|
65.97 |
120 |
112.75 |
−0.8 |
0.146 |
0.153 |
1.365 |
|
66.97 |
120 |
113.11 |
−0.8 |
0.159 |
0.165 |
1.530 |
|
67.97 |
120 |
113.44 |
−0.8 |
0.171 |
0.178 |
1.708 |
|
68.97 |
120 |
113.76 |
−0.7 |
0.185 |
0.191 |
1.899 |
|
69.97 |
120 |
114.07 |
−0.7 |
0.198 |
0.205 |
2.104 |
|
70.97 |
120 |
114.36 |
−0.7 |
0.212 |
0.219 |
2.323 |
|
71.97 |
120 |
114.63 |
−0.6 |
0.225 |
0.233 |
2.555 |
|
72.97 |
120 |
114.9 |
−0.6 |
0.240 |
0.247 |
2.802 |
|
73.97 |
120 |
115.15 |
−0.6 |
0.254 |
0.261 |
3.063 |
|
74.97 |
120 |
115.38 |
−0.6 |
0.268 |
0.275 |
3.338 |
|
76 |
25 |
115.61 |
−0.5 |
0.282 |
0.290 |
3.628 |
|
77 |
25 |
115.83 |
−0.5 |
0.297 |
0.304 |
3.932 |
|
78 |
25 |
116.02 |
−0.5 |
0.310 |
0.316 |
4.248 |
|
79 |
25 |
116.17 |
−0.5 |
0.321 |
0.322 |
4.570 |
|
80 |
25 |
116.19 |
−0.5 |
0.323 |
0.315 |
4.885 |
|
81 |
25 |
115.97 |
−0.5 |
0.307 |
0.290 |
5.175 |
|
82 |
25 |
115.45 |
−0.6 |
0.272 |
0.248 |
5.422 |
|
83 |
25 |
114.58 |
−0.7 |
0.223 |
0.196 |
5.618 |
|
84 |
25 |
113.36 |
−0.8 |
0.168 |
0.143 |
5.761 |
|
85 |
25 |
111.81 |
−0.9 |
0.118 |
0.097 |
5.858 |
|
86 |
25 |
109.96 |
−1.1 |
0.077 |
0.062 |
5.920 |
|
87 |
25 |
107.87 |
−1.3 |
0.048 |
0.038 |
5.958 |
|
88 |
25 |
105.57 |
−1.6 |
0.028 |
0.022 |
5.980 |
|
89 |
25 |
103.12 |
−1.8 |
0.016 |
0.012 |
5.992 |
|
90 |
25 |
100.57 |
−2.1 |
0.009 |
0.007 |
5.999 |
|
91 |
25 |
97.94 |
−2.3 |
0.005 |
0.004 |
6.003 |
|
92 |
25 |
95.26 |
−2.6 |
0.003 |
0.002 |
6.005 |
|
93 |
25 |
92.58 |
−2.9 |
0.001 |
0.001 |
6.006 |
|
94 |
25 |
89.91 |
−3.1 |
0.001 |
0.001 |
6.007 |
|
95 |
25 |
87.26 |
−3.4 |
0.000 |
0.000 |
6.007 |
|
96 |
25 |
84.66 |
−3.6 |
0.000 |
0.000 |
6.007 |
|
97 |
25 |
82.11 |
−3.9 |
0.000 |
0.000 |
6.007 |
|
98 |
25 |
79.63 |
−4.1 |
0.000 |
0.000 |
6.007 |
|
99 |
25 |
77.22 |
−4.4 |
0.000 |
0.000 |
6.007 |
|
100 |
25 |
74.88 |
−4.6 |
0.000 |
0.000 |
6.007 |
|
101 |
25 |
72.62 |
−4.8 |
0.000 |
0.000 |
6.007 |
|
102 |
25 |
70.45 |
−5.1 |
0.000 |
0.000 |
6.007 |
|
103 |
25 |
68.35 |
−5.3 |
0.000 |
0.000 |
6.007 |
|
104 |
25 |
66.34 |
−5.5 |
0.000 |
0.000 |
6.007 |
|
105 |
25 |
64.41 |
−5.7 |
0.000 |
0.000 |
6.007 |
|
106 |
25 |
62.55 |
−5.9 |
0.000 |
0.000 |
6.007 |
|
107 |
25 |
60.78 |
−6.0 |
0.000 |
0.000 |
6.007 |
|
108 |
25 |
59.08 |
−6.2 |
0.000 |
0.000 |
6.007 |
|
109 |
25 |
57.46 |
−6.4 |
0.000 |
0.000 |
6.007 |
|
110 |
25 |
55.91 |
−6.5 |
0.000 |
0.000 |
6.007 |
|
111 |
25 |
54.43 |
−6.7 |
0.000 |
0.000 |
6.007 |
|
112 |
25 |
53.01 |
−6.8 |
0.000 |
0.000 |
6.007 |
|
113 |
25 |
51.67 |
−6.9 |
0.000 |
0.000 |
6.007 |
|
114 |
25 |
50.38 |
−7.1 |
0.000 |
0.000 |
6.007 |
|
115 |
25 |
49.15 |
−7.2 |
0.000 |
0.000 |
6.007 |
|
116 |
25 |
47.99 |
−7.3 |
0.000 |
0.000 |
6.007 |
|
117 |
25 |
46.87 |
−7.4 |
0.000 |
0.000 |
6.007 |
|
118 |
25 |
45.81 |
−7.5 |
0.000 |
0.000 |
6.007 |
|
119 |
25 |
44.8 |
−7.6 |
0.000 |
0.000 |
6.007 |
|
120 |
25 |
43.84 |
−7.7 |
0.000 |
0.000 |
6.007 |
|
121 |
25 |
42.92 |
−7.8 |
0.000 |
0.000 |
6.007 |
|
122 |
25 |
42.05 |
−7.9 |
0.000 |
0.000 |
6.007 |
|
123 |
25 |
41.22 |
−8.0 |
0.000 |
0.000 |
6.007 |
|
124 |
25 |
40.43 |
−8.1 |
0.000 |
0.000 |
6.007 |
Discusión:
La letalidad acumulada, F 0, fue de aproximadamente 6.01 min, lo que significa que el proceso es seguro de acuerdo con los requisitos de la FDA, es decir, F 0 ≥ 3 min (ver la sección Criterio y Cálculo de Esterilización de Alimentos anterior).
Ejemplo\(\PageIndex{4}\)
Ejemplo 4: Letalidad del procesamiento térmico de una lata de mejillones
Problema:
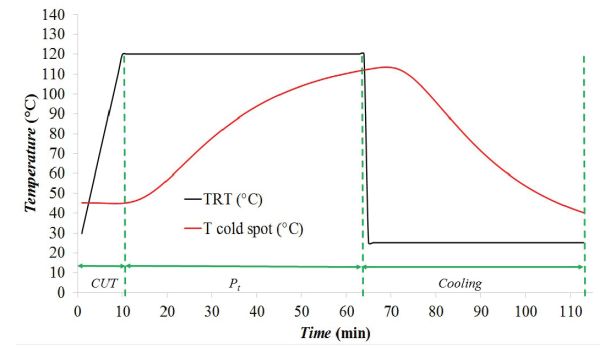
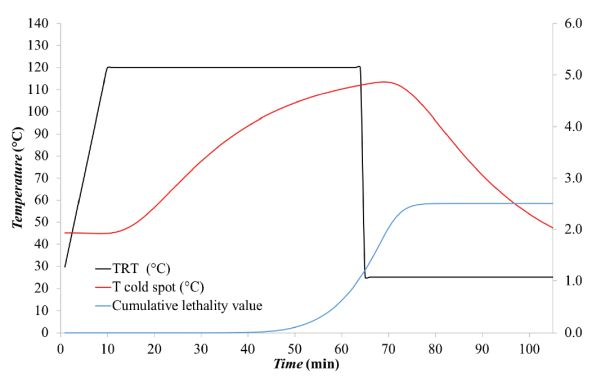
Se registraron las temperaturas medidas en la retorta y la temperatura medida en el punto frío de una lata de mejillones durante un proceso térmico realizado a 120°C. El tiempo total del proceso fue de 113 min hasta que el producto estuvo lo suficientemente frío como para ser retirado de la retorta. Se graficaron los perfiles térmicos medidos (TRT y punto frío T), como se hizo en el Ejemplo 6.2.3. La gráfica resultante (Figura 6.2.8) muestra que CUT fue aproximadamente 10 min y P t fue aproximadamente 53 min. El valor de letalidad, F 0, se obtuvo a través de la integración numérica de la Ecuación 6.2.9. En este caso, el F 0 alcanzado en la lata de mejillones con una temperatura de procesamiento de 120 °C fue de 2.508 min. La evolución de F 0 a lo largo del proceso térmico se muestra en la Figura 6.2.9 como la línea azul.
Discusión:
La letalidad acumulada, F 0, alcanzada a lo largo del proceso térmico fue de 2.5 min, lo que significa que el proceso no es seguro según los requisitos de la FDA (F 0 ≥ 3 min). Por lo tanto, se debe extender el tiempo de procesamiento térmico del proceso de enlatado de mejillones para alcanzar el valor de seguridad recomendado por la FDA.
Ejemplo\(\PageIndex{5}\)
Ejemplo 5: Tiempo de procesamiento a diferentes temperaturas de retorta
Problema:
Determinar el tiempo de procesamiento requerido para obtener una letalidad de 6 min (F 0 = 6 min) cuando la temperatura de retorta es de (a) 120°C y considerada igual a la temperatura del punto frío, (b) 110°C, y (c) 130°C.
Solución
El F 0 se establece típicamente para el valor 12D para dar una reducción logarítmica de 12 especies resistentes al calor de esporas mesófilas (típicamente tomadas como C. botulinum). La T ref = 121.1°C y z = 10°C. Por lo tanto, la Ecuación 6.2.9 se puede usar directamente reemplazando T por la temperatura de retorta, dado que la temperatura del punto frío puede asumirse igual a la temperatura de retorta:
\( F_{0} = \int^{t}_{0}10^{\dfrac{T-121.1}{z}}dt \)(Ecuación\(\PageIndex{9}\))
\( 6 = \int^{t}_{0}10^{\dfrac{120-121.1}{10}}dt \)
\( t = \dfrac{6}{10^{\dfrac{120-121.1}{10}}} \)
Resolver la integral produce un tiempo de procesamiento, t, de 7.7 min.
- b) Cuando la temperatura de la retorta se reduzca a 110°C, la letalidad deberá mantenerse a los 6 min. Resolviendo la Ecuación 6.2.9:
\( 6 = \int^{t}_{0} 10^{\dfrac{110-121.1}{10}} dt \)
- da el tiempo de procesamiento requerido t de 77.2 min.
- (c) Cuando la temperatura de la retorta se incrementa a 130°C, y manteniendo el F 0 = 6 min, el tiempo de procesamiento se reduce a 0.77 min
\( 6 = \int^{t}_{0} 10^{\dfrac{130-121.1}{10}} dt \)
Discusión:
Los resultados mostraron que a medida que la temperatura en los alimentos aumentaba en incrementos de 10°C, el tiempo de procesamiento se redujo en una reducción decimal. Esta variación se debe a un valor z de 10°C.
Apéndice: La regla trapezoidal
Un trapecio es una región de cuatro lados con dos lados opuestos paralelos (Figura 6.2.10). El área de un trapecio es la longitud promedio de los dos lados paralelos multiplicada por la distancia entre los dos lados. En la Figura 6.2.11, el área (A) bajo la función f (x) entre los puntos x 0 y x n viene dada por:

\[ A=\int^{b}_{a} f(x)dx \]
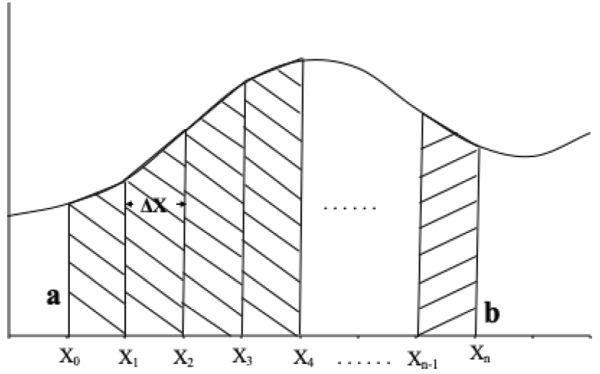
Una aproximación del área A es la suma de las áreas de los trapecios individuales (T), donde T se puede calcular usando la Ecuación 6.2.11:
\[ T=\dfrac{1}{2}\Delta x_{1}[f(x_{0})+f(x_{1})]+\dfrac{1}{2}\Delta x_{2}[f(x_{1})+f(x_{2})]+…+\dfrac{1}{2}\Delta x_{n}[f(x_{n-1})+f(x_{n})] \]
donde\(\Delta x_{i}=x_{i}-x_{i-1}\), para i = 1, 2, 3,.,., n
En el caso particular donde ∆x 1 = ∆x 2 = ∆x 3 =. = ∆x n = ∆x, la Ecuación 6.2.11 puede expresarse como:
\[ T=\Delta x[\dfrac{f(x_{0})}{2} + f(x_{1})+ f(x_{2})+ f(x_{3})+…+\dfrac{f(x_{n})}{2} \]
o bien, en la siguiente forma reducida:
\[ T=\Delta x[\dfrac{f(x_{0})}{2} +\sum^{n-1}_{i=1}f(x_{i})+\dfrac{f(x_{n})}{2} \]
Finalmente, para estimar el área A bajo la regla trapezoidal,
\[ A=\int^{x_{n}}_{x_{0}}f(x)dx\cong\dfrac{1}{2}\Delta x_{1}[f(x_{0})+f(x_{1})]+\dfrac{1}{2}\Delta x_{2}[f(x_{1})+f(x_{2})]+…+\dfrac{1}{2}\Delta x_{n}[f(x_{n-1})+f(x_{n})] \]
Cuando todos los intervalos son del mismo tamaño (∆x 1 = ∆x 2 = ∆x 3 =.. = ∆x n = ∆x), se puede aplicar la siguiente expresión:
\[ A=\int^{x_{n}}_{x_{0}}f(x)dx\cong\Delta x(\dfrac{f(x_{0})}{2} +\sum^{n-1}_{i=1}f(x_{i})+\dfrac{f(x_{n})}{2}) =\dfrac{1}{2}\Delta x(f(x_{0}) +2\sum^{n-1}_{i=1}f(x_{i})+f(x_{n})) \]
Ejemplo\(\PageIndex{6}\)
Ejemplo
Problema:
Utilizando los datos de penetración de calor en el punto frío de un alimento enlatado en el Cuadro 6.2.4, calcular la letalidad acumulada, F 0, en el rango de 23 a 27 min usando la regla trapezoidal.
Tabla\(\PageIndex{4}\): Datos de penetración de calor en el punto de calentamiento más lento.
| Tiempo (min) | Temperatura (C) |
|---|---|
|
... |
... |
|
23 |
118.5 |
|
24 |
118.7 |
|
25 |
118.9 |
|
26 |
119.1 |
|
27 |
119.3 |
|
... |
... |
Solución
De la Ecuación 6.2.9,
\( F_{0}=\int^{27}_{23}10^{\dfrac{T-121.1}{10}}dt \)
Aplicando la regla trapezoidal y considerando que todos los pasos de tiempo son iguales (∆t = 1 min), calcula F 0 usando la Ecuación 6.2.15,
\( F_{0}=\int^{27}_{23}10^{\dfrac{T-121.1}{10}}dt \cong \dfrac{1}{2}[f(23)+2f(24)+2f(25)+2f(26)+f(27)] \)
donde ∆t = 1 (intervalo de 1 min), y:
\( f(23)=10^{\dfrac{118.5-121.1}{10}} = 0.549541 \)
\( f(24)=10^{\dfrac{118.7-121.1}{10}} = 0.57544 \)
\( f(25)=10^{\dfrac{118.9-121.1}{10}} = 0.6025596 \)
\( f(26)=10^{\dfrac{119.1-121.1}{10}} = 0.63095734 \)
\( f(27)=10^{\dfrac{119.3-121.1}{10}} = 0.66069345 \)
Sustitución en la ecuación (6.2.15):
\( F_{0}=\int^{27}_{23}10^{\dfrac{T-121.1}{10}}dt \cong \dfrac{1}{2}(0.549541+2\times0.57544+2\times0.6025596+2\times 0.63095734+0.66069345) \)
Por lo tanto, F 0 ~ 2.41407394 ~ 2.41 min.
Discusión:
El proceso aplicado para esterilizar el alimento objetivo no es seguro ya que F 0 < 3 minutos.
Créditos de imagen
Figura 1. Simpson, R. (CC Por 4.0). (2020). Principales mecanismos de transferencia de calor involucrados en el procesamiento térmico de alimentos envasados. Recuperado a partir de onlinelibrary.wiley.com
Figura 2. Holdsworth, S. Donald-Simpson, R. (CC Por 4.0). (2020). Curva semilogarítmica de superviviente. Recuperado a partir de https://www.springer.com/la/book/9783319249025
Figura 3. Holdsworth, S. Donald-Simpson, R. (CC Por 4.0). (2020). Curva de tiempo de muerte térmica (TDT). Recuperado de https://www.springer.com/la/book/9783319249025.
Figura 4. Simpson, R. (CC Por 4.0). (2020). Etapas de una fábrica de conservas comerciales de alimentos típicos.
Figura 5. Ramírez, C. (CC Por 4.0). (2020). Perfiles de temperatura para un proceso térmico típico, donde CUT es el tiempo de llegada y P t es el tiempo del operador.
Figura 6. Ramírez, C. (CC Por 4.0). (2020). Perfil de temperatura de los datos de procesamiento térmico en la tabla 2.
Figura 7. Ramírez, C. (CC Por 4.0). (2020). Perfiles de temperatura del proceso térmico incluyendo el valor de letalidad acumulada (F en cualquier momento t).
Figura 8. Ramírez, C. (CC Por 4.0). (2020). Perfil de temperatura de los datos de procesamiento térmico (Cuadro 4).
Figura 9. Ramírez, C. (CC Por 4.0). (2020). Perfiles de temperatura del proceso térmico incluyendo el valor de letalidad acumulada (F en cualquier momento t).
Figura 10. Simpson, R. (CC Por 4.0). (2020). Ejemplo de trapecio.
Figura 11. Simpson, R. (CC Por 4.0). (2020). Curva dividida en n partes iguales cada una de longitud Δ X.
Referencias
Ball, C. O., & Olson, F. C. (1957). Esterilización en la tecnología de los alimentos—Teoría, práctica y cálculos. Nueva York, NY: McGraw-Hill.
Bigelow, W. D. (1921). La naturaleza logarítmica de las curvas de tiempo de muerte térmica. J. Infecciosas Dis., 29 (5), 528-536. https://doi.org/10.1093/infdis/29.5.528.
Bigelow, W. D., & Esty, J. R. (1920). El punto de muerte térmica en relación con el tiempo de los organismos termófilos típicos. J. Infecciosas Dis., 27 (6), 602-617. doi.org/10.1093/infdis/27.6.602.
Bigelow, W. D., Bohart, G. S., Richardson, A. C., & Ball, C. O. (1920). Penetración térmica en el procesamiento de alimentos enlatados Toro. No. 16. Washington, DC: Laboratorio de Investigación, Asociación Nacional de Canners.
Esty, J. R., & Meyer, K. F. (1922). La resistencia al calor de las esporas de B. botulinus y anaerobios aliados. J. Infecciosas Dis., 31 (6), 650-663. https://doi.org/10.1093/infdis/31.6.650.
FDA. (1972). Símbolos esterilizantes. Alimentos enlatados bajos en ácido. Guía técnica de inspección. Ch. 7. ORO/ETSB (HFC-133). Washington, DC: FDA.
Featherstone, S. (2015). 7: Envases flexibles retortables para envasado de alimentos. En Un curso completo en conservas y procesos afines (14ª ed.). Vol. 2: Microbiología, empaque, HACCP e ingredientes (pp. 137-146). Sawston, Cambridge, Reino Unido: Woodhead Publ. https://doi.org/10.1016/B978-0-85709-678-4.00007-5.
Holdsworth, S. D., & Simpson, R. (2016). Procesamiento térmico de alimentos envasados (3ª ed.). Springer. doi.org/10.1007/978-3-319-24904-9.
Patashnik, M. (1953). Un procedimiento simplificado para la evaluación de procesos térmicos. Food Technol., 7 (1), 1-6.
Simpson, R., Almonacid, S., & Teixeira, A. (2003). Revisión del método general de Bigelow: Desarrollo de una nueva técnica de cálculo. J. Alimentación Sci., 68 (4), 1324-1333. doi.org/10.1111/j.1365-2621.2003.tb09646.x.
Stumbo, C. R. (1973). Termobacteriología en el procesamiento de alimentos (2da. ed.). Nueva York, NY: Prensa Académica.
Teixeira, A., Almonacid, S., & Simpson, R. (2006). Mantener el botulismo fuera de los alimentos enlatados. Food Technol., 60 (2), Volver página.


