13.3: Método Directo de Lyapunov

Idea General

Considere el sistema de tiempo continuo

\[\dot{x}(t)=f(x(t)) \ \tag{13.8}\]

con un punto de equilibrio en\(x = 0\). Se trata de un sistema invariante en el tiempo (o “autónomo”), ya que\(f\) no depende explícitamente de\(t\). El análisis de estabilidad del punto de equilibrio en dicho sistema es una tarea difícil en general. Esto se debe a que no podemos escribir una fórmula simple que relacione la trayectoria con el estado inicial. La idea detrás del método “directo” de Lyapunov es establecer propiedades del punto de equilibrio (o, más generalmente, del sistema no lineal) mediante el estudio de cómo ciertas funciones escalares cuidadosamente seleccionadas del estado evolucionan a medida que evoluciona el estado del sistema. (El término “directo” es para contrastar este enfoque con el método “indirecto” de Lyapunov, que intenta establecer propiedades del punto de equilibrio mediante el estudio del comportamiento del sistema linealizado en ese punto. Estudiaremos este próximo Capítulo.)

Consideremos, por ejemplo, una función escalar continua\(V (x)\) que es 0 en el origen y positiva en otra parte en alguna bola que encierra el origen, es decir\(V (0) = 0\) y\(V (x) > 0\) para\(x \neq 0\) en esta bola. Tal\(V (x)\) puede pensarse como una función de “energía”. Dejar\(\dot{V} (x)\) denotar la derivada del tiempo\(V (x)\) a lo largo de cualquier trayectoria del sistema, es decir, su tasa de cambio\(x(t)\) varía según (13.8). Si esta derivada es negativa en toda la región (excepto en el origen), entonces esto implica que la energía está disminuyendo estrictamente con el tiempo. En este caso, debido a que la energía es menor delimitada por 0, la energía debe ir a 0, lo que implica que todas las trayectorias convergen al estado cero. Formalizaremos esta idea en los siguientes apartados.

Lyapunov Funciones

Definición 13.2

Dejar\(V\) ser un mapa continuo de\(\mathbb{R}^{n}\) a\(\mathbb{R}\). Llamamos a\(V (x)\) una función definida localmente positiva (lpd) alrededor de\(x = 0\) si

1. \(V(0)=0\)
2. \(V(x)>0,0<\|x\|<r\)para algunos\(r\).

Del mismo modo, la función se denomina localmente semidefinita positiva (lpsd) si la estricta desigualdad en la función en la segunda condición es reemplazada por\(V(x) \geq 0\). La función\(V (x)\) es localmente negativa definida (lnd) si\(-V (x)\) es lpd, y localmente negativa semidefinita (lnsd) si\(-V (x)\) es lpsd. Lo que puede ser útil para formar una imagen mental de una función lpd\(V (x)\) es pensar que tiene “contornos” de constante\(V\) que forman (al menos en una pequeña región alrededor del origen) un conjunto anidado de superficies cerradas que rodean el origen. La situación para\(n = 2\) se ilustra en la Figura 13.2.

\ (c_ {1} < c_ {2} < c_ {3}\)” src=” https://eng.libretexts.org/@api/deki...2.29.42_PM.png "/>

Figura\(\PageIndex{1}\): Líneas de nivel para una función Lyapunov, donde\(c_{1} < c_{2} < c_{3}\)

A lo largo de nuestro tratamiento del caso de TC, nos limitaremos a\(V (x)\) que tengan continuas primeras derivadas parciales. (No será necesaria la diferenciabilidad en el caso DT; ahí bastará la continuidad). Denotaremos la derivada de tal\(V\) con respecto al tiempo a lo largo de una trayectoria del sistema (13.8) por\(\dot{V} (x(t))\). Esta derivada viene dada por

\[\dot{V}(x(t))=\frac{d V(x)}{d x} \dot{x}=\frac{d V(x)}{d x} f\tag{x}\]

donde\(\frac{d V(x)}{d x}\) es un vector de fila - el vector gradiente o jacobiano de\(V\) con respecto a\(x\) - que contiene las derivadas parciales por componentes\(\frac{\partial V}{\partial x_{i}}\).

Definición 13.3

Dejar\(V\) ser una función lpd (una “función candidata de Lyapunov”), y dejar\(\dot{V}\) ser su derivada a lo largo de trayectorias de sistema (13.8). Si\(\dot{V}\) es lnsd, entonces\(V\) se llama una función Lyapunov del sistema (13.8).

Teorema de Lyapunov para la estabilidad local

Teorema 13.1

Si existe una función Lyapunov de sistema (13.8), entonces\(x = 0\) es un punto de equilibrio estable en el sentido de Lyapunov. Si además\(\dot{V}(x)<0,0<\|x\|<r_{1}\) para algunos\(r_{1}\), es decir, si\(\dot{V}\) es lnd, entonces\(x = 0\) es un punto de equilibrio asintóticamente estable.

Prueba

Primero, demostramos estabilidad en el sentido de Lyapunov. Supongamos que\(\epsilon>0\) se da. Tenemos que encontrar un\(\delta>0\) tal que para todos\(\|x(0)\|<\delta\), de ello se deduce\(\|x(t)\|<\epsilon, \forall t>0\). La Figura 19.6 ilustra las construcciones de la prueba para el caso\(n = 2\). Vamos\(\epsilon_{1}=\min (\epsilon, r)\). Definir

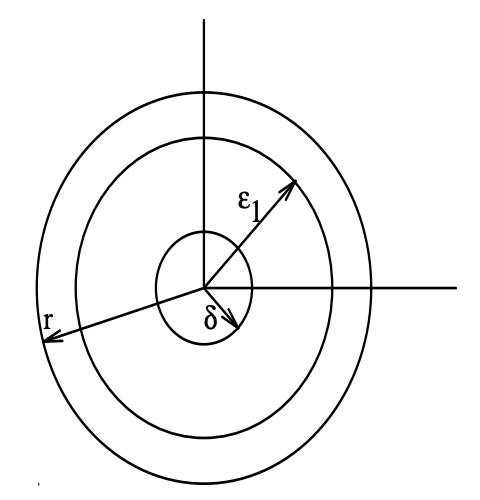
Figura\(\PageIndex{2}\): Ilustración de los barrios utilizados en la prueba

\[m=\min _{\|x\|=\epsilon_{1}} V\tag{x}\]

Dado que\(V (x)\) es continuo, lo anterior\(m\) está bien definido y positivo. Elija\(\delta\)\(0<\delta<\epsilon_{1}\) satisfactoriamente tal que para todos\(\|x\|<\delta, V(x)<m\). Tal elección siempre es posible, nuevamente por la continuidad de\(V (x)\). Ahora bien, considere cualquiera de\(x(0)\) tales que\(\|x(0)\|<\delta, V(x(0))<m\), y deje que\(x(t)\) sea la trayectoria resultante. \(V (x(t))\)es no creciente (es decir\(\dot{V}(x(t)) \leq 0)\)) lo que resulta en\(V (x(t)) < m\). Demostraremos que esto implica eso\(\|x(t)\|<\epsilon_{1}\). Supongamos que existe\(t_{1}\) tal que\(\left\|x\left(t_{1}\right)\right\|>\epsilon_{1}\), entonces por continuidad debemos tener eso en un momento anterior\(t_{2}\),\(\left\|x\left(t_{2}\right)\right\|=\epsilon_{1}\), y\(\min _{\|x\|=\epsilon_{1}}\|V(x)\|=m>V\left(x\left(t_{2}\right)\right)\), que es una contradicción. Así se mantiene la estabilidad en el sentido de Lyapunov.

Para probar la estabilidad asintótica cuando\(\dot{V}\) es primero, necesitamos demostrar que como\(t \rightarrow \infty, V(x(t)) \rightarrow 0\) entonces, por continuidad de\(V,\|x(t)\| \rightarrow 0\). Ya que\(V (x(t))\) es estrictamente decreciente, y lo\(V(x(t)) \geq 0\) sabemos\(V(x(t)) \rightarrow c\), con\(c \geq 0\). Queremos demostrar que de hecho\(c\) es cero. Podemos argumentar por contradicción y suponer eso\(c > 0\). Deje que el conjunto\(S\) se defina como

\[S=\left\{x \in \mathbb{R}^{n} \mid V(x) \leq c\right\}\nonumber\]

y dejar\(B_{\alpha}\) ser una bola dentro\(S\) del radio\(\alpha\),

\[B_{\alpha}=\{x \in S \mid\|x\|<\alpha\}\nonumber\]

Supongamos que\(x(t)\) es una trayectoria del sistema que inicia en\(x(0)\), sabemos que\(V (x(t))\) está disminuyendo monótonamente a\(c\) y\(V(x(t))>c\) para todos\(t\). Por lo tanto,\(x(t) \notin B_{\alpha}\); recordemos aquello\(B_{\alpha} \subset S\) que se define como todos los elementos en\(\mathbb{R}^{n}\) los que\(V(x) \leq c\). En la primera parte de la prueba, hemos establecido que si\(\|x(0)\|<\delta\) entonces\(\|x(t)\|<\epsilon\). Podemos definir el derivado más grande de\(V (x)\) como

\[-\gamma=\max _{\alpha \leq\|x\| \leq \epsilon} \dot{V}\tag{x}\]

Claramente\(-\gamma<0\) ya que\(\dot{V} (x)\) es lnd. Observe que,

\ [\ comenzar {alineado}
V (x (t) &=V (x (0)) +\ int_ {0} ^ {t}\ punto {V} (x (\ tau)) d\ tau\\
&\ leq V (x (0)) -\ gamma t
\ final {alineado}\ nonumber\]

lo que implica que\(V (x(t))\) será negativo lo que se traducirá en una contradicción estableciendo el hecho de que\(c\) debe ser cero.

Ejemplo 13.2

Consideremos el sistema dinámico que se rige por la ecuación diferencial

\[\dot{x}=-g\tag{x}\]

donde\(g(x)\) tiene la forma dada en la Figura 13.4. Claramente el origen es un punto de equilibrio. Si definimos una función

\[V(x)=\int_{0}^{x} g(y) d y\nonumber\]

entonces es claro que\(V (x)\) es localmente positivo definido (lpd) y

\[\dot{V}(x)=-g(x)^{2}\nonumber\]

que es localmente negativo definido (lnd). Esto implica que\(x = 0\) es un punto de equilibrio asintóticamente estable.

Figura\(\PageIndex{3}\): Descripción gráfica de g (x)

Teorema de Lyapunov para la estabilidad asintótica global

La región en el espacio estatal para la que se mantienen nuestros resultados anteriores está determinada por la región sobre la que\(V (x)\) sirve como función de Lyapunov. Es de especial interés determinar la “cuenca de atracción” de un punto de equilibrio asintóticamente estable, es decir, el conjunto de condiciones iniciales cuyas trayectorias posteriores terminan en este punto de equilibrio. Un punto de equilibrio es globalmente asintóticamente estable (o asintóticamente estable “en lo grande”) si su cuenca de atracción es todo el espacio estatal.

Si una función\(V (x)\) es positiva definida en todo el espacio de estado, y tiene la propiedad adicional que\(|V(x)| \nearrow \infty\) as\(\|x\| \nearrow \infty\), y si su derivada\(V\) es negativa definida en todo el espacio de estado, entonces el punto de equilibrio en el origen es globalmente asintóticamente estable. Omitimos la prueba de este resultado. Se pueden afirmar otras versiones de dichos resultados, pero también se omiten.

Ejemplo 13.3

Considere el sistema\(n\) de orden th-order

\[\dot{x}=-C\tag{x}\]

con la propiedad que\(C(0)=0\) y\(x^{\prime} C(x)>0\) si\(x \neq 0\). Convénzase de que el punto de equilibrio único del sistema está en 0. Consideremos ahora la función candidata Lyapunov

\[V(x)=x^{\prime} x\nonumber\]

que satisface todas las propiedades deseadas, incluyendo\(|V(x)| \nearrow \infty\) as\(\|x\| \nearrow \infty\). Evaluando su derivada a lo largo de trayectorias, obtenemos

\[\dot{V}(x)=2 x^{\prime} \dot{x}=-2 x^{\prime} C(x)<0 \quad \text { for } x \neq 0\nonumber\]

De ahí que el sistema sea globalmente asintóticamente estable.

Ejemplo 13.4

Considere el siguiente sistema dinámico

\ [\ begin {alineado}
\ punto {x} _ {1} &=-x_ {1} +4 x_ {2}\
\ punto {x} _ {2} &=-x_ {1} -x_ {2} ^ {3}
\ end {alineado}\ nonumber\]

El único punto de equilibrio para este sistema es el origen\(x = 0\). Para investigar la estabilidad del origen proponemos una función cuadrática de Lyapunov\(V=x_{1}^{2}+a x_{2}^{2}\), donde\(a\) es una constante positiva por determinar. Es claro que\(V\) es positivo definido en todo el espacio estatal\(\mathbb{R}^{2}\). Además,\(V\) es radialmente ilimitado, es decir satisface\(|V(x)| \nearrow \infty\) como\(\|x\| \nearrow \infty\). La derivada de V a lo largo de las trayectorias del sistema viene dada por

\ [\ begin {alineado}
\ punto {V} &=\ left [\ begin {array} {cc}
2 x_ {1} & 2 a x_ {2}
\ end {array}\ right]\ left [\ begin {array} {c}
-x_ {1} +4 x_ {2}\\
-x_ {1} -x_ {2} ^ {3}
\ end {array}\ derecha]\\
&=-2 x_ {1} ^ {2} + (8-2 a) x_ {1 } x_ {2} -2 a x_ {2} ^ {4}
\ final {alineado}\ nonumber\]

Si elegimos\(a = 4\) entonces podemos eliminar el término cruzado\(x_{1}x_{2}\), y la derivada de\(V\) se convierte

\[\dot{V}=-2 x_{1}^{2}-8 x_{2}^{4},\nonumber\]

que es claramente una función definida negativa en todo el espacio estatal. Por lo tanto, concluimos que\(x = 0\) es un punto de equilibrio globalmente asintóticamente estable.

Ejemplo 13.5

Un ejemplo muy estudiado en el área de sistemas dinámicos y caos es el famoso sistema Lorenz, que es un sistema no lineal que evoluciona en\(\mathbb{R}^{3}\) cuyas ecuaciones están dadas por

\ [\ comenzar {alineado}
\ punto {x} &=\ sigma (y-x)\
\ punto {y} &=r x-y-x z\
\ punto {z} &=x y-b z
\ final {alineado}\ nonumber\]

donde\(\sigma\),\(r\) y\(b\) son constantes positivas. Este sistema de ecuaciones proporciona un modelo aproximado de una capa de fluido horizontal que se calienta desde abajo. El fluido más cálido del fondo se eleva y así provoca corrientes de convección. Esto se aproxima a lo que sucede en la atmósfera. Bajo calentamiento intenso, este modelo exhibe un comportamiento dinámico complejo. Sin embargo, en este ejemplo nos gustaría analizar la estabilidad del origen bajo la condición\(r < 1\), que se sabe que no conduce a comportamientos complejos. Le definimos\(V=\alpha_{1} x^{2}+\alpha_{2} y^{2}+\alpha_{3} z^{2}\), dónde\(\alpha_{1}\)\(\alpha_{2}\),, y\(\alpha_{3}\) son constantes positivas por determinar. Es claro que\(V\) es positivo definido\(\mathbb{R}^{3}\) y está radialmente sin límites. La derivada de\(V\) a lo largo de las trayectorias del sistema viene dada por

\ [\ punto {V} =\ left [\ begin {array} {ccc}
2\ alpha_ {1} x & 2\ alpha_ {2} y & 2\ alpha_ {3} z
\ end {array}\ right]\ left [\ begin {array} {c}
\ sigma (y-x)\
r x-y-x z\\
x y-umbb z
\ end {array}\ right]\ nonor er\]

\ [\ begin {alineado}
=&-2\ alpha_ {1}\ sigma x^ {2} -2\ alpha_ {2} y^ {2} -2\ alpha_ {3} b z^ {2}\\
&+x y\ izquierda (2\ alpha_ {1}\ sigma+2 r\ alpha_ {2}\ derecha) +\ izquierda (2\ alpha_ {3} -2\ alpha_ {2}\ derecha) x y z
\ final {alineado}\ nonumber\]

Si elegimos\(\alpha_{2}=\alpha_{3}=1\) y\(\alpha_{1}=\frac{1}{\sigma}\) luego se\(\dot{V}\) convierte en

\ [\ begin {alineado}
\ punto {V} &=-2\ izquierda (x^ {2} +y^ {2} +2 b z^ {2} - (1+r) x y\ derecha)\\
&=-2\ izquierda [\ izquierda (x-\ frac {1} {2} (1+r) y\ derecha) ^ {2} +\ izquierda (1-\ izquierda (\ frac {r} {2}\ derecha) ^ {2}\ derecha) y^ {2} +b z^ {2}\ derecha]
\ final {alineado}\ nonumber\]

Ya que\(0 < r < 1\) se deduce eso\(0<\frac{1+r}{2}<1\) y por lo tanto\(\dot{V}\) es negativo definido en todo el espacio estatal\(\mathbb{R}^{3}\). Esto implica que el origen es globalmente asintóticamente estable.

Ejemplo 13.6 (Péndulo)

La ecuación dinámica de un péndulo que comprende una masa\(M\) al final de una varilla rígida pero sin masa de longitud\(R\) es

\[M R \ddot{\theta}+M g \sin \theta=0\nonumber\]

donde\(\theta\) está el ángulo hecho con la dirección hacia abajo, y\(g\) es la aceleración debida a la gravedad. Para poner el sistema en forma estado-espacio, dejar\(x_{1} = \theta\), y\(x_{1} = \dot{\theta}\); luego

\ [\ begin {alineado}
\ punto {x_ {1}} &=x_ {2}\
\ punto {x_ {2}} &=-\ frac {g} {R}\ sin x_ {1}
\ end {alineado}\ nonumber\]

Tomar como candidato Lyapunov funcionar la energía total en el sistema. Entonces

\ [\ begin {alineado}
V (x) &=\ frac {1} {2} M R^ {2} x_ {2} ^ {2} +M g R\ izquierda (1-\ cos x_ {1}\ derecha) =\ texto {cinético} +\ texto {potencial}\
\ punto {V} =\ frac {d V} {d x} f (x) &= izquierda [M g R\ sin x_ {1}\ quad M R^ {2} x_ {2}\ derecha]\ izquierda [\ comenzar {matriz} {c}
x_ {2}\\
-\ frac { g} {R}\ sin x_ {1}
\ end {array}\ right]\\
&=0
\ end {alineado}\ nonumber\]

Por lo tanto,\(V\) es una función de Lyapunov y el sistema es estable I.s.l. No podemos concluir la estabilidad asintótica con este análisis.

Considere ahora agregar un par de amortiguación proporcional a la velocidad, de modo que la descripción del espacio de estado se convierta en

\ [\ begin {array} {l}
\ punto {x_ {1}} =x_ {2}\
\ punto {x_ {2}} =-D x_ {2} -\ frac {g} {R}\ sin x_ {1}
\ end {array}\ nonumber\]

Con este cambio, pero\(V\) igual que antes, encontramos

\[\dot{V}=-D M R^{2} x_{2}^{2} \leq 0\nonumber\]

De esto podemos concluir estabilidad I.s.l. Todavía no podemos concluir directamente la estabilidad asintótica. Observe sin embargo que\(\dot{V}=0 \Rightarrow \dot{\theta}=0\). Bajo esta condición,\(\ddot{\theta}=-(g / R) \sin \theta\). Por lo tanto,\(\ddot{\theta} \neq 0\) si\(\theta \neq k \pi\) para entero\(k\), es decir, si el péndulo no está verticalmente hacia abajo o verticalmente hacia arriba. Esto implica que, a menos que estemos en la parte inferior o superior con velocidad cero, tendremos\(\ddot{\theta} \neq 0\) cuándo\(\dot{V} = 0\), así no\(\dot{\theta}\) quedaremos en 0, y de ahí la función Lyapunov comenzará a disminuir de nuevo. El único lugar donde el sistema puede terminar, por lo tanto, es con velocidad cero, colgando verticalmente hacia abajo o de pie verticalmente, es decir, en uno de los dos equilibrios. La prueba formal de este resultado en el caso general (“teorema de conjunto invariante de LaSalle”) está fuera del alcance de este curso.

La conclusión de la estabilidad asintótica local también se puede obtener directamente a través de una elección alternativa de la función de Lyapunov. Considerar al candidato a la función Lyapunov

\[V(x)=\frac{1}{2} x_{2}^{2}+\frac{1}{2}\left(x_{1}+x_{2}\right)^{2}+2\left(1-\cos x_{1}\right)\nonumber\]

De ello se deduce que

\[\dot{V}=-\left(x_{2}^{2}+x_{1} \sin x_{1}\right)=--\left(\dot{\theta}^{2}+\theta \sin \theta\right) \leq 0\nonumber\]

También,\(\dot{\theta}^{2}+\theta \sin \theta=0 \Rightarrow \dot{\theta}^{2}=0, \theta \sin \theta=0 \Rightarrow \theta=0, \dot{\theta}=0\). De ahí\(\dot{V}\) que sea estrictamente negativo en un pequeño barrio alrededor de 0. Esto demuestra estabilidad asintótica.

Sistemas Discretos de Tiempo

Resultados esencialmente idénticos para el sistema

\[x(k+1)=f(x(k))\ \tag{13.9}\]

siempre que interpretemos\(\dot{V}\) como

\[\dot{V}(x) \triangleq V(f(x))-V\tag{x}\]

es decir, como

\[\text{V (next state)} - \text{V (present state)}\]

Ejemplo 13.7 (Sistema DT)

Considerar el sistema

\ [\ begin {alineado}
x_ {1} (k+1) &=\ frac {x_ {2} (k)} {1+x_ {2} ^ {2} (k)}\\
x_ {2} (k+1) &=\ frac {x_ {1} (k)} {1+x_ {2} ^ {2} (k)}
\ fin {alineado}\ umber\]

que tiene su único equilibrio en el origen. Si elegimos la función cuadrática de Lyapunov

\[V(x)=x_{1}^{2}+x_{2}^{2}\nonumber\]

encontramos

\[\dot{V}(x(k))=V(x(k))\left(\frac{1}{\left[1+x_{2}^{2}(k)\right]^{2}}-1\right) \leq 0\nonumber\]

de donde podemos concluir que el punto de equilibrio es estable I.s.l. De hecho, examinando las relaciones anteriores con más cuidado (en el mismo estilo que hicimos para el péndulo con amortiguación), es posible concluir que el punto de equilibrio es en realidad globalmente asintóticamente estable.

Nota

El sistema del Ejemplo 2 está tomado del texto eminentemente legible de F. Verhulst, Ecuaciones diferenciales no lineales y sistemas dinámicos, Springer-Verlag, 1990.