1.25: El Pozo Cuadrado

Última actualización
Guardar como PDF

Page ID: 84555

Marc Baldo
Massachusetts Institute of Technology via MIT OpenCourseWare

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

A continuación consideramos un solo electrón dentro de un potencial cuadrado así como se muestra en la Figura 1.25.1. Como se mencionó en la discusión del efecto fotoeléctrico, los electrones dentro de los sólidos están unidos por fuerzas nucleares atractivas.

Al modelar la energía de unión dentro de un sólido como un pozo cuadrado, ignoramos completamente la estructura de escala fina dentro del sólido. De ahí que el pozo cuadrado, o partícula en una caja, como a menudo se le conoce, es una de las aproximaciones más crudas para un electrón dentro de un sólido. La simplicidad de la aproximación del pozo cuadrado, sin embargo, lo convierte en uno de los problemas más útiles en toda la mecánica cuántica.

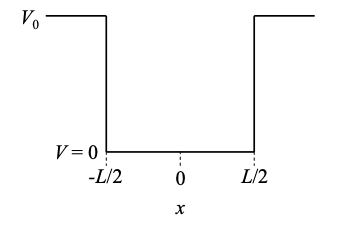
Captura de pantalla 2021-04-15 a las 10.50.18.png — Figura\(\PageIndex{1}\): El pozo cuadrado. Dentro del sólido el potencial se define como cero. En el espacio libre, fuera del sólido, el potencial repulsivo es\(V_{0}\).

Dado que el potencial cambia abruptamente, tratamos cada región de potencial constante por separado. Posteriormente, debemos conectar las soluciones en las diferentes regiones. Abordar el problema de esta manera se conoce como una solución por partes.

Ahora, la Ecuación de Schrödinger es una declaración de la conservación de la energía

\[ \text{total energy (E)} = \text{kinetic energy (KE)}+\text{Potential energy (V)} \nonumber \]

En la mecánica clásica, nunca se puede tener una energía cinética negativa. Por lo tanto, la mecánica clásica requiere que E > V. Esto se conoce como la región clásicamente permitida.

Pero en nuestro análisis cuántico, encontraremos soluciones para E < V. Esto se conoce como el régimen clásicamente prohibido.

La región clásicamente permitida

La ecuación de reorganización (1.23.5) da la ecuación diferencial de segundo orden:

\[ \frac{d^{2}\psi}{dx^{2}} = -\frac{2m(E-V)}{\hbar^{2}}\psi \nonumber \]

En esta región, E > V, las soluciones son de la forma

\[ \psi(x)=Ae^{ikx}+Be^{-ikx} \nonumber \]

\[ \psi(x)=A\ sin(kx)+B\ cos(kx) \nonumber \]

donde

\[ k =\sqrt{\frac{2m(E-V)}{\hbar^{2}}} \nonumber \]

En la región clásicamente permitida tenemos soluciones oscilantes.

La región clásicamente prohibida

En esta región, E < V, y las soluciones son de la forma

\[ \psi(x)=Ae^{\alpha x} +Be^{-\alpha x} \nonumber \]

es decir, están creciendo o decayendo exponenciales donde

\[ \alpha = \sqrt{\frac{2m(V-E)}{\hbar^{2}}} \nonumber \]