3.4: Permittividad compleja

La relación entre la intensidad del campo eléctrico\({\bf E}\) (unidades base SI de V/m) y la densidad de flujo eléctrico\({\bf D}\) (unidades base SI de C/m\(^2\)) es:

\[{\bf D} = \epsilon{\bf E} \label{m0134_eD} \]

donde\(\epsilon\) está la permitividad (SI unidades base de F/m). En los medios simples,\(\epsilon\) es un valor positivo real el cual no depende de la variación temporal de\({\bf E}\). Es decir, la respuesta (\({\bf D}\)) a un cambio en\({\bf E}\) se observa instantáneamente y sin demora.

En los materiales prácticos, sin embargo, el cambio\({\bf D}\) en respuesta a un cambio en\({\bf E}\) puede depender de la manera en que\({\bf E}\) cambia. La respuesta puede no ser instantánea, sino que podría tardar algún tiempo en manifestarse completamente. Este comportamiento se puede modelar usando la siguiente generalización de la Ecuación\ ref {M0134_ED}:

\[{\bf D} = a_0{\bf E} + a_1 \frac{\partial}{\partial t} {\bf E} + a_2 \frac{\partial^2}{\partial t^2} {\bf E} + a_3 \frac{\partial^3}{\partial t^3} {\bf E} + ... \label{m0134_ee} \]

donde\(a_0\),\(a_1\)\(a_2\), y así sucesivamente son constantes de valor real, y el número de términos es infinito. En los materiales prácticos, la importancia de los términos tiende a disminuir con el orden creciente. Por lo tanto, es común que sólo los primeros términos sean significativos. En muchas aplicaciones que involucran materiales comunes, solo el primer término es significativo; es decir,\(a_0\approx\epsilon\) y\(a_n\approx 0\) para\(n\ge 1\). Como veremos en un momento, esta distinción suele depender de la frecuencia.

En el dominio fasor, la diferenciación con respecto al tiempo se convierte en multiplicación por\(j\omega\). Así, la Ecuación\ ref {m0134_ee} se convierte

\[\begin{align} \widetilde{\bf D} &= a_0\widetilde{\bf E} + a_1\left(j\omega\right)\widetilde{\bf E} + a_2\left(j\omega\right)^2\widetilde{\bf E} + a_3\left(j\omega\right)^3\widetilde{\bf E} + ... \nonumber \\ &= a_0\widetilde{\bf E} + j\omega a_1\widetilde{\bf E} - \omega^2 a_2\widetilde{\bf E} - j\omega^3 a_3\widetilde{\bf E} + ... \nonumber \\ &= \left(a_0 + j\omega a_1 - \omega^2 a_2 - j\omega^3 a_3 + ... \right) \widetilde{\bf E} \end{align} \nonumber \]

Obsérvese que el factor entre paréntesis es un número de valor complejo que depende de parámetros de frecuencia\(\omega\) y materiales\(a_0\),\(a_1\),... Podemos resumir esto de la siguiente manera:

\[\widetilde{\bf D} = \epsilon_c \widetilde{\bf E} \label{m0134_eDc} \]

donde\(\epsilon_c\) es una constante de valor complejo que depende de la frecuencia.

La notación “\(\epsilon_c\)” se utiliza en otras partes de este libro (p. ej., Sección 3.3) para representar una generalización de permitividad simple que acomoda la pérdida asociada a la conductividad distinta de cero\(\sigma\). En la Sección 3.3, definimos

\[\epsilon_c \triangleq \epsilon' -j\epsilon'' \nonumber \]

donde\(\epsilon' \triangleq \epsilon\) (es decir, permitividad simple de valor real) y\(\epsilon'' \triangleq \sigma/\omega\) (es decir, el efecto de la conductividad distinta de cero). Del mismo modo,\(\epsilon_c\) en la Ecuación\ ref {M0134_EDC} se puede expresar como

\[\epsilon_c \triangleq \epsilon' -j\epsilon'' \nonumber \]

pero en este caso

\[\epsilon' \triangleq a_0 - \omega^2a_2 + ... \nonumber \]

y

\[\epsilon'' \triangleq -\omega a_1 + \omega^3a_3 - ... \nonumber \]

Cuando se expresa como fasores, la relación temporal entre la densidad de flujo eléctrico y la intensidad del campo eléctrico se puede expresar como una permitividad de valor complejo.

Así, ahora vemos dos posibles aplicaciones para el concepto de permitividad compleja: Modelar la respuesta retardada de\({\bf D}\) al cambio\({\bf E}\), como se describió anteriormente; y modelar la pérdida asociada con conductividad distinta de cero. En el trabajo práctico, puede que no siempre quede claro con precisión qué combinación de efectos\(\epsilon_c = \epsilon'-j\epsilon''\) está tomando en cuenta la permitividad compleja. Por ejemplo, si\(\epsilon_c\) se obtiene por medición, pueden representarse tanto la respuesta retardada como la pérdida de conducción. Por lo tanto, no es razonable suponer que un valor de\(\epsilon''\) obtenido por medición representa solo la pérdida de conducción (es decir, es igual a\(\sigma/\omega\)); de hecho, la medición también puede incluir una contribución significativa dependiente de la frecuencia asociada con el comportamiento de respuesta retardada identificado en este sección.

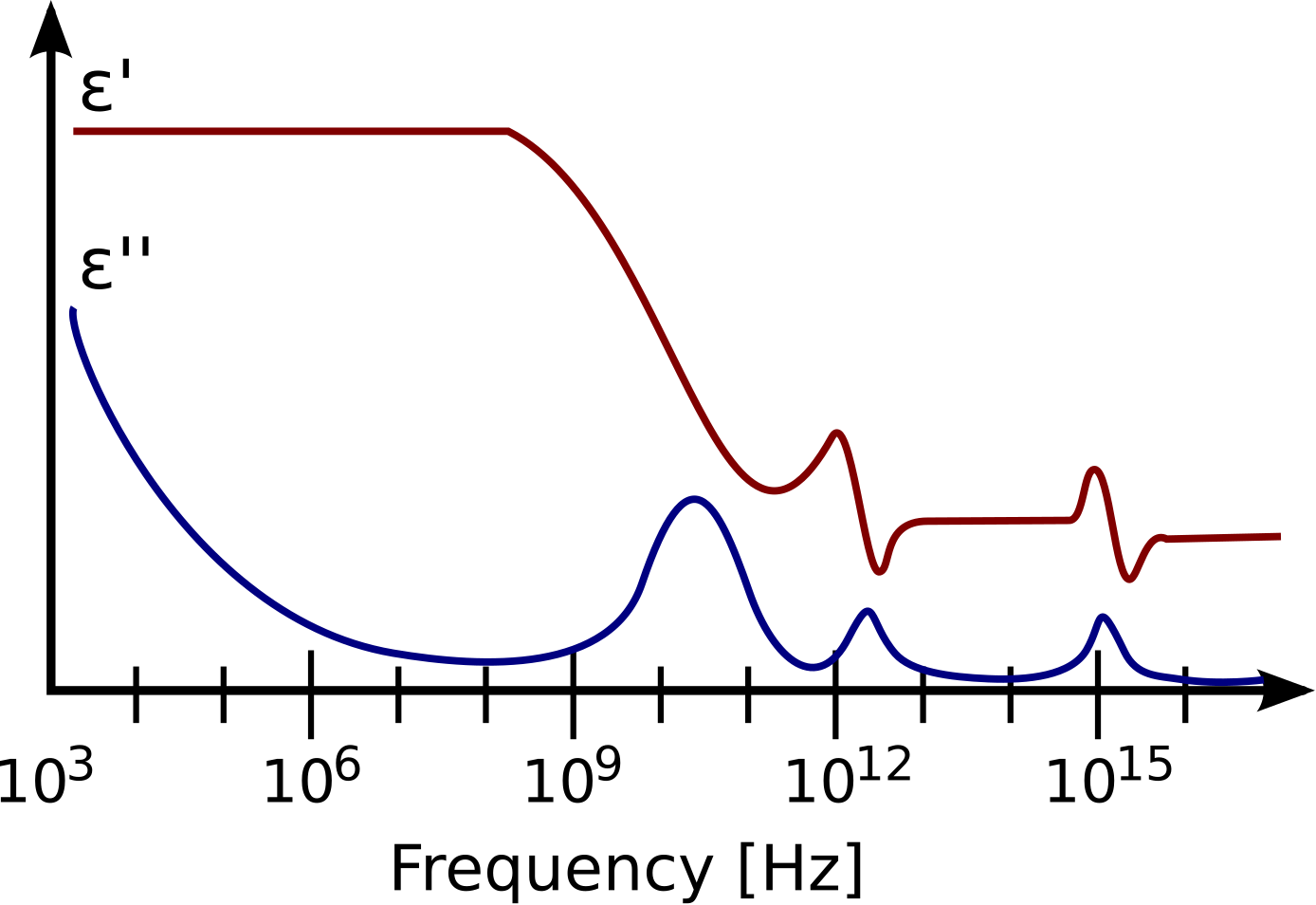
Un ejemplo de la permitividad compleja de un material dieléctrico típico se muestra en la Figura\(\PageIndex{1}\). Tenga en cuenta que la dependencia de la frecuencia es bastante simple y varía poco a bajas frecuencias por debajo de 1 GHz más o menos, pero se vuelve relativamente compleja a frecuencias más altas.

Figura\(\PageIndex{1}\): Las contribuciones relativas de los componentes reales e imaginarios de permitividad para un material dieléctrico típico (en este caso, un polímero). (K.A. Mauritz modificado)

Lectura adicional:

• “Permittividad” en Wikipedia.