9.5: Radiación de un dipolo eléctrico corto
- Page ID
- 83727
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La distribución más simple de la corriente radiante que se encuentra en la práctica común es el dipolo eléctricamente corto (ESD). Esta distribución de corriente se muestra en la Figura\(\PageIndex{1}\).
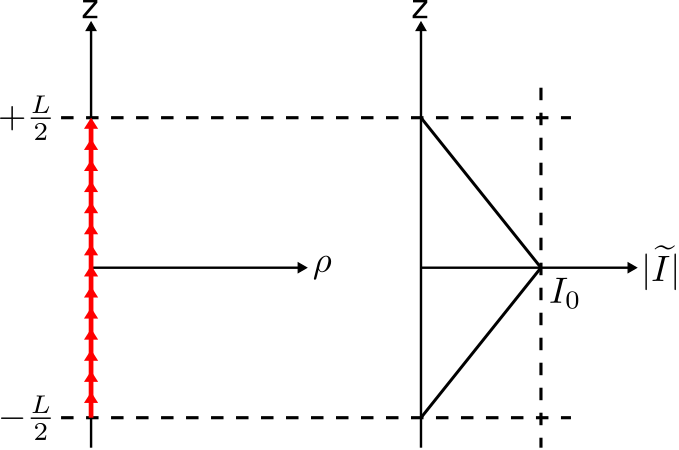
Las dos características que definen la ESD son (1) la corriente se alinea a lo largo de una línea recta, y (2) la longitud\(L\) de la línea es mucho menor que la mitad de una longitud de onda; es decir,\(L\ll\lambda/2\). Esta última característica es lo que queremos decir con “eléctricamente-corto”. 1
La distribución de corriente de una ESD es aproximadamente triangular en magnitud y aproximadamente constante en fase. ¿Cómo sabemos esto? Primero, tenga en cuenta que las distribuciones de corriente no pueden cambiar de manera compleja o rápida a lo largo de tales distancias que son mucho menores que una longitud de onda. Si esto no es inmediatamente aparente, recuerde el comportamiento de las líneas de transmisión: La onda estacionaria actual en una línea de transmisión exhibe un periodo de\(\lambda/2\), independientemente de la fuente o terminación. Para la ESD,\(L\ll\lambda/2\) y así esperamos una variación aún más simple. También, sabemos que la corriente en los extremos del dipolo debe ser cero, simplemente porque ahí termina el dipolo. Estas consideraciones implican que la distribución actual de la EDS es bien aproximada como triangular en magnitud. 2 Expresado matemáticamente:
\[\widetilde{I}(z) \approx I_0 \left(1-\frac{2}{L}\left|z\right|\right) \nonumber \]
donde\(I_0\) (Unidades base SI de A) es una constante de valor complejo que indica la magnitud y fase de corriente máxima.
Hay dos enfoques que podríamos considerar para encontrar el campo eléctrico irradiado por una ESD. El primer enfoque es calcular el potencial del vector magnético\(\widetilde{\bf A}\) por integración sobre la distribución de corriente\(\widetilde{\bf H}=(1/\mu)\nabla\times\widetilde{\bf A}\), calcular y finalmente calcular\(\widetilde{\bf E}\) a\(\widetilde{\bf H}\) partir de la ley de Ampere. Emplearemos un enfoque más sencillo, que se muestra en la Figura\(\PageIndex{2}\).

Imagínese la ESD como una colección de muchos segmentos más cortos de corriente que irradian independientemente. El campo total es entonces la suma de estos segmentos cortos. Debido a que estos segmentos son muy cortos en relación con la longitud del dipolo además de ser cortos en relación con una longitud de onda, podemos aproximar la corriente sobre cada segmento como aproximadamente constante. En otras palabras, podemos interpretar cada uno de estos segmentos como siendo, a una buena aproximación, un dipolo hertziano.
La ventaja de este enfoque es que ya tenemos una solución para cada uno de los segmentos. En la Sección 9.4, se muestra que un dipolo hertziano\(\hat{\bf z}\) -dirigido en el origen irradia el campo eléctrico
\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j\eta \frac{\widetilde{I}\cdot\beta \Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]
donde\(\widetilde{I}\) y\(\Delta l\) puede interpretarse como la corriente y la longitud del dipolo, respectivamente. En esta expresión,\(\eta\) se encuentra la impedancia de onda del medio en el que irradia el dipolo (por ejemplo,\(\approx 377~\Omega\) para el espacio libre), y hemos presumido medios sin pérdidas tales que la constante de atenuación\(\alpha\approx 0\) y la constante de propagación de fase\(\beta=2\pi/\lambda\). Esta expresión también asume puntos de campo alejados del dipolo; específicamente, distancias\(r\) que son mucho mayores que\(\lambda\). Reproponiendo esta expresión para el presente problema, el segmento en el origen irradia el campo eléctrico:
\[\widetilde{\bf E}({\bf r};z'=0) \approx \hat{\bf \theta} j\eta \frac{I_0\cdot\beta \Delta l}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]
donde la notación\(z'=0\) indica que el dipolo hertziano se encuentra en el origen. Dejando que la longitud\(\Delta l\) de este segmento se encoja a la longitud diferencial\(dz'\), podemos describir la contribución de este segmento al campo irradiado por la ESD de la siguiente manera:
\[d\widetilde{\bf E}({\bf r};z'=0) \approx \hat{\bf \theta} j\eta \frac{I_0\cdot\beta dz'}{4\pi}~\left(\sin\theta\right) \frac{e^{-j\beta r}}{r} \nonumber \]
Usando este enfoque, el campo eléctrico irradiado por cualquier segmento puede escribirse:
\[d\widetilde{\bf E}({\bf r};z') \approx \hat{\bf \theta}' j\eta\beta \frac{\widetilde{I}(z')}{4\pi}\left(\sin\theta'\right) \frac{e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}}{\left|{\bf r}-\hat{\bf z}z'\right|}~dz' \nonumber \]
Tenga en cuenta que\(\theta\) se sustituye por\(\theta'\) ya que el rayo\({\bf r}-\hat{\bf z}z'\) forma un ángulo diferente (i.e.,\(\theta'\)) con respecto a\(\hat{\bf z}\). De igual manera,\(\hat{\bf \theta}\) se sustituye por\(\hat{\bf \theta}'\), ya que también varía con\(z'\). El campo eléctrico irradiado por la ESD se obtiene por integración sobre estas contribuciones:
\[\widetilde{\bf E}({\bf r}) \approx \int_{-L/2}^{+L/2} d\widetilde{\bf E}(\hat{\bf r};z') \nonumber \]
rindiendo:
\[\widetilde{\bf E}({\bf r}) \approx j \frac{\eta\beta}{4\pi} \int_{-L/2}^{+L/2} \hat{\bf \theta}' \widetilde{I}(z')~\left(\sin\theta'\right) \frac{e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}}{\left|{\bf r}-\hat{\bf z}z'\right|} dz' \nonumber \]
Dados algunos de los supuestos que ya hemos hecho, esta expresión puede simplificarse aún más. Por ejemplo, tenga en cuenta que\(\theta'\approx\theta\) desde\(L\ll r\). Por la misma razón,\(\hat{\bf \theta}'\approx\hat{\bf \theta}\). Dado que estas variables son aproximadamente constantes sobre la longitud del dipolo, podemos moverlas fuera de la integral, produciendo:
\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta\beta}{4\pi}~\left(\sin\theta\right) \int_{-L/2}^{+L/2} \widetilde{I}(z') \frac{e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}}{\left|{\bf r}-\hat{\bf z}z'\right|} dz' \label{m0198_eE1} \]
También es posible simplificar la expresión\(\left|{\bf r}-\hat{\bf z}z'\right|\). Considera Figura\(\PageIndex{3}\).
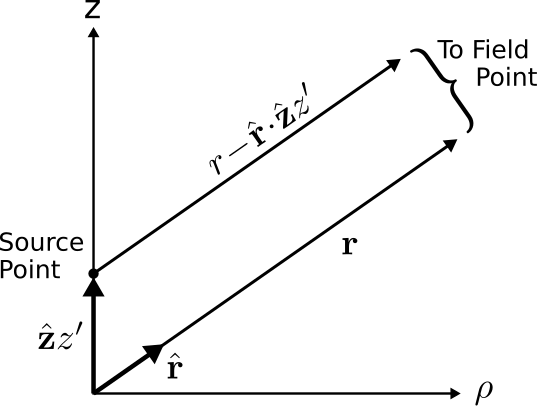
Dado que ya asumimos que\(r\gg L\) (es decir, la distancia a los puntos de campo es mucho mayor que la longitud del dipolo), el vector\({\bf r}\) es aproximadamente paralelo al vector\({\bf r}-\hat{\bf z}z'\). Posteriormente, debe ser cierto que
\[\left|{\bf r}-\hat{\bf z}z'\right| \approx r-\hat{\bf r}\cdot\hat{\bf z}z' \label{m0198_ePRA} \]
Tenga en cuenta que la magnitud de\(r-\hat{\bf r}\cdot\hat{\bf z}z'\) debe ser aproximadamente igual a\(r\), ya que\(r\gg L\). Entonces, en la medida en que\(\left|{\bf r}-\hat{\bf z}z'\right|\) determine la magnitud de\(\widetilde{\bf E}({\bf r})\), podemos usar la aproximación:
\[\left|{\bf r}-\hat{\bf z}z'\right| \approx r ~~~\mbox{(magnitude)} \nonumber \]
En la medida en que\(\left|{\bf r}-\hat{\bf z}z'\right|\) determine la fase, tenemos que ser un poco más cuidadosos. La parte del integrando de la Ecuación\ ref {M0198_EE1} que exhibe fase variable es\(e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|}\). Usando la ecuación\ ref {M0198_epra}, encontramos
\[e^{-j\beta\left|{\bf r}-\hat{\bf z}z'\right|} \approx e^{-j\beta r} e^{+j\beta\hat{\bf r}\cdot\hat{\bf z}z'} \nonumber \]
El peor caso en términos de variación de fase dentro de la integral es para puntos de campo a lo largo del\(z\) eje. Para estos puntos,\(\hat{\bf r}\cdot\hat{\bf z}=\pm 1\) y posteriormente\(\left|{\bf r}-\hat{\bf z}z'\right|\) varía de\(z-L/2\) a\(z+L/2\) dónde\(z\) está la ubicación del punto de campo. Sin embargo, dado que\(L\ll\lambda\) (es decir, debido a que el dipolo es eléctricamente corto), esta diferencia en longitudes es mucho menor que\(\lambda/2\). Por lo tanto, la fase\(\beta \hat{\bf r}\cdot\hat{\bf z}z'\) varía mucho menos que\(\pi\) los radianes, y posteriormente\(e^{-j\beta\hat{\bf r}\cdot\hat{\bf z}z'}\approx 1\). Concluimos que en estas condiciones,
\[e^{-j\beta \left|{\bf r}-\hat{\bf z}z'\right|} \approx e^{-j\beta r} ~~~\mbox{(phase)} \nonumber \]
Aplicando estas simplificaciones para magnitud y fase a la Ecuación\ ref {M0198_EE1}, obtenemos:
\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta\beta}{4\pi} \left(\sin\theta\right) \frac{e^{-j\beta r}}{r}~\int_{-L/2}^{+L/2} \widetilde{I}(z') dz' \nonumber \]
La integral en esta ecuación es muy fácil de evaluar; de hecho, a partir de la inspección (Figura\(\PageIndex{1}\)), determinamos que es igual a\(I_0L/2\). Finalmente, obtenemos:
\[\boxed{ \widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \eta \frac{I_0\cdot\beta L}{8\pi} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} } \label{m0198_eESDE} \]
Resumiendo:
La intensidad del campo eléctrico irradiado por una ESD localizada en el origen y alineada a lo largo del\(z\) eje viene dada por la Ecuación\ ref {M0198_EESDE}. Esta expresión es válida para\(r\gg\lambda\).
Cabe señalar que la variación en magnitud, fase y polarización de la ESD con ubicación de punto de campo es idéntica a la de un solo dipolo hertziano que tiene momento actual\(\hat{\bf z} I_0 L/2\) (Sección 9.4). Sin embargo, la magnitud del campo irradiado por la ESD es exactamente la mitad de la del dipolo hertziano. ¿Por qué la mitad? Simplemente porque la integral sobre la distribución de corriente triangular asumida para el ESD es la mitad de la integral sobre la distribución uniforme de corriente que define el dipolo hertziano. Esto de manera similar a veces causa confusión entre los dipolos hertzianos y las ESD. Recuerde que las ESD son físicamente realizables, mientras que los dipolos hertzianos no lo son.
Es común eliminar el factor de\(\beta\) en la magnitud utilizando la relación\(\beta=2\pi/\lambda\), produciendo:
\[\widetilde{\bf E}({\bf r}) \approx \hat{\bf \theta} j \frac{\eta I_0}{4} \frac{L}{\lambda} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} \nonumber \]
En los puntos de campo\(r\gg\lambda\), la onda parece ser localmente plana. Por lo tanto, estamos justificados usando la relación de onda plana\(\widetilde{\bf H} = \frac{1}{\eta} \hat{\bf r} \times \widetilde{\bf E}\) para calcular\(\widetilde{\bf H}\). El resultado es:
\[\widetilde{\bf H}({\bf r}) \approx \hat{\bf \phi} j \frac{I_0}{4} \frac{L}{\lambda} ~\left(\sin\theta\right) ~\frac{e^{-j\beta r}}{r} \label{m0198_eESDH} \]
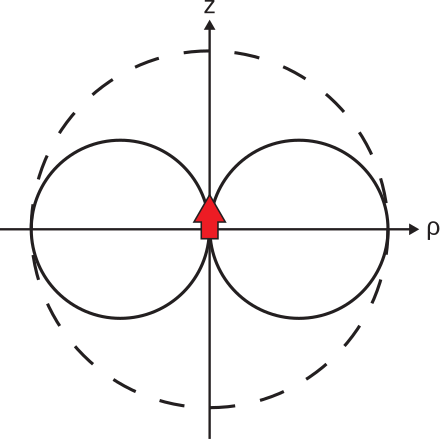
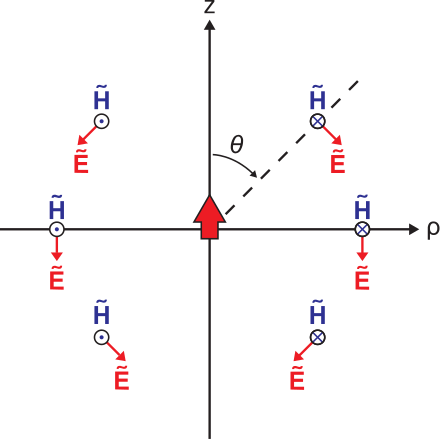
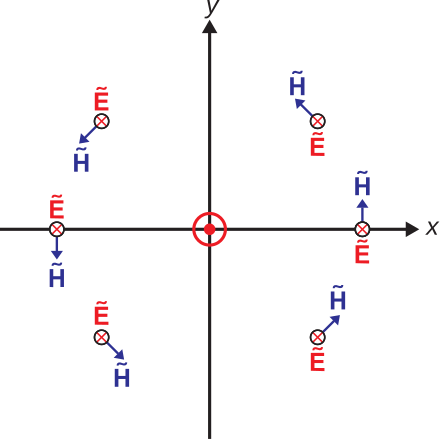
Finalmente, consideremos las características espaciales del campo radiado. Las figuras\(\PageIndex{4}\) y\(\PageIndex{5}\) muestran el resultado en un plano de constante\(\phi\). Las figuras\(\PageIndex{6}\) y\(\PageIndex{7}\) muestran el resultado en el\(z=0\) plano. Tenga en cuenta que las orientaciones de los vectores de campo eléctrico y magnético indican un vector Poynting\(\widetilde{\bf E}\times\widetilde{\bf H}\) que siempre se dirige radialmente hacia afuera desde la ubicación del dipolo. Esto confirma que el flujo de potencia siempre se dirige radialmente hacia afuera desde el dipolo. Debido a la simetría del problema, las Figuras\(\PageIndex{4}\) —\(\PageIndex{7}\) proporcionan una caracterización completa de las magnitudes y orientaciones relativas de los campos radiados.
- Una fuente potencial de confusión es que el dipolo hertziano es también un “dipolo” que es “eléctricamente corto”. La distinción es que la corriente que comprende un dipolo hertziano es constante a lo largo de su longitud. Esta condición se ve raramente y solo aproximadamente en la práctica, mientras que la distribución de magnitud triangular es una aproximación relativamente buena a una clase amplia de antenas de cable eléctrico corto comúnmente encontradas. Así, el término “dipolo eléctricamente corto”, como se usa en este libro, se refiere a la distribución triangular a menos que se indique lo contrario. ↩
- Un análisis más riguroso que lleve a la misma conclusión es posible, pero está más allá del alcance de este libro. ↩


