10.1: Cómo irradian las antenas
- Page ID
- 83705
Una antena es un transductor; es decir, un dispositivo que convierte señales de una forma en otra forma. En el caso de una antena, estas dos formas son (1) señales de voltaje y corriente ligadas al conductor y (2) ondas electromagnéticas. Las antenas pasivas tradicionales son capaces de esta conversión en cualquier dirección. En esta sección, consideramos el caso de transmisión, en el que una señal ligada a un conductor se convierte en una onda electromagnética radiante. La radiación de una antena se debe a la corriente variable en el tiempo que es excitada por la señal eléctrica ligada aplicada a los terminales de la antena.
Por qué las líneas de transmisión ideales no irradian
Para describir el proceso que permite que una antena transmita, es útil considerar primero el escenario representado en la Figura\(\PageIndex{1}\).
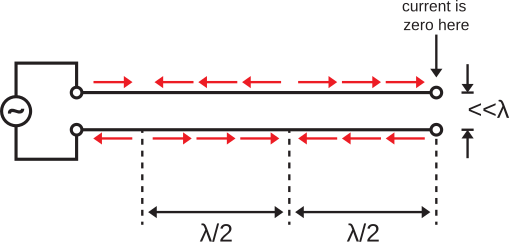
Aquí se aplica una fuente sinusoidal a la entrada de una línea de transmisión de doble cable ideal. El espaciamiento entre conductores es mucho menor que una longitud de onda, y la salida de la línea de transmisión termina en un circuito abierto.
Sin ninguna información adicional, ya sabemos dos cosas sobre la corriente en esta línea de transmisión. Primero, sabemos que la corriente debe ser idéntica a cero al final de la línea de transmisión. Segundo, sabemos que la corriente en los dos conductores que componen la línea de transmisión debe estar relacionada como se indica en la Figura\(\PageIndex{1}\). Es decir, en cualquier posición dada en la línea de transmisión, la corriente en cada conductor es igual en magnitud y fluye en direcciones opuestas.
Obsérvese además que la Figura\(\PageIndex{1}\) representa solo la situación a lo largo de un intervalo de la mitad del periodo de la fuente sinusoidal. Para el otro medio periodo, la dirección de la corriente será en la dirección opuesta a la representada en la Figura\(\PageIndex{1}\). Es decir: La fuente varía periódicamente, por lo que el signo de la corriente está cambiando cada medio periodo. Generalmente, las corrientes variables en el tiempo dan lugar a la radiación. Por lo tanto, debemos esperar que las corrientes representadas en la Figura\(\PageIndex{1}\) puedan irradiar. Podemos estimar la radiación de la línea de transmisión interpretando la corriente como una colección de dipolos hertzianos. Para una revisión de los dipolos hertzianos, véase la Sección 9.4; sin embargo, todo lo que necesitamos saber para abordar el problema actual es que se aplica la superposición. Es decir, la radiación total es la suma de la radiación de los dipolos hertzianos individuales. Una vez más mirando hacia atrás en la Figura\(\PageIndex{1}\), tenga en cuenta que cada dipolo hertziano que representa la corriente en un conductor tiene un dipolo hertziano asociado que representa la corriente en el otro conductor, y es solo una pequeña fracción de una longitud de onda distante. Además, estos pares de dipolos hertzianos son idénticos en magnitud pero de signo opuesto. Por lo tanto, el campo radiado de cualquier par de dipolos hertzianos es aproximadamente cero a distancias suficientemente alejadas de la línea de transmisión. Continuando sumando todos esos pares de dipolos hertzianos, el campo radiado permanece aproximadamente cero a distancias suficientemente alejadas de la línea de transmisión. Llegamos a la siguiente conclusión notable:
La radiación de una línea de transmisión de doble cable ideal con terminación de circuito abierto es insignificante a distancias mucho mayores que la separación entre los conductores.
Antes de continuar, seamos claros sobre una cosa: La situación a distancias que no son grandes en relación con la separación entre los conductores es bastante diferente. Esto se debe a que los pares de dipolos hertzianos no parecen estar tan precisamente ubicados en puntos de campo cercanos a la línea de transmisión. Posteriormente la cancelación de campos de pares de dipolos hertzianos es menos precisa. Los campos de suma resultantes no son despreciables y dependen de la separación entre los conductores. Para la presente discusión, basta con restringir nuestra atención al caso más simple del “campo lejano”.
Una antena simple formada por la modificación de la línea de transmisión de dos conductores
Consideremos ahora una modificación al escenario anterior, que se muestra en la Figura\(\PageIndex{2}\).
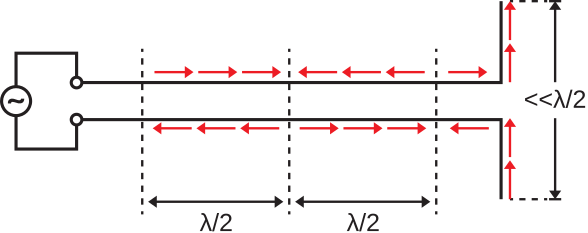
En el nuevo escenario, los extremos del cable gemelo se doblan en ángulos rectos. Esta nueva sección tiene una longitud total que es mucho menor que la mitad de la longitud de onda. Para determinar la distribución de corriente en la sección modificada, primero observamos que la corriente debe seguir siendo precisamente cero en los extremos de los conductores, pero no necesariamente en el punto en el que se doblan. Dado que la sección modificada es mucho más corta que la mitad de la longitud de onda, la distribución de corriente en esta sección debe ser muy simple. De hecho, la distribución de corriente debe ser la del dipolo eléctrico corto (ESD), exhibiendo una magnitud máxima en el centro y disminuyendo aproximadamente linealmente a cero en los extremos. (Véase la Sección 9.5 para una revisión de la EDS.) Por último, observamos que la corriente debe ser continua en el cruce entre las secciones no modificadas y modificadas.
Habiendo establecido que la sección modificada exhibe la distribución de corriente de una ESD, y habiendo determinado previamente que la sección no modificada de la línea de transmisión no irradia, concluimos que este sistema irradia precisamente como lo hace una ESD. Tenga en cuenta también que no necesitamos interpretar la porción ESD de la línea de transmisión como una modificación de la línea de transmisión: En cambio, podemos ver este sistema como una línea de transmisión no modificada unida a una antena, que en este caso en un ESD.
El caso general
Aunque desarrollamos esta perspicacia para la EDS específicamente, el principio se aplica de manera general. Es decir, cualquier antena —no solo dipolos— puede verse como una estructura que puede soportar una distribución de corriente que irradia. Elaborando:
Una antena transmisora es un dispositivo que, cuando es accionado por una fuente apropiada, soporta una distribución de corriente variable en el tiempo dando como resultado una onda electromagnética que irradia lejos del dispositivo.
Aunque esto pueda parecer simplemente una reexpresión de la definición al inicio de esta sección —y lo es—, ahora vemos cómo puede suceder esto, y también por qué las líneas de transmisión normalmente no son también antenas.