10.11: Potencial inducido en un dipolo
- Page ID
- 83657
Una onda electromagnética incidente en una antena inducirá un potencial en los terminales de la antena. En esta sección, derivaremos este potencial. Para simplificar la derivación, consideraremos el caso especial de un dipolo delgado recto de longitud arbitraria que es iluminado por una onda plana. Sin embargo, ciertos aspectos de la derivación se aplicarán a las antenas en general. En particular, los conceptos de longitud efectiva (también conocida como altura efectiva) y longitud efectiva vectorial emergen naturalmente de esta derivación, por lo que esta sección también sirve como un escalón en el desarrollo de un modelo de circuito equivalente para una antena receptora. La derivación se basa en las propiedades de transmisión de los dipolos así como en el principio de reciprocidad, por lo que se recomienda conocer esos temas antes de leer esta sección.
El escenario de interés se muestra en la Figura\(\PageIndex{1}\). Aquí se localiza en el origen un dipolo recto delgado\(\hat{\bf z}\) alineado. La longitud total del dipolo es\(L\). Los brazos del dipolo son perfectamente conductores. Los terminales constan de un pequeño hueco de longitud\(\Delta l\) entre los brazos. La onda plana incidente se describe en términos de su intensidad de campo eléctrico\(\widetilde{\bf E}^i\). La pregunta es: ¿Cuál es\(\widetilde{V}_{OC}\), el potencial en los terminales cuando los terminales están en circuito abierto?
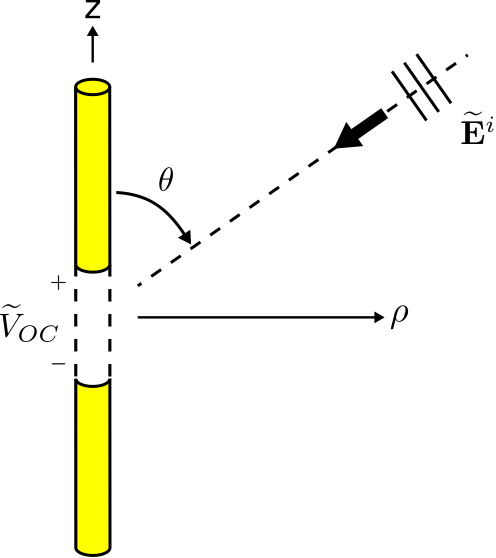
Existen múltiples enfoques para resolver este problema. Un ataque directo consiste en invocar el principio de que el potencial es igual a la integral de la intensidad del campo eléctrico sobre una trayectoria. En este caso, el trayecto comienza en el terminal “\(-\)” y termina en el terminal “\(+\)”, cruzando el hueco que define los terminales de antena. Así:
\[\widetilde{V}_{OC} = -\int_{gap} \widetilde{\bf E}_{gap} \cdot d{\bf l} \label{m0215_eVoc-General} \]
donde\(\widetilde{\bf E}_{gap}\) está el campo eléctrico en la brecha. El problema con este enfoque es que el valor de no\(\widetilde{\bf E}_{gap}\) está fácilmente disponible. No es simplemente\(\widetilde{\bf E}^i\), porque la estructura de la antena (en particular, las condiciones de límite electromagnético) modifican el campo eléctrico en las proximidades de la antena. 1
Afortunadamente, podemos sortear este obstáculo utilizando el principio de reciprocidad. En una estrategia basada en la reciprocidad, establecemos una relación entre dos escenarios que ocurren dentro de un mismo sistema electromagnético. El primer escenario se muestra en la Figura\(\PageIndex{2}\).
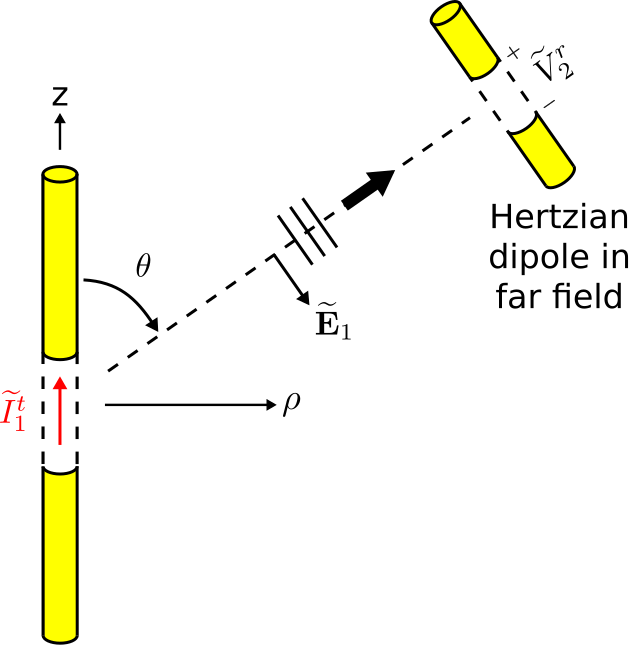
En este escenario, tenemos dos dipolos. El primer dipolo es precisamente el dipolo de interés (Figura\(\PageIndex{1}\)), excepto que\(\widetilde{I}_1^t\) se aplica una corriente a los terminales de la antena. Esto da lugar a una distribución de corriente\(\widetilde{I}(z)\) (unidades base SI de A) a lo largo del dipolo, y posteriormente el dipolo irradia el campo eléctrico (Sección 9.6):
\ begin {align}\ Widetilde {\ bf E} _1 ({\ bf r}) &\ approx\ hat {\ bf\ theta} j\ frac {\ eta} {2}\ frac {e^ {-j\ beta r}} {r} ~\ izquierda (\ sin\ theta\ derecha)\ nonumber\ & ~~~\ cdot\ izquierda [\ frac {1} {\ lambda}\ int_ {-L/2} ^ {+L/2}\ Widetilde {I} (z') e^ {+j\ beta z'\ cos {\ theta}} dz'\ derecha]\ etiqueta {M0215_eesde}\ end {align}
La segunda antena es un dipolo hertziano\(\hat{\bf \theta}\) -alineado en el campo lejano, que recibe\(\widetilde{\bf E}_1\). (Para un repaso sobre las propiedades de los dipolos hertzianos, ver Sección 9.4. Un punto clave es que los dipolos hertzianos son muy pequeños.) Específicamente, medimos (conceptualmente, al menos) el potencial de circuito abierto\(\widetilde{V}_2^r\) en los terminales del dipolo hertziano. Seleccionamos un dipolo hertziano para este propósito porque, a diferencia de esencialmente todas las demás antenas, es simple determinar el potencial de circuito abierto. Como se explicó anteriormente:
\[\widetilde{V}_2^r = -\int_{gap} \widetilde{\bf E}_{gap} \cdot d{\bf l} \nonumber \]
Para el dipolo hertziano,\(\widetilde{\bf E}_{gap}\) es simplemente el campo eléctrico incidente, ya que hay una estructura insignificante (en particular, una cantidad insignificante de material) presente para modificar el campo eléctrico. Así, simplemente tenemos:
\[\widetilde{V}_2^r = -\int_{gap} \widetilde{\bf E}_1 \cdot d{\bf l} \label{m0215_eV2r1} \]
Dado que el dipolo hertziano es muy corto y muy alejado del dipolo transmisor,\(\widetilde{\bf E}_1\) es esencialmente constante sobre la brecha. También recordemos que requerimos que el dipolo hertziano estuviera alineado con\(\widetilde{\bf E}_1\). Al elegir integrar en línea recta a través de la brecha, la ecuación\ ref {m0215_EV2R1} se reduce a:
\[\widetilde{V}_2^r = -\widetilde{\bf E}_1({\bf r}_2) \cdot \hat{\bf \theta}\Delta l \label{m0215_eV2r2} \]
donde\(\Delta l\) es la longitud de la brecha y\({\bf r}_2\) es la ubicación del dipolo hertziano. Sustituyendo la expresión por\(\widetilde{\bf E}_1\) de Ecuación\ ref {M0215_EESDE}, obtenemos:
\ begin {align}\ Widetilde {V} _2^r\ approx &- j\ frac {\ eta} {2}\ frac {e^ {-j\ beta r_2}} {r_2} ~\ izquierda (\ sin\ theta\ derecha)\ nonumber\\ & ~~~\ cdot\ izquierda [\ frac {1} {\ lambda}\ int_ {-L/2} ^ {+L/2}\ tilde ancho {I} (z') e^ {+j\ beta z'\ cos {\ theta}} dz'\ derecha]\ Delta l\ etiqueta {m0215_EV2r3}\ end {align}
donde\(r_2=\left|{\bf r}_2\right|\).
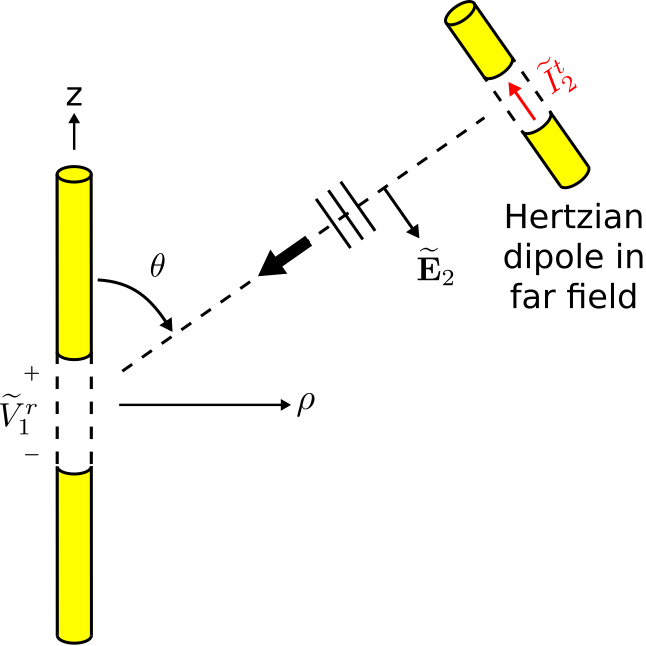
El segundo escenario se muestra en la Figura\(\PageIndex{3}\). Este escenario es idéntico al primer escenario, con la excepción de que el dipolo hertziano transmite y el dipolo de interés recibe. El campo irradiado por el dipolo hertziano en respuesta a la corriente aplicada\(\widetilde{I}_2^t\), evaluada en el origen, es (Sección 9.4):
\[\widetilde{\bf E}_2({\bf r}=0) \approx \hat{\bf \theta} j\eta \frac{\widetilde{I}_2^t\cdot\beta \Delta l}{4\pi}~(1)~\frac{e^{-j\beta r_2}}{r_2} \label{m0215_eE} \]
El factor “\(\sin\theta\)” en la expresión general es igual a 1 en este caso, ya que, como se muestra en la Figura\(\PageIndex{3}\), el origen se localiza de lado ancho (es decir, en\(\pi/2\) rad) con relación al eje del dipolo hertziano. También tenga en cuenta que debido a que se presume que el dipolo hertziano está en el campo lejano,\({\bf E}_2\) puede interpretarse como una onda plana en la región del dipolo receptor de interés.
Ahora nos preguntamos: ¿Cuál es el potencial inducido\(\widetilde{V}_1^r\) en el dipolo de interés? Una vez más, la Ecuación\ ref {M0215_EVOC-General} no es de mucha ayuda, porque no se conoce el campo eléctrico en la brecha. No obstante, sí sabemos que\(\widetilde{V}_1^r\) debe ser proporcional a\(\widetilde{\bf E}_2({\bf r}=0)\), ya que se presume que se trata de un sistema lineal. Con base solo en esta cantidad de información, debe haber algún vector\({\bf l}_e=\hat{\bf l} l_e\) para el cual
\[\widetilde{V}_1^r = \widetilde{\bf E}_2({\bf r}=0) \cdot {\bf l}_e \label{m0215_eVEL1} \]
Esto no define de manera única ni el vector unitario\(\hat{\bf l}\) ni la parte escalar\(l_e\), ya que un cambio en la definición de la primera puede ser compensado por un cambio en la definición de esta última y viceversa. Por lo que en este punto invocamos la definición estándar de\({\bf l}_e\) como la longitud efectiva del vector, introducida en la Sección 10.9. Así,\(\hat{\bf l}\) se define como la dirección en la que se polarizaría un campo eléctrico transmitido desde la antena. En el presente ejemplo,\(\hat{\bf l}=-\hat{\bf \theta}\), donde el signo menos refleja el hecho de que el potencial terminal positivo da como resultado una corriente terminal que fluye en la\(-\hat{\bf z}\) dirección. Así, la Ecuación\ ref {M0215_evel1} se convierte en:
\[\widetilde{V}_1^r = -\widetilde{\bf E}_2({\bf r}=0) \cdot \hat{\bf \theta} l_e \nonumber \]
Podemos ir un poco más allá y sustituir la expresión\(\widetilde{\bf E}_2({\bf r}=0)\) de la ecuación\ ref {M0215_EE}:
\[\widetilde{V}_1^r \approx - j\eta~\frac{\widetilde{I}_2^t\cdot\beta \Delta l}{4\pi}~\frac{e^{-j\beta r_2}}{r_2} l_e \label{m0215_eV1r1} \]
Ahora invocamos la reciprocidad. Como sistema lineal de dos puertos invariante en el tiempo, debe ser cierto que:
\[\widetilde{I}_1^t \widetilde{V}_1^r = \widetilde{I}_2^t \widetilde{V}_2^r \nonumber \]
Así:
\[\widetilde{V}_1^r = \frac{\widetilde{I}_2^t}{\widetilde{I}_1^t} \widetilde{V}_2^r \nonumber \]
Sustituyendo la expresión\(\widetilde{V}_2^r\) de la ecuación\ ref {m0215_EV2r3}:
\[\begin{aligned} \widetilde{V}_1^r \approx &- \frac{\widetilde{I}_2^t}{\widetilde{I}_1^t} \cdot j \frac{\eta}{2} \frac{e^{-j\beta r_2}}{r_2}~\left(\sin\theta\right) \nonumber \\ & ~~~\cdot\left[\frac{1}{\lambda}\int_{-L/2}^{+L/2} \widetilde{I}(z') e^{+j\beta z'\cos{\theta}} dz'\right] \Delta l\end{aligned} \nonumber \]
Así, la reciprocidad ha proporcionado una segunda expresión para\(\widetilde{V}_1^r\). Podemos resolver para\(l_e\) estableciendo esta expresión igual a la expresión de la ecuación\ ref {m0215_EV1r1}, rindiendo
\[l_e \approx \frac{2\pi}{\beta \widetilde{I}_1^t} \left[\frac{1}{\lambda}\int_{-L/2}^{+L/2} \widetilde{I}(z') e^{+j\beta z'\cos{\theta}} dz'\right] \sin\theta \nonumber \]
Señalando que\(\beta=2\pi/\lambda\), esto simplifica para:
\[l_e \approx \left[ \frac{1}{\widetilde{I}_1^t}\int_{-L/2}^{+L/2} \widetilde{I}(z') e^{+j\beta z'\cos{\theta}} dz' \right] \sin\theta \label{m0215_ele} \]
Así, se puede calcular\(l_e\) utilizando el siguiente procedimiento:
- Aplicar una corriente\(\widetilde{I}_1^t\) al dipolo de interés.
- Determinar la distribución de corriente resultante\(\widetilde{I}(z)\) a lo largo de la longitud del dipolo. (Obsérvese que precisamente esto se hace para el dipolo eléctricamente corto en la Sección 9.5 y para el dipolo de media onda en la Sección 9.7.)
- Integrar\(\widetilde{I}(z)\) sobre la longitud del dipolo como se indica en la Ecuación\ ref {m0215_ele}. Luego divide (“normaliza”) por\(\widetilde{I}_1^t\) (que es simplemente\(\widetilde{I}(0)\)). Obsérvese que el resultado es independiente de la excitación\(\widetilde{I}_1^t\), como se esperaba ya que se trata de un sistema lineal.
- Multiplicar por\(\sin\theta\).
Ahora hemos determinado que el potencial terminal de circuito abierto\(\widetilde{V}_{OC}\) en respuesta a un campo eléctrico incidente\(\widetilde{\bf E}^i\) es
\[\boxed{ \widetilde{V}_{OC} = \widetilde{\bf E}^i \cdot {\bf l}_e } \label{m0215_eVOCEL} \]
donde\({\bf l}_e = \hat{\bf l} l_e\) es la longitud efectiva del vector definida previamente.
Este resultado es notable. En inglés sencillo, hemos encontrado que:
El potencial inducido en un dipolo es el componente copolarizado del campo eléctrico incidente multiplicado por una integral normalizada de la distribución de corriente de transmisión sobre la longitud del dipolo, tiempos seno del ángulo entre el eje del dipolo y la dirección de incidencia.
En otras palabras, la propiedad de reciprocidad de los sistemas lineales permite que esta propiedad de una antena receptora se determine con relativa facilidad si se conocen las características de transmisión de la antena.
A explicado en la Sección 9.5, la distribución de corriente en una ESD delgada es
\[\widetilde{I}(z) \approx I_0 \left(1-\frac{2}{L}\left|z\right|\right) \nonumber \]
donde\(L\) es la longitud del dipolo y\(I_0\) es la corriente terminal. Aplicando la Ecuación\ ref {m0215_ele}, encontramos:
\[\begin{aligned} l_e \approx & \left[ \frac{1}{I_0}\int_{-L/2}^{+L/2} I_0 \left(1-\frac{2}{L}\left|z'\right|\right) e^{+j\beta z'\cos{\theta}} dz' \right] \nonumber \\ &\cdot \sin\theta\end{aligned} \nonumber \]
Recordemos\(\beta=2\pi/\lambda\), entonces\(\beta z'=2\pi\left(z'/\lambda\right)\). Dado que se trata de un dipolo eléctricamente corto,\(z' \ll \lambda\) sobre toda la integral, y posteriormente podemos asumir\(e^{+j\beta z'\cos{\theta}}\approx 1\) sobre toda la integral. Así:
\[l_e \approx \left[ \int_{-L/2}^{+L/2} \left(1-\frac{2}{L}\left|z'\right|\right) dz' \right] \sin\theta \nonumber \]
La integral se resuelve fácilmente usando métodos estándar, o simplemente reconocer que el “área bajo la curva” en este caso es simplemente la mitad de “base” (\(L\)) por “altura” (\(1\)). De cualquier manera, encontramos
\[l_e\approx \frac{L}{2} \sin\theta \nonumber \]
El Ejemplo 10.9.1 (Sección 10.9) demuestra cómo se usa la Ecuación\ ref {M0215_evocel} con la longitud efectiva del vector determinada en el ejemplo anterior para obtener el potencial inducido.
- Además, si esto fuera cierto, entonces la antena en sí no importaría; ¡solo importaría el espaciado relativo y la orientación de los terminales de la antena! ↩