10.14: Ecuación de Transmisión Friis
- Page ID
- 83645
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Una tarea común en las aplicaciones de sistemas de radio es determinar la potencia entregada a un receptor debido a un transmisor distante. El escenario se muestra en la Figura\(\PageIndex{1}\):
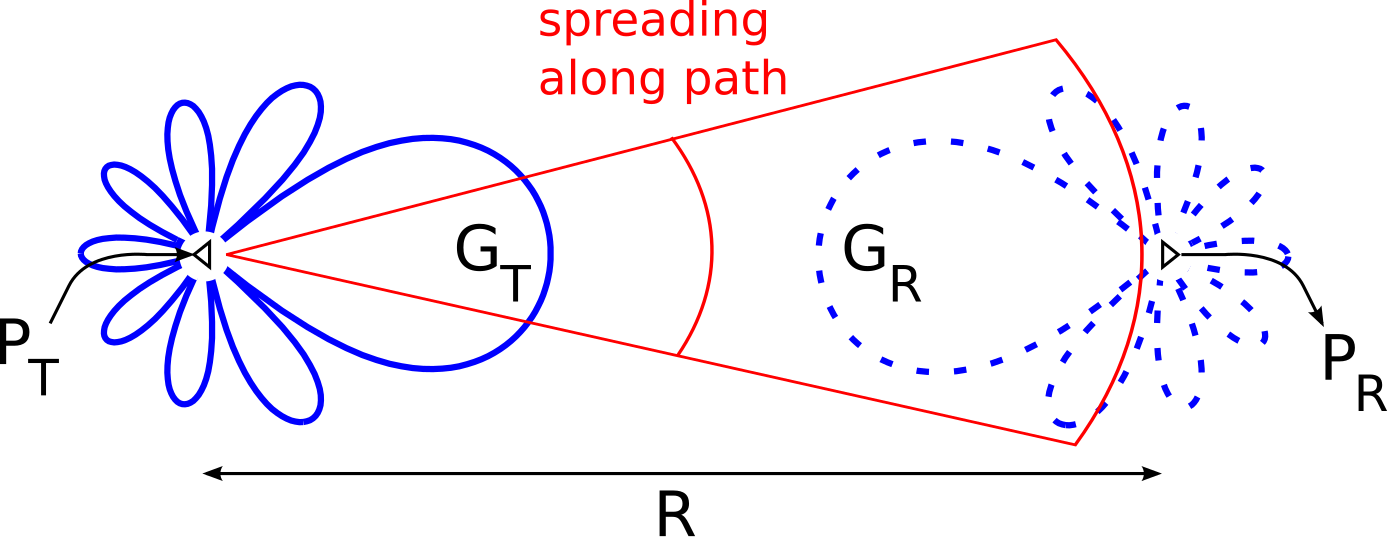
Un transmisor entrega energía\(P_T\) a una antena que tiene ganancia\(G_T\) en la dirección del receptor. La antena del receptor tiene ganancia\(G_R\). Como siempre, la ganancia de la antena es igual a los tiempos de directividad eficiencia de radiación, por lo que\(G_T\) y\(G_R\) cuenta las pérdidas internas a la antena, pero no pérdidas debidas a la falta de coincidencia de impedancia.
Una expresión simple para se\(P_R\) puede derivar de la siguiente manera. Primero, supongamos “condiciones de espacio libre”; es decir, supongamos que el terreno intermedio exhibe una absorción insignificante, reflexión u otra dispersión de la señal transmitida. En este caso, la densidad de potencia espacial en el rango\(R\) desde el transmisor que irradia esta potencia a través de una antena isotrópica y sin pérdidas sería:
\[\frac{P_T}{4\pi R^2} \nonumber \]
es decir, la potencia total transmitida dividida por el área de una esfera de radio\(R\) a través de la cual debe fluir toda la potencia. La densidad de potencia real\(S^i\) es esta cantidad multiplicada por la ganancia de la antena transmisora, es decir:
\[S^i = \frac{P_T}{4\pi R^2} G_T \nonumber \]
La potencia máxima recibida es la densidad de potencia copolarizada incidente multiplicada por la apertura efectiva\(A_e\) de la antena receptora:
\ begin {align} P_ {R, max} &= A_e S^i_ {co}\ nonumber\\ &= a_E\ frac {P_T} {4\ pi R^2} G_T\ label {M0219_EprMax1}\ end {align}
Esto supone que la antena receptora está copolarizada con el campo eléctrico incidente, y que el receptor está conjugado-emparejado con la antena. La apertura efectiva también se puede expresar en términos de la ganancia\(G_R\) de la antena receptora:
\[A_e = \frac{\lambda^2}{4\pi} G_R \nonumber \]
Así, la Ecuación\ ref {M0219_EPRmax1} puede escribirse de la siguiente forma:
\[\boxed{ P_{R,max} = P_T G_T \left(\frac{\lambda}{4\pi R}\right)^2 G_R } \label{m0219_eFTE} \]
Esta es la ecuación de transmisión de Friis. Resumiendo:
La ecuación de transmisión de Friis (Ecuación\ ref {M0219_EFTE}) da la potencia entregada a un receptor conjugado-emparejado en respuesta a un transmisor distante, asumiendo antenas copolarizadas y condiciones de espacio libre.
El factor\(\left(\lambda/4\pi R\right)^2\) que aparece en la ecuación de transmisión de Friis se conoce como ganancia de trayectoria de espacio libre. Más a menudo esto se expresa como la cantidad recíproca:
\[\boxed{ L_p \triangleq \left(\frac{\lambda}{4\pi R}\right)^{-2} } \nonumber \]
que se conoce como pérdida de trayectoria de espacio libre. Por lo tanto, la Ecuación\ ref {M0219_EFTE} puede expresarse de la siguiente manera:
\[P_{R,max} = P_T G_T L_p^{-1} G_R \label{m0219_eFTE2} \]
La utilidad del concepto de pérdida de trayectoria es que también se puede determinar para condiciones que son diferentes del espacio libre. La ecuación de transmisión de Friis todavía se aplica; uno simplemente usa el valor apropiado (y probablemente significativamente diferente) de\(L_p\).
Un concepto erróneo común es que la pérdida de ruta es igual a la reducción en la densidad de potencia debido a la propagación a lo largo de la trayectoria entre antenas, y por lo tanto esta “pérdida de propagación” aumenta con la frecuencia. De hecho, la reducción en la densidad de potencia debido a la dispersión entre dos distancias cualesquiera\(R_1 < R_2\) es:
\[\frac{P_T/4\pi R_1^2}{P_T/4\pi R_2^2} = \left(\frac{R_1}{R_2}\right)^2 \nonumber \]
que es claramente independiente de la frecuencia. La pérdida de trayectoria\(L_p\), en contraste, depende únicamente de la distancia total\(R\) y sí depende de la frecuencia. La dependencia de la frecuencia refleja la dependencia de la apertura efectiva de la longitud de onda. Por lo tanto, la pérdida de trayectoria no es pérdida en el sentido tradicional, sino que explica una combinación de propagación y la\(\lambda^2\) dependencia de apertura efectiva que es común a todas las antenas receptoras.
Finalmente, tenga en cuenta que la Ecuación\ ref {M0219_EFTE2} es meramente la forma más simple de la ecuación de transmisión de Friis. Las formas alternativas comúnmente encontradas incluyen formas en las que\(G_T\) y/o en su lugar\(G_R\) están representadas por las aberturas efectivas asociadas, y formas en las que se tienen en cuenta los efectos de la falta de coincidencia de impedancia de antena y/o polarización cruzada.
Los sistemas de telecomunicaciones terrestres suelen agregar un gran número de enlaces de comunicaciones individuales en un solo enlace de alto ancho de banda. Esto a menudo se implementa como un enlace de radio entre antenas tipo plato que tienen una ganancia de aproximadamente\(27\) dBi (eso es dB en relación con una antena isotrópica sin pérdidas) montadas en torres muy altas y operando a frecuencias alrededor de 6 GHz. Suponiendo que la potencia de recepción mínima aceptable es\(-120\) dBm (es decir\(-120\) dB en relación con 1 mW; es decir,\(10^{-15}\) W) y el rango requerido es de 30 km, ¿cuál es la potencia de transmisión mínima aceptable?
Solución
De la declaración del problema:
\[G_T=G_R=10^{27/10}\cong 501 \nonumber \]
\[\lambda =\frac{c}{f} \cong \frac{3 \times 10^8~\mbox{m/s}}{6 \times 10^9~\mbox{Hz}} \cong 5.00~\mbox{cm} \nonumber \]
\(R=30\)km, y\(P_R\ge 10^{-15}\) W. Suponemos que la altura y alta directividad de las antenas producen condiciones suficientemente cercanas al espacio libre. Además, asumimos conjugado-coincidencia en el receptor, y que las antenas están copolarizadas. Bajo estas condiciones,\(P_R=P_{R,max}\) y se aplica la Ecuación\ ref {M0219_EFTE}. Encontramos:
\[\begin{aligned} P_T &\ge \frac{ P_{R,max} }{ G_T \left(\lambda/4\pi R\right)^2 G_R } \\ &\cong 2.26 \times 10^{-7}~\mbox{W} \nonumber \\ &\cong 2.26 \times 10^{-4}~\mbox{mW} \nonumber \\ &\cong \underline{-36.5~\mbox{dBm}} \nonumber\end{aligned} \nonumber \]
Lectura adicional:
- “Pérdida de ruta de espacio libre” en Wikipedia.
- “Ecuación de transmisión de Friis” en Wikipedia.


