10.13: Apertura efectiva
- Page ID
- 83643
Cuando se trabaja con sistemas que involucran antenas receptoras, es conveniente tener un solo parámetro que relacione la potencia incidente (a diferencia del campo eléctrico incidente) con la energía entregada a la electrónica del receptor. Este parámetro se conoce comúnmente como la apertura efectiva o apertura de antena.
A partir de la teoría elemental de circuitos, la potencia entregada a una carga\(Z_L\) se maximiza cuando la carga se corresponde conjugada con la impedancia de la antena; es decir, cuándo\(Z_L=Z_A^*\) dónde\(Z_A\) está la impedancia de la antena. Por lo tanto, una definición conveniente para una apertura efectiva\(A_e\) emplea la relación:
\[P_{R,max} \triangleq S^i_{co} A_e \label{m0218_eAedef} \]
donde\(S^i_{co}\) esta la densidad de potencia incidente (unidades base SI de W/m\(^2\)) que se copolariza con la antena, y\(P_{R,max}\) es la potencia entregada a una carga que se corresponde conjugada con la impedancia de la antena. Resumiendo:
La apertura efectiva (unidades base SI de m\(^2\)) es la relación de potencia entregada por una antena a una carga conjugada conjugada, a la densidad de potencia copolarizada incidente.
Según se define, un método para el cálculo de la apertura efectiva no es obvio, excepto quizás a través de la medición directa. De hecho, hay al menos tres formas de calcular la apertura efectiva: (a) vía longitud efectiva, (b) vía termodinámica y (c) vía reciprocidad. Cada uno de estos métodos arroja cierta perspicacia y se consideran a su vez.
Apertura efectiva a través de la longitud efectiva
El potencial y la corriente a la carga de la antena receptora se pueden determinar utilizando el modelo de circuito equivalente que se muestra en la Figura\(\PageIndex{1}\), utilizando el modelo de circuito equivalente Thévenin para la antena desarrollado en la Sección 10.9.
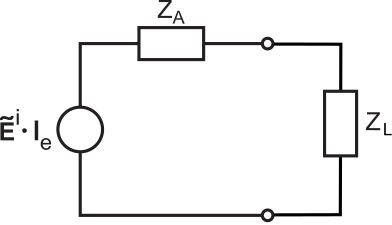
En este modelo, la fuente de voltaje está determinada por la intensidad del campo eléctrico incidente\(\widetilde{\bf E}^i\) y la longitud efectiva del vector\({\bf l_e}=\hat{\bf l}_el_e\) de la antena. Determinamos la apertura efectiva asociada de la siguiente manera. Considere una onda plana co-polarizada que varía sinusoidalmente\(\widetilde{\bf E}_{co}^i\) incidente en la antena. Además, vamos
\[\widetilde{\bf E}_{co}^i = E^i \hat{\bf e} \nonumber \]
donde\(\hat{\bf e}\) está la dirección de referencia de\(\widetilde{\bf E}_{co}^i\). La densidad de potencia copolarizada incidente en la antena es:
\[S^i_{co} = \frac{\left|E^i\right|^2}{2\eta} \label{m0218_Sico} \]
donde\(\eta\) es la impedancia de onda del medio (por ejemplo,\(\cong 377~\Omega\) para una antena en el espacio libre). En respuesta, la potencia promedio en el tiempo entregada a la carga es
\[P_R = \frac{1}{2}\mbox{Re}\left\{\widetilde{V}_L \widetilde{I}_L^*\right\} \label{m0218_ePA1} \]
donde\(\widetilde{V}_L\) y\(\widetilde{I}_L\) son los fasores potenciales y actuales, respectivamente, a la carga. Podemos determinar\(\widetilde{V}_L\) y\(\widetilde{I}_L\) a partir del modelo de circuito equivalente de la Figura\(\PageIndex{1}\) utilizando la teoría básica de circuitos. Primero, tenga en cuenta que la magnitud y fase de la fuente de voltaje es:
\[\widetilde{\bf E}_{co}^i \cdot {\bf l}_e = E^i l_e \left( \hat{\bf e} \cdot \hat{\bf l}_e \right) \nonumber \]
y como hemos definido\(\hat{\bf l}_e\) para ser iguales a\(\hat{\bf e}\),
\[\widetilde{\bf E}_{co}^i \cdot {\bf l}_e = E^i l_e \nonumber \]
A continuación, tenga en cuenta que la impedancia de carga crea un divisor de voltaje con la impedancia de fuente (antena) de tal manera que
\[\widetilde{V}_L = \left( E^i l_e \right) \frac{Z_L}{Z_A+Z_L} \nonumber \]
Del mismo modo,\(\widetilde{I}_L\) es la salida de la fuente de voltaje dividida por la resistencia total en serie:
\[\widetilde{I}_L = \frac{E^i l_e }{Z_A+Z_L} \nonumber \]
Sustituyendo estas expresiones en la Ecuación\ ref {M0218_EPA1}, obtenemos:
\[P_R = \frac{1}{2} \left|E^i l_e \right|^2 \frac{R_L}{\left|Z_A+Z_L\right|^2} \nonumber \]
Identificemos los componentes reales e imaginarios de\(Z_A\) y\(Z_L\) explícitamente, de la siguiente manera:
\[Z_A = R_A +jX_A \nonumber \]
\[Z_L = R_L +jX_L \nonumber \]
Además, supongamos que la pérdida interna a la antena es insignificante, entonces\(R_A \approx R_{rad}\). Si\(Z_L\) es conjugado emparejado para la transferencia de potencia máxima, entonces\(Z_L=Z_A^*=R_{rad}-jX_A\). Por lo tanto:
\ begin {align} P_ {R, max} &=\ frac {1} {2}\ izquierda|e^I l_e\ derecha|^2\ frac {R_ {rad}} {\ izquierda|z_a+z_a^*\ derecha|^2}\ nonumber\\ &=\ frac {1} {2}\ izquierda|E^i l_e\ derecha|^2\ frac {R_ {rad}} {\ izquierda|2R_ {rad}\ derecha|^2}\ nonumber\\ &=\ frac {\ izquierda|e^I l_e\ derecha|^2} {8R_ {rad}}\ label {M0219_prmax}\ end {align}
Ahora usando Ecuaciones\ ref {M0218_EAEdef},\ ref {M0218_SICO}, y\ ref {M0219_prmax}, encontramos:
\[A_e = \frac{\left|E^i l_e \right|^2 / 8R_{rad} }{ \left|E^i\right|^2 / 2\eta } \nonumber \]
lo que reduce a:
\[\boxed{ A_e = \frac{ \eta \left|l_e\right|^2 }{ 4 R_{rad} } } \label{m0218_eAeel} \]
No es sorprendente que la apertura efectiva deba ser proporcional al cuadrado de la magnitud de la longitud efectiva. Sin embargo, vemos que el medio y la resistencia a la radiación de la antena también juegan un papel.
La longitud efectiva y la resistencia a la radiación son fáciles de calcular para las antenas de alambre, por lo que es natural usar la Ecuación\ ref {M0218_EAEel} para calcular las aberturas efectivas de las antenas de cable. Para el dipolo eléctricamente corto (ESD) de longitud\(L\),\(l_e\approx(L/2)\sin\theta\) y\(R_{rad} \approx 20\pi^2\left(L/\lambda\right)^2\). Así, encontramos la apertura efectiva asumiendo que el espacio libre (es decir,\(\eta=\eta_0\)) es:
\[A_e \approx 0.119\lambda^2 \left|\sin\theta\right|^2 ~~~\mbox{(lossless ESD)} \nonumber \]
Sorprendentemente, la apertura efectiva de la ESD no depende de su longitud. De hecho, depende sólo de la frecuencia de operación.
También vale la pena señalar que la apertura efectiva máxima (es decir, la apertura efectiva en la\(\theta=\pi/2\) dirección) es
\[\boxed{ A_e \approx 0.119\lambda^2 } ~~~\mbox{(lossless ESD, max.)} \nonumber \]
Los dipolos que no son eléctricamente cortos exhiben resistencia a la radiación que es proporcional a\(L^p\), donde\(p>2\). Por lo tanto, la apertura efectiva de dipolos no eléctricamente cortos sí aumenta con\(L\), como se esperaba. Sin embargo, este incremento no es dramático a menos que\(L\) sea significativamente mayor que\(\lambda/2\). Aquí hay un ejemplo:
El dipolo de media onda eléctricamente delgado exhibe resistencia a la radiación\(\cong 73~\Omega\) y longitud efectiva\(\lambda/\pi\). Suponiendo que el dipolo no tiene pérdidas y está en el espacio libre, la ecuación\ ref {M0218_eaeel} produce:
\[A_e \approx 0.131\lambda^2 ~~~\mbox{(half-wave dipole, max.)} \nonumber \]
Nuevamente, esta es la apertura efectiva para una ola incidente desde el costado hacia el dipolo.
Apertura efectiva a través de termodinámica
Una visión útil del concepto de apertura efectiva se puede deducir haciendo la siguiente pregunta: ¿Cuánta potencia recibe una antena cuando llegan ondas de igual densidad de potencia desde todas las direcciones simultáneamente? Esta pregunta es sorprendentemente fácil de responder utilizando principios básicos de la termodinámica. La termodinámica es un campo de la física que aborda el calor y su relación con la radiación y la energía eléctrica. No se asume ninguna experiencia previa con la termodinámica en esta derivación.
Consideremos el escenario representado en la Figura\(\PageIndex{2}\).
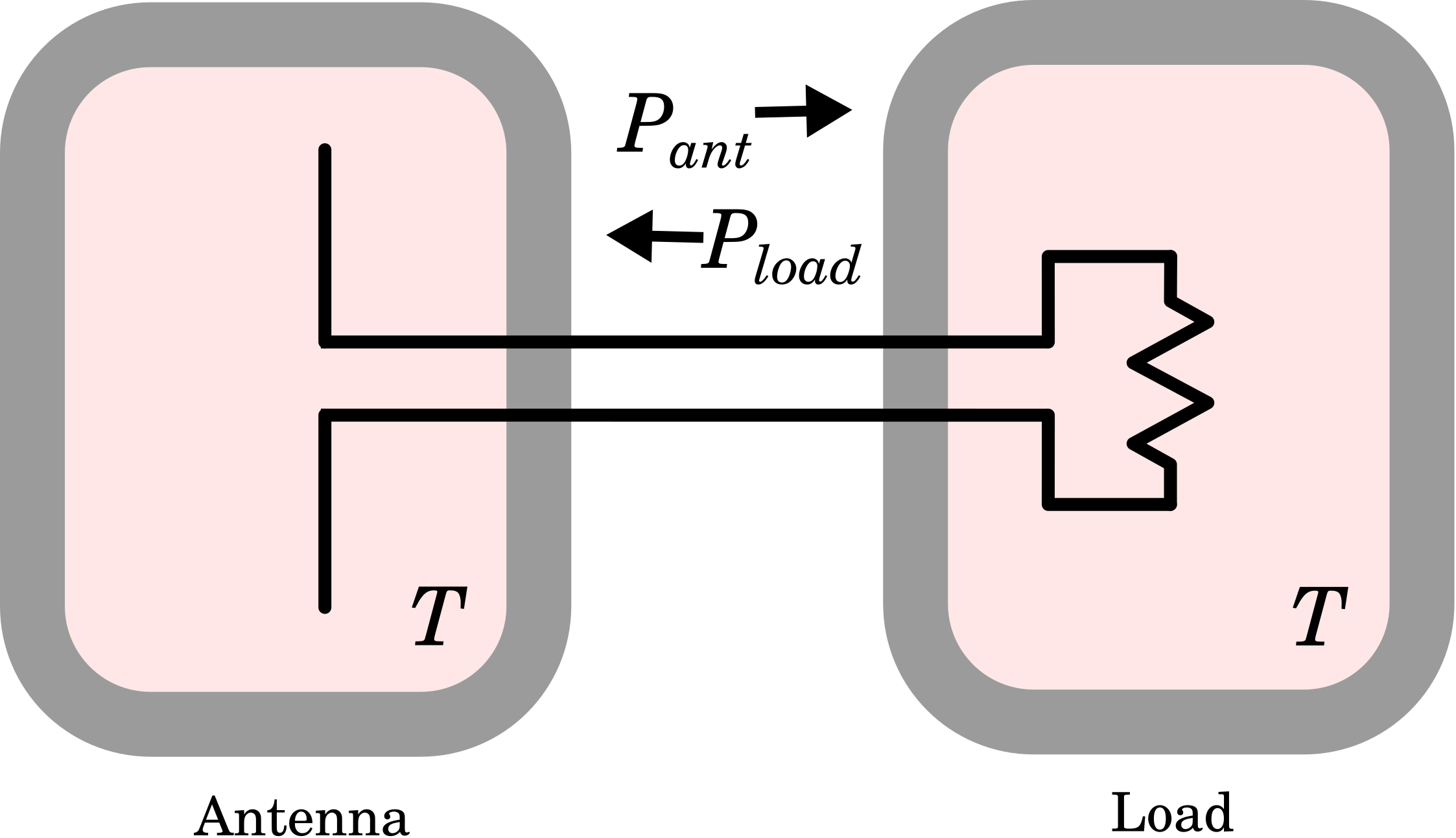
En este escenario, la antena está completamente encerrada en una cámara cuyas paredes no afectan el comportamiento de la antena y que tienen una temperatura uniforme\(T\). La carga (aún conjugada emparejada a la antena) está completamente encerrada por una cámara separada pero idéntica, también a temperatura\(T\).
Considera primero la cámara de carga. El calor provoca una aceleración aleatoria de los portadores de carga constituyentes en la carga, dando lugar a una corriente que varía aleatoriamente en los terminales de carga. (Esto se conoce como ruido Johnson-Nyquist.) Esta corriente, que fluye a través de la carga, da lugar a un potencial; por lo tanto, la carga —a pesar de ser un dispositivo pasivo— es en realidad una fuente de energía. La potencia asociada a este ruido es:
\[P_{load} = kTB \label{m0218_ePload} \]
donde\(k\cong 1.38 \times 10^{-23}\) J/K es la constante de Boltzmann y\(B\) es el ancho de banda dentro del cual\(P_{load}\) se mide.
De igual manera, la antena es una fuente de energía de ruido\(P_{ant}\). \(P_{ant}\)también puede interpretarse como radiación térmica capturada, es decir, ondas electromagnéticas estimuladas por la aceleración aleatoria de partículas cargadas que comprenden las paredes de la cámara. Estas ondas irradian desde las paredes y viajan hasta la antena. La ley Rayleigh-Jeans de la termodinámica nos dice que esta radiación debe tener una densidad de potencia (es decir, unidades base SI de W/m\(^2\)) igual a
\[\frac{2kT}{\lambda^2}~B \nonumber \]
por esteradiano de ángulo sólido. 1 La potencia total accesible a la antena es la mitad de esta cantidad, ya que una antena es sensible a una sola polarización a la vez, mientras que la radiación térmica se distribuye equitativamente entre dos polarizaciones ortogonales cualesquiera. \(P_A\)es el poder restante, obtenido integrando sobre todos los\(4\pi\) esteradianos. Por lo tanto, la antena captura una potencia total igual a 2
\ begin {align} P_ {ant} &=\ oint {a_E (\ theta',\ phi')\ izquierda (\ frac {1} {2} ~\ frac {2kT} {\ lambda^2} ~B\ derecha)\ sin\ theta' d\ theta' d\ phi'}\ nonumber\\ &=\ izquierda (\ frac {kT}\ lambda^2} ~B\ derecha)\ oint {a_E (\ theta',\ phi')\ sin\ theta' d\ theta' d\ phi'}\ etiqueta {M0218_epant}\ end {align}
Dadas las condiciones del experimento, y en particular dado que la cámara de antena y la cámara de carga están a la misma temperatura, la antena y la carga están en equilibrio termodinámico. Una consecuencia de este equilibrio es que la potencia\(P_{ant}\) capturada por la antena y entregada a la carga debe ser igual a la potencia\(P_{load}\) generada por la carga y entregada a la antena; es decir,
\[P_{ant} = P_{load} \label{m0218_eTE} \]
Combinando Ecuaciones\ ref {M0218_epload},\ ref {M0218_EPANT}, y\ ref {M0218_ETE}, obtenemos:
\[\left(\frac{kT}{\lambda^2}~B \right) \oint { A_e(\theta',\phi') \sin\theta' d\theta' d\phi' } = kTB \nonumber \]
lo que reduce a:
\[\oint { A_e(\theta',\phi') \sin\theta' d\theta' d\phi' } = \lambda^2 \label{m0218_fAT1} \]
\(\left<A_e\right>\)Sea la apertura efectiva media de la antena; es decir,\(A_e\) promediada sobre todas las direcciones posibles. Este promedio es simplemente Ecuación\ ref {M0218_FAT1} dividido por el\(4\pi\) sr de ángulo sólido que comprende todas las direcciones posibles. Así:
\[\left<A_e\right> = \frac{\lambda^2}{4\pi} \nonumber \]
Recordemos que una antena isotrópica es aquella que tiene la misma apertura efectiva en todas las direcciones. Dichas antenas no existen en la práctica, pero el concepto de antena isotrópica es bastante útil como veremos pronto. Dado que la apertura efectiva de una antena isotrópica debe ser la misma que su apertura efectiva media, encontramos:
\[\boxed{ A_e = \frac{\lambda^2}{4\pi} \approx 0.080\lambda^2 ~~~\mbox{(isotropic antenna)} } \nonumber \]
Tenga en cuenta además que este debe ser el valor mínimo posible de la apertura máxima efectiva para cualquier antena.
Apertura efectiva a través de la reciprocidad
El hecho de que todas las antenas tengan una apertura efectiva máxima mayor que la de una antena isotrópica hace de la antena isotrópica un punto de referencia lógico con el que comparar la apertura efectiva de las antenas. Podemos caracterizar la apertura efectiva de cualquier antena como una constante de valor real sin unidad\(D\) multiplicada por la apertura efectiva de una antena isotrópica; es decir:
\[\boxed{ A_e \triangleq D \frac{\lambda^2}{4\pi} ~~~\mbox{(any antenna)} } \label{m0218_eAe1} \]
donde\(D\) debe ser mayor o igual a 1.
Los lectores astutos podrían notar que se\(D\) parece mucho a la directividad. La directividad se define en la Sección 10.7 como el factor por el cual una antena transmisora aumenta la densidad de potencia de su radiación sobre la de una antena isotrópica. Consideremos una vez más la EDS, para la cual determinamos previamente (vía el concepto de longitud efectiva) aquella\(A_e\cong 0.119\lambda^2\) en la dirección en la que es máxima. Aplicando la Ecuación\ ref {M0218_EAE1} a la ESD, encontramos:
\[D \triangleq A_e \frac{4\pi}{\lambda^2} \cong 1.50 ~~~\mbox{(ESD, max.)} \nonumber \]
Efectivamente,\(D\) es igual a la directividad de la ESD en el caso de transmisión.
Este resultado resulta ser generalmente cierto; es decir:
La apertura efectiva de cualquier antena viene dada por la Ecuación\ ref {M0218_EAE1} donde\(D\) está la directividad de la antena al transmitir.
Una derivación de este resultado para el caso general es posible utilizando análisis similares a la termodinámica presentada anteriormente, o utilizando el teorema de reciprocidad desarrollado en la Sección 10.10.
El hecho de que la apertura efectiva se calcule fácilmente a partir de la directividad de transmisión es una herramienta enormemente útil en la ingeniería de antenas. Sin esta herramienta, la determinación de la apertura efectiva se limita a la medición directa o cálculo a través de la longitud efectiva; y la longitud efectiva es generalmente difícil de calcular para antenas que no están bien descritas como distribuciones de corriente a lo largo de una línea. Por lo general, es mucho más fácil calcular la directividad de una antena al transmitir, y luego usar la Ecuación\ ref {M0218_EAE1} para obtener una apertura efectiva para la operación de recepción.
Obsérvese que este principio es en sí mismo una expresión de reciprocidad. Es decir, se puede decir justamente que la “directividad” no es exclusivamente un concepto de transmisión ni un concepto de recepción, sino que es una única característica cuantificable de una antena que se aplica tanto en el caso de transmisión como en el de recepción. Recordemos que los patrones de radiación se utilizan para cuantificar la manera en que la directividad (transmitir) varía con la dirección. De pronto, ¡hemos encontrado que precisamente los mismos patrones se aplican al caso de recepción! Resumiendo:
Siempre y cuando se cumplan las condiciones requeridas para la reciprocidad formal, la directividad de una antena receptora (definida a través de la Ecuación\ ref {M0218_EAE1}) es igual a la directividad de la misma antena al transmitir, y los patrones que describen la directividad de recepción son iguales a los de la directividad de transmisión.
Por último, observamos que la equivalencia de directividad de transmisión y recepción puede, nuevamente a través de la Ecuación\ ref {M0218_EAE1}, ser utilizada para definir una apertura efectiva para el caso de transmisión. En otras palabras, podemos definir la apertura efectiva de una antena transmisora para que sea\(\lambda^2/4\pi\) veces la directividad de la antena. Aquí no hay nueva física en funcionamiento; simplemente estamos aprovechando que los conceptos de apertura efectiva y directividad describen esencialmente la misma característica de una antena, y que esta característica es la misma tanto para la operación de transmisión como de recepción.
- Divulgación completa: Esta es una aproximación a la expresión exacta, pero es muy precisa en frecuencias de radio. Consulte “Lectura adicional” al final de esta sección para obtener detalles adicionales. ↩
- La recuperación\(\sin\theta' d\theta' d\phi'\) es el elemento diferencial del ángulo sólido. ↩