2.6: Transformaciones horizontales
- Page ID
- 110843
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En la sección anterior, introdujimos el concepto de transformaciones. Hicimos un cambio a la ecuación básica y = f (x), como y = af (x), y = −f (x), y = f (x) − c, o y = f (x) + c, luego estudiamos cómo estos cambios afectaban la forma de la gráfica de y = f (x). En esa sección, nos concentramos estrictamente en las transformaciones que se aplicaban en la dirección vertical. En esta sección, estudiaremos las transformaciones que afectarán la forma de la gráfica en la dirección horizontal.
Comenzamos nuestra tarea con un ejemplo que requiere que leamos la gráfica de una función para capturar varios puntos clave que se encuentran en la gráfica de la función.
Ejemplo\(\PageIndex{1}\)
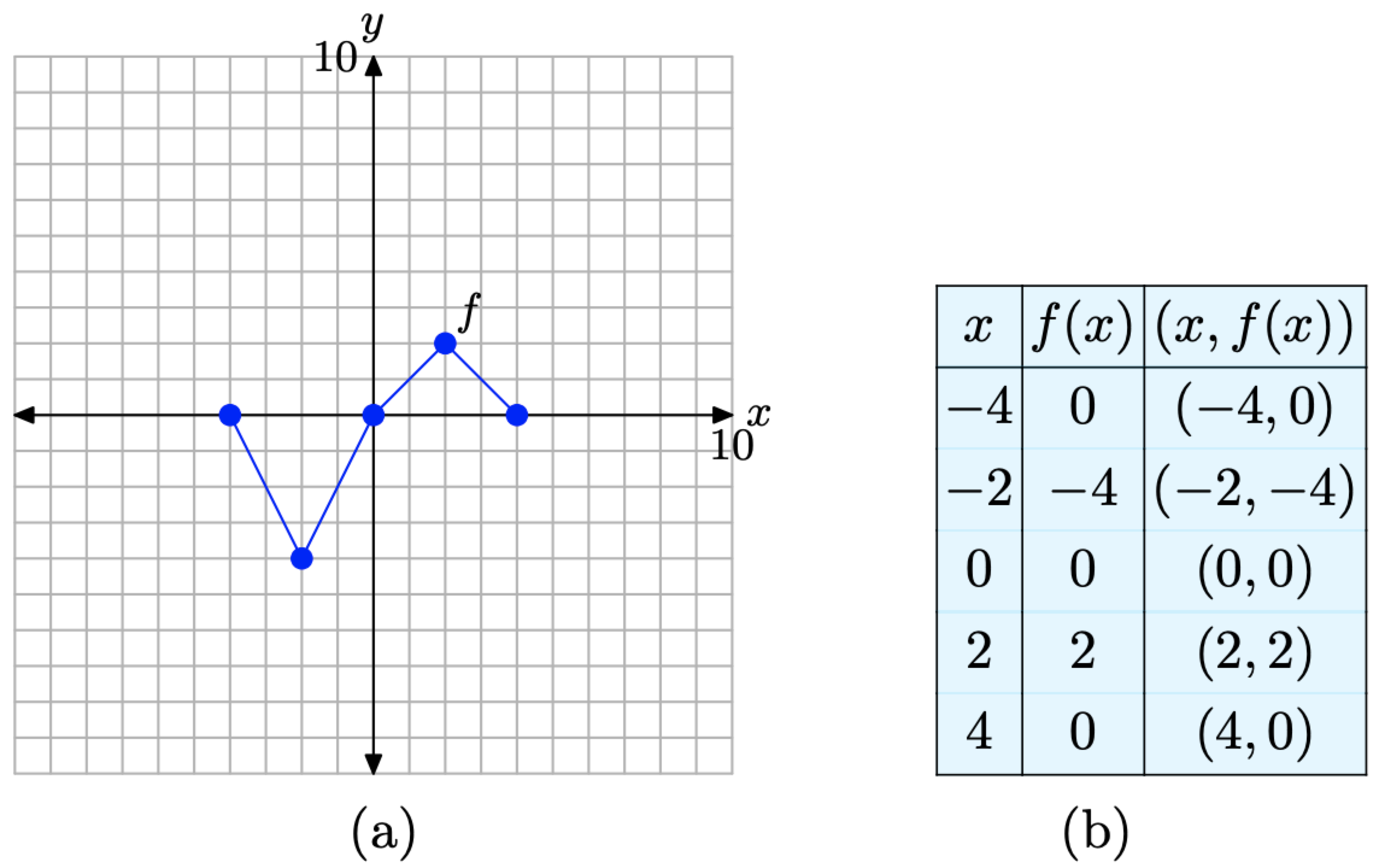
Considera la gráfica de f presentada en la Figura\(\PageIndex{1}\) (a). Utilice la gráfica de f para completar la tabla de la Figura\(\PageIndex{1}\) (b).
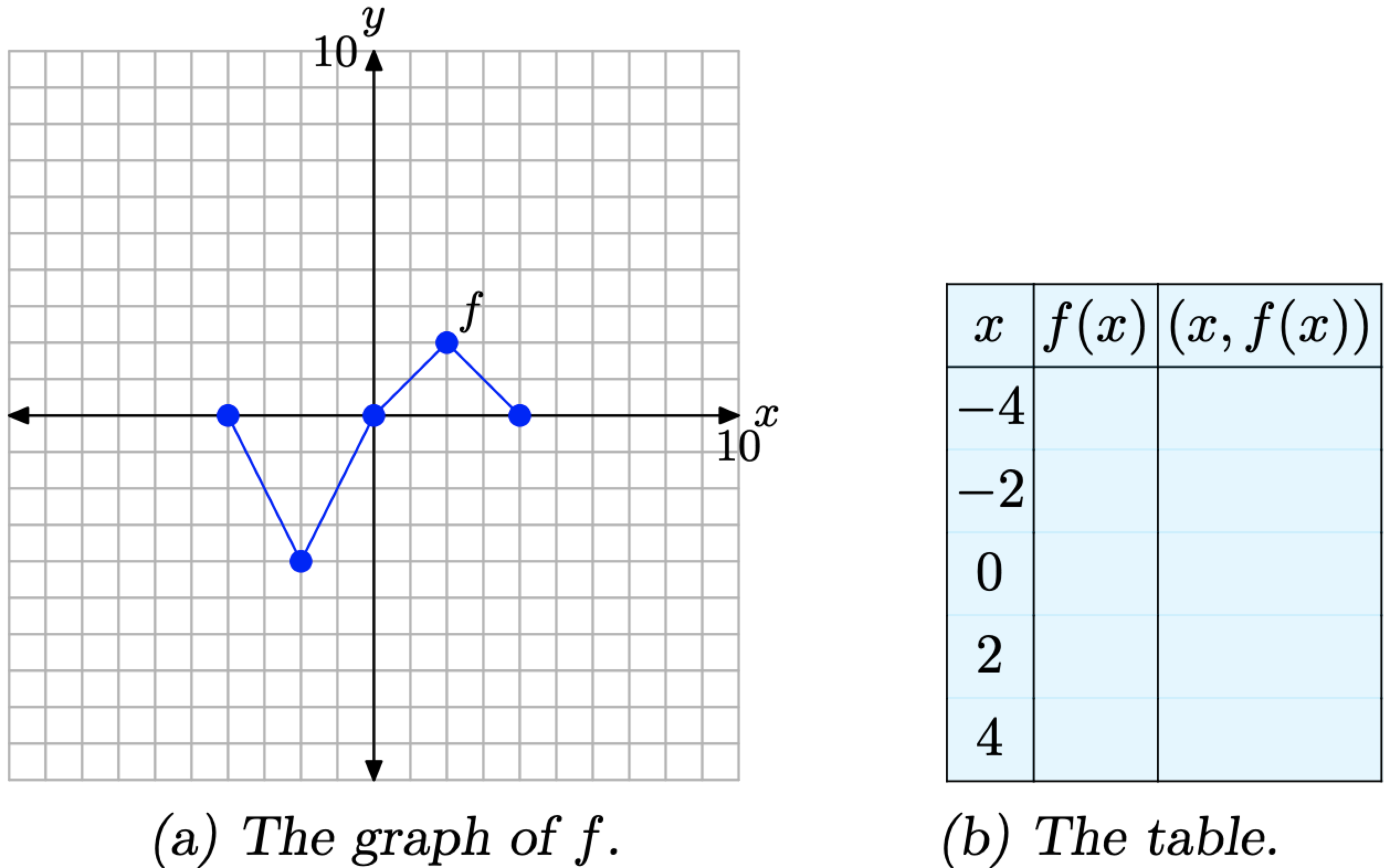
Figura\(\PageIndex{1}\). Lectura de valores clave de la gráfica de f.
Solución
Para calcular f (−2), por ejemplo, primero ubicaríamos −2 en el eje x, dibujaríamos una flecha vertical a la gráfica de f, luego una flecha horizontal al eje y, como se muestra en la Figura\(\PageIndex{2}\) (a). El valor y de este destino final es el valor de f (−2). Es decir, f (−2) = −4. Esto nos permite completar una entrada en la tabla, como se muestra en la Figura\(\PageIndex{2}\) (b). Continuar de esta manera para completar todas las entradas en la tabla. El resultado se muestra en la Figura\(\PageIndex{2}\) (c).
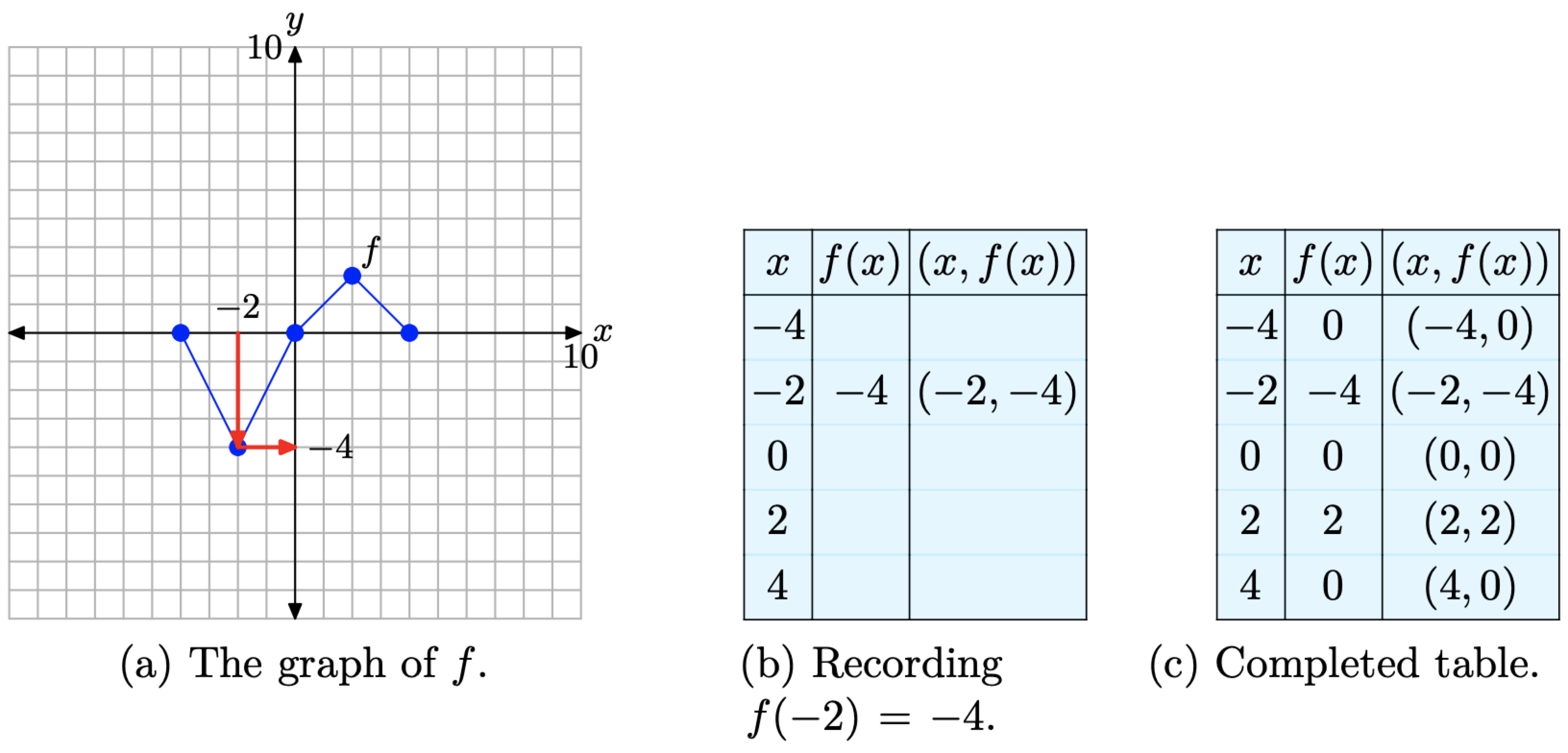
Figura\(\PageIndex{2}\). Grabación de coordenadas de puntos en la gráfica de f en las tablas
Escalado Horizontal
En la narrativa que sigue, tendremos necesidad repetida de la gráfica en la Figura\(\PageIndex{2}\) (a) y la tabla en la Figura\(\PageIndex{2}\) (c). Caracterizan la función básica que será el punto de partida para los conceptos de escalado, reflexión y traducción que desarrollamos en esta sección. En consecuencia, coloquemos uno al lado del otro para enfatizarlos en la Figura\(\PageIndex{3}\).
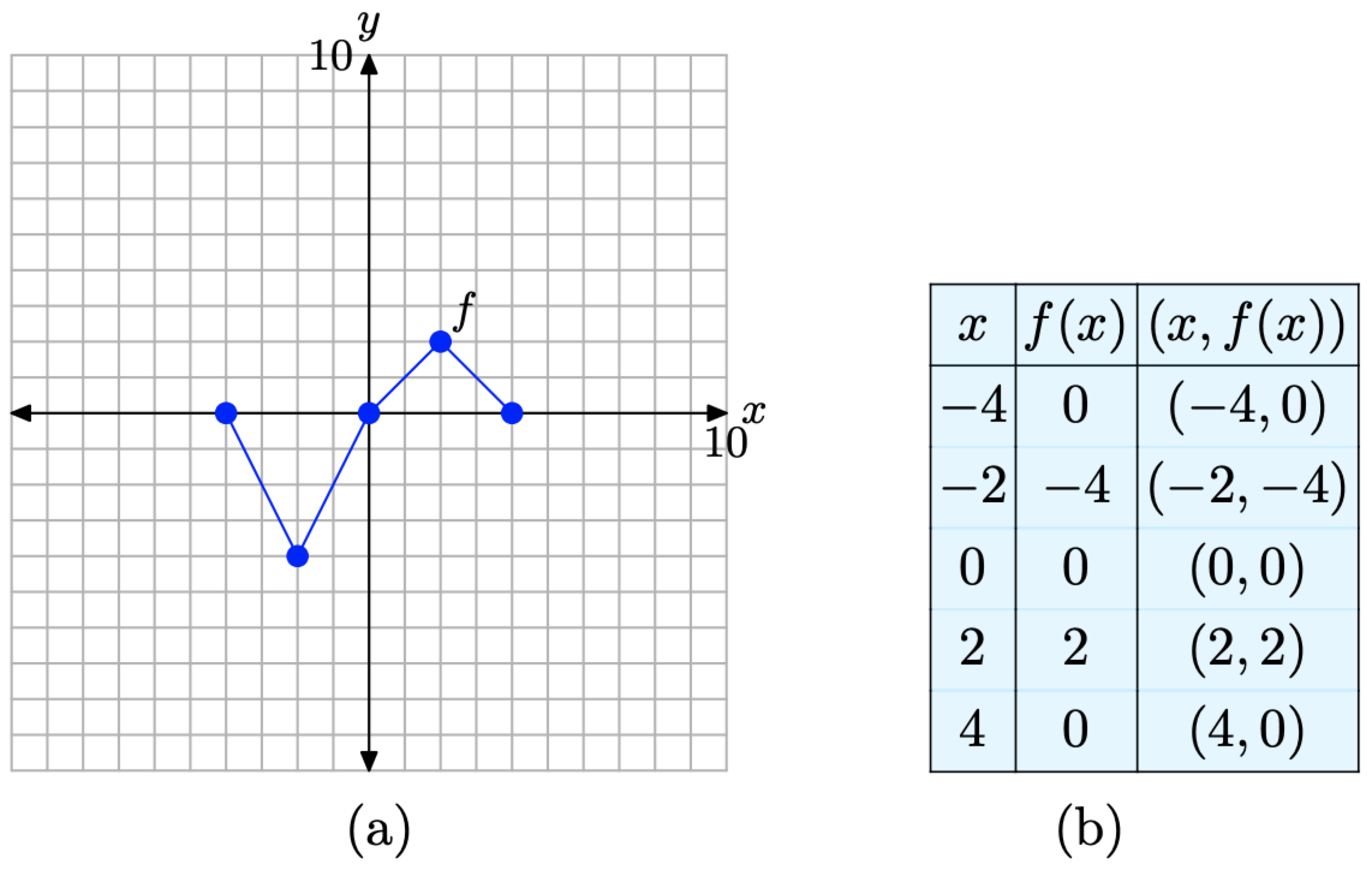
Figura\(\PageIndex{3}\). La gráfica original de f y una tabla de puntos clave en la gráfica de f
Ahora vamos a escalar la gráfica de f en la dirección horizontal.
Ejemplo\(\PageIndex{2}\)
Si y = f (x) tiene la gráfica mostrada en la Figura\(\PageIndex{3}\) (a), esboce la gráfica de y = f (2x).
Solución
En la sección anterior, se investigó la gráfica de y = 2f (x). El número 2 estaba fuera de la notación de función y como resultado estiramos la gráfica de y = f (x) verticalmente por un factor de 2. Sin embargo, tenga en cuenta que el 2 ahora está dentro de la notación de función y = f (2x). La intuición exigiría que esto pudiera tener algo que ver con el escalado en la dirección x (dirección horizontal), pero ¿cómo?
Nuevamente, cuando no estamos seguros de la forma de la gráfica, confiamos en trazar una tabla de puntos. Comenzamos escogiendo estos valores x: x = −2, −1, 0, 1 y 2. Obsérvese que estos son precisamente la mitad de cada uno de los valores x presentados en la tabla de la Figura\(\PageIndex{3}\) (b). Ahora evaluaremos la función y = f (2x) en cada uno de estos valores x. Por ejemplo, para calcular y = f (2x) en x = −2, primero insertamos x = −2 para x para obtener\[y=f(2(-2))=f(-4)\]
Para completar el cálculo, ahora debemos evaluar f (−4). Sin embargo, este resultado se registra en la tabla de la Figura\(\PageIndex{3}\) (b). Ahí encontramos que f (−4) = 0, y podemos completar el cómputo iniciado anteriormente.
\[y=f(2(-2))=f(-4)=0\]
De manera similar, para evaluar la función y = f (2x) a x = −1, primero sustituya x = −1 en y = f (2x) para obtener
\[y=f(2(-1))=f(-2)\]
Ahora, tenga en cuenta que f (−2) es el siguiente valor registrado en la tabla de la Figura\(\PageIndex{3}\) (b). Ahí encontramos que f (−2) = −4, así podemos completar el cómputo iniciado anteriormente.
\[y=f(2(-1))=f(-2)=-4\]
En este punto, es posible que veas por qué elegimos los valores x: −2, −1, 0, 1 y 2. Estos son precisamente la mitad de los valores x en la tabla de valores originales para la función y = f (x) en la Figura\(\PageIndex{3}\) (b). Cuando los valores −2, −1, 0, 1 y 2 se sustituyen en la función y = f (2x), primero se duplican antes de ir a buscar el valor de la función en la tabla de la Figura\(\PageIndex{3}\) (b).
Continuando de esta manera, evaluamos la función y = f (2x) en los valores restantes de x, es decir, 0, 1 y 2.
\[\begin{aligned} y &=f(2(0))=f(0)=0 \\ y &=f(2(1))=f(2)=2 \\ y &=f(2(2))=f(4)=0 \end{aligned}\]
Ingresamos estos valores en la tabla de la Figura 4 (b) y los trazamos para determinar la gráfica de y = f (2x) en la Figura\(\PageIndex{4}\) (a).
En este punto, hay una serie de comparaciones que puedes hacer.
1. Comparar los datos de la tabla de la Figura\(\PageIndex{4}\) (b) con los datos de función originales en la tabla de la Figura\(\PageIndex{3}\) (b). Tenga en cuenta que los valores y en cada tabla son idénticos. Sin embargo, tenga en cuenta que cada valor x en la tabla de la Figura\(\PageIndex{4}\) (b) es precisamente la mitad del valor x correspondiente en la tabla de la Figura\(\PageIndex{3}\) (b).
2. Compare la gráfica de y = f (2x) en la Figura\(\PageIndex{4}\) (a) con la gráfica original de y = f (x) en la Figura\(\PageIndex{3}\) (a). Tenga en cuenta que cada valor x en cada punto de la gráfica de y = f (2x) en
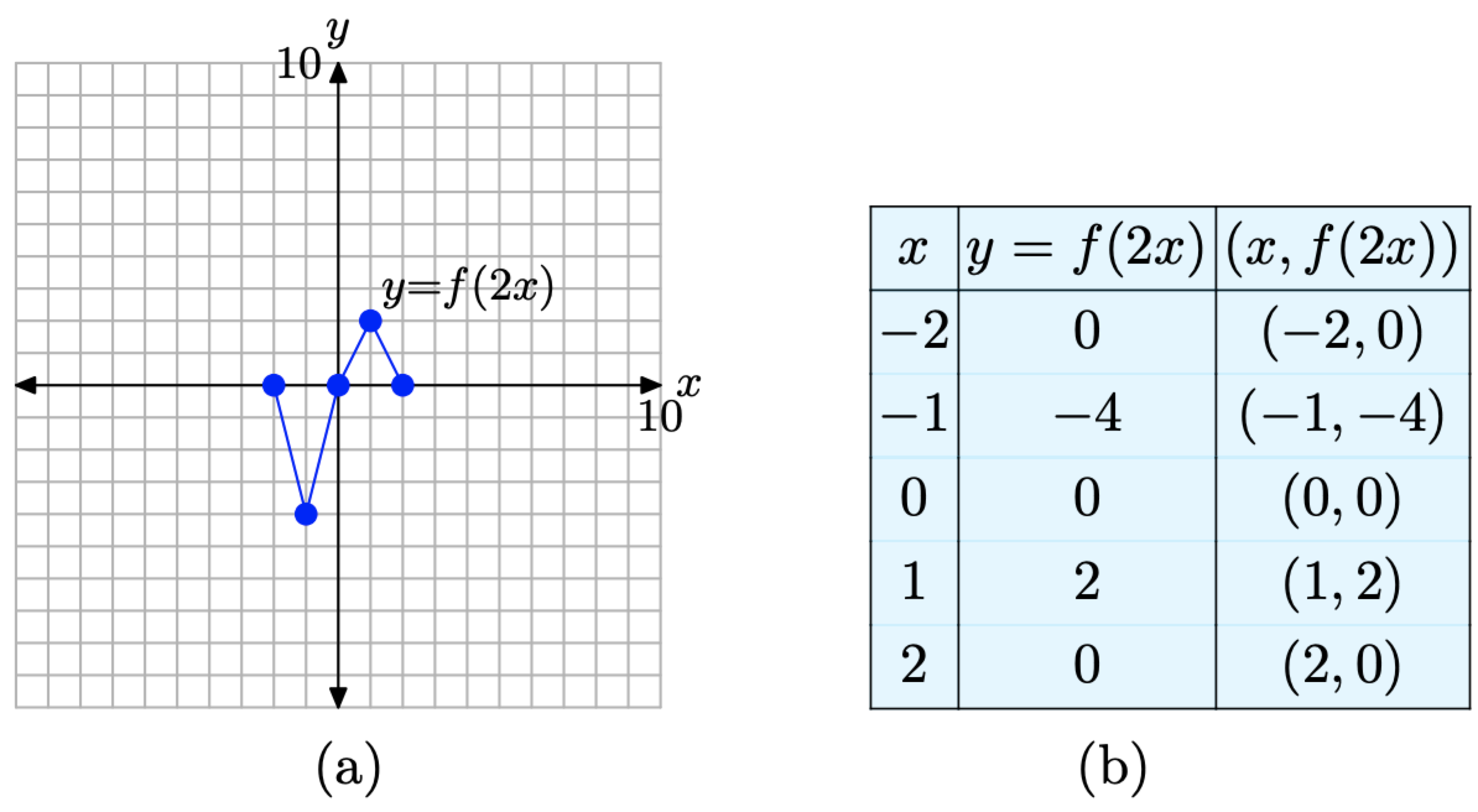
Figura\(\PageIndex{4}\). Los puntos en la tabla son puntos en la gráfica de y = f (2x).
La Figura\(\PageIndex{4}\) (a) es precisamente la mitad del valor x del punto correspondiente en la gráfica de y = f (x) en la Figura\(\PageIndex{3}\) (a).
Anote el resultado. La gráfica de y = f (2x) se comprime horizontalmente (hacia el eje y), tanto positiva como negativamente, por un factor de 2. Tenga en cuenta que esto es exactamente lo contrario de lo que podría esperar por intuición, pero un examen cuidadoso de los datos en las tablas de las Figuras\(\PageIndex{3}\) (b) y\(\PageIndex{4}\) (b) explicará por qué.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{3}\)
Si y = f (x) tiene la gráfica mostrada en la Figura\(\PageIndex{3}\) (a), esboce la gráfica de y = f ((1/2) x).
Solución
En lugar de duplicar cada valor de x al inicio, esta función primero reduce a la mitad cada valor de x Por lo tanto, vamos a querer evaluar la función y = f ((1/2) x) en x = −8, −4, 0, 4 y 8. Por ejemplo, para evaluar la función y = f ((1/2) x) a x = −8, primero sustituya x = −8 para obtener\[y=f((1 / 2)(-8))=f(-4)\]
Ahora, busque este valor en la tabla de la Figura\(\PageIndex{3}\) (b) y observe que f (−4) = 0. Así, podemos completar el cómputo de la siguiente manera.
\[y=f((1 / 2)(-8))=f(-4)=0\]
Del mismo modo, para evaluar la función y = f ((1/2) x) a x = −4, primero sustituya x = −4 para obtener
\[y=f((1 / 2)(-4))=f(-2)\]
Ahora, busque este valor en la tabla de la Figura\(\PageIndex{3}\) (b) y observe que f (−2) = −4. Así, podemos completar el cómputo de la siguiente manera.
\[y=f((1 / 2)(-4))=f(-2)=-4\]
En este punto, verá por qué elegimos los valores x: −8, −4, 0, 4 y 8. Estos valores son precisamente el doble de los valores x en la tabla de valores originales para la función y = f (x) en la Figura\(\PageIndex{3}\) (b). Cuando los valores −8, −4, 0, 4 y 8 se sustituyen en la función y = f ((1/2) x), primero se reducen a la mitad antes de ir a buscar el valor de la función en la tabla de la Figura\(\PageIndex{3}\) (b). Esta reducción a la mitad conduce a los valores −4, −2, 0, 2 y 4, que son precisamente los valores disponibles en la tabla de la Figura\(\PageIndex{3}\) (b).
Hacemos cálculos similares en los valores restantes de x, es decir, x = 0, 4 y 8.
\[\begin{aligned} y &=f((1 / 2)(0))=f(0)=0 \\ y &=f((1 / 2)(4))=f(2)=2 \\ y &=f((1 / 2)(8))=f(4)=0 \end{aligned}\]
Esperemos que estos cálculos expliquen nuestra elección de los valores x anteriores. Cada uno de estos resultados se registra en la tabla de la Figura\(\PageIndex{5}\) (b) y se grafica en la gráfica mostrada en la Figura\(\PageIndex{5}\) (a).
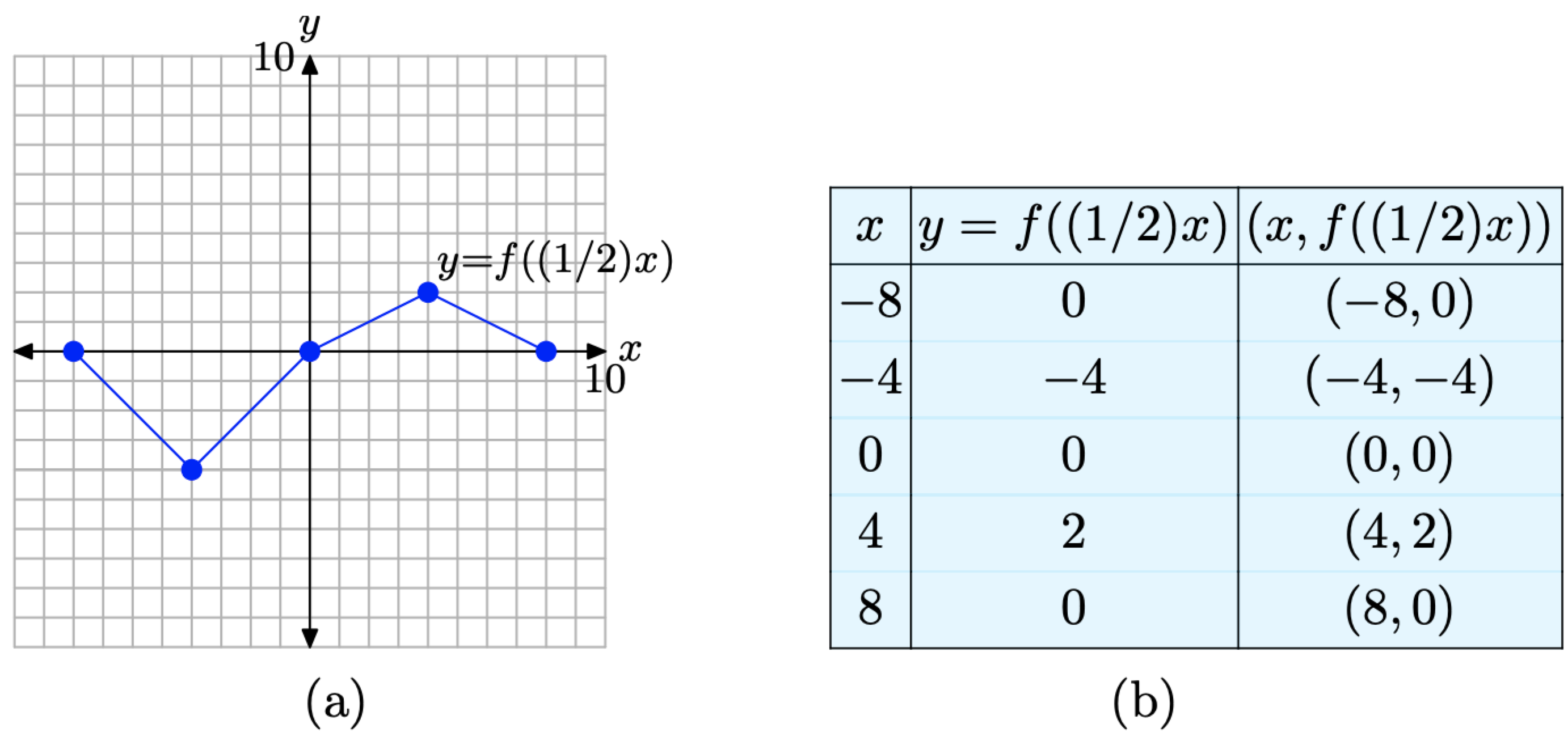
Figura\(\PageIndex{5}\). Los puntos en la tabla son puntos en la gráfica de y = f ((1/2) x).
Nuevamente, tenga en cuenta que los valores y en la tabla de la Figura\(\PageIndex{5}\) (b) son idénticos a los valores y en la tabla de la Figura\(\PageIndex{3}\) (b). Sin embargo, cada valor x en la tabla de la Figura\(\PageIndex{5}\) (b) es precisamente el doble del valor x correspondiente en la tabla de la Figura\(\PageIndex{3}\) (b).
Esta duplicación de los valores x es evidente en la gráfica de y = f ((1/2) x) mostrada en la Figura\(\PageIndex{5}\) (a), donde la gráfica se estira en un factor de 2 horizontalmente (alejándose del eje y), tanto positiva como negativamente. Tenga en cuenta que esto es exactamente lo contrario de lo que podría esperar por intuición, pero un examen cuidadoso de los datos en las tablas de las Figuras\(\PageIndex{3}\) (b) y\(\PageIndex{5}\) (b) explicará por qué.
Resumimos nuestros hallazgos.
Un resumen visual: escalado horizontal
Considera las imágenes en la Figura\(\PageIndex{6}\).
- En la Figura\(\PageIndex{6}\) (a), vemos representado el gráfico de la función original y = f (x).
- En la Figura\(\PageIndex{6}\) (b), observe que cada punto clave en la gráfica de y = f (2x) tiene un valor x que es precisamente la mitad del valor x del punto correspondiente en la gráfica de y = f (x) en la Figura\(\PageIndex{6}\) (a).
- En la Figura\(\PageIndex{6}\) (c), nótese que cada punto clave en la gráfica de y = f ((1/2) x) tiene un valor x que es el doble del valor x del punto correspondiente en la gráfica de y = f (x) en la Figura\(\PageIndex{6}\) (a).
- Tenga en cuenta que el valor y de cada punto transformado sigue siendo el mismo.
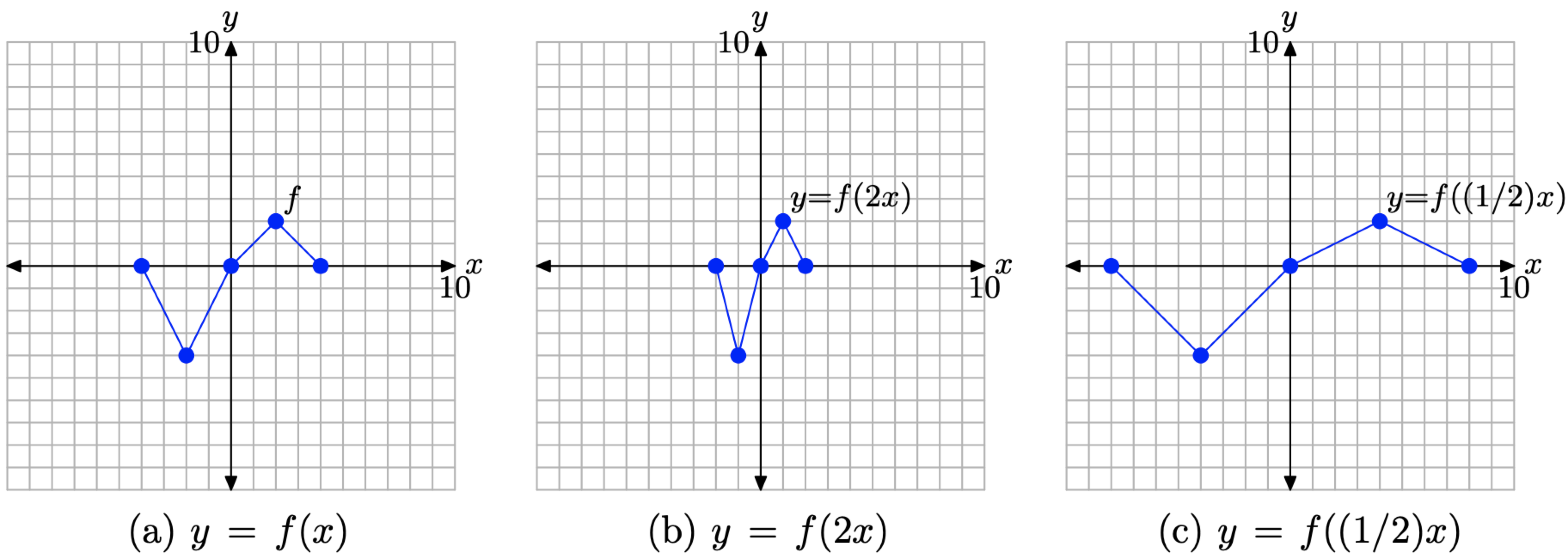
Figura\(\PageIndex{6}\). La gráfica de y = f (2x) comprime horizontalmente (hacia el eje y) por un factor de 2. La gráfica de y = f ((1/2) x) se estira horizontalmente (alejándose del eje y) por un factor de 2.
El resumen visual en Figura\(\PageIndex{6}\) hace que el bosquejo de las gráficas de y = f (2x) e y = f (1/2) x) sea una tarea fácil.
- Dada la gráfica de y = f (x), para bosquejar la gráfica de y = f (2x), simplemente tome cada punto de la gráfica de y = f (x) y corte su valor x a la mitad, manteniendo el mismo valor y.
- Dada la gráfica de y = f (x), para bosquejar la gráfica de y = f ((1/2) x), simplemente tome cada punto de la gráfica de y = f (x) y duplique su valor x, manteniendo el mismo valor y.
Siga los mismos procedimientos para otros factores de escalado. Por ejemplo, en el caso de y = f (3x), tomar cada punto de la gráfica de y = f (x) y dividir su valor x por 3, manteniendo el mismo valor y. Por otro lado, para dibujar la gráfica de y = f ((1/3) x), tomar cada punto de la gráfica de f y multiplicar su valor x por 3, manteniendo el mismo valor y.
En general, podemos exponer lo siguiente.
resumen
Supongamos que se nos da la gráfica de y = f (x).
- Si a > 1, la gráfica de y = f (ax) comprime horizontalmente (hacia el eje y), tanto positiva como negativamente, por un factor de a.
- Si 0 < a < 1, la gráfica de y = f (ax) se estira horizontalmente (alejándose del eje y), tanto positiva como negativamente, por un factor de 1/a.
En el caso del primer ítem en Resumen, cuando comparamos la forma general y = f (ax) con y = f (2x), vemos que a = 2. En este caso, tenga en cuenta que a > 1 y la gráfica de y = f (2x) se comprime horizontalmente por un factor de 2 cuando se compara con la gráfica de y = f (x) (ver Figura\(\PageIndex{6}\) (b)).
En el caso del segundo ítem en Resumen, cuando comparamos la forma general y = f (ax) con la ecuación y = f ((1/2) x), vemos que a = 1/2, entonces
\[\frac{1}{a}=\frac{1}{1 / 2}=2\]
El segundo ítem del Resumen 4 dice que cuando 0 < a < 1, la gráfica de y = f (ax) se estira horizontalmente por un factor de 1/a De hecho, esto es exactamente lo que sucedió en el caso de y = f ((1/2) x), que se estiró en la dirección horizontal por un factor de 1/ (1/2), o 2 (ver Figura\(\PageIndex{6}\) (c)).
Reflexiones horizontales
Por conveniencia, comenzamos repitiendo la gráfica original de y = f (x) y sus datos acompañantes en la Figura\(\PageIndex{7}\). Ahora vamos a reflejar la gráfica de y = f (x) en la dirección horizontal (a través del eje y).
Figura\(\PageIndex{7}\). La gráfica original de f y una tabla de puntos clave en la gráfica de f
Ejemplo\(\PageIndex{4}\)
Si y = f (x) tiene la gráfica mostrada en la Figura\(\PageIndex{7}\) (a), dibuje la gráfica de y = f (−x).
Solución
En la sección anterior, se nos pidió dibujar la gráfica de y = −f (x). Observe cómo aparece el signo menos en el exterior de la función. Claramente, los valores y de y = −f (x) deben ser opuestos en signo a los valores y de y = f (x). Es por ello que la gráfica de y = −f (x) fue un reflejo de la gráfica de y = f (x) a través del eje x.
Sin embargo, en este ejemplo, el signo menos está dentro de la función, dejando uno para intuir que son los valores x, no los valores y, los que están siendo negados. Escogeremos los siguientes valores x: x = 4, 2, 0, −2 y −4. Esto es un poco engañoso, ya que parece que estamos eligiendo los mismos valores x, solo en orden inverso. Este no es el caso. Estamos eligiendo el negativo de cada valor x en la tabla de la Figura\(\PageIndex{7}\) (b).
Para evaluar y = f (−x) en nuestro primer valor x, concretamente x = 4, realizamos el siguiente cálculo. Primer sustituto x = 4 para obtener
\[y=f(-(4))=f(-4)\]
Ahora, busque este valor en la tabla de la Figura\(\PageIndex{7}\) (b) y observe que f (−4) = 0. Así, podemos completar el cómputo de la siguiente manera.
\[y=f(-(4))=f(-4)=0\]
Del mismo modo, para evaluar la función y = f (−x) a x = 2, primero sustituya x = 2 para obtener
\[y=f(-(2))=f(-2)\]
Ahora, busque este valor en la tabla de la Figura\(\PageIndex{7}\) (b) y observe que f (−2) = −4. Así, podemos completar el cómputo de la siguiente manera.
\[y=f(-(2))=f(-2)=-4\]
En este punto, verá por qué elegimos los valores x: 4, 2, 0, −2 y −4. Estos valores son los negativos de los valores x en la tabla de valores originales para la función y = f (x) en la Figura\(\PageIndex{7}\) (b). Cuando los valores 4, 2, 0, −2 y −4 se sustituyen en la función y = f (−x), primero se anulan antes de ir a buscar el valor de la función en la tabla de la Figura\(\PageIndex{7}\) (b). Esta negación conduce a los valores −4, −2, 0, 2 y 4, que son precisamente los valores disponibles en la tabla de la Figura\(\PageIndex{7}\) (b).
Hacemos cálculos similares en los valores restantes de x, es decir, x = 0, −2 y −4.
\[\begin{array}{l}{y=f(-(0))=f(0)=0} \\ {y=f(-(-2))=f(2)=2} \\ {y=f(-(-4))=f(4)=0}\end{array}\]
Organizamos estos puntos en la tabla de la Figura\(\PageIndex{8}\) (b), luego los trazamos en la Figura\(\PageIndex{8}\) (a).
Cuando compare las entradas de la tabla de la Figura\(\PageIndex{8}\) (b) con las de la tabla de la Figura\(\PageIndex{7}\) (b), tenga en cuenta que los valores y aparecen en el mismo orden, pero los valores x de la tabla en la Figura\(\PageIndex{7}\) (b) han sido negados en la tabla de la Figura\(\PageIndex{8}\) (b). Esto significa que un punto anterior como (−2, −4) se transforma en el punto (2, −4), que es una reflexión del punto (−2, −4) a través del eje y.
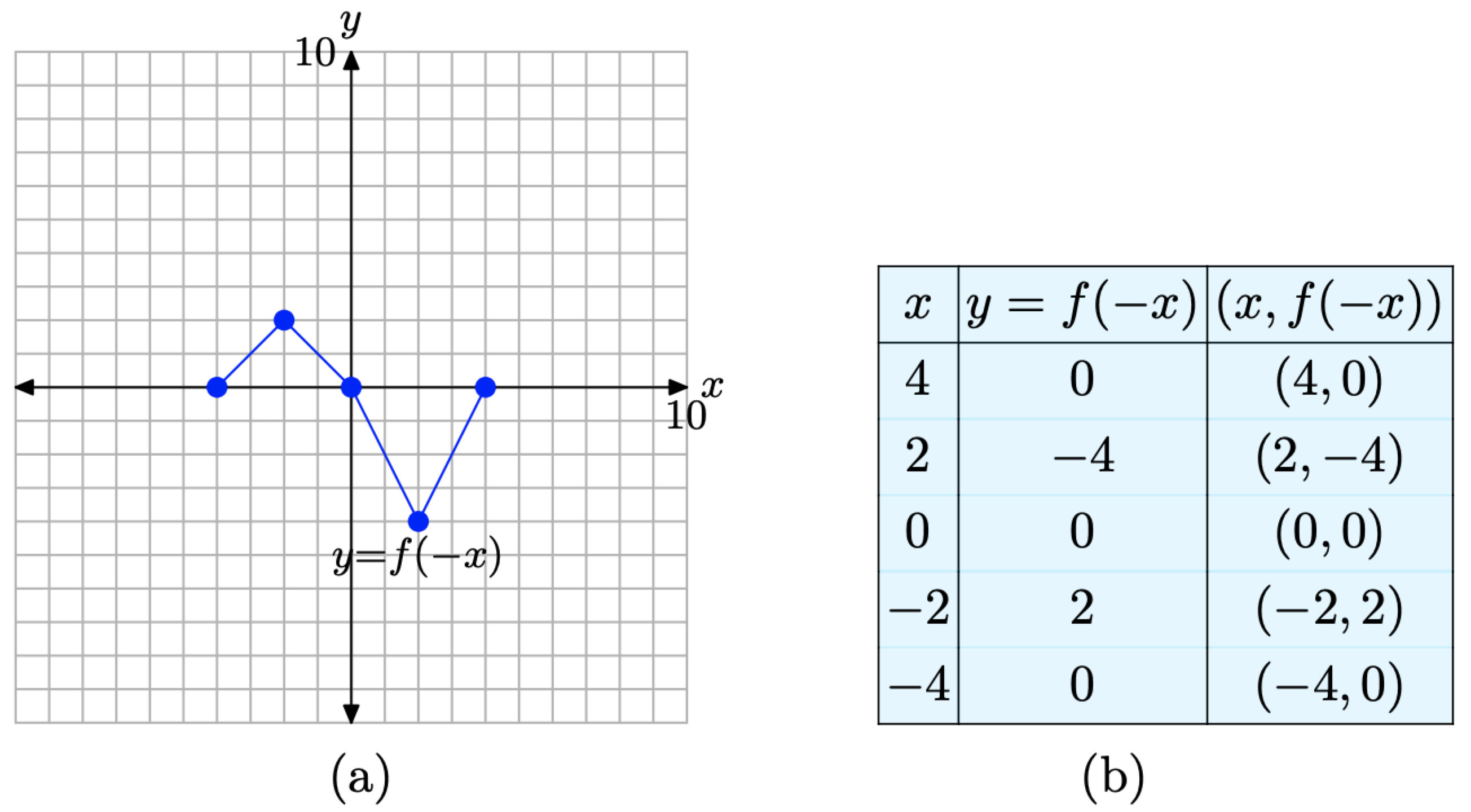
Figura\(\PageIndex{8}\). La gráfica de y = f (−x) y una tabla de puntos clave en la gráfica.
Así, para producir la gráfica de y = f (−x), simplemente refleje la gráfica de y = f (x) a través del eje y.
Resumimos lo que hemos aprendido sobre las reflexiones horizontales.
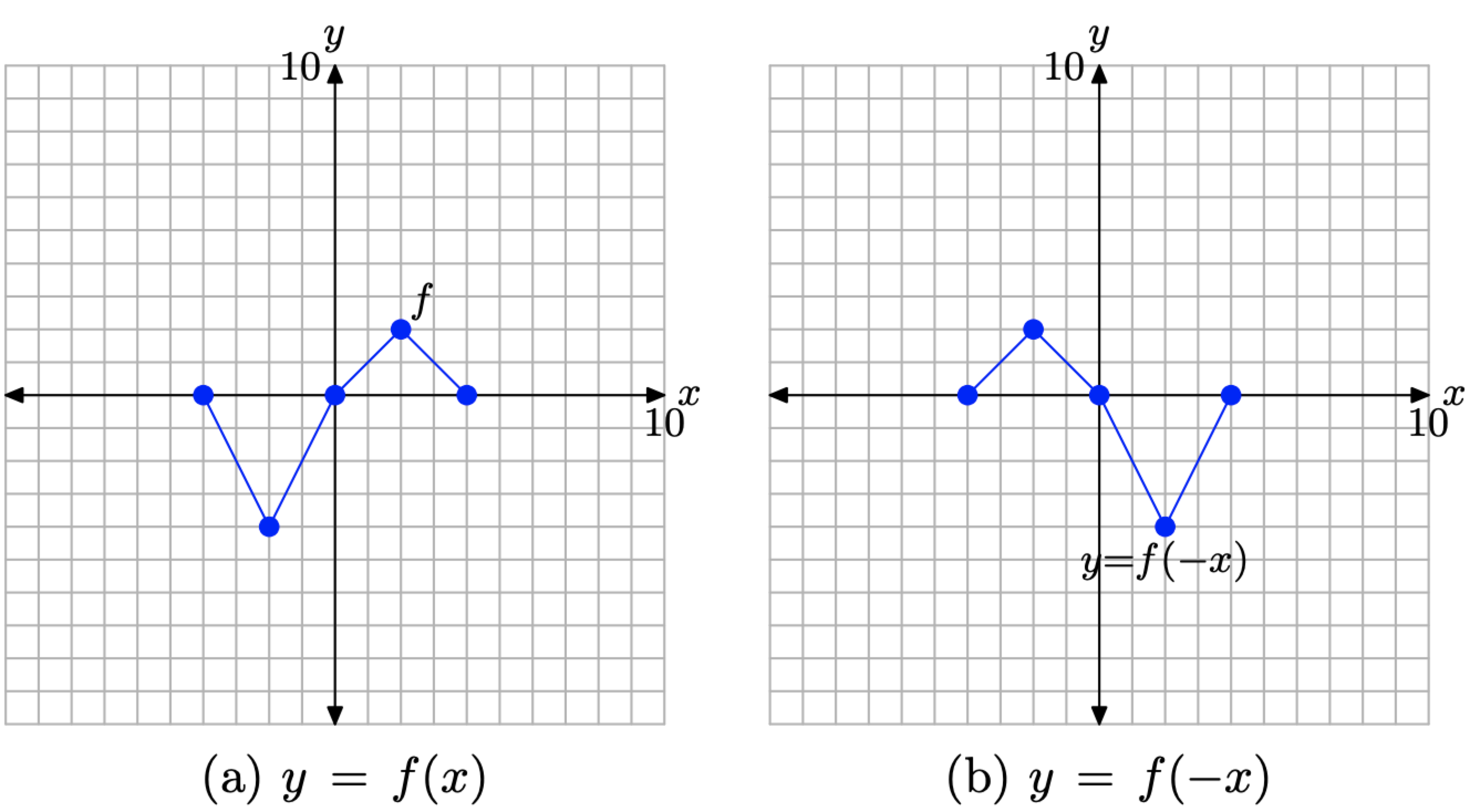
Figura\(\PageIndex{9}\). La gráfica de y = f (−x) es un reflejo de la gráfica de y = f (x) a través del eje y.
Un resumen visual — Reflexiones horizontales
Considera las imágenes en la Figura\(\PageIndex{9}\).
- En la Figura\(\PageIndex{9}\) (a), vemos en la imagen la gráfica original de y = f (x).
- En la Figura\(\PageIndex{9}\) (b), la gráfica de y = f (−x) es un reflejo de la gráfica de y = f (x) a través del eje y.
Así, dada la gráfica de y = f (x), es una tarea sencilla dibujar la gráfica de y = f (−x).
- Para dibujar la gráfica de y = f (−x), toma cada punto de la gráfica de y = f (x) y reflejarla a través del eje y, manteniendo el valor y igual, pero negando el valor x.
Traducciones Horizontales
En la sección anterior, vimos que las gráficas de y = f (x) + c e y = f (x) − c eran traducciones verticales de la gráfica de y = f (x). Si c es un número positivo, entonces la gráfica de y = f (x) + c desplaza c unidades hacia arriba mientras que la gráfica de y = f (x) − c desplaza c unidades hacia abajo.
En esta sección, estudiaremos las traducciones horizontales. Por conveniencia, comenzamos repitiendo la gráfica original de y = f (x) y sus datos acompañantes en la Figura 10.
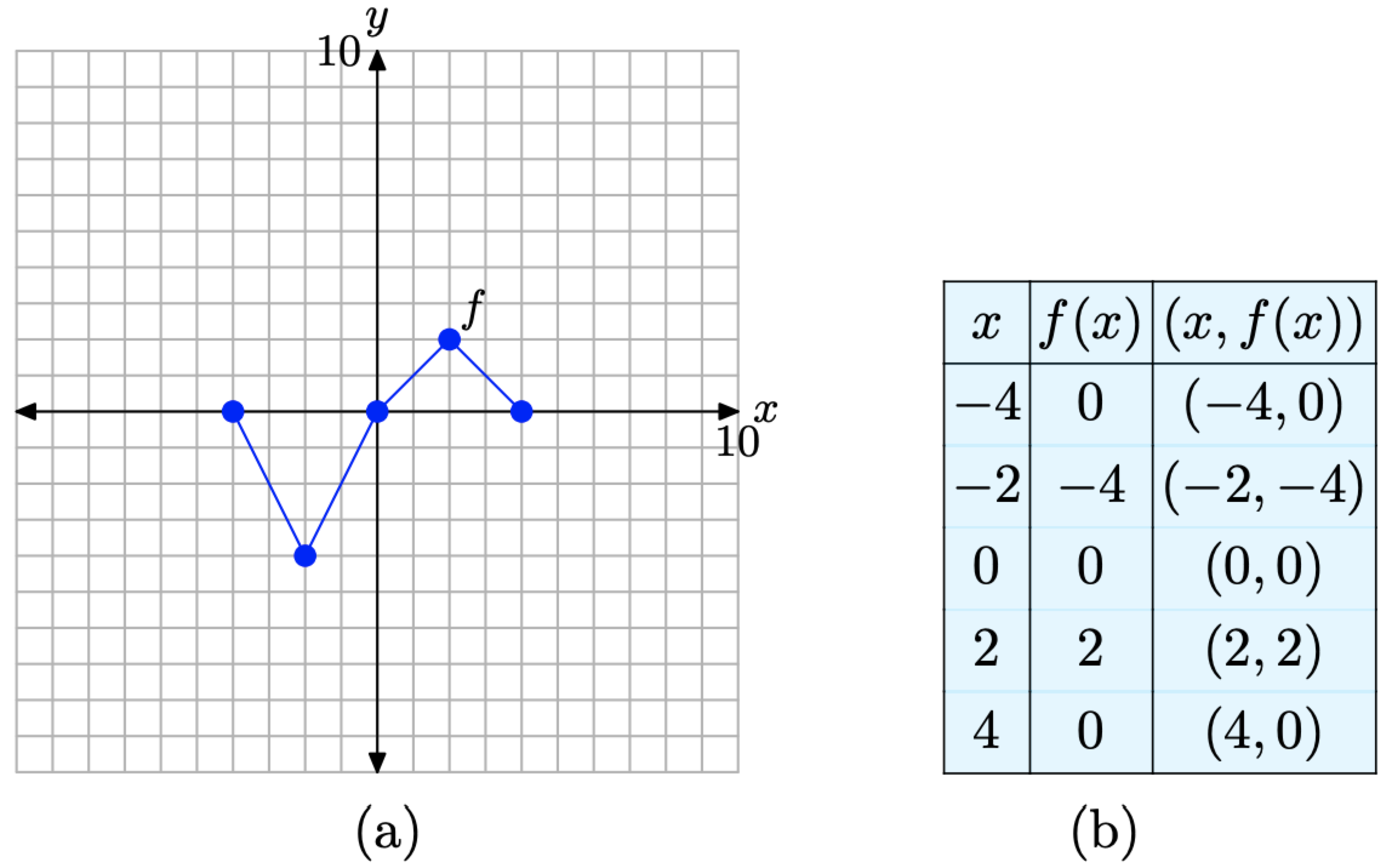
Figura\(\PageIndex{10}\). La gráfica original de f y una tabla de puntos clave en la gráfica de f
Ejemplo\(\PageIndex{5}\)
Si y = f (x) tiene la gráfica mostrada en la Figura\(\PageIndex{10}\) (a), esboce la gráfica de y = f (x + 1).
Solución
En la sección anterior, dibujamos la gráfica de y = f (x) +1. Tenga en cuenta que en y = f (x) +1, el número 1 está fuera de la función. El resultado fue una gráfica que se desplazó 1 unidad hacia arriba en la dirección y.
En este caso, y = f (x + 1) y el 1 está dentro de la notación de función, lo que lleva a uno a intuir que la traducción podría estar en la dirección horizontal (dirección x). Pero, ¿cómo?
Nuevamente, configuraremos una tabla de puntos que satisfagan la ecuación y = f (x + 1), luego los trazaremos. Debido a que esta función requiere que primero agreguemos 1 a cada valor x antes de insertarlo en la función, elegiremos los valores x apropiadamente, es decir, x = −5, −3, −1, 1 y 3. En un momento, quedará claro por qué hemos elegido estos valores particulares de x ¿Quizás ya veas por qué?
Necesitamos evaluar la función y = f (x + 1) en cada uno de estos valores elegidos de x Para evaluar y = f (x+ 1) en el primer valor, es decir, x = −5, insertamos x = −5 y hacemos el cálculo\[y=f(-5+1)=f(-4)\]
Para completar el cálculo, ahora debemos evaluar f (−4). Sin embargo, este resultado se registra en la tabla de la Figura\(\PageIndex{10}\) (b). Ahí encontramos que f (−4) = 0, y podemos completar el cálculo iniciado anteriormente.
\[y=f(-5+1)=f(-4)=0\]
De manera similar, podemos evaluar la función y = f (x+1) a x = −3. Primero, sustituya x = −3 en y = f (x + 1) para obtener
\[y=f(-3+1)=f(-2)\]
Para completar el cálculo, ahora debemos evaluar f (−2). Sin embargo, este resultado se registra en la tabla de la Figura\(\PageIndex{10}\) (b). Ahí encontramos que f (−2) = −4, y podemos completar el cálculo iniciado anteriormente.
\[y=f(-3+1)=f(-2)=-4\]
En este punto, es posible que veas por qué elegimos los valores x: −5, −3, −1, 1 y 3. Estos son precisamente uno menos que los valores x en la tabla de valores originales para la función y = f (x) en la Figura\(\PageIndex{10}\) (b). Cuando los valores −5, −3, −1, 1 y 3 se sustituyen en la función y = f (x + 1), primero agregamos 1 a cada valor antes de ir a buscar el valor de la función en la tabla de la Figura\(\PageIndex{10}\) (b). Esta suma de 1 conduce a los valores −4, −2, 0, 2 y 4, que son precisamente los valores disponibles en la tabla de la Figura\(\PageIndex{10}\) (b).
Continuando de esta manera, evaluamos la función y = f (x + 1) en los valores restantes de x, a saber, −1, 1 y 3.
\[\begin{aligned} y &=f(-1+1)=f(0)=0 \\ y &=f(1+1)=f(2)=2 \\ y &=f(3+1)=f(4)=0 \end{aligned}\]
Ensamblamos estos resultados en la tabla de la Figura\(\PageIndex{11}\) (b) y los trazamos en la Figura\(\PageIndex{11}\) (a).
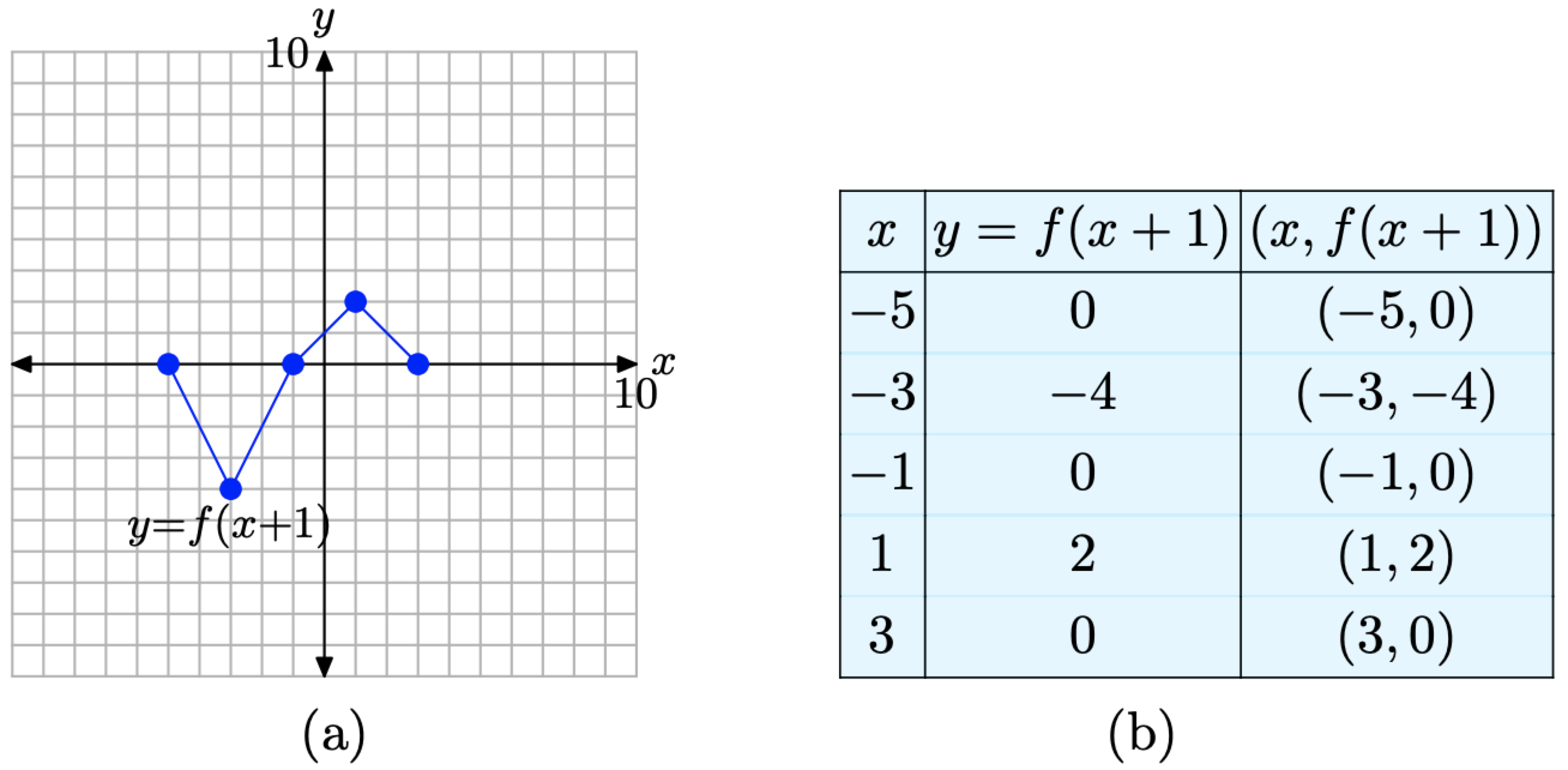
Figura\(\PageIndex{11}\). La gráfica de y = f (x + 1) y una tabla de puntos clave en la gráfica
Al comparar los puntos en la gráfica de y = f (x+1) en la tabla de la Figura\(\PageIndex{11}\) (b) con los puntos originales en la gráfica de y = f (x) en la tabla de la Figura\(\PageIndex{10}\) (b), tenga en cuenta que los valores y son idénticos, pero los valores x en la tabla de la Figura\(\PageIndex{11}\) (b) son todos 1 unidad menos que el valores x correspondientes en la tabla de la Figura\(\PageIndex{10}\) (b). No es de extrañar que la gráfica de y = f (x + 1) en la Figura\(\PageIndex{11}\) (a) se desplace 1 unidad a la izquierda de la gráfica original de y = f (x) en la Figura\(\PageIndex{10}\) (a).
Tenga en cuenta que esto es algo contradictorio, porque aparentemente estamos agregando 1 a cada valor x en y = f (x + 1). ¿Por qué la gráfica no mueve una unidad a la derecha? Bueno, una comparación cuidadosa de los valores x en las tablas de las Figuras\(\PageIndex{10}\) (b) y\(\PageIndex{11}\) (b) revela la respuesta. Para poder utilizar los datos de la tabla de la Figura\(\PageIndex{10}\) (b), primero debemos restar 1 de cada valor x para producir los valores x en la tabla de la Figura\(\PageIndex{11}\) (b). Es por ello que la gráfica de y = f (x + 1) mueve 1 unidad a la izquierda en lugar de 1 unidad a la derecha.
También podría recordar que la función y = f (2x) comprimida por un factor de 2, que también es lo contrario de lo que la intuición podría dictar. De igual manera, la función y = f ((1/2) x) se estira en un factor de 2, lo que también va en contra de la intuición. Con estos pensamientos en mente, no es de extrañar que y = f (x+ 1) desplace una unidad hacia la izquierda. Aún así, una comparación de los valores x en las tablas de las Figuras\(\PageIndex{10}\) (b) y\(\PageIndex{11}\) (b) proporciona evidencia irrefutable de que el desplazamiento es de 1 unidad a la izquierda.
Veamos otro ejemplo.
Ejemplo\(\PageIndex{6}\)
Si y = f (x) tiene la gráfica mostrada en la Figura\(\PageIndex{10}\) (a), esboce la gráfica de y = f (x − 2).
Solución
Nuevamente, configuraremos una tabla de puntos que satisfagan la ecuación y = f (x − 2), luego los trazaremos. Debido a que esta función requiere que primero restemos 2 de cada valor x antes de insertarlo en la función, elegiremos valores x: −2, 0, 2, 4 y 6. Necesitamos evaluar la función y = f (x − 2) en cada uno de estos valores de x.
Para evaluar y = f (x − 2) en el primer valor, concretamente x = −2, inserte x = −2 en la función y = f (x − 2) para obtener\[y=f(-2-2)=f(-4)\]
En la tabla de la Figura\(\PageIndex{10}\) (b), encontramos que f (−4) = 0, lo que nos permite completar el cálculo anterior.
\[y=f(-2-2)=f(-4)=0\]
De manera similar, evaluamos y = f (x − 2) a x = 0 para obtener
\[y=f(0-2)=f(-2)\]
En la tabla de la Figura\(\PageIndex{10}\) (b), encontramos que f (−2) = −4, lo que nos permite completar el cálculo anterior.
\[y=f(0-2)=f(-2)=-4\]
Ojalá veas por qué elegimos los valores x: −2, 0, 2, 4 y 6. Estos valores son 2 mayores que los valores x en la tabla de valores originales para la función y = f (x) en la Figura\(\PageIndex{10}\) (b). Cuando los valores −2, 0, 2, 4 y 6 se sustituyen en la función y = f (x − 2), primero restamos 2 de cada valor antes de ir a buscar el valor de la función en la tabla de la Figura\(\PageIndex{10}\) (b). Esta resta de 2 conduce a −4, −2, 0, 2 y 4, precisamente los valores que están disponibles en la tabla de la Figura\(\PageIndex{10}\) (b).
Continuando de esta manera, evaluamos y = f (x − 2) en los valores restantes de x, es decir, x = 2, 4 y 6.
\[\begin{array}{l}{y=f(2-2)=f(0)=0} \\ {y=f(4-2)=f(2)=2} \\ {y=f(6-2)=f(4)=0}\end{array}\]
Ensamblamos estos resultados en la tabla de la Figura\(\PageIndex{12}\) (b) y los trazamos en la Figura\(\PageIndex{12}\) (a).
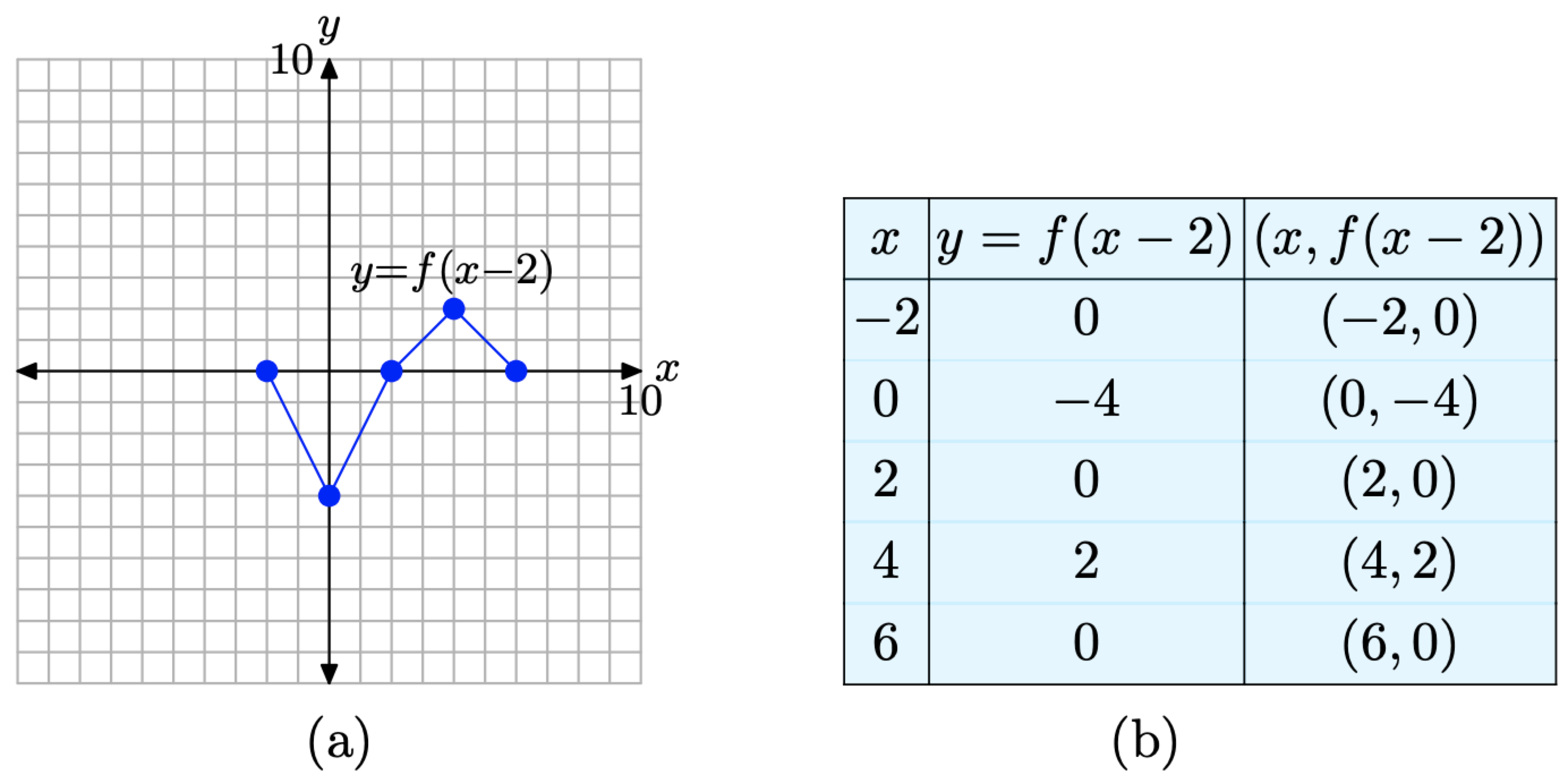
Figura\(\PageIndex{12}\). La gráfica de y = f (x − 2) y una tabla de puntos clave en la gráfica.
Al comparar los puntos en la gráfica de y = f (x−2) en la tabla de la Figura\(\PageIndex{12}\) (b) con los puntos originales en la gráfica de y = f (x) en la tabla de la Figura\(\PageIndex{10}\) (b), tenga en cuenta que los valores y son idénticos, pero los valores x en la tabla de la Figura\(\PageIndex{12}\) (b) son todos 2 mayores que los correspondientes valores x en la tabla de la Figura\(\PageIndex{10}\) (b). No es de extrañar que la gráfica de y = f (x − 2) en la Figura\(\PageIndex{12}\) (a) se desplace 2 unidades a la derecha de la gráfica original de y = f (x) en la Figura\(\PageIndex{10}\) (a).
Nuevamente, esto corre contradictorio (¿por qué la gráfica de y = f (x − 2) no desplaza 2 unidades hacia la izquierda?) , pero una comparación de los valores x en las tablas de las Figuras\(\PageIndex{10}\) (b) y\(\PageIndex{12}\) (b) indica claramente un desplazamiento hacia la derecha.
Resumimos lo que hemos aprendido sobre las traducciones horizontales.
Resumen Visual — Traducciones Horizontales (Turnos)
Considera las imágenes en la Figura\(\PageIndex{13}\).
- En la Figura\(\PageIndex{13}\) (a), vemos representado el gráfico de la función original y = f (x).
- En la Figura\(\PageIndex{13}\) (b), nótese que cada punto de la gráfica de y = f (x + 1) tiene un valor x que es 1 unidad menor que el valor x del punto correspondiente en la gráfica de y = f (x) en la Figura\(\PageIndex{13}\) (a).
- En la Figura\(\PageIndex{13}\) (c), nótese que cada punto de la gráfica de y = f (x − 2) tiene un valor x que es 2 unidades mayor que el valor x del punto correspondiente en la gráfica de y = f (x) en la Figura\(\PageIndex{13}\) (a).
- Tenga en cuenta que el valor y de cada punto transformado sigue siendo el mismo.
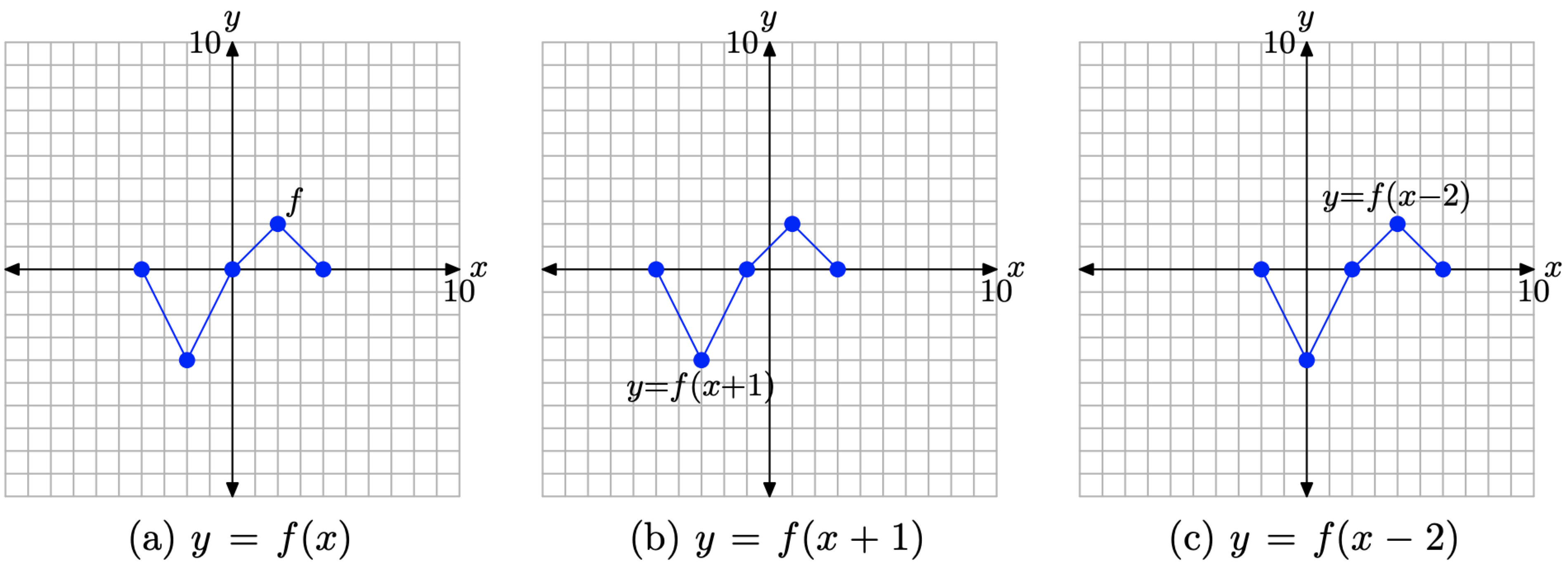
Figura\(\PageIndex{13}\). La gráfica de y = f (x + 1) se forma desplazando (horizontalmente) la gráfica de y = f (x) una unidad hacia la izquierda. La gráfica de y = f (x − 2) se forma desplazando (horizontalmente) la gráfica de y = f (x) dos unidades a la derecha.
El resumen visual de la Figura\(\PageIndex{13}\) hace que bosquejar las gráficas de y = f (x + 1) e y = f (x − 2) sea una tarea fácil.
- Dada la gráfica de y = f (x), para bosquejar la gráfica de y = f (x + 1), simplemente tomar cada punto de la gráfica de y = f (x) y desplazarlo 1 unidad hacia la izquierda, manteniendo el mismo valor y.
- Dada la gráfica de y = f (x), para bosquejar la gráfica de y = f (x − 2), simplemente tomar cada punto de la gráfica de y = f (x) y desplazarlo 2 unidades hacia la derecha, manteniendo el mismo valor y.
En general, podemos exponer lo siguiente.
Resumen
Supongamos que se nos da la gráfica de y = f (x) y supongamos que c es cualquier número real positivo.
- La gráfica de y = f (x+c) se desplaza c unidades a la izquierda de la gráfica de y = f (x).
- La gráfica de y = f (x−c) se desplaza c unidades a la derecha de la gráfica de y = f (x).
Cuando observamos las traducciones verticales en la sección anterior, se describió una traducción imaginando primero una gráfica sobre una hoja de plástico transparente, luego deslizando la transparencia (sin girarla) sobre un sistema de coordenadas en una hoja de papel cuadrilátero. Las traducciones horizontales pueden pensarse de la misma manera, como deslizar la gráfica sobre las unidades c de transparencia hacia la izquierda, o c unidades a la derecha.
Práctica Extra
En esta sección, tomemos los conceptos de los Resúmenes Visuales y pongámoslos a trabajar en algunos ejemplos finales.
Ejemplo\(\PageIndex{7}\)
Considera la gráfica de f en la Figura\(\PageIndex{14}\).
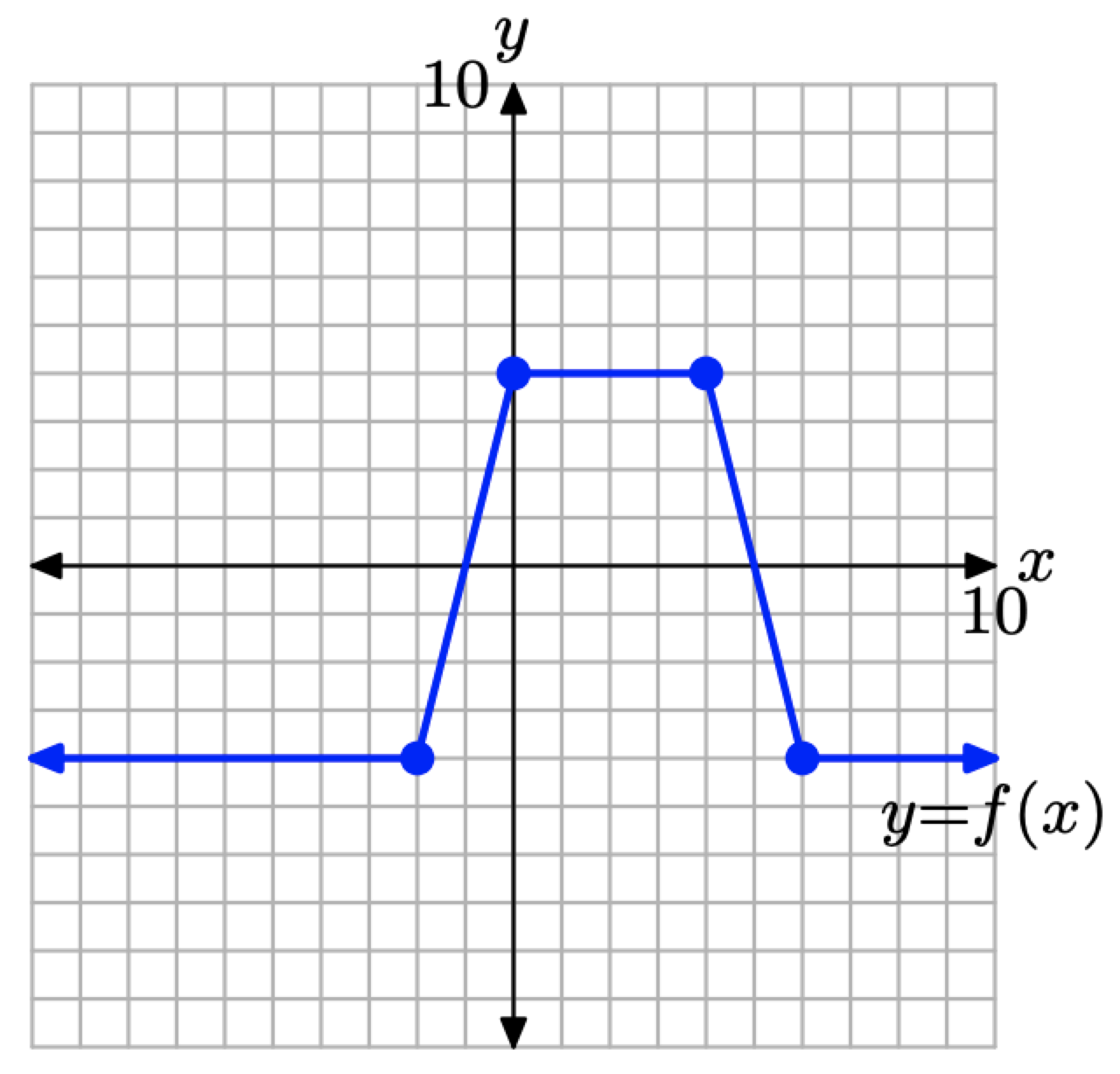
Figura\(\PageIndex{14}\). La gráfica de y = f (x) para Ejemplo\(\PageIndex{7}\).
Utilice los conceptos de los Resúmenes Visuales (escala, reflexión y traducción) para bosquejar las gráficas de y = f (2x), y = f (−x) e y = f (x + 2) sin crear y hacer referencia a tablas.
Solución
Para bosquejar la gráfica de y = f (2x), simplemente tome cada punto de la gráfica de y = f (x) en la Figura\(\PageIndex{15}\) (a) y divida su valor x por 2, manteniendo el mismo valor y. El resultado se muestra en la Figura\(\PageIndex{15}\) (b).
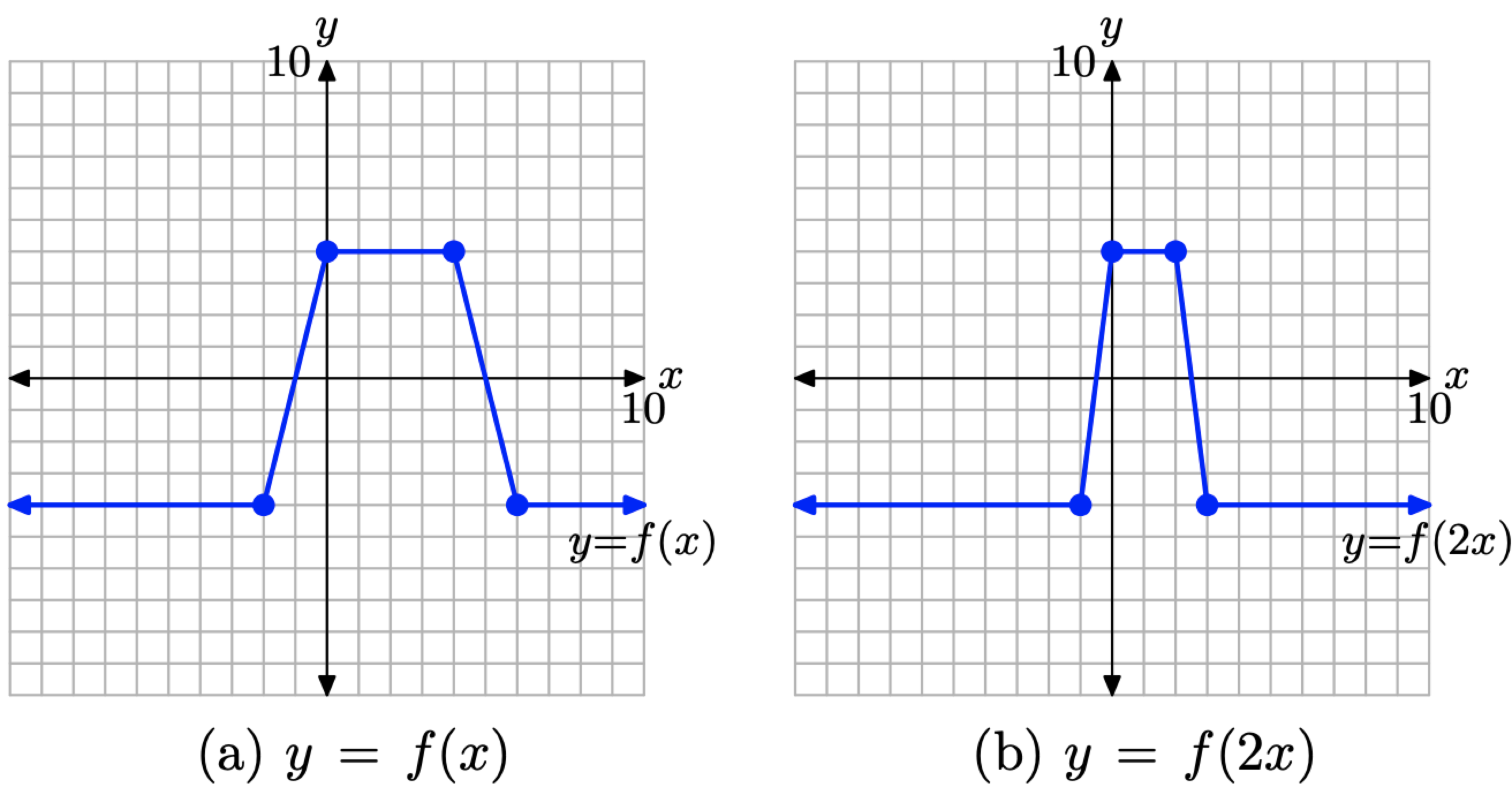
Figura\(\PageIndex{15}\). Comprimir la gráfica de y = f (x) por un factor de 2 para producir la gráfica de y = f (2x).
Para bosquejar la gráfica de y = f (−x), simplemente tome cada punto de la gráfica de y = f (x) en la Figura\(\PageIndex{16}\) (a) y anule su valor x, manteniendo el mismo valor y. El resultado se muestra en la Figura\(\PageIndex{16}\) (b).
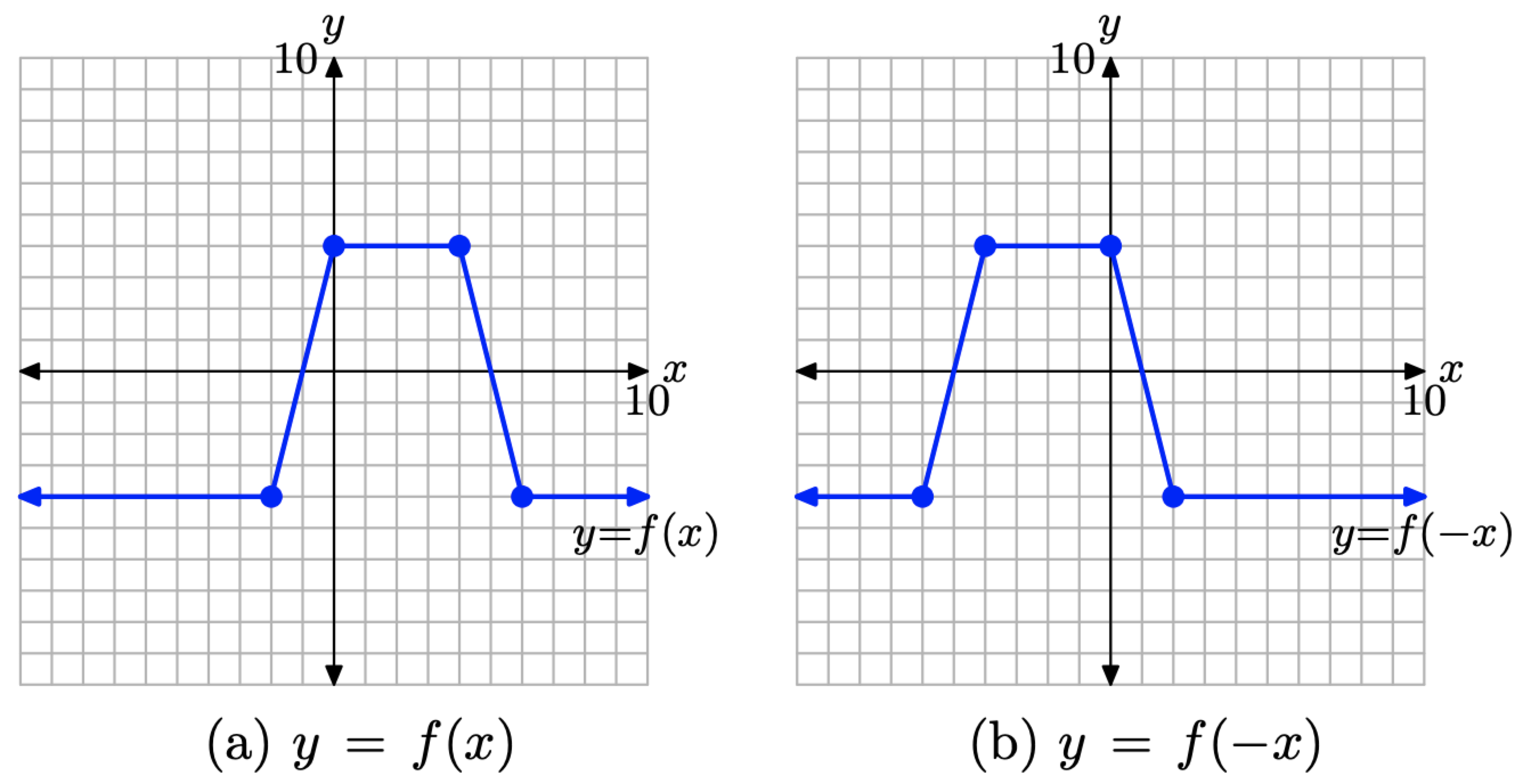
Figura\(\PageIndex{16}\). Refleja la gráfica de y = f (x) a través del eje y para producir la gráfica de y = f (−x).
Para bosquejar la gráfica de y = f (x + 2), simplemente tome cada punto de la gráfica de y = f (x) en la Figura\(\PageIndex{17}\) (a) y reste 2 de su valor x, manteniendo el mismo valor y. El resultado se muestra en la Figura\(\PageIndex{17}\) (b).
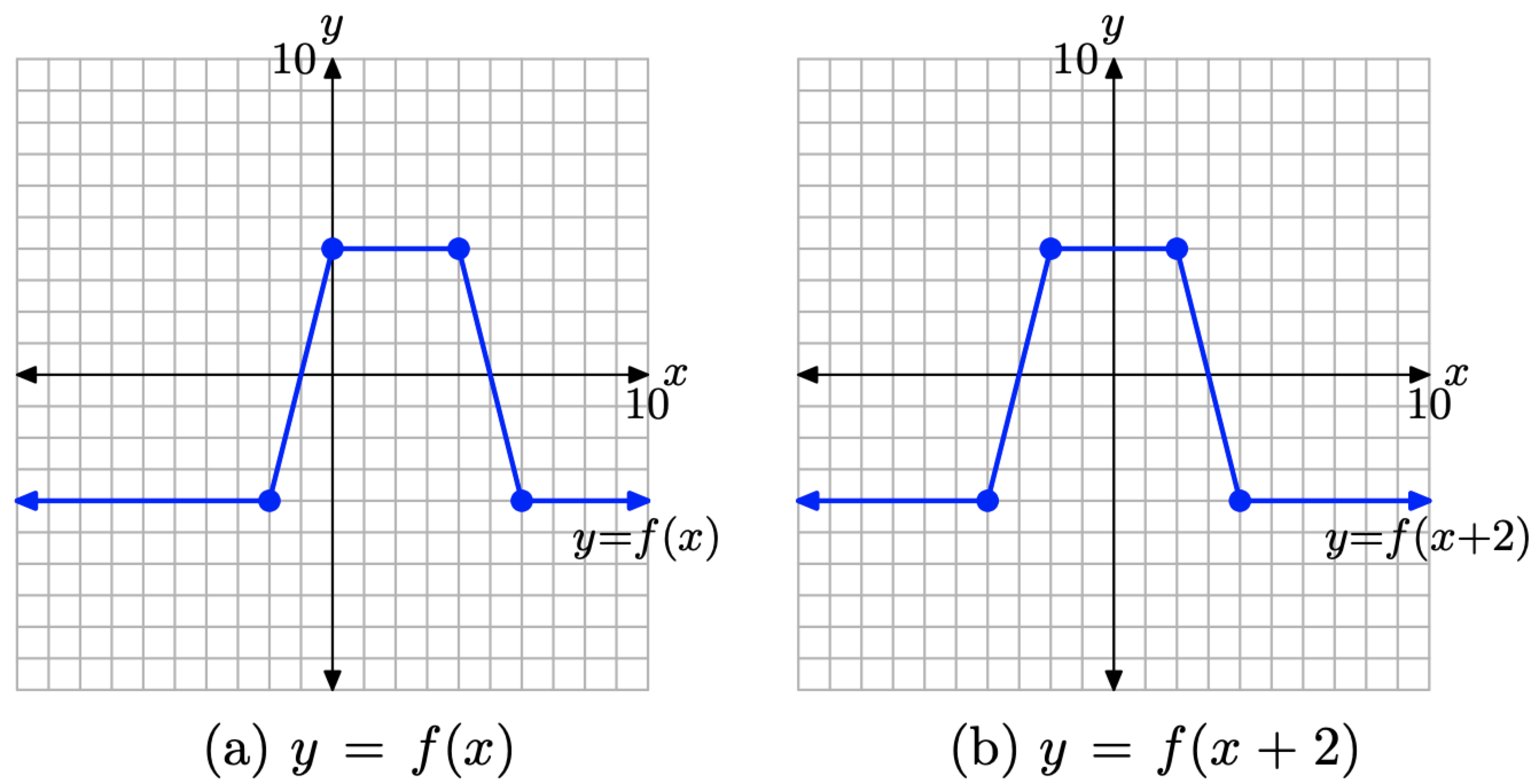
Figura\(\PageIndex{17}\). Desplace la gráfica de y = f (x) hacia la izquierda 2 unidades para producir la gráfica de y = f (x + 2).
Resumen
En esta sección hemos visto cómo un puñado de transformaciones mejoran enormemente nuestra capacidad de graficar. Terminamos esta sección enumerando las transformaciones que se presentan en esta sección y sus efectos en la gráfica de una función.
Transformaciones Verticales
Supongamos que se nos da la gráfica de y = f (x).
- Si a > 1, la gráfica de y = f (ax) comprime horizontalmente (hacia el eje y), tanto positiva como negativamente, por un factor de a.
- Si 0 < a < 1, la gráfica de y = f (ax) se estira horizontalmente (alejándose del eje y), tanto positiva como negativamente, por un factor de 1/a.
- La gráfica de y = f (−x) es un reflejo de la gráfica de y = f (x) a través del eje y.
- Si c > 0, entonces la gráfica de y = f (x + c) se desplaza c unidades a la izquierda de la gráfica de y = f (x).
- Si c > 0, entonces la gráfica de y = f (x − c) se desplaza c unidades a la derecha de la gráfica de y = f (x).


