2.7: Capítulo 2 Ejercicios con Soluciones
- Page ID
- 110849
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)2.1 Ejercicios
En Ejercicios\(\PageIndex{1}\) -\(\PageIndex{6}\), indicar el dominio y el rango de la relación dada.
Ejercicio\(\PageIndex{1}\)
R = {(1, 3), (2, 4), (3, 4)}
- Responder
-
El dominio es el conjunto de todas las primeras coordenadas = {1, 2, 3}. El rango es el conjunto de todas las segundas coordenadas {3, 4} (tenga en cuenta que en un conjunto no listas un objeto dos veces, así que solo enumeramos 4 una vez).
Ejercicio\(\PageIndex{2}\)
R = {(1, 3), (2, 4), (2, 5)}
Ejercicio\(\PageIndex{3}\)
R = {(1, 4), (2, 5), (2, 6)}
- Responder
-
El dominio es el conjunto de todas las primeras coordenadas = {1, 2} (tenga en cuenta que en un conjunto no listas un objeto dos veces, así que solo enumeramos 2 una vez). El rango es el conjunto de todas las segundas coordenadas {4, 5, 6}.
Ejercicio\(\PageIndex{4}\)
R = {(1, 5), (2, 4), (3, 6)}
Ejercicio\(\PageIndex{5}\)
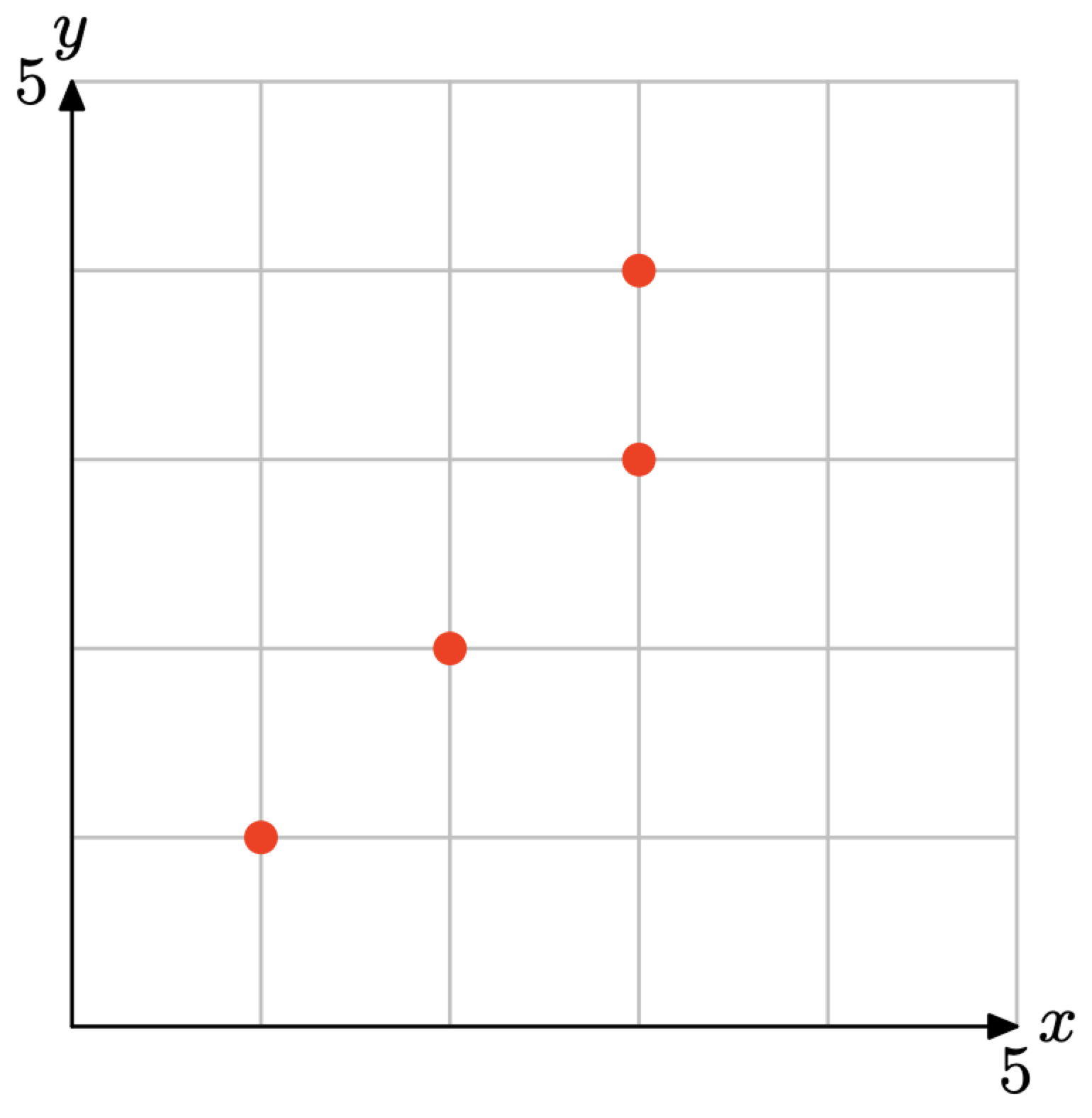
- Responder
-
Lee la coordenada x de cada punto para obtener que el dominio sea {1, 2, 3}. Luego lee las coordenadas y para obtener que el rango es {1, 2, 3, 4}
Ejercicio\(\PageIndex{6}\)
En Ejercicios\(\PageIndex{7}\) -\(\PageIndex{12}\), crea un diagrama de mapeo para la relación dada y establece si es o no una función.
Ejercicio\(\PageIndex{7}\)
La relación en el ejercicio\(\PageIndex{1}\).
- Responder
-
Crear un diagrama de mapeo para R.
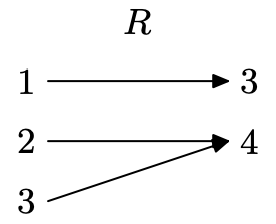
Dado que ningún valor de dominio se empareja con dos valores de rango, esta es una función (cada x se asigna a una y única). Tenga en cuenta que tener dos valores de dominio diferentes ir a un solo valor de rango (2 y 3 ambos mapean a 4) es permisible para una función.
Ejercicio\(\PageIndex{8}\)
La relación en el ejercicio\(\PageIndex{2}\).
Ejercicio\(\PageIndex{9}\)
La relación en el ejercicio\(\PageIndex{3}\).
- Responder
-
Crear un diagrama de mapeo para R.
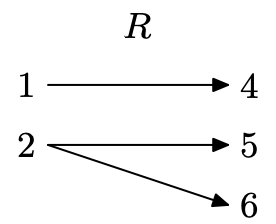
El número 2 se mapea a dos valores de rango diferentes (una x se asigna a dos y), por lo que esta no es una función.
Ejercicio\(\PageIndex{10}\)
La relación en el ejercicio\(\PageIndex{4}\).
Ejercicio\(\PageIndex{11}\)
La relación en el ejercicio\(\PageIndex{5}\).
- Responder
-
Crear un diagrama de mapeo para R.
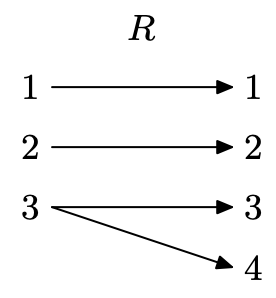
El número 3 se mapea a dos valores de rango diferentes (una x se asigna a dos y), por lo que esta no es una función.
Ejercicio\(\PageIndex{12}\)
La relación en el ejercicio\(\PageIndex{6}\).
Ejercicio\(\PageIndex{13}\)
Dado que g toma un número real y lo duplica, entonces\(g : x \rightarrow ?\).
- Responder
-
Dobles significa 'multiplica por 2', entonces\(g : x \rightarrow 2x\).
Ejercicio\(\PageIndex{14}\)
Dado que f toma un número real y lo divide por 3, entonces\(f : x \rightarrow ?\).
Ejercicio\(\PageIndex{15}\)
Dado que g toma un número real y le suma 3, entonces\(g : x \rightarrow ?\).
- Responder
-
\(g : x \rightarrow x + 3\)
Ejercicio\(\PageIndex{16}\)
Dado que h toma un número real y le resta 4, entonces\(h : x \rightarrow ?\).
Ejercicio\(\PageIndex{17}\)
Dado que g toma un número real, lo duplica, luego suma 5, luego\(g : x \rightarrow ?\)
- Responder
-
Para una x poner en g, g la duplica, dando 2x, y luego agrega cinco, resultando en 2x + 5. Por lo tanto,\(g : x \rightarrow 2x + 5\)
Ejercicio\(\PageIndex{18}\)
Dado que h toma un número real, le resta 3, luego divide el resultado por 4, luego\(h : x \rightarrow ?\)
Dado que la función f está definida por la regla\(h : x \rightarrow 3x − 5\), determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{19}\) -\(\PageIndex{22}\).
Ejercicio\(\PageIndex{19}\)
\(f : 3 \rightarrow ?\)
- Responder
-
Poner 3 en f. esto significa, reemplazar x por 3 y computar la salida. \(f : 3 \rightarrow 3(3) − 5 = 4\), entonces\(f : 3 \rightarrow 4\).
Ejercicio\(\PageIndex{20}\)
\(f : -5 \rightarrow ?\)
Ejercicio\(\PageIndex{21}\)
\(f : a \rightarrow ?\)
- Responder
-
Pon a en f, igual que lo harías con un número. Esto significa, reemplazar x por a y calcular la salida. \(f : a \rightarrow 3(a) − 5 = 3a − 5\), entonces\(f : 3 \rightarrow 3a − 5\).
Ejercicio\(\PageIndex{22}\)
\(f : 2a+3 \rightarrow ?\)
Dado que la función f está definida por la regla\(f : x \rightarrow 4-5x\), determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{23}\) -\(\PageIndex{26}\).
Ejercicio\(\PageIndex{23}\)
\(f : 2 \rightarrow ?\)
- Responder
-
Pon 2 en f reemplazando x con él. \(f : 2 \rightarrow 4 − 5(2) = −6\), entonces\(f : 2 \rightarrow −6\).
Ejercicio\(\PageIndex{24}\)
\(f : -3 \rightarrow ?\)
Ejercicio\(\PageIndex{25}\)
\(f : a \rightarrow ?\)
- Responder
-
Pon a en f reemplazando x por ella, tal como lo harías con un número. \(f : a \rightarrow 4 − 5(a)\), entonces\(f : 2 \rightarrow 4 − 5a\).
Ejercicio\(\PageIndex{26}\)
\(f : 2a+11 \rightarrow ?\)
Dado que la función f está definida por la regla\(f : x \rightarrow x^{2}-4x-6\), determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{27}\) -\(\PageIndex{30}\).
Ejercicio\(\PageIndex{27}\)
\(f : 1 \rightarrow ?\)
- Responder
-
Pon 1 en f reemplazando x con él. \(f : 1 \rightarrow (1)2 − 4(1) − 6 = 1 − 4 − 6 = −9\), entonces\(f : 1 \rightarrow −9\).
Ejercicio\(\PageIndex{28}\)
\(f : -2 \rightarrow ?\)
Ejercicio\(\PageIndex{29}\)
\(f : -1 \rightarrow ?\)
- Responder
-
Pon −1 en f reemplazando x por él. \(f : −1 \rightarrow (−1)2 −4(−1)−6 = 1+4−6 = −1\), entonces\(f : 1 \rightarrow −1\).
Ejercicio\(\PageIndex{30}\)
\(f : a \rightarrow ?\)
Dado que la función f está definida por la regla\(f : x \rightarrow 3x-9\), determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{31}\) -\(\PageIndex{34}\).
Ejercicio\(\PageIndex{31}\)
\(f : a \rightarrow ?\)
- Responder
-
Pon a en f reemplazando x por ella, tal como lo harías con un número. \(f : a \rightarrow 3a − 9\).
Ejercicio\(\PageIndex{32}\)
\(f : a+1 \rightarrow ?\)
Ejercicio\(\PageIndex{33}\)
\(f : 2a-5 \rightarrow ?\)
- Responder
-
Pon 2a − 5 en f reemplazando x por él, tal como lo harías con un número. Obtenemos\(f : 2a − 5 \rightarrow 3(2a − 5) − 9 = 6a − 15 − 9 = 6a − 24\), entonces\(f : 2a − 5 \rightarrow 6a − 24\)
Ejercicio\(\PageIndex{34}\)
\(f : a+h \rightarrow ?\)
Dado que las funciones f y g están definidas por las reglas\(f : x \rightarrow 2x+3\) y\(g : x \rightarrow 4-x\), determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{35}\) -\(\PageIndex{38}\).
Ejercicio\(\PageIndex{35}\)
\(f : 2 \rightarrow ?\)
- Responder
-
Pon 2 en f reemplazando x con él. Lo conseguimos\(f : 2 \rightarrow 2(2)+3 = 7\), entonces\(f : 2 \rightarrow 7\).
Ejercicio\(\PageIndex{36}\)
\(f : 2 \rightarrow ?\)
Ejercicio\(\PageIndex{37}\)
\(f : a+1 \rightarrow ?\)
- Responder
-
Pon un + 1 en f reemplazando x por él, tal como lo harías con un número. Obtenemos\(f : a + 1 \rightarrow 2(a + 1) + 3 = 2a + 2 + 3 = 2a + 5\), entonces\(f : a + 1 \rightarrow 2a + 5\)
Ejercicio\(\PageIndex{38}\)
\(f : a-3 \rightarrow ?\)
Ejercicio\(\PageIndex{39}\)
Dado que g toma un número real y lo triplica, entonces g (x) =?.
- Responder
-
Triples significa 'multiplica por 3, 'así g (x) = 3x
Ejercicio\(\PageIndex{40}\)
Dado que f toma un número real y lo divide por 5, entonces f (x) =?.
Ejercicio\(\PageIndex{41}\)
Dado que g toma un número real y lo resta de 10, entonces g (x) =?.
- Responder
-
g toma una entrada x y la resta DE 10, entonces g (x) = 10 − x.
Ejercicio\(\PageIndex{42}\)
Dado que f toma un número real, lo multiplica por 5 y luego suma 4 al resultado, luego f (x) =?.
Ejercicio\(\PageIndex{43}\)
Dado que f toma un número real, lo duplica, luego resta el resultado de 11, luego f (x) =?.
- Responder
-
f toma una entrada x, la duplica para obtener 2x, y le quita esto DE 11, obteniendo 11 − 2x. Por lo tanto, f (x) = 11 − 2x.
Ejercicio\(\PageIndex{44}\)
Dado que h toma un número real, lo duplica, suma 5, luego toma la raíz cuadrada del resultado, después h (x) =?.
En Ejercicios\(\PageIndex{45}\) -\(\PageIndex{54}\), evaluar la función dada en el valor dado b.
Ejercicio\(\PageIndex{45}\)
f (x) = 12x + 2 para b = 6.
- Responder
-
Sustituye 6 por x en 12x + 2 y simplifica para obtener 74: f (6) = 12 (6) + 2 = 74.
Ejercicio\(\PageIndex{46}\)
f (x) = −11x − 4 para b = −3.
Ejercicio\(\PageIndex{47}\)
f (x) = −9x − 1 para b = −5.
- Responder
-
Sustituye −5 por x en −9x−1 y simplifica para obtener 44: f (−5) = −9 (−5) −1 = 44.
Ejercicio\(\PageIndex{48}\)
f (x) = 11x + 4 para b = −4.
Ejercicio\(\PageIndex{49}\)
f (x) = 4 para b = −12.
- Responder
-
f es una función constante, por lo que f (x) = 4 para todo x Por lo tanto, f (−12) = 4.
Ejercicio\(\PageIndex{50}\)
f (x) = 7 para b = −7.
Ejercicio\(\PageIndex{51}\)
f (x) = 0 para b = −7.
- Responder
-
f es una función constante, por lo que f (x) = 0 para todos x Por lo tanto, f (−7) = 0.
Ejercicio\(\PageIndex{52}\)
f (x) = 12x + 8 para b = −3.
Ejercicio\(\PageIndex{53}\)
f (x) = −9x + 3 para b = −1.
- Responder
-
Sustituye −1 por x en −9x+3 y simplifica para obtener 12: f (−1) = −9 (−1) +3 = 12
Ejercicio\(\PageIndex{54}\)
f (x) = 6x − 3 para b = 3.
En Ejercicios\(\PageIndex{55}\) -\(\PageIndex{58}\), dado que la función f está definida por la regla f (x) = 2x+ 7, determinar dónde se mapea el número de entrada.
Ejercicio\(\PageIndex{55}\)
f (a) =?
- Responder
-
Pon a en f reemplazando x por ella, tal como lo harías con un número. Esto produce f (a) = 2a + 7.
Ejercicio\(\PageIndex{56}\)
f (a + 1) =?
Ejercicio\(\PageIndex{57}\)
f (3a − 2) =?
- Responder
-
Pon 3a − 2 en f reemplazando x por él, tal como lo harías con un número. Esto produce f (3a − 2) = 2 (3a − 2) + 7 = 6a − 4 + 7 = 6a + 3.
Ejercicio\(\PageIndex{58}\)
f (a + h) =?
En Ejercicios\(\PageIndex{59}\) -\(\PageIndex{62}\), dado que la función g está definida por la regla g (x) = 3 − 2x, determinar dónde se mapea el número de entrada.
Ejercicio\(\PageIndex{59}\)
g (a) =?
- Responder
-
Pon a en g reemplazando x con él, tal como lo harías con un número. Esto produce g (a) = 3 − 2a.
Ejercicio\(\PageIndex{60}\)
g (a + 3) =?
Ejercicio\(\PageIndex{61}\)
g (2 − 5a) =?
- Responder
-
Pon 2 − 5a en g reemplazando x con él, tal como lo harías con un número. Esto produce g (2 − 5a) = 3 − 2 (2 − 5a) = 3 − 4 + 10a = −1 + 10a o 10a − 1.
Ejercicio\(\PageIndex{62}\)
g (a + h) =?
Dado que las funciones f y g están definidas por las reglas f (x) = 1 − x y g (x) = 2x + 13, determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{63}\) -\(\PageIndex{66}\).
Ejercicio\(\PageIndex{63}\)
f (a) =?
- Responder
-
Pon a en f reemplazando x por ella, tal como lo harías con un número. Esto produce f (a) = 1 − a.
Ejercicio\(\PageIndex{64}\)
g (a) =?
Ejercicio\(\PageIndex{65}\)
f (a + 3) =?
- Responder
-
Pon un + 3 en f reemplazando x por él, tal como lo harías con un número. Esto produce f (a + 3) = 1 − (a + 3) = 1 − a − 3 = −a − 2.
Ejercicio\(\PageIndex{66}\)
g (4 − a) =?
Dado que las funciones f y g están definidas por las reglas f (x) = 3x + 4 y g (x) = 2x−5, determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{67}\) -\(\PageIndex{70}\).
Ejercicio\(\PageIndex{67}\)
f (g (2)) =?
- Responder
-
Primero computa g (2) = 2 (2) − 5 = −1. Esto significa que f (g (2)) es realmente f (−1). Conectando −1 para x en la función f, obtenemos f (g (2)) = f (−1) = 3 (−1) + 4 = −3 + 4 = 1.
Ejercicio\(\PageIndex{68}\)
g (f (2)) =?
Ejercicio\(\PageIndex{69}\)
f (g (a)) =?
- Responder
-
Primero computa g (a) = 2a−5. Esto significa que f (g (a)) es realmente f (2a−5). Conectando 2a − 5 in para x en la función f, obtenemos f (g (a)) = f (2a − 5) = 3 (2a − 5) + 4 = 6a − 15 + 4 = 6a − 11.
Ejercicio\(\PageIndex{70}\)
g (f (a)) =?
Dado que las funciones f y g están definidas por las reglas f (x) = 2x − 9 y g (x) = 11, determinar dónde se mapea el número de entrada en Ejercicios\(\PageIndex{71}\) -\(\PageIndex{74}\).
Ejercicio\(\PageIndex{71}\)
f (g (2)) =?
- Responder
-
Primero computa g (2) = 11 (tenga en cuenta que, no importa lo que pongas en g, genera 11). Esto significa que f (g (2)) es realmente f (11). Conectando 11 in para x en la función f, obtenemos f (g (2)) = f (11) = 2 (11) − 9 = 22 − 9 = 13.
Ejercicio\(\PageIndex{72}\)
g (f (2)) =?
Ejercicio\(\PageIndex{73}\)
f (g (a)) =?
- Responder
-
Primero computa g (a) = 11 (tenga en cuenta que, no importa lo que pongas en g, genera 11). Esto significa que f (g (a)) es realmente f (11). Conectando 11 in para x en la función f, obtenemos f (g (2)) = f (11) = 2 (11) − 9 = 22 − 9 = 13.
Ejercicio\(\PageIndex{74}\)
g (f (a)) =?
Utilice la notación set-builder para describir el dominio de cada una de las funciones definidas en Ejercicios\(\PageIndex{75}\) -\(\PageIndex{78}\).
Ejercicio\(\PageIndex{75}\)
\(f(x) = \dfrac{93}{x+98}\)
- Responder
-
Una entrada de x = −98 causaría división por cero, por lo que −98 no está en el dominio. Todas las demás entradas posibles son válidas. El dominio, en notación set-builder, es\(\{x : x \neq −98\}\).
Ejercicio\(\PageIndex{76}\)
\(f(x) = \dfrac{54}{x+65}\)
Ejercicio\(\PageIndex{77}\)
\(f(x) = -\dfrac{87}{x-88}\)
- Responder
-
Una entrada de x = 88 causaría división por cero, por lo que 88 no está en el dominio. Todas las demás entradas posibles son válidas. El dominio, en notación set-builder, es\(\{x : x \neq 88\}\)..
Ejercicio\(\PageIndex{78}\)
\(f(x) = -\dfrac{30}{x-52}\)
Utilice set-builder y notación de intervalos para describir el dominio de las funciones definidas en Ejercicios\(\PageIndex{79}\) -\(\PageIndex{82}\).
Ejercicio\(\PageIndex{79}\)
\(f(x) = \sqrt{x+69}\)
- Responder
-
La raíz cuadrada de un número negativo no se define como un número real. Así, x + 69 debe ser mayor o igual a cero. Entonces\(x + 69 geq 0\) implica eso\(x \geq −69\), entonces el dominio es el intervalo\([−69,\infty)\), o en notación set-builder,\(\{x : x \geq −69\}\).
Ejercicio\(\PageIndex{80}\)
\(f(x) = \sqrt{x+62}\)
Ejercicio\(\PageIndex{81}\)
\(f(x) = \sqrt{x-81}\)
- Responder
-
La raíz cuadrada de un número negativo no se define como un número real. Así, x − 81 debe ser mayor o igual a cero. Entonces\(x − 81 \geq 0\) implica eso\(x \geq 81\), entonces el dominio es el intervalo\([81,\infty)\), o en notación set-builder,\(\{x : x \geq 81\}\).
Ejercicio\(\PageIndex{82}\)
\(f(x) = \sqrt{x-98}\)
Se dice que dos enteros son relativamente primos si su divisor más común es 1. Por ejemplo, el divisor más común de 6 y 35 es 1, por lo que 6 y 35 son relativamente primos. Por otro lado, el divisor más común de 14 y 21 no es 1 (es 7), por lo que 14 y 21 no son relativamente primos. La\(\phi\) función Euler se define de la siguiente manera:
• Si n = 1, entonces\(\phi (n) = 1\).
• Si n > 1, entonces\(\phi (n)\) es el número de enteros positivos menor que n que son relativamente primos a n. En Ejercicios\(\PageIndex{83}\) -\(\PageIndex{84}\), evalúe la\(\phi\) función Euler en la entrada dada.
Ejercicio\(\PageIndex{83}\)
\(\phi (12)\)
- Responder
-
1, 5, 7 y 11 son menores de 12 y cada uno es relativamente primo a 12. Por lo tanto,\(\phi(12) = 4\).
Ejercicio\(\PageIndex{84}\)
\(\phi (36)\)
2.2 Ejercicios
Realizar cada una de las siguientes tareas para las funciones definidas por las ecuaciones en Ejercicios\(\PageIndex{1}\) -\(\PageIndex{8}\).
i. Establecer una tabla de puntos que satisfagan la ecuación dada. Por favor, coloque esta tabla de puntos junto a su gráfica en su papel cuadriculado.
ii. Configura un sistema de coordenadas en una hoja de papel gráfico. Etiqueta y escala cada eje, luego traza cada uno de los puntos de tu tabla en tu sistema de coordenadas.
iii. Si estás seguro de que “ves” la forma de la gráfica, haz un “salto de fe” y traza todos los pares que satisfagan la ecuación dada dibujando una curva suave (a mano alzada) en tu sistema de coordenadas que contenga todos los puntos previamente trazados (usa una regla solo si la gráfica de la ecuación es una línea). Si no estás seguro de que “ves” la forma de la gráfica, entonces agrega más puntos a tu tabla, grácalos en tu sistema de coordenadas y ve si esto ayuda. Continúe con este proceso hasta que “vea” la forma de la gráfica y pueda rellenar el resto de los puntos que satisfagan la ecuación dibujando una curva (o línea) suave en su sistema de coordenadas.
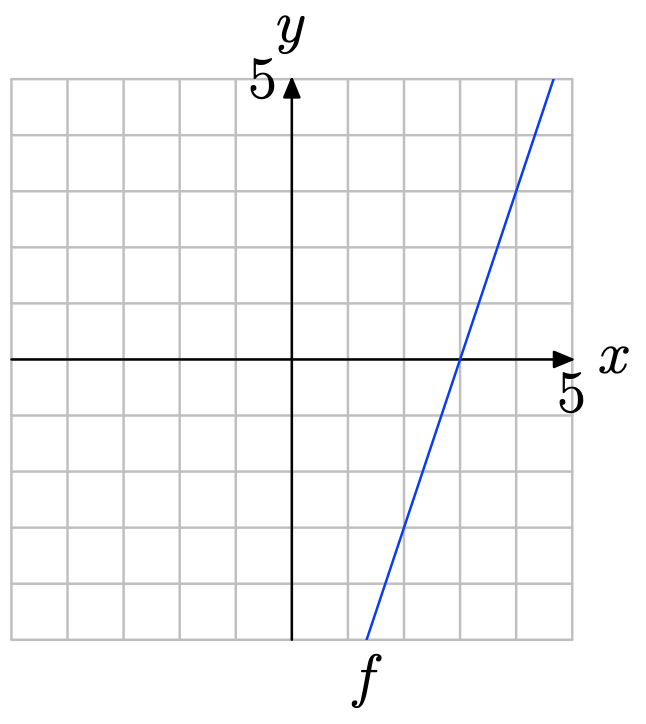
Ejercicio\(\PageIndex{1}\)
\(f(x) = 2x + 1\)
- Responder
-
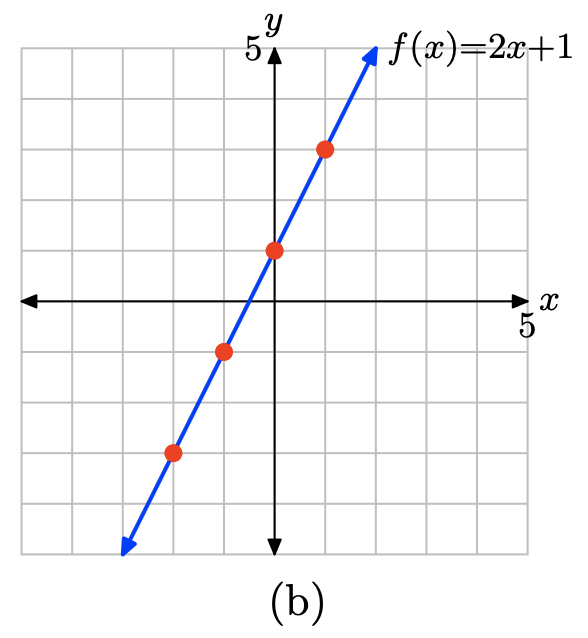
Evalúe la función\(f(x) = 2x + 1\) en −2, −1, 0 y 1.
\[\begin{array} {ccc} f(−2) &=& 2(−2) + 1 &=& −3 \\ f(−1) & = &2(−1) + 1 &=& −1 \\ f(0) &=& 2(0) + 1 &=& 1 \\ f(1) &=& 2(1) + 1 &=& 3 \end{array}\]
Colocar estos resultados en la tabla (a) y trazarlos como se muestra en (b). Aquí hay pruebas suficientes para intuir que la gráfica de f es la línea que se muestra en (b).
x \(f(x) = 2x + 1\) (x, f (x)) -2 \ (f (x) = 2x + 1\) ">-3 (−2, −3) -1 \ (f (x) = 2x + 1\) ">-1 (−1, −1) 0 \ (f (x) = 2x + 1\) ">1 (0,1) 1 \ (f (x) = 2x + 1\) ">3 (1,3) - (a)
Ejercicio\(\PageIndex{2}\)
\(f(x) = 1 − x\)
Ejercicio\(\PageIndex{3}\)
\(f(x) = 3 − \dfrac{1}{2} x\)
- Responder
-
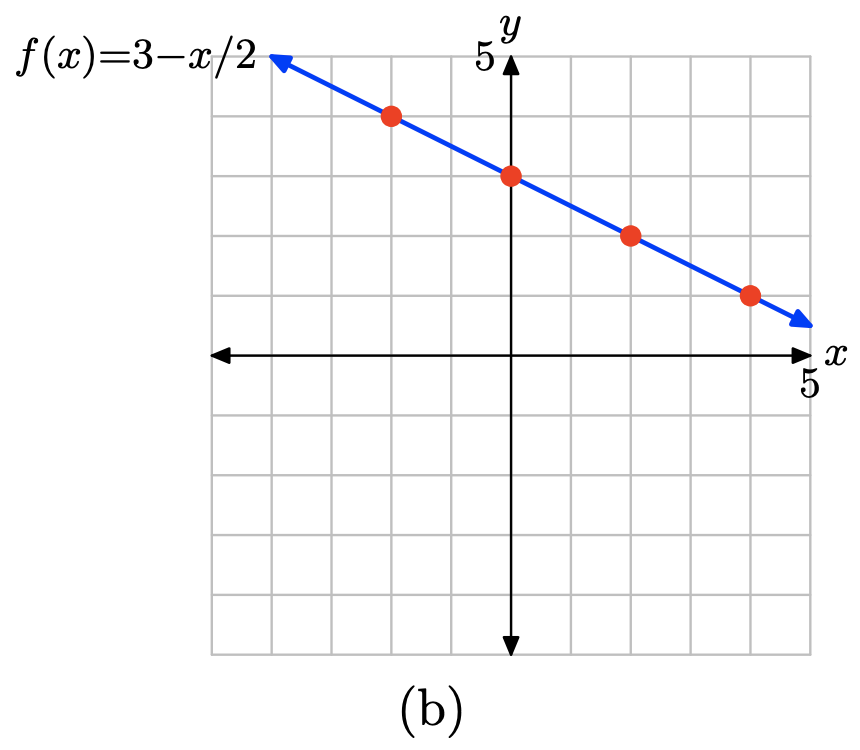
Evalúe la función f (x) = 3 − (1/2) x en x = −2, 0, 2 y 4.
\[f(−2) = 3 − (1/2)(−2) = 4 \\ f(0) = 3 − (1/2)(0) = 3 \\ f(2) = 3 − (1/2)(2) = 2 \\ f(4) = 3 − (1/2)(4) = 1 \]
Colocar estos resultados en la tabla (a) y trazarlos como se muestra en (b). Aquí hay pruebas suficientes para intuir que la gráfica de f es la línea que se muestra en (b).
x \(f(x) = 3 - x/2\) (x, f (x)) -2 \ (f (x) = 3 - x/2\) ">4 (−2, 4) 0 \ (f (x) = 3 - x/2\) ">3 (0,3) 2 \ (f (x) = 3 - x/2\) ">2 (2,2) 4 \ (f (x) = 3 - x/2\) ">1 (4,1)
(a)
Ejercicio\(\PageIndex{4}\)
\(f(x) = −1 + \dfrac{1}{2}x\)
Ejercicio\(\PageIndex{5}\)
\(f(x) = x^2 − 2\)
- Responder
-
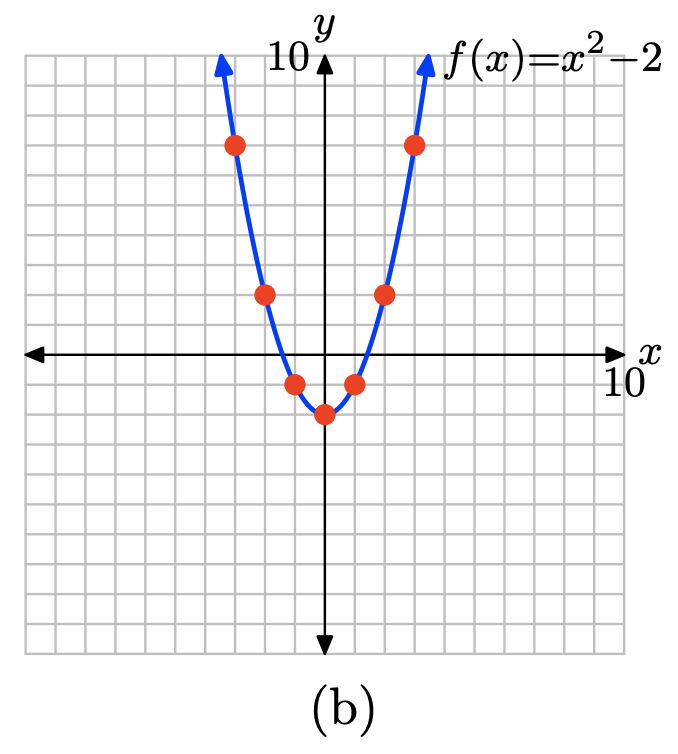
Evalúa\(f(x) = x^2 − 2\) en x = −3, −2, −1, 0, 1, 2 y 3.
\[f(−3) = (−3)^2 − 2 = 7 \\ f(−2) = (−2)^2 − 2 = 2 \\ f(−1) = (−1)^2 − 2 = −1 \\ f(0) = (0)^2 − 2 = −2 \\ f(1) = (1)^2 − 2 = −1 \\ f(2) = (2)^2 − 2 = 2 \\ f(3) = (3)^2 − 2 = 7\]
Colocar estos resultados en la tabla (a) y trazarlos como se muestra en (b). Aquí hay evidencia suficiente para intuir que la gráfica de f es la curva mostrada en (b).
x \(f(x) = x^2 − 2\) (x, f (x)) -3 \ (f (x) = x^2 − 2\) ">7 (−3, 7) -2 \ (f (x) = x^2 − 2\) ">2 (-2,2) -1 \ (f (x) = x^2 − 2\) ">-1 (-1, -1) 0 \ (f (x) = x^2 − 2\) ">-2 (0, -2) 1 \ (f (x) = x^2 − 2\) ">-1 (1, -1) 2 \ (f (x) = x^2 − 2\) ">2 (2,2) 3 \ (f (x) = x^2 − 2\) ">7 (3,7) (a)
Ejercicio\(\PageIndex{6}\)
\(f(x) = 4 − x^{2}\)
Ejercicio\(\PageIndex{7}\)
\(f(x) = \dfrac{1}{2} x^{2} − 6\)
- Responder
-
Evalúa\(f(x) = x^2/2 − 6\) en x = −4, −2, 0, 2 y 4.
\[f(−4) = (−4)^2/2 − 6 = 2 \\ f(−2) = (−2)^2/2 − 6 = −4 \\ f(0) = (0)^2/2 − 6 = −6 \\ f(2) = (2)^2/2 − 6 = −4 \\ f(4) = (4)^2/2 − 6 = 2\]
Colocar estos resultados en la tabla (a) y trazarlos como se muestra en (b). Aquí hay evidencia suficiente para intuir que la gráfica de f es la curva mostrada en (b).
x \(f(x) = x^2 − 2\) (x, f (x)) -4 \ (f (x) = x^2 − 2\) ">2 (−4, 2) -2 \ (f (x) = x^2 − 2\) ">-4 (-2, -4) 0 \ (f (x) = x^2 − 2\) ">-6 (0, -6) 2 \ (f (x) = x^2 − 2\) ">-4 (2, -4) 4 \ (f (x) = x^2 − 2\) ">2 (4,2)
(a)
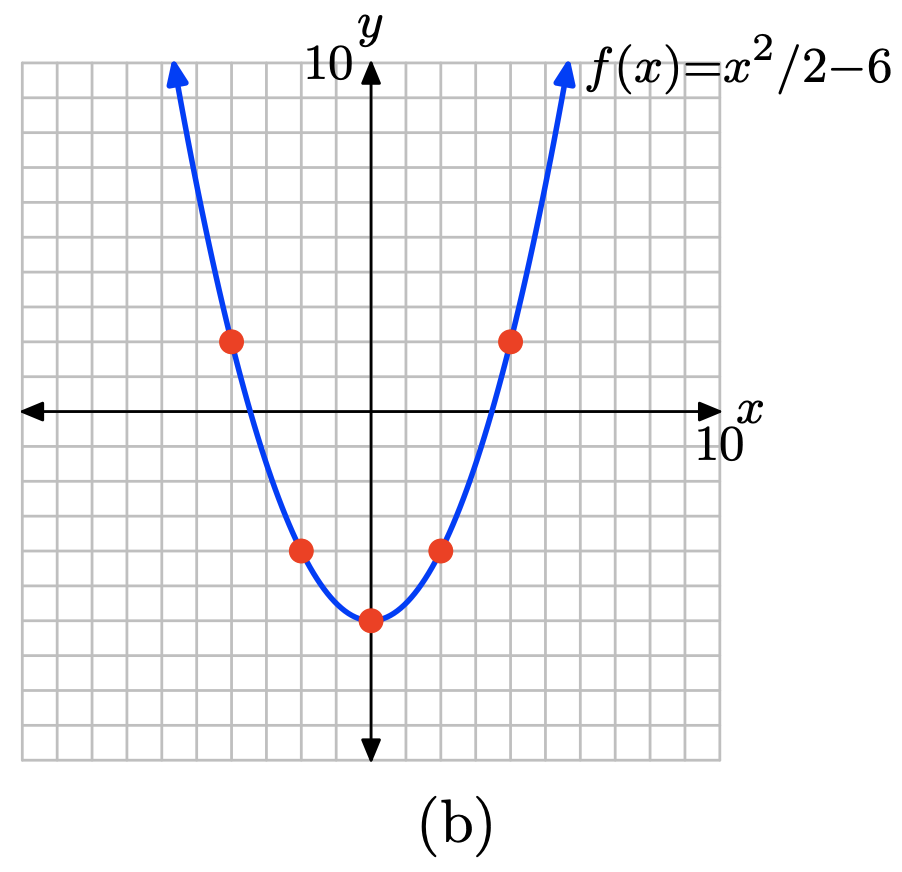
Ejercicio\(\PageIndex{8}\)
\(f(x) = 8-\dfrac{1}{2} x^2\)
Realizar cada una de las siguientes tareas para las funciones Ejercicios\(\PageIndex{9}\) -\(\PageIndex{10}\).
i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje.
ii. Utilice la función de tabla de su calculadora gráfica para evaluar la función a los valores dados de x. Registre estos resultados en una tabla junto a su sistema de coordenadas en su papel cuadriculado.
iii. Trace los puntos de la tabla en su sistema de coordenadas y luego utilícelos para dibujar la gráfica de la función dada. Etiquete la gráfica con su ecuación.
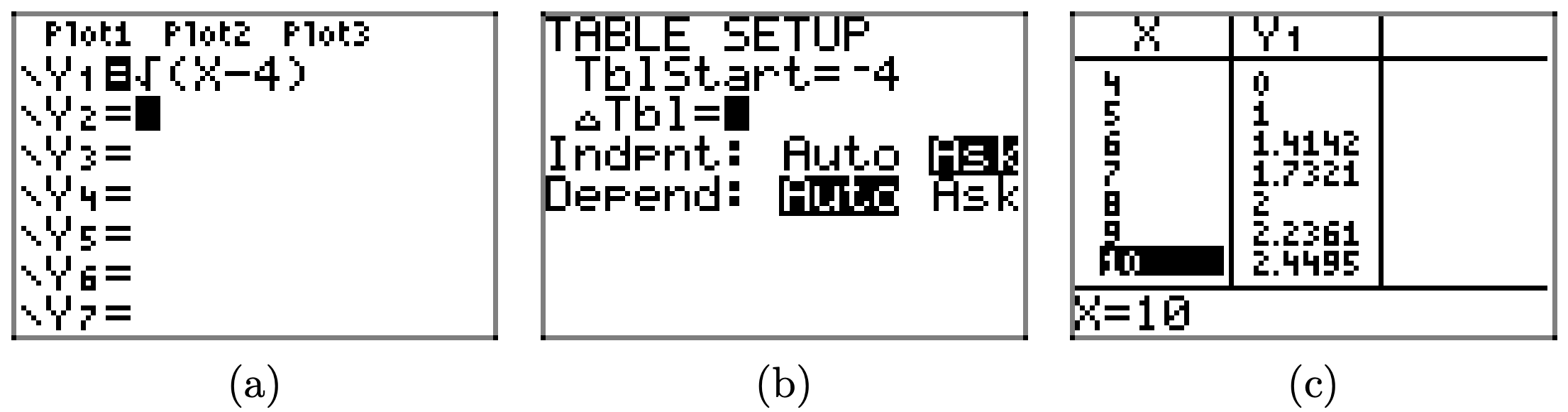
Ejercicio\(\PageIndex{9}\)
\(f(x) = \sqrt{x − 4}\)a x = 4, 5, 6, 7, 8, 9 y 10.
- Responder
-
Cargue la función\(f(x) = \sqrt{x − 4}\) en Y1 como se muestra en (a). Seleccione TBLSET, luego resalte ASK para la variable independiente y presione ENTRAR (ver (b)). No importa lo que se ingrese para TblStart o ∆Tbl. Seleccione TABLE e ingrese los valores x 4, 5, 6, 7, 8, 9 y 10, como se muestra en (c).
Trazar los puntos en la tabla (c) en (d). Esto es suficiente para intuir que la gráfica de f es la curva mostrada en (d).
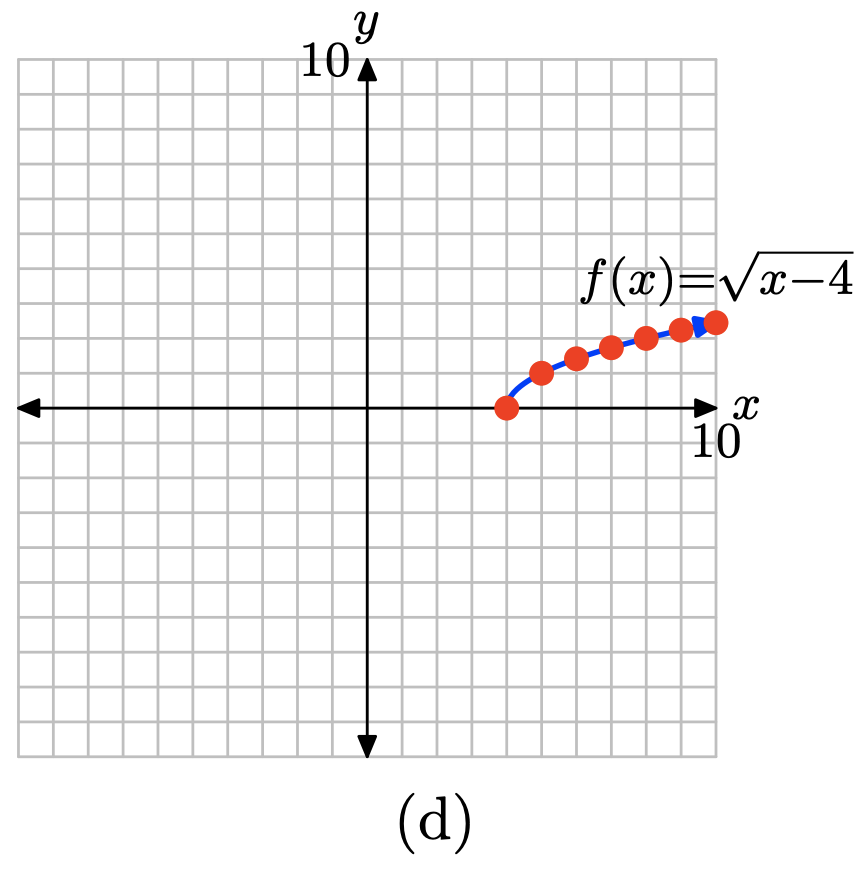
Ejercicio\(\PageIndex{10}\)
\(f(x) = \sqrt{4 − x}\)en x = −10, −8, −6, −4, −2, 0, 2 y 4.
En Ejercicios\(\PageIndex{11}\) -\(\PageIndex{14}\), la gráfica de la función dada es una parábola, una gráfica que tiene una “forma de U”. Una parábola tiene sólo un punto de inflexión. Para cada ejercicio, realice las siguientes tareas.
i. Cargue la ecuación en el menú Y= de su calculadora gráfica. Ajusta los parámetros WINDOW para que el “punto de inflexión” (realmente llamado vértice) sea visible en la ventana de visualización.
ii. Haga una copia razonable de la imagen en la ventana de visualización en su papel de tarea. Dibuja todas las líneas con una regla (incluyendo los ejes), pero dibuja curvas a mano alzada. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax. Etiquete la gráfica con su ecuación.
Ejercicio\(\PageIndex{11}\)
\(f(x) = x^{2} − x − 30\)
- Responder
-
Cargue la función\(f(x) = x^{2} − x − 30\) en Y1 como se muestra en (a). Ajuste los parámetros de VENTANA como se muestra en (b). Presione el botón GRAPAR para obtener la gráfica de f en (c).
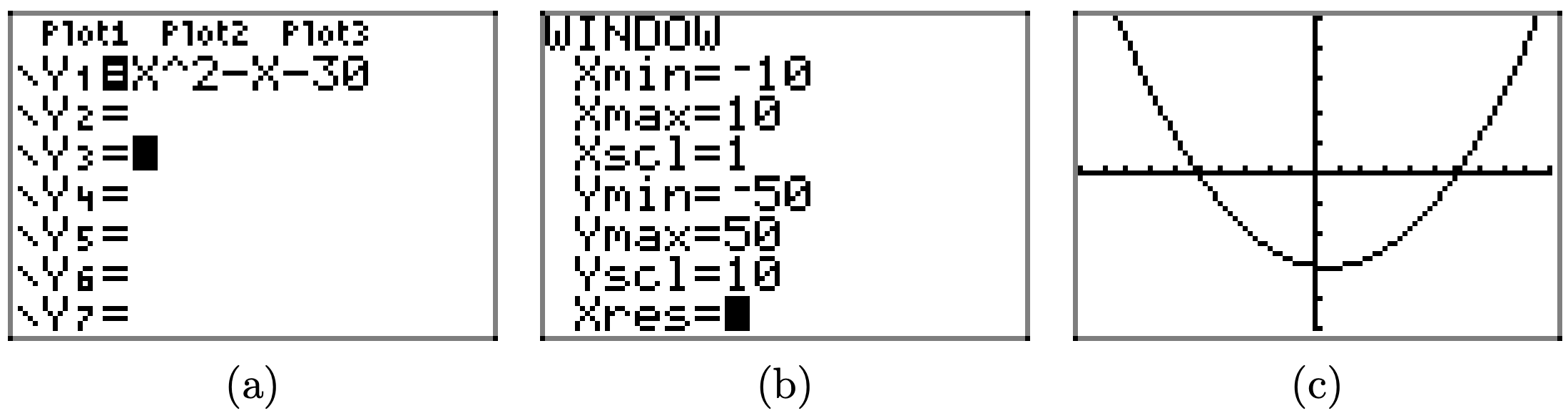
Copia la imagen en tu tarea como se muestra en (d).
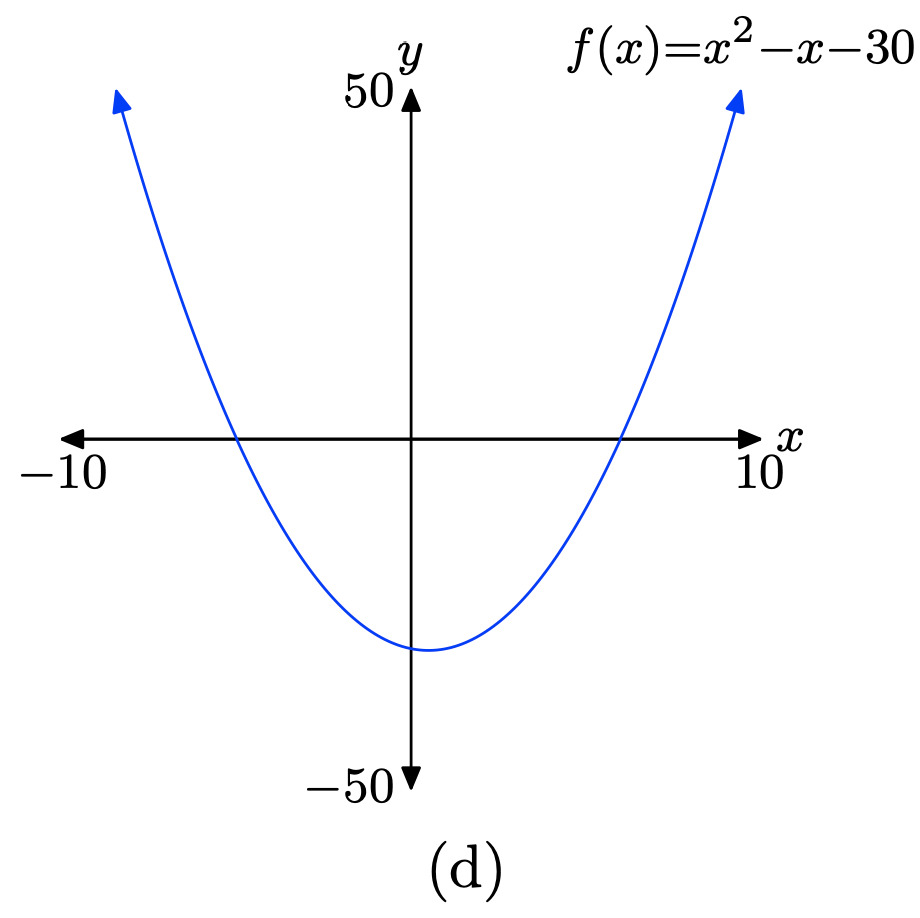
Ejercicio\(\PageIndex{12}\)
\(f(x) = 24 − 2x − x^2\)
Ejercicio\(\PageIndex{13}\)
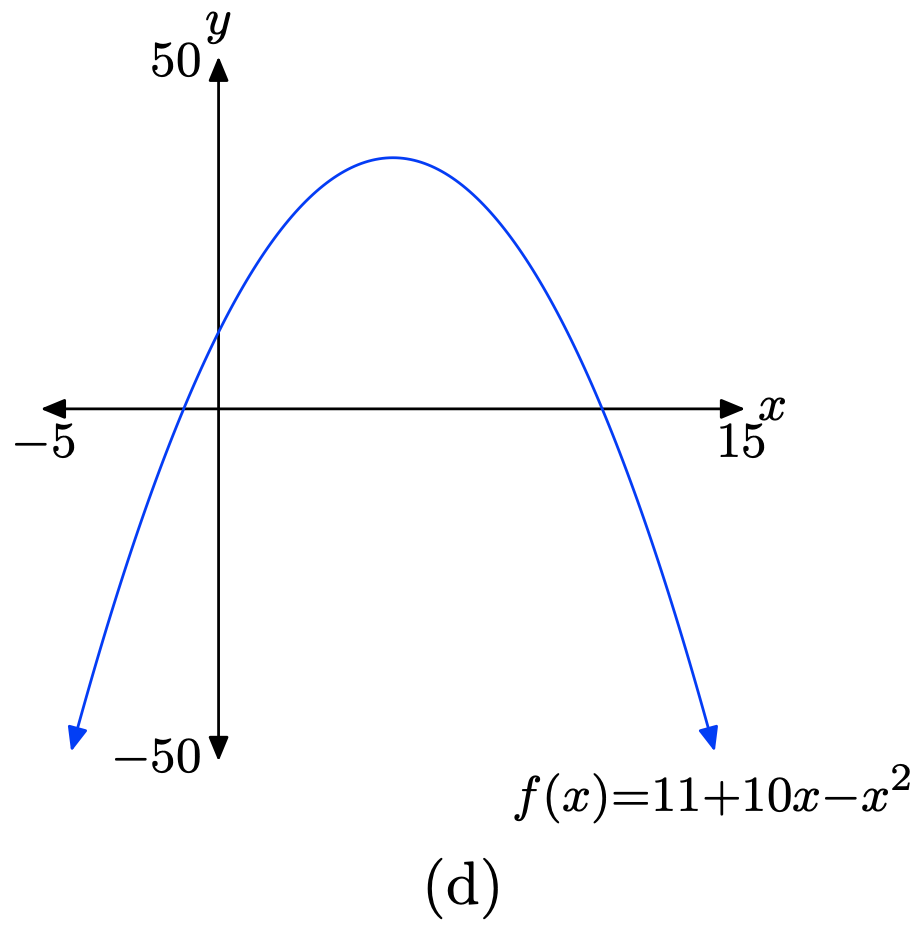
\(f(x) = 11 + 10x − x^2\)
- Responder
-
Cargue la función\(f(x) = 11 + 10x − x^2\) en Y1 como se muestra en (a). Ajuste los parámetros de VENTANA como se muestra en (b). Presione el botón GRAPAR para obtener la gráfica de f en (c).
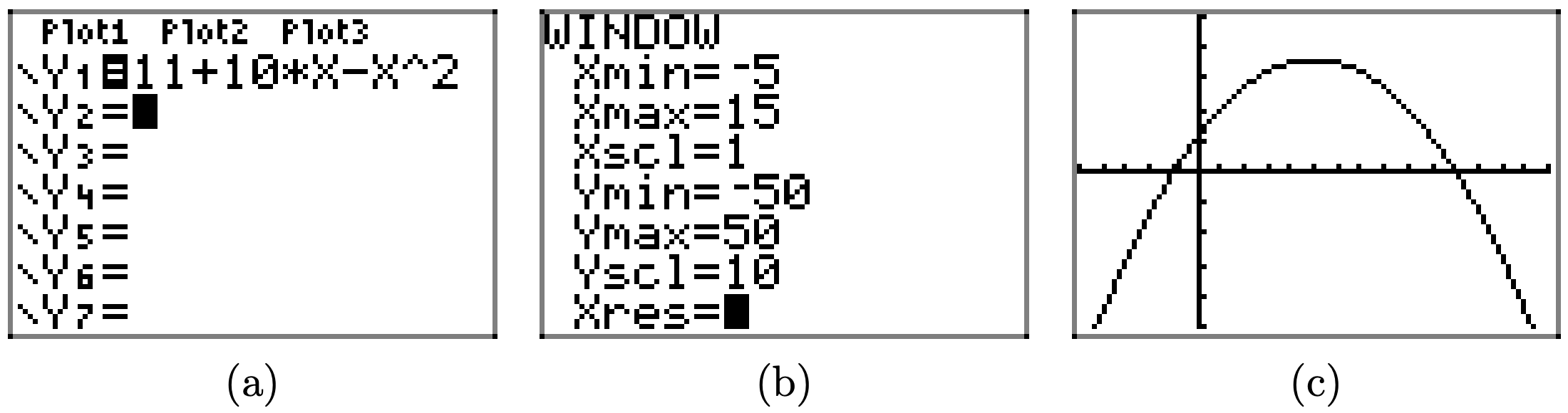
Copia la imagen en tu tarea como se muestra en (d).
Ejercicio\(\PageIndex{14}\)
\(f(x) = x^2 + 11x − 12\)
Cada una de las ecuaciones en Ejercicios\(\PageIndex{15}\) -\(\PageIndex{18}\) se llaman “polinomios cúbicos”. Cada ecuación ha sido cuidadosamente elegida para que su gráfica tenga exactamente dos “puntos de inflexión”. Para cada ejercicio, realice cada una de las siguientes tareas. i. Cargue la ecuación en el menú Y= de su calculadora gráfica y ajuste los parámetros WINDOW para que ambos “puntos de inflexión” sean visibles en la ventana de visualización. ii. Haga una copia razonable del gráfico en la ventana de visualización en su papel de tarea. Marque y escale cada eje con xmin, xmax, ymin e ymax, luego etiquete la gráfica con su ecuación. Recuerda dibujar todas las líneas con una regla.
Ejercicio\(\PageIndex{15}\)
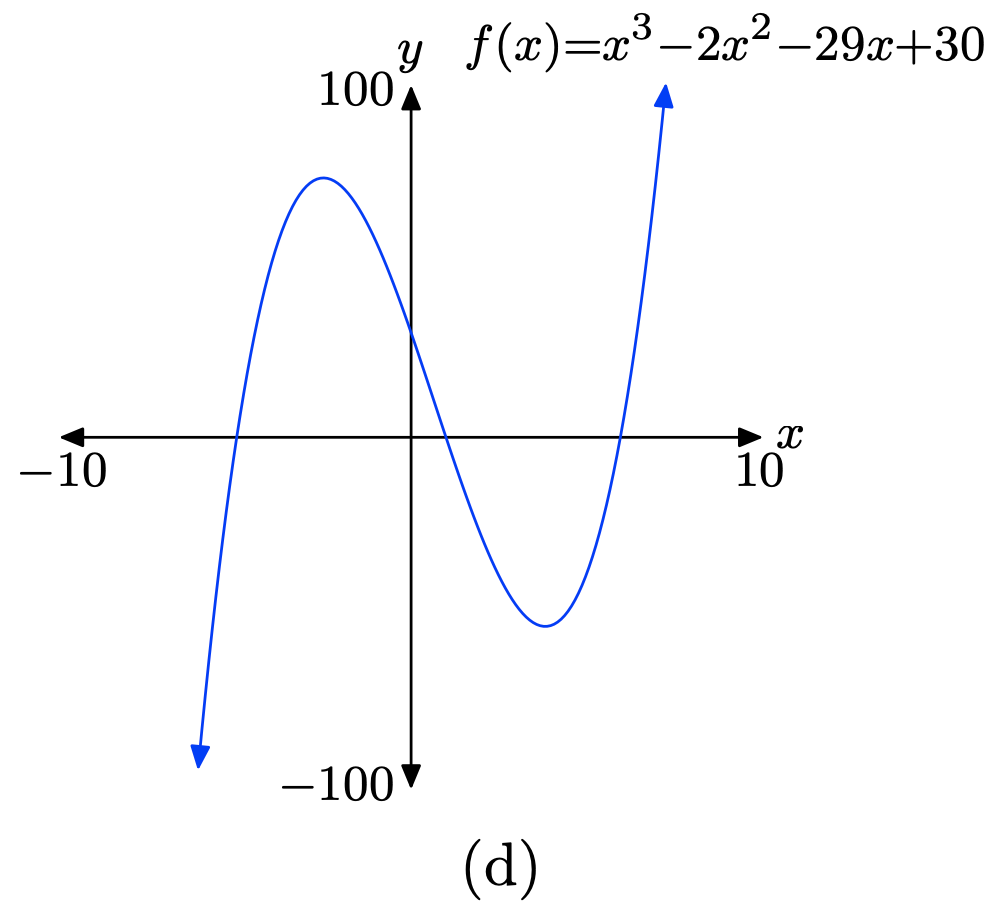
\(f(x) = x^3 − 2x^2 − 29x + 30\)
- Responder
-
Cargue la función\(f(x) = x^3 − 2x^2 − 29x + 30\) en Y1 como se muestra en (a). Ajuste los parámetros de VENTANA como se muestra en (b). Presione el botón GRAPAR para obtener la gráfica de f en (c).
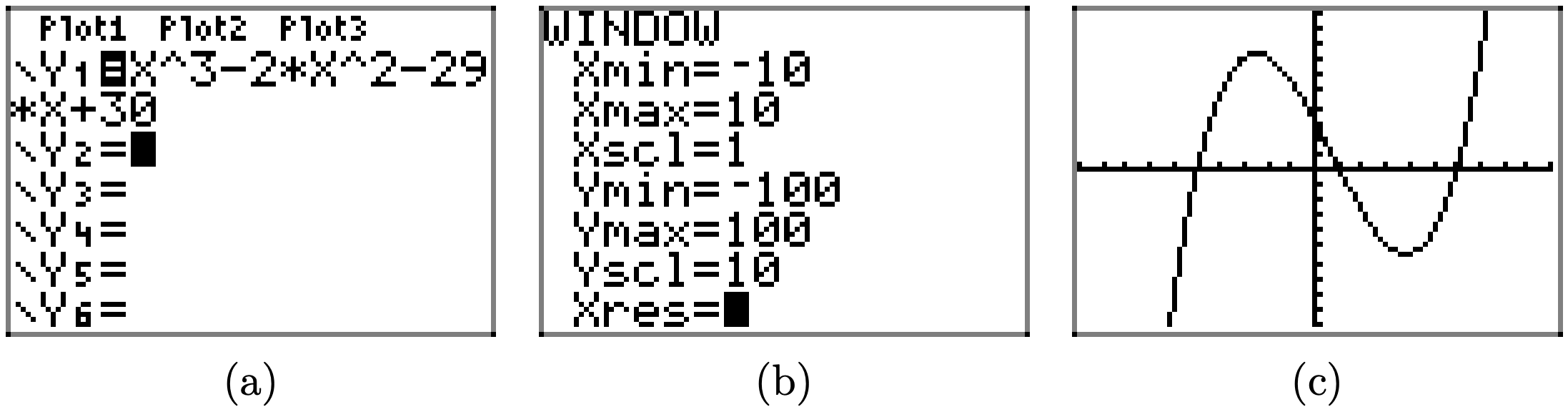
Copia la imagen en tu tarea como se muestra en (d).
Ejercicio\(\PageIndex{16}\)
\(f(x) = −x^3 + 2x^2 + 19x − 20\)
Ejercicio\(\PageIndex{17}\)
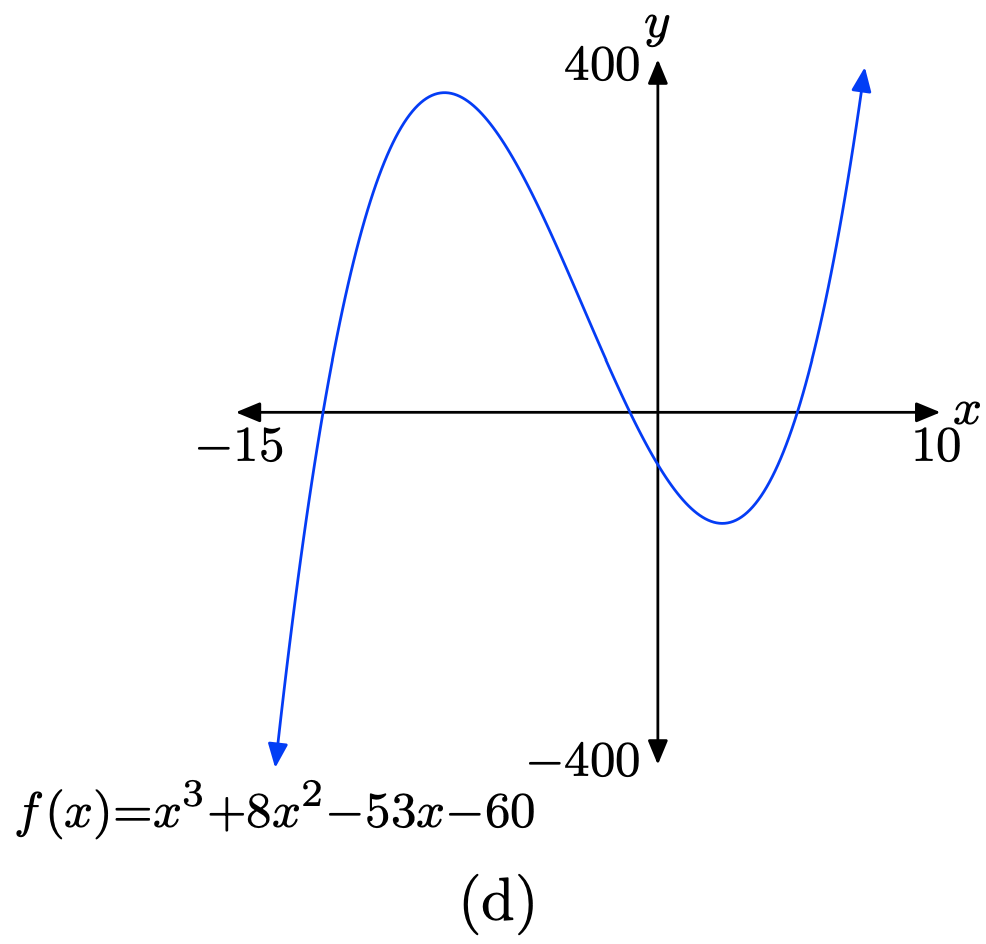
\(f(x) = x^3 + 8x^2 − 53x − 60\)
- Responder
-
Cargue la función\(f(x) = x^3 + 8x^2 − 53x − 60\) en Y1 como se muestra en (a). Ajuste los parámetros de VENTANA como se muestra en (b). Presione el botón GRAPAR para obtener la gráfica de f en (c).
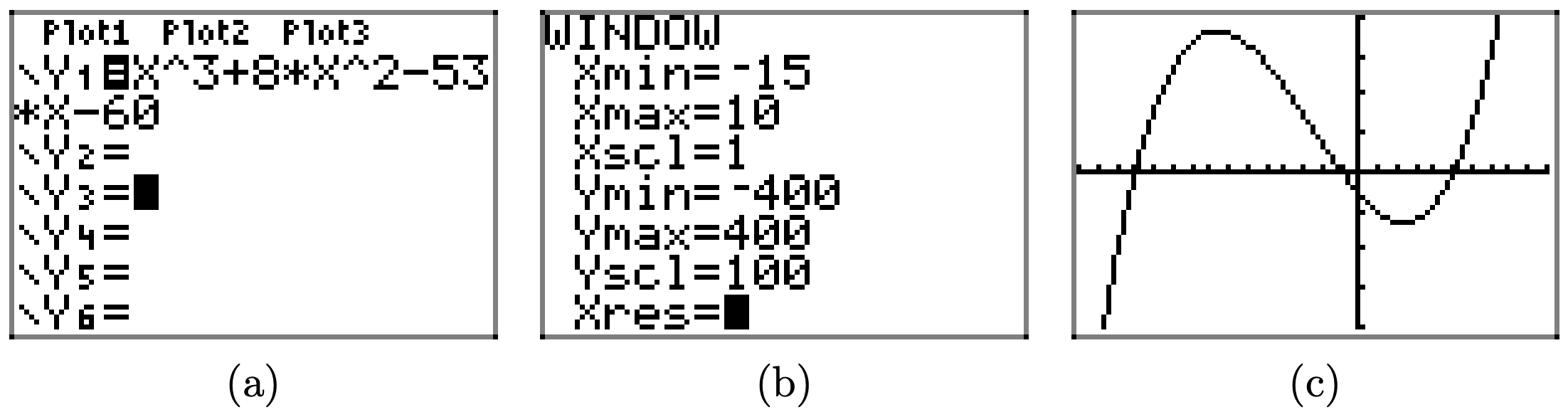
Copia la imagen en tu tarea como se muestra en (d).
Ejercicio\(\PageIndex{18}\)
\(f(x) = −x^3 + 16x^2 − 43x − 60\)
Realizar cada una de las siguientes tareas para las ecuaciones en Ejercicios\(\PageIndex{19}\) -\(\PageIndex{22}\).
i. Cargar la ecuación en el menú Y=. Ajuste los parámetros de VENTANA hasta que piense que todo el comportamiento importante (“puntos de inflexión”, etc.) es visible en la ventana de visualización. Nota: Esto es más difícil de lo que parece, particularmente cuando no tenemos una noción anticipada de cómo podría ser la gráfica. Sin embargo, experimenta con varios escenarios hasta que “descubras” los escenarios que exhiben el comportamiento más importante.
ii. Copia la imagen en la pantalla en tu papel de tarea. Etiquetar y escalar cada eje con xmin, xmax, ymin e ymax. Etiquete la gráfica con su ecuación.
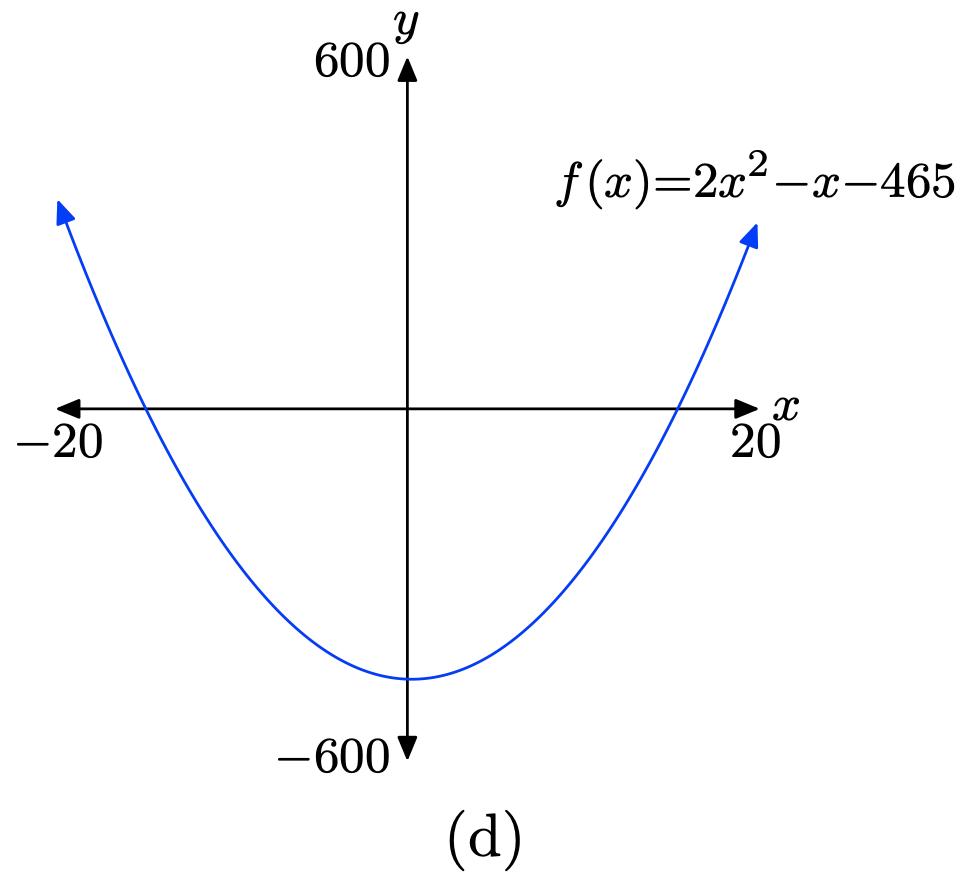
Ejercicio\(\PageIndex{19}\)
\(f(x) = 2x^2 − x − 465\)
- Contestar
-
Cargue la función\(f(x) = 2x^2 − x − 465\) en Y1 como se muestra en (a). Ajuste los parámetros de VENTANA como se muestra en (b). Presione el botón GRAPAR para obtener la gráfica de f en (c).

Copia la imagen en tu tarea como se muestra en (d).
Ejercicio\(\PageIndex{20}\)
\(f(x) = x^3 − 24x^2 + 65x + 1050\)
Ejercicio\(\PageIndex{21}\)
\(f(x) = x^4 − 2x^3 − 168x^2 + 288x + 3456\)
- Contestar
-
Cargue la función\(f(x) = x^4 − 2x^3 − 168x^2 + 288x + 3456\) en Y1 como se muestra en (a). Ajuste los parámetros de VENTANA como se muestra en (b). Presione el botón GRAPAR para obtener la gráfica de f en (c).
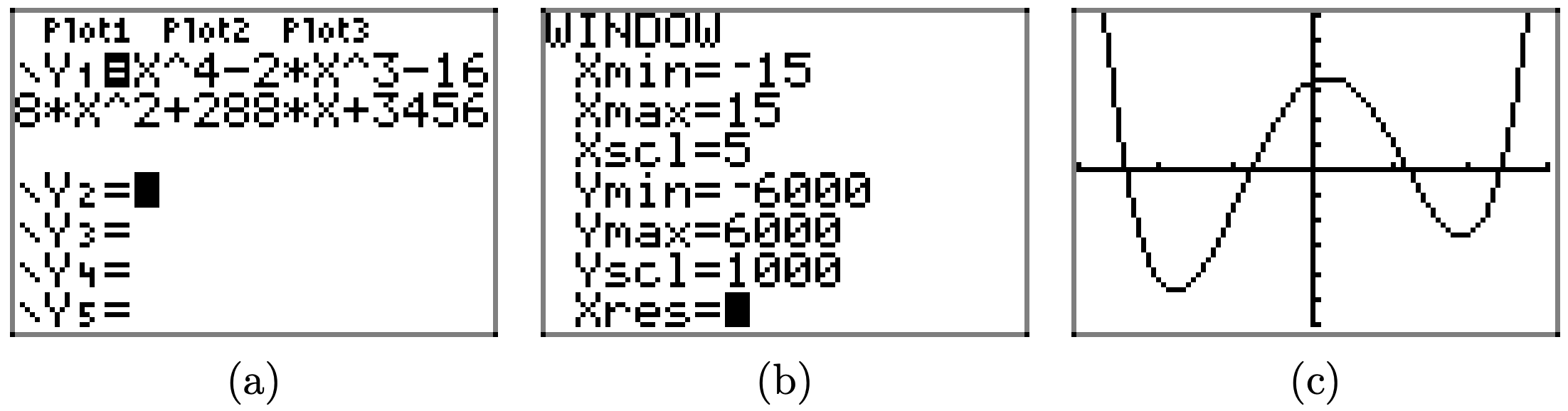
Copia la imagen en tu tarea como se muestra en (d)
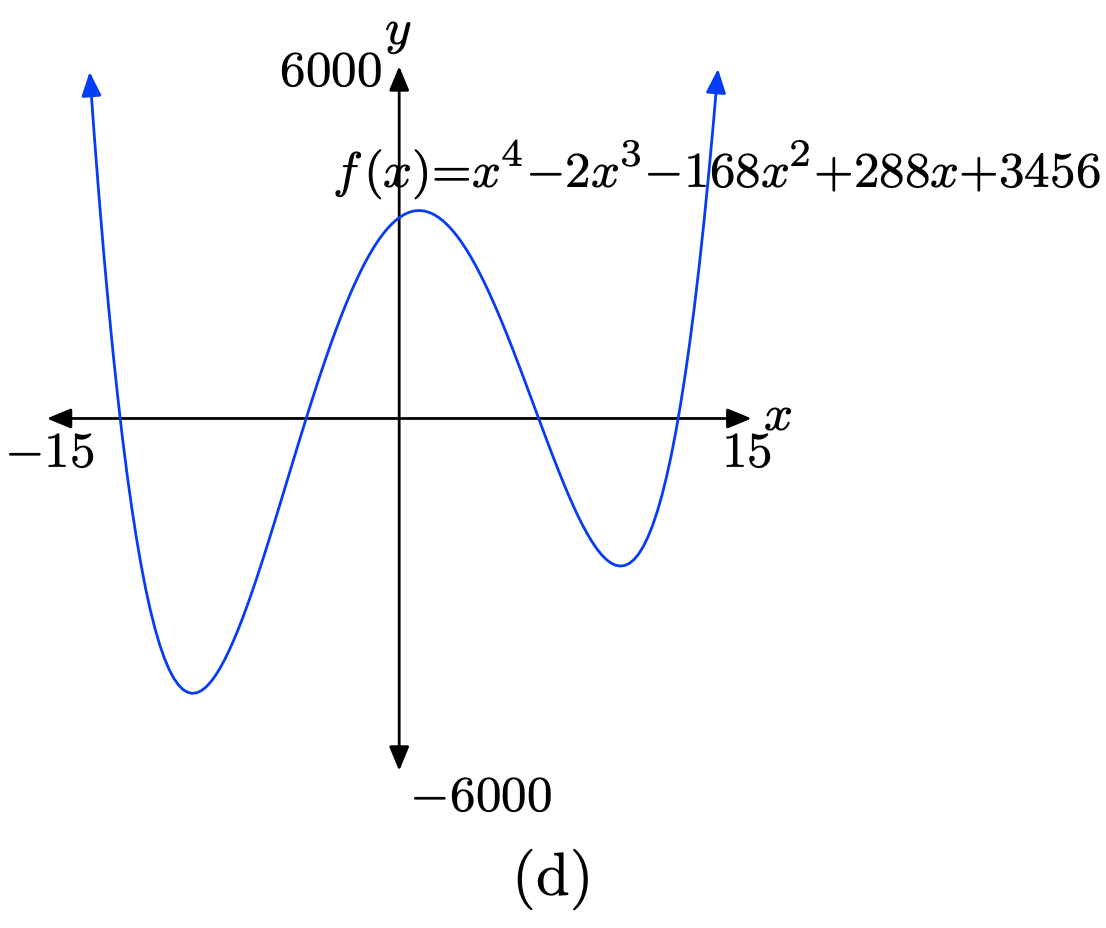
Ejercicio\(\PageIndex{22}\)
\(f(x) = −x^4 −3x^3 +141x^2 +523x− 660\)
2.3 Ejercicios
Para Ejercicios\(\PageIndex{1}\) -\(\PageIndex{6}\), realizar cada una de las siguientes tareas.
i. Hacer una copia de la gráfica en una hoja de papel cuadriculado y aplicar la prueba de línea vertical.
ii. Escribe una oración completa indicando si la gráfica representa o no una función. Explica el motivo de tu respuesta.
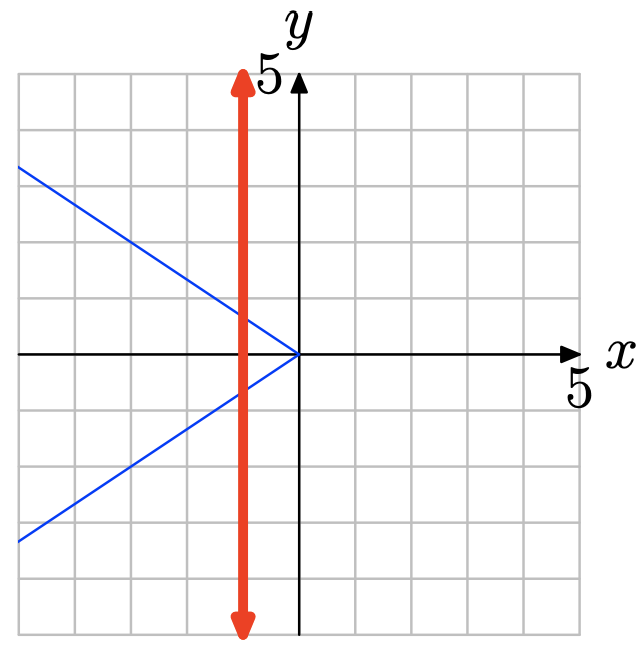
Ejercicio\(\PageIndex{1}\)
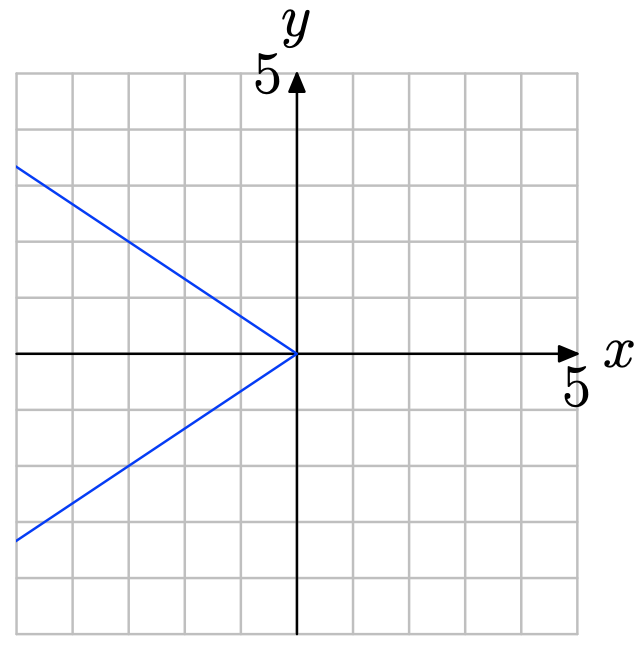
- Contestar
-
Obsérvese que en la figura de abajo una línea vertical corta la gráfica más de una vez. Por lo tanto, la gráfica no representa la gráfica de una función.
Ejercicio\(\PageIndex{2}\)
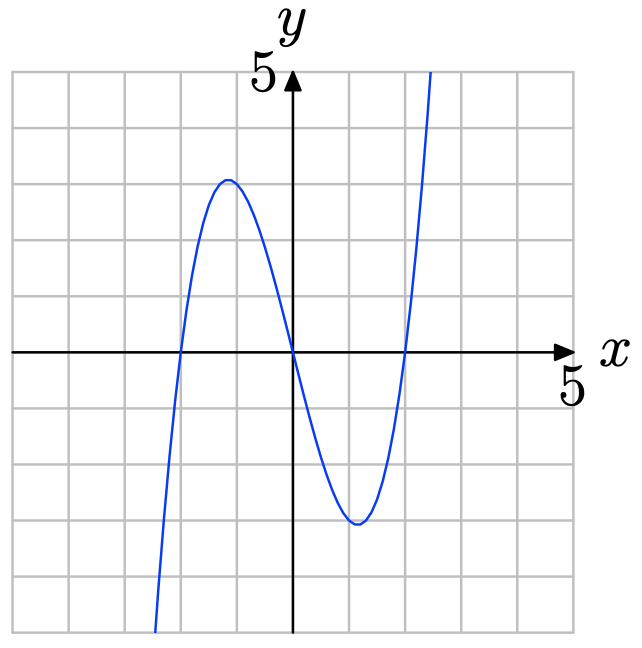
Ejercicio\(\PageIndex{3}\)
- Contestar
-
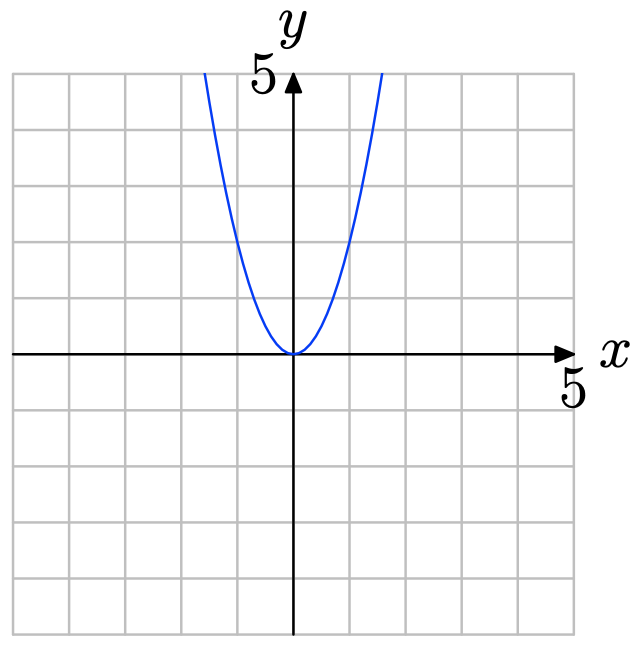
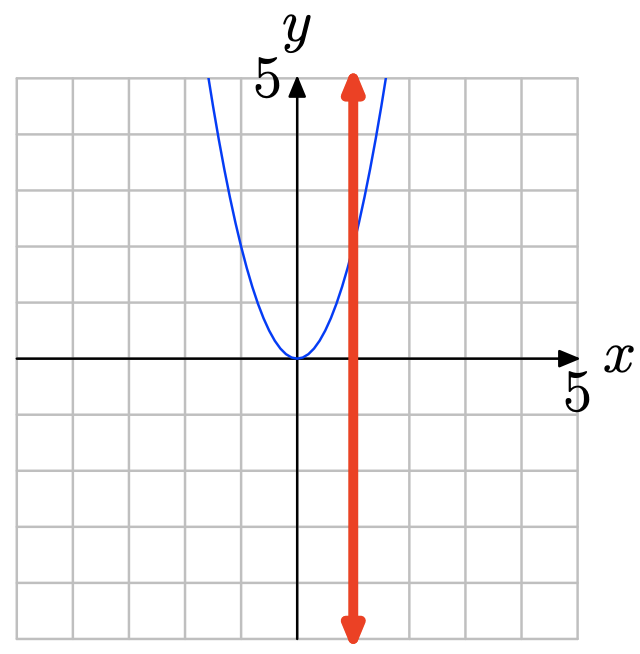
Ninguna línea vertical corta la gráfica más de una vez (ver figura a continuación). Por lo tanto, la gráfica representa una función.
Ejercicio\(\PageIndex{4}\)
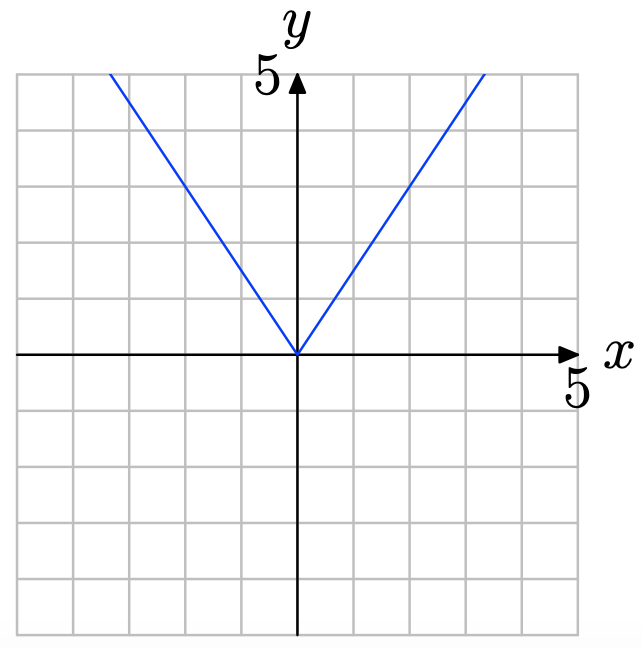
Ejercicio\(\PageIndex{5}\)
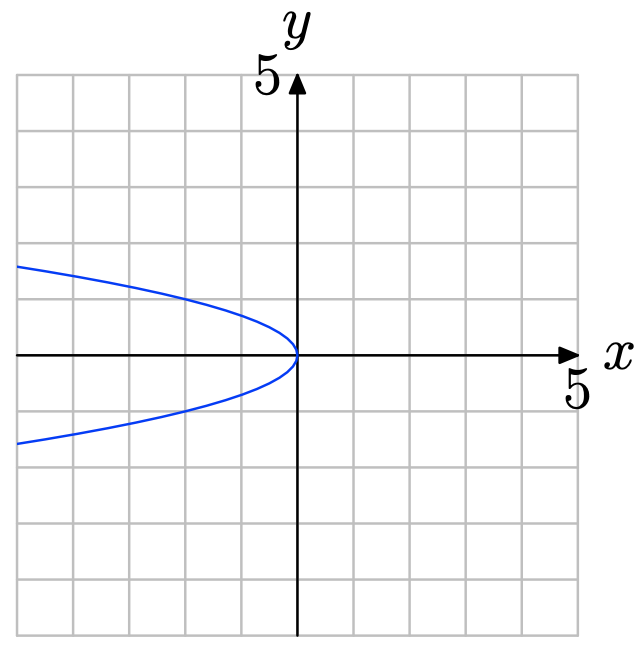
- Contestar
-
Obsérvese que en la figura de abajo una línea vertical corta la gráfica más de una vez. Por lo tanto, la gráfica no representa la gráfica de una función.
Ejercicio\(\PageIndex{6}\)
En Ejercicios\(\PageIndex{7}\) -\(\PageIndex{12}\), realizar cada una de las siguientes tareas.
i. Hacer una copia exacta de la gráfica de la función f en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
ii. Utilizar la técnica de los Ejemplos 3 y 4 en la narrativa para evaluar la función en el valor dado. Dibuja y etiqueta las flechas como se muestra en las figuras 4 y 5 de la narrativa.
Ejercicio\(\PageIndex{7}\)
Utilice la gráfica de f para determinar f (2).
- Contestar
-
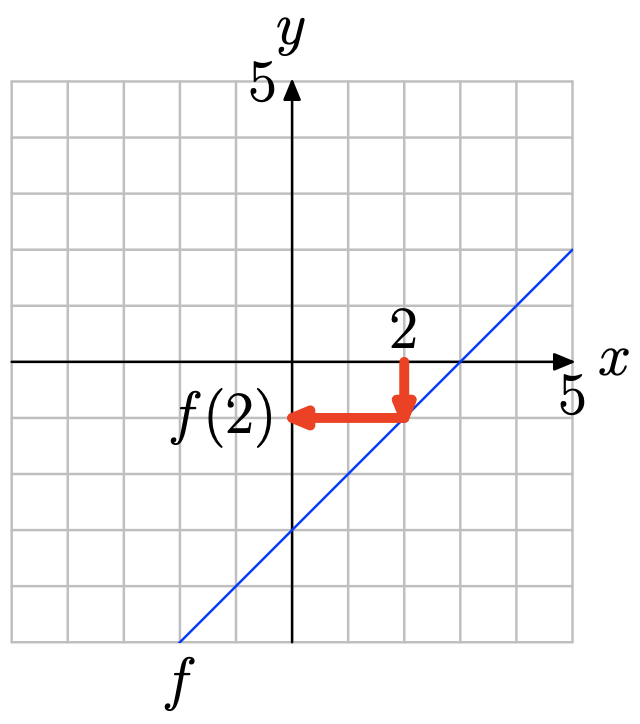
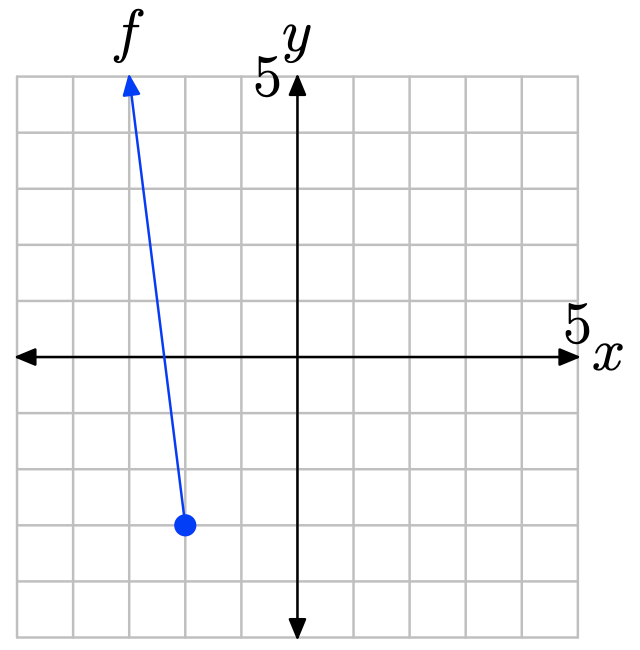
Localice x = 2 en el eje x (vea la figura a continuación), dibuje una flecha vertical a la gráfica de f, luego una flecha horizontal al eje y. Así, f (2) = −1.
Ejercicio\(\PageIndex{8}\)
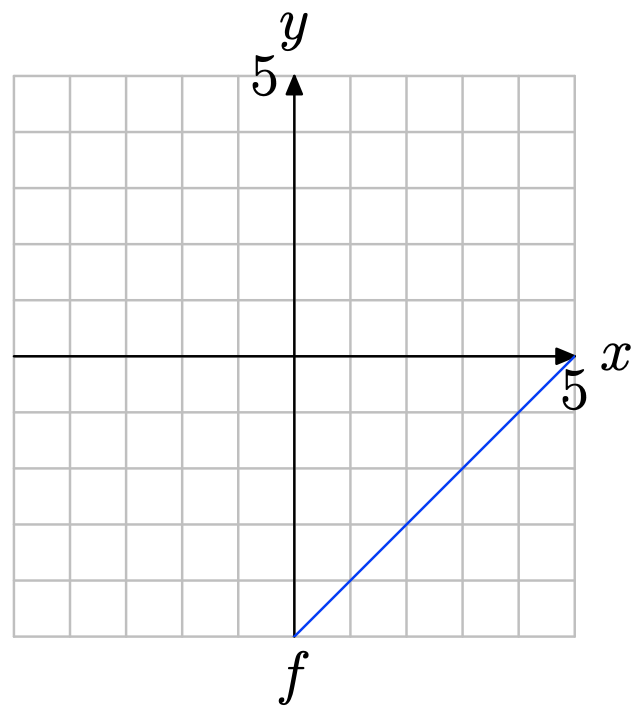
Utilice la gráfica de f para determinar f (3).
Ejercicio\(\PageIndex{9}\)
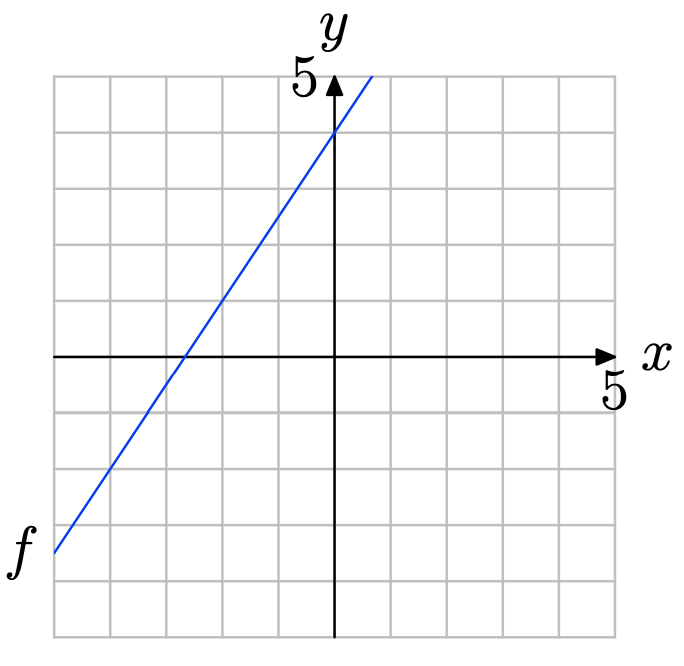
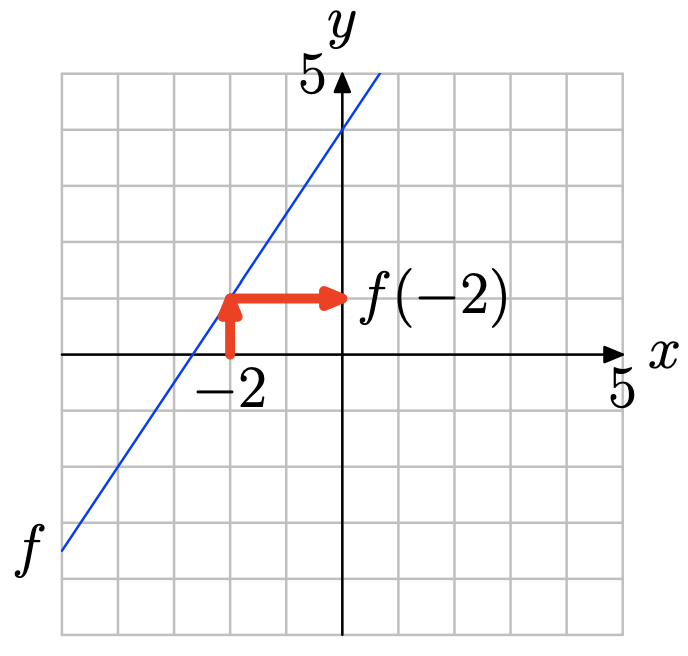
Utilice la gráfica de f para determinar f (−2).
- Contestar
-
Localice x = −2 en el eje x (vea la figura a continuación), dibuje una flecha vertical a la gráfica de f, luego una flecha horizontal al eje y. Así, f (−2) = 1.
Ejercicio\(\PageIndex{10}\)
Utilice la gráfica de f para determinar f (1).
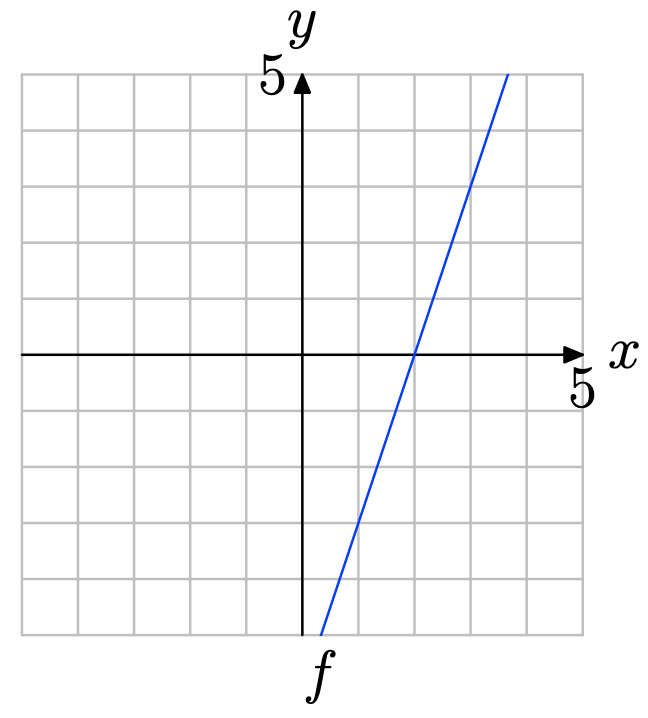
Ejercicio\(\PageIndex{11}\)
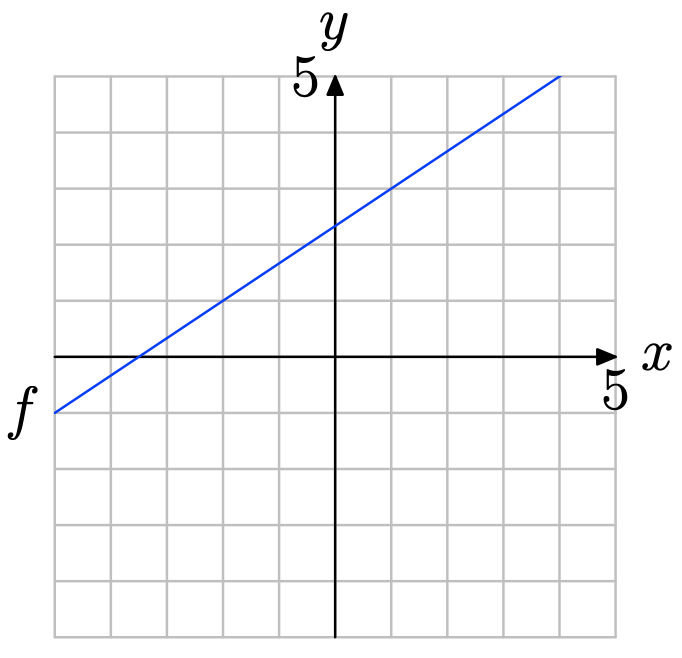
Utilice la gráfica de f para determinar f (1).
- Contestar
-
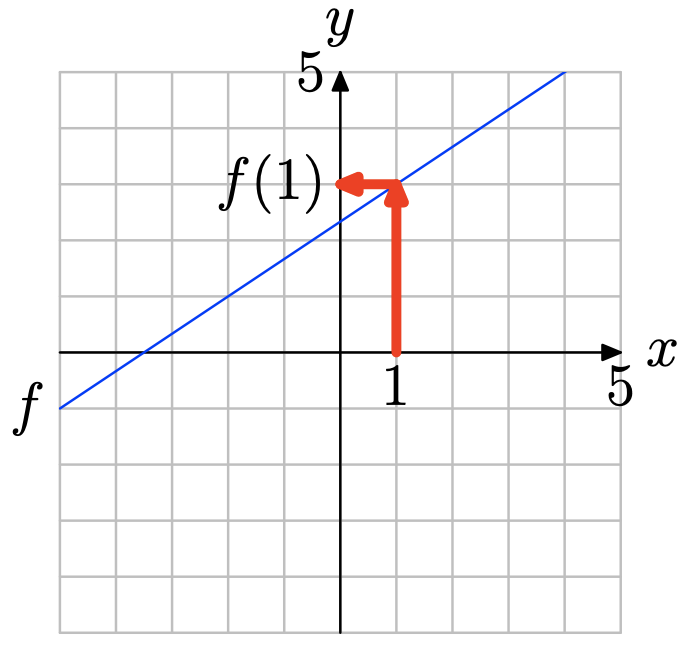
Localice x = 1 en el eje x (vea la figura a continuación), dibuje una flecha vertical a la gráfica de f, luego una flecha horizontal al eje y. Así, f (1) = 3.
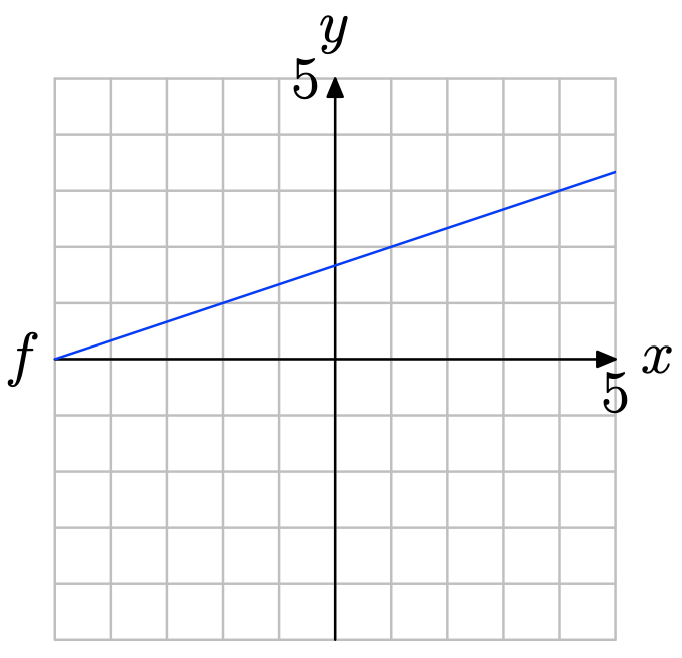
Ejercicio\(\PageIndex{12}\)
Utilice la gráfica de f para determinar f (−2).
En Ejercicios\(\PageIndex{13}\) -\(\PageIndex{18}\), realizar cada una de las siguientes tareas.
i. Hacer una copia exacta de la gráfica de la función f en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
ii. Utilice la técnica del Ejemplo 5 en la narrativa para encontrar el valor de x que se mapea sobre el valor dado. Dibuje y etiquete las flechas como se muestra en la Figura 6 en la narrativa.
Ejercicio\(\PageIndex{13}\)
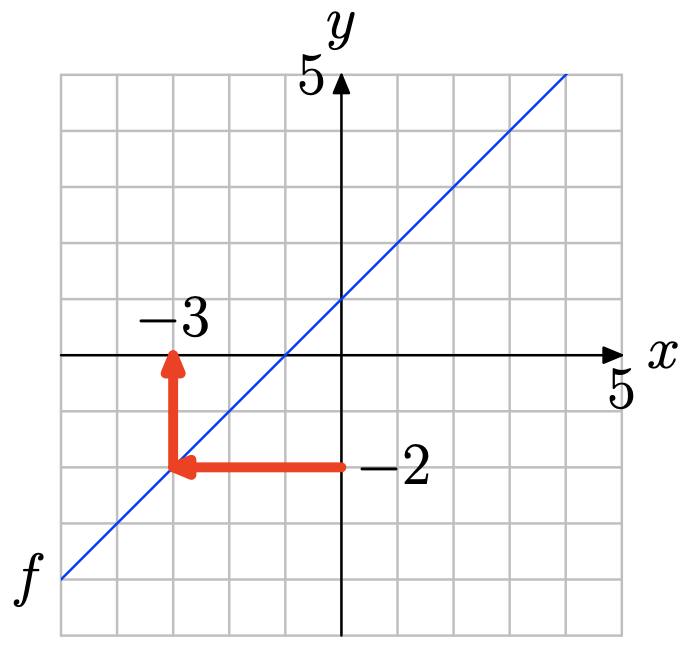
Usa la gráfica de f para resolver la ecuación f (x) = −2.
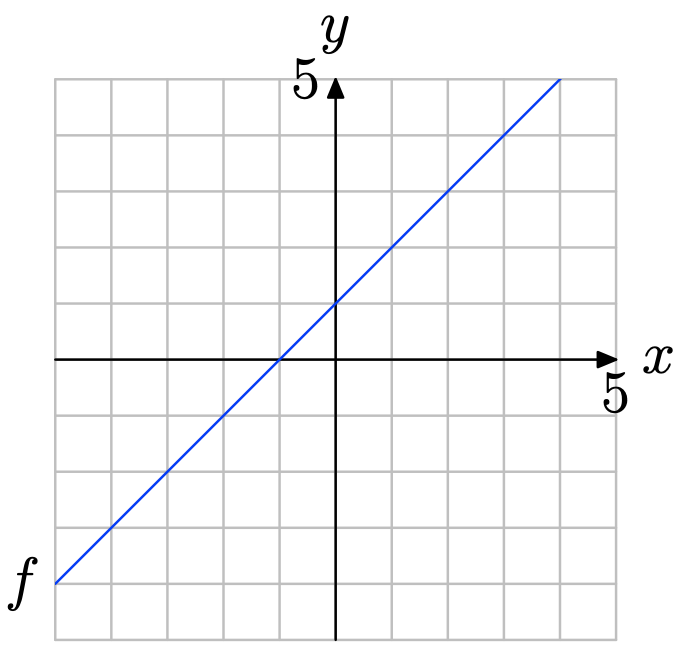
- Contestar
-
Localice y = −2 en el eje y (vea la figura a continuación), dibuje una flecha horizontal a la gráfica de f, luego una flecha vertical al eje y. Así, la solución de f (x) = −2 es x = −3.
Ejercicio\(\PageIndex{14}\)
Usa la gráfica de f para resolver la ecuación f (x) = 1.
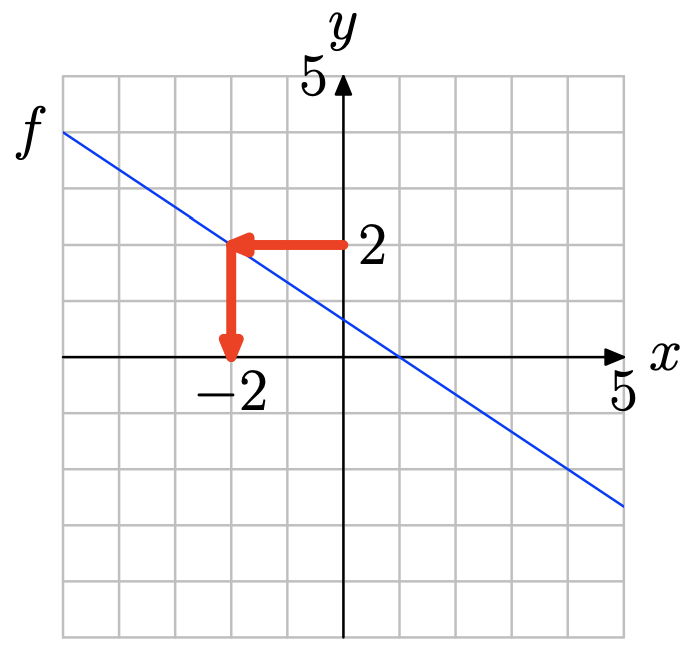
Ejercicio\(\PageIndex{15}\)
Usa la gráfica de f para resolver la ecuación f (x) = 2
- Contestar
-
Localice y = 2 en el eje y (vea la figura a continuación), dibuje una flecha horizontal a la gráfica de f, luego una flecha vertical al eje y. Así, la solución de f (x) = 2 es x = −2.
Ejercicio\(\PageIndex{16}\)
Usa la gráfica de f para resolver la ecuación f (x) = −2.
Ejercicio\(\PageIndex{17}\)
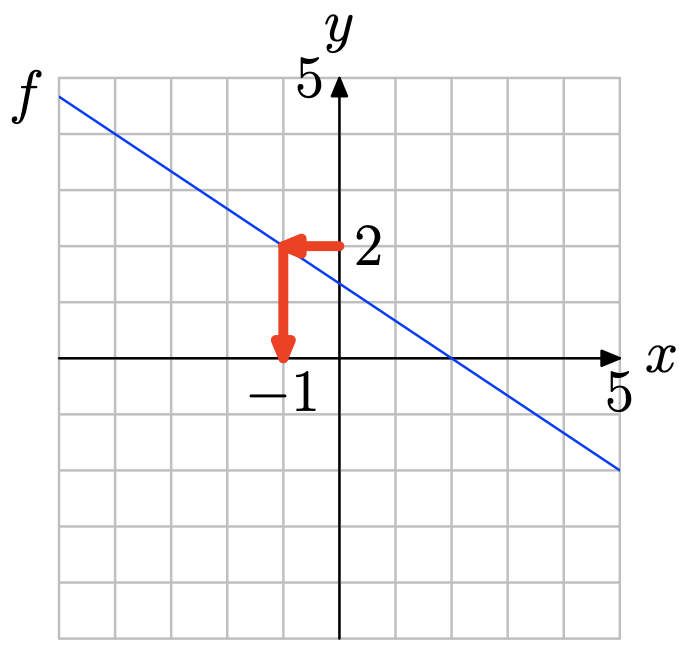
Usa la gráfica de f para resolver la ecuación f (x) = 2.
- Contestar
-
Localice y = 2 en el eje y (vea la figura a continuación), dibuje una flecha horizontal a la gráfica de f, luego una flecha vertical al eje y. Así, la solución de f (x) = 2 es x = −1.
Ejercicio\(\PageIndex{18}\)
Usa la gráfica de f para resolver la ecuación f (x) = −3.
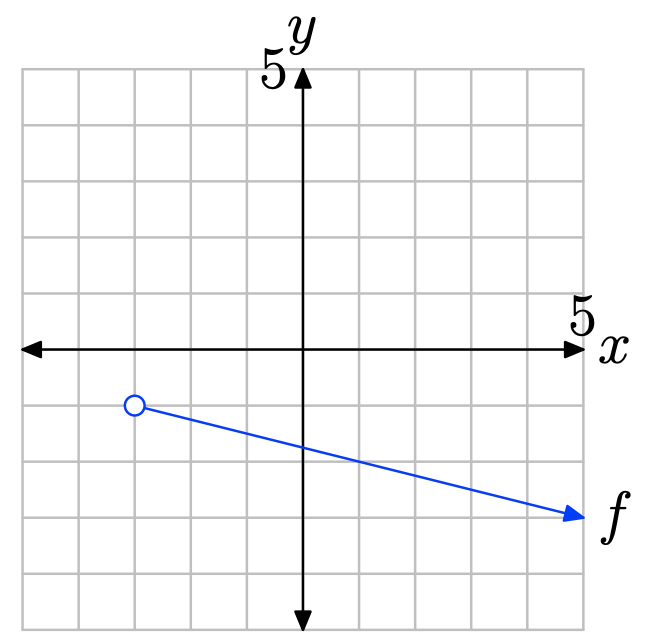
En los Ejercicios\(\PageIndex{19}\) -\(\PageIndex{22}\), realizar cada una de las siguientes tareas.
i. Hacer copia de la gráfica de f en una hoja de papel cuadriculado. Etiquetar y escalar cada eje.
ii. Usando una pluma o lápiz de diferentes colores, proyecte cada punto de la gráfica de f en el eje x. Sombra el dominio resultante en el eje x.
iii. Utilice tanto el generador de conjuntos como la notación de intervalos para describir el dominio.
Ejercicio\(\PageIndex{19}\)
- Contestar
-
Para encontrar el dominio de la función, proyecte la gráfica de f sobre el eje x. Tenga en cuenta que todos los valores de x que se encuentran a la derecha de −3 se encuentran en sombra y, por lo tanto, están en el dominio de f. Por lo tanto, el dominio se describe mejor con la notación\(\{x : x > −3\} = (−3,\infty)\).
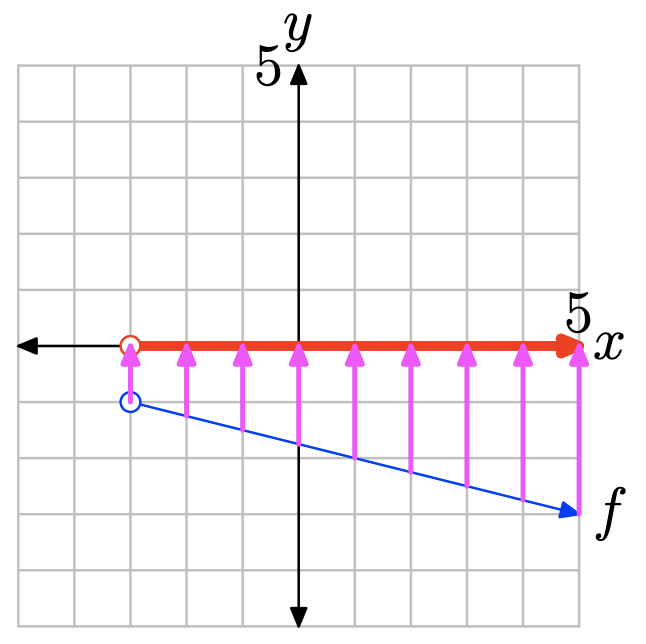
Ejercicio\(\PageIndex{20}\)
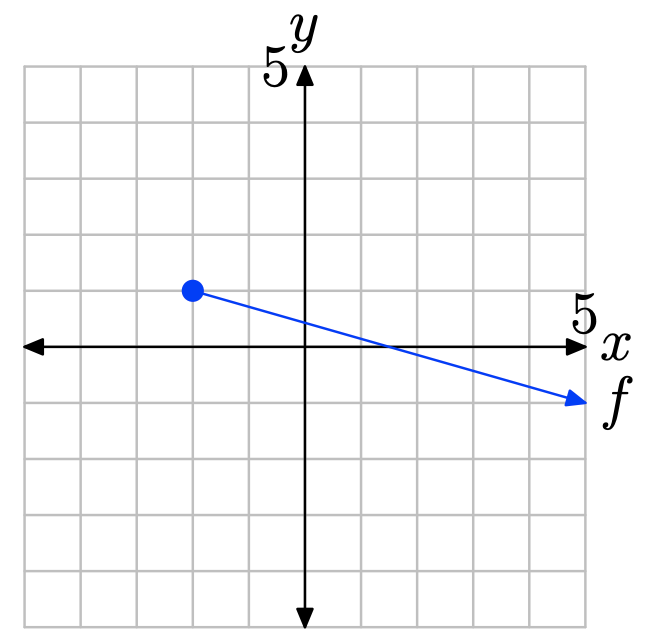
Ejercicio\(\PageIndex{21}\)
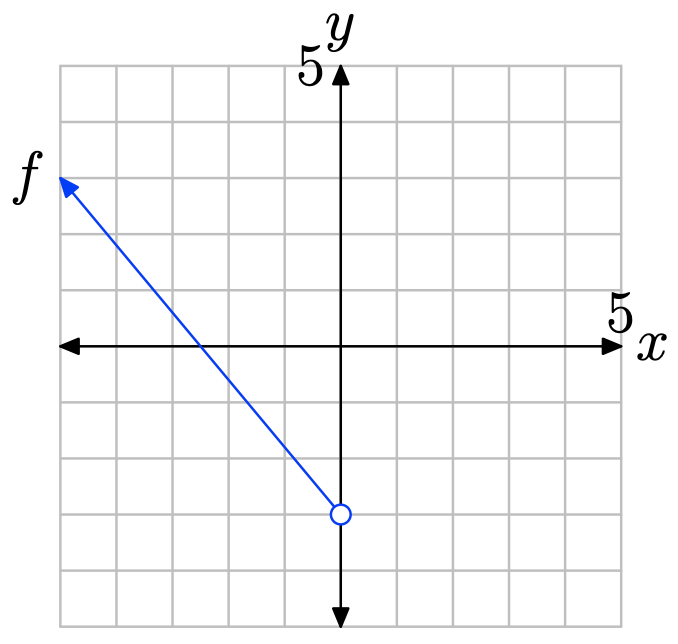
- Contestar
-
Para encontrar el dominio de la función, proyecte la gráfica de f sobre el eje x. Tenga en cuenta que todos los valores de x que se encuentran a la izquierda de 0 se encuentran en sombra y, por lo tanto, están en el dominio de f Por lo tanto, el dominio se describe mejor con la notación de intervalo\(\{x : x < 0\} = (−\infty, 0)\).
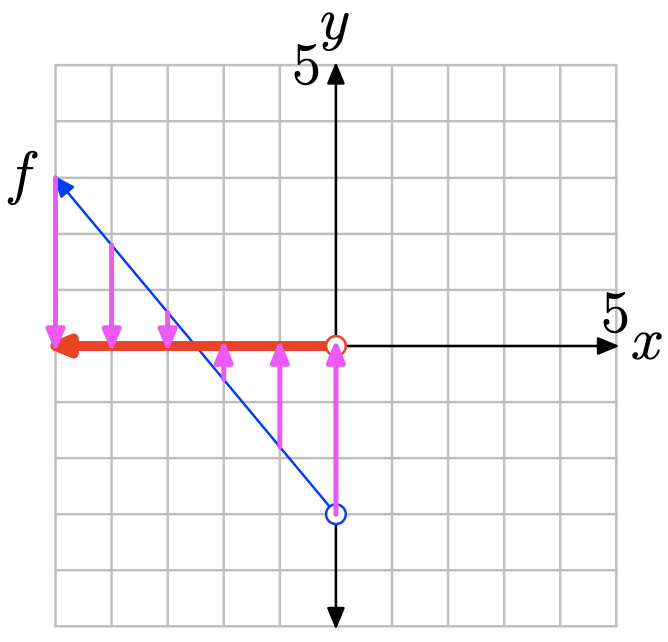
Ejercicio\(\PageIndex{22}\)
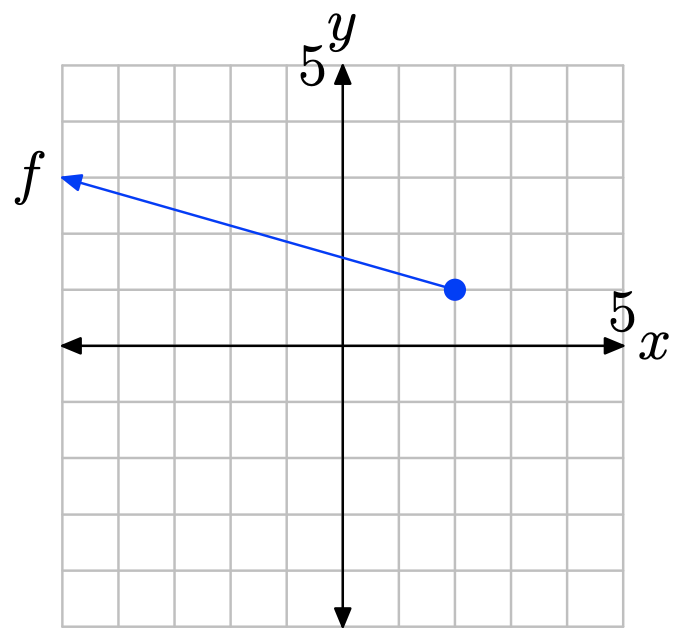
En Ejercicios\(\PageIndex{23}\) -\(\PageIndex{26}\), realizar cada una de las siguientes tareas.
i. Hacer copia de la gráfica de f en una hoja de papel cuadriculado. Etiquetar y escalar cada eje.
ii. Usando una pluma o lápiz de diferentes colores, proyecte cada punto de la gráfica de f sobre el eje y. Sombra el rango resultante en el eje y. iii. Utilice tanto el generador de conjuntos como la notación de intervalos para describir el rango.
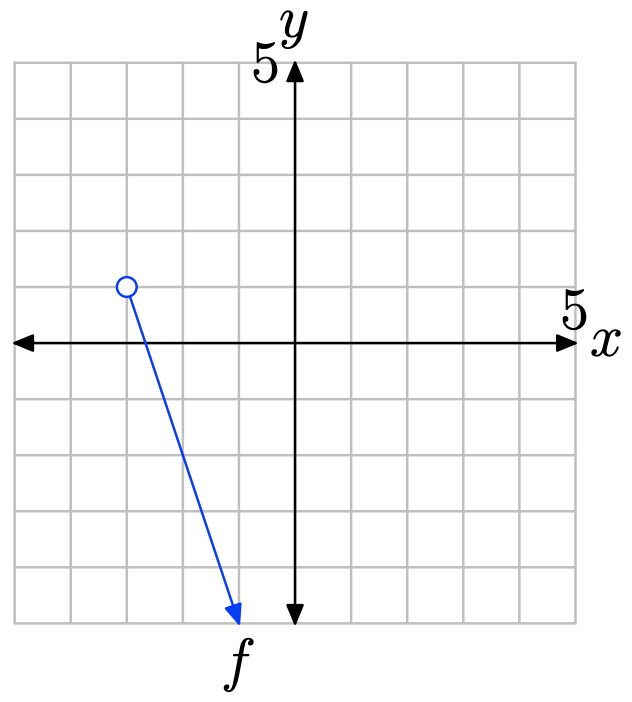
Ejercicio\(\PageIndex{23}\)
- Contestar
-
Para encontrar el rango de la función, proyecte la gráfica de f sobre el eje y. Tenga en cuenta que todos los valores de y que se encuentran por debajo de 1 se encuentran en sombra y, por lo tanto, están en el rango de f Por lo tanto, el rango se describe mejor con la notación de intervalo\(\{y : y < 1\} = (−\infty, 1)\).
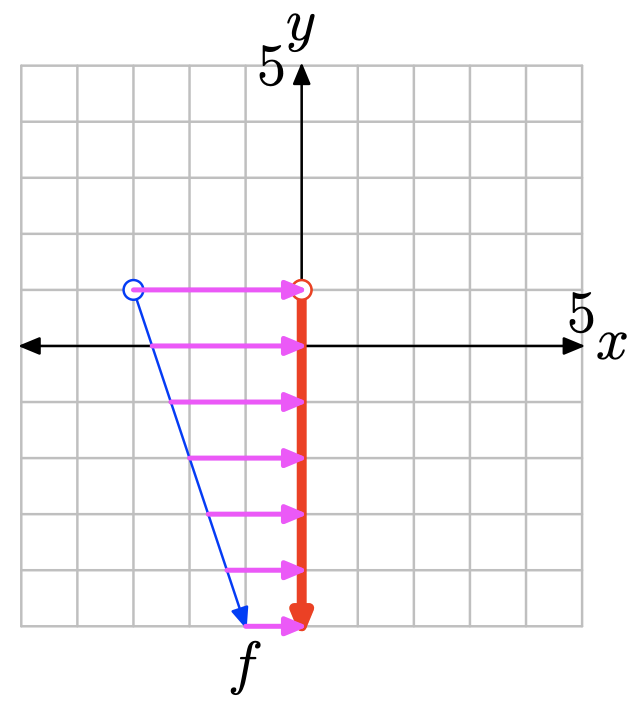
Ejercicio\(\PageIndex{24}\)
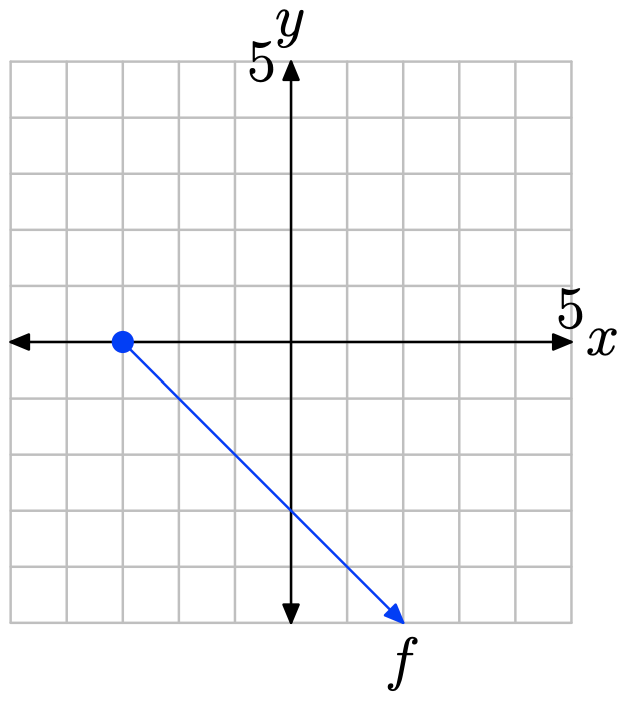
Ejercicio\(\PageIndex{25}\)
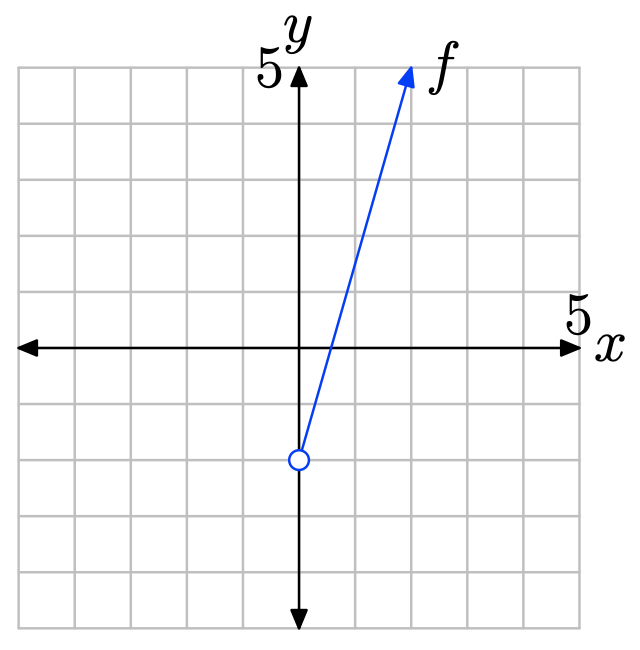
- Contestar
-
Para encontrar el rango de la función, proyecte la gráfica de f sobre el eje y. Tenga en cuenta que todos los valores de y que se encuentran por encima de −2 se encuentran en sombra y por lo tanto están en el rango de f. Por lo tanto, el rango se describe mejor con la notación de intervalo\(\{y : y > −2\} = (−2,\infty)\).
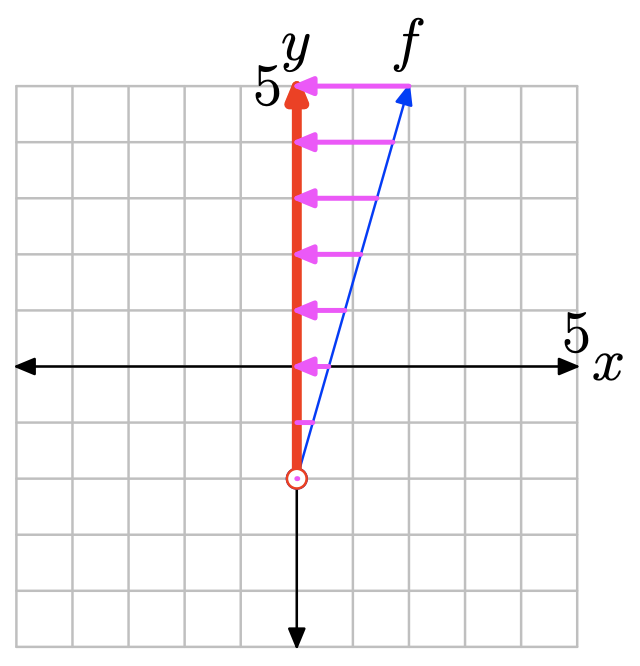
Ejercicio\(\PageIndex{26}\)
En Ejercicios\(\PageIndex{27}\) -\(\PageIndex{30}\), realizar cada una de las siguientes tareas.
i. Usa tu calculadora gráfica para dibujar la gráfica de la función dada. Haga una copia razonablemente precisa de la imagen en su pantalla de visualización en su papel de tarea. Etiquete y escale cada eje con los parámetros VENTANA xmin, xmax, ymin e ymax. Etiquete la gráfica con su ecuación.
ii. Usando un lápiz de color, proyecte cada punto de la gráfica en el eje x; es decir, sombree el dominio en el eje x. Utilice la notación de intervalo y set-builder para describir el dominio.
iii. Utilizar una técnica puramente algebraica, como se demuestra en el Ejemplo 8 en la narrativa, para encontrar el dominio. Comparar este resultado con el encontrado en la parte (ii).
iv. Usando un lápiz de diferentes colores, proyecte cada punto de la gráfica sobre el eje y; es decir, sombree el rango en el eje y. Utilice la notación de intervalo y generador de conjuntos para describir el rango.
Ejercicio\(\PageIndex{27}\)
\(f(x) = \sqrt{x + 5}\).
- Contestar
-
Cargue la función\(f(x) = \sqrt{x + 5}\) en Y1 como se muestra en (a). Seleccione 6:zStandRD en el menú ZOOM para producir la gráfica en (b).
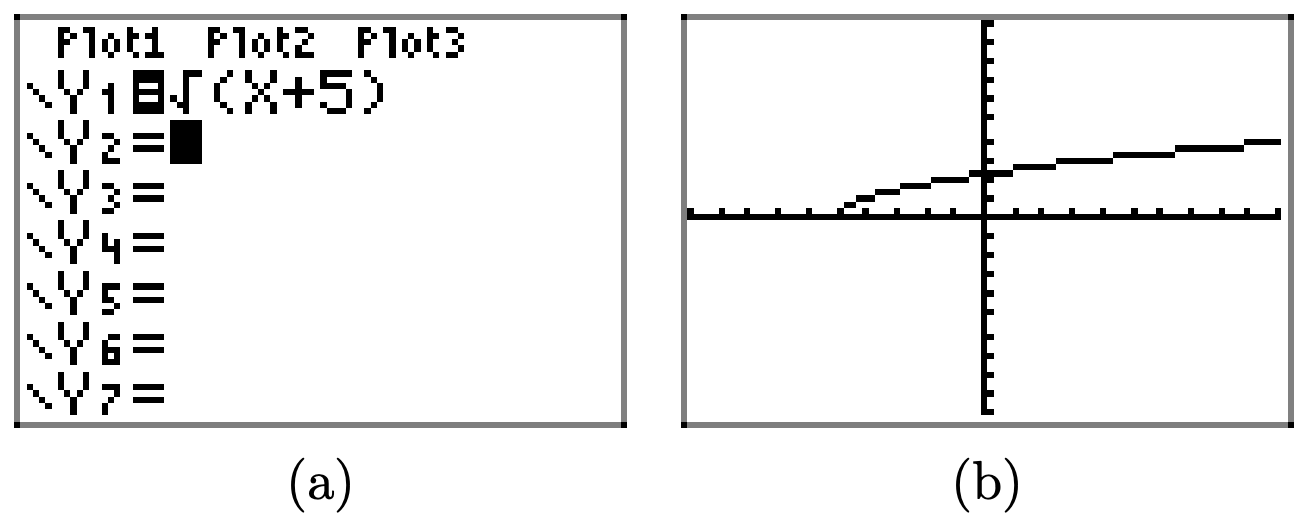
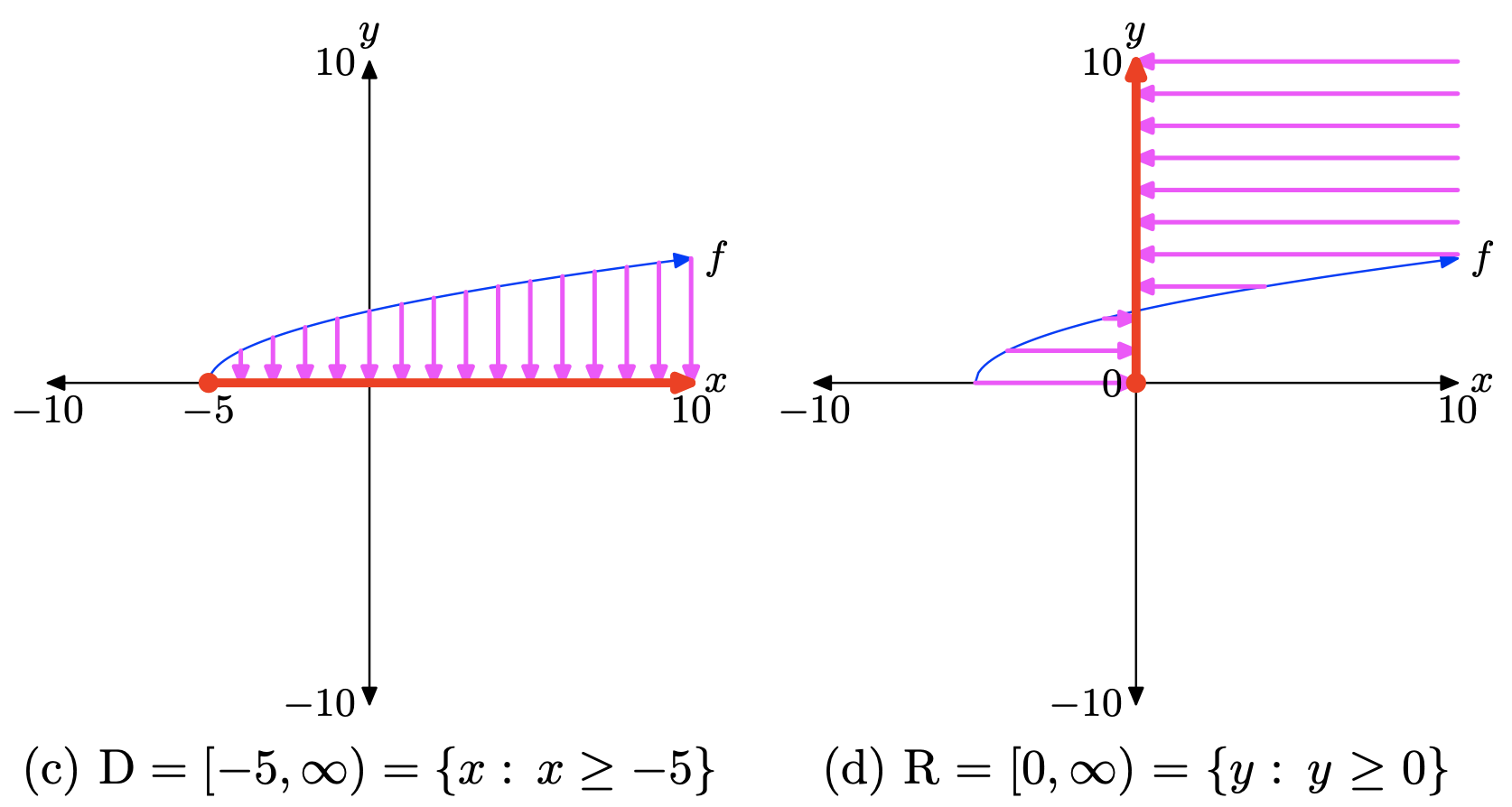
Copia la imagen en (b) en tu trabajo de tarea, luego proyecta el dominio y el rango en los ejes x e y, como se muestra en (c) y (d), respectivamente.
Para encontrar el dominio algebraicamente, tenga en cuenta que no se puede tomar la raíz cuadrada de un número negativo, por lo que la expresión bajo el radical in\(f(x) = \sqrt{x + 5}\), es decir x+5, debe ser positiva o cero (no negativa). Es decir,
\[x + 5 \geq 0\]
o equivalentemente,
\[x\geq -5\]
Así, el dominio de f es Domain =\([−5,\infty)\), o en notación set-builder, Domain =\({x : x \geq −5}\).
Ejercicio\(\PageIndex{28}\)
\(f(x) = \sqrt{5-x}\)
Ejercicio\(\PageIndex{29}\)
\(f(x) = − \sqrt{4 − x}\).
- Contestar
-
Cargue la\(f(x) = − \sqrt{4 − x}\) función. en Y1 como se muestra en (a). Seleccione 6:zStandRD en el menú ZOOM para producir la gráfica en (b).
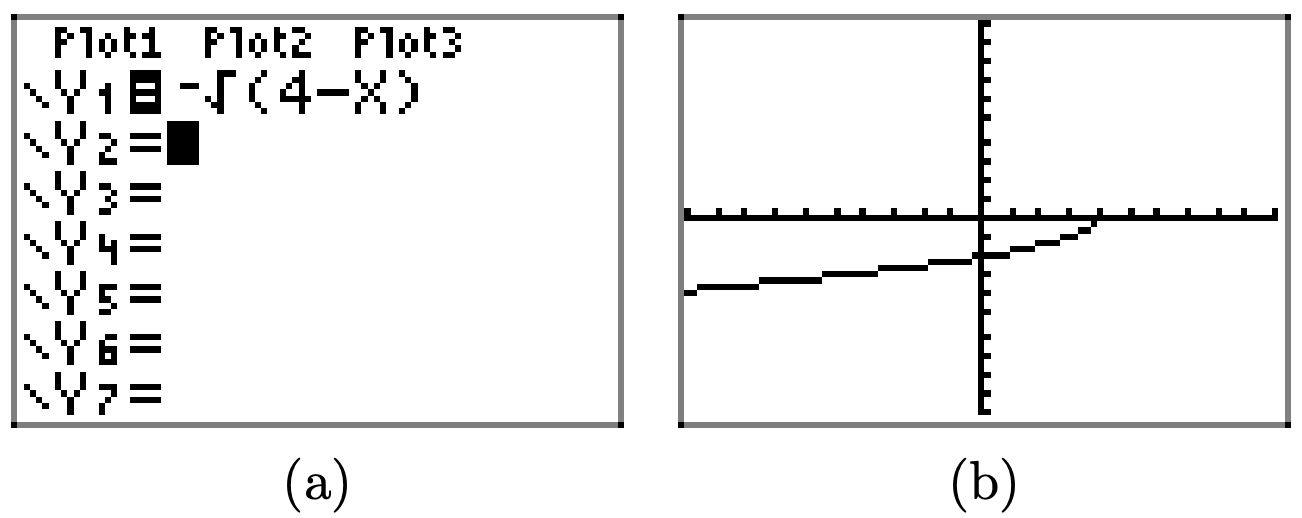
Copia la imagen en (b) en tu trabajo de tarea, luego proyecta el dominio y el rango en los ejes x e y, como se muestra en (c) y (d), respectivamente.
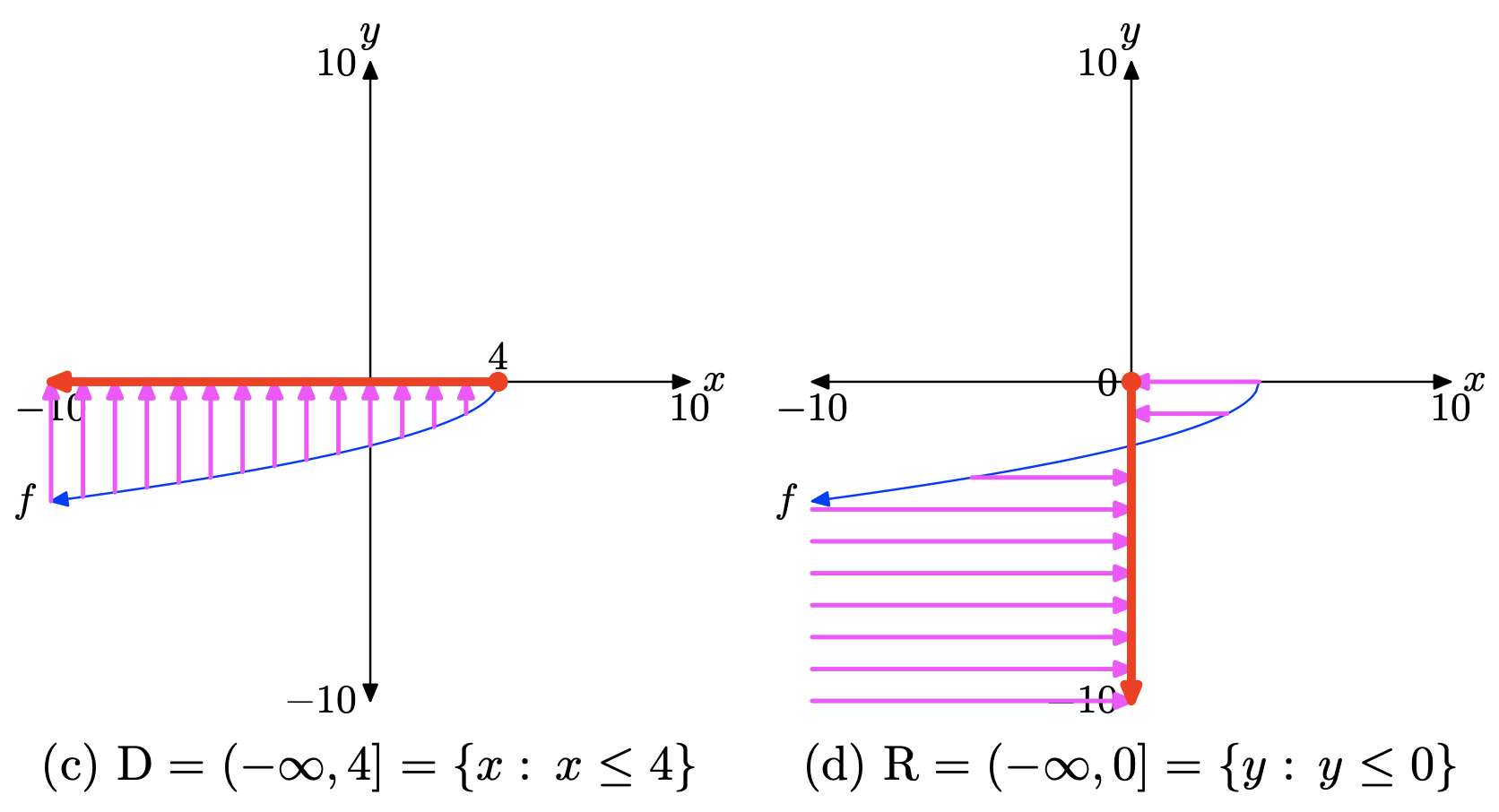
Para encontrar el dominio algebraicamente, tenga en cuenta que no se puede tomar la raíz cuadrada de un número negativo, por lo que la expresión bajo el radical in\(f(x) = − \sqrt{4 − x}\), es decir 4−x, debe ser positiva o cero (no negativa). Es decir,
\[4-x\geq 0\]
o equivalentemente,
\[-x \geq -4 \\ x\leq 4\]
Así, el dominio de f es Domain =\((\infty, 4]\), o en notación set-builder, Domain =\(\{x : x \leq 4\}\).
Ejercicio\(\PageIndex{30}\)
\(f(x) = − \sqrt{x + 4}\)
2.4 Ejercicios
En Ejercicios\(\PageIndex{1}\) -\(\PageIndex{6}\), se le da la definición de dos funciones f y g. Compare las funciones, como en el Ejemplo 1 de la narrativa, a los valores dados de x.
Ejercicio\(\PageIndex{1}\)
f (x) = x+2, g (x) = 4−x a x = −3, 1 y 2.
- Contestar
-
Se nos da que f (x) = x + 2 y g (x) = 4 − x A x = −3,
\[f(−3) = −3 + 2 = −1 \\ g(−3) = 4 − (−3) = 7\]
Por lo tanto, f (−3) < g (−3). A x = 1,
\[f(1) = 1 + 2 = 3 \\ g(1) = 4 − 1 = 3.\]
Por lo tanto, f (1) = g (1). A x = 2,
\[f(2) = 2 + 2 = 4 \\ g(2) = 4 − 2 = 2.\]
Por lo tanto, f (2) > g (2).
Ejercicio\(\PageIndex{2}\)
f (x) = 2x − 3, g (x) = 3 − x a x = −4, 2 y 5.
Ejercicio\(\PageIndex{3}\)
f (x) = 3−x, g (x) = x+9 en x = −4, −3 y −2.
- Contestar
-
Se nos da que f (x) = 3 − x y g (x) = x + 9. A x = −4,
\[f(−4) = 3 − (−4) = 7 \\ g(−4) = −4 + 9 = 5\]
Por lo tanto, f (−4) > g (−4). A x = −3,
\[f(−3) = 3 − (−3) = 6 \\ g(−3) = −3 + 9 = 6\]
Por lo tanto, f (−3) = g (−3). A x = −2,
\[f(−2) = 3 − (−2) = 5 \\ g(−2) = −2 + 9 = 7\]
Por lo tanto, f (−2) < g (−2).
Ejercicio\(\PageIndex{4}\)
\(f(x) = x^2\), g (x) = 4x + 5 a x = −2, 1 y 6.
Ejercicio\(\PageIndex{5}\)
\(f(x) = x^2\), g (x) = −3x − 2 a x = −3, −1 y 0.
- Contestar
-
Se nos da eso\(f(x) = x^2\) y g (x) = −3x − 2. A x = −3,
\[f(−3) = (−3)2 = 9 \\ g(−3) = −3(−3) − 2 = 7\]
Por lo tanto, f (−3) > g (−3). A x = −1,
\[f(−1) = (−1)2 = 1 \\ g(−1) = −3(−1) − 2 = 1\]
Por lo tanto, f (−1) = g (−1). A x = 0,
\[f(0) = (0)2 = 0 \\ g(0) = −3(0) − 2 = −2\]
Por lo tanto, f (0) > g (0).
Ejercicio\(\PageIndex{6}\)
f (x) = |x|, g (x) = 4 − x en x = 1, 2 y 3.
En Ejercicios\(\PageIndex{7}\) -\(\PageIndex{12}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Hacer una copia precisa de la imagen en papel cuadriculado (etiquetar cada ecuación, etiquetar y escalar cada eje), colocar una línea vertical discontinua a través del punto de intersección, luego etiquetar y sombrear la solución de f (x) = g (x) en el eje x.
ii. Haga una segunda copia de la imagen en papel cuadriculado, coloque una línea discontinua y vertical a través del punto de intersección, luego etiquete y sombree la solución de f (x) > g (x) en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
iii. Haga una tercera copia de la imagen en papel cuadriculado, coloque una línea discontinua y vertical a través del punto de intersección, luego etiquete y sombree la solución de f (x) < g (x) en el eje x. Utilice setbuilder y notación de intervalos para describir su conjunto de soluciones.
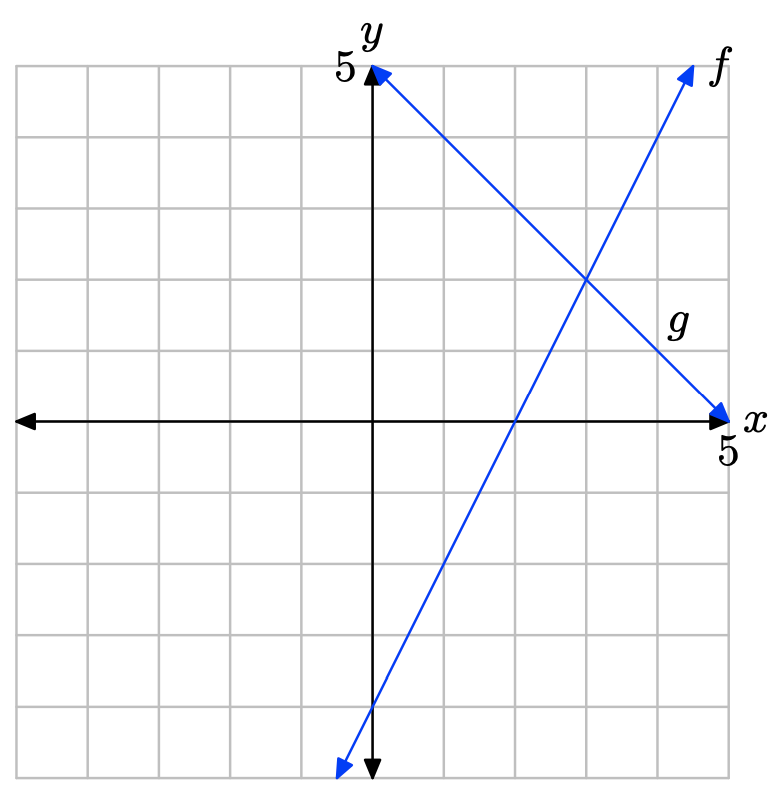
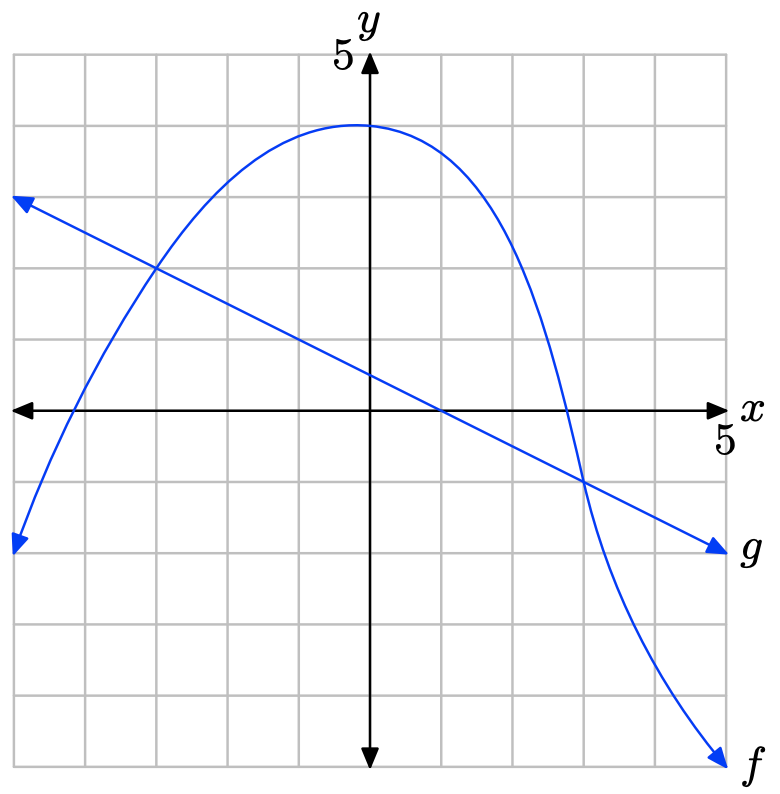
Ejercicio\(\PageIndex{7}\)
- Contestar
-
La gráfica de f cruza la gráfica de g a x = 3. La solución de f (x) = g (x) es x = 3.
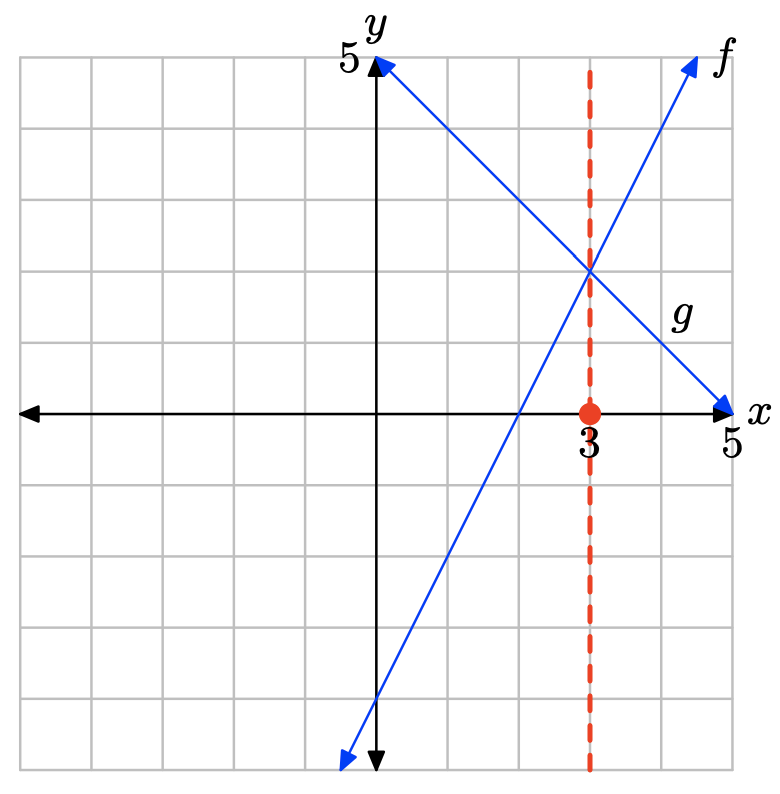
La gráfica de f se encuentra por encima de la gráfica de g a la derecha de x = 3. La solución de f (x) > g (x) es\((3,\infty) = \{x : x > 3\}\).
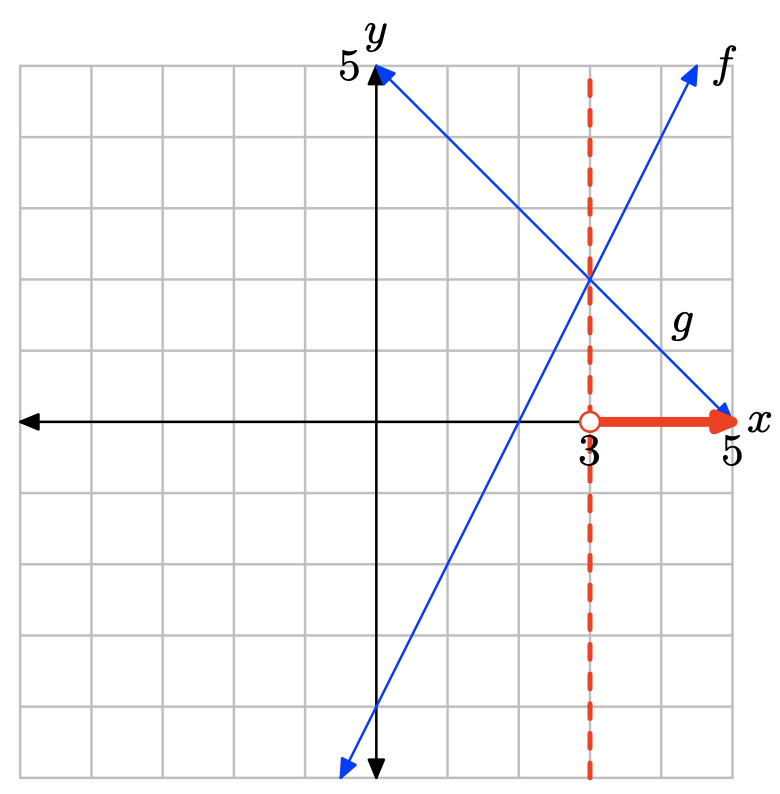
La gráfica de f se encuentra debajo de la gráfica de g a la izquierda de x = 3. La solución de f (x) < g (x) es\((−\infty, 3) = \{x : x < 3\}\).
Ejercicio\(\PageIndex{8}\)
Ejercicio\(\PageIndex{9}\)
- Contestar
-
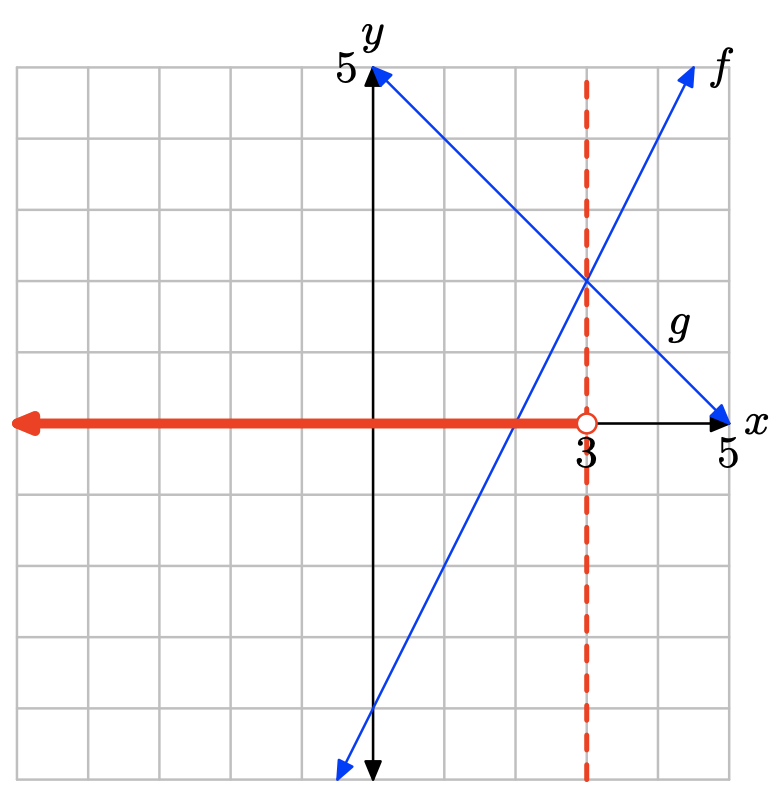
La gráfica de f cruza la gráfica de g a x = −2. La solución de f (x) = g (x) es x = −2.
La gráfica de f se encuentra por encima de la gráfica de g a la izquierda de x = −2. La solución de f (x) > g (x) es\((−\infty, −2) = \{x : x < −2\}\).
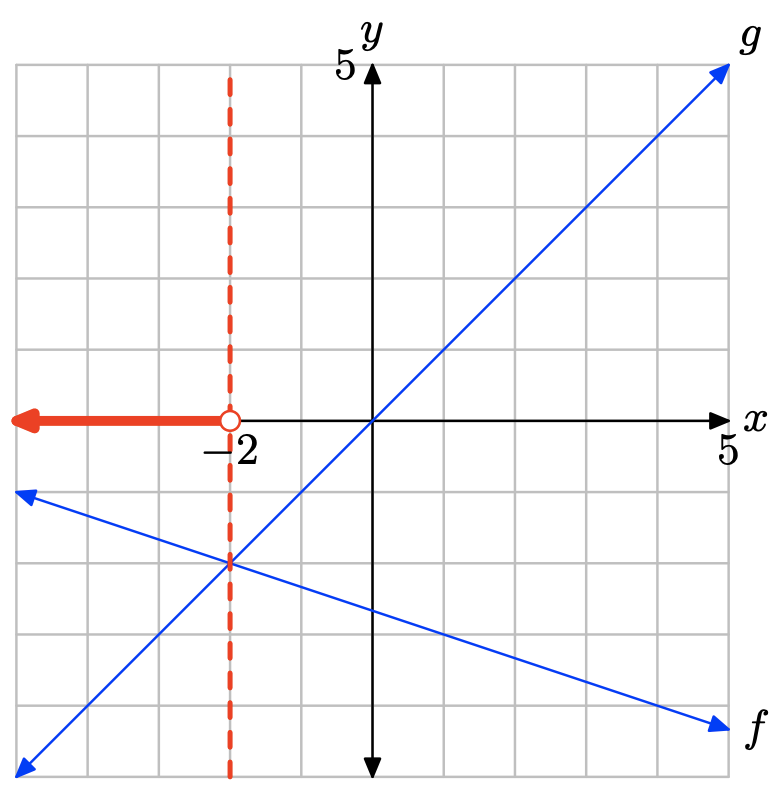
La gráfica de f se encuentra debajo de la gráfica de g a la derecha de x = −2. La solución de f (x) < g (x) es\((−2,\infty) = {\x : x > −2\}\).
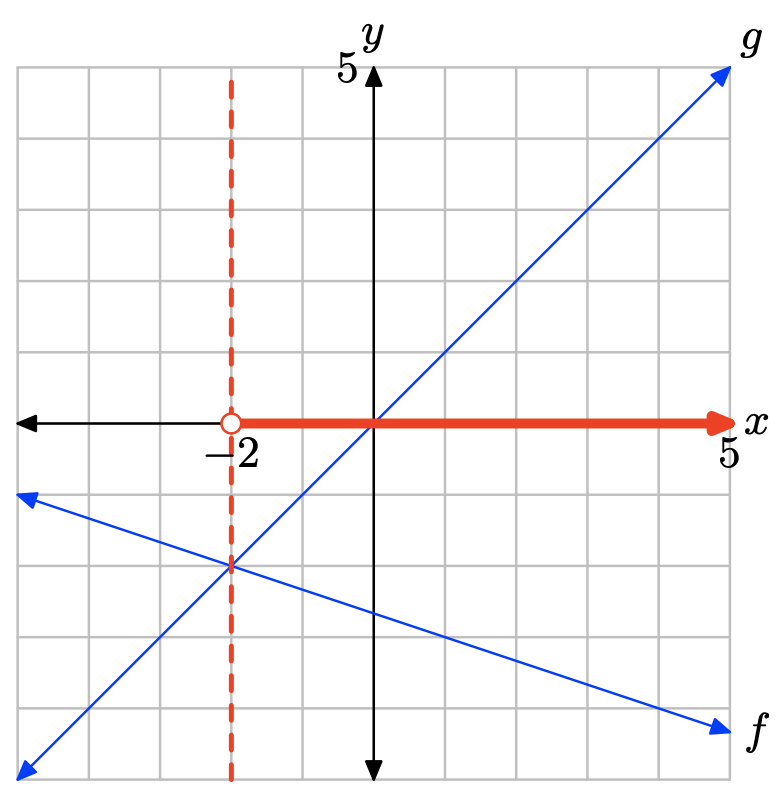
Ejercicio\(\PageIndex{10}\)
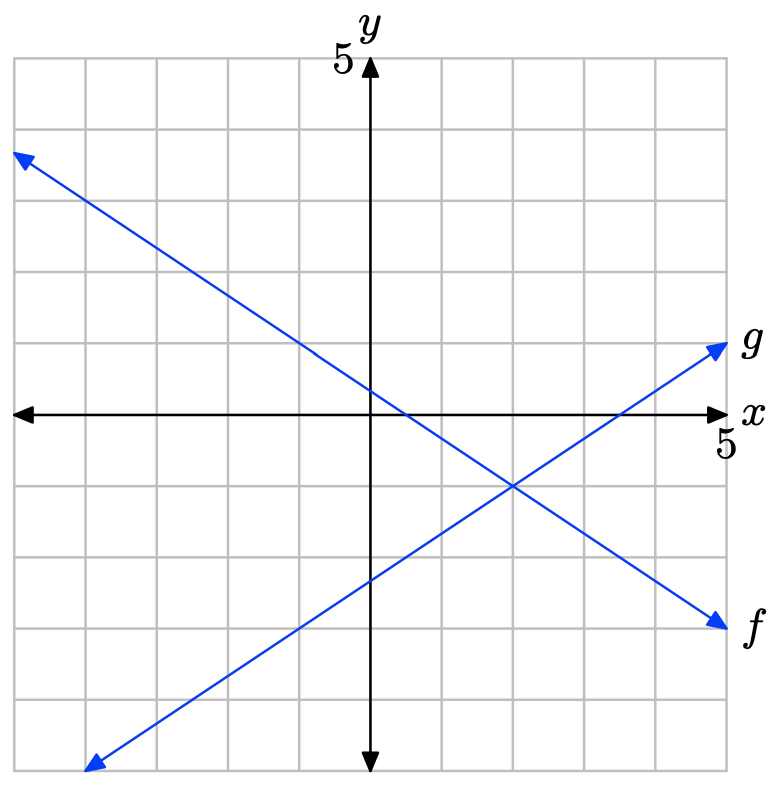
Ejercicio\(\PageIndex{11}\)
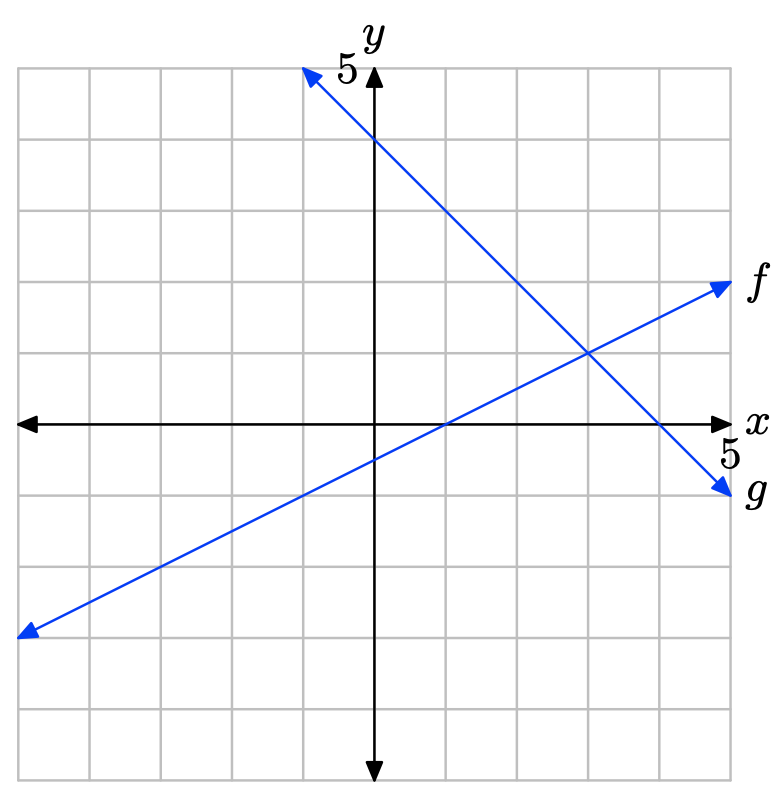
- Contestar
-
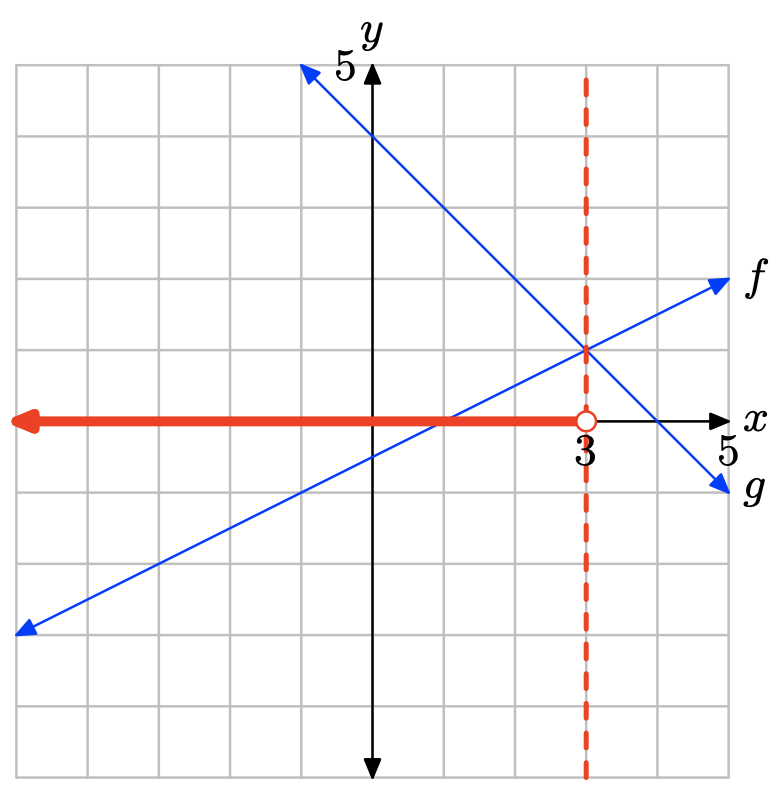
La gráfica de f cruza la gráfica de g a x = 3. La solución de f (x) = g (x) es x = 3.
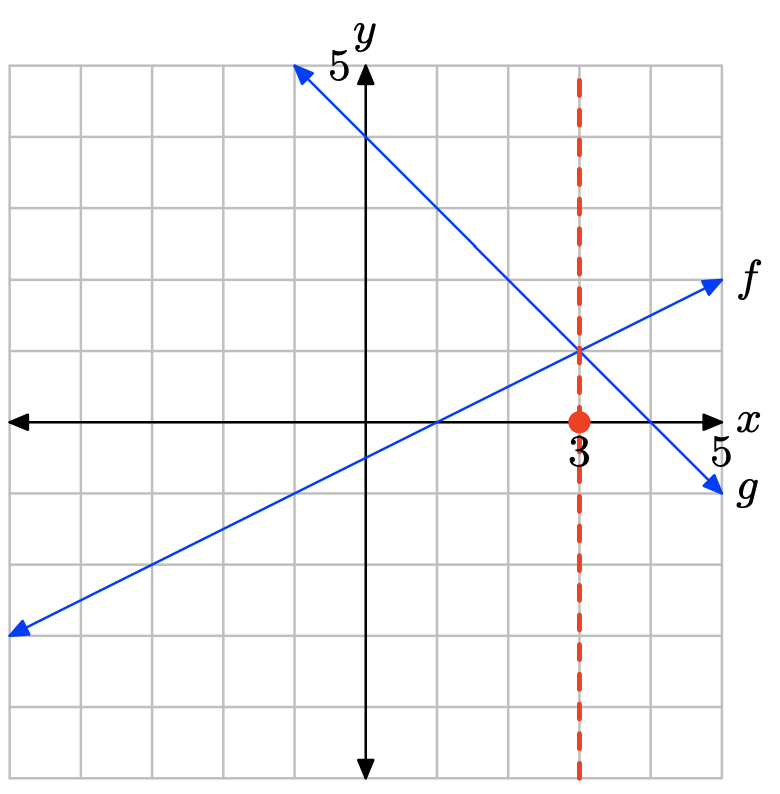
La gráfica de f está por encima de la gráfica de g a la derecha de x = 3. La solución de f (x) > g (x) es\((3,\infty) = \{x : x > 3\}\).
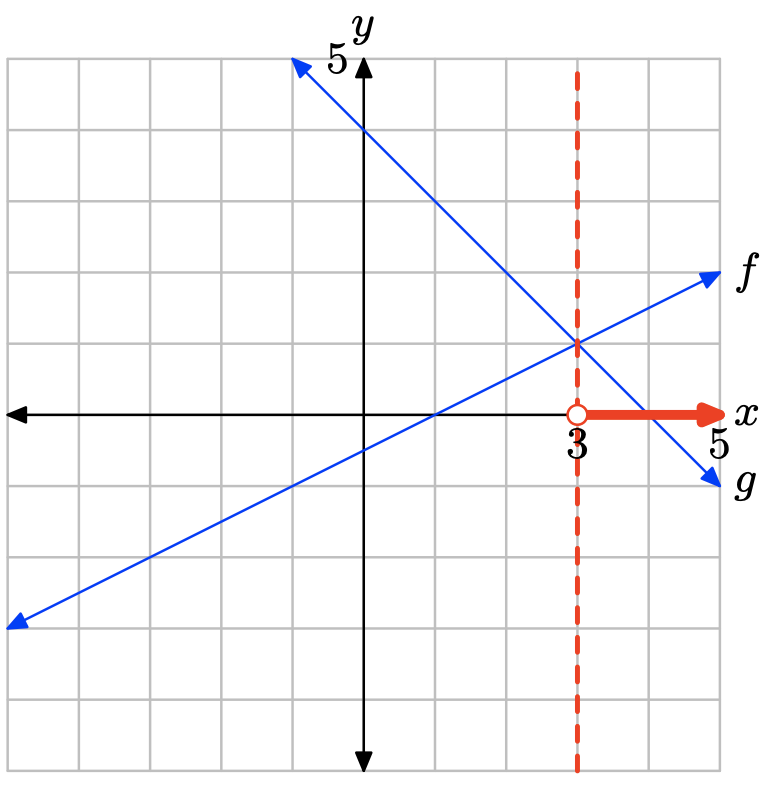
La gráfica de f está debajo de la gráfica de g a la izquierda de x = 3. La solución de f (x) < g (x) es\((−\infty, 3) = \{x : x < 3\}\).
Ejercicio\(\PageIndex{12}\)
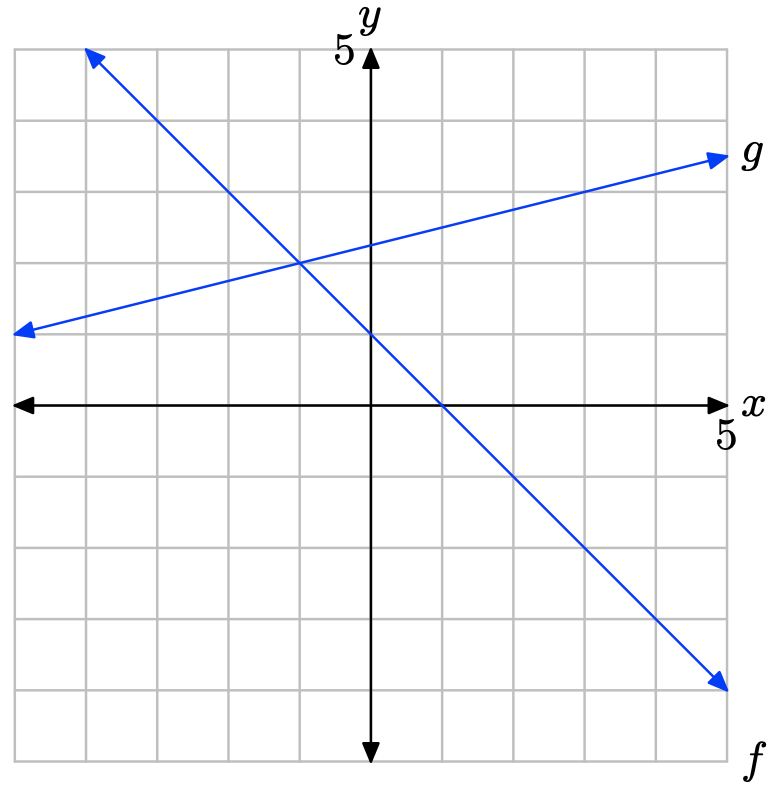
En Ejercicios\(\PageIndex{13}\) -\(\PageIndex{16}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Hacer una copia precisa de la imagen en papel cuadriculado, soltar líneas discontinuas y verticales a través de los puntos de intersección, luego etiquetar y sombrear la solución de\(f(x) \geq g(x)\) en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
ii. Haga una segunda copia de la imagen en papel cuadriculado, suelte líneas discontinuas y verticales a través de los puntos de intersección, luego etiquete y sombree la solución de f (x) < g (x) en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
Ejercicio\(\PageIndex{13}\)
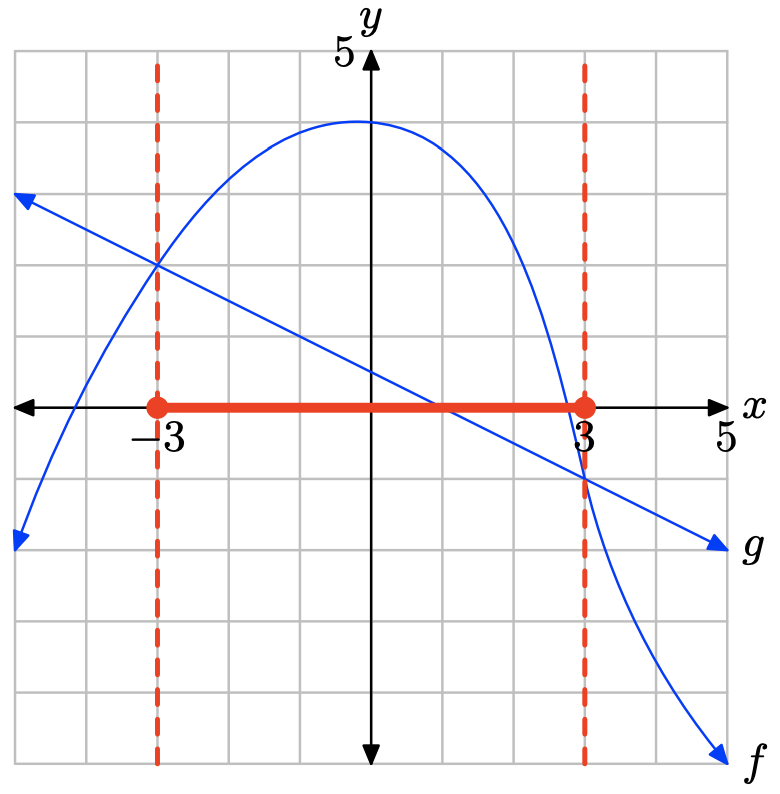
- Contestar
-
La gráfica de f cruza la gráfica de g a x = −3 y x = 3. La gráfica de f se encuentra por encima de la gráfica de g para valores de x que se encuentran entre −3 y 3. Por lo tanto, la solución de\(f(x) \geq g(x)\) es\([−3, 3] = \{x : −3 \leq x \leq 3\}\).
La gráfica de f está debajo de la gráfica de g para valores de x que se encuentran a la izquierda de −3 o a la derecha de 3. Por lo tanto, la solución de f (x) < g (x) es\((−\infty, −3) \cup (3,\infty)\) o\(\{x : x < −3 or x > 3\}\).
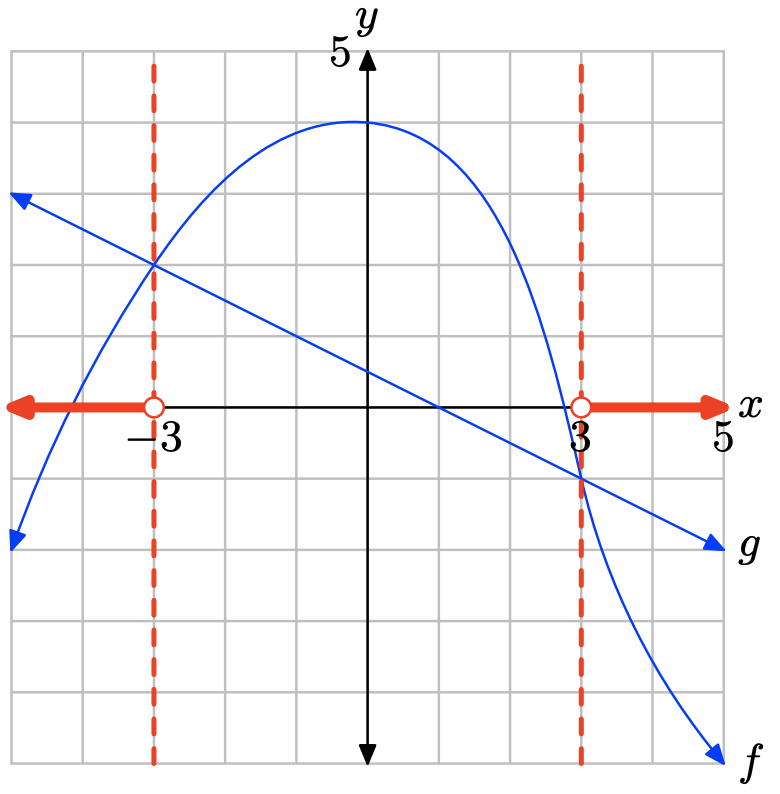
Ejercicio\(\PageIndex{14}\)
Ejercicio\(\PageIndex{15}\)
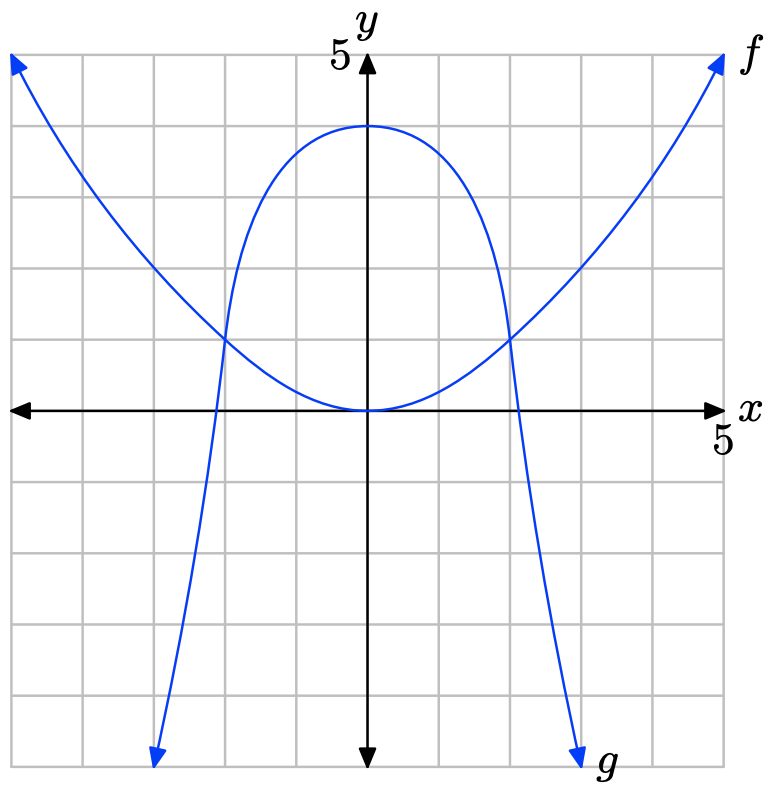
- Contestar
-
La gráfica de f cruza la gráfica de g a x = −2 y a x = 2. La gráfica de f se encuentra por encima de la gráfica de g para todos los valores de x que se encuentran a la izquierda de −2 o a la derecha de 2. Por lo tanto, la solución de\(f(x) \geq g(x)\) es\((−\infty, −2] \cup [2,\infty)\) o\(\{x : x \leq −2 or x \geq 2\}\).
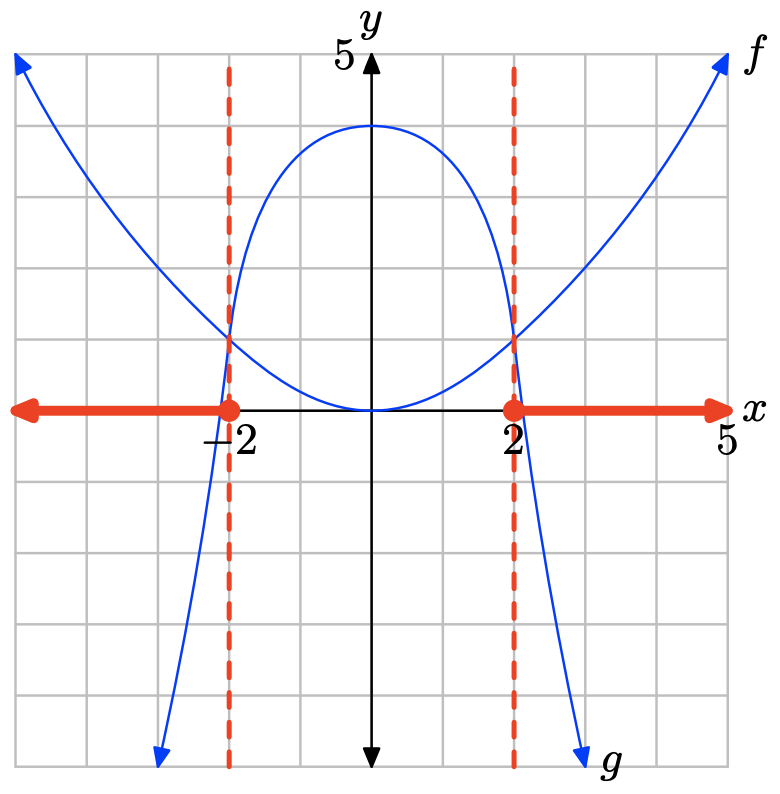
La gráfica de f se encuentra debajo de la gráfica de g para valores de x que se encuentran entre −2 y 2. Por lo tanto, la solución de f (x) < g (x) es\((−2, 2) = \{x : −2 < x < 2\}\).
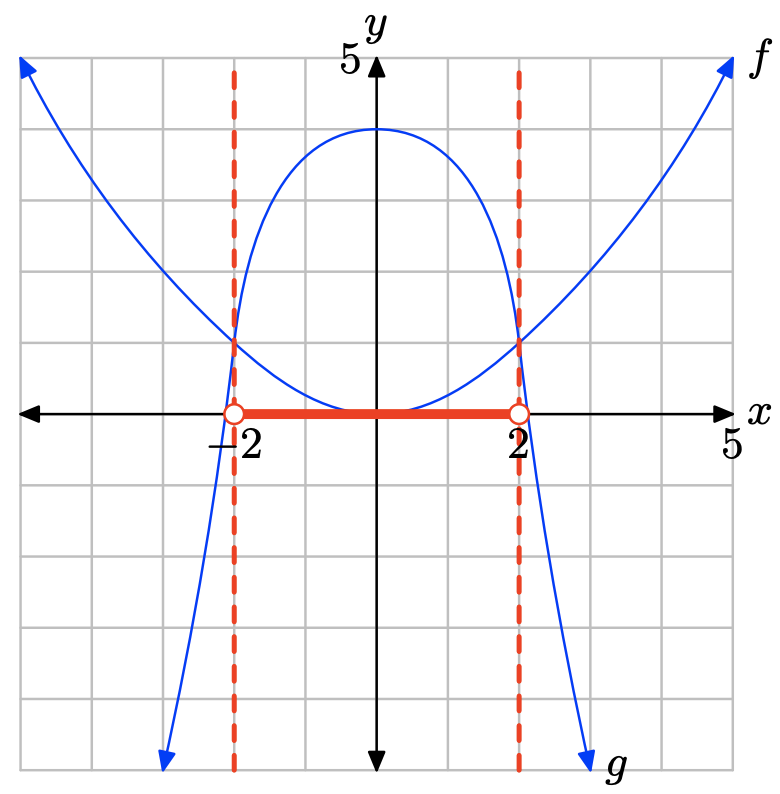
Ejercicio\(\PageIndex{16}\)
En Ejercicios\(\PageIndex{17}\) -\(\PageIndex{20}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Cargue cada lado de la ecuación en el menú Y= de su calculadora. Ajuste los parámetros VENTANA para que el punto de intersección de las gráficas sea visible en la ventana de visualización. Utilice la utilidad de intersección en el menú CALC de su calculadora para determinar la coordenada x del punto de intersección.
ii. Haga una copia exacta de la imagen en su ventana de visualización en su papel de tarea. Marque y escale cada eje con xmin, xmax, ymin e ymax, y etiquete cada gráfico con su ecuación.
iii. Dibuja una línea discontinua y vertical a través del punto de intersección. Sombra y etiqueta la solución de la ecuación en el eje x.
Ejercicio\(\PageIndex{17}\)
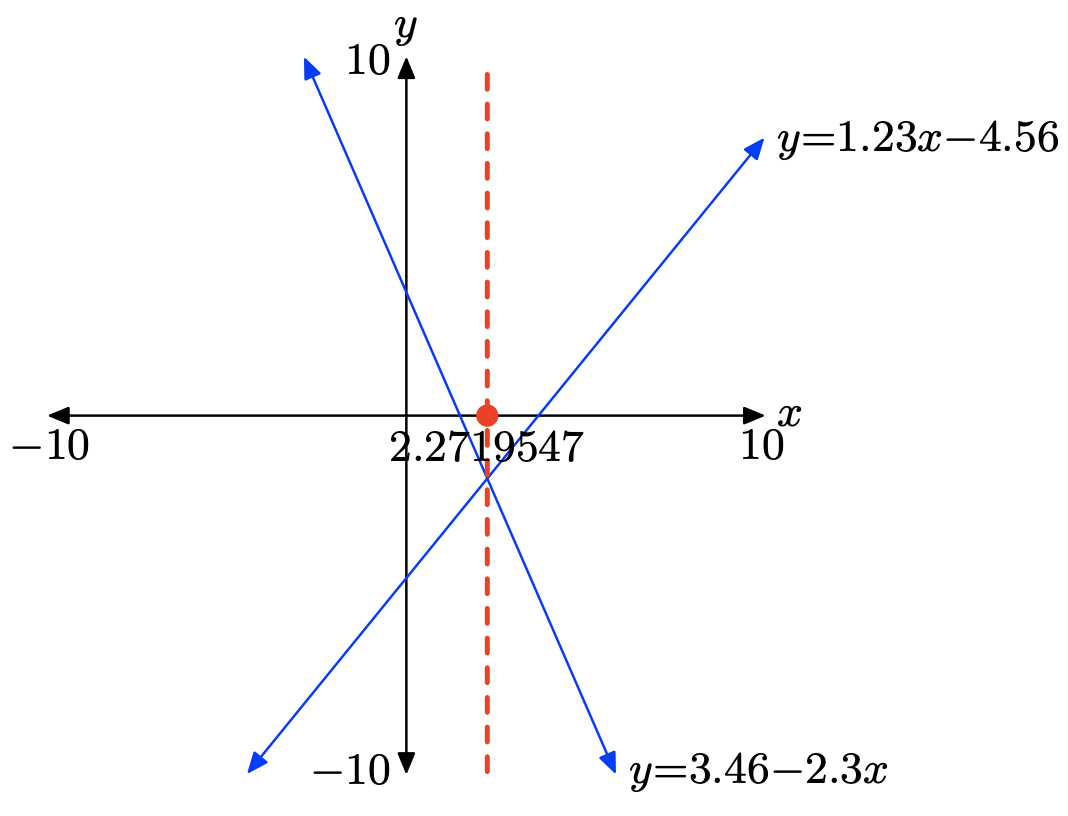
1.23x − 4.56 = 3.46 − 2.3x
- Contestar
-
Para resolver la ecuación 1.23x − 4.56 = 3.46 − 2.3x gráficamente, comience cargando los lados izquierdo y derecho de la ecuación en Y1 e Y2, respectivamente, como se muestra en (a). Utilice la utilidad de intersección en el menú CALC para determinar el punto de intersección, como se muestra en (c).
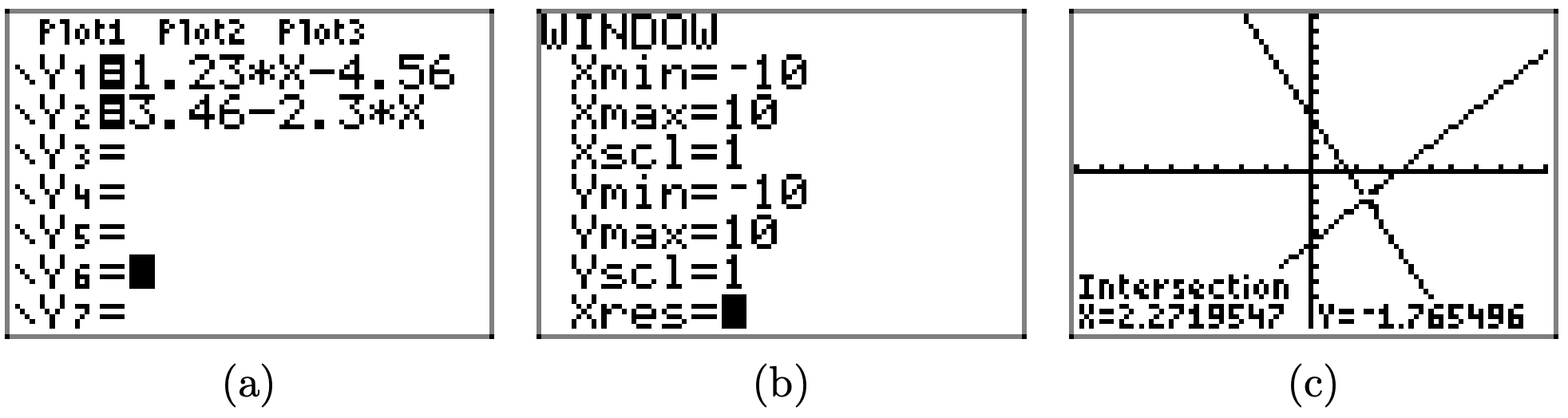
Por lo tanto, la solución de la ecuación es x = 2.2719547, que se sombrea en el eje x en la imagen que sigue. Las respuestas pueden variar debido a un error de redondear.
Ejercicio\(\PageIndex{18}\)
2.23x − 1.56 = 5.46 − 3.3x
Ejercicio\(\PageIndex{19}\)
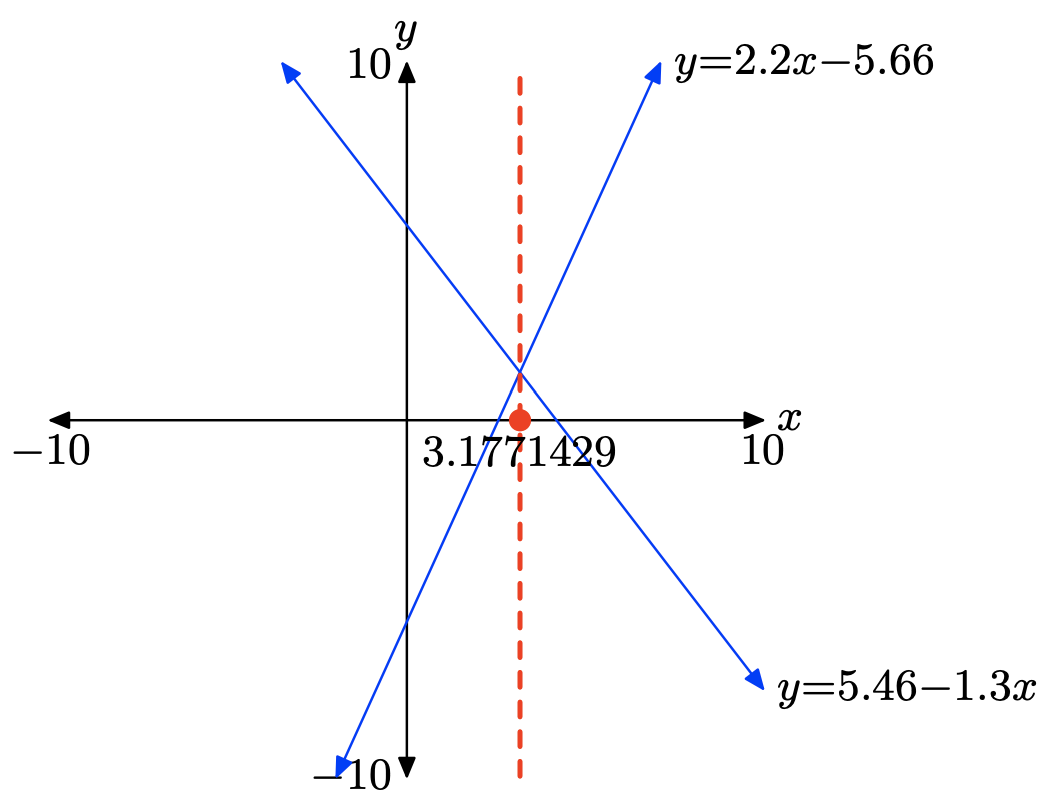
5.46 − 1.3x = 2.2x − 5.66
- Contestar
-
Para resolver gráficamente la ecuación 5.46 − 1.3x = 2.2x − 5.66, comience cargando los lados izquierdo y derecho de la ecuación en Y1 e Y2, respectivamente, como se muestra en (a). Utilice la utilidad de intersección en el menú CALC para determinar el punto de intersección, como se muestra en (c).
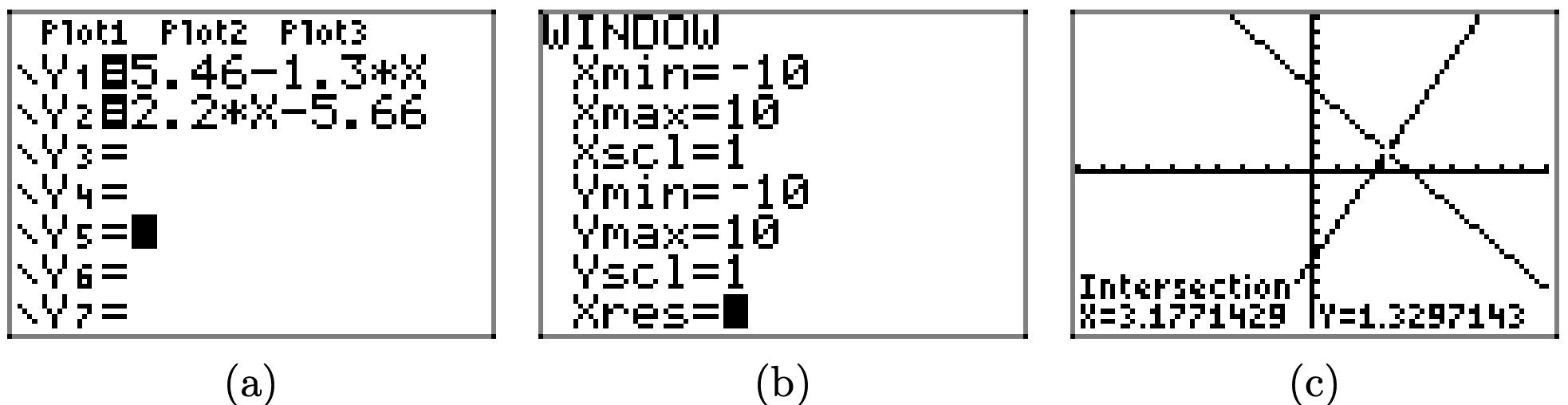
Por lo tanto, la solución de la ecuación es x = 3.1771429, que se sombrea en el eje x en la imagen que sigue. Las respuestas pueden variar debido a un error de redondear.
Ejercicio\(\PageIndex{20}\)
2.46 − 1.4x = 1.2x − 2.66
En Ejercicios\(\PageIndex{21}\) -\(\PageIndex{26}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Cargue cada lado de la desigualdad en el menú Y= de su calculadora. Ajuste los parámetros de VENTANA para que los puntos de intersección de las gráficas sean visibles en la ventana de visualización. Utilice la utilidad de intersección en el menú CALC de su calculadora para determinar las coordenadas del punto (s) de intersección.
ii. Haga una copia exacta de la imagen en su ventana de visualización en su papel de tarea. Marque y escale cada eje con xmin, xmax, ymin e ymax, y etiquete cada gráfico con su ecuación.
iii. Dibuje una línea discontinua y vertical a través de los puntos de intersección. Sombrear y etiquetar la solución de la desigualdad en el eje x. Utilice tanto el generador de conjuntos como la notación de intervalos para describir el conjunto de soluciones.
Ejercicio\(\PageIndex{21}\)
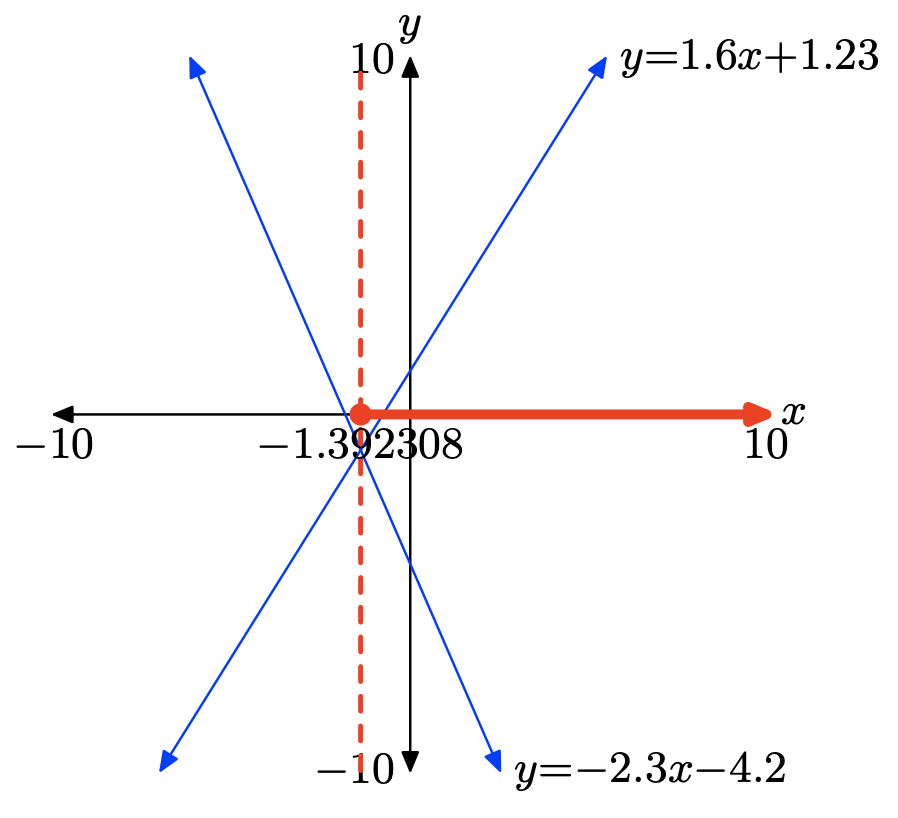
\(1.6x + 1.23 \geq −2.3x − 4.2\)
- Contestar
-
Para resolver la desigualdad\(1.6x+1.23 \geq −2.3x−4.2\) gráficamente, comience cargando los lados izquierdo y derecho de la desigualdad en Y1 e Y2, respectivamente, como se muestra en (a). Utilice la utilidad de intersección en el menú CALC para determinar el punto de intersección, como se muestra en (c).
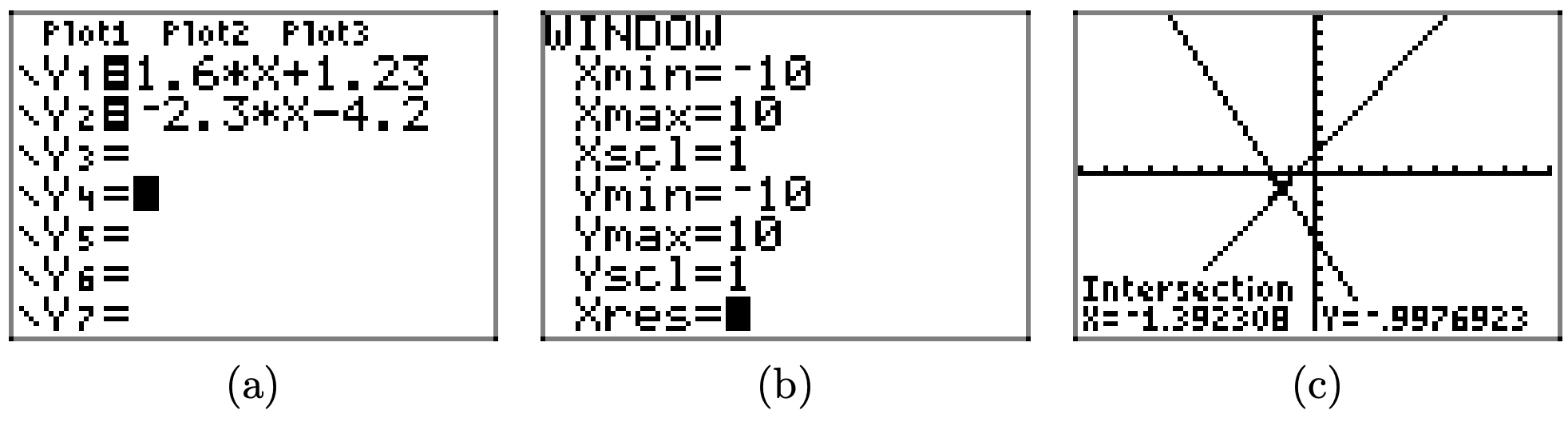
Las dos gráficas se cruzan en x = −1.392308. La gráfica de y = 1.6x + 1.23 está por encima de la gráfica de y = −2.3x−4.2 para todos los valores de x que se encuentran a la derecha de −1.392308. Por lo tanto, la solución de\(1.6x + 1.23 \geq −2.3x − 4.2\) es\([−1.392308,\infty) = \{x : x \geq −1.392308\}\).
Ejercicio\(\PageIndex{22}\)
1.24x + 5.6 < 1.2 − 0.52x
Ejercicio\(\PageIndex{23}\)
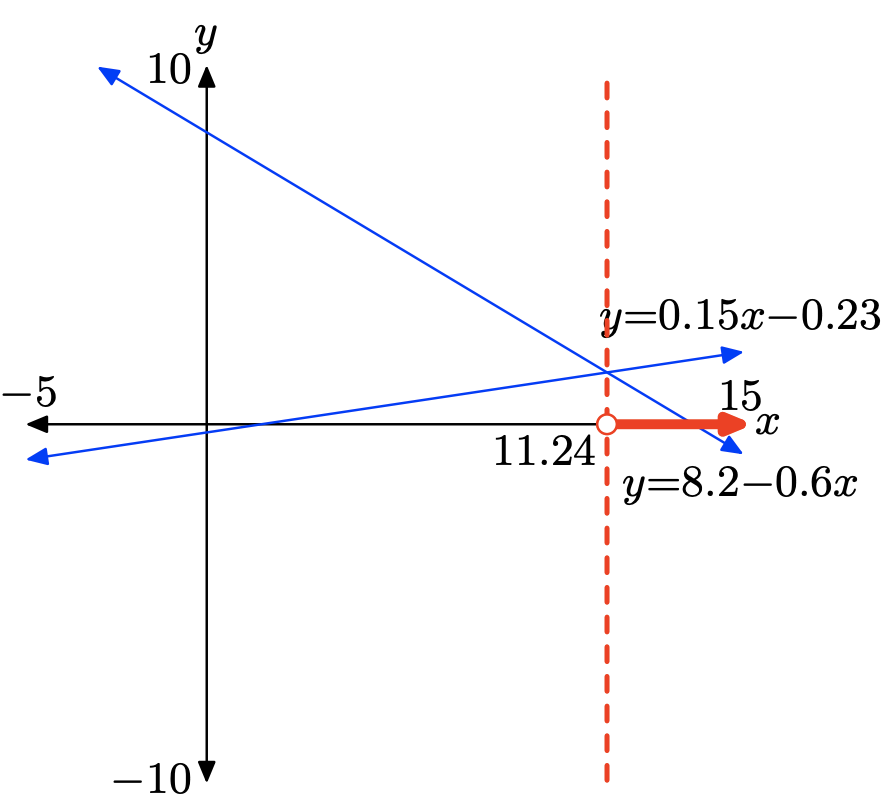
0.15x − 0.23 > 8.2 − 0.6x
- Contestar
-
Para resolver la desigualdad 0.15x − 0.23 > 8.2 − 0.6x gráficamente, comience cargando los lados izquierdo y derecho de la desigualdad en Y1 e Y2, respectivamente, como se muestra en (a). Ajuste la ventana de visualización como se muestra en (b). Utilice la utilidad de intersección en el menú CALC para determinar el punto de intersección, como se muestra en (c).
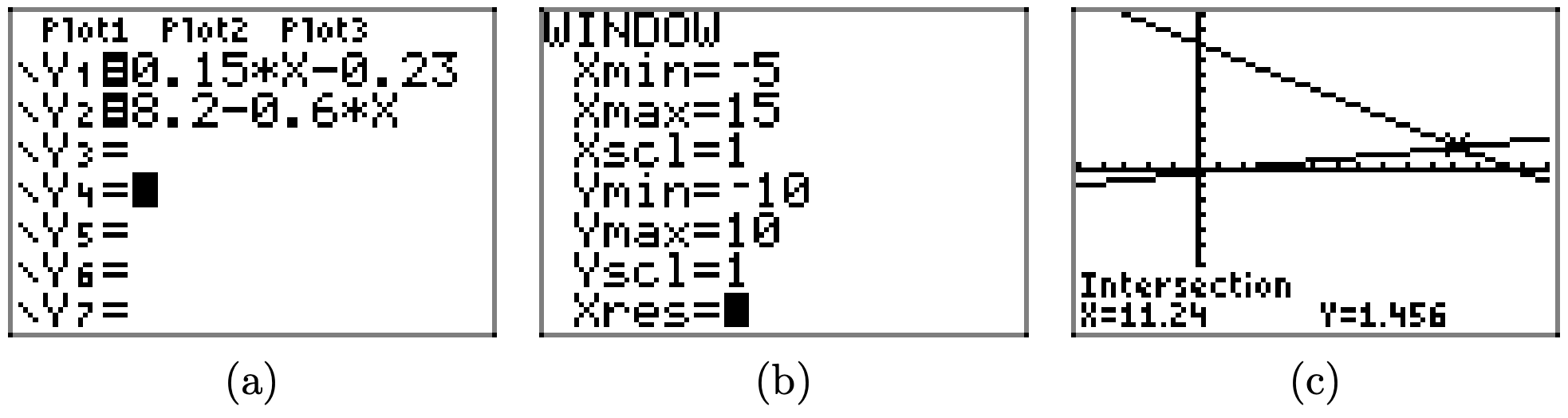
La gráfica de y = 0.15x − 0.23 está por encima de la gráfica de y = 8.2 − 0.6x para todos los valores de x que se encuentran a la derecha de 11.24. Por lo tanto, la solución de 0.15x − 0.23 > 8.2 − 0.6x es\((11.24,\infty) = \{x : x > 11.24\}\)
Ejercicio\(\PageIndex{24}\)
\(−1.23x − 9.76 \leq 1.44x + 22.8\)
Ejercicio\(\PageIndex{25}\)
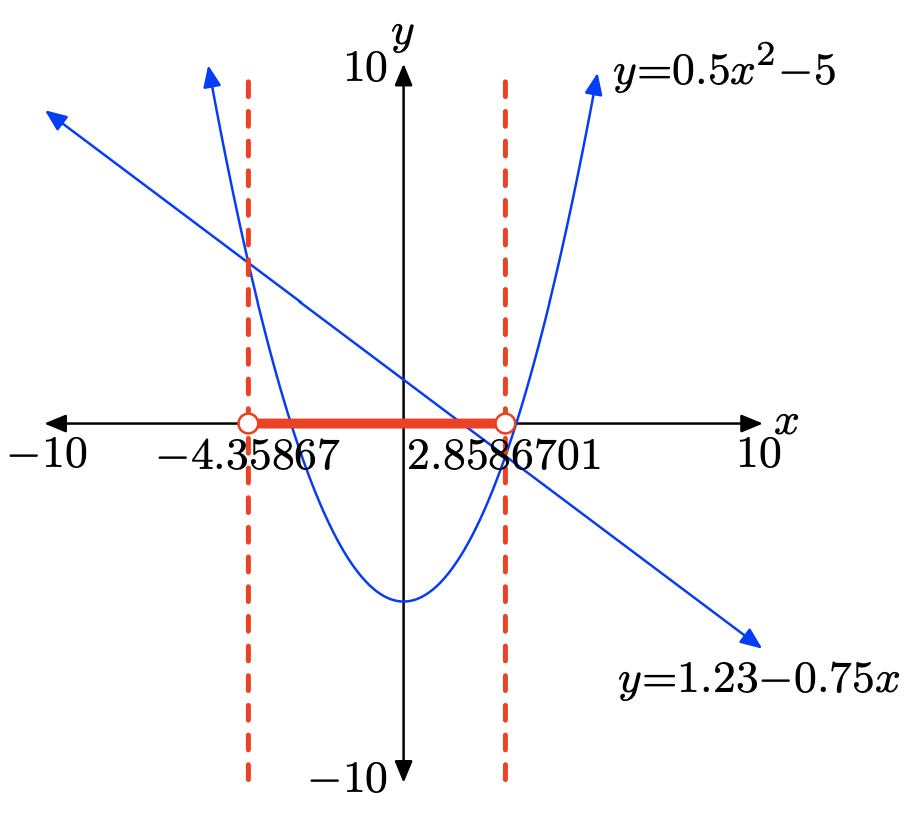
\(0.5x^2 − 5 < 1.23 − 0.75x\)
- Contestar
-
Para resolver la desigualdad\(0.5x^2 − 5 < 1.23 − 0.75x\) gráficamente, comience cargando los lados izquierdo y derecho de la desigualdad en Y1 e Y2, respectivamente, como se muestra en (a). Utilice la utilidad de intersección en el menú CALC para determinar los puntos de intersección, como se muestra en (b) y (c).
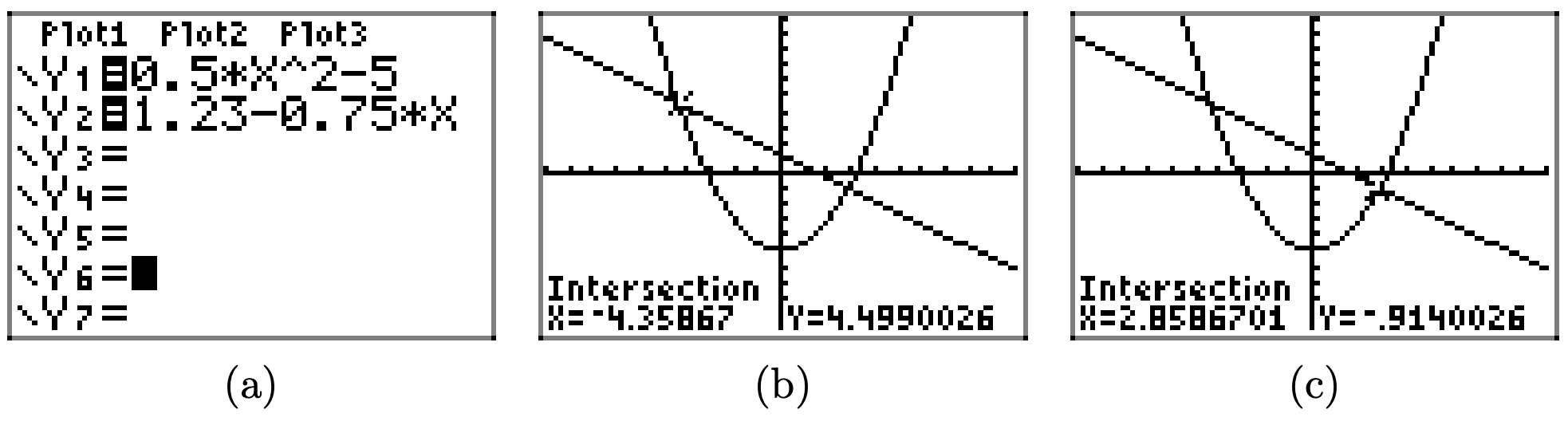
La gráfica de y = 0.5x2−5 está por debajo de la gráfica de y = 1.23−0.75x para todos los valores de x que se encuentran entre −4.35867 y 2.8586701. Por lo tanto, la solución de\(0.5x^2−5 < 1.23−0.75x\) es (−4.35867, 2.8586701) o {x: −4.35867 < x < 2.8586701}.
Ejercicio\(\PageIndex{26}\)
\(4 − 0.5x^2 \leq 0.72x − 1.34\)
En Ejercicios\(\PageIndex{27}\) -\(\PageIndex{30}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Hacer una copia precisa de la imagen en papel cuadriculado (etiquetar la gráfica con la letra f y etiquetar y escalar cada eje), colocar una línea vertical discontinua a través de la intersección x de la gráfica de f, luego etiquetar y sombrear la solución de f (x) = 0 en el eje x. Utilice la notación set-builder para describir su solución.
ii. Hacer una segunda copia de la imagen en papel cuadriculado, colocar una línea discontinua y vertical a través de la intersección x de la gráfica de f, luego etiquetar y sombrear la solución de f (x) > 0 en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
iii. Hacer una tercera copia de la imagen en papel cuadriculado, colocar una línea discontinua y vertical a través de la intersección x de la gráfica de f, luego etiquetar y sombrear la solución de f (x) < 0 en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
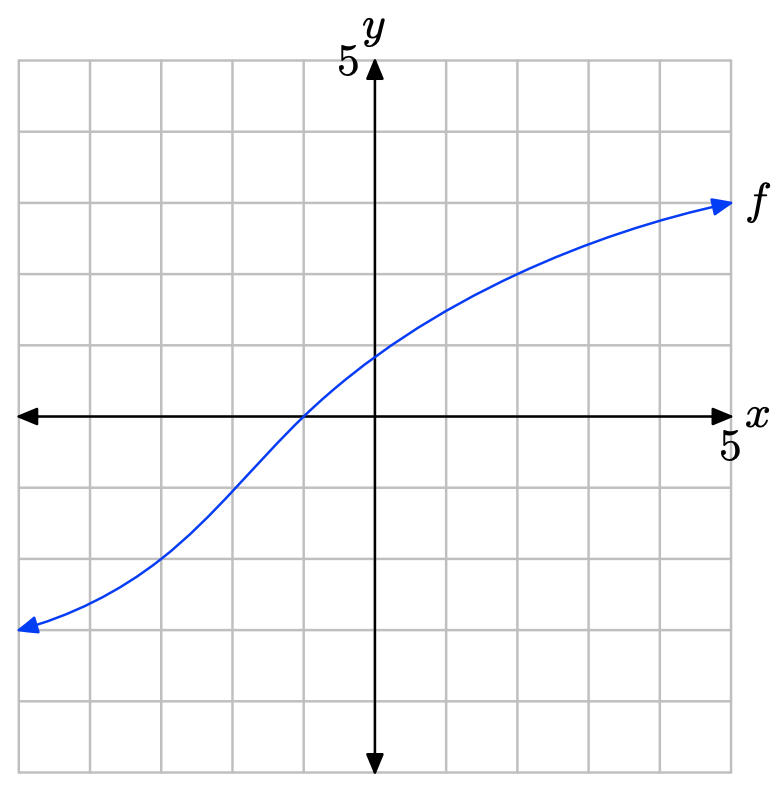
Ejercicio\(\PageIndex{27}\)
- Contestar
-
La gráfica de f intercepta el eje x en x = −1. Por lo tanto, la solución de f (x) = 0 es x = −1.
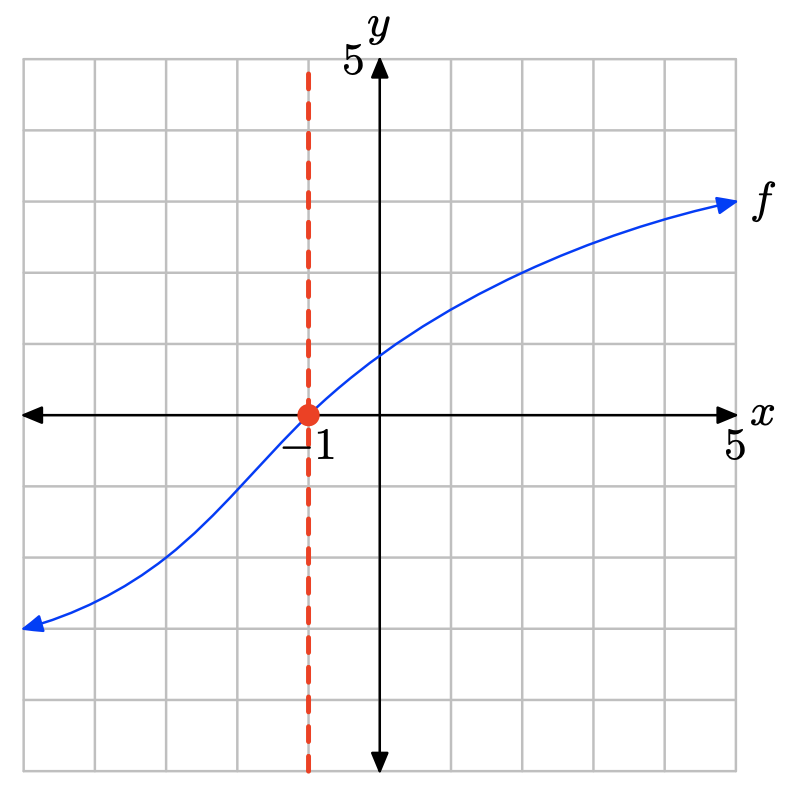
La gráfica de f se encuentra por encima del eje x para todos los valores de x que se encuentran a la derecha de −1. Por lo tanto, la solución de f (x) > 0 es\((−1,\infty) = \{x : x > −1\}\).
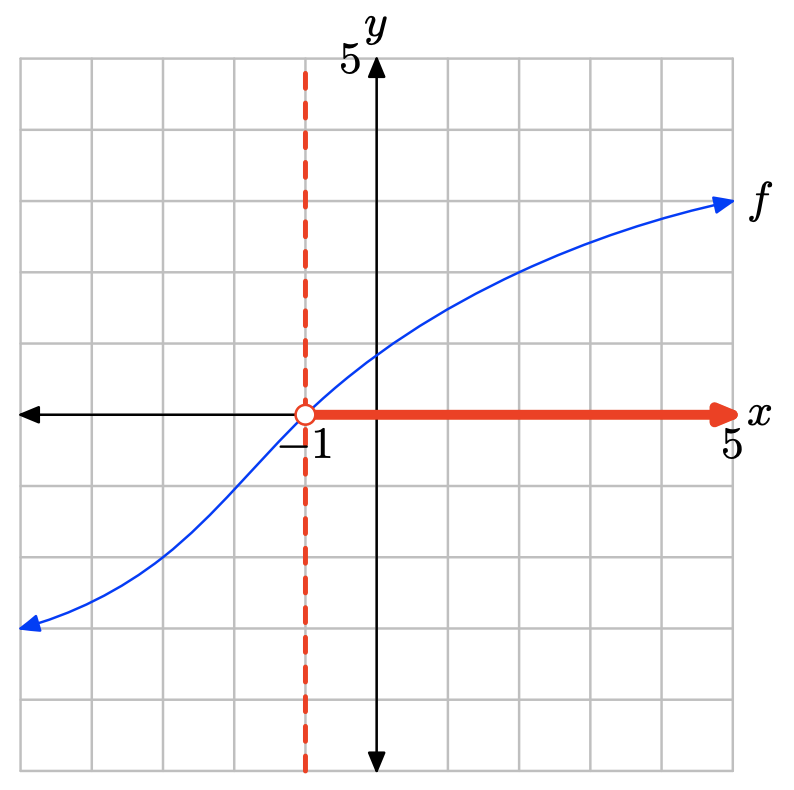
La gráfica de f se encuentra debajo del eje x para todos los valores de x que se encuentran a la izquierda de −1. Por lo tanto, la solución de f (x) < 0 es\((−\infty, −1) = \{x : x < −1\}\)
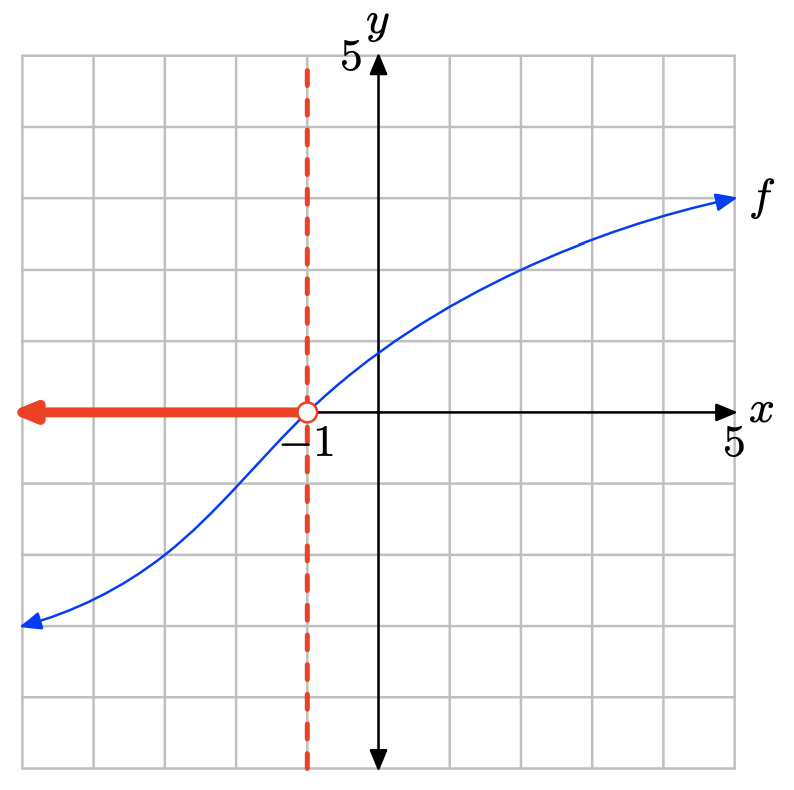
Ejercicio\(\PageIndex{28}\)
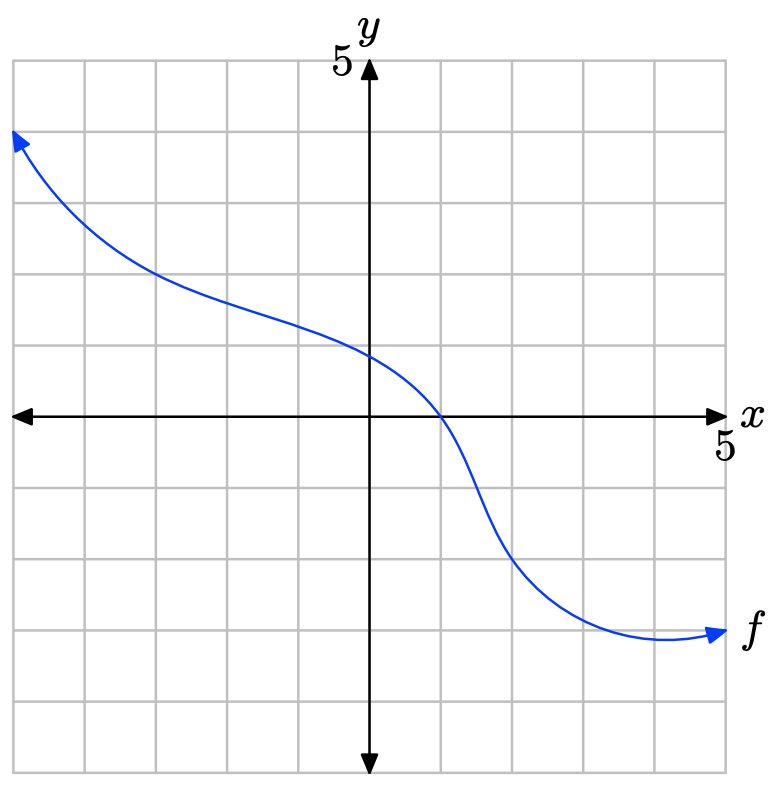
Ejercicio\(\PageIndex{29}\)
- Contestar
-
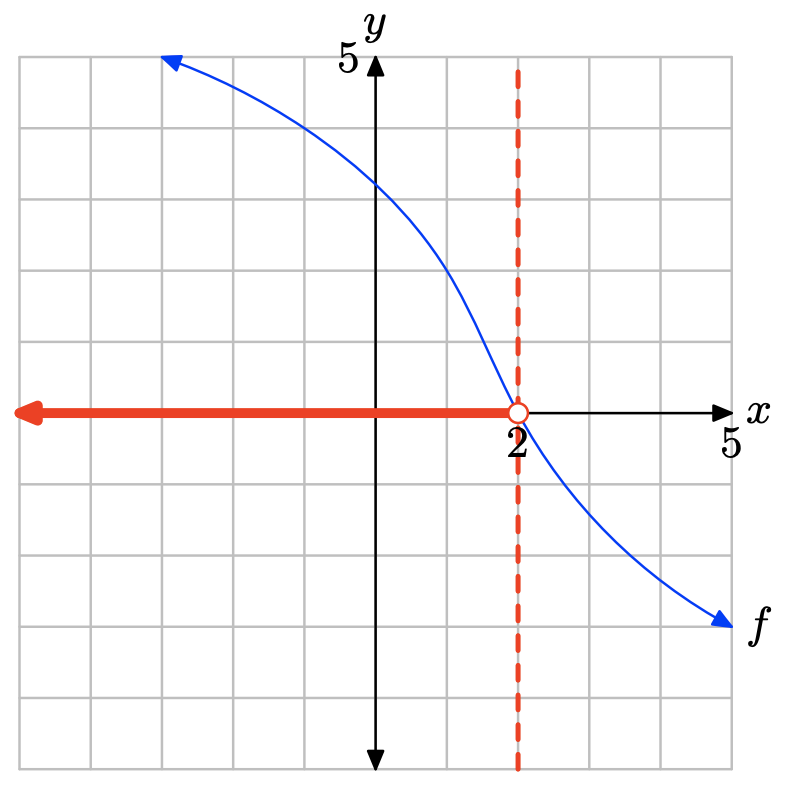
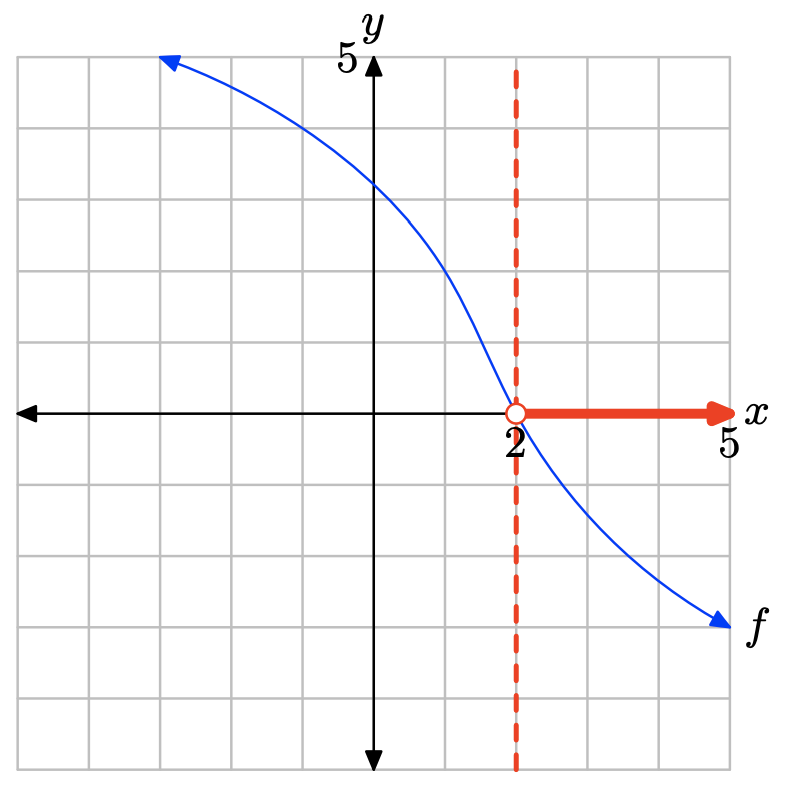
La gráfica de f intercepta el eje x en x = 2. Por lo tanto, la solución de f (x) = 0 es x = 2.
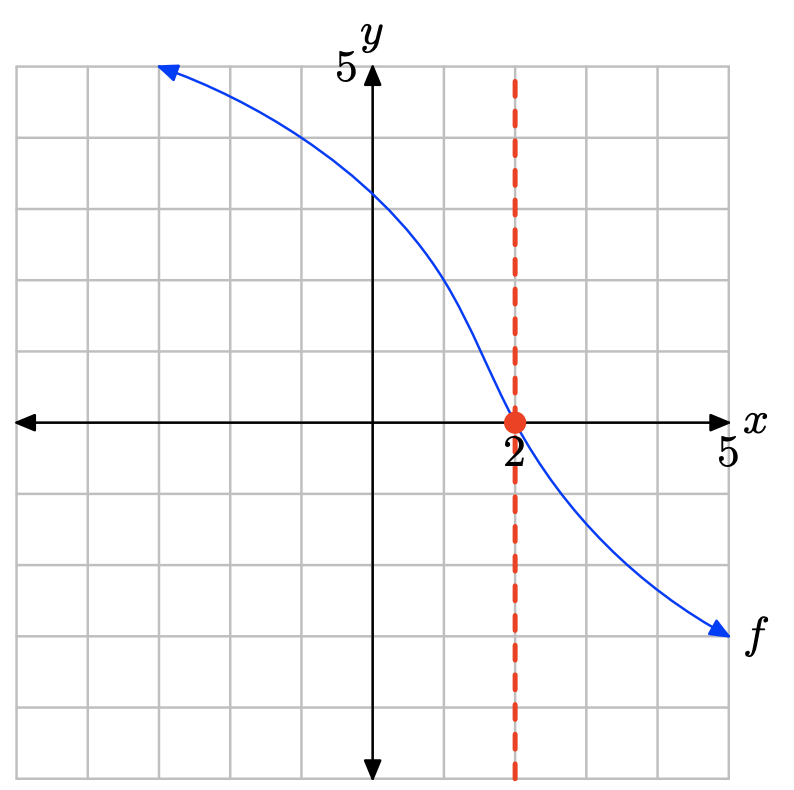
La gráfica de f se encuentra por encima del eje x para todos los valores de x que se encuentran a la izquierda de x = 2. Por lo tanto, la solución de f (x) > 0 es\((−\infty, 2) = \{x : x < 2\}\).
La gráfica de f se encuentra debajo del eje x para todos los valores de x que se encuentran a la derecha de x = 2. Por lo tanto, la solución de f (x) < 0 es\((2,\infty) = \{x : x > 2\}\)
Ejercicio\(\PageIndex{30}\)
En Ejercicios\(\PageIndex{31}\) -\(\PageIndex{34}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Hacer una copia precisa de la imagen en papel cuadriculado, soltar líneas discontinuas y verticales a través de las intercepciones x, luego etiquetar y sombrear la solución de\(f(x) \geq 0\) en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
ii. Haga una segunda copia de la imagen en papel cuadriculado, suelte líneas discontinuas y verticales a través de las intercepciones x, luego etiquete y sombree la solución de f (x) < 0 en el eje x. Utilice el generador de conjuntos y la notación de intervalos para describir su conjunto de soluciones.
Ejercicio\(\PageIndex{31}\)
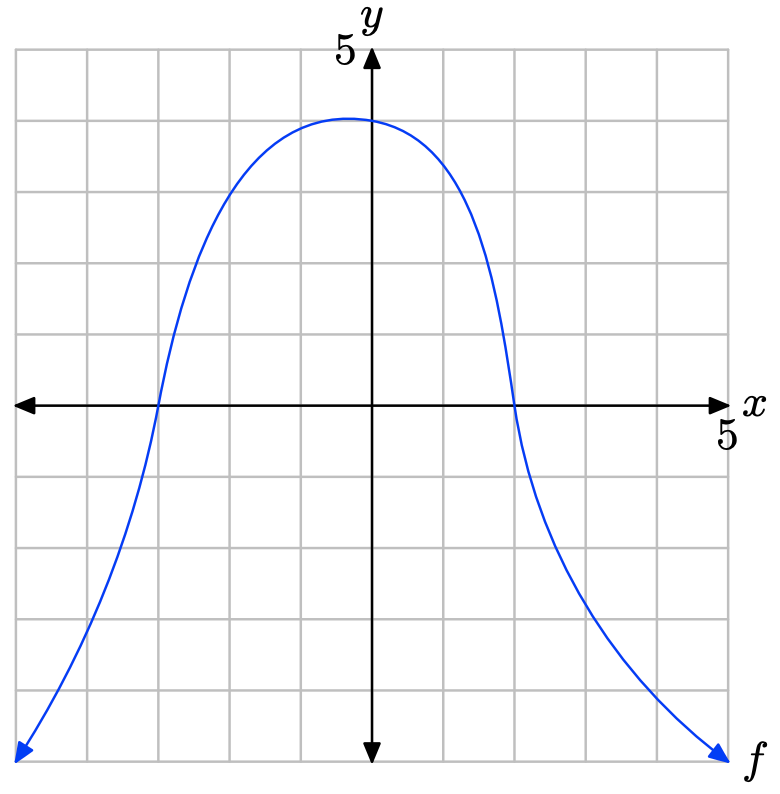
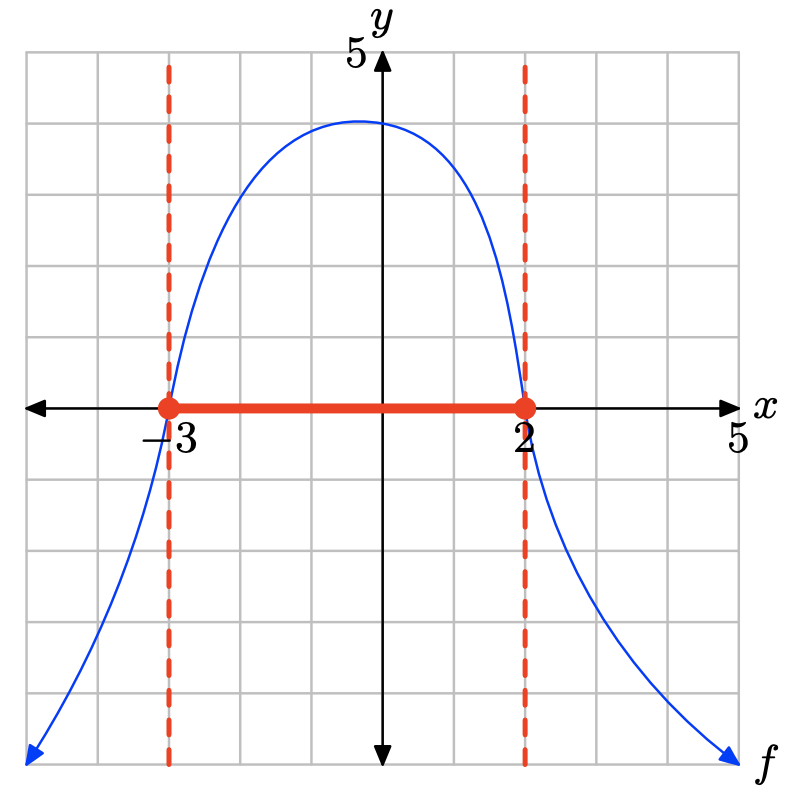
- Contestar
-
La gráfica de f intercepta el eje x en x = −3 y x = 2. La gráfica de f se encuentra por encima del eje x para todos los valores de x que se encuentran entre x = −3 y x = 2. Por lo tanto, la solución de\(f(x) \geq 0\) es\([−3, 2] = \{x : −3 \leq x \leq 2\}\).
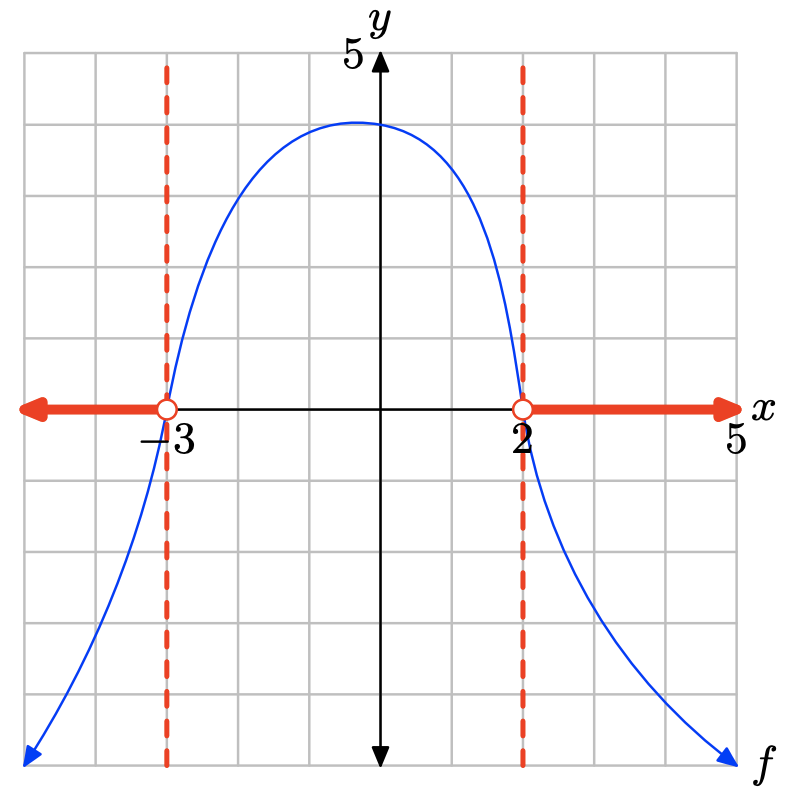
La gráfica de f se encuentra debajo del eje x para todos los valores de x que se encuentran a la izquierda de x = −3 o a la derecha de x = 2. Por lo tanto, la solución de f (x) < 0 es\((−\infty, −3) \cup (2,\infty) = \{x : x < −3 or x > 2\}\).
Ejercicio\(\PageIndex{32}\)
Ejercicio\(\PageIndex{33}\)
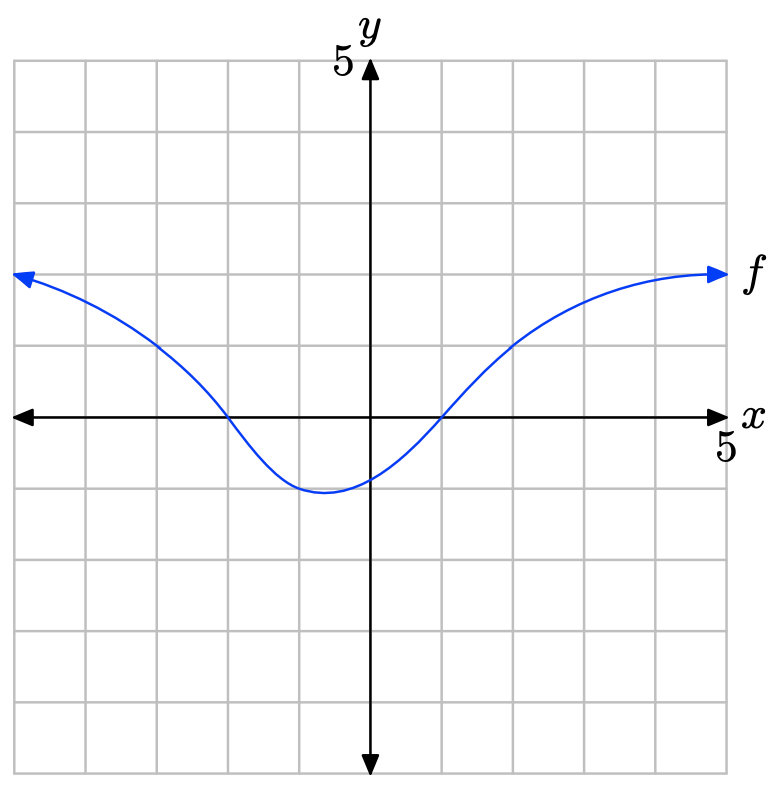
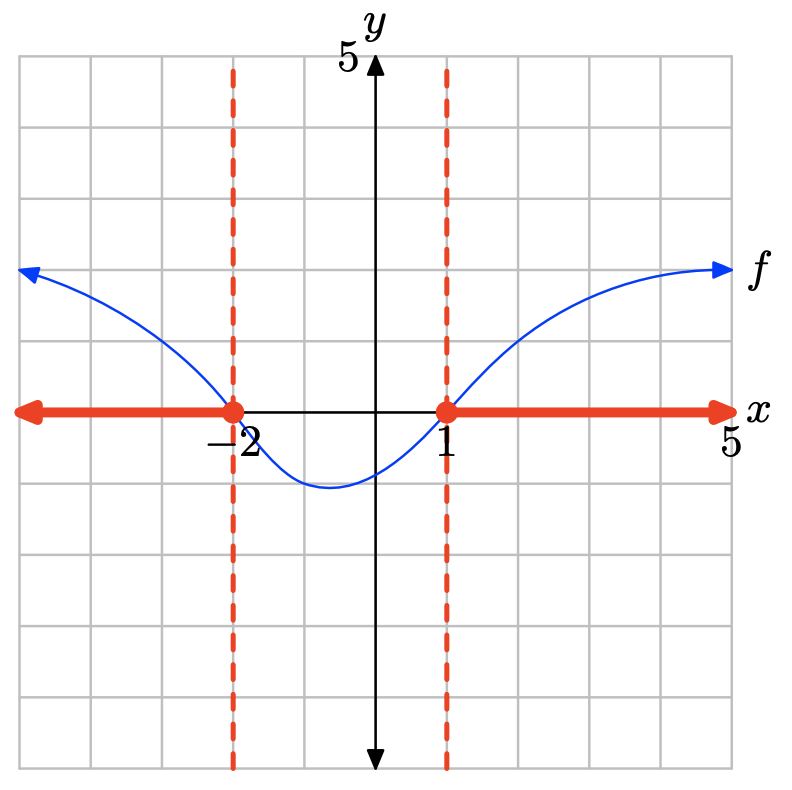
- Contestar
-
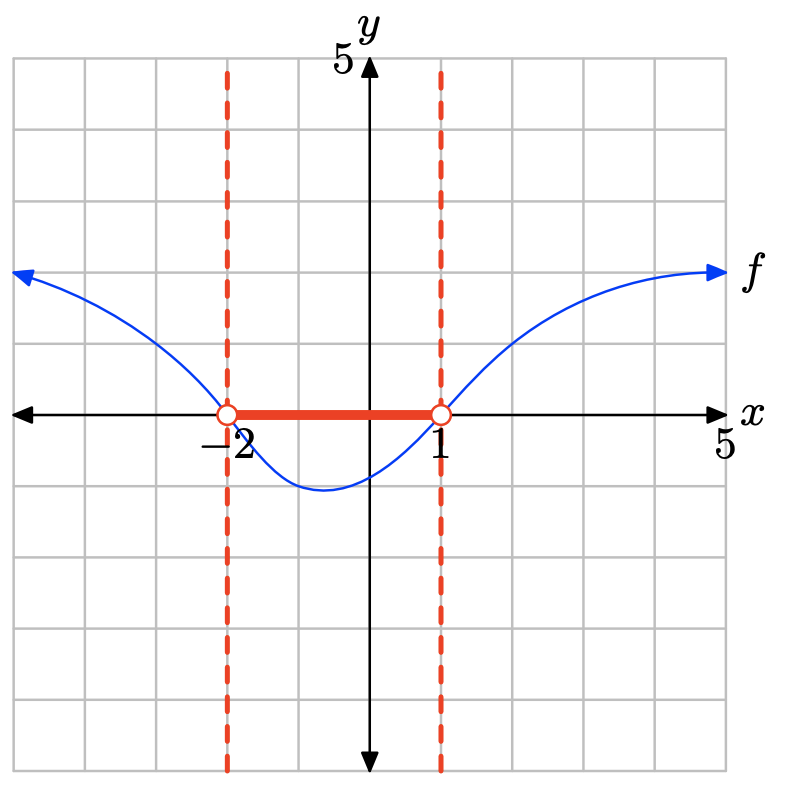
La gráfica de f intercepta el eje x en x = −2 y x = 1. La gráfica de f se encuentra por encima del eje x para todos los valores de x que se encuentran a la izquierda x = −2 o a la derecha de x = 1. Por lo tanto, la solución de\(f(x) \geq 0\) es\((−\infty, −2] \cup [1,\infty) = \{x : x \leq −2 or x \geq 1\}\).
La gráfica de f se encuentra debajo del eje x para todos los valores de x que se encuentran entre x = −2 y x = 1. Por lo tanto, la solución de f (x) < 0 es\((−2, 1) = \{x : −2 < x < 1\}\).
Ejercicio\(\PageIndex{34}\)
En Ejercicios\(\PageIndex{35}\) -\(\PageIndex{38}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Cargue la función dada f en el menú Y= de su calculadora. Ajuste los parámetros WINDOW para que la (s) intercepción (es) x de la gráfica de f sea visible en la ventana de visualización. Utilice la utilidad cero en el menú CALC de su calculadora para determinar las coordenadas de las intercepciones x de la gráfica de f.
ii. Haga una copia exacta de la imagen en su ventana de visualización en su papel de tarea. Marque y escale cada eje con xmin, xmax, ymin e ymax, y etiquete la gráfica con su ecuación.
iii. Dibuja una línea discontinua y vertical a través de las intercepciones x. Sombra y etiqueta la solución de la desigualdad f (x) > 0 en el eje x. Utilice tanto el generador de conjuntos como la notación de intervalos para describir el conjunto de soluciones.
Ejercicio\(\PageIndex{35}\)
f (x) = −1.25x + 3.58
- Contestar
-
Para resolver la desigualdad f (x) > 0 gráficamente, comience cargando f (x) = −1.25x+3.58 en Y1. Utilice la utilidad cero en el menú CALC para determinar el cero de f, como se muestra en (c).
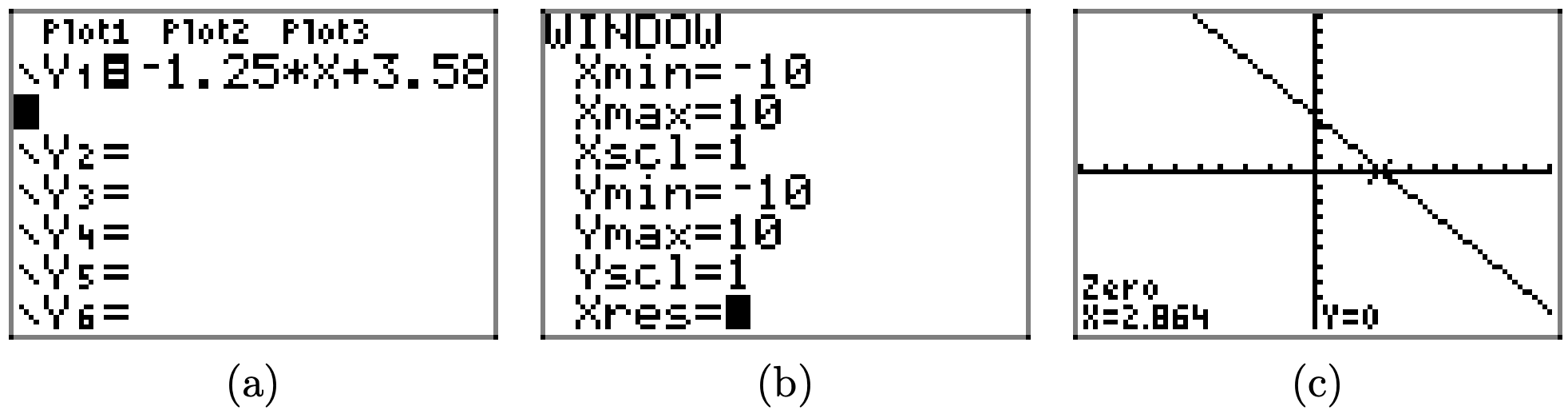
La gráfica de f se encuentra por encima del eje x para todos los valores de x que se encuentran a la izquierda de x = 2.864. Por lo tanto, la solución de f (x) > 0 es\((−\infty, 2.864) = \{x : x < 2.864\}\). Las respuestas pueden variar debido a un error de redondeo.

Ejercicio\(\PageIndex{36}\)
f (x) = 1.34x − 4.52
Ejercicio\(\PageIndex{37}\)
\(f(x) = 1.25x^2 + 4x − 5.9125\)
- Contestar
-
Para resolver la desigualdad f (x) > 0 gráficamente, comience cargando\(f(x) = 1.25x^2 + 4x − 5.9125\) en Y1. Utilice la utilidad cero en el menú CALC para determinar los ceros de f, como se muestra en (b) y (c).
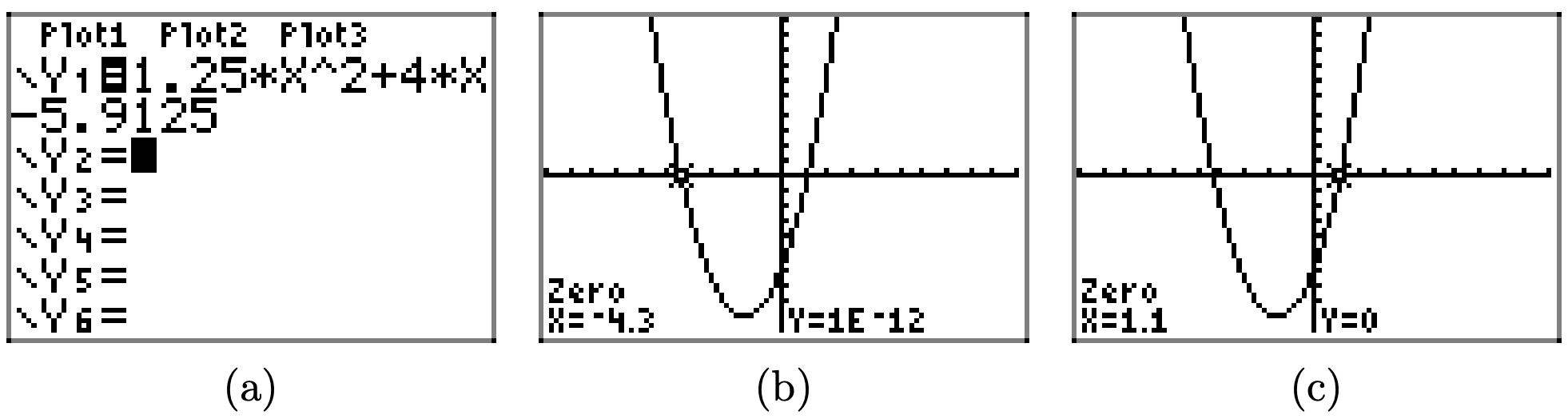
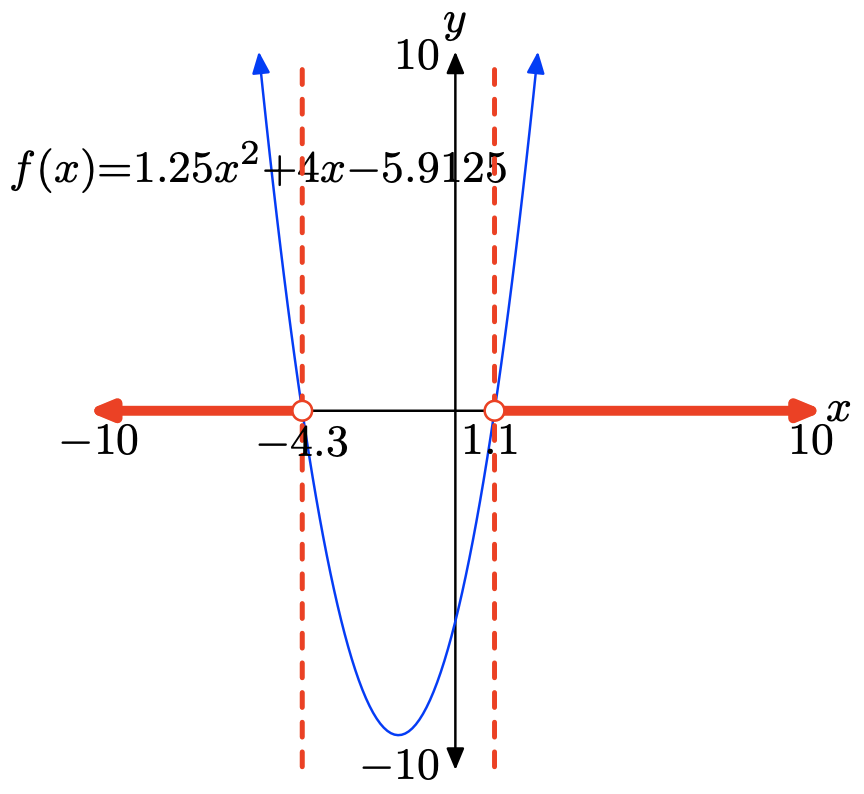
La gráfica de f se encuentra por encima del eje x para todos los valores de x que se encuentran a la izquierda de x = −4.3 o a la derecha de x = 1.1. Por lo tanto, la solución de f (x) > 0 es\((−\infty, −4.3) \cup (1.1,\infty)\) o\(\{x : x < −4.3 or x > 1.1\}\). Las respuestas pueden variar debido a un error de redondeo.
Ejercicio\(\PageIndex{38}\)
\(f(x) = −1.32x^2 − 3.96x + 5.9532\)
En Ejercicios\(\PageIndex{39}\) -\(\PageIndex{42}\), realizar cada una de las siguientes tareas. Recuerda usar una regla para dibujar todas las líneas.
i. Cargue la función dada f en el menú Y= de su calculadora. Ajuste los parámetros WINDOW para que la (s) intercepción (es) x de la gráfica de f sea visible en la ventana de visualización. Utilice la utilidad cero en el menú CALC de su calculadora para determinar las coordenadas de las intercepciones x de la gráfica de f.
ii. Haga una copia exacta de la imagen en su ventana de visualización en su papel de tarea. Marque y escale cada eje con xmin, xmax, ymin e ymax, y etiquete la gráfica con su ecuación.
iii. Dibuja una línea discontinua y vertical a través de las intercepciones x. Sombrear y etiquetar la solución de la desigualdad\(f(x) \leq 0\) en el eje x. Utilice tanto el generador de conjuntos como la notación de intervalos para describir el conjunto de soluciones.
Ejercicio\(\PageIndex{39}\)
f (x) = −1.45x − 5.6
- Contestar
-
Para resolver la desigualdad\(f(x) \leq 0\) gráficamente, comience cargando f (x) = −1.45x−5.6 en Y1. Utilice la utilidad cero en el menú CALC para determinar el cero de f, como se muestra en (c).
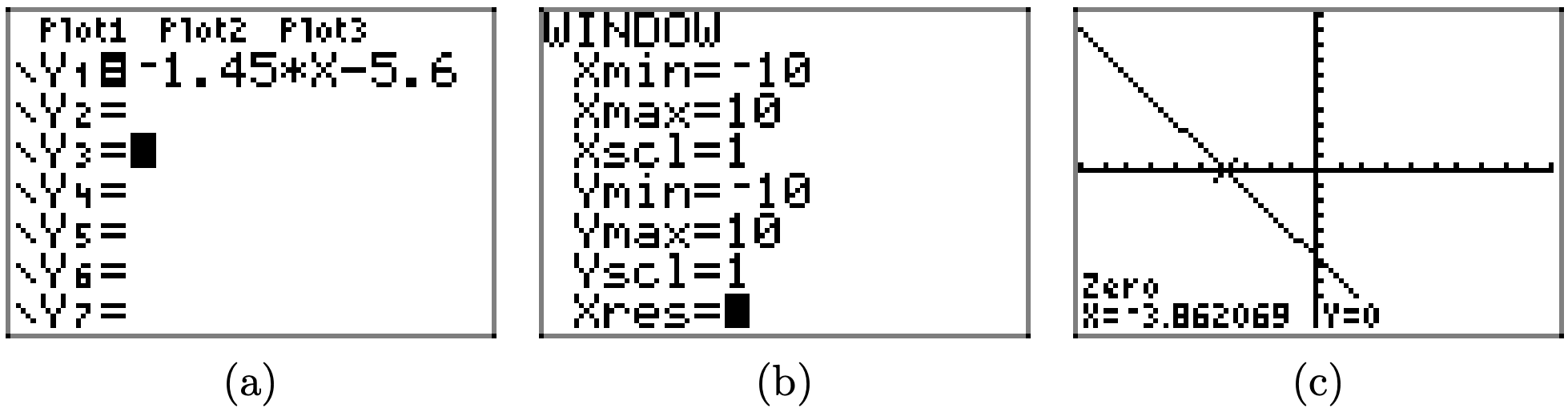
La gráfica de f intercepta el eje x en x = −3.862069. La gráfica de f se encuentra debajo del eje x para todos los valores de x que se encuentran a la derecha de x = −3.862069. Por lo tanto, la solución de\(f(x) \leq 0\) es\([−3.862069,\infty) = \{x : x \geq −3.862069\}\). Las respuestas pueden variar debido a un error de redondear.
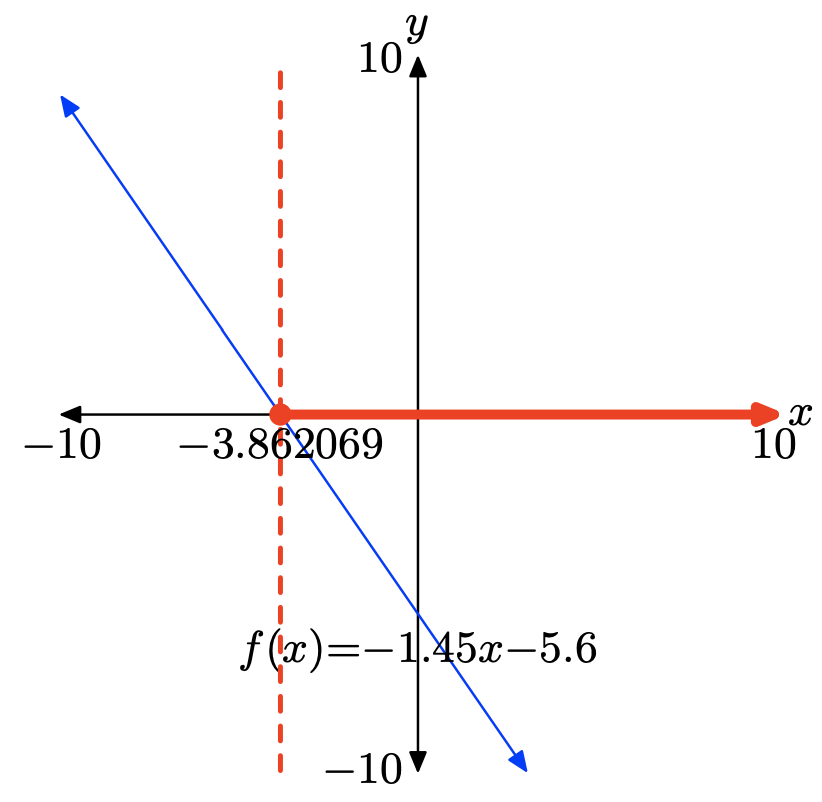
Ejercicio\(\PageIndex{40}\)
f (x) = 1.35x + 8.6
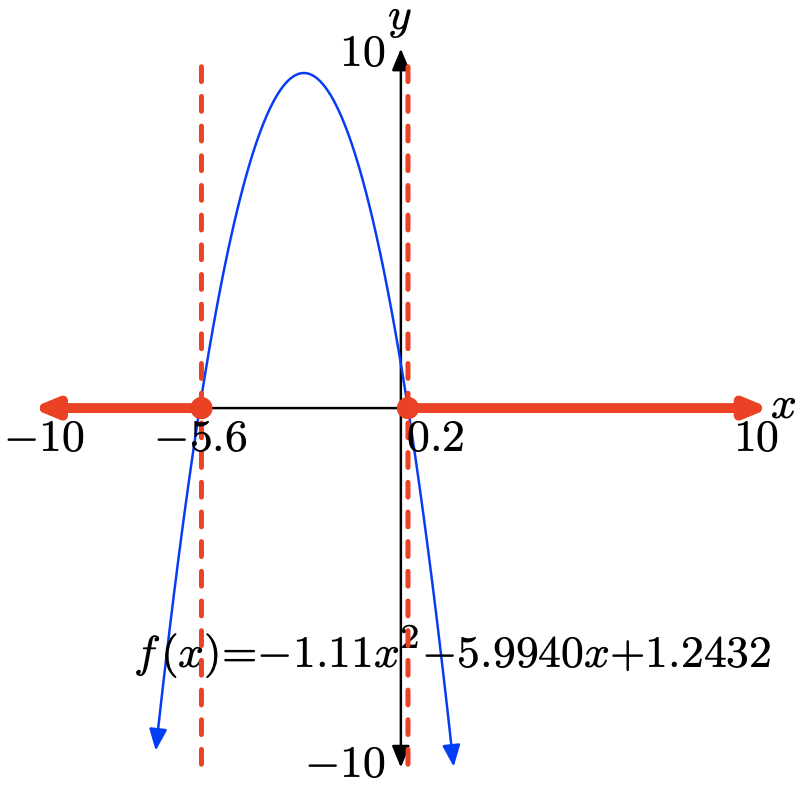
Ejercicio\(\PageIndex{41}\)
\(f(x) = −1.11x^2 −5.9940x+1.2432\)
- Contestar
-
Para resolver la desigualdad\(f(x) \leq 0\) gráficamente, comience cargando\(f(x) = −1.11x^2 − 5.9940x+1.2432\) en Y1. Utilice la utilidad cero en el menú CALC para determinar los ceros de f, como se muestra en (b) y (c).
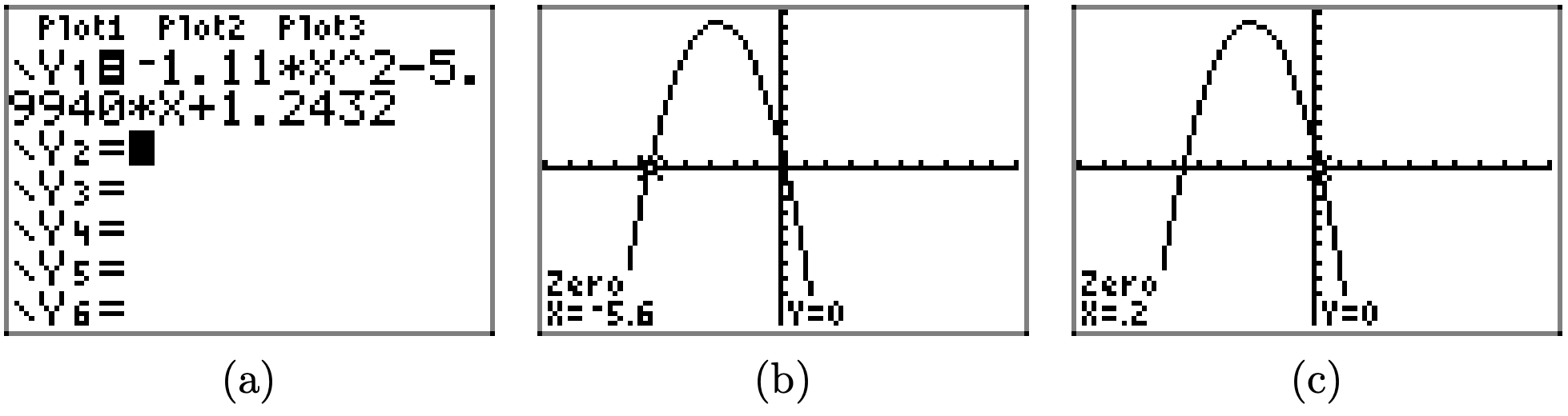
La gráfica de f intercepta el eje x en x = −5.6 y x = 0.2. La gráfica de f se encuentra debajo del eje x para todos los valores de x que se encuentran a la izquierda de x = −5.6 o a la derecha de x = 0.2. Por lo tanto, la solución de\(f(x) \leq 0\) es\((−\infty, −5.6] \cup [0.2,\infty)\) o\(\{x : x \leq −5.6 or x \geq 0.2\}\). Las respuestas pueden variar debido a un error de redondear.
Ejercicio\(\PageIndex{42}\)
\(f(x) = 1.22x^2 − 6.3440x + 1.3176\)
2.5 Ejercicios
A continuación se muestra la gráfica de una función f.
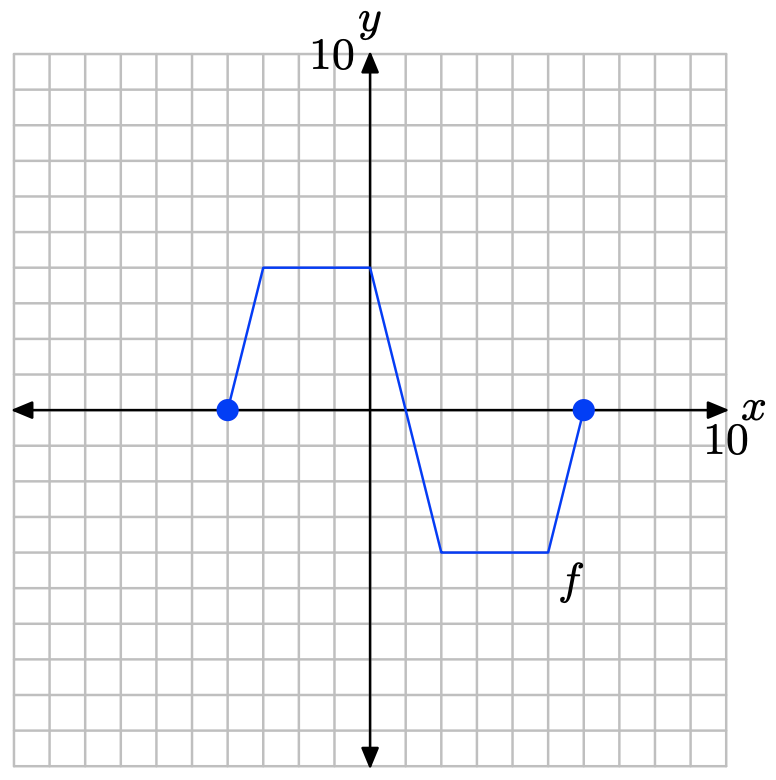
La tabla que sigue evalúa la función f en la gráfica a valores clave de x Observe el formato horizontal, donde el primer punto de la tabla es el par ordenado (−4, 0).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| f (x) | 0 | 4 | 4 | -4 | -4 | 0 |
Utilice la gráfica y la tabla para completar cada una de las siguientes tareas para Ejercicios\(\PageIndex{1}\) -\(\PageIndex{10}\).
i. Establecer un sistema de coordenadas en papel de gráfico. Etiquete y escale cada eje, luego copie y etiquete la gráfica original de f en su sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. Utilice la tabla original para ayudar a completar la tabla para la función dada en el ejercicio.
iii. Usando un lápiz de color diferente, traza los datos de tu tabla terminada en el mismo sistema de coordenadas que la gráfica original de f. Usa estos puntos para ayudar a completar la gráfica de la función dada en el ejercicio, luego etiqueta esta gráfica con su ecuación dada en el ejercicio.
Ejercicio\(\PageIndex{1}\)
y= 2f (x).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
- Contestar
-
La tabla de funciones original.
x -4 -3 0 2 5 6 f (x) 0 4 4 -4 -4 0
Evalúe la función y = 2f (x) en x = −4, −3, 0, 2, 5 y 6.
\[y= 2f(−4) = 2(0) = 0 \\ y = 2f(−3) = 2(4) = 8 \\ y = 2f(0) = 2(4) = 8 \\ y = 2f(2) = 2(−4) = −8 \\ y = 2f(5) = 2(−4) = −8 \\ y = 2f(6) = 2(0) = 0 \]
Puntos satisfactorios y = 2f (x).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y | 0 | 8 | 8 | -8 | -8 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = 2f (x).
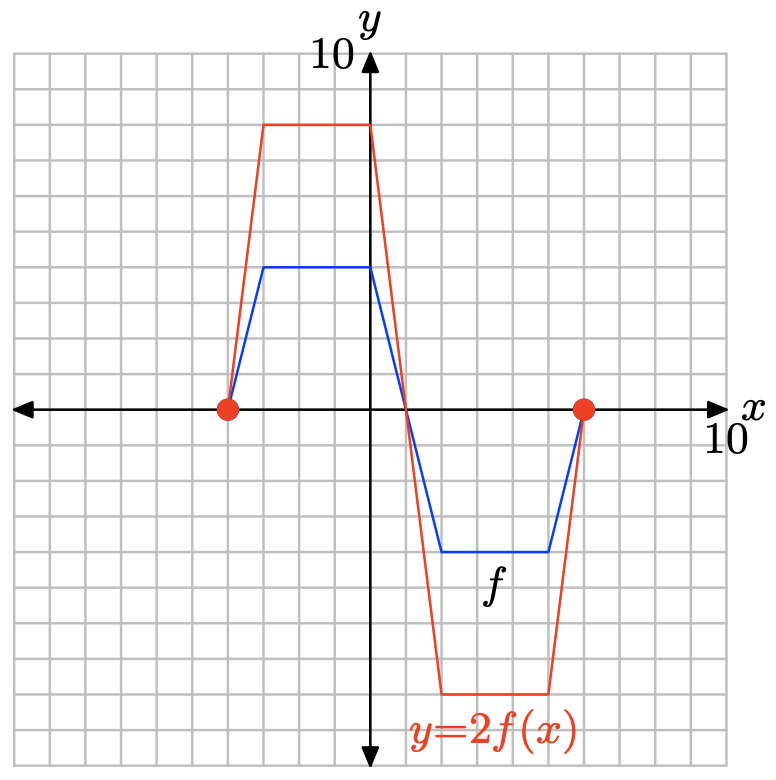
Obsérvese que multiplicando por 2, como en y = 2f (x), estira la gráfica de y = f (x) verticalmente por un factor de 2.
Ejercicio\(\PageIndex{2}\)
y = (1/2) f (x).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
Ejercicio\(\PageIndex{3}\)
y = −f (x).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
- Contestar
-
La tabla de funciones original.
x -4 -3 0 2 5 6 f (x) 0 4 4 -4 -4 0
Evalúe la función y = −f (x) en x = −4, −3, 0, 2, 5 y 6.
\[y = −f(−4) = −(0) = 0 \\ y = −f(−3) = −(4) = −4 \\ y = −f(0) = −(4) = −4 \\ y = −f(2) = −(−4) = 4 \\ y = −f(5) = −(−4) = 4 \\ y = −f(6) = −(0) = 0\]
Puntos satisfactorios y = −f (x).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y | 0 | -4 | -4 | 4 | 4 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = −f (x).
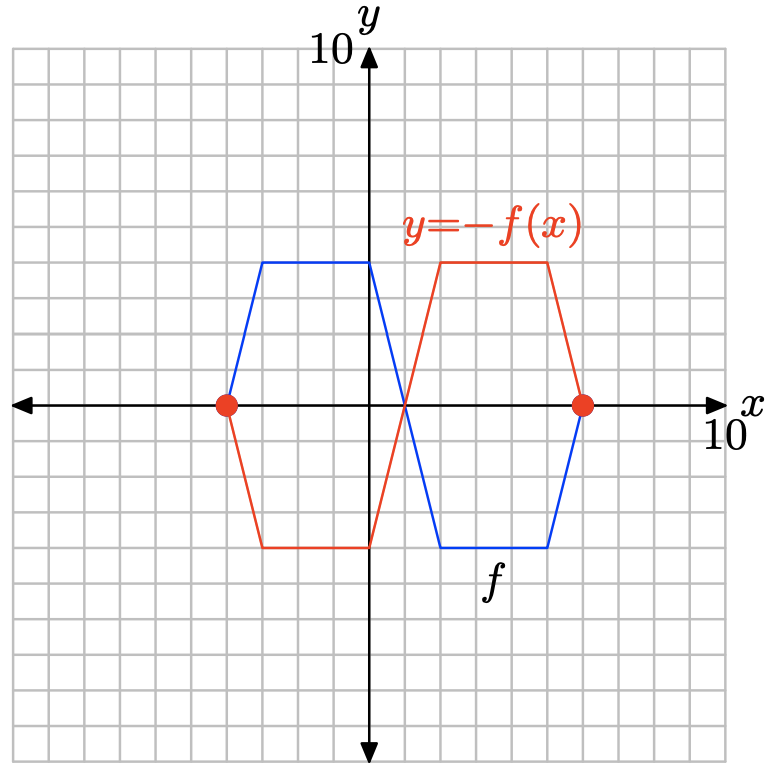
Tenga en cuenta que la negación de la función, como en y = −f (x), refleja la gráfica de y = f (x) a través del eje x.
Ejercicio\(\PageIndex{4}\)
y = f (x) − 2.
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
Ejercicio\(\PageIndex{5}\)
y = f (x) + 4.
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
- Contestar
-
La tabla de funciones original.
x -4 -3 0 2 5 6 f (x) 0 4 4 -4 -4 0
Evalúa la función y = f (x) + 4 a x = −4, −3, 0, 2, 5 y 6.
\[y = f(−4) + 4 = (0) + 4 = 4 \\y = f(−3) + 4 = (4) + 4 = 8 \\y = f(0) + 4 = (4) + 4 = 8 \\y = f(2) + 4 = (−4) + 4 = 0 \\y = f(5) + 4 = (−4) + 4 = 0 \\y = f(6) + 4 = (0) + 4 = 4\]
Puntos satisfactorios y = f (x) + 4.
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y | 4 | 8 | 8 | 0 | 0 | 4 |
Trace los puntos en la tabla para obtener la gráfica de y = f (x) + 4.
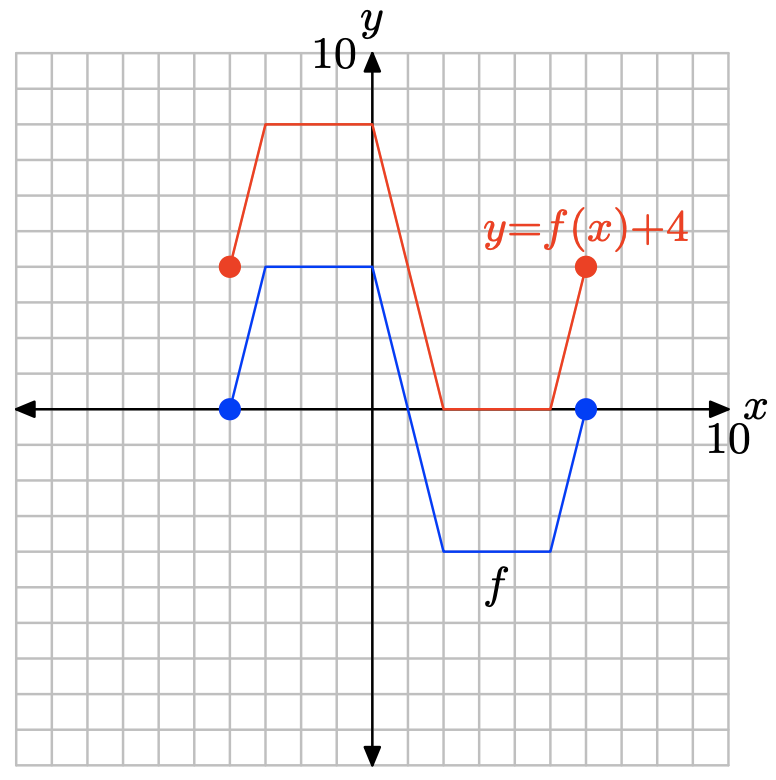
Obsérvese que sumar 4, como en y = f (x) + 4, traduce la gráfica de y = f (x) hacia arriba 4 unidades.
Ejercicio\(\PageIndex{6}\)
y = −2f (x)
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
Ejercicio\(\PageIndex{7}\)
y = (−1/2) f (x)
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
- Contestar
-
La tabla de funciones original.
x -4 -3 0 2 5 6 f (x) 0 4 4 -4 -4 0
Evalúe la función y = (−1/2) f (x) en x = −4, −3, 0, 2, 5 y 6.
\[y = (−1/2)f(−4) = (−1/2)(0) = 0 \\ y = (−1/2)f(−3) = (−1/2)(4) = −2 \\ y = (−1/2)f(0) = (−1/2)(4) = −2 \\ y = (−1/2)f(2) = (−1/2)(−4) = 2 \\ y = (−1/2)f(5) = (−1/2)(−4) = 2 \\ y = (−1/2)f(6) = (−1/2)(0) = 0 \]
Puntos satisfactorios y = (−1/2) f (x).
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y | 0 | -2 | -2 | 2 | 2 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = (−1/2) f (x).
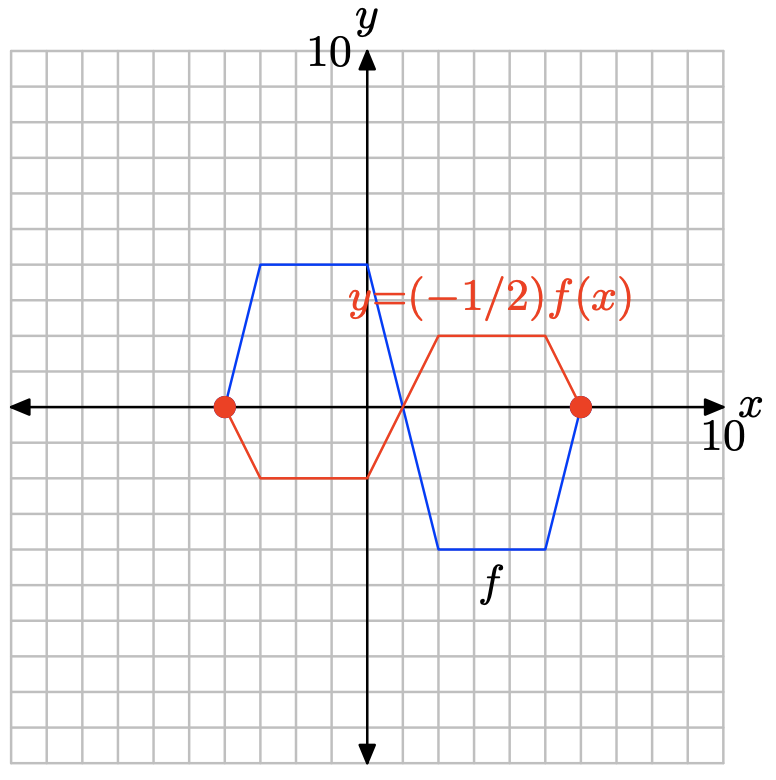
Tenga en cuenta que multiplicando por −1/2, como en y = (−1/2) f (x), comprime la gráfica de y = f (x) verticalmente por un factor de 2, luego refleja el resultado a través del eje x.
Ejercicio\(\PageIndex{8}\)
y = −f (x) + 3.
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
Ejercicio\(\PageIndex{9}\)
y = −f (x) − 2
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
- Contestar
-
La tabla de funciones original.
x -4 -3 0 2 5 6 f (x) 0 4 4 -4 -4 0
Evalúe la función y = −f (x) − 2 en x = −4, −3, 0, 2, 5 y 6.
\[y = −f(−4) − 2 = −(0) − 2 = −2 \\ y = −f(−3) − 2 = −(4) − 2 = −6\\ y = −f(0) − 2 = −(4) − 2 = −6 \\y = −f(2) − 2 = −(−4) − 2 = 2 \\y = −f(5) − 2 = −(−4) − 2 = 2 \\y = −f(6) − 2 = −(0) − 2 = −2 \]
Puntos satisfactorios y = −f (x) − 2.
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y | -2 | -6 | -6 | 2 | 2 | -2 |
Trace los puntos en la tabla para obtener la gráfica de y = −f (x) − 2.
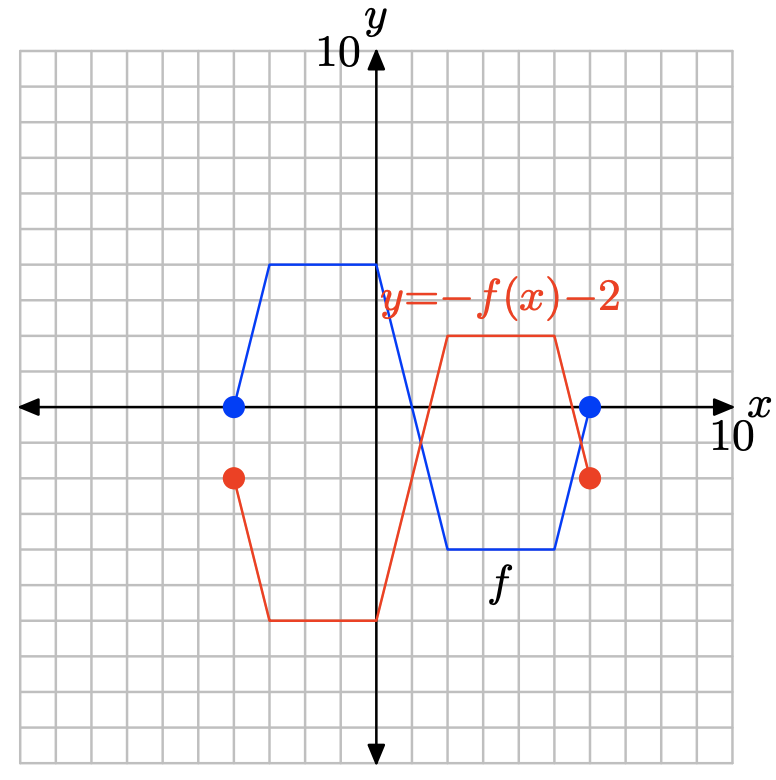
Tenga en cuenta que negando luego restando 2, como en y = −f (x) − 2, primero refleja la gráfica de y = f (x) a través del eje x, luego traduce la reflexión resultante 2 unidades hacia abajo.
Ejercicio\(\PageIndex{10}\)
y = (−1/2) f (x) + 3
| x | -4 | -3 | 0 | 2 | 5 | 6 |
| y |
Ejercicio\(\PageIndex{11}\)
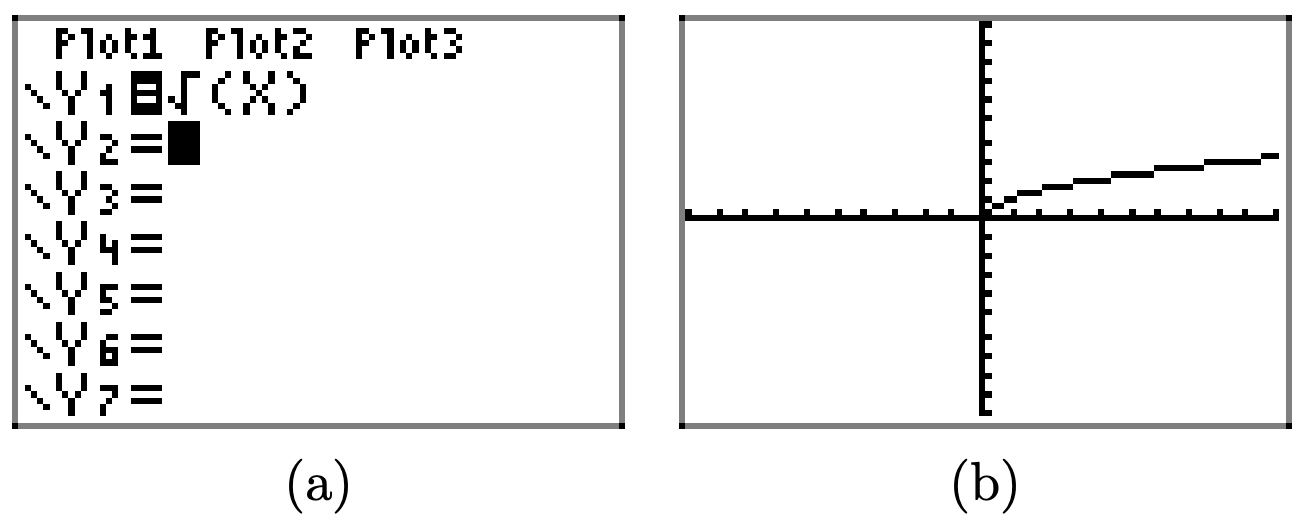
Usa tu calculadora gráfica para dibujar la gráfica de\(y = \sqrt{x}\). Después, dibuja la gráfica de\(y = \sqrt{x}\). En sus propias palabras, explique lo que aprendió de este ejercicio.
- Contestar
-
Primero, dibuja la gráfica de\(y = \sqrt{x}\).
La gráfica de\(y = -\sqrt{x}\) es un reflejo de la gráfica de\(y = \sqrt{x}\) a través del eje x.
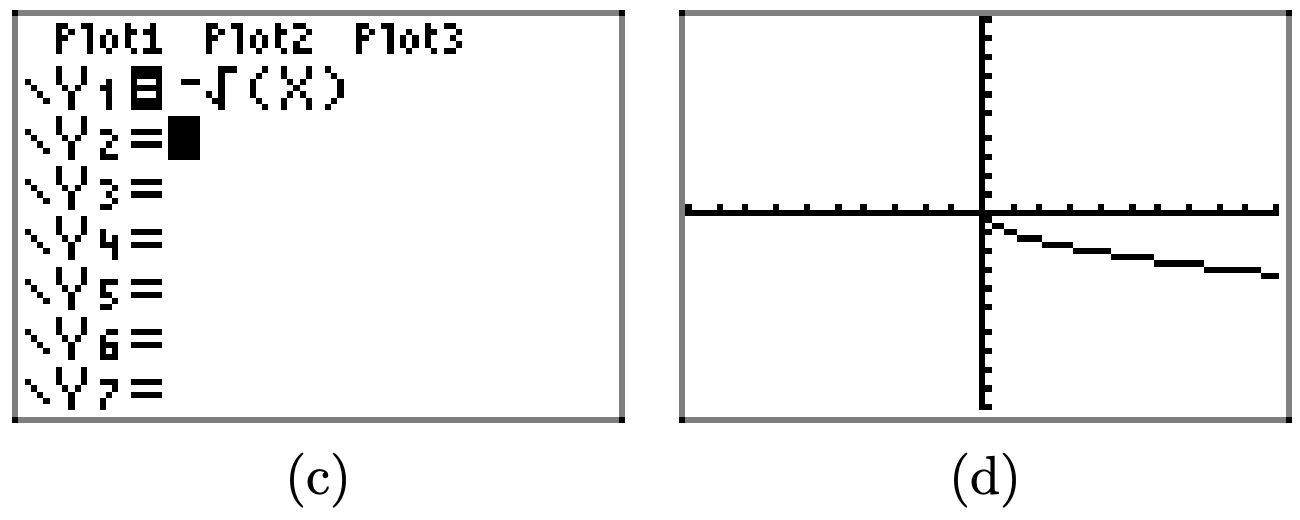
La negación de una función parece reflejar la gráfica de la función a través del eje x.
Ejercicio\(\PageIndex{12}\)
Usa tu calculadora gráfica para dibujar la gráfica de y = |x|. Luego, dibuja la gráfica de y = −|x|. En sus propias palabras, explique lo que aprendió de este ejercicio.
Ejercicio\(\PageIndex{13}\)
Usa tu calculadora gráfica para dibujar la gráfica de\(y = x^2\). Después, en sucesión, dibujar las gráficas de\(y = x^2−2\),\(y = x^2−4\), y\(y = x^2 − 6\). En sus propias palabras, explique lo que aprendió de este ejercicio.
- Contestar
-
Primero, dibuja la gráfica de\(y = x^2\).
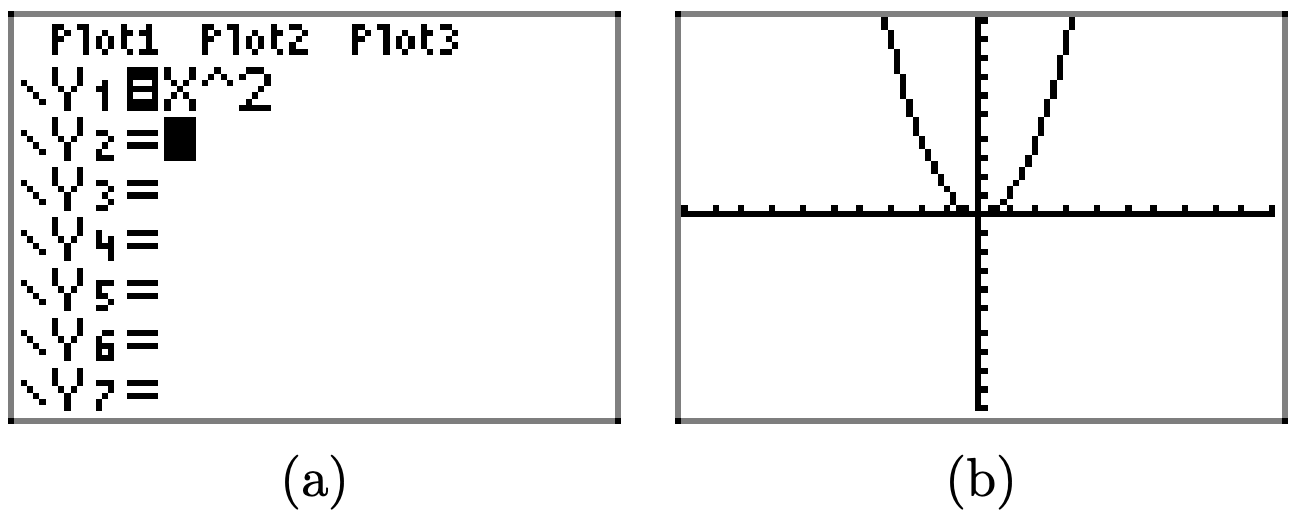
Restar 2 (como en\(y = x^2-2\)) traduce la gráfica de\(y = x^2\) dos unidades hacia abajo en la dirección y.
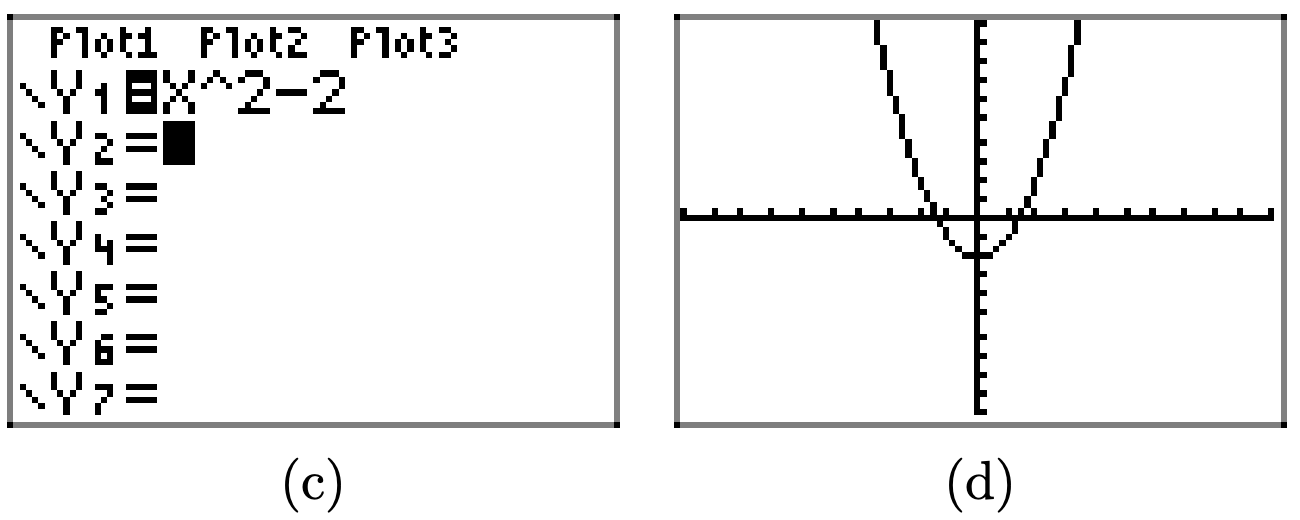
De igual manera, restando 4 y 6 traduce la gráfica de\(y = x^2\) cuatro unidades y 6 unidades a la baja, respectivamente
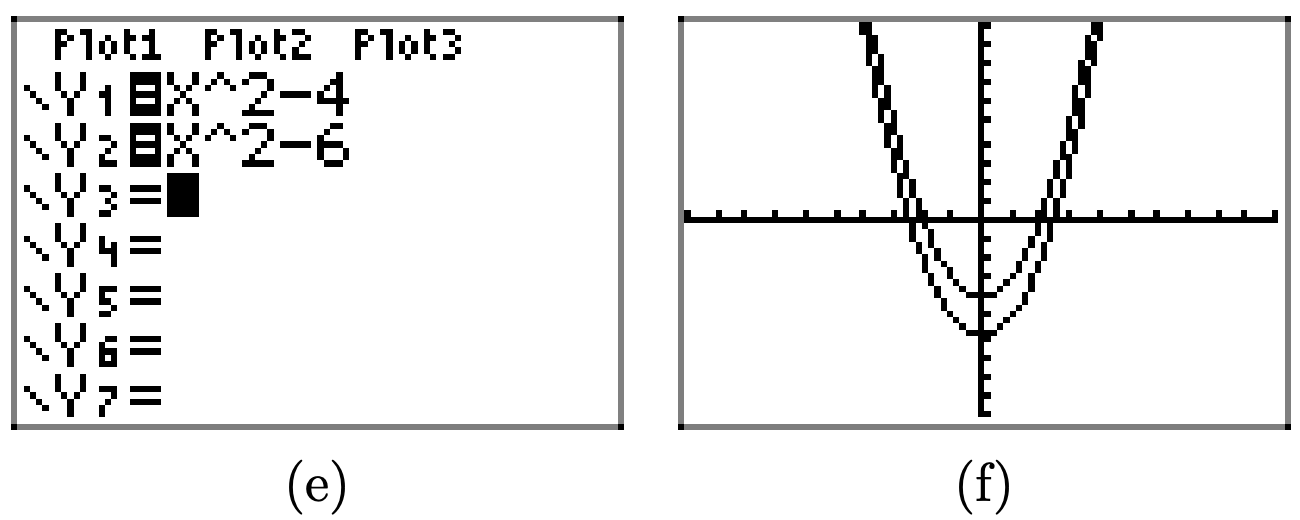
En general, si c es positivo, entonces la gráfica de y = f (x) − c se obtiene traduciendo la gráfica de y = f (x) hacia abajo c unidades.
Ejercicio\(\PageIndex{14}\)
Usa tu calculadora gráfica para dibujar la gráfica de\(y = x^2\). Después, en sucesión, dibujar las gráficas de\(y = x^2+2\),\(y = x^2+4\), y\(y = x^2 + 6\). En sus propias palabras, explique lo que aprendió de este ejercicio.
Ejercicio\(\PageIndex{15}\)
Usa tu calculadora gráfica para dibujar la gráfica de y = |x|. Después, en sucesión, dibuje las gráficas de y = 2|x|, y = 3|x|, e y = 4|x|. En sus propias palabras, explique lo que aprendió de este ejercicio.
- Contestar
-
Primero, dibuja la gráfica de y = |x|.
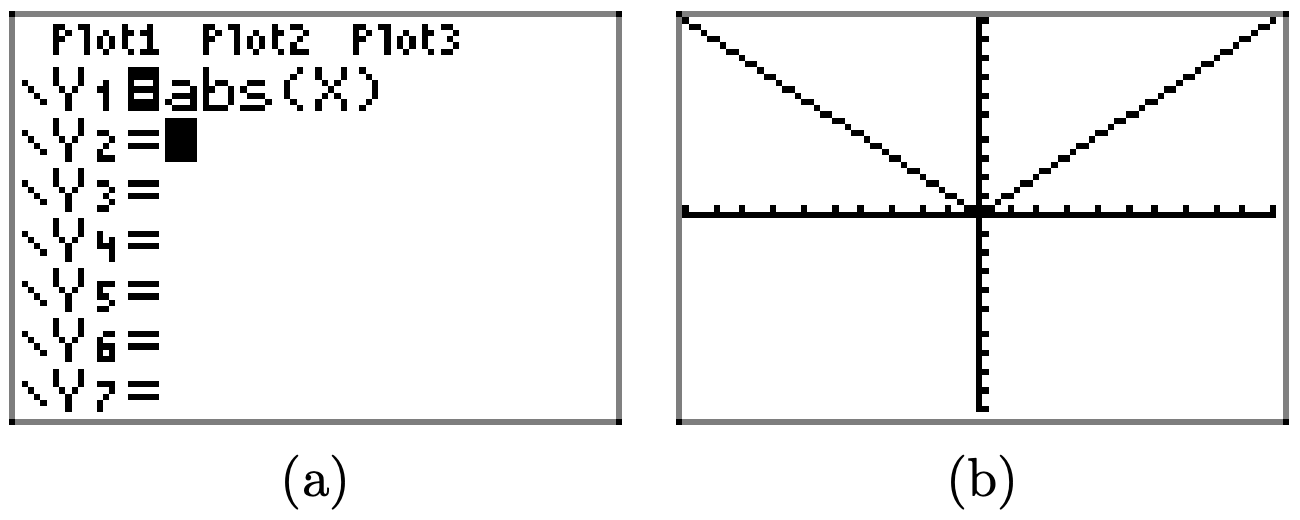
Multiplicando por 2, como en y = 2|x|, estira la gráfica de y = |x| verticalmente por un factor de 2.
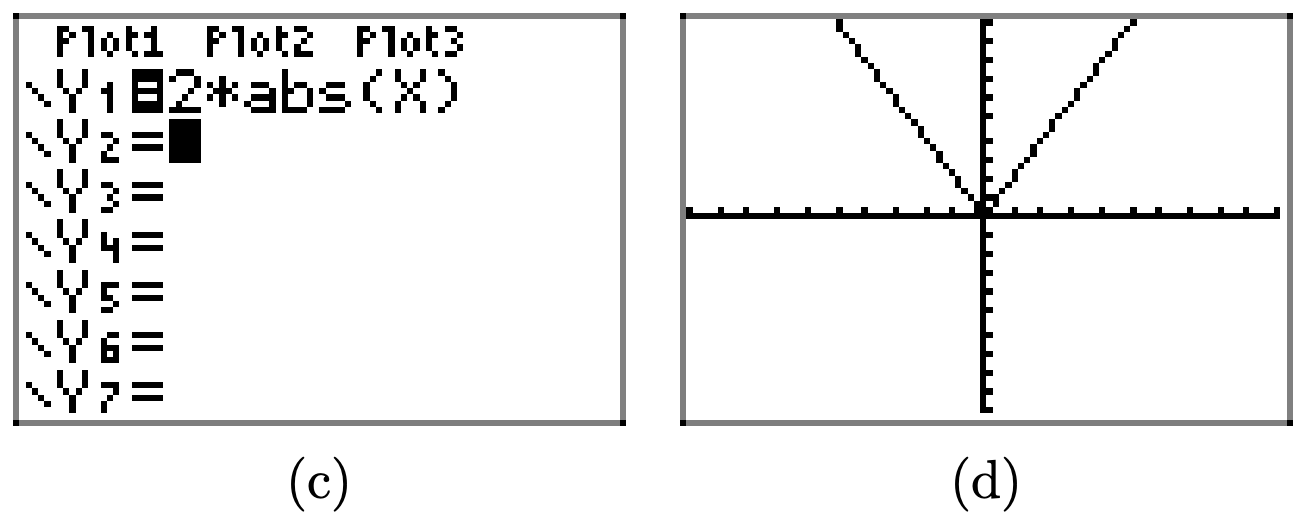
De igual manera, multiplicando por 3 y 4, como en y = 3|x| e y = 4|x|, estira la gráfica de y = |x| verticalmente por factores de 3 y 4, respectivamente.
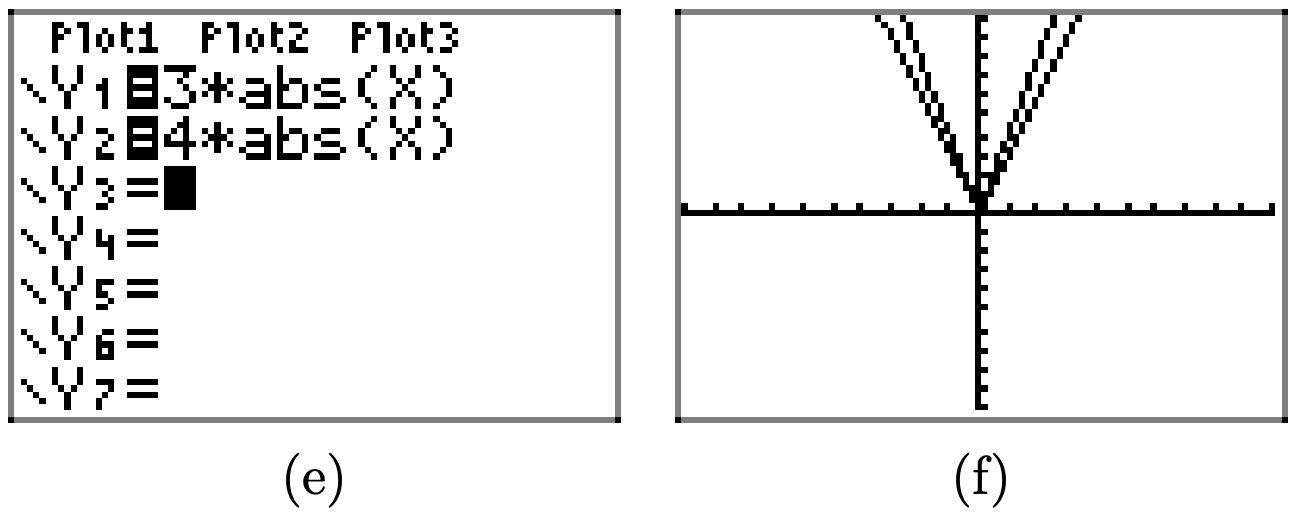
En general, si a > 1, entonces la gráfica de y = af (x) se obtiene estirando la gráfica de y = f (x) verticalmente por un factor de a.
Ejercicio\(\PageIndex{16}\)
Usa tu calculadora gráfica para dibujar la gráfica de y = |x|. Después, en sucesión, dibuje las gráficas de y = (1/2) |x|, y = (1/3) |x|, e y = (1/4) |x|. En sus propias palabras, explique lo que aprendió de este ejercicio.
A continuación se muestra la gráfica de una función f. en Ejercicios\(\PageIndex{17}\) -\(\PageIndex{22}\), utilice esta gráfica para realizar cada una de las siguientes tareas.
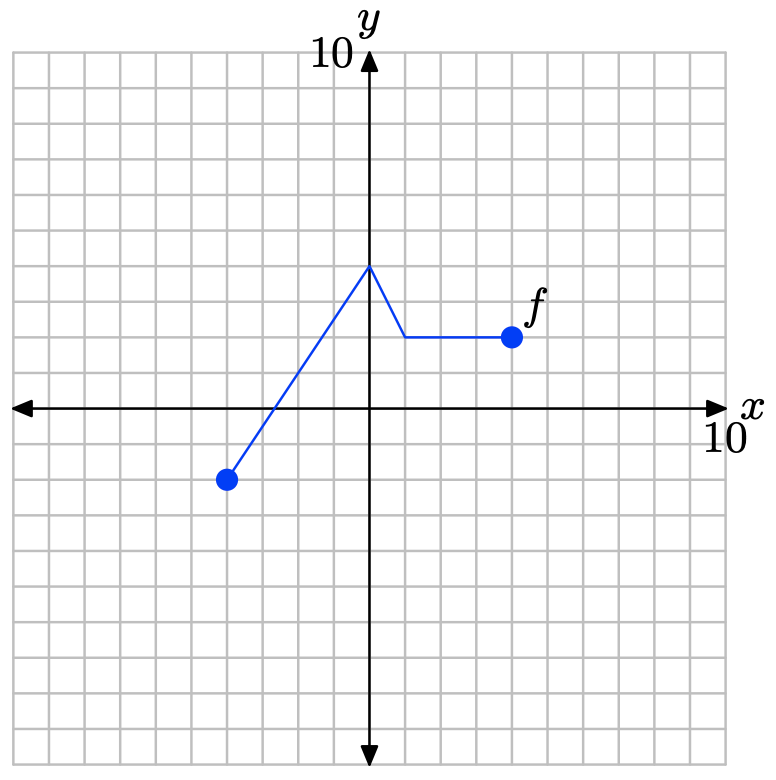
i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Haz una copia exacta de la gráfica de f en tu sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. En la narrativa, una caja de sombra al final de la sección resume los conceptos y la técnica de escalado vertical, reflexión vertical y traducción vertical. Utilice las ideas de atajo que se presentan en este cuadro de sombra de resumen para dibujar las gráficas de las funciones que siguen sin usar tablas.
iii. Usa un lápiz de diferente color para dibujar la gráfica de la función dada en el ejercicio. Etiquete esta gráfica con su ecuación. Asegúrese de que los puntos clave estén trazados con precisión. En cada ejercicio, se ruega trazar exactamente dos gráficas por sistema de coordenadas, la gráfica de la función original f y la gráfica de la función en el ejercicio.
Ejercicio\(\PageIndex{17}\)
y = (1/2) f (x).
- Contestar
-
Para obtener la gráfica de y = (1/2) f (x), simplemente multiplique el valor y de cada punto en la gráfica de y = f (x) por 1/2, manteniendo el valor x igual.
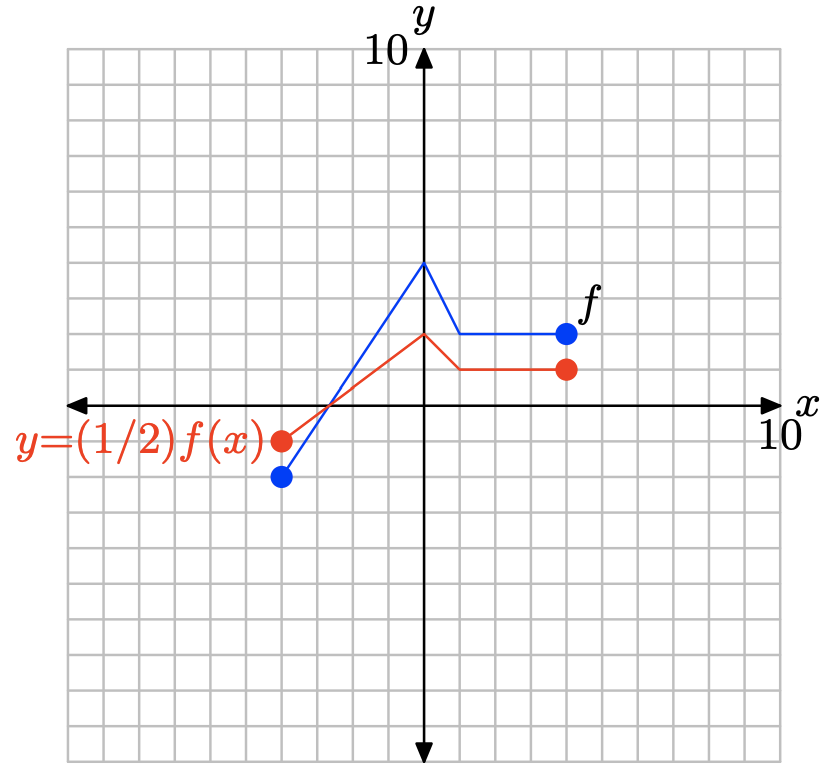
Obsérvese que multiplicando por 1/2, como en y = (1/2) f (x), comprime la gráfica de y = f (x) verticalmente por un factor de 2.
Ejercicio\(\PageIndex{18}\)
y = 2f (x).
Ejercicio\(\PageIndex{19}\)
y= −f (x).
- Contestar
-
Para obtener la gráfica de y = −f (x), simplemente niega el valor y de cada punto en la gráfica de y = f (x).
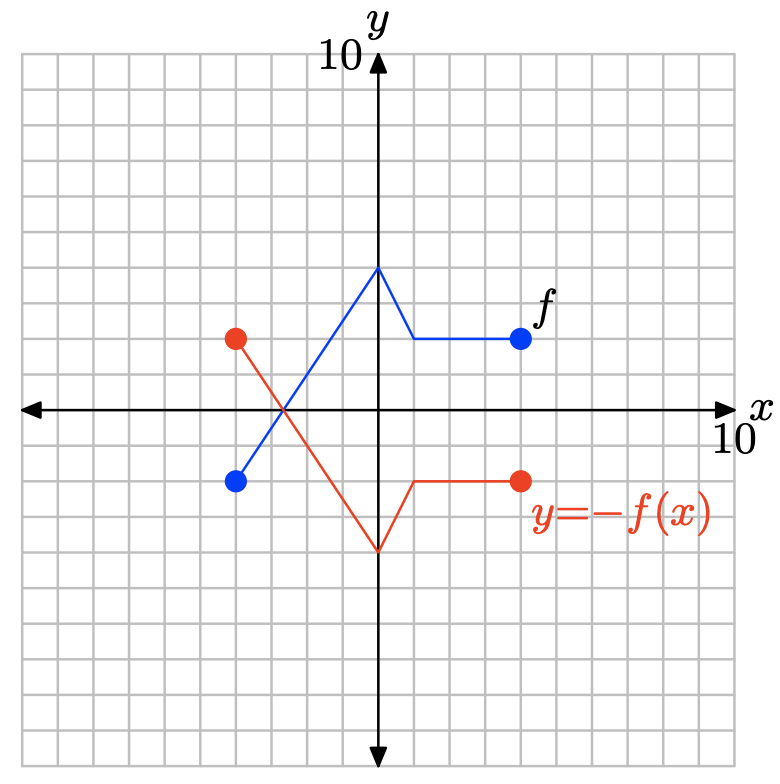
Tenga en cuenta que la negación, como en y = −f (x), refleja la gráfica de y = f (x) a través del eje x.
Ejercicio\(\PageIndex{20}\)
y = f (x) − 1
Ejercicio\(\PageIndex{21}\)
y = f (x) + 3.
- Contestar
-
Para obtener la gráfica de y = f (x) + 3, simplemente agregue 3 al valor y de cada punto en la gráfica de y = f (x).
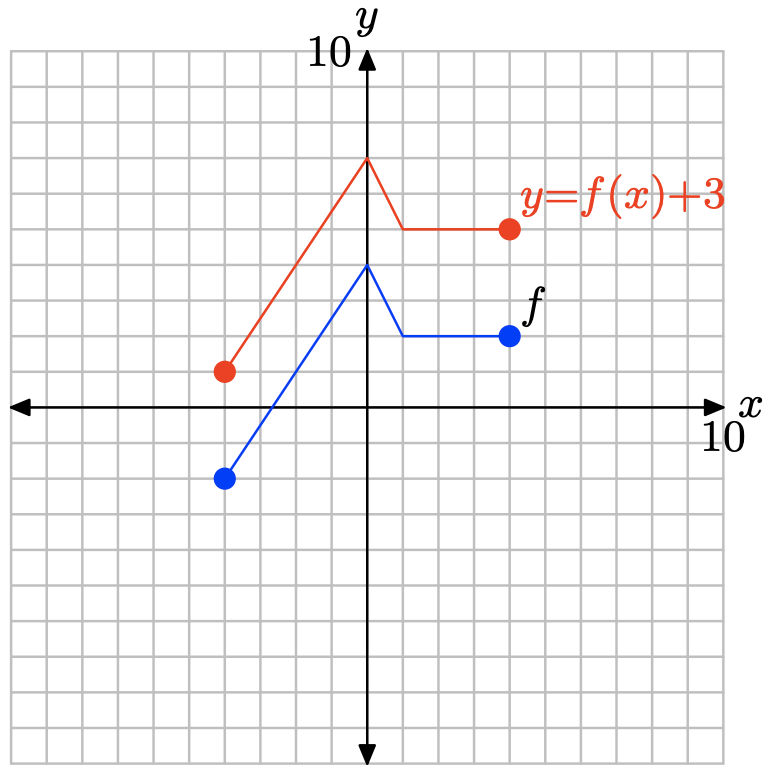
Obsérvese que sumar 3, como en y = f (x) + 3, traduce la gráfica de y = f (x) hacia arriba 3 unidades.
Ejercicio\(\PageIndex{22}\)
y = f (x) − 4
A continuación se muestra la gráfica de una función f. en Ejercicios\(\PageIndex{23}\) -\(\PageIndex{28}\), utilice esta gráfica para realizar cada una de las siguientes tareas.
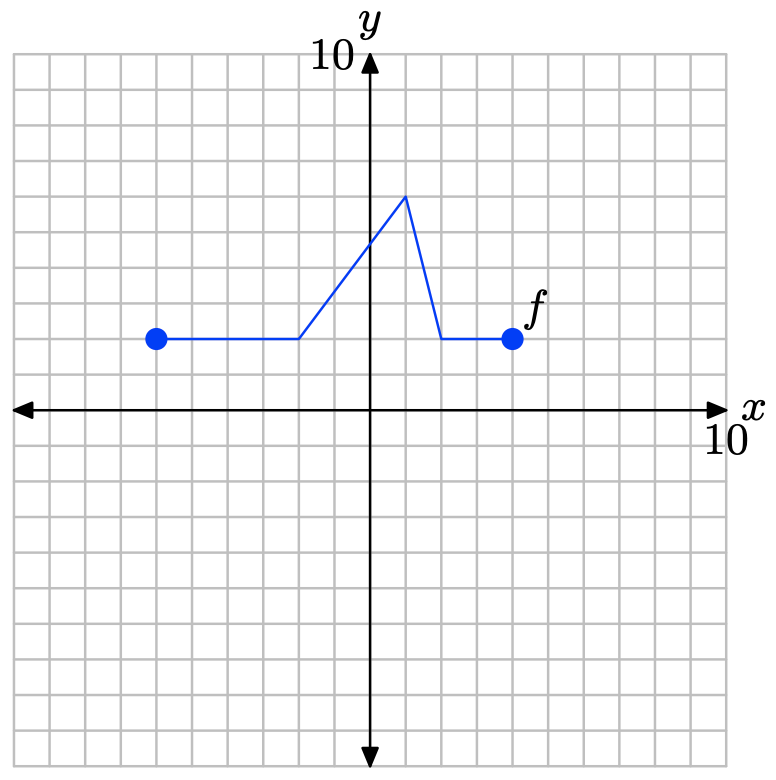
i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Haz una copia exacta de la gráfica de f en tu sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. En la narrativa, una caja de sombra al final de la sección resume los conceptos y la técnica de escalado vertical, reflexión vertical y traducción vertical. Utilice las ideas de atajo que se presentan en este cuadro de sombra de resumen para dibujar las gráficas de las funciones que siguen sin usar tablas.
iii. Usa un lápiz de diferente color para dibujar la gráfica de la función dada en el ejercicio. Etiquete esta gráfica con su ecuación. Asegúrese de que los puntos clave estén trazados con precisión. En cada ejercicio, se ruega trazar exactamente dos gráficas por sistema de coordenadas, la gráfica de la función original f y la gráfica de la función en el ejercicio.
Ejercicio\(\PageIndex{23}\)
y = 2f (x)
- Contestar
-
Para obtener la gráfica de y = 2f (x), simplemente multiplique el valor y de cada punto de y = f (x) por 2.
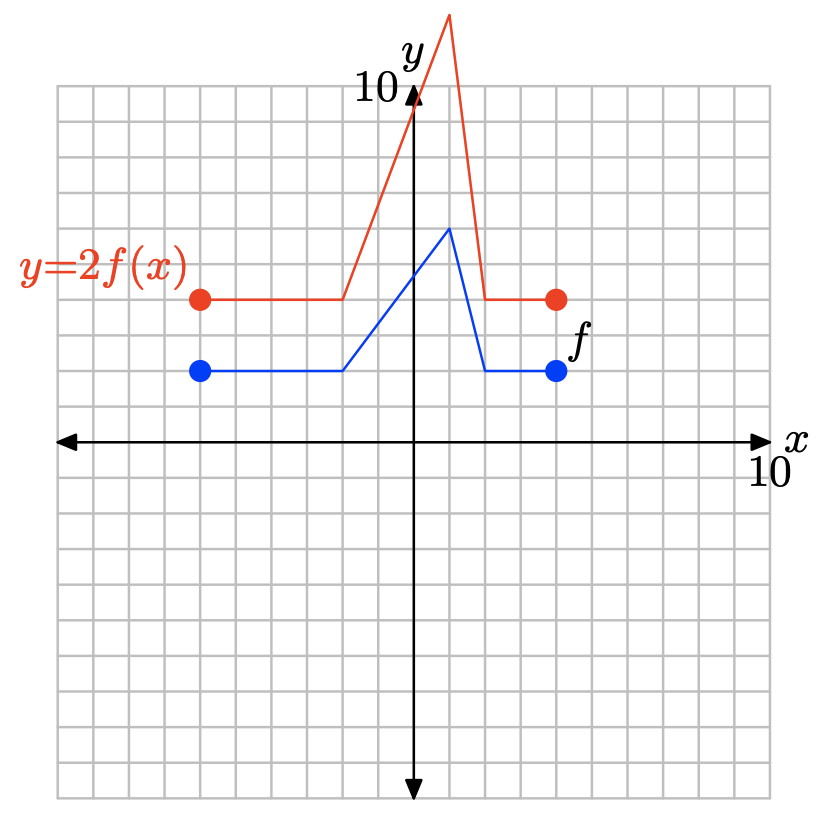
Obsérvese que multiplicando por 2, como en y = 2f (x), estira la gráfica de y = f (x) verticalmente por un factor de 2.
Ejercicio\(\PageIndex{24}\)
y = (1/2) f (x)
Ejercicio\(\PageIndex{25}\)
y = −f (x).
- Contestar
-
Para obtener la gráfica de y = −f (x), simplemente niega el valor y de cada punto en la gráfica de y = f (x).
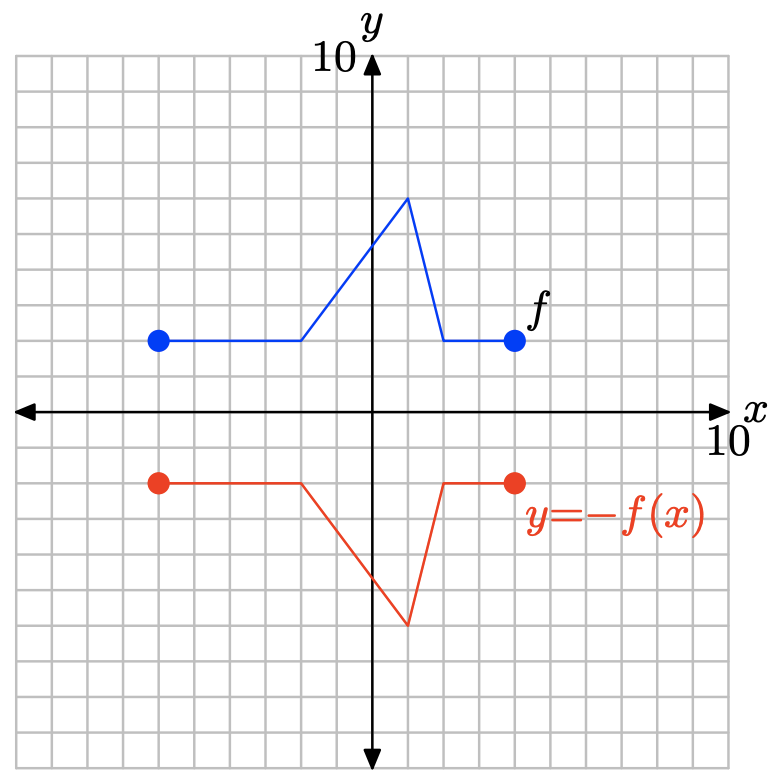
Tenga en cuenta que negar una función, como en y = −f (x), refleja la gráfica de y = f (x) a través del eje x.
Ejercicio\(\PageIndex{26}\)
y = f (x) + 3
Ejercicio\(\PageIndex{27}\)
y = f (x) − 2
- Contestar
-
Para obtener la gráfica de y = f (x) − 2, simplemente resta 2 del valor y de cada punto en la gráfica de y = f (x).
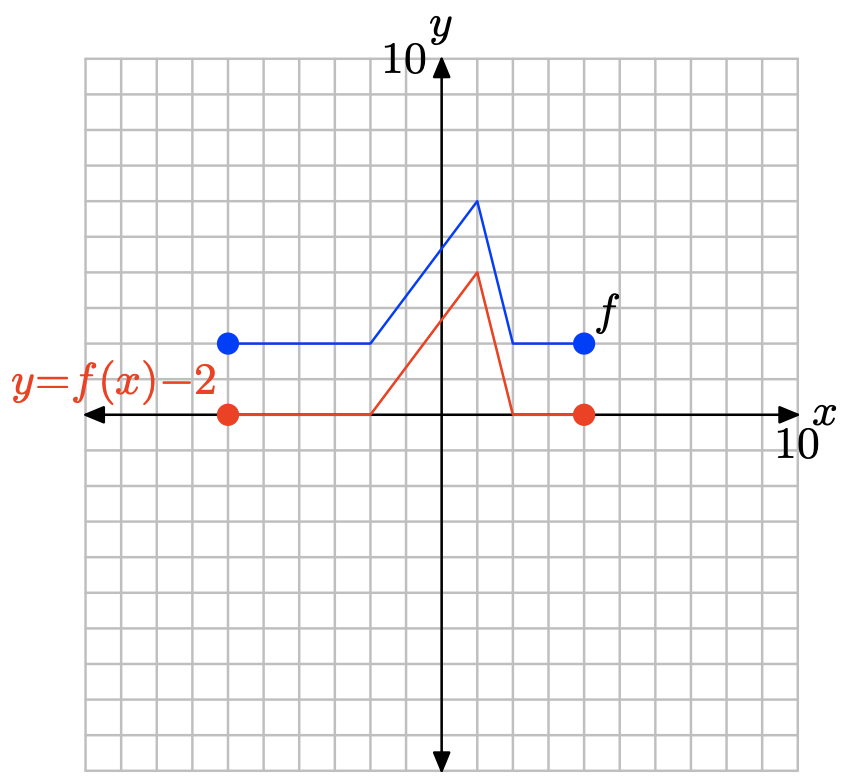
Obsérvese que restando 2, como en y = f (x) −2, traduce la gráfica de y = f (x) hacia abajo 2 unidades.
Ejercicio\(\PageIndex{28}\)
y = f (x) − 1
A continuación se muestra la gráfica de una función f. en Ejercicios\(\PageIndex{29}\) -\(\PageIndex{34}\), utilice esta gráfica para realizar cada una de las siguientes tareas.
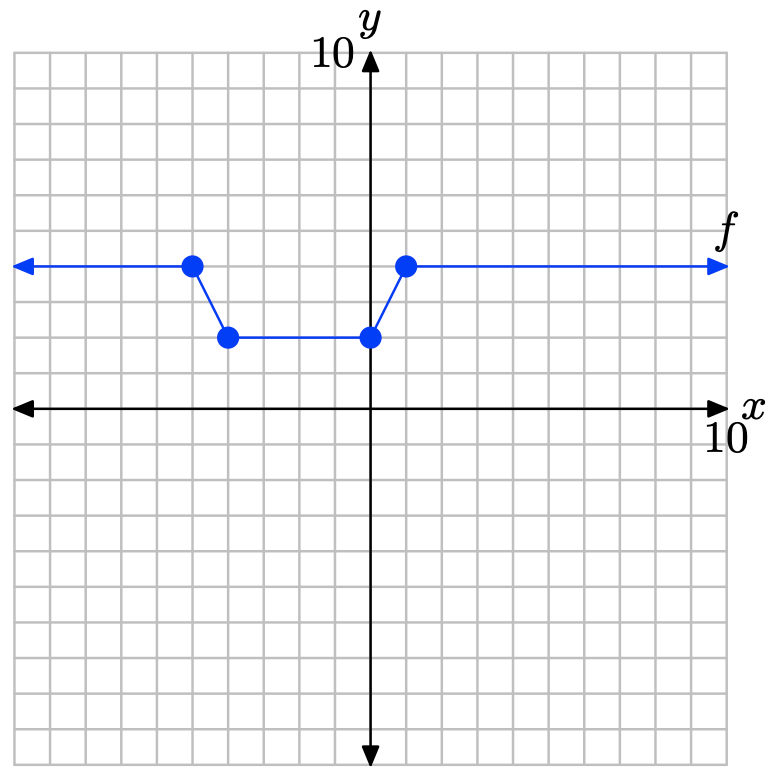
i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Haz una copia exacta de la gráfica de f en tu sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. En la narrativa, una caja de sombra al final de la sección resume los conceptos y la técnica de escalado vertical, reflexión vertical y traducción vertical. Utilice las ideas de atajo que se presentan en este cuadro de sombra de resumen para dibujar las gráficas de las funciones que siguen sin usar tablas.
iii. Usa un lápiz de diferente color para dibujar la gráfica de la función dada en el ejercicio. Etiquete esta gráfica con su ecuación. Asegúrese de que los puntos clave estén trazados con precisión. En cada ejercicio, se ruega trazar exactamente dos gráficas por sistema de coordenadas, la gráfica de la función original f y la gráfica de la función en el ejercicio.
Ejercicio\(\PageIndex{29}\)
y = (−1/2) f (x)
- Contestar
-
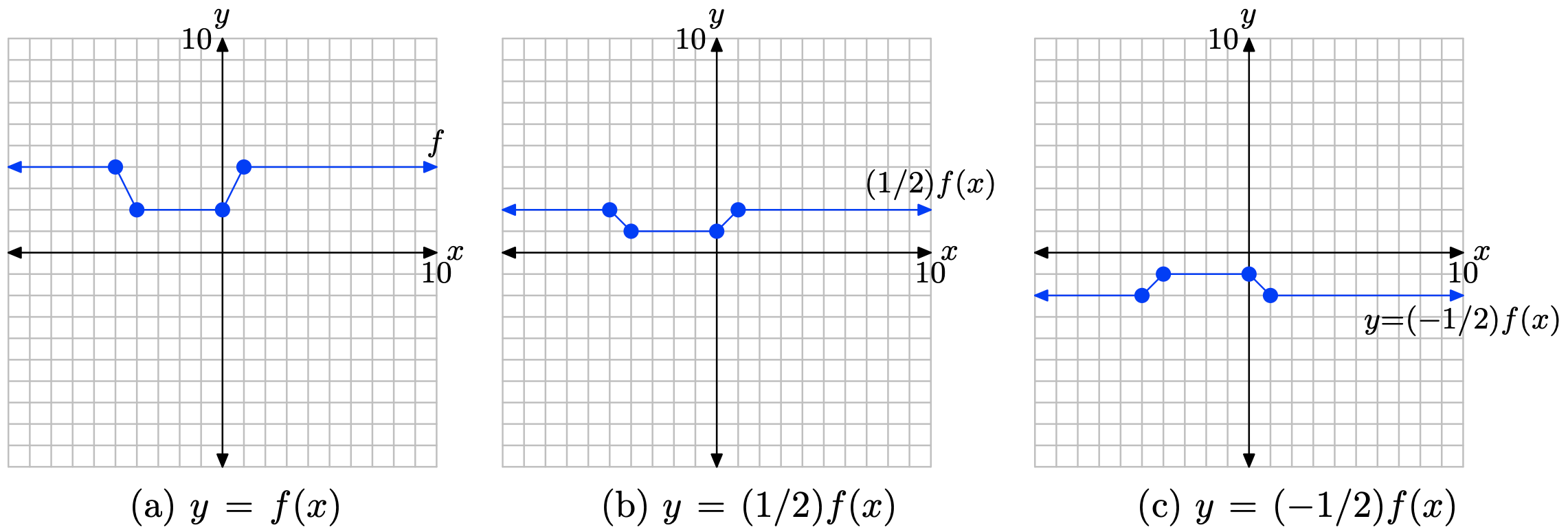
Se procede en dos pasos:
1. Primero, multiplique el valor y de cada punto en la gráfica de y = f (x) por 1/2 para producir la gráfica de y = (1/2) f (x) en (b). Esto comprime la gráfica de y = f (x) por un factor de 2.
2. En segundo lugar, multiplique el valor y de cada punto en la gráfica de y = (1/2) f (x) por −1 para producir la gráfica de y = (−1/2) f (x) en (c). Esto refleja la gráfica de y = (1/2) f (x) a través del eje x.
Ejercicio\(\PageIndex{30}\)
y = −2f (x).
Ejercicio\(\PageIndex{31}\)
y = −f (x) + 2
- Contestar
-
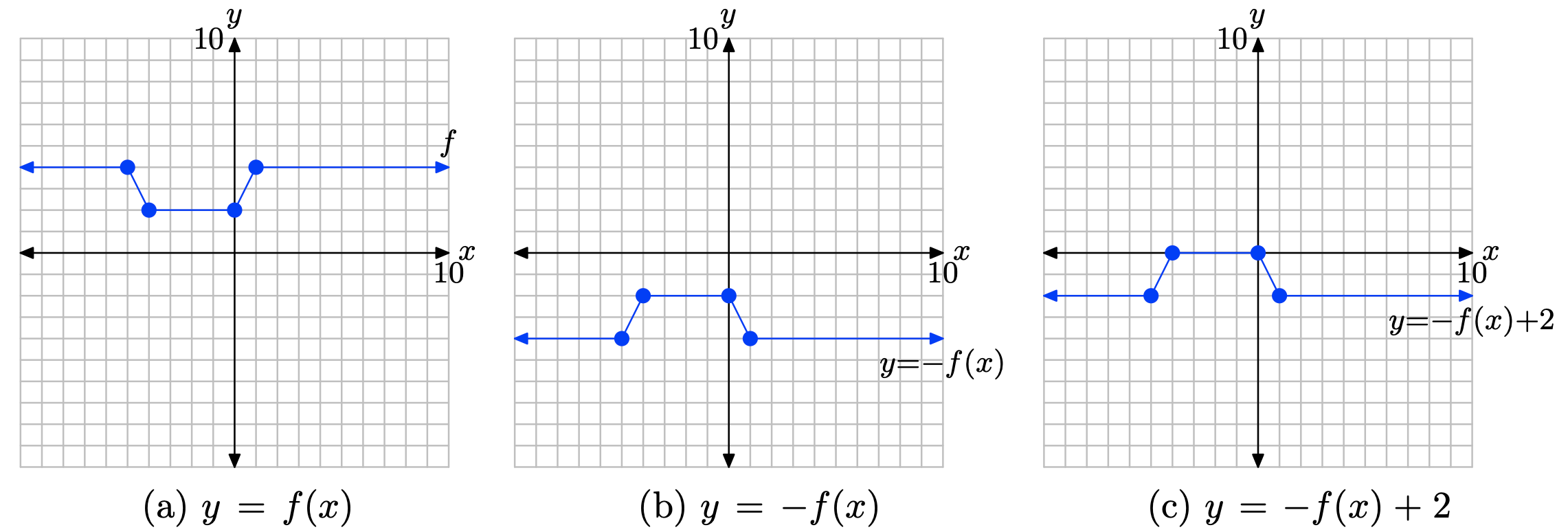
Se procede en dos pasos:
1. Primero, multiplica el valor y de cada punto en la gráfica de y = f (x) por −1 para producir la gráfica de y = −f (x) en (b). Esto refleja la gráfica de y = f (x) a través del eje x.
2. En segundo lugar, sumar 2 al valor y de cada punto en la gráfica de y = −f (x) para producir la gráfica de y = −f (x) + 2 en (c). Esto desplaza la gráfica de y = −f (x) hacia arriba 2 unidades.
Ejercicio\(\PageIndex{32}\)
y = −f (x) − 3
Ejercicio\(\PageIndex{33}\)
y = 2f (x) − 3.
- Contestar
-
Se procede en dos pasos:
1. Primero, multiplica el valor y de cada punto en la gráfica de y = f (x) por 2 para producir la gráfica de y = 2f (x) en (b). Esto estira la gráfica de y = f (x) verticalmente por un factor de 2.
2. En segundo lugar, restar 3 del valor y de cada punto en la gráfica de y = 2f (x) para producir la gráfica de y = 2f (x) − 3 en (c). Esto desplaza la gráfica de y = 2f (x) hacia abajo 3 unidades.
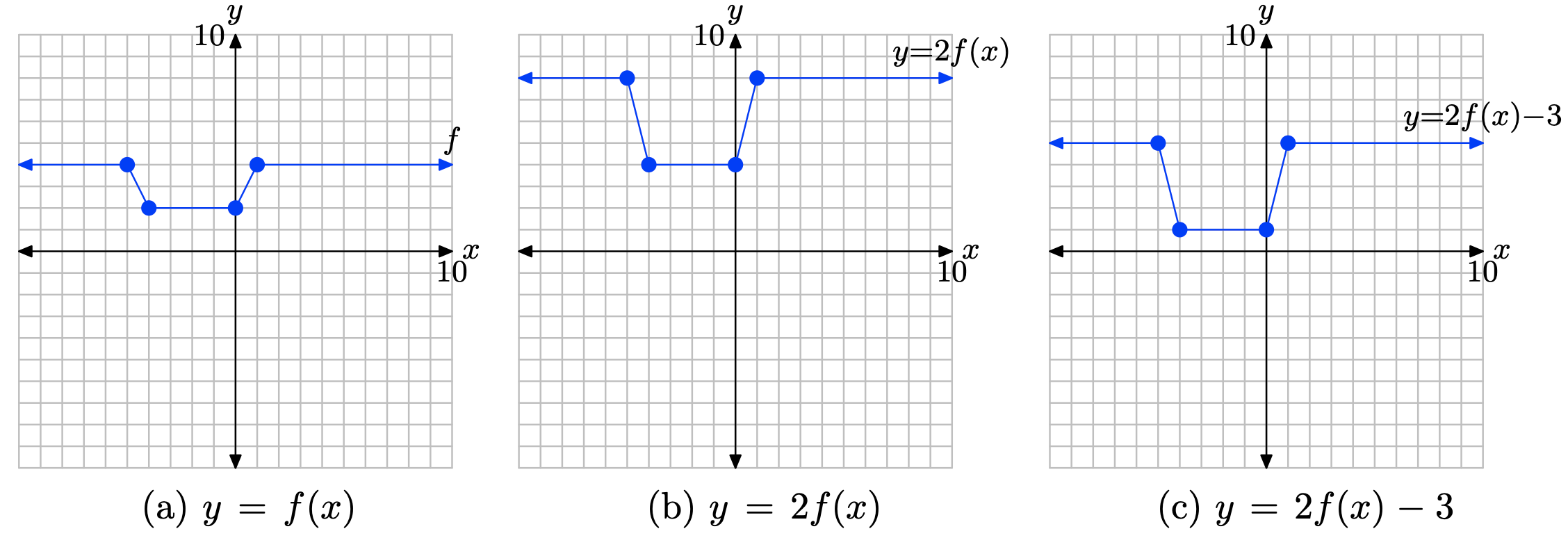
Ejercicio\(\PageIndex{34}\)
y = (−1/2) f (x) + 1
2.6 Ejercicios
A continuación se muestra la gráfica de una función f.
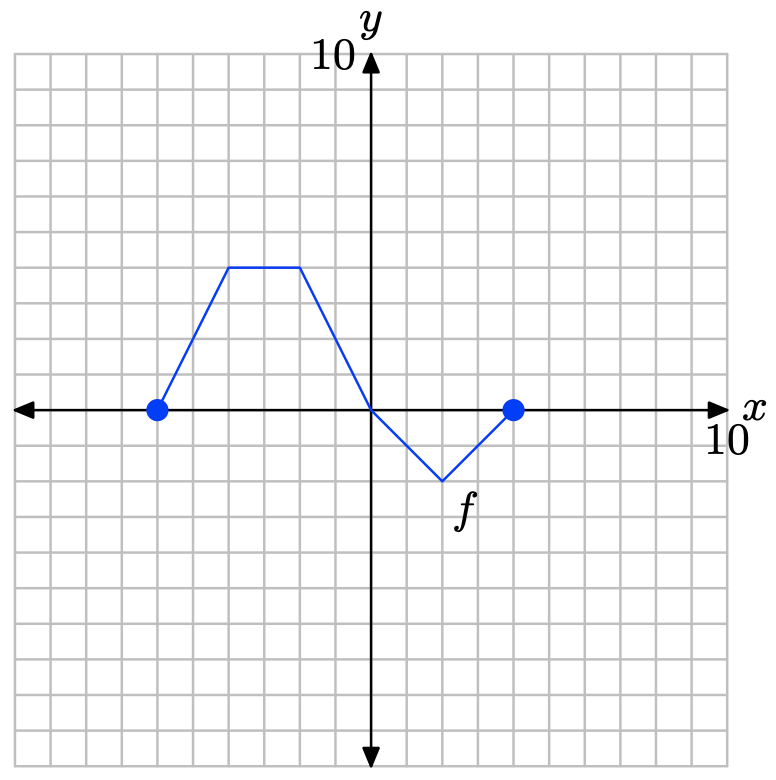
La tabla que sigue evalúa la función f en la gráfica a valores clave de x Observe el formato horizontal, donde el primer punto de la tabla es el par ordenado (−6, 0).
| x | -6 | -4 | -2 | 0 | 2 | 4 |
| f (x) | 0 | 4 | 4 | 0 | -2 | 0 |
Utilice la gráfica y la tabla para completar cada una de las siguientes tareas para Ejercicios\(\PageIndex{1}\) -\(\PageIndex{10}\).
i. Establecer un sistema de coordenadas en papel de gráfico. Etiquete y escale cada eje, luego copie y etiquete la gráfica original de f en su sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. Utilice la tabla original para ayudar a completar la tabla para la función dada en el ejercicio.
iii. Usando un lápiz de color diferente, traza los datos de tu tabla terminada en el mismo sistema de coordenadas que la gráfica original de f. Usa estos puntos para ayudar a completar la gráfica de la función dada en el ejercicio, luego etiqueta esta gráfica con su ecuación dada en el ejercicio.
Ejercicio\(\PageIndex{1}\)
y = f (2x).
| x | -3 | -2 | -1 | 0 | 1 | 2 |
| y |
- Contestar
-
La tabla de funciones original.
x -6 -4 -2 0 2 4 f (x) 0 4 4 0 -2 0
Evalúe la función y = f (2x) en x = −3, −2, −1, 0, 1 y 2.
\[y = f(2(−3)) = f(−6) = 0 \\ y = f(2(−2)) = f(−4) = 4 \\ y = f(2(−1)) = f(−2) = 4 \\ y = f(2(0)) = f(0) = 0 \\ y = f(2(1)) = f(2) = −2 \\ y = f(2(2)) = f(4) = 0 \]
Puntos satisfactorios y = f (2x).
| x | -3 | -2 | -1 | 0 | 1 | 2 |
| y | 0 | 4 | 4 | 0 | -2 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = f (2x).
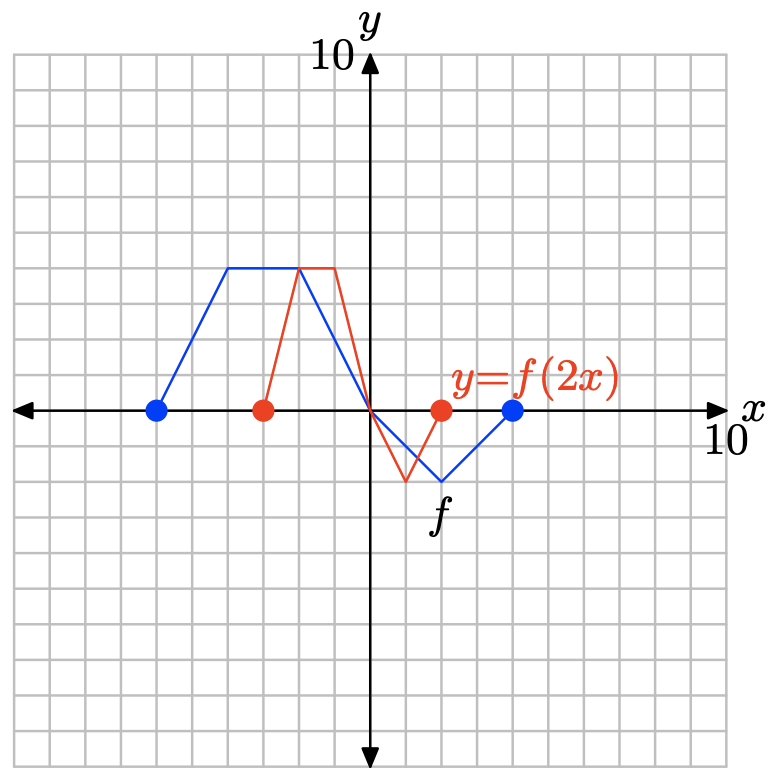
Tenga en cuenta que al reemplazar x por 2x, como en y = f (2x), comprime la gráfica de y = f (x) horizontalmente por un factor de 2.
Ejercicio\(\PageIndex{2}\)
y = f ((1/2) x).
| x | -12 | -8 | -4 | 0 | 4 | 8 |
| y |
Ejercicio\(\PageIndex{3}\)
y = f (−x).
| x | -4 | -2 | 0 | 2 | 4 | 6 |
| y |
- Contestar
- La tabla de funciones original.
-
x -6 -4 -2 0 2 4 f (x) 0 4 4 0 -2 0
Evalúe la función y = f (−x) en x = −4, −2, 0, 2, 4 y 6.
\[y = f(−(−4)) = f(4) = 0 \\ y = f(−(−2)) = f(2) = −2 \\ y = f(−(0)) = f(0) = 0 \\ y = f(−(2)) = f(−2) = 4 \\ y = f(−(4)) = f(−4) = 4 \\ y = f(−(6)) = f(−6) = 0 \]
Puntos satisfactorios y = f (−x).
| x | -4 | -2 | 0 | 2 | 4 | 6 |
| y | 0 | -2 | 0 | 4 | 4 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = f (−x).
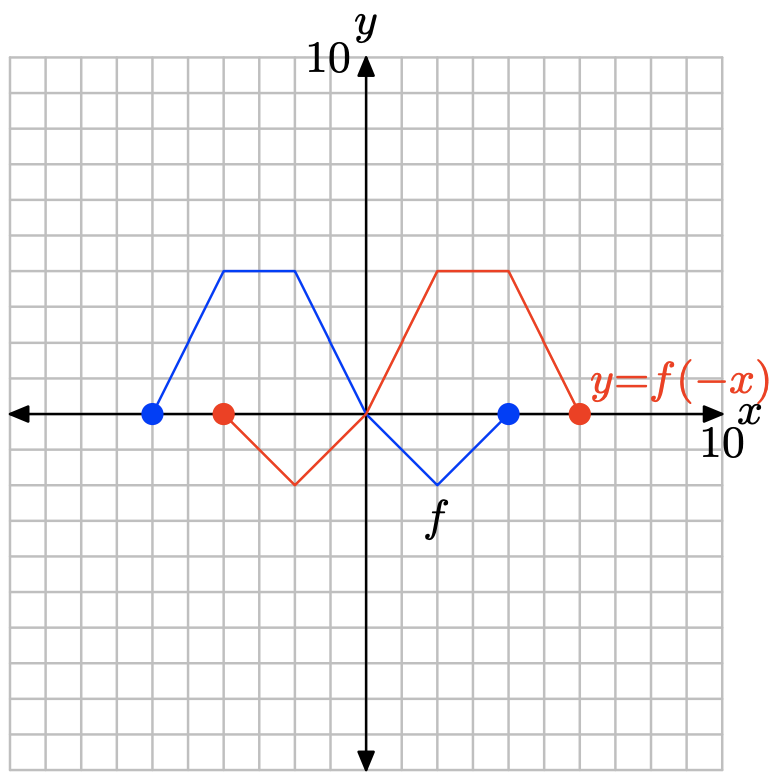
Tenga en cuenta que reemplazar x por −x, como en y = f (−x), refleja la gráfica de y = f (x) a través del eje y.
Ejercicio\(\PageIndex{4}\)
y = f (x + 3).
| x | -9 | -7 | -5 | -3 | -1 | 1 |
| y |
Ejercicio\(\PageIndex{5}\)
y = f (x − 1).
| x | -5 | -3 | -1 | 1 | 3 | 5 |
| y |
- Contestar
-
La tabla de funciones original.
x -6 -4 -2 0 2 4 f (x) 0 4 4 0 -2 0
Evalúe la función y = f (x − 1) en x = −5, −3, −1, 1, 3 y 5.
\[y = f((−5) − 1) = f(−6) = 0 \\ y = f((−3) − 1) = f(−4) = 4 \\ y = f((−1) − 1) = f(−2) = 4 \\ y = f((1) − 1) = f(0) = 0 \\ y = f((3) − 1) = f(2) = −2 \\ y = f((5) − 1) = f(4) = 0\]
Puntos satisfactorios y = f (x − 1).
| x | -5 | -3 | -1 | 1 | 3 | 5 |
| y | 0 | 4 | 4 | 0 | -2 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = f (x − 1).
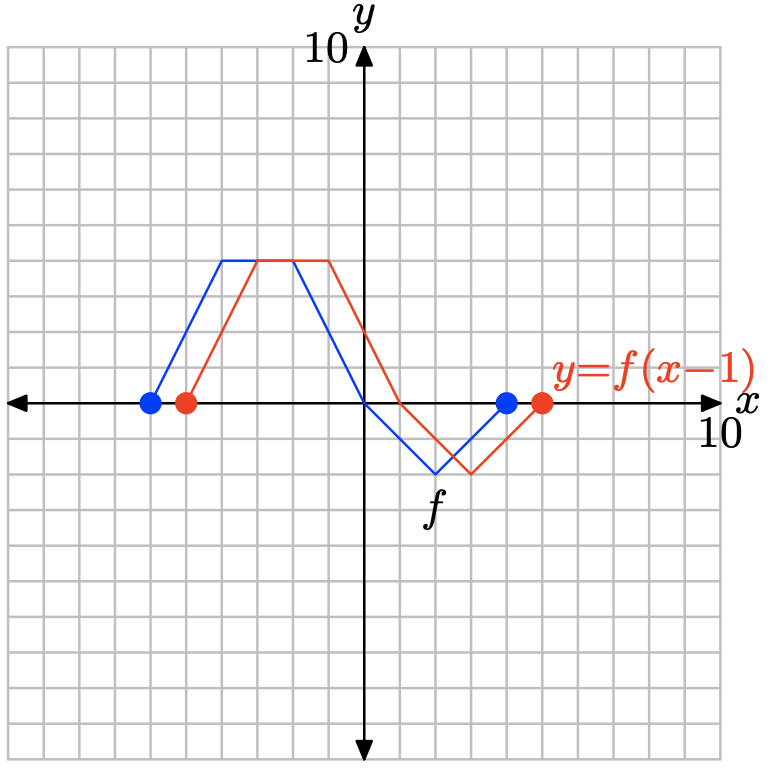
Tenga en cuenta que al reemplazar x por x − 1, como en y = f (x − 1), traduce la gráfica de y = f (x) horizontalmente 1 unidad a la derecha.
Ejercicio\(\PageIndex{6}\)
y = f (−2x).
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y |
Ejercicio\(\PageIndex{7}\)
y = f ((−1/2) x).
| x | -8 | -4 | 0 | 4 | 8 | 12 |
| y |
- Contestar
-
La tabla de funciones original.
x -6 -4 -2 0 2 4 f (x) 0 4 4 0 -2 0
Evalúe la función y = f ((−1/2) x) en x = −8, −4, 0, 4, 8 y 12.
\[y = f((−1/2)(−8)) = f(4) = 0 \\ y = f((−1/2)(−4)) = f(2) = −2 \\ y = f((−1/2)(0)) = f(0) = 0 \\ y = f((−1/2)(4)) = f(−2) = 4 \\ y = f((−1/2)(8)) = f(−4) = 4 \\ y = f((−1/2)(12)) = f(−6) = 0\]
Puntos satisfactorios y = f ((−1/2) x).
| x | -8 | -4 | 0 | 4 | 8 | 12 |
| y | 0 | -2 | 0 | 4 | 4 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = f ((−1/2) x).
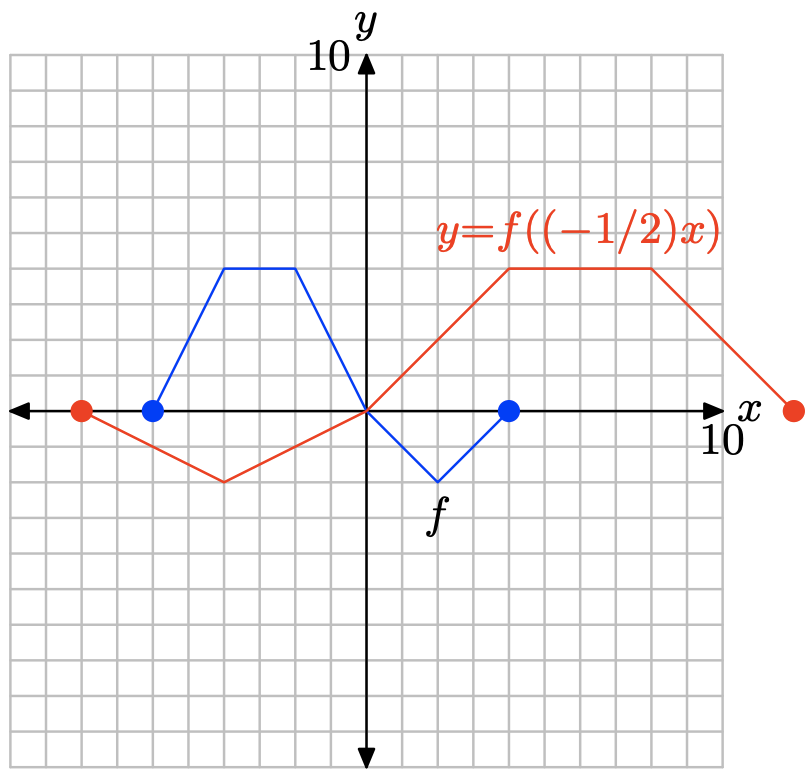
Tenga en cuenta que reemplazar x con (−1/2) x, como en y = f ((−1/2) x), estira la gráfica por un factor de 2, luego refleja el resultado a través del eje y.
Ejercicio\(\PageIndex{8}\)
y= f (−x − 2)
| x | -6 | -4 | -2 | 0 | 2 | 4 |
| y |
Ejercicio\(\PageIndex{9}\)
y= f (−x + 1).
| x | -3 | -1 | 1 | 3 | 5 | 7 |
| y |
- Contestar
-
La tabla de funciones original.
x -6 -4 -2 0 2 4 f (x) 0 4 4 0 -2 0
Evalúe la función y = f (−x + 1) en x = −3, −1, 1, 3, 5 y 7.
\[y = f(−(−3) + 1) = f(4) = 0 \\ y = f(−(−1) + 1) = f(2) = −2 \\ y = f(−(1) + 1) = f(0) = 0 \\ y = f(−(3) + 1) = f(−2) = 4 \\ y = f(−(5) + 1) = f(−4) = 4 \\ y = f(−(7) + 1) = f(−6) = 0 \]
Puntos satisfactorios y = f (−x + 1).
| x | -3 | -1 | 1 | 3 | 5 | 7 |
| y | 0 | -2 | 0 | 4 | 4 | 0 |
Trace los puntos en la tabla para obtener la gráfica de y = f (−x + 1).
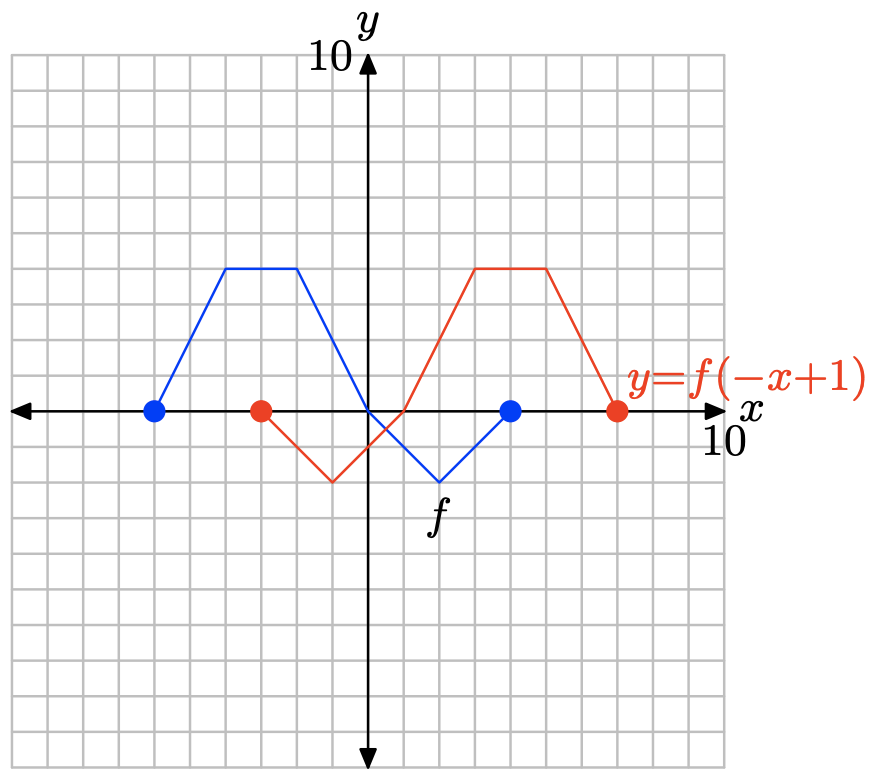
Tenga en cuenta que y = f (−x + 1) es lo mismo que y = f (− (x − 1)). Si reemplazamos x con −x para obtener y = f (−x), entonces x en este último resultado con x − 1 para obtener y = f (− (x − 1)), esto tiene el efecto de reflejar primero la gráfica de y = f (x) a través del eje y, luego, desplazando el resultado a la derecha 1 unidad.
Ejercicio\(\PageIndex{10}\)
y = f (−x/4).
| x | -16 | -8 | 0 | 8 | 16 | 24 |
| y |
Ejercicio\(\PageIndex{11}\)
Usa tu calculadora gráfica para dibujar la gráfica de\(y = \sqrt{x}\). Después, dibuja la gráfica de\(y = \sqrt{-x}\). En sus propias palabras, explique lo que aprendió de este ejercicio.
- Contestar
-
Primero, dibuja la gráfica de\(y = \sqrt{x}\).
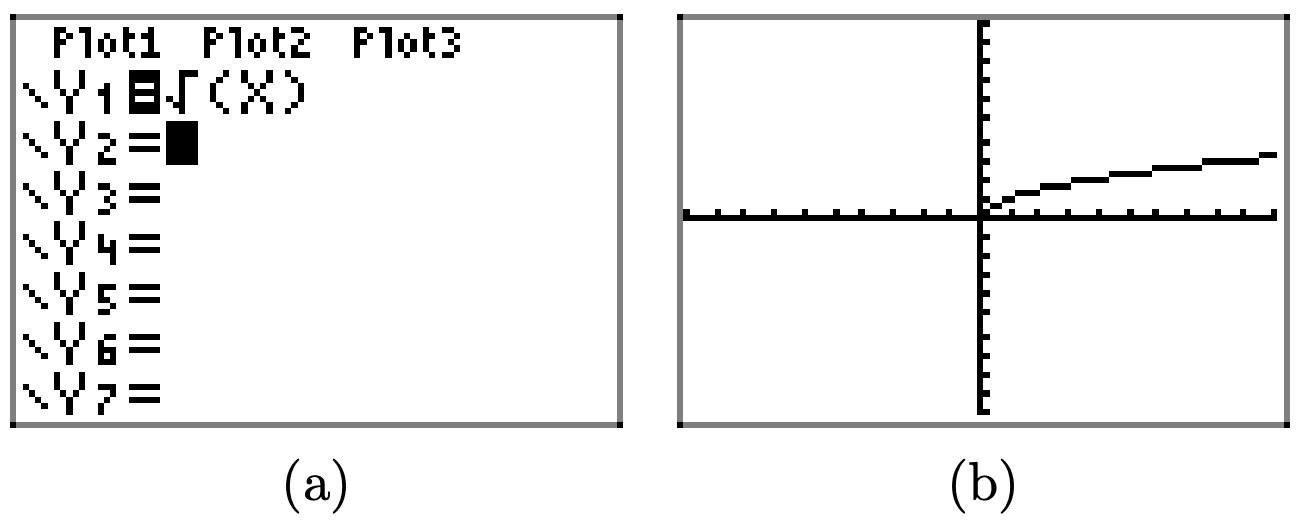
La gráfica de\(y = \sqrt{-x}\) es un reflejo de la gráfica de\(y = \sqrt{x}\) a través del eje y.
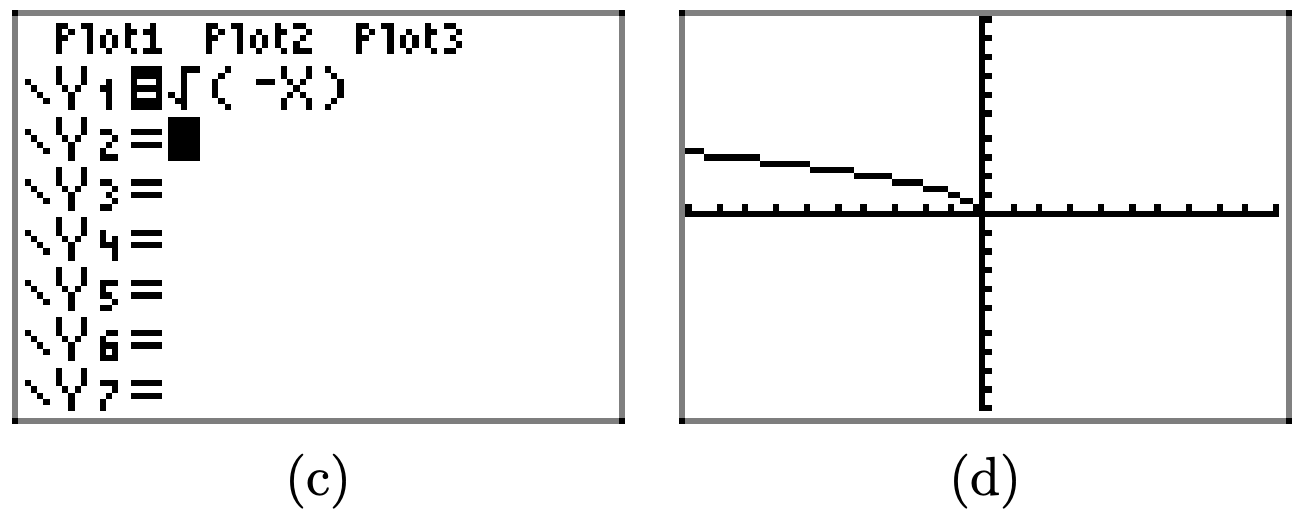
Reemplazar x por −x, como en y = f (−x), refleja la gráfica de y = f (x) a través del eje y.
Ejercicio\(\PageIndex{12}\)
Usa tu calculadora gráfica para dibujar la gráfica de y = |x|. Después, dibuja la gráfica de y = | − x|. En sus propias palabras, explique lo que aprendió de este ejercicio.
Ejercicio\(\PageIndex{13}\)
Usa tu calculadora gráfica para dibujar la gráfica de\(y = x^2\). Después, en sucesión, dibujar las gráficas de\(y = (x − 2)^2, y = (x − 4)^2\), y\(y = (x − 6)^2\). En sus propias palabras, explique lo que aprendió de este ejercicio.
- Contestar
-
Primero, dibuja la gráfica de\(y = x^2\).
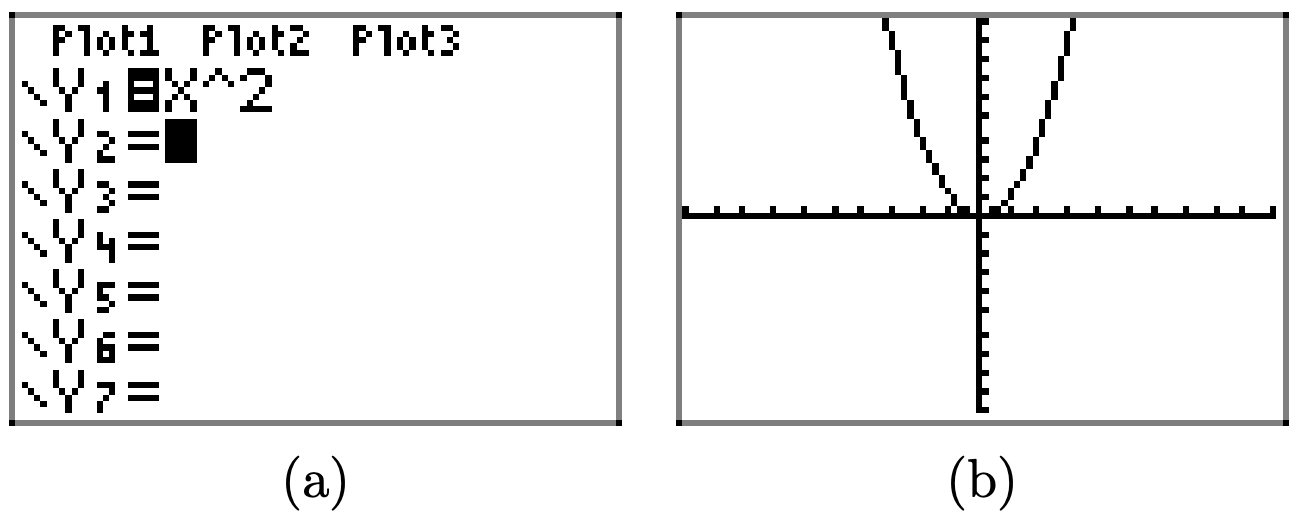
Reemplazar x por x − 2 traduce la gráfica de\(y = x^2\) dos unidades a la derecha en la dirección horizontal.
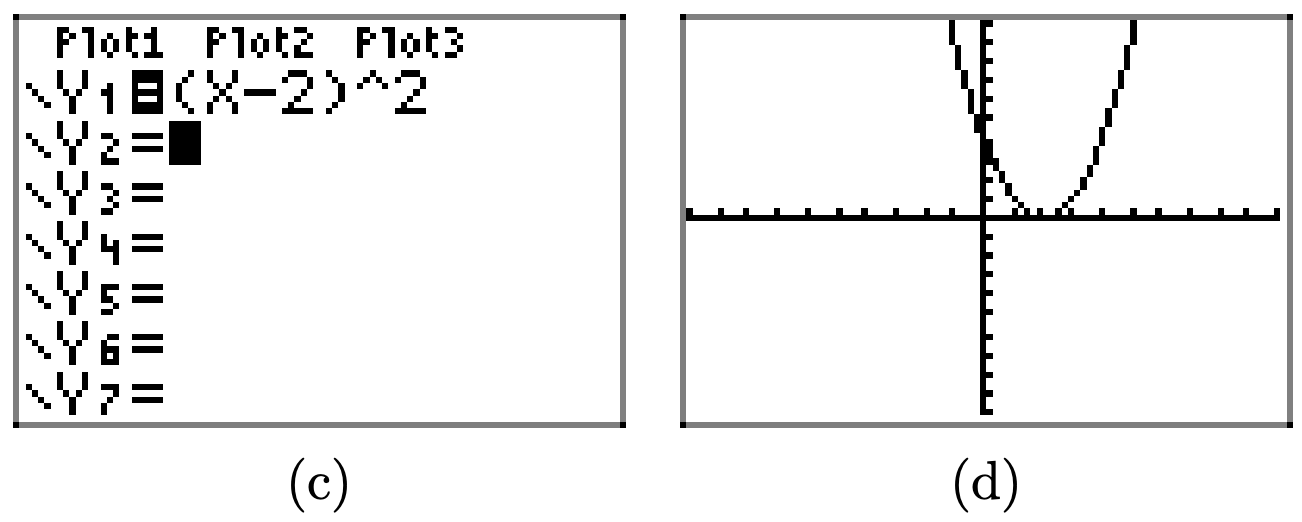
De igual manera, al reemplazar x por x − 4 y x − 6 se traduce la gráfica de\(y = x^2\) cuatro unidades y 6 unidades a la derecha, respectivamente.
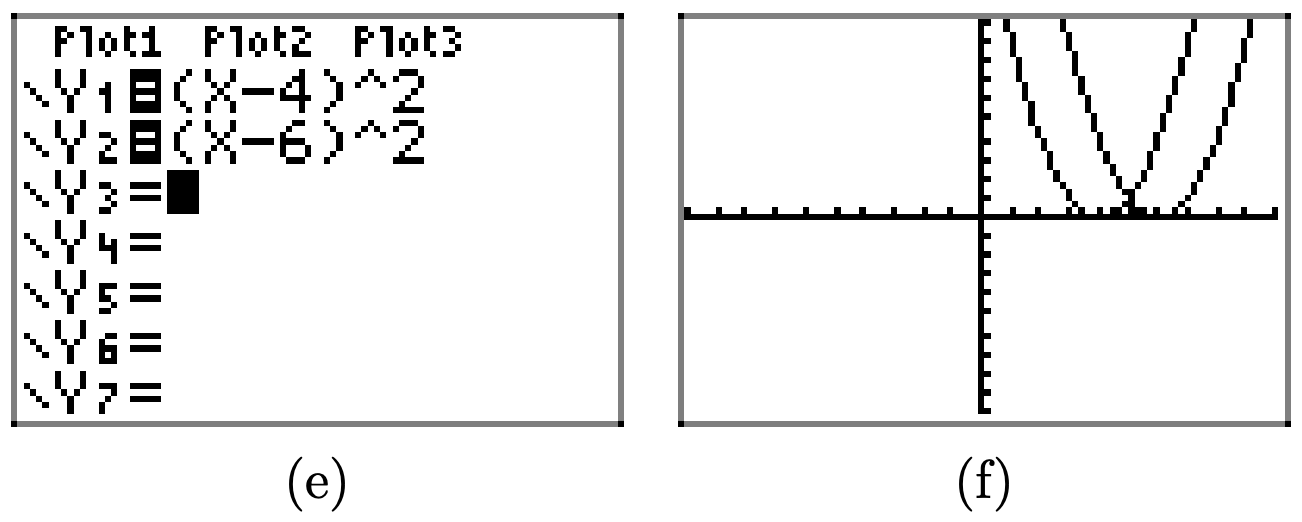
En general, si c es positivo, entonces la gráfica de y = f (x − c) se obtiene traduciendo la gráfica de y = f (x) a la derecha c unidades.
Ejercicio\(\PageIndex{14}\)
Usa tu calculadora gráfica para dibujar la gráfica de\(y = x^2\). Después, en sucesión, dibujar las gráficas de\(y = (x + 2)^2, y = (x + 4)^2\), y\(y = (x + 6)^2\). En sus propias palabras, explique lo que aprendió de este ejercicio.
Ejercicio\(\PageIndex{15}\)
Usa tu calculadora gráfica para dibujar la gráfica de y = |x|. Después, en sucesión, dibuje las gráficas de y = |2x|, y = |3x|, e y = |4x|. En sus propias palabras, explique lo que aprendió de este ejercicio.
- Contestar
-
Primero, dibuja la gráfica de y = |x|.
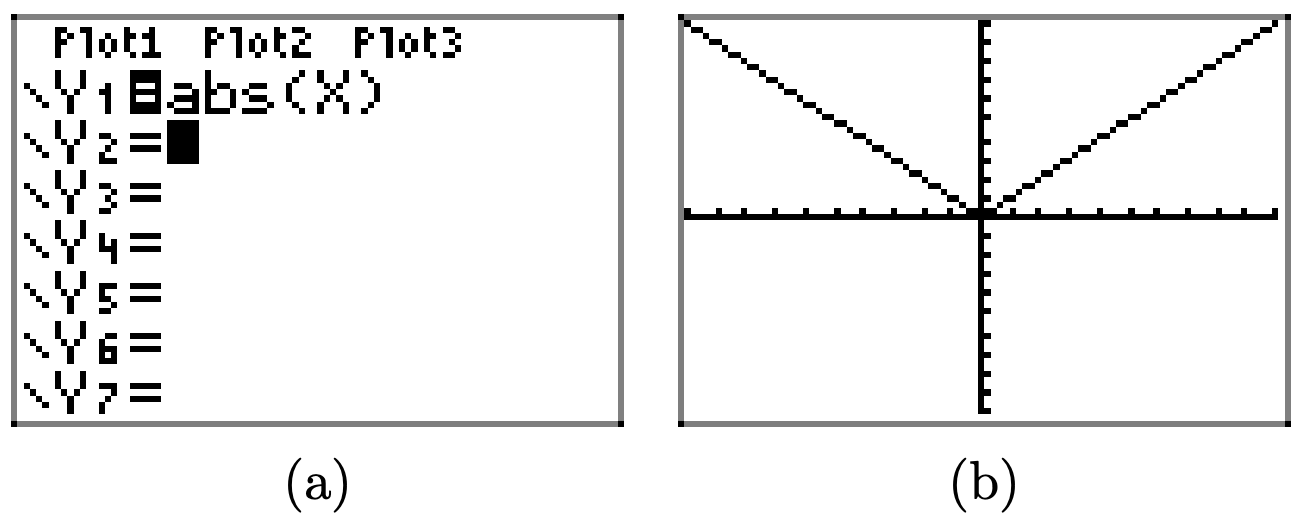
Al reemplazar x por 2x se comprime la gráfica de y = |x| por un factor de 2 en la dirección horizontal.
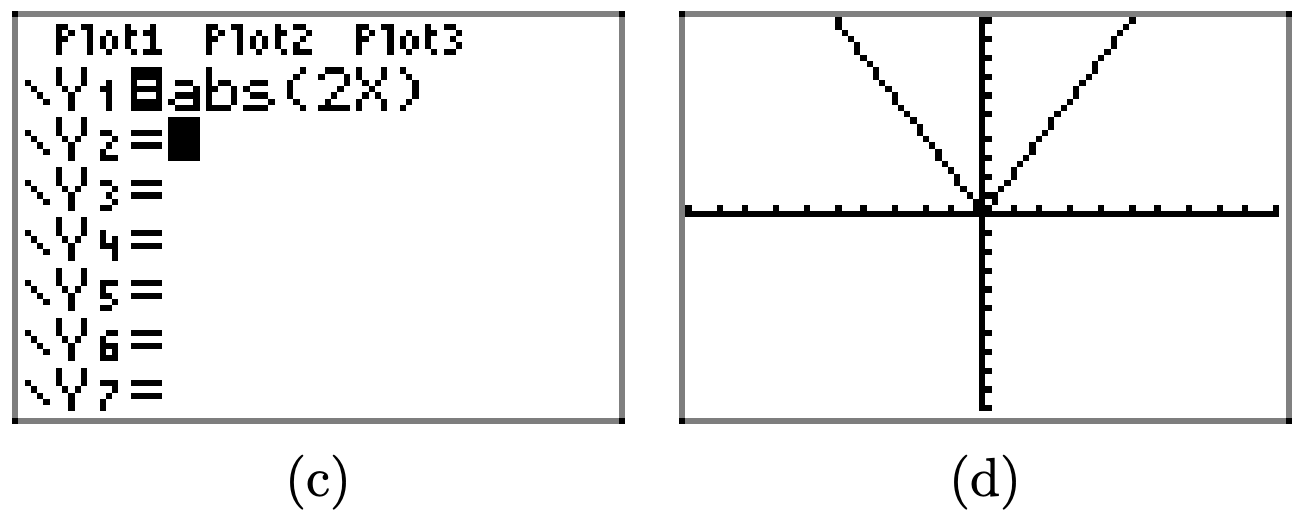
De igual manera, reemplazando x por 3x y 4x por un factor de 3 y 4 en la dirección horizontal, respectivamente.
En general, si a > 1, entonces la gráfica de y = f (ax) se obtiene comprimiendo la gráfica de y = f (x) por un factor de a en la dirección horizontal.
Ejercicio\(\PageIndex{16}\)
Usa tu calculadora gráfica para dibujar la gráfica de y = |x|. Después, en sucesión, dibuja las gráficas de y = | (1/2) x|, y = | (1/3) x|, e y = | (1/4) x|. En sus propias palabras, explique lo que aprendió de este ejercicio.
A continuación se muestra la gráfica de una función f. en Ejercicios\(\PageIndex{17}\) -\(\PageIndex{22}\), utilice esta gráfica para realizar cada una de las siguientes tareas.
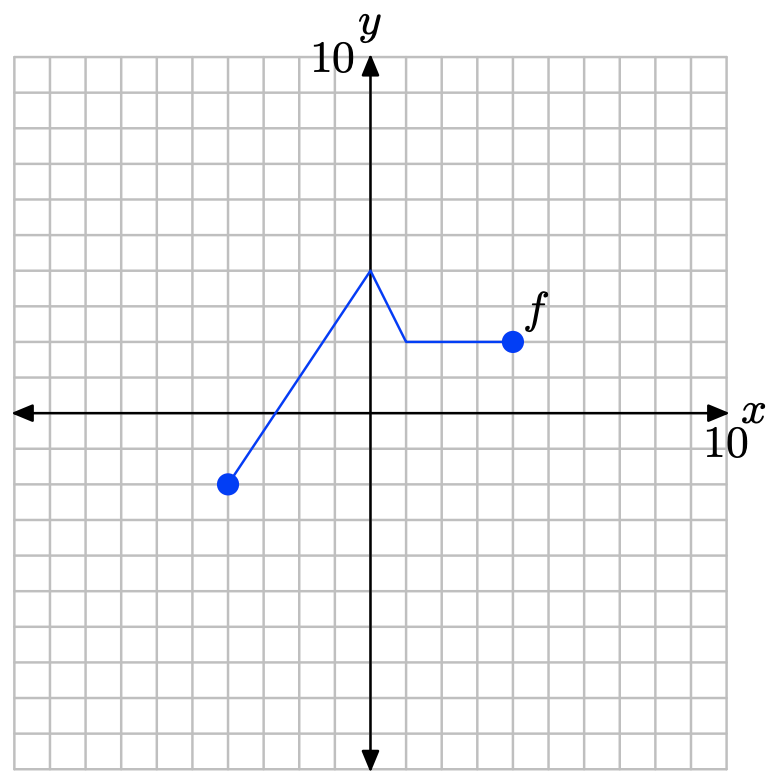
i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Haz una copia exacta de la gráfica de f en tu sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. En la narrativa, una caja de sombra al final de la sección resume los conceptos y la técnica de escalado horizontal, reflexión horizontal y traducción horizontal. Utilice las ideas de atajo que se presentan en este cuadro de sombra de resumen para dibujar las gráficas de las funciones que siguen sin usar tablas.
iii. Usa un lápiz de diferente color para dibujar la gráfica de la función dada en el ejercicio. Etiquete esta gráfica con su ecuación. Asegúrese de que los puntos clave estén trazados con precisión. En cada ejercicio, se ruega trazar exactamente dos gráficas por sistema de coordenadas, la gráfica de la función original f y la gráfica de la función en el ejercicio.
Ejercicio\(\PageIndex{17}\)
y = f (2x).
- Contestar
-
Para obtener una gráfica para y = f (2x), tome cada punto de la gráfica de y = f (x) y divida su valor x por 2, manteniendo el valor y igual.
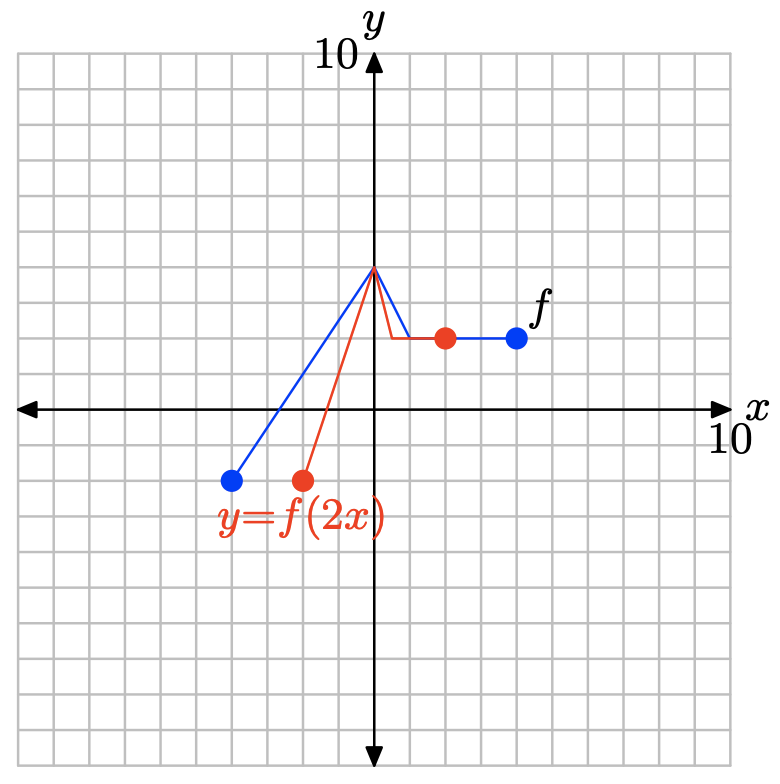
Tenga en cuenta que al reemplazar x por 2x, como en y = f (2x), comprime la gráfica de y = f (x) en la dirección horizontal por un factor de 2.
Ejercicio\(\PageIndex{18}\)
y = f ((1/2) x).
Ejercicio\(\PageIndex{19}\)
y = f (−x).
- Contestar
-
Para obtener una gráfica de y = f (−x), toma cada punto de la gráfica de y = f (x) y niega su valor x, manteniendo el valor y igual.
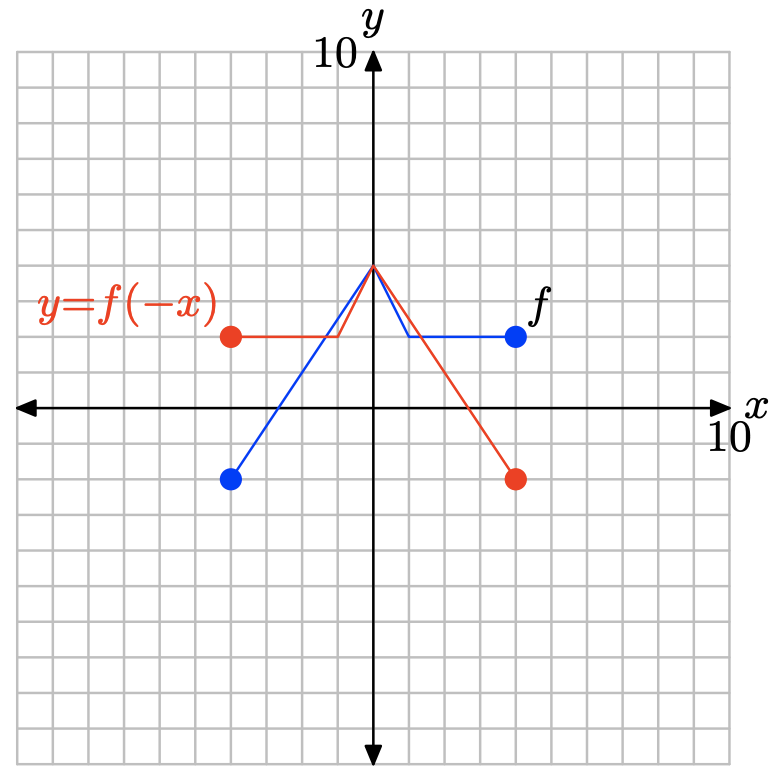
Tenga en cuenta que reemplazar x por −x, como en y = f (−x), refleja la gráfica de f a través del eje y.
Ejercicio\(\PageIndex{20}\)
y = f (x − 1).
Ejercicio\(\PageIndex{21}\)
y = f (x + 3).
- Contestar
-
Para obtener una gráfica de y = f (x + 3), tomar cada punto de la gráfica de y = f (x) y restar 3 de su valor x, manteniendo el valor y igual.
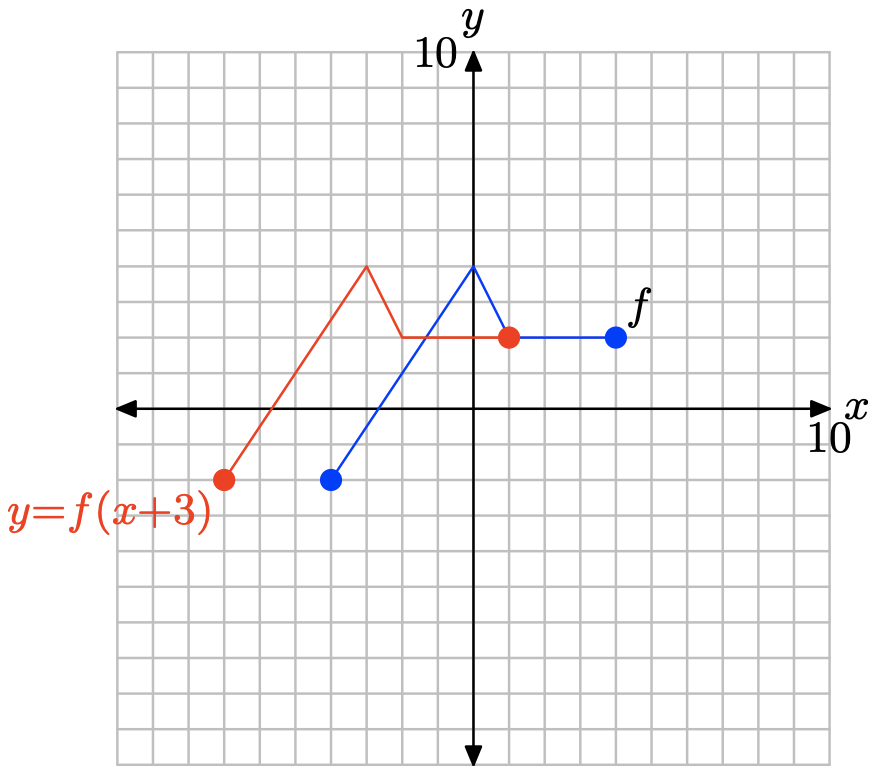
Obsérvese que reemplazando x por x + 3, como en y = f (x + 3), traduce la gráfica de y = f (x) a la izquierda 3 unidades.
Ejercicio\(\PageIndex{22}\)
y = f (x − 2).
A continuación se muestra la gráfica de una función f. en Ejercicios\(\PageIndex{23}\) -\(\PageIndex{28}\), utilice esta gráfica para realizar cada una de las siguientes tareas.
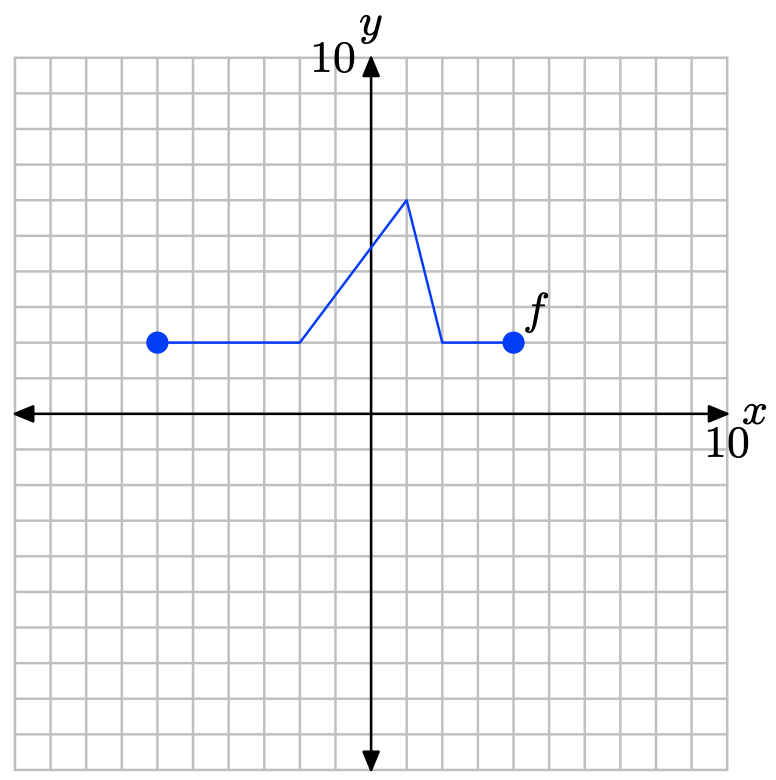
i. Establecer un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje. Haz una copia exacta de la gráfica de f en tu sistema de coordenadas. Recuerda dibujar todas las líneas con una regla.
ii. En la narrativa, una caja de sombra al final de la sección resume los conceptos y la técnica de escalado horizontal, reflexión horizontal y traducción horizontal. Utilice las ideas de atajo que se presentan en este cuadro de sombra de resumen para dibujar las gráficas de las funciones que siguen sin usar tablas.
iii. Usa un lápiz de diferente color para dibujar la gráfica de la función dada en el ejercicio. Etiquete esta gráfica con su ecuación. Asegúrese de que los puntos clave estén trazados con precisión. En cada ejercicio, se ruega trazar exactamente dos gráficas por sistema de coordenadas, la gráfica de la función original f y la gráfica de la función en el ejercicio.
Ejercicio\(\PageIndex{23}\)
y = f (2x).
- Contestar
-
Para obtener una gráfica de y = f (2x), tome cada punto de la gráfica de y = f (x) y divida su valor x por 2, manteniendo el valor y igual.
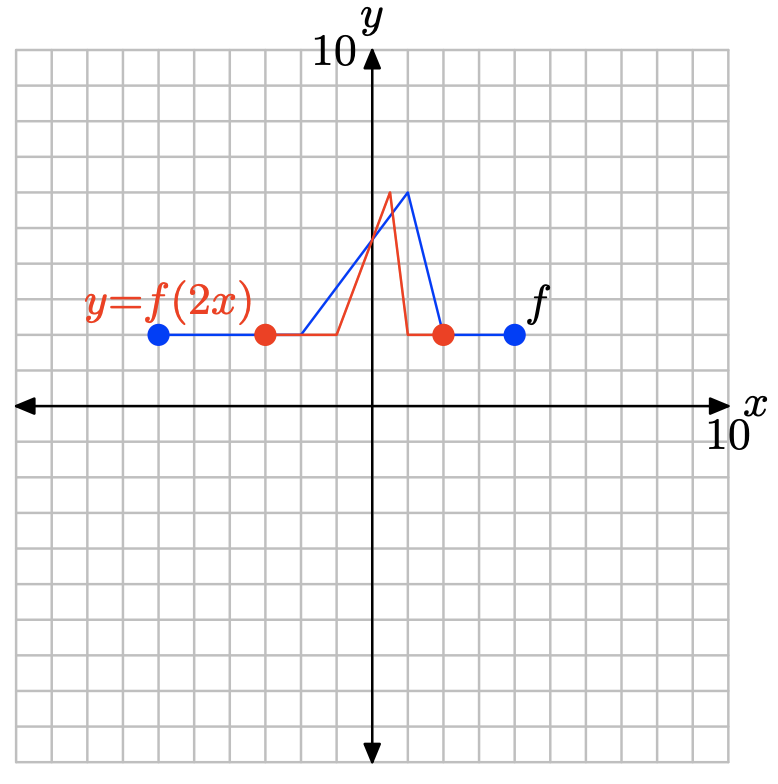
Al reemplazar x por 2x, como en y = f (2x), comprime la gráfica de y = f (x) horizontalmente por un factor de 2.
Ejercicio\(\PageIndex{24}\)
y = f ((1/2) x).
Ejercicio\(\PageIndex{25}\)
y = f (−x).
- Contestar
-
Para obtener una gráfica de y = f (−x), toma cada punto de la gráfica de y = f (x) y niega su valor x, manteniendo el mismo valor y.
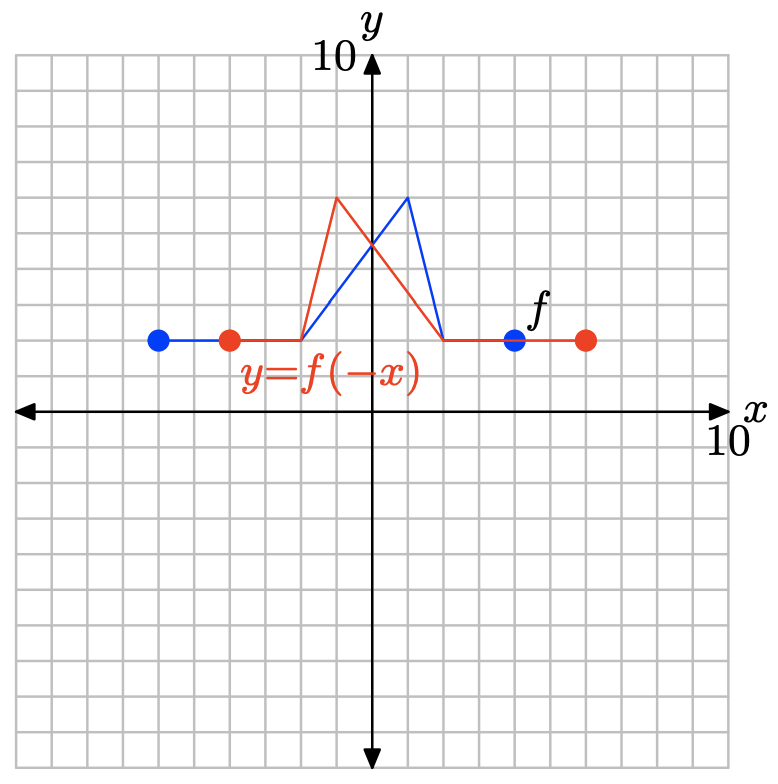
Reemplazar x por −x, como en y = f (−x), refleja la gráfica de y = f (x) a través del eje y.
Ejercicio\(\PageIndex{26}\)
y = f (x + 3)
Ejercicio\(\PageIndex{27}\)
y= f (x − 2).
- Contestar
-
Para obtener una gráfica de y = f (x − 2), toma cada punto de la gráfica de y = f (x) y suma 2 a su valor x, manteniendo igual su valor y.
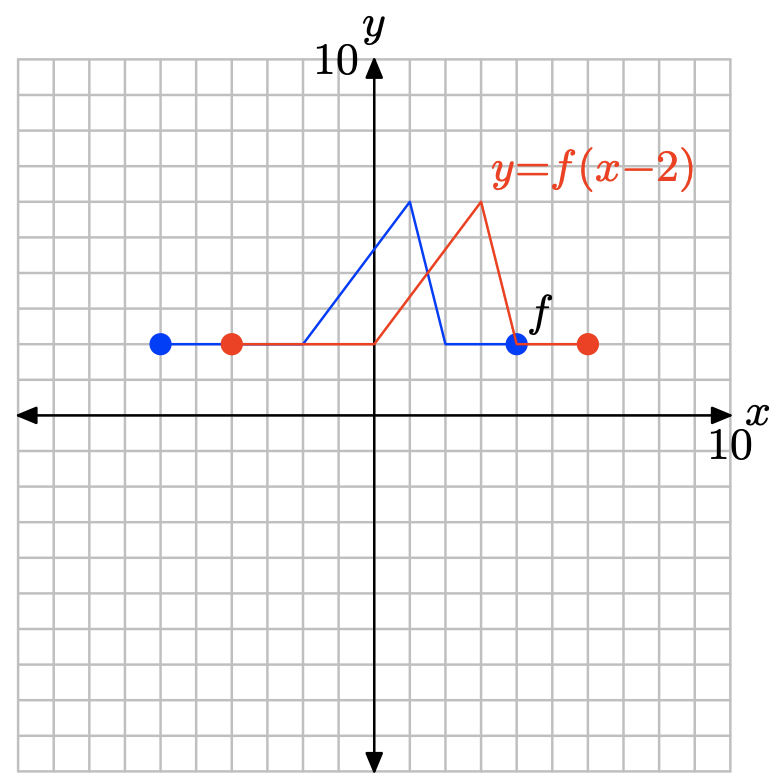
Al reemplazar x por x − 2, como en y = f (x − 2), desplaza la gráfica de y = f (x) hacia la derecha 2 unidades.
Ejercicio\(\PageIndex{28}\)
y = f (x + 1).

