7.7: Resolver ecuaciones racionales

Al simplificar fracciones complejas en la sección anterior, vimos que multiplicar tanto el numerador como el denominador por la expresión apropiada podría “borrar” todas las fracciones del numerador y denominador, simplificando enormemente la expresión racional.

En esta sección se utiliza una técnica similar.

Borrar las fracciones a partir de una ecuación racional

Si tu ecuación tiene expresiones racionales, multiplica ambos lados de la ecuación por el mínimo denominador común para borrar la ecuación de expresiones racionales.

Veamos un ejemplo.

Ejemplo\(\PageIndex{1}\)

Resuelve la siguiente ecuación para x.

\[\frac{x}{2}-\frac{2}{3}=\frac{3}{4}\]

Solución

Para borrar esta ecuación de fracciones, multiplicaremos ambos lados por el denominador común para 2, 3 y 4, que es 12. Distribuye 12 en el segundo paso.

\[\begin{aligned} \color{blue}{12}\left(\frac{x}{2}-\frac{2}{3}\right) &=\left(\frac{3}{4}\right) \color{blue}{12} \\ \color{blue}{12}\left(\frac{x}{2}\right)-\color{blue}{12}\left(\frac{2}{3}\right) &=\left(\frac{3}{4}\right) \color{blue}{12} \end{aligned}\]

Multiplicar.

\[6 x-8=9\]

Hemos logrado borrar las expresiones racionales de la ecuación multiplicando por el denominador común. Ahora tenemos una ecuación lineal simple que se puede resolver sumando primero 8 a ambos lados de la ecuación, seguido de dividir ambos lados de la ecuación por 6.

\[\begin{aligned} 6 x &=17 \\ x &=\frac{17}{6} \end{aligned}\]

Dejaremos que nuestros lectores comprueben esta solución.

Probemos otro ejemplo.

Ejemplo\(\PageIndex{2}\)

Resuelve la siguiente ecuación para x.\[6=\frac{5}{x}+\frac{6}{x^{2}}\]

Solución

En esta ecuación, los denominadores son 1, x, y\(x^2\), y el denominador común para ambos lados de la ecuación es\(x^2\). En consecuencia, comenzamos la solución multiplicando primero ambos lados de la ecuación por\(x^2\).

\[\begin{array}{l}{\color{blue}{x^{2}}(6)=\left(\frac{5}{x}+\frac{6}{x^{2}}\right) \color{blue}{x^{2}}} \\ {\color{blue}{x^{2}}(6)=\left(\frac{5}{x}\right) \color{blue}{x^{2}}+\left(\frac{6}{x^{2}}\right) \color{blue}{x^{2}}}\end{array}\]

Simplificar.

\[6 x^{2}=5 x+6\]

Obsérvese que multiplicar ambos lados de la ecuación original por el mínimo denominador común borra la ecuación de todas las expresiones racionales. Esta última ecuación es no lineal, así que haz que un lado de la ecuación sea igual a cero restando 5x y 6 de ambos lados de la ecuación.

\[6 x^{2}-5 x-6=0\]

Para factorizar el lado izquierdo de esta ecuación, tenga en cuenta que es un trinomio cuadrático con ac = (6) (−6) = −36. El par entero 4 y −9 tienen producto −36 y suma −5. Dividir el término medio usando este par y factorial por agrupación.

\[\begin{aligned} 6 x^{2}+4 x-9 x-6 &=0 \\ 2 x(3 x+2)-3(3 x+2) &=0 \\(2 x-3)(3 x+2) &=0 \end{aligned}\]

La propiedad cero del producto obliga a

\[2 x-3=0 \quad \text { or } \quad 3 x+2=0\]

Cada una de estas ecuaciones lineales se resuelve fácilmente.

\[x=\frac{3}{2} \quad \text { or } \quad x=-\frac{2}{3}\]

Por supuesto, siempre debemos revisar nuestras soluciones. Sustituyendo x = 3/2 en el lado derecho de la ecuación original (4),

\[\frac{5}{x}+\frac{6}{x^{2}}=\frac{5}{3 / 2}+\frac{6}{(3 / 2)^{2}}=\frac{5}{3 / 2}+\frac{6}{9 / 4}\]

En la expresión final, multiplique la parte superior e inferior de la primera fracción por 2, la parte superior e inferior de la segunda fracción por 4.

\[\frac{5}{3 / 2} \cdot \color{blue}{\frac{2}{2}}+\frac{6}{9 / 4} \cdot \color{blue}{\frac{4}{4}}=\frac{10}{3}+\frac{24}{9}\]

Hacer fracciones equivalentes con un denominador común de 9 y sumar.

\[\frac{10}{3} \cdot \color{blue}{\frac{3}{3}}+\frac{24}{9}=\frac{30}{9}+\frac{24}{9}=\frac{54}{9}=6\]

Tenga en cuenta que este resultado es idéntico al lado izquierdo de la ecuación original (4). Así, x = 3/2 cheques.

Este ejemplo demuestra claramente que la comprobación puede ser tan difícil y laboriosa como el cálculo utilizado para resolver originalmente la ecuación. Por esta razón, tendemos a ponernos perezosos y no revisar nuestras respuestas como deberíamos. Hay ayuda, sin embargo, ya que la calculadora gráfica puede ayudarnos a verificar las soluciones de ecuaciones.

Primero, ingrese la solución 3/2 en la pantalla de su calculadora, presione el botón STOI, luego presione el botón X y ejecute el comando resultante en la pantalla presionando la tecla ENTER. El resultado se muestra en la Figura\(\PageIndex{1}\) (a).

A continuación, ingrese la expresión 5/X+6/X2 y ejecute el comando resultante en la pantalla presionando la tecla ENTER. El resultado se muestra en la Figura\(\PageIndex{1}\) (b). Obsérvese que el resultado es 6, el mismo que el calculado a mano arriba, y coincide con el lado izquierdo de la ecuación original (4). También hemos utilizado la calculadora para verificar la segunda solución x = −2/3. Esto se muestra en la Figura\(\PageIndex{4}\) (c).

Figura\(\PageIndex{1}\). Usando la calculadora gráfica para verificar las soluciones de la ecuación (4).

Veamos otro ejemplo.

Ejemplo\(\PageIndex{3}\)

Resuelve la siguiente ecuación para x.

\[\frac{2}{x^{2}}=1-\frac{2}{x}\]

Solución

Primero, multiplica ambos lados de la ecuación (6) por el denominador común\(x^2\).

\[\begin{aligned} \color{blue}{x^{2}}\left(\frac{2}{x^{2}}\right) &=\left(1-\frac{2}{x}\right) \color{blue}{x^{2}} \\ 2 &=x^{2}-2 x \end{aligned}\]

Hacer un lado cero.

\[0=x^{2}-2 x-2\]

El lado derecho es un trinomio cuadrático con ac = (1) (−2) = −2. No hay pares enteros con el producto −2 que sumen a −2, por lo que este trinomio cuadrático no factoriza. Afortunadamente, la ecuación es cuadrática (segundo grado), por lo que podemos usar la fórmula cuadrática con a = 1, b = −2 y c = −2.

\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-2) \pm \sqrt{(-2)^{2}-4(1)(-2)}}{2(1)}=\frac{2 \pm \sqrt{12}}{2}\]

Esto nos da dos soluciones,\(x=(2-\sqrt{12}) / 2\) y\(x=(2+\sqrt{12}) / 2\). Comprobemos la solución\(x=(2-\sqrt{12}) / 2\). Primero ingresa este resultado en tu calculadora, presiona el botón STOI, presiona X, luego presiona la tecla ENTER para ejecutar el comando y almacenar la solución en la variable X. Este comando se muestra en la Figura\(\PageIndex{2}\) (a).

Ingresa el lado izquierdo de la ecuación original (6) como 2/x́2 y presiona la tecla INTRO para ejecutar este comando. Esto se muestra en la Figura\(\PageIndex{2}\) (b).

Ingrese el lado derecho de la ecuación original (6) como 1-2/X y presione la tecla ENTER para ejecutar este comando. Esto se muestra en la Figura\(\PageIndex{2}\) (c). Obsérvese que los lados izquierdo y derecho de la ecuación (6) se muestran ambos iguales a 3.732050808 en\(x=(2-\sqrt{12}) / 2\) (a X = -0.7320508076), como se muestra en la Figura\(\PageIndex{2}\) (c). Esto demuestra que\(x=(2-\sqrt{12}) / 2\) es una solución de la ecuación (6).

Dejamos a nuestros lectores comprobar la segunda solución,\(x=(2+\sqrt{12}) / 2\).

Figura\(\PageIndex{2}\). Usando la calculadora gráfica para verificar las soluciones de la ecuación (6).

Veamos otro ejemplo, este que involucra la notación de funciones.

Ejemplo\(\PageIndex{4}\)

Considere la función definida por\[f(x)=\frac{1}{x}+\frac{1}{x-4}\] Resolver la ecuación f (x) = 2 para x usando técnicas gráficas y analíticas, luego compare las soluciones. Realizar cada una de las siguientes tareas.

a. Dibuje la gráfica de f en papel cuadriculado. Etiquetar los ceros de f con sus coordenadas y las asíntotas de f con sus ecuaciones.

b. Agrega la gráfica de y = 2 a tu parcela y estima las coordenadas de donde la gráfica de f se cruza con la gráfica de y = 2.

c. Utilice la utilidad de intersección en su calculadora para encontrar mejores aproximaciones de los puntos donde se cruzan las gráficas de f e y = 2.

d. Resuelve la ecuación f (x) = 2 algebraicamente y compara tus soluciones con las que se encuentran en la parte (c).

Solución

Para la gráfica en la parte (a), necesitamos encontrar los ceros de f y las ecuaciones de cualquier asíntota vertical u horizontal.

Para encontrar el cero de la función f, encontramos un denominador común y sumamos las dos expresiones racionales en la ecuación (8).

\[f(x)=\frac{1}{x}+\frac{1}{x-4}=\frac{x-4}{x(x-4)}+\frac{x}{x(x-4)}=\frac{2 x-4}{x(x-4)}\]

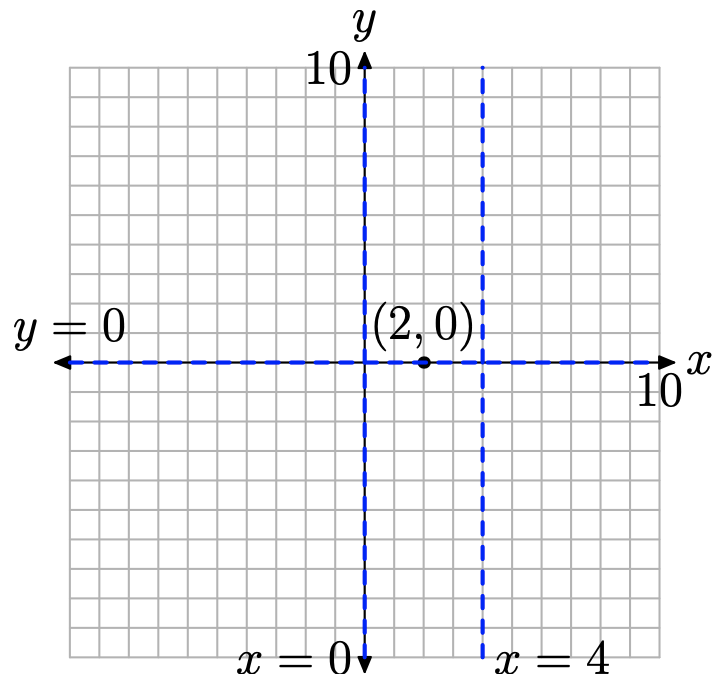
Tenga en cuenta que el numerador de este resultado es igual a cero (pero no al denominador) cuando x = 2. Este es el cero de f. Así, la gráfica de f tiene intercepción x en (2, 0), como se muestra en la Figura\(\PageIndex{4}\).

Obsérvese que la función racional en la ecuación (9) se reduce a los términos más bajos. Los denominadores de x y x + 4 en la ecuación (9) son cero cuando x = 0 y x = 4. Estas son nuestras asíntotas verticales, como se muestra en la Figura\(\PageIndex{4}\).

Para encontrar las asíntotas horizontales, necesitamos examinar qué sucede con los valores de la función a medida que x aumenta (o disminuye) sin límite. Ingrese la función en el menú Y= con 1/X+1/ (X-4), como se muestra en la Figura\(\PageIndex{3}\) (a). Presione 2do TBLSET, luego resalte ASK para la variable independiente y presione ENTRAR para hacer esta selección permanente, como se muestra en la Figura\(\PageIndex{3}\) (b).

Presione 2nd TABLE, luego ingrese 10, 100, 1,000 y 10,000, como se muestra en la Figura\(\PageIndex{3}\) (c). Observe cómo los valores de Y1 se acercan a cero. En la Figura\(\PageIndex{3}\) (d), a medida que x disminuye sin límite, el comportamiento final es el mismo. Esta es una indicación de una asíntota horizontal en y = 0, como se muestra en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{3}\). Examinar el comportamiento final de f con la calculadora gráfica.

Figura\(\PageIndex{4}\). Colocando las asíntotas horizontales y verticales y la intercepción x de la gráfica de la función f.

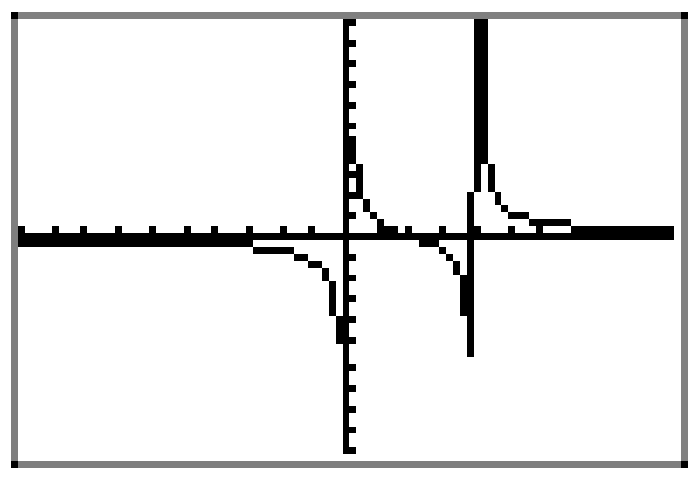
En este punto, ya tenemos nuestra función f cargada en Y1, por lo que podemos presionar el botón ZOOM y seleccionar 6:ZStandard para producir la gráfica que se muestra en la Figura\(\PageIndex{5}\). Como era de esperar, la calculadora gráfica no hace un muy buen trabajo con la función racional f, particularmente cerca de las discontinuidades en las asíntotas verticales. Sin embargo, hay suficiente información en Figura\(\PageIndex{5}\), en pareja con nuestro trabajo avanzado resumido en Figura\(\PageIndex{4}\), para dibujar una gráfica muy agradable de la función racional en nuestro papel cuadriculado, como se muestra en la Figura\(\PageIndex{6}\) (a). Nota: No hemos etiquetado asíntotas con ecuaciones, ni ceros con coordenadas, en la Figura\(\PageIndex{6}\) (a), ya que pensamos que la imagen podría estar un poco abarrotada. No obstante, debes etiquetar cada una de estas partes en tu papel cuadriculado, como hicimos en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{5}\). El gráfico de f como se dibuja en la calculadora.

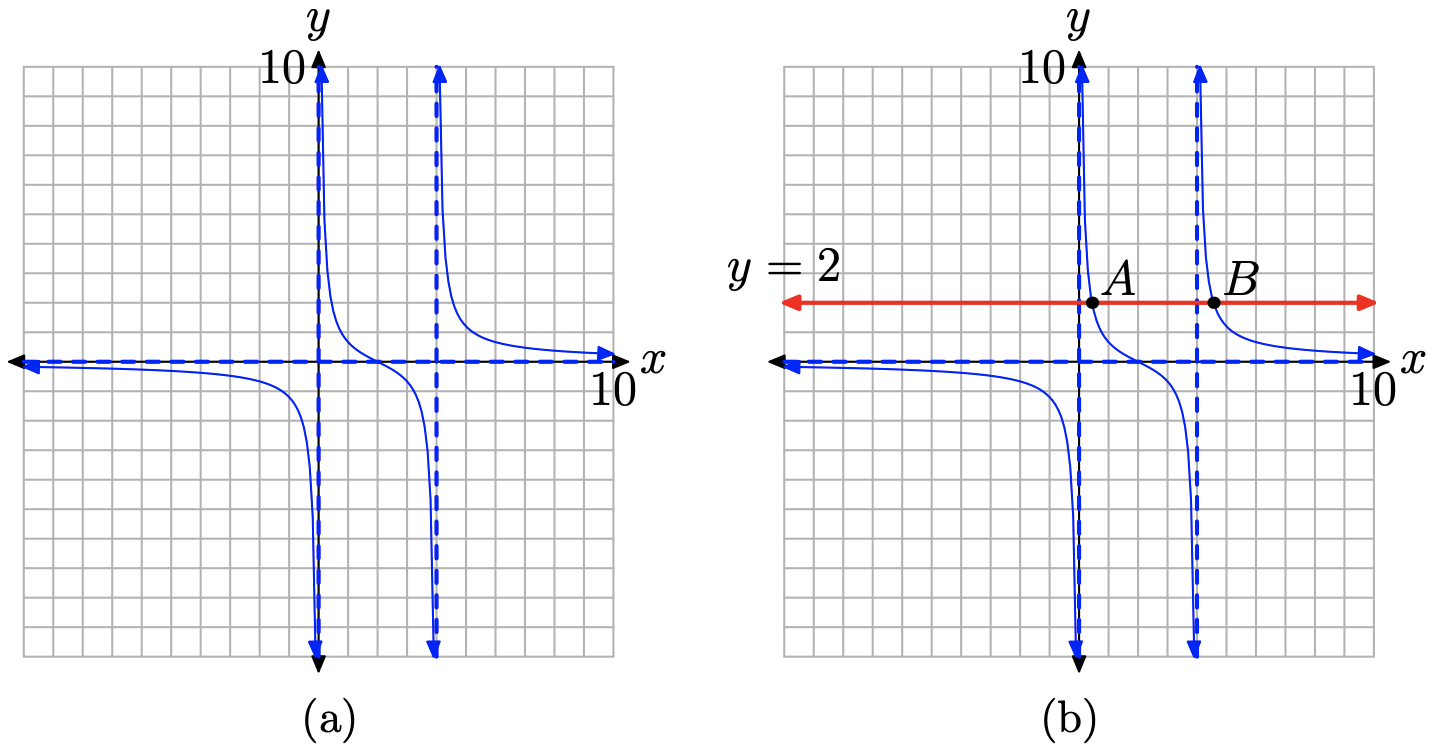
Abordemos ahora la parte (b) sumando la línea horizontal y = 2 a la gráfica, como se muestra en la Figura\(\PageIndex{6}\) (b). Obsérvese que la gráfica de y = 2 cruza la gráfica de la función racional f en dos puntos A y B. Los valores x de los puntos A y B son las soluciones a nuestra ecuación f (x) = 2.

Podemos obtener una estimación bruta de las coordenadas x de los puntos A y B directamente de nuestro papel cuadriculado. El valor x del punto A es aproximadamente\(x \approx 0.3\), mientras que el valor x del punto B parece ser aproximadamente\(x \approx 4.6\).

Figura\(\PageIndex{6}\). Resolviendo f (x) = 2 gráficamente.

A continuación, abordemos la tarea requerida en la parte (c). Tenemos estimaciones muy razonables de las soluciones de f (x) = 2 con base en los datos presentados en la Figura\(\PageIndex{6}\) (b). Usemos la calculadora gráfica para mejorar estas estimaciones.

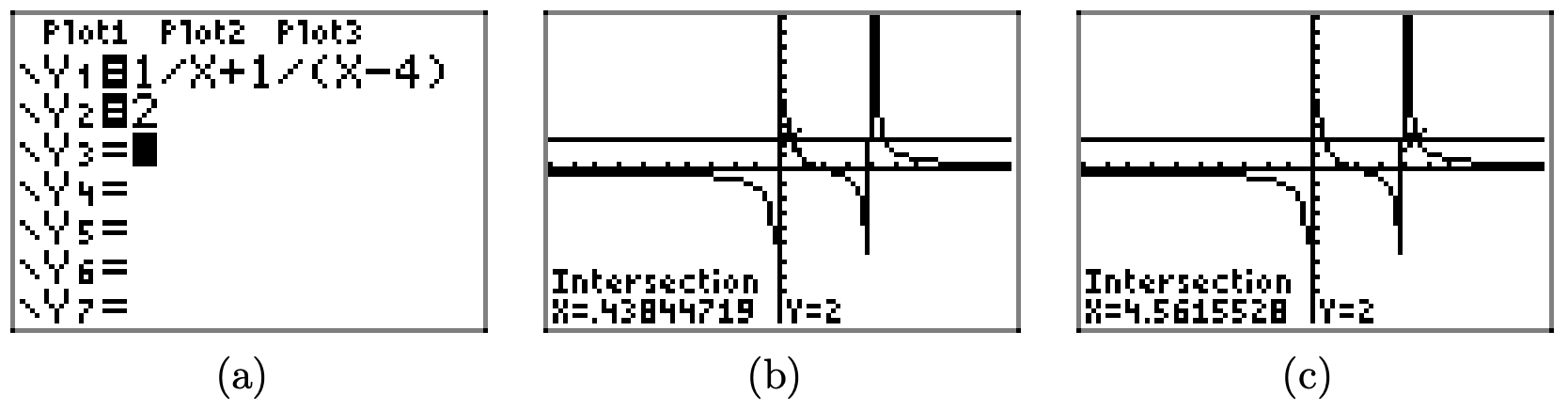
Primero, cargue la ecuación Y2=2 en el menú Y=, como se muestra en la Figura\(\PageIndex{7}\) (a). Necesitamos encontrar donde la gráfica de Y1 se cruza con la gráfica de Y2, así que presionamos 2do CALC y seleccionamos 5:intersectar del menú. De la manera habitual, selecciona “Primera curva”, “Segunda curva” y mueve el cursor cerca del punto que deseas estimar. Este es tu “Guess”. Realizar tareas similares para el segundo punto de intersección.

Nuestros resultados se muestran en las Figuras\(\PageIndex{7}\) (b) y Figuras\(\PageIndex{7}\) (c). La estimación en la Figura\(\PageIndex{7}\) (b) tiene\(x \approx 0.43844719\), mientras que la de la Figura\(\PageIndex{7}\) (c) tiene\(x \approx 4.5615528\). Tenga en cuenta que estos son más precisos que las aproximaciones\(x \approx 0.3\) y\(x \approx 4.6\) capturados a partir de nuestra imagen dibujada a mano en la Figura\(\PageIndex{6}\) (b).

Figura\(\PageIndex{7}\). Resolviendo f (x) = 2 gráficamente.

Por último, abordemos la solicitud de una solución algebraica de f (x) = 2 en la parte (d). Primero, reemplace f (x) por 1/x + 1/ (x − 4) para obtener

\[\begin{aligned} f(x) &=2 \\ \frac{1}{x}+\frac{1}{x-4} &=2 \end{aligned}\]

Multiplique ambos lados de esta ecuación por el denominador común x (x − 4).

\[\begin{aligned} \color{blue}{x(x-4)}\left[\frac{1}{x}+\frac{1}{x-4}\right] &=[2] \color{blue}{x(x-4)} \\ \color{blue}{x(x-4)}\left[\frac{1}{x}\right]+\color{blue}{x(x-4)}\left[\frac{1}{x-4}\right] &=[2] \color{blue}{x(x-4)}\end{aligned}\]

Cancelar.

\[\begin{aligned} \color{blue}{\not{x}(x-4)}\left[\frac{1}{\not{x}}\right]+\color{blue}{x(x-4)}\left[\frac{1}{x-4}\right] &=[2] \color{blue}{x(x-4)} \\(x-4)+x &=2 x(x-4) \end{aligned}\]

Simplifica cada lado.

\[2 x-4=2 x^{2}-8 x\]

Esta última ecuación es no lineal, por lo que hacemos un lado cero restando 2x y sumando 4 a ambos lados de la ecuación.

\[\begin{array}{l}{0=2 x^{2}-8 x-2 x+4} \\ {0=2 x^{2}-10 x+4}\end{array}\]

Tenga en cuenta que cada coeficiente del lado derecho de esta última ecuación es divisible por 2. Dividamos ambos lados de la ecuación por 2, distribuyendo la división a través de cada término en el lado derecho de la ecuación.

\[0=x^{2}-5 x+2\]

El trinomio de la derecha es un cuadrático con ac = (1) (2) = 2. No hay pares enteros que tengan producto 2 y suma −5, por lo que este trinomio no factorial. En su lugar usaremos la fórmula cuadrática, con a = 1, b = −5 y c = 2.

\[x=\frac{-b \pm \sqrt{b^{2}-4 a c}}{2 a}=\frac{-(-5) \pm \sqrt{(-5)^{2}-4(1)(2)}}{2(1)}=\frac{5 \pm \sqrt{17}}{2}\]

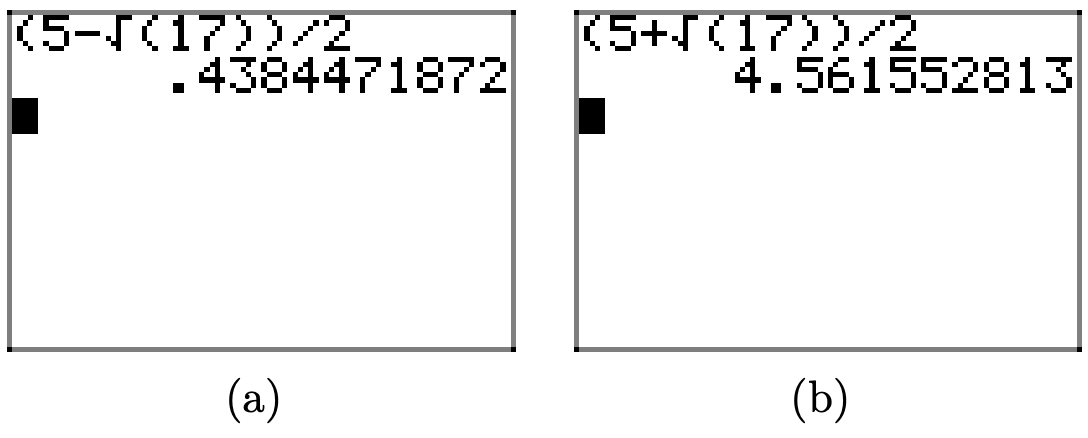
Queda por compararlos con las soluciones gráficas que se encuentran en la parte (c). Entonces, ingresa la solución\((5-\sqrt{( } 17) ) /(2)\) en la pantalla de tu calculadora, como se muestra en la Figura\(\PageIndex{8}\) (a). Ingrese\((5+\sqrt{( } 17) ) /(2)\), como se muestra en la Figura\(\PageIndex{8}\) (b). Por lo tanto,

\[\(\frac{5-\sqrt{17}}{2} \approx 0.4384471872 \quad\) and \(\quad \frac{5+\sqrt{17}}{2} \approx 4.561552813\)\]

Obsérvese el estrecho acuerdo con las aproximaciones encontradas en la parte (c).

Figura\(\PageIndex{8}\). Aproximando las soluciones exactas.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{5}\)

Resolver la siguiente ecuación para x, tanto gráfica como analíticamente\[\frac{1}{x+2}-\frac{x}{2-x}=\frac{x+6}{x^{2}-4}\]

Solución

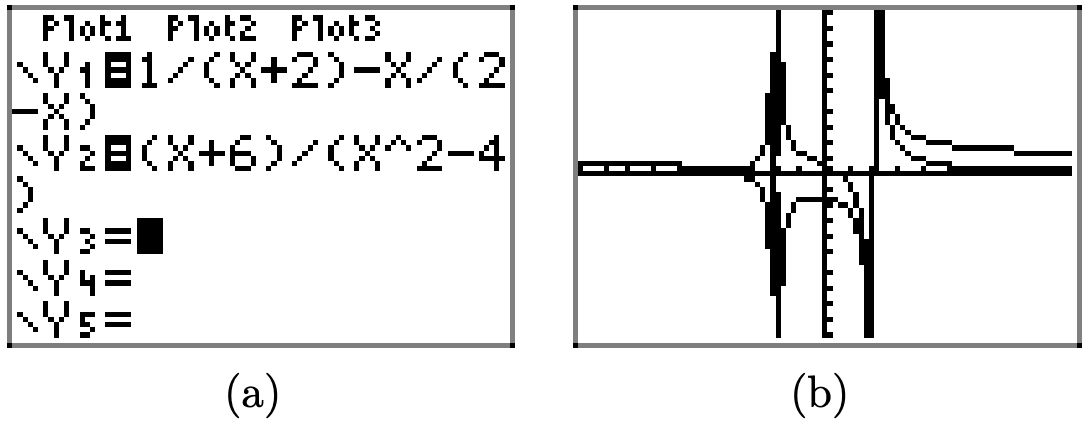
Iniciamos la solución gráfica de la manera habitual, cargando los lados izquierdo y derecho de la ecuación (11) en Y1 e Y2, como se muestra en la Figura\(\PageIndex{9}\) (a). Obsérvese que en la gráfica resultante, mostrada en la Figura\(\PageIndex{9}\) (b), es muy difícil de interpretar donde la gráfica del lado izquierdo se cruza con la gráfica del lado derecho de la ecuación (11).

Figura\(\PageIndex{9}\). Dibuje los lados izquierdo y derecho de la ecuación (11).

En esta situación, una mejor estrategia es hacer que un lado de la ecuación (11) sea igual a cero.

\[\frac{1}{x+2}-\frac{x}{2-x}-\frac{x+6}{x^{2}-4}=0\]

Nuestro enfoque cambiará ahora. Trazaremos el lado izquierdo de la ecuación (12), luego encontraremos dónde el lado izquierdo es igual a cero; es decir, encontraremos dónde la gráfica del lado izquierdo de la ecuación (12) intercepta el eje x.

Con este pensamiento en mente, cargue el lado izquierdo de la ecuación (12) en Y1, como se muestra en la Figura\(\PageIndex{10}\) (a). Tenga en cuenta que la gráfica de la Figura\(\PageIndex{10}\) (b) parece tener solo una asíntota vertical en x = −2 (alguna cancelación debe eliminar el factor de x − 2 del denominador cuando se combinan los términos del lado izquierdo de la ecuación (12) 3). Además, cuando usa la utilidad cero en el menú CALC de la calculadora gráfica, parece haber un cero en x = −4, como se muestra en la Figura\(\PageIndex{10}\) (b).

Figura\(\PageIndex{10}\). Encontrar el cero del lado izquierdo de la ecuación (12).

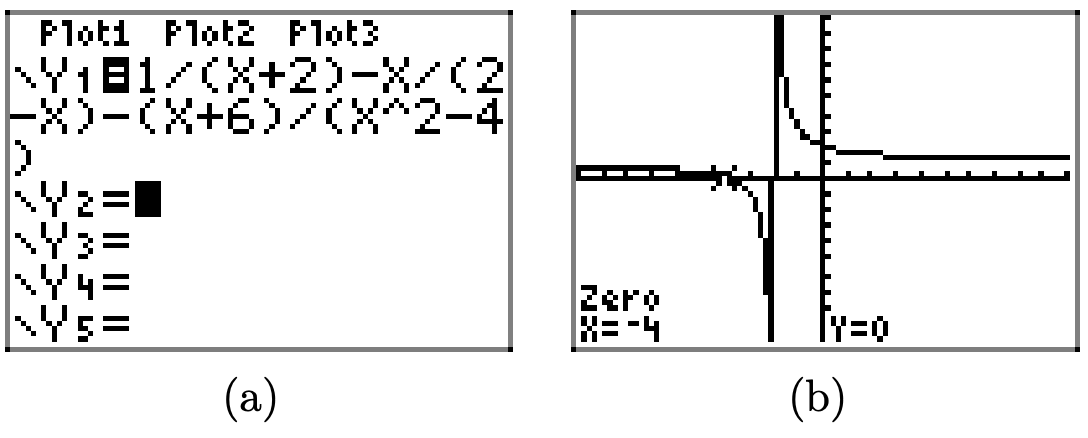
Por lo tanto, la ecuación (12) parece tener una sola solución, a saber x = 4.

A continuación, busquemos una solución analítica de la ecuación (11). Habrá que facturar los denominadores para descubrir un denominador común.

\[\frac{1}{x+2}-\frac{x}{2-x}=\frac{x+6}{(x+2)(x-2)}\]

Es tentador usar un denominador de\((x + 2)(2 − x)(x − 2)\). Sin embargo, el denominador del segundo término en el lado izquierdo de esta última ecuación, 2 − x, está en un orden diferente al de los factores en los otros denominadores, x−2 y x+2, así que vamos a realizar un cambio de signo en este término e invertir el orden. Negaremos la barra de fracción y negaremos el denominador. Eso son dos cambios de signo, por lo que el término permanece sin cambios cuando escribimos

\[\frac{1}{x+2}+\frac{x}{x-2}=\frac{x+6}{(x+2)(x-2)}\]

Ahora vemos que bastará con un denominador común de (x + 2) (x − 2). Multipliquemos ambos lados de la última ecuación por\((x + 2)(x − 2)\).

\[\begin{aligned}\color{blue}{(x+2)(x-2)}\left[\frac{1}{x+2}+\frac{x}{x-2}\right] &=\left[\frac{x+6}{(x+2)(x-2)}\right]\color{blue}{(x+2)(x-2)} \\\color{blue}{(x+2)(x-2)}\left[\frac{1}{x+2}\right]+\color{blue}{(x+2)(x-2)}\left[\frac{x}{x-2}\right] &=\left[\frac{x+6}{(x+2)(x-2)}\right]\color{blue}{(x+2)(x-2)} \end{aligned}\]

Cancelar.

\[\begin{aligned}\color{blue}{(x+2)(x-2)}\left[\frac{1}{x+2}\right]+\color{blue}{(x+2)(x-2)}\left[\frac{x}{x-2}\right] &=\left[\frac{x+6}{(x+2)(x-2)}\right]\color{blue}{(x+2)(x-2)} \\(x-2)+x(x+2) &=x+6 \end{aligned}\]

Simplificar.

\[\begin{array}{r}{x-2+x^{2}+2 x=x+6} \\ {x^{2}+3 x-2=x+6}\end{array}\]

Esta última ecuación es no lineal debido a la presencia de una potencia de x mayor que 1 (tenga en cuenta el\(x^2\) término). Por lo tanto, la estrategia es hacer que un lado de la ecuación sea igual a cero. Vamos a restar x y restar 6 de ambos lados de la ecuación.

\[\begin{aligned} x^{2}+3 x-2-x-6 &=0 \\ x^{2}+2 x-8 &=0 \end{aligned}\]

El lado izquierdo es un trinomio cuadrático con ac = (1) (−8) = −8. El par entero 4 y −2 tienen producto −8 y suma 2. Por lo tanto,

\[(x+4)(x-2)=0\]

Usando la propiedad cero del producto, ya sea

\[x+4=0 \quad \text { or } \quad x-2=0\]

por lo\[x=-4 \quad \text { or } \quad x=2\]

El hecho de que hayamos encontrado dos respuestas usando un método analítico es preocupante. Después de todo, la gráfica de la Figura\(\PageIndex{10}\) (b) indica solo una solución, a saber x = −4. Es reconfortante que una de nuestras soluciones analíticas sea también x = −4, pero sigue siendo desconcertante que nuestro enfoque analítico revele una segunda “respuesta”, es decir, x = 2.

No obstante, fíjense que no hemos prestado atención alguna a las restricciones ocasionadas por los denominadores hasta este punto. De hecho, una cuidadosa consideración de la ecuación (11) revela factores de x+2 y x−2 en los denominadores. Por lo tanto, x = −2 y x = 2 son restricciones.

Tenga en cuenta que una de nuestras respuestas, a saber x = 2, es un valor restringido. Hará que algunos de los denominadores en la ecuación (11) sean iguales a cero, por lo que no puede ser una solución. Así, la única solución viable es x = −4. Ciertamente se puede verificar esta solución a mano, pero usemos la calculadora gráfica para ayudarnos en el cheque.

Primero, ingrese -4, presione el\(\blacktriangleright\) botón STO, presione X, luego presione ENTRAR para ejecutar el comando resultante y almacene -4 en la variable X. El resultado se muestra en la Figura\(\PageIndex{11}\) (a).

A continuación, calculamos el valor del lado izquierdo de la ecuación (11) a este valor de X. Ingresamos el lado izquierdo de la ecuación (11) como 1/ (X+2) -X/ (2-X), luego presionamos la tecla ENTER para ejecutar la sentencia y producir el resultado mostrado en la Figura\(\PageIndex{11}\) (b).

Finalmente, ingresa el lado derecho de la ecuación (11) como (X+6)/(x́2-4) y presiona la tecla INTRO para ejecutar la sentencia. El resultado se muestra en la Figura\(\PageIndex{11}\) (c). Obsérvese que ambos lados de la ecuación son iguales a .1666666667 en X=-4. Así, la solución x = −4 comprueba.

Figura\(\PageIndex{11}\). Usando la calculadora gráfica para verificar la solución x = −4 de la ecuación (11).

Ejercicio

Para cada una de las funciones racionales dadas en los Ejercicios 1 - 6, realizar cada una de las siguientes tareas.

1. Configure un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.
2. Traza el cero de la función racional en tu sistema de coordenadas y etiquétalo con sus coordenadas. Traza las asíntotas verticales y horizontales en tu sistema de coordenadas y etiquétalas con sus ecuaciones. Usa esta información (y tu calculadora gráfica) para dibujar la gráfica de f.
3. Trace la línea horizontal y = k en su sistema de coordenadas y etiquete esta línea con su ecuación.
4. Utilice la utilidad de intersección de su calculadora para ayudar a determinar la solución de f (x) = k. Etiquete este punto en su gráfica con sus coordenadas.
5. Resuelve la ecuación f (x) = k algebraicamente, colocando el trabajo para esta solución en tu papel cuadriculado junto a tu sistema de coordenadas que contiene la solución gráfica. ¿Están de acuerdo las respuestas?

Ejercicio\(\PageIndex{1}\)

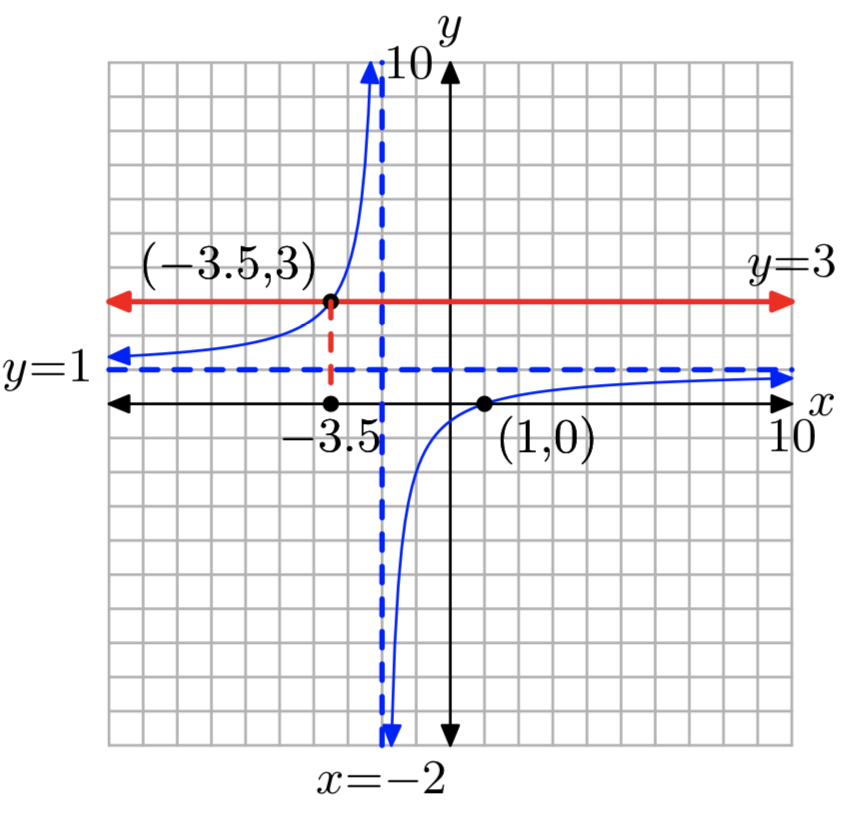
\(f(x) = \frac{x−1}{x+2}\); k = 3

Contestar

\(x = −\frac{7}{2}\)

Ejercicio\(\PageIndex{2}\)

\(f(x) = \frac{x+1}{x−2}\); k = −3

Ejercicio\(\PageIndex{3}\)

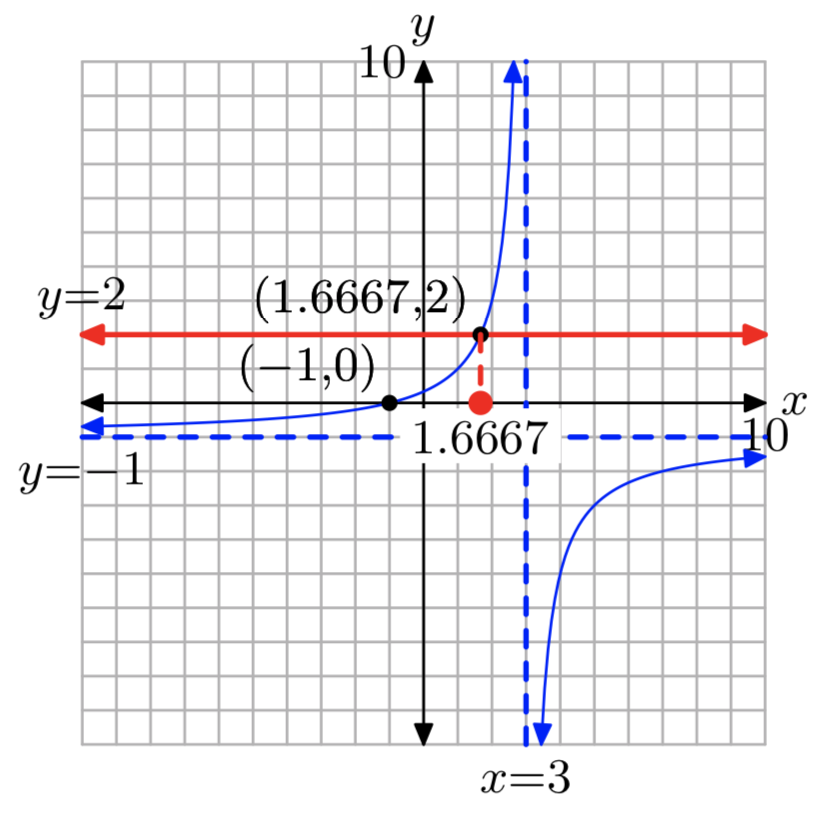
\(f(x) = \frac{x+1}{3−x}\); k = 2

Contestar

\(x = \frac{5}{3}\)

Ejercicio\(\PageIndex{4}\)

\(f(x) = \frac{x+3}{2−x}\); k = 2

Ejercicio\(\PageIndex{5}\)

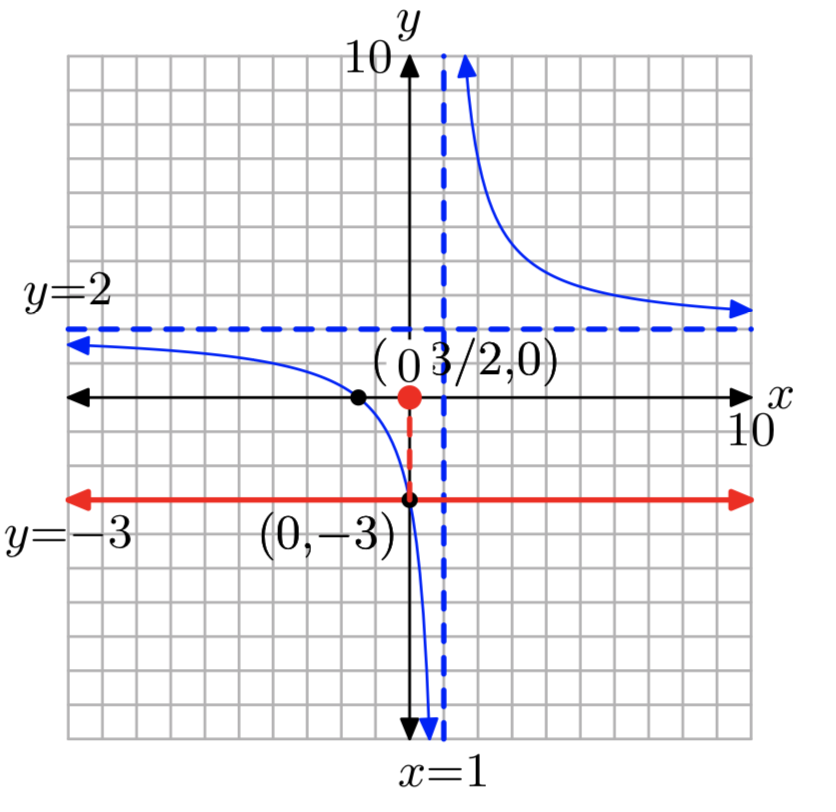
\(f(x) = \frac{2x+3}{x−1}\); k = −3

Contestar

x = 0

Ejercicio\(\PageIndex{6}\)

\(f(x)= \frac{5−2x}{x−1}\); k = 3

En los Ejercicios 7 - 14, utilice una técnica estrictamente algebraica para resolver la ecuación f (x) = k para la función dada y el valor de k Se le anima a verificar su resultado con su calculadora.

Ejercicio\(\PageIndex{7}\)

\(f(x) = \frac{16x−9}{2x−1}\); k = 8

Contestar

ninguno

Ejercicio\(\PageIndex{8}\)

\(f(x) = \frac{10x−3}{7x+7}\); k = 1

Ejercicio\(\PageIndex{9}\)

\(f(x) = \frac{5x+8}{4x+1}\); k = −11

Contestar

\(−\frac{19}{49}\)

Ejercicio\(\PageIndex{10}\)

\(f(x) = −\frac{6x−11}{7x−2}\); k = −6

Ejercicio\(\PageIndex{11}\)

\(f(x) = −\frac{35x}{7x+1​​2}\); k = −5

Contestar

ninguno

Ejercicio\(\PageIndex{12}\)

\(f(x) = −\frac{66x−5}{6x−10}\); k = −11

Ejercicio\(\PageIndex{13}\)

\(f(x) = \frac{8x+2}{x−11}\); k = 11

Contestar

41

Ejercicio\(\PageIndex{14}\)

\(f(x) = \frac{36x−7}{3x−4}\); k = 12

En los Ejercicios 15 - 20, utilizar una técnica estrictamente algebraica para resolver la ecuación dada. Se le anima a verificar su resultado con su calculadora.

Ejercicio\(\PageIndex{15}\)

\(\frac{x}{7}+\frac{8}{9} = −\frac{8}{7}\)

Contestar

\(−\frac{128}{9}\)

Ejercicio\(\PageIndex{16}\)

\(\frac{x}{3}+\frac{9}{2} = −\frac{3}{8}\)

Ejercicio\(\PageIndex{17}\)

\(−\frac{57}{x}=27−\frac{40}{x^2}\)

Contestar

\(−\frac{8}{5}, \frac{3}{9}\)

Ejercicio\(\PageIndex{18}\)

\(−\frac{117}{x} = 54+\frac{54}{x^2}\)

Ejercicio\(\PageIndex{19}\)

\(\frac{7}{x} = 4−\frac{3}{x^2}\)

Responder

\(\frac{7+\sqrt{97}}{8}, \frac{7−\sqrt{97}}{8}\)

Ejercicio\(\PageIndex{20}\)

\(\frac{3}{x^2} = 5−\frac{3}{x}\)

Para cada una de las funciones racionales dadas en los Ejercicios 21 - 26, realizar cada una de las siguientes tareas.

1. Configure un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje. Re- miembro para dibujar todas las líneas con una regla.
2. Traza el cero de la función racional en tu sistema de coordenadas y etiquétalo con sus coordenadas. Puede usar la utilidad cero de su calculadora para encontrar esto, si lo desea.
3. Traza las asíntotas verticales y horizontales en tu sistema de coordenadas y etiquétalas con sus ecuaciones. Usa la asíntota y la información cero (y tu calculadora gráfica) para dibujar la gráfica de f.
4. Trace la línea horizontal y = k en su sistema de coordenadas y etiquete esta línea con su ecuación.
5. Utilice la utilidad de intersección de su calculadora para ayudar a determinar la solución de f (x) = k. Etiquete este punto en su gráfica con sus coordenadas.
6. Resuelve la ecuación f (x) = k algebraicamente, colocando el trabajo para esta solución en tu papel cuadriculado junto a tu sistema de coordenadas que contiene la solución gráfica. ¿Están de acuerdo las respuestas?

Ejercicio\(\PageIndex{21}\)

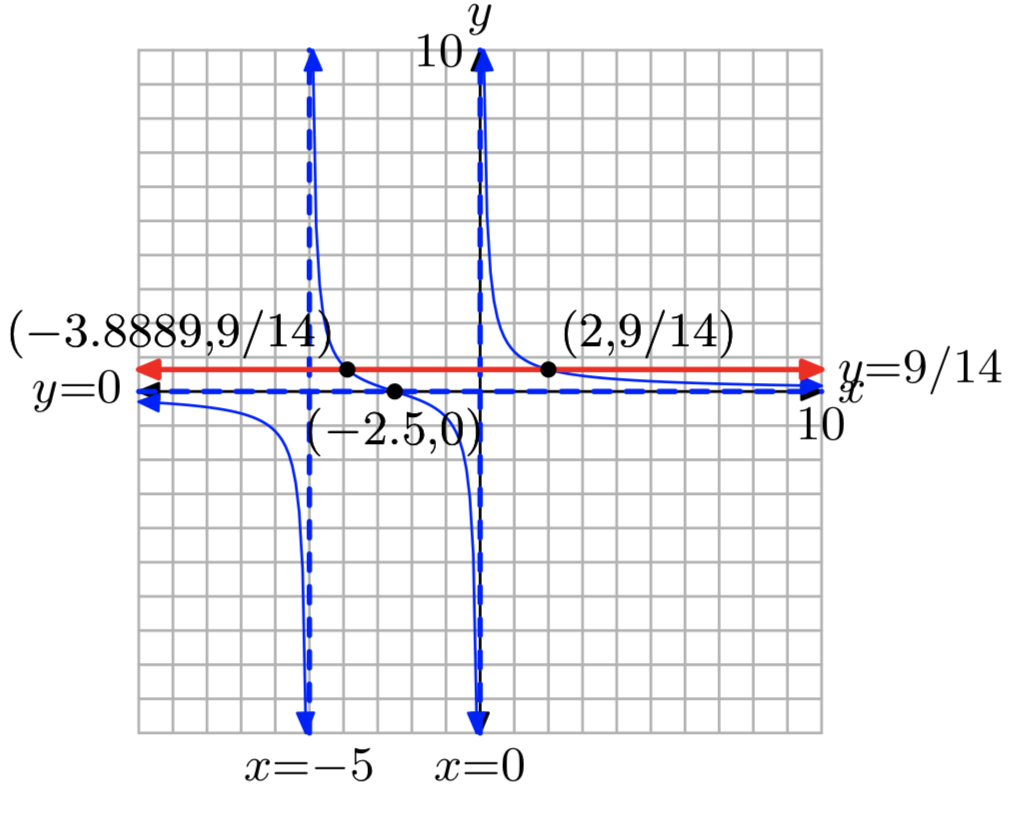
\(f(x) = \frac{1}{x}+\frac{1}{x+5}\),\(k = \frac{9}{14}\)

Responder

\(x = −\frac{35}{9}\)o x = 2

Ejercicio\(\PageIndex{22}\)

\(f(x) = \frac{1}{x}+\frac{1}{x−2}\),\(k = \frac{8}{15}\)

Ejercicio\(\PageIndex{23}\)

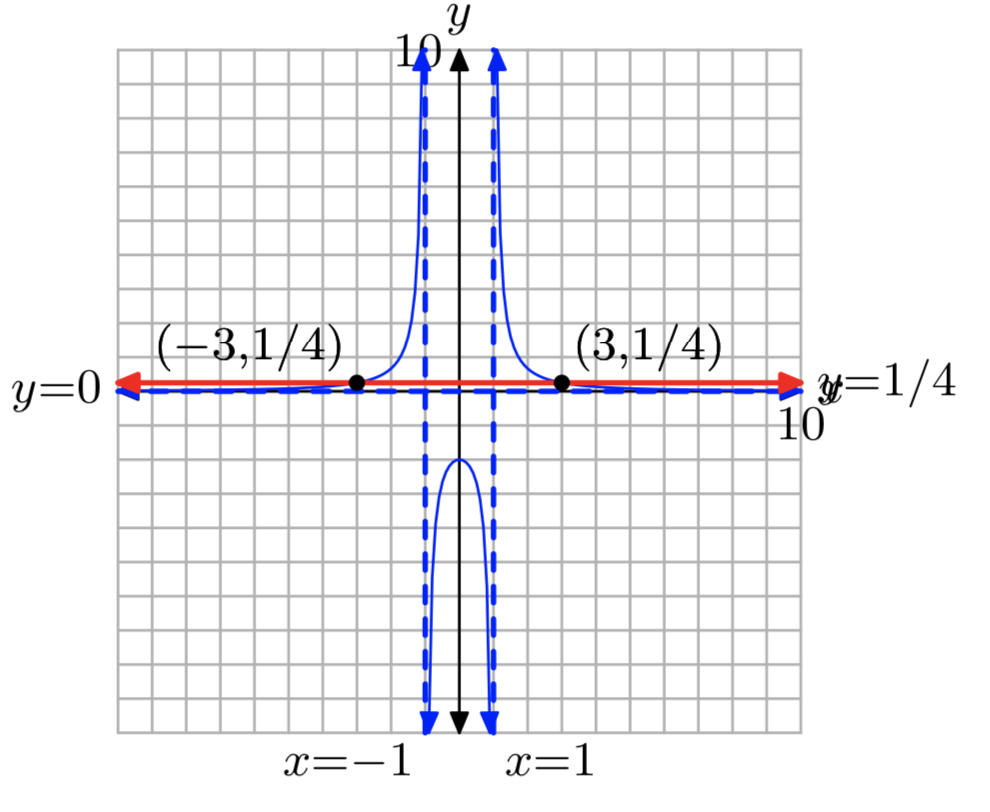
\(f(x) = \frac{1}{x−1}−\frac{1}{x+1}\),\(k = \frac{1}{4}\)

Responder

x = −3 o x = 3

Ejercicio\(\PageIndex{24}\)

\(f(x) = \frac{1}{x−1}−\frac{1}{x+2}\),\(k = \frac{1}{6}\)

Ejercicio\(\PageIndex{25}\)

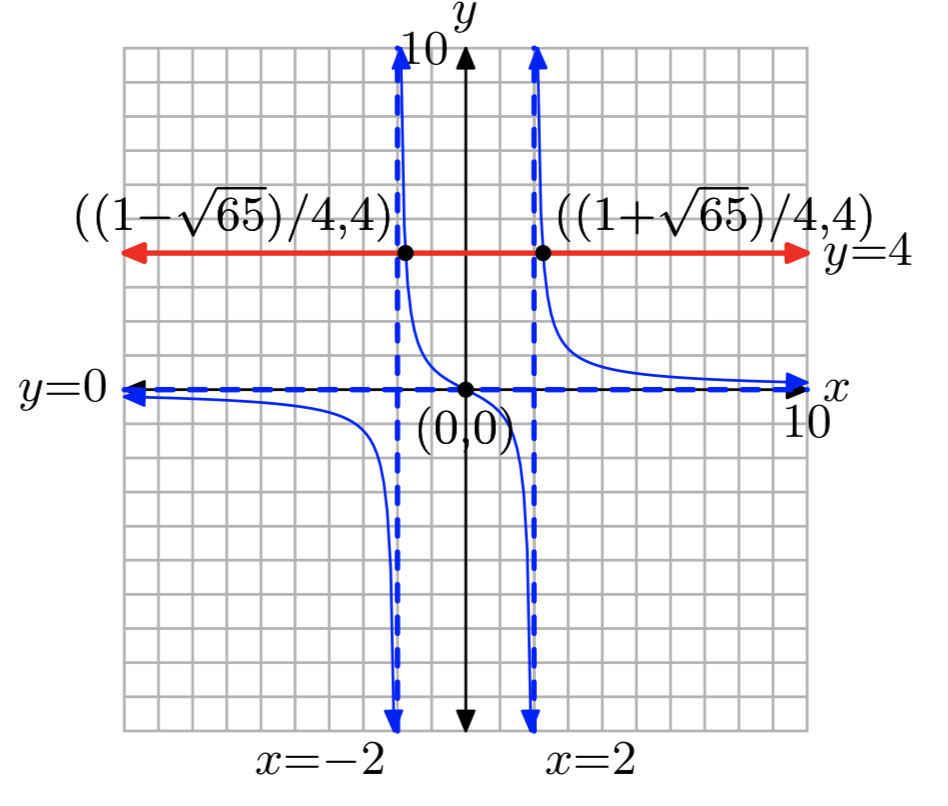
\(f(x) = \frac{1}{x−2}+\frac{1}{x+2}\), k = 4

Responder

\(x = \frac{1+\sqrt{65}}{4}, \frac{1−\sqrt{65}}{4}\)

Ejercicio\(\PageIndex{26}\)

\(f(x) = \frac{1}{x−3}+\frac{1}{x+2}\), k = 5

En los Ejercicios 27 - 34, utilizar una técnica estrictamente algebraica para resolver la ecuación dada. Se le anima a verificar su resultado con su calculadora.

Ejercicio\(\PageIndex{27}\)

\(\frac{2}{x+1}+\frac{4}{x+2} = −3\)

Responder

\(\frac{−15+\sqrt{57}}{6}, \frac{−15−\sqrt{57}}{6}\)

Ejercicio\(\PageIndex{28}\)

\(\frac{2}{x−5}−\frac{7}{x−7} = 9\)

Ejercicio\(\PageIndex{29}\)

\(\frac{3}{x+9}−\frac{2}{x+7} = −3\)

Responder

\(\frac{−49+\sqrt{97}}{6}, \frac{−49−\sqrt{97}}{6}\)

Ejercicio\(\PageIndex{30}\)

\(\frac{3}{x+9}−\frac{6}{x+7} = 9\)

Ejercicio\(\PageIndex{31}\)

\(\frac{2}{x+9}+\frac{2}{x+6} = −1\)

Responder

−7, −12

Ejercicio\(\PageIndex{32}\)

\(\frac{5}{x−6}−\frac{8}{x−7} = −1\)

Ejercicio\(\PageIndex{33}\)

\(\frac{3}{x+3}+\frac{6}{x+2} = −2\)

Responder

\(\frac{−19+\sqrt{73}}{4}, \frac{−19−\sqrt{73}}{4}\)

Ejercicio\(\PageIndex{34}\)

\(\frac{2}{x−4}−\frac{2}{x−1} = 1\)

Para cada una de las ecuaciones de los Ejercicios 35 - 40, realice cada una de las siguientes tareas.

1. Siga el ejemplo del Ejemplo 10 en el texto. Hacer que un lado de la ecuación sea igual a cero. Carga el lado distinto de cero en tu calculadora y dibuja su gráfica.
2. Determine las asíntotas verticales de analizando la ecuación y la gráfica resultante en su calculadora. Utilice la función TABLE de su calculadora para determinar cualquier comportamiento de asíntota horizontal.
3. Utilice la utilidad de búsqueda de cero en el menú CALC para determinar el cero del lado distinto de cero de la ecuación resultante.
4. Configure un sistema de coordenadas en papel cuadriculado. Etiquetar y escalar cada eje. Recuerda dibujar todas las líneas con una regla.Dibuja la gráfica del lado distinto de cero de la ecuación. Dibuja las asíntotas verticales y horizontales y etiquétalas con sus ecuaciones. Trazar la intersección x y etiquetarla con sus coordenadas.
5. Utilizar una técnica algebraica para disuadir- minar la solución de la ecuación y compararla con la solución encontrada por el análisis gráfico anterior.

Ejercicio\(\PageIndex{35}\)

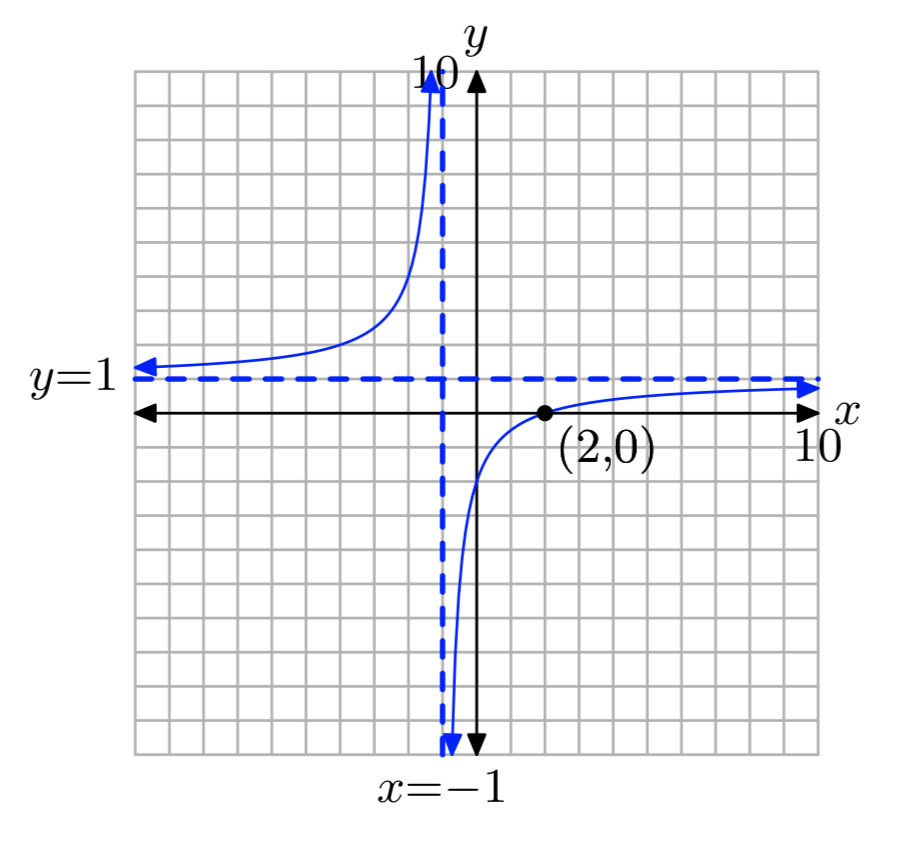
\(\frac{x}{x+1}+\frac{8}{x^2−2x−3} = \frac{2}{x−3}\)

Responder

x = 2

Ejercicio\(\PageIndex{36}\)

\(\frac{x}{x+4}−\frac{2}{x+1} = \frac{12}{x^2+5x+4}\)

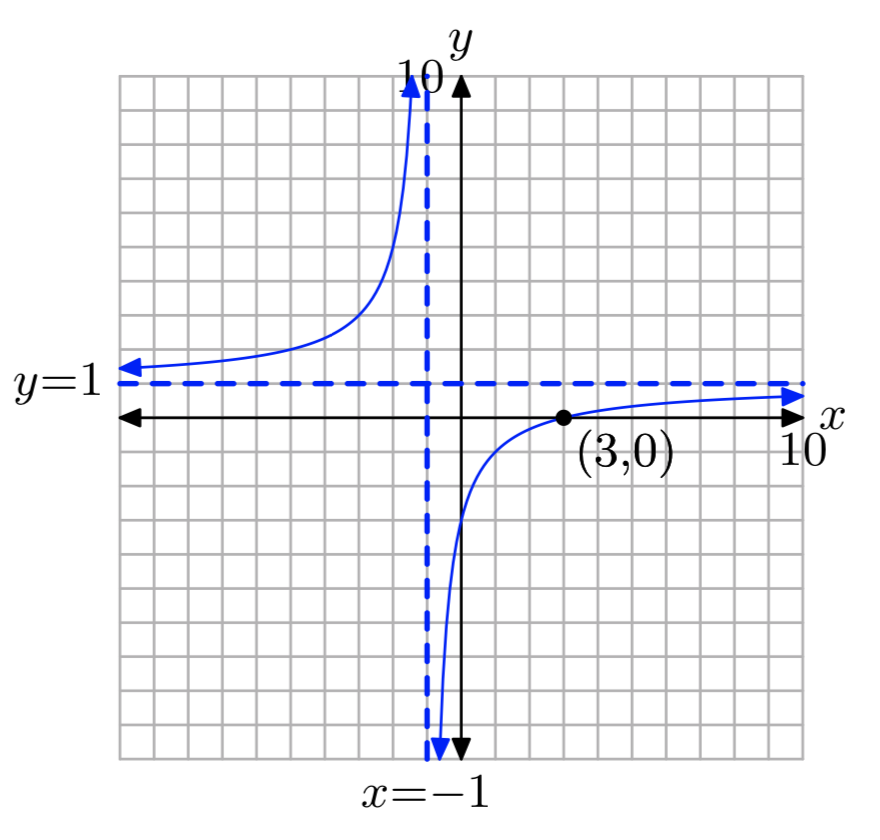
Ejercicio\(\PageIndex{37}\)

\(\frac{x}{x+1}−\frac{4}{2x+1} = \frac{2x−1}{2x^2+3x+2}\)

Responder

x = 3

Ejercicio\(\PageIndex{38}\)

\(\frac{2x}{x−4}−\frac{1}{x+1} = \frac{4x+24}{x^2−3x−4}\)

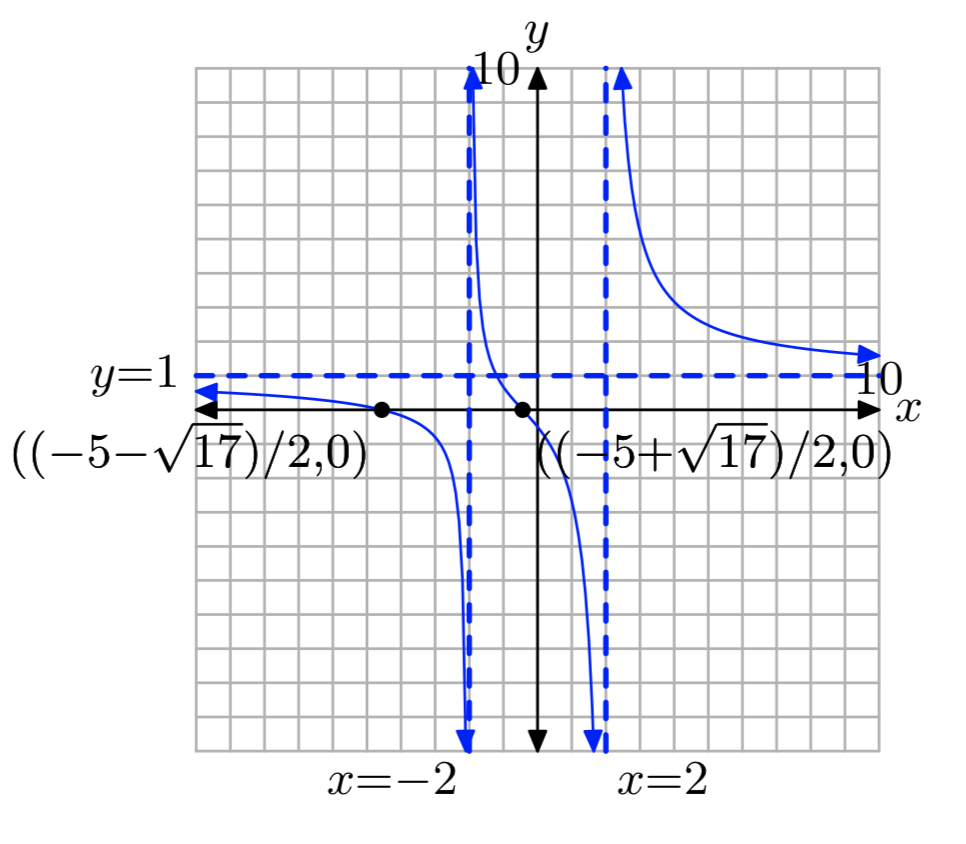
Ejercicio\(\PageIndex{39}\)

\(\frac{x}{x−2}+\frac{3}{x+2} = \frac{8}{4−x^2}\)

Responder

\(x = \frac{5−\sqrt{17}}{2}, \frac{−5−\sqrt{17}}{2}\)

Ejercicio\(\PageIndex{40}\)

\(\frac{x}{x−6​​​​​1​}−\frac{4}{x+1} = \frac{x−6}{1−x^2}\)

En los Ejercicios 41 - 68, utilizar una técnica estrictamente algebraica para resolver la ecuación dada. Se le anima a verificar su resultado con su calculadora.

Ejercicio\(\PageIndex{41}\)

\(\frac{x}{3x−9}−\frac{9}{x} = \frac{1}{x−3}\)

Responder

27

Ejercicio\(\PageIndex{42}\)

\(\frac{5x}{x+2}+\frac{5}{x−5} = \frac{x+6}{x^2−3x−10}\)

Ejercicio\(\PageIndex{43}\)

\(\frac{3x}{x+2}−\frac{7}{x} = −\frac{1}{2x+4}\)

Responder

\(\frac{7}{2}, −\frac{4}{3}\)

Ejercicio\(\PageIndex{44}\)

\(\frac{4x}{x+6}−\frac{4}{x+4} = \frac{x−4}{x^2+10x+24}\)

Ejercicio\(\PageIndex{45}\)

\(\frac{x}{x−5}+\frac{9}{4−x} = \frac{x+5}{x^2−9x+20}\)

Responder

10

Ejercicio\(\PageIndex{46}\)

\(\frac{6x}{x−5}−\frac{2}{x−3} = \frac{x−8}{x^2−8x+15}\)

Ejercicio\(\PageIndex{47}\)

\(\frac{2x}{x−4}+\frac{5}{2−x} = \frac{x+8}{x^2−6x+8}\)

Responder

3

Ejercicio\(\PageIndex{48}\)

\(\frac{x}{x−7}−\frac{8}{5−x} = \frac{x+7}{x^2−12x+35}\)

Ejercicio\(\PageIndex{49}\)

\(−\frac{x}{2x+2}−\frac{6}{x} = −\frac{2}{x+1}\)

Responder

−6, −2

Ejercicio\(\PageIndex{50}\)

\(\frac{7x}{x+3}−\frac{4}{2−x} = \frac{x+8}{x^2+x−6}\)

Ejercicio\(\PageIndex{51}\)

\(\frac{2x}{x+5}−\frac{2}{6−x} = \frac{x−2}{x^2−x−30}\)

Responder

4,\(\frac{3}{2}\)

Ejercicio\(\PageIndex{52}\)

\(\frac{4x}{x+1}+\frac{6}{x+3} = \frac{x−9}{x^2+4x+3}\)

Ejercicio\(\PageIndex{53}\)

\(\frac{x}{x+7}−\frac{2}{x+5}​​​​​​​ = \frac{x+1}{x^2+12x+35}\)

Responder

3

Ejercicio\(\PageIndex{54}\)

\(\frac{5x}{6x+4}+\frac{6}{x} = \frac{1}{3x+2}\)

Ejercicio\(\PageIndex{55}\)

\(\frac{2x}{3x+9​​​​​​​}−\frac{4}{x} = −\frac{2}{x+3}\)

Responder

6

Ejercicio\(\PageIndex{56}\)

\(\frac{7x}{x+1}−\frac{4}{x+2} = \frac{x+6}{x^2+3x+2}\)

Ejercicio\(\PageIndex{57}\)

\(\frac{x}{2x−8​​​​​​​} + \frac{8}{x} = \frac{2}{x−4}\)

Responder

−16

Ejercicio\(\PageIndex{58}\)

\(\frac{3x}{x−6}+\frac{6}{x−6} = \frac{x+2}{x^2−12x+36}\)

Ejercicio\(\PageIndex{59}\)

\(\frac{x}{x+2}+\frac{2}{x} = −\frac{5}{2x+4}\)

Responder

\(\frac{−9+\sqrt{17}}{4}, \frac{−9−\sqrt{17}}{4}\)

Ejercicio\(\PageIndex{60}\)

\(\frac{4x}{x−2}+\frac{2}{2−x} = \frac{x+4}{x^2−4x+4}\)

Ejercicio\(\PageIndex{61}\)

\(−\frac{2x}{3x−9​​​​​​​}−\frac{3}{x} = −\frac{2}{x−3}\)

Responder

\(−\frac{9}{2}\)

Ejercicio\(\PageIndex{62}\)

\(\frac{2x}{x+1}−\frac{2}{x} = \frac{1}{2x+2}\)

Ejercicio\(\PageIndex{63}\)

\(\frac{x}{x+1}+\frac{5}{x} = \frac{1}{4x+4}\)

Responder

\(\frac{−19+\sqrt{41}}{8}, \frac{−19−\sqrt{41}}{8}\)

Ejercicio\(\PageIndex{64}\)

\(\frac{2x}{x−4}−\frac{8}{x−7} = \frac{x+2}{x^2−11x+28}\)

Ejercicio\(\PageIndex{65}\)

\(−\frac{9x}{x−2}+\frac{2}{x} = −\frac{2}{4x−1}\)

Responder

\(\frac{9}{2}\), 5

Ejercicio\(\PageIndex{66}\)

\(\frac{2x}{x−3​​​​​​​}−\frac{4}{4−x} = \frac{x−9}{x^2−7x+12}\)

Ejercicio\(\PageIndex{67}\)

\(\frac{4x}{x+6}−\frac{5}{7−x} = \frac{x−5}{x^2−x−42}\)

Responder

\(\frac{7}{2}, \frac{5}{2}\)

Ejercicio\(\PageIndex{68}\)

\(\frac{x}{x−1​​​​​​​}−\frac{4}{x} = \frac{1}{5x−5}\)

​​​​​​​