7.1: Introducción de funciones racionales
- Page ID
- 110784
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)En el capítulo anterior, estudiamos polinomios, funciones que tienen forma de ecuación
\[p(x)=a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}\]
A pesar de que este polinomio se presenta en potencias ascendentes de\(x\), el término principal del polinomio sigue siendo\(a_{n} x^{n}\), el término con mayor poder de\(x\). El grado del polinomio es el mayor poder de (x\) presente, por lo que en este caso, el grado del polinomio es\(n\).
En esta sección, nuestro estudio nos conducirá a las funciones racionales. Observe la palabra raíz “ratio” en el término “racional”. ¿Te recuerda a la palabra “fracción”? Debería, ya que las funciones racionales son funciones en una forma fraccionaria muy específica.
Definición: Funciones racionales
Una función racional es una función que puede escribirse como cociente de dos funciones polinómicas. En símbolos, la función
\[f(x)=\frac{a_{0}+a_{1} x+a_{2} x^{2}+\cdots+a_{n} x^{n}}{b_{0}+b_{1} x+b_{2} x^{2}+\cdots+b_{m} x^{m}}\]
se llama una función racional.
Por ejemplo,
\[f(x)=\frac{1+x}{x+2}, \quad g(x)=\frac{x^{2}-2 x-3}{x+4}, \quad \text { and } \quad h(x)=\frac{3-2 x-x^{2}}{x^{3}+2 x^{2}-3 x-5} \label{4}\]
son funciones racionales, mientras
\[f(x)=\frac{1+\sqrt{x}}{x^{2}+1}, \quad g(x)=\frac{x^{2}+2 x-3}{1+x^{1 / 2}-3 x^{2}}, \quad \text { and } \quad h(x)=\sqrt{\frac{x^{2}-2 x-3}{x^{2}+4 x-12}} \label{5}\]
no son funciones racionales.
Cada una de las funciones en la Ecuación\ ref {4} son funciones racionales, porque en cada caso, el numerador y denominador de la expresión dada es un polinomio válido.
Sin embargo, en la Ecuación\ ref {5}, el numerador de no\(f(x)\) es un polinomio (los polinomios no permiten la raíz cuadrada de la variable independiente). Por lo tanto, no\(f\) es una función racional. Del mismo modo, el denominador de\(g(x)\) en la Ecuación\ ref {5} no es un polinomio. Las fracciones no están permitidas como exponentes en polinomios. Así, no\(g\) es una función racional. Finalmente, en el caso de la función\(h\) en la Ecuación\ ref {5}, aunque el radicando (la expresión dentro del radical) es una función racional, la raíz cuadrada impide que h sea una función racional.
Una habilidad importante a desarrollar es la capacidad de dibujar la gráfica de una función racional. Empecemos dibujando la gráfica de una de las funciones racionales más simples (pero más fundamentales).
La Gráfica de y = 1/x
En todas las situaciones nuevas, cuando se nos presenta una ecuación cuya gráfica no hemos considerado o no reconocemos, comenzamos el proceso de dibujar la gráfica creando una tabla de puntos que satisfagan la ecuación. Es importante recordar que la gráfica de una ecuación es el conjunto de todos los puntos que satisfacen la ecuación. Observamos que cero no está en el dominio de\(y = 1/x\) (la división por cero no tiene sentido y no está definida), y creamos una tabla de puntos que satisfaga la ecuación mostrada en la Figura\(\PageIndex{1}\).
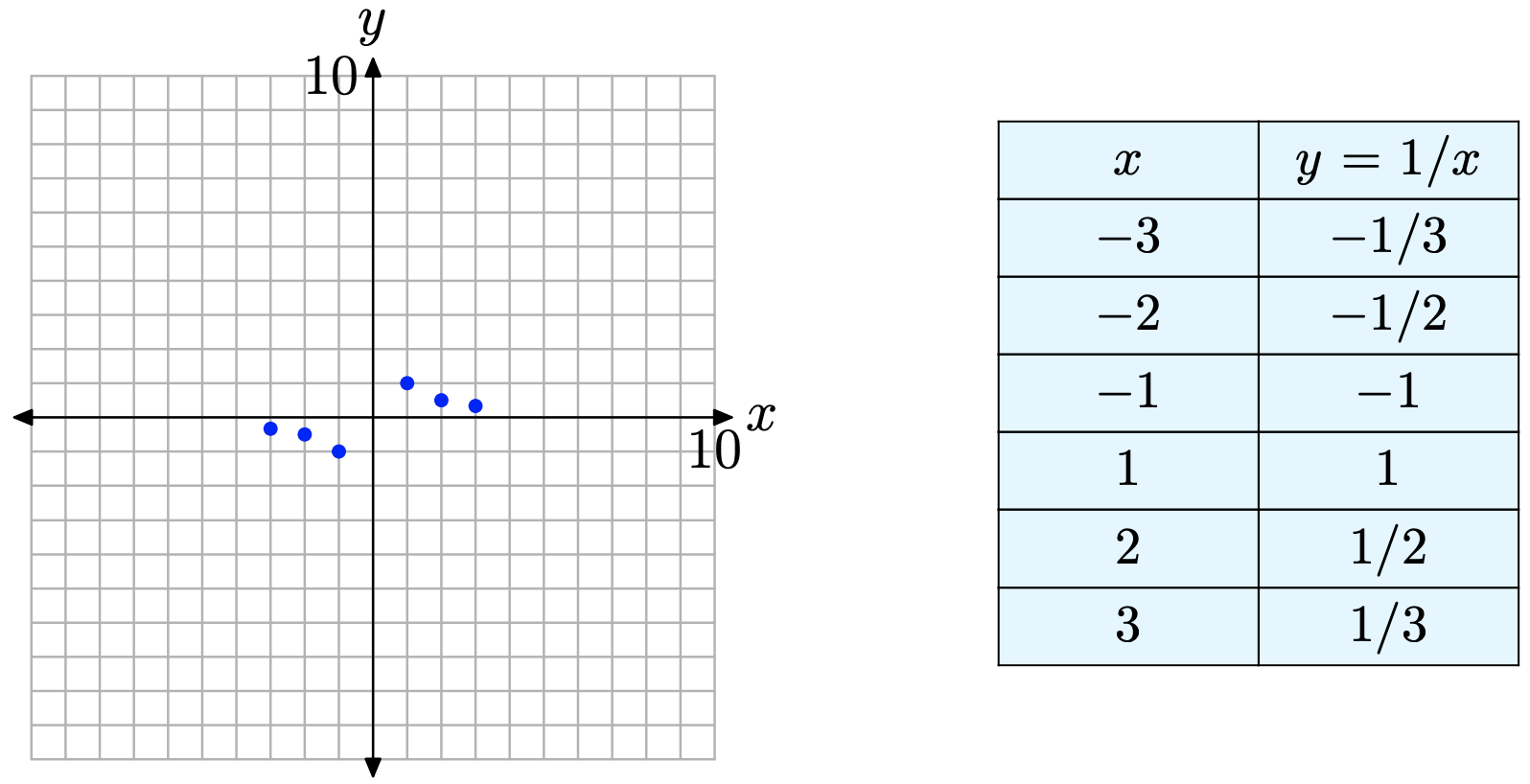
En este punto (Figura\(\PageIndex{1}\)), está bastante claro qué está haciendo la gráfica entre\(x = −3\) y\(x = −1\). De igual manera, queda claro lo que está sucediendo entre x = 1 y x = 3. No obstante, existen algunas áreas abiertas de preocupación.
- ¿Qué pasa con la gráfica a medida que x aumenta sin encuadernación? Es decir, ¿qué pasa con la gráfica a medida que x se mueve hacia\(\infty\)?
- ¿Qué pasa con la gráfica a medida que x disminuye sin encuadernación? Es decir, ¿qué pasa con la gráfica a medida que x se mueve hacia\(-\infty\)?
- ¿Qué pasa con la gráfica a medida que x se acerca a cero desde la derecha?
- ¿Qué pasa con la gráfica cuando x se acerca a cero desde la izquierda?
Respondamos cada una de estas preguntas a su vez. Comenzaremos discutiendo el “comportamiento final” de la función racional definida por y = 1/x Primero, el extremo derecho. ¿Qué sucede a medida que x aumenta sin límite? Es decir, ¿qué sucede a medida que x aumenta hacia ∞? En la Tabla\(\PageIndex{1a}\), calculamos y = 1/x para x igual a 100, 1000 y 10000. Observe cómo los valores y en la Tabla\(\PageIndex{1a}\) son todos positivos y se acercan a cero.
Los estudiantes en cálculo utilizan la siguiente notación para esta idea.
\[\lim _{x \rightarrow \infty} y=\lim _{x \rightarrow \infty} \frac{1}{x}=0\]
Dicen que “el límite de y a medida que x se acerca al infinito es cero”. Es decir, a medida que x se acerca al infinito, y se acerca a cero.
| x | y = 1/x |
|---|---|
| 100 | 0.01 |
| 1000 | 0.001 |
| 10000 | 0.0001 |
Un evento completamente similar ocurre en el extremo izquierdo. A medida que x disminuye sin límite, es decir, a medida que x disminuye hacia\(-\infty\), tenga en cuenta que los valores y en la Tabla\(\PageIndex{1}\) (b) son todos negativos y se acercan a cero. Los estudiantes de Cálculo tienen una notación similar para esta idea.
\[\lim _{x \rightarrow-\infty} y=\lim _{x \rightarrow-\infty} \frac{1}{x}=0\]
Dicen que “el límite de y a medida que x se acerca al infinito negativo es cero”. Es decir, a medida que x se acerca al infinito negativo, y se acerca a cero.
| x | y=1/x |
|---|---|
| -100 | -0.01 |
| -1000 | -0.001 |
| -10000 | -0.0001 |
Estos números en Tablas\(\PageIndex{1a}\) y\(\PageIndex{1b}\), y las ideas descritas anteriormente, predicen el correcto comportamiento final de la gráfica de\(y = 1/x\). En cada extremo del eje x, los valores y deben acercarse a cero. Esto significa que la gráfica de\(y = 1/x\) debe acercarse al eje x para los valores x en el extremo derecho e izquierdo de la gráfica. En este caso, decimos que el eje x actúa como asíntota horizontal para la gráfica de\(y = 1/x\). A medida que\(x\) se acerca al infinito positivo o negativo, la gráfica de\(y = 1/x\) se acerca al eje x. Este comportamiento se muestra en la Figura\(\PageIndex{2}\).

Nuestra última investigación será en el intervalo de\(x = −1\) a\(x = 1\). Nuevamente se recuerda a los lectores que la función y = 1/x no está definida en x = 0. En consecuencia, partiremos esta región a la mitad, investigando primero lo que sucede en la región entre x = 0 y x = 1. Evaluamos y = 1/x a x = 1/2, x = 1/4 y x = 1/8, como se muestra en la tabla de la Figura\(\PageIndex{3}\), luego graficamos los puntos resultantes.
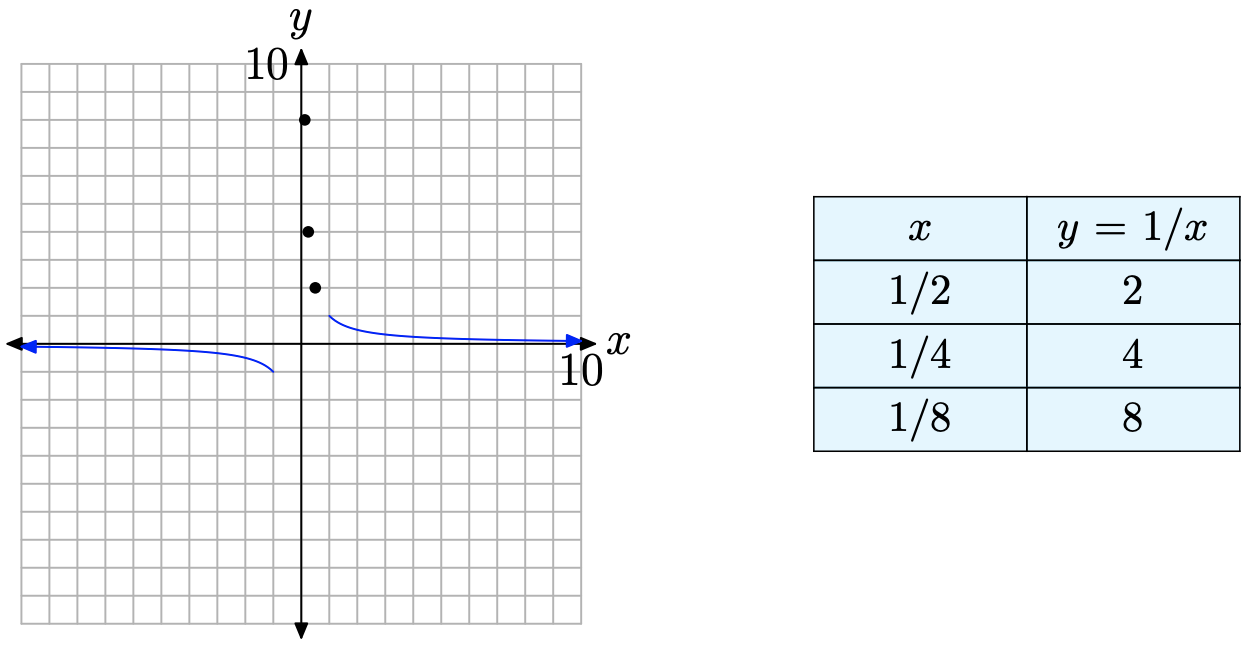
Tenga en cuenta que los valores x en la tabla de la Figura se\(\PageIndex{3}\) acercan a cero desde la derecha, luego tenga en cuenta que los valores y correspondientes son cada vez más grandes. Podríamos seguir en esta línea, sumando puntos. Por ejemplo, si\(x = 1/16\), entonces\(y = 16\). Si\(x = 1/32\), entonces\(y = 32\). Si\(x = 1/64\), entonces\(y = 64\). Cada vez que reducimos a la mitad nuestro valor de x, el valor resultante de x está más cerca de cero, y el valor y correspondiente duplica su tamaño. Estudiantes de Cálculo describen este comportamiento con la notación
\[\lim _{x \rightarrow 0^{+}} y=\lim _{x \rightarrow 0^{+}} \frac{1}{x}=\infty\]
Es decir, a medida que “x se acerca a cero desde la derecha, el valor de y crece hasta el infinito”. Esto es evidente en la gráfica de la Figura\(\PageIndex{3}\), donde vemos que los puntos trazados se acercan al eje vertical mientras que al mismo tiempo se mueven hacia arriba sin límite. Algo similar sucede en el otro lado del eje vertical, como se muestra en la Figura\(\PageIndex{4}\).
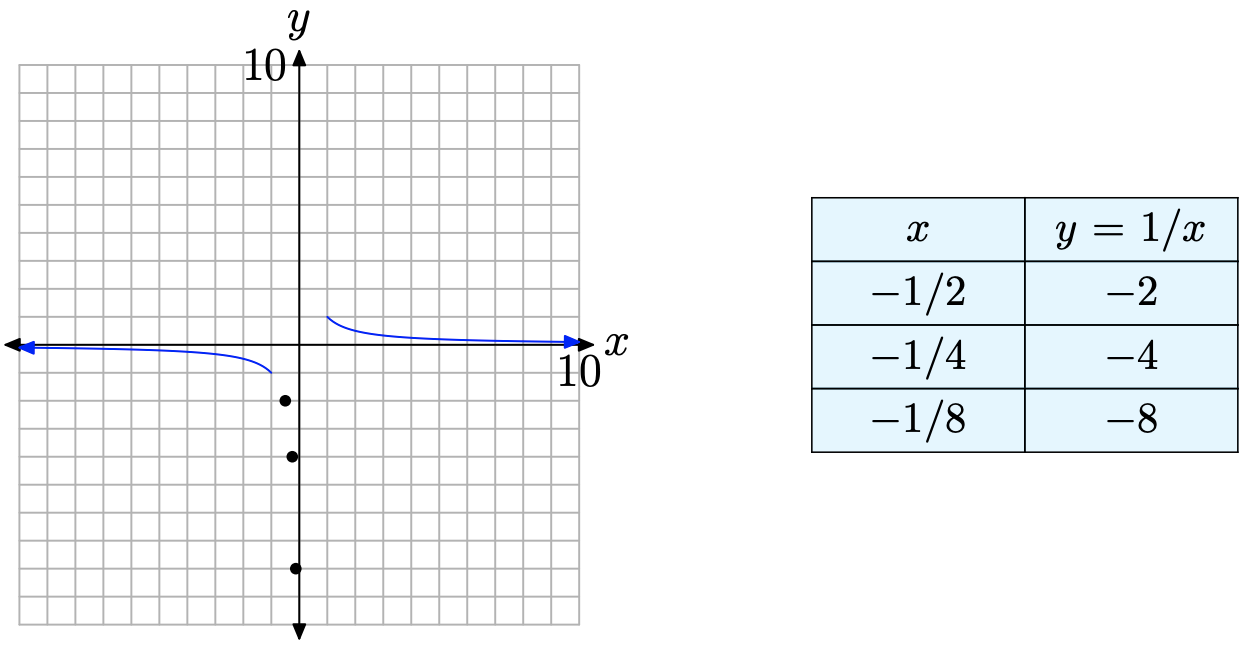
Nuevamente, los estudiantes de cálculo escribirían\[\lim _{x \rightarrow 0^{-}} y=\lim _{x \rightarrow 0^{-}} \frac{1}{x}=-\infty\]
Es decir, “a medida que x se acerca a cero desde la izquierda, los valores de y disminuyen a infinito negativo”. En la Figura\(\PageIndex{4}\), es claro que a medida que los puntos se acercan al eje vertical (a medida que x se acerca a cero) desde la izquierda, la gráfica disminuye sin límite. Las pruebas reunidas a este punto indican que
La evidencia reunida hasta este punto indica que el eje vertical está actuando como asíntota vertical. A medida que x se acerca a cero desde cualquier lado, la gráfica se acerca al eje vertical, ya sea subiendo al infinito o cayendo al infinito negativo. La gráfica no puede cruzar el eje vertical porque ahí la función no está definida. La gráfica terminada se muestra en la Figura\(\PageIndex{5}\).
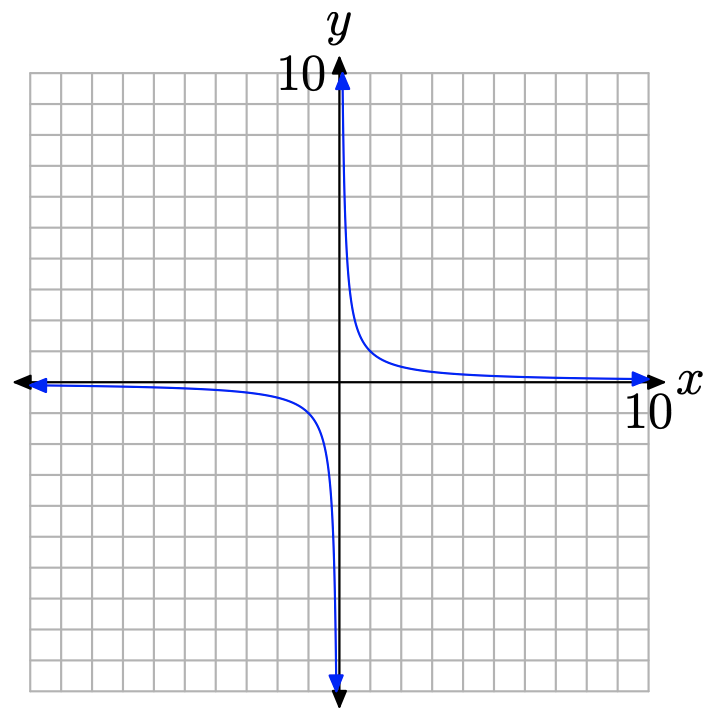
La gráfica completa de y = 1/x en la Figura\(\PageIndex{5}\) se denomina hipérbola y sirve como punto de partida fundamental para toda discusión posterior en esta sección.
Señalamos anteriormente que el dominio de la función definida por la ecuación y = 1/x es el conjunto\(D=\{x : x \neq 0\}\). Cero se excluye del dominio porque la división por cero no está definida. No es casualidad que la gráfica tenga una asíntota vertical en x = 0. Veremos esta relación reforzada en otros ejemplos.
Traducciones
En esta sección, traduciremos la gráfica de y = 1/x tanto en la dirección horizontal como en la vertical.
Ejemplo\(\PageIndex{1}\)
Esbozar el gráfico de
\[y=\frac{1}{x+3}-4 \nonumber\]
Solución
Técnicamente, la función definida por y = 1/ (x + 3) − 4 no tiene la forma general (3) de una función racional. Sin embargo, en capítulos posteriores mostraremos cómo y = 1/ (x + 3) − 4 puede ser manipulado en la forma general de una función racional.
Sabemos cómo se ve la gráfica de y = 1/x. Si reemplazamos x por x + 3, esto desplazará la gráfica de y = 1/x tres unidades hacia la izquierda, como se muestra en la Figura\(\PageIndex{6}\) (a). Tenga en cuenta que la asíntota vertical también ha desplazado 3 unidades a la izquierda de su posición original (el eje y) y ahora tiene la ecuación x = −3. Por tradición, dibujamos la asíntota vertical como una línea discontinua.
Si restamos 4 del resultado en la Figura\(\PageIndex{6}\) (a), esto desplazará la gráfica de la Figura\(\PageIndex{6}\) (a) cuatro unidades hacia abajo para producir la gráfica mostrada en la Figura\(\PageIndex{6}\) (b). Tenga en cuenta que la asíntota horizontal también desplazó 4 unidades hacia abajo desde su posición original (el eje x) y ahora tiene la ecuación y = −4.
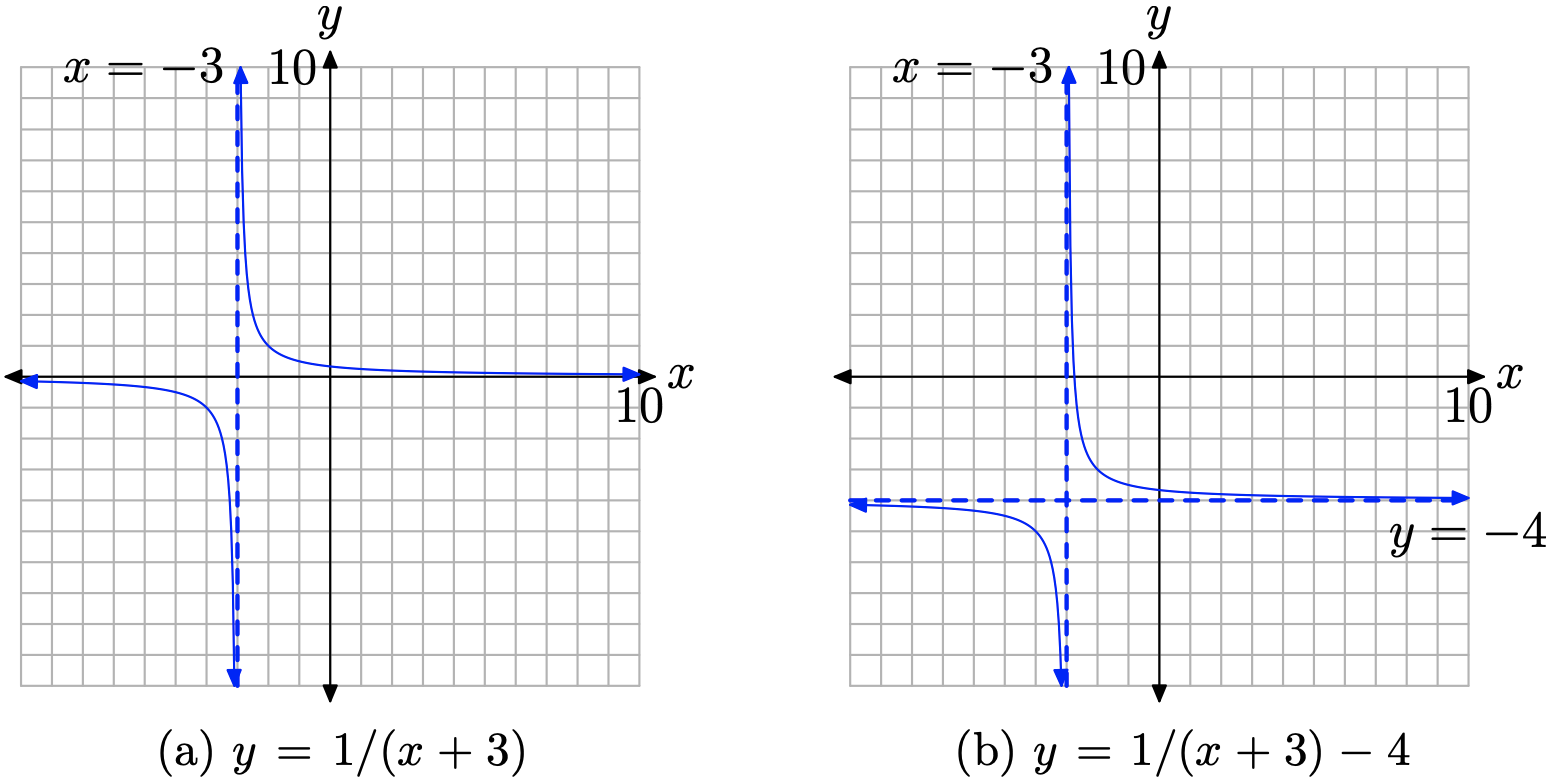
Si examina la ecuación (11), observa que no puede usar x = −3 ya que esto hará que el denominador de la ecuación (11) sea igual a cero. En la Figura\(\PageIndex{6}\) (b), observe que hay una asíntota vertical en la gráfica de la ecuación (11) a x = −3. Esta es una ocurrencia común, que será un tema central de este capítulo.
Hagamos otra pregunta clave.
Ejemplo\(\PageIndex{2}\)
¿Cuáles son el dominio y el rango de la función racional que se presenta en Ejemplo\(\PageIndex{1}\)?
Solución
Puedes echarle un vistazo a la ecuación
\[y=\frac{1}{x+3}-4\nonumber\]
de Ejemplo\(\PageIndex{1}\) y tenga en cuenta que x = −3 hace que el denominador sea cero y debe ser excluido del dominio. De ahí que el dominio de esta función sea\(D=\{x : x \neq-3\}\).
Sin embargo, también se puede determinar el dominio examinando la gráfica de la función en la Figura\(\PageIndex{6}\) (b). Tenga en cuenta que la gráfica se extiende indefinidamente hacia la izquierda y hacia la derecha. Primero se podría adivinar que el dominio es todo números reales si no fuera por la asíntota vertical en x = −3 interrumpiendo la continuidad de la gráfica. Debido a que la gráfica de la función se acerca arbitrariamente a esta asíntota vertical (a cada lado) sin tocar realmente la asíntota, la gráfica no contiene un punto que tenga un valor x igual a −3. De ahí que el dominio sea el anterior,\(D=\{x : x \neq-3\}\). Esto es reconfortante que el análisis gráfico concuerda con nuestra determinación analítica anterior del dominio.
El gráfico es especialmente útil para determinar el rango de la función. Tenga en cuenta que la gráfica sube al infinito positivo y cae al infinito negativo. Primero se adivinaría que el rango es todo números reales si no fuera por la asíntota horizontal en y = −4 interrumpiendo la continuidad de la gráfica. Debido a que la gráfica se acerca arbitrariamente a la asíntota horizontal (a cada lado) sin tocar realmente la asíntota, la gráfica no contiene un punto que tenga un valor y igual a −4. Por lo tanto, −4 se excluye del rango. Es decir,\(R=\{y : y \neq-4\}\).
Escalado y Reflexión
En esta sección, escalaremos y reflejaremos la gráfica de y = 1/x Para medida extra, también lanzamos traducciones en las direcciones horizontal y vertical.
Ejemplo\(\PageIndex{3}\)
Esbozar el gráfico de\[y=-\frac{2}{x-4}+3\nonumber\]
Solución
Primero, multiplicamos la ecuación y = 1/x por −2 para obtener
\[y=-\frac{2}{x}\nonumber\]
Al multiplicar por 2 se debe estirar la gráfica en las direcciones verticales (tanto positiva como negativa) por un factor de 2. Tenga en cuenta que los puntos que están muy cerca del eje x, cuando se duplican, no van a desviarse demasiado del eje x, por lo que la asíntota horizontal seguirá siendo la misma. Finalmente, multiplicar por −2 no solo estirará la gráfica, sino que también reflejará la gráfica a través del eje x, como se muestra en la Figura\(\PageIndex{7}\) (b).
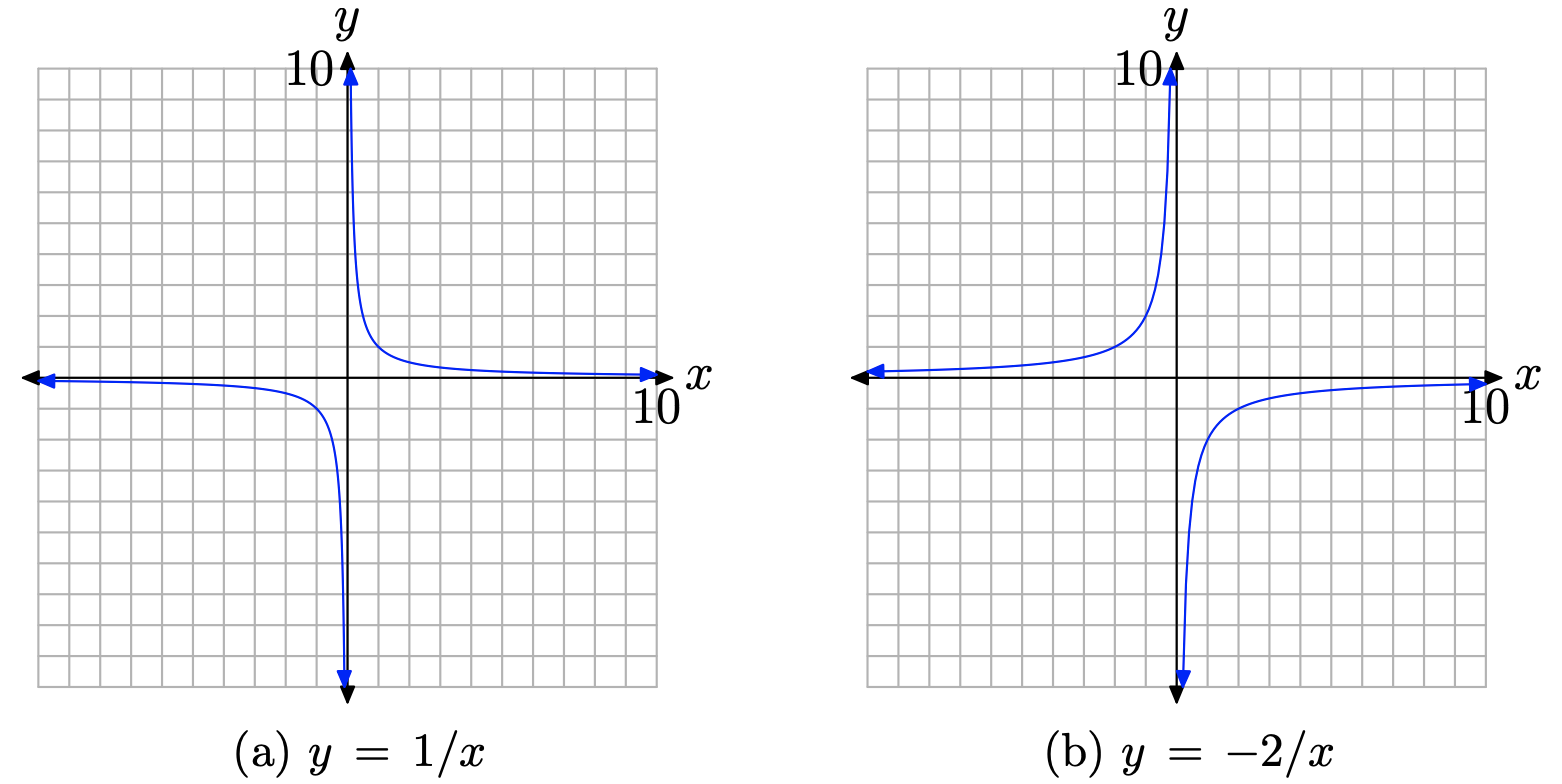
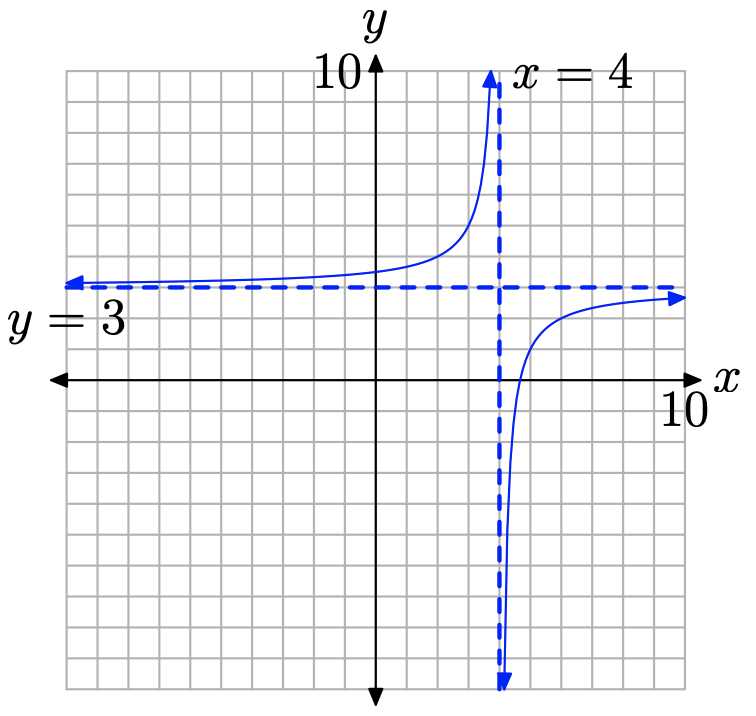
Reemplazar x por x − 4 desplazará la gráfica 4 unidades hacia la derecha, luego agregando 3 desplazará la gráfica 3 unidades hacia arriba, como se muestra en la Figura\(\PageIndex{8}\). Observe nuevamente que x = 4 hace que el denominador de y = −2/ (x − 4) + 3 sea igual a cero y hay una asíntota vertical en x = 4. El dominio de esta función es\(D=\{x : x \neq 4\}\).
A medida que x se acerca al infinito positivo o negativo, los puntos en la gráfica de y = −2/ (x−4) + 3 se acercan arbitrariamente a la asíntota horizontal y = 3 pero nunca la tocan. Por lo tanto, no hay ningún punto en la gráfica que tenga un valor y de 3. Así, el rango de la función es el conjunto\(R=\{y : y \neq 3\}\).
Dificultades con la Calculadora Gráfica
La calculadora gráfica hace un muy buen trabajo dibujando los gráficos de “funciones continuas”.
Una función continua es aquella que se puede dibujar en un trazo continuo, nunca levantando pluma o lápiz del papel durante el dibujo.
Los polinomios, como el de la Figura\(\PageIndex{9}\), son funciones continuas.
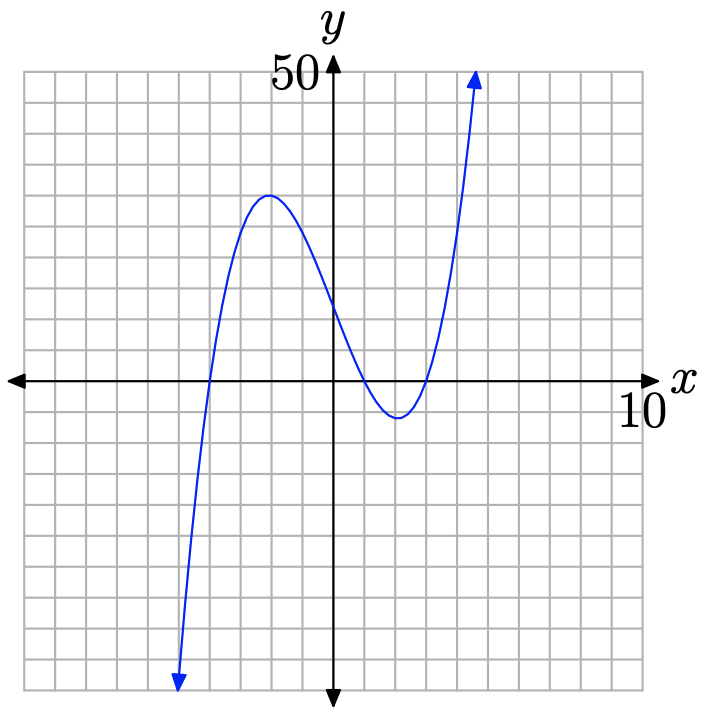
Desafortunadamente, una función racional con asíntota (s) vertical (s) no es una función continua. Primero, hay que levantar la pluma en puntos donde el denominador es cero, porque la función no está definida en estos puntos. En segundo lugar, no es raro tener que saltar del infinito positivo al infinito negativo (o viceversa) al cruzar una asíntota vertical. Cuando esto sucede, tenemos que levantar nuestro bolígrafo y cambiarlo antes de continuar con nuestro dibujo.
Sin embargo, la calculadora gráfica no sabe cómo hacer este “levantamiento” de la pluma cerca de asíntotas verticales. La calculadora gráfica solo conoce una técnica, traza un punto, luego lo conecta con un segmento al último punto trazado, mueve una distancia incremental y repite. En consecuencia, cuando la calculadora gráfica cruza una asíntota vertical donde hay un desplazamiento de un tipo de infinito a otro (por ejemplo, de positivo a negativo), la calculadora dibuja una “línea falsa” de conexión, una que no debe dibujar. Demostremos esta aberración con un ejemplo.
Ejemplo\(\PageIndex{4}\)
Utilice una calculadora gráfica para dibujar la gráfica de la función racional en Ejemplo\(\PageIndex{3}\).
Solución
Cargue la ecuación en su calculadora, como se muestra en la Figura\(\PageIndex{10}\) (a). Ajuste la ventana como se muestra en la Figura\(\PageIndex{10}\) (b), luego presione el botón GRAPADO para dibujar la gráfica que se muestra en la Figura\(\PageIndex{10}\) (c). Los resultados pueden diferir en algunas calculadoras, pero en nuestro caso, anotar la “línea falsa” dibujada desde la parte superior de la pantalla hasta la parte inferior, intentando “conectar” las dos ramas de la hipérbola.
Algunos podrían regocijarse y afirmar: “Oye, mi calculadora gráfica dibuja asíntotas verticales”. Sin embargo, antes de que te excites demasiado, ten en cuenta que en\(\PageIndex{8}\) la Figura la asíntota vertical debe ocurrir exactamente en x = 4. Si miras con mucho cuidado la “línea vertical” de la Figura\(\PageIndex{10}\) (c), notará que simplemente pierde la marca de graduación en x = 4. Esta “línea vertical” es una línea que la calculadora no debe dibujar. La calculadora está intentando dibujar una función continua donde no existe.

Una posible solución alternativa es presionar el botón MODE en su teclado, que abre el menú que se muestra en la Figura\(\PageIndex{11}\) (a). Usa las teclas de flecha para resaltar DOT en lugar de CONECTADO y presiona la tecla ENTER para hacer la selección permanente. Pulse el botón GRAPAR para dibujar la gráfica en la Figura\(\PageIndex{11}\) (b).
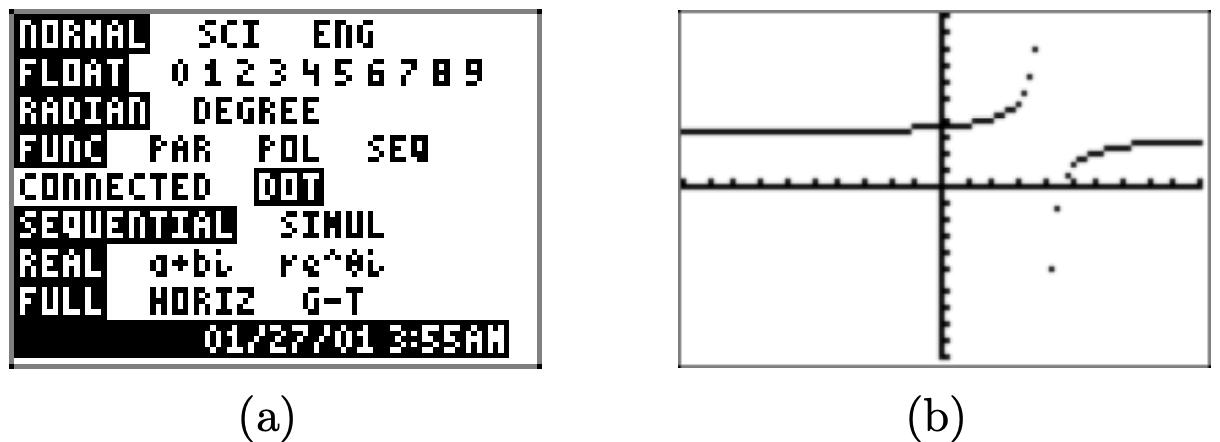
Este “modo punto” en tu calculadora calcula el siguiente punto en la gráfica y traza el punto, pero no lo conecta con un segmento de línea al punto previamente trazado. Este modo es útil para demostrar que la línea vertical en la Figura\(\PageIndex{10}\) (c) no es realmente parte de la gráfica, pero perdemos algunas partes de la gráfica que realmente nos gustaría ver. El compromiso está en orden.
Este ejemplo muestra claramente que el uso inteligente de la calculadora es un componente requerido de este curso. La calculadora no es simplemente una “caja negra” que automáticamente hace lo que quieres que haga. En particular, cuando se están dibujando funciones racionales, ayuda conocer con anticipación la colocación de las asíntotas verticales. El conocimiento de las asíntotas, aunado a lo que ve en la pantalla de su calculadora, debería permitirle dibujar una gráfica tan precisa como la que se muestra en la Figura\(\PageIndex{8}\).
Recordatorio suave. Querrás volver a configurar tu calculadora en “modo conectado”. Para ello, presiona el botón MODE de tu teclado para volver a abrir el menú de la Figura\(\PageIndex{10}\) (a). Usa tus teclas de flecha para resaltar CONNECTED, luego presiona la tecla ENTRAR para que la selección sea permanente.
Ejercicio
En los Ejercicios 1 - 14, realizar cada una de las siguientes tareas para la función racional dada.
- Configure un sistema de coordenadas en una hoja de papel cuadriculado. Etiquetar y escalar cada eje.
- Utilice transformaciones geométricas como en los Ejemplos 10, 12 y 13 para dibujar las gráficas de cada una de las siguientes funciones racionales. Dibuja las asíntotas verticales y horizontales como líneas discontinuas y etiquete cada una con su ecuación. Puede usar su calculadora para verificar su solución, pero debería poder dibujar la función racional sin el uso de una calculadora.
- Utilice la notación set-builder para describir el dominio y el rango de la función racional dada.
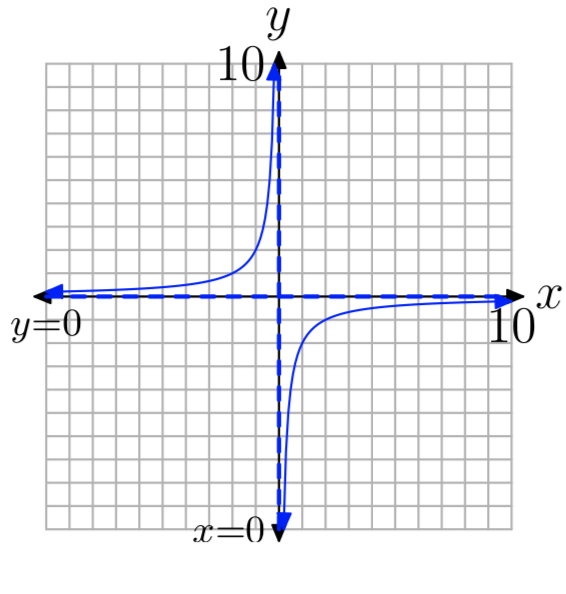
Ejercicio\(\PageIndex{1}\)
\(f(x) = −\frac{2}{x}\)
- Contestar
-
D = {x:\(x \ne 0\)}, R = {y:\(y \ne 0\)}
Ejercicio\(\PageIndex{2}\)
\(f(x) = \frac{3}{x}\)
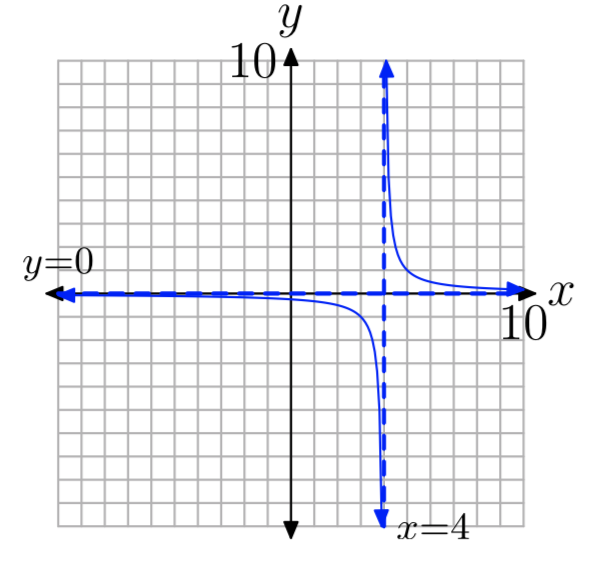
Ejercicio\(\PageIndex{3}\)
\(f(x) = \frac{1}{x−4}\)
- Contestar
-
D = {x:\(x \ne 4\)}, R = {y:\(y \ne 0\)}
Ejercicio\(\PageIndex{4}\)
\(f(x) = \frac{1}{x+3}\)
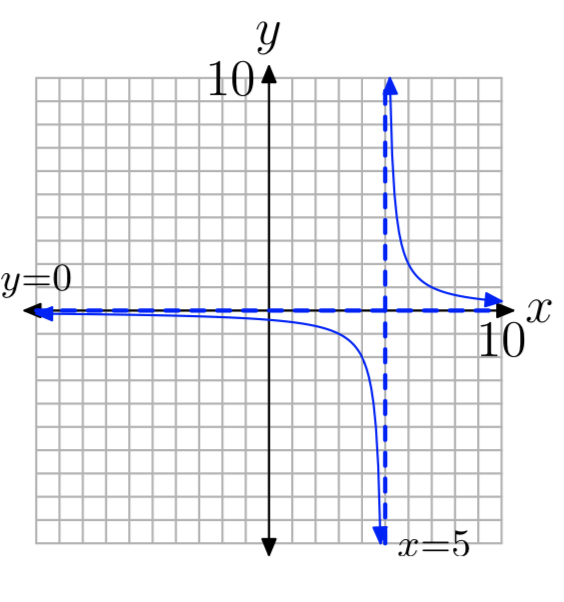
Ejercicio\(\PageIndex{5}\)
\(f(x) = \frac{2}{x−5}\)
- Contestar
-
D = {x:\(x \ne 5\)}, R = {y:\(y \ne 0\)}
Ejercicio\(\PageIndex{6}\)
\(f(x) = −\frac{3}{x+6}\)
Ejercicio\(\PageIndex{7}\)
\(f(x) = \frac{1}{x}−2\)
- Contestar
-
D = {x:\(x \ne 0\)}, R = {y:\(y \ne −2\)}
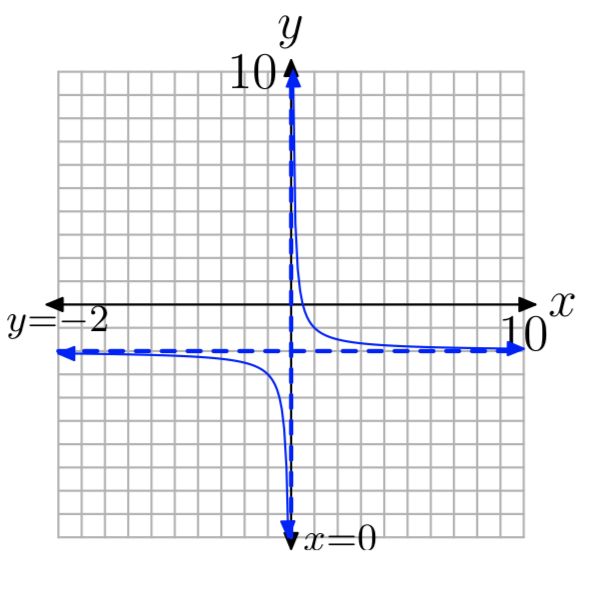
Ejercicio\(\PageIndex{8}\)
\(f(x) = −\frac{1}{x}+4\)
Ejercicio\(\PageIndex{9}\)
\(f(x) = −\frac{2}{x}−5\)
- Contestar
-
D = {x:\(x \ne 0\)}, R = {y:\(y \ne −5\)}
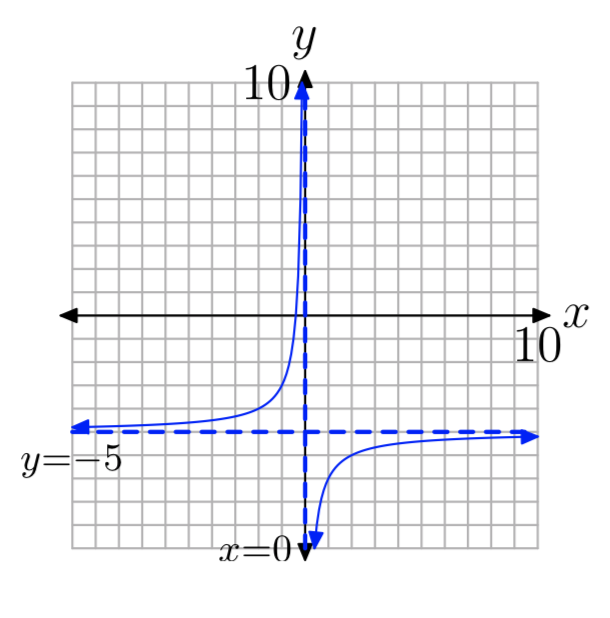
Ejercicio\(\PageIndex{10}\)
\(f(x) = \frac{3}{x}−5\)
Ejercicio\(\PageIndex{11}\)
\(f(x) = \frac{1}{x−2}−3\)
- Contestar
-
D = {x:\(x \ne 2\)}, R = {y:\(y \ne −3\)}
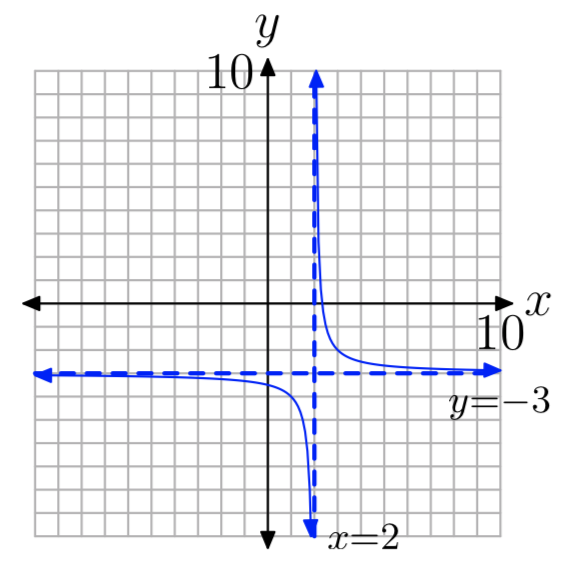
Ejercicio\(\PageIndex{12}\)
\(f(x) = −\frac{1}{x+1}+5\)
Ejercicio\(\PageIndex{13}\)
\(f(x) = −\frac{2}{x−3}−4\)
- Contestar
-
D = {x:\(x \ne 3\)}, R = {y:\(y \ne −4\)}
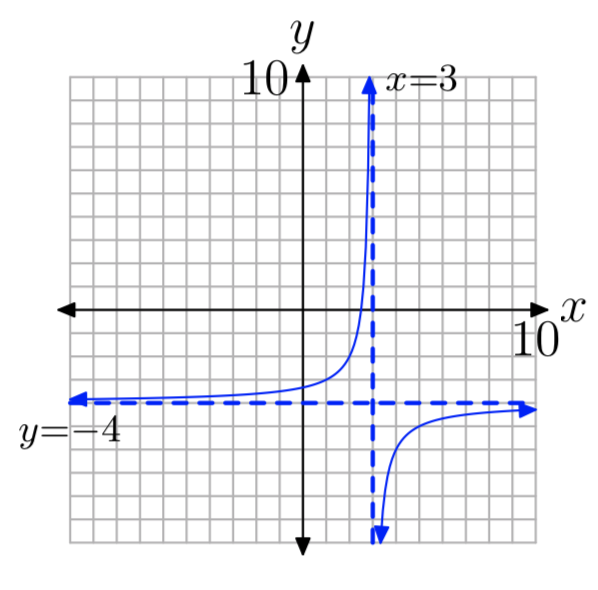
Ejercicio\(\PageIndex{14}\)
\(f(x) = \frac{3}{x+5}−2\)
En los Ejercicios 15 - 22, encuentra todos los verticales como ymptotes, en su caso, de la gráfica de la función dada.
Ejercicio\(\PageIndex{15}\)
\(f(x) = −\frac{5}{x+1}−3\)
- Contestar
-
Asymptota vertical: x = −1
Ejercicio\(\PageIndex{16}\)
\(f(x) = \frac{6}{x+8}+2\)
Ejercicio\(\PageIndex{17}\)
\(f(x) = −\frac{9}{x+2}−6\)
- Contestar
-
Asymptota vertical: x = −2
Ejercicio\(\PageIndex{18}\)
\(f(x) = −\frac{8}{x−4}−5\)
Ejercicio\(\PageIndex{19}\)
\(f(x) = \frac{2}{x+5}+1\)
- Contestar
-
Asymptota vertical: x = −5
Ejercicio\(\PageIndex{20}\)
\(f(x) = −\frac{3}{x+9}+2\)
Ejercicio\(\PageIndex{21}\)
\(f(x) = \frac{7}{x+8}−9\)
- Contestar
-
Asymptota vertical: x = −8
Ejercicio\(\PageIndex{22}\)
\(f(x) = \frac{6}{x−5}−8\)
En los Ejercicios 23 - 30, encuentra todas las asíntotas horizontales, en su caso, de la gráfica de la función dada.
Ejercicio\(\PageIndex{23}\)
\(f(x) = \frac{5}{x+7}+9\)
- Contestar
-
Aíntota horizontal: y = 9
Ejercicio\(\PageIndex{24}\)
\(f(x) = −\frac{8}{x+7}−4\)
Ejercicio\(\PageIndex{25}\)
\(f(x) = \frac{8}{x+5}−1\)
- Contestar
- Asymptota horizontal: y = −1
Ejercicio\(\PageIndex{26}\)
\(f(x) = −\frac{2}{x+3}+8\)
Ejercicio\(\PageIndex{27}\)
\(f(x) = \frac{7}{x+1}−9\)
- Contestar
-
Asymptota horizontal: y = −9
Ejercicio\(\PageIndex{28}\)
\(f(x) = −\frac{2}{x−1}+5\)
Ejercicio\(\PageIndex{29}\)
\(f(x) = \frac{5}{x+2}−4\)
- Contestar
-
Asymptota horizontal: y = −4
Ejercicio\(\PageIndex{30}\)
\(f(x) = −\frac{6}{x−1}−2\)
En los Ejercicios 31 - 38, indique el dominio de la función racional dada utilizando la notación set-builder.
Ejercicio\(\PageIndex{31}\)
\(f(x) = −\frac{4}{x+5}+5\)
- Contestar
-
Dominio = {x:\(x \ne −5\)}
Ejercicio\(\PageIndex{32}\)
\(f(x) = −\frac{7}{x−6}+1\)
Ejercicio\(\PageIndex{33}\)
\(f(x) = \frac{6}{x−5}+1\)
- Contestar
-
Dominio = {x:\(x \ne 5\)}
Ejercicio\(\PageIndex{34}\)
\(f(x) = −\frac{5}{x−3}−9\)
Ejercicio\(\PageIndex{35}\)
\(f(x) = \frac{1}{x+7}+2\)
- Contestar
-
Dominio = {x:\(x \ne −7\)}
Ejercicio\(\PageIndex{36}\)
\(f(x) = −\frac{2}{x−5}+4\)
Ejercicio\(\PageIndex{37}\)
\(f(x) = −\frac{4}{x+2}+2\)
- Contestar
-
Dominio = {x:\(x \ne −2\)}
Ejercicio\(\PageIndex{38}\)
\(f(x) = \frac{2}{x+6}+9\)
En Ejercicios 39 - 46, encuentra el rango de la función dada, y expresa tu respuesta en notación fija.
Ejercicio\(\PageIndex{39}\)
\(f(x) = \frac{2}{x−3}+8\)
- Contestar
-
Rango = {y:\(y \ne 8\)}
Ejercicio\(\PageIndex{40}\)
\(f(x) = \frac{4}{x−3}+5\)
Ejercicio\(\PageIndex{41}\)
\(f(x) = −\frac{5}{x−8}−5\)
- Contestar
-
Rango = {y:\(y \ne −5\)}
Ejercicio\(\PageIndex{42}\)
\(f(x) = −\frac{2}{x+1}+6\)
Ejercicio\(\PageIndex{43}\)
\(f(x) = \frac{7}{x+7}+5\)
- Contestar
-
Rango = {y:\(y \ne 5\)}
Ejercicio\(\PageIndex{44}\)
\(f(x) = −\frac{8}{x+3}+9\)
Ejercicio\(\PageIndex{45}\)
\(f(x) = \frac{4}{x+3}−2\)
- Contestar
-
Rango = {y:\(y \ne −2\)}
Ejercicio\(\PageIndex{46}\)
\(f(x) = −\frac{5}{x−4}+9\)


