7.6: Fracciones Complejas

En esta sección aprendemos a simplificar lo que se llaman fracciones complejas, de lo que sigue un ejemplo.

\[\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}}\]

Tenga en cuenta que tanto el numerador como el denominador son problemas de fracción por derecho propio, dando crédito a por qué nos referimos a tal estructura como una “fracción compleja”.

Existen dos técnicas muy diferentes que podemos utilizar para simplificar la fracción compleja (1). La primera técnica es una elección “natural”.

Simplificación de Fracciones Complejas — Primera Técnica

Para simplificar una fracción compleja, proceda de la siguiente manera:

1. Simplifica el numerador.
2. Simplifica el denominador.
3. Simplifica el problema de división que queda.

Sigamos este esquema para simplificar la fracción compleja (1). Primero, sumar las fracciones en el numerador de la siguiente manera.

\[\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{3}{6}+\dfrac{2}{6}=\dfrac{5}{6}\]

En segundo lugar, sumar las fracciones en el denominador de la siguiente manera.

\[\dfrac{1}{4}+\dfrac{2}{3}=\dfrac{3}{12}+\dfrac{8}{12}=\dfrac{11}{12}\]

Sustituir los resultados de (2) y (3) en el numerador y denominador de (1), respectivamente.

\[\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}}=\dfrac{\dfrac{5}{6}}{\dfrac{11}{12}}\]

El lado derecho de (4) es equivalente a

\[\dfrac{5}{6} \div \dfrac{11}{12}\]

Esto es un problema de división, entonces invertir y multiplicar, faccionar, luego cancelar factores comunes.

\[\begin{aligned} \dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}} &=\dfrac{5}{6} \cdot \dfrac{12}{11} \\ &=\dfrac{5}{2 \cdot 3} \cdot \dfrac{2 \cdot 2 \cdot 3}{11} \\ &=\dfrac{5}{\not{2} \cdot \not{3}} \cdot \dfrac{\not{2} \cdot 2 \cdot \not{3}}{11} \\ &=\dfrac{10}{11} \end{aligned}\]

Aquí se presenta un arreglo de la obra, de principio a fin, presentada sin comentarios. Esta es una buena plantilla para emular a la hora de hacer tu tarea.

\[\begin{aligned} \dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}} &=\dfrac{\dfrac{3}{6}+\dfrac{2}{6}}{\dfrac{3}{12}+\dfrac{8}{12}} \\ &=\dfrac{\dfrac{5}{6}}{\dfrac{11}{12}} \\ &=\dfrac{5}{6} \cdot \dfrac{12}{11} \\ &=\dfrac{5}{2 \cdot 3} \cdot \dfrac{2 \cdot 2 \cdot 3}{11}\\ &=\dfrac{5}{\not{2} \cdot \not{3}} \cdot \dfrac{\not{2} \cdot 2 \cdot \not{3}}{11} \\ &=\dfrac{10}{11} \end{aligned}\]

Ahora, veamos una segunda aproximación al problema. Vimos que simplificar el numerador en (2) requería un denominador común de 6. Simplificar el denominador en (3) requería un denominador común de 12. Entonces, escojamos otro denominador común, éste un denominador común tanto para el numerador como para el denominador, es decir, 12. Ahora, multiplique la parte superior e inferior (numerador y denominador) de la fracción compleja (1) por 12, de la siguiente manera.

\[\dfrac{\dfrac{1}{2}+\dfrac{1}{3}}{\dfrac{1}{4}+\dfrac{2}{3}}=\dfrac{\left(\dfrac{1}{2}+\dfrac{1}{3}\right) \color{blue}{12}}{\left(\dfrac{1}{4}+\dfrac{2}{3}\right) \color{blue}{12}}\]

Distribuir el 12 tanto en numerador como denominador y simplificar.

\[\dfrac{\left(\dfrac{1}{2}+\dfrac{1}{3}\right) \color{blue}{12}}{\left(\dfrac{1}{4}+\dfrac{2}{3}\right) \color{blue}{12}}=\dfrac{\left(\dfrac{1}{2}\right) \color{blue}{12}+\left(\dfrac{1}{3}\right) \color{blue}{12}}{\left(\dfrac{1}{4}\right) \color{blue}{12}+\left(\dfrac{2}{3}\right) \color{blue}{12}}=\dfrac{6+4}{3+8}=\dfrac{10}{11}\]

Resumimos esta segunda técnica.

Simplificación de Fracciones Complejas — Segunda Técnica

Para simplificar una fracción compleja, proceda de la siguiente manera:

1. Encuentra un denominador común tanto para el numerador como para el denominador.
2. Borrar fracciones del numerador y denominador multiplicando cada una por el denominador común que se encuentra en el primer paso.

Tenga en cuenta que para este problema en particular, el segundo método es mucho más eficiente. Ahorra espacio y tiempo y es más estéticamente agradable. Es la técnica que vamos a favorecer en el resto de esta sección.

Veamos otro ejemplo.

Ejemplo\(\PageIndex{1}\)

Utilice tanto la Primera como la Segunda Técnicas para simplificar la expresión\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}\] Estado todas las restricciones.

Solución

Usemos la primera técnica, simplificando el numerador y el denominador por separado antes de dividirlos. Primero, hacer fracciones equivalentes con denominador común para el problema de resta en el numerador de (7) y simplificar. Haz lo mismo para el denominador.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=\dfrac{\dfrac{1}{x}-\dfrac{x}{x}}{\dfrac{x^{2}}{x^{2}}-\dfrac{1}{x^{2}}}=\dfrac{\dfrac{1-x}{x}}{\dfrac{x^{2}-1}{x^{2}}}\]

A continuación, invertir y multiplicar, luego factorial.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=\dfrac{1-x}{x} \cdot \dfrac{x^{2}}{x^{2}-1}=\dfrac{1-x}{x} \cdot \dfrac{x^{2}}{(x+1)(x-1)}\]

Invoquemos la regla de cambio de signo y negemos dos partes de la fracción (1 − x) /x, el numerador y la barra de fracciones, luego cancelemos los factores comunes.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x-1}{x} \cdot \dfrac{x^{2}}{(x+1)(x-1)}=-\dfrac{x-1}{\not{x}} \cdot \dfrac{x \not{x}}{(x+1)(x-1)}\]

Por lo tanto,

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x}{x+1}\]

Ahora, probemos el problema por segunda vez, multiplicando el numerador y el denominador por\(x^2\) para borrar fracciones tanto del numerador como del denominador.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=\dfrac{\left(\dfrac{1}{x}-1\right) \color{blue}{x^{2}}}{\left(1-\dfrac{1}{x^{2}}\right)\color{blue}{x^{2}}}=\dfrac{\left(\dfrac{1}{x}\right) \color{blue}{x^{2}}-(1) \color{blue}{x^{2}}}{(1) \color{blue}{x^{2}}-\left(\dfrac{1}{x^{2}}\right) \color{blue}{x^{2}}}=\dfrac{x-x^{2}}{x^{2}-1}\]

El orden en el numerador de la última fracción intima que sería útil un cambio de signo. Nigue el numerador y la barra de fracción, factor, luego cancele los factores comunes.

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x^{2}-x}{x^{2}-1}=-\dfrac{x(x-1)}{(x+1)(x-1)}=-\dfrac{x(x-1)}{(x+1)(x-1)}=-\dfrac{x}{x+1}\]

Esta es precisamente la misma respuesta que se encontró con la primera técnica. Para enumerar las restricciones, debemos asegurarnos de que ningún valor de x haga que ningún denominador sea igual a cero, al inicio del problema, en el cuerpo de nuestro trabajo, o en la respuesta final.

En el problema original, si x = 0, entonces tanto 1/x como\(1/x^{2}\) están indefinidos, entonces x = 0 es una restricción. En el cuerpo de nuestro trabajo, los factores x + 1 y x − 1 encontrados en diversos denominadores hacen restricciones x = −1 y x = 1. Ningún otro denominador suministra restricciones que aún no hayan sido listadas. Por lo tanto, para todas las x que no sean −1, 0 y 1, el lado izquierdo de

\[\dfrac{\dfrac{1}{x}-1}{1-\dfrac{1}{x^{2}}}=-\dfrac{x}{x+1}\]

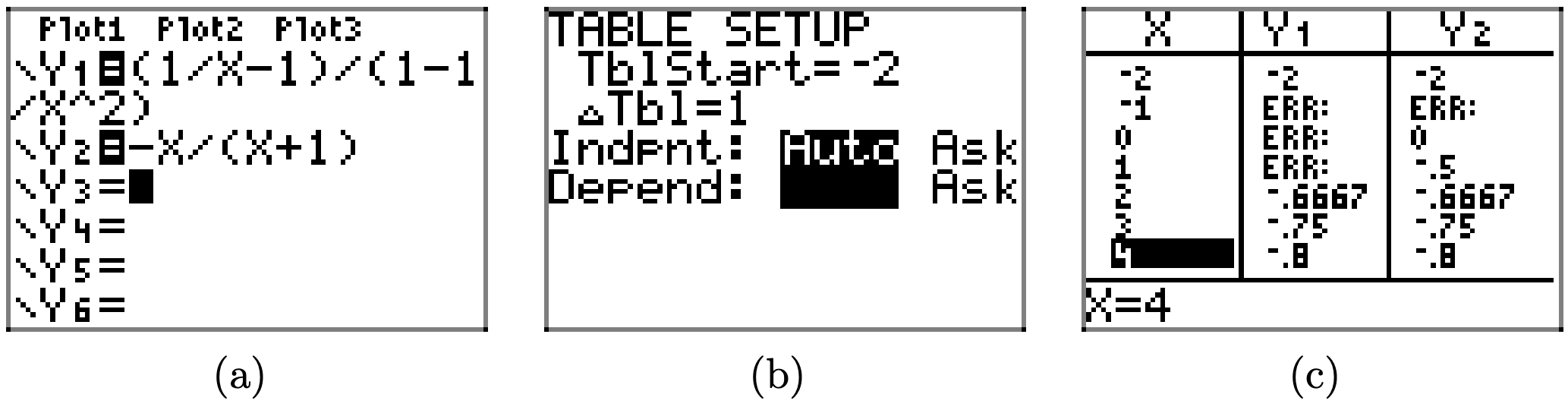
es idéntico al lado derecho. Nuevamente, la utilidad de tabla de la calculadora proporciona amplia evidencia de este hecho en las capturas de pantalla que se muestran en la Figura\(\PageIndex{1}\).

Anote los mensajes ERR (error) en cada uno de los valores restringidos de x, pero también anote el acuerdo perfecto de Y1 e Y2 en todos los demás valores de x.

Veamos otro ejemplo, un ejemplo importante que involucra la notación de funciones.

Figura\(\PageIndex{1}\). Usando la función de tabla de la calculadora gráfica para verificar la identidad en (8).

Ejemplo\(\PageIndex{2}\)

Ante eso\[f(x)=\dfrac{1}{x}\], simplificar la expresión\[\dfrac{f(x)-f(2)}{x-2}\]. Enumere todas las restricciones.

Solución

Recuerda, f (2) significa sustituir 2 por x. Porque f (x) = 1/x, sabemos que f (2) = 1/2, entonces

\[\dfrac{f(x)-f(2)}{x-2}=\dfrac{\dfrac{1}{x}-\dfrac{1}{2}}{x-2}\]

Para borrar las fracciones del numerador, usaríamos un denominador común de 2x. No hay fracciones en el denominador que necesiten aclaramiento, por lo que el denominador común para numerador y denominador es 2x. Multiplica el numerador y el denominador por 2x.

\[\dfrac{f(x)-f(2)}{x-2}=\dfrac{\left(\dfrac{1}{x}-\dfrac{1}{2}\right) \color{blue}{2x}}{(x-2) \color{blue}{2x}}=\dfrac{\left(\dfrac{1}{x}\right) \color{blue}{2x}-\left(\dfrac{1}{2}\right) \color{blue}{2x}}{(x-2) \color{blue}{2x}}=\dfrac{2-x}{2 x(x-2)}\]

Nigue el numerador y la barra de fracciones, luego cancele los factores comunes.

\[\dfrac{f(x)-f(2)}{x-2}=-\dfrac{x-2}{2 x(x-2)}=-\dfrac{x-2}{2 x(x-2)}=-\dfrac{1}{2 x}\]

En el problema original, tenemos un denominador de x − 2, entonces x = 2 es una restricción. Si el cuerpo de nuestro trabajo, hay una fracción 1/x, que es indefinida cuando x = 0, entonces x = 0 también es una restricción. Los denominadores restantes no ofrecen otras restricciones. Por lo tanto, para todos los valores de x excepto 0 y 2, el lado izquierdo de

\[\dfrac{f(x)-f(2)}{x-2}=-\dfrac{1}{2 x}\]

es idéntico al lado derecho.

Veamos otro ejemplo que involucra la notación de funciones.

Ejemplo\(\PageIndex{3}\)

Dado\[f(x)=\dfrac{1}{x^{2}}\], simplifique la expresión\[\dfrac{f(x+h)-f(x)}{h}\] Listar todas las restricciones.

Solución

La notación de función f (x + h) nos está pidiendo reemplazar cada instancia de x en la fórmula 1\(/ x^{2}\) por x + h\(f(x+h)=1 /(x+h)^{2}\).

Aquí hay otra forma de pensar en esta sustitución. Supongamos que eliminamos la x de

\[f(x)=\dfrac{1}{x^{2}}\]

para que se lea

\[f( \space)=\dfrac{1}{( \space)^{2}}\]

Ahora, si quieres calcular f (2), simplemente inserta un 2 en el área en blanco entre paréntesis. En nuestro caso, queremos calcular f (x + h), así que insertamos una x + h en el espacio en blanco entre paréntesis en (12) para obtener

\[f(x+h)=\dfrac{1}{(x+h)^{2}}\]

Con estas observaciones preliminares en mente, volvamos al problema. Primero, interpretamos la notación de funciones como en nuestras observaciones preliminares y escribimos

\[\dfrac{f(x+h)-f(x)}{h}=\dfrac{\\(\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{x^{2}-\left(x^{2}+2 x h+h^{2}\right)}{h x^{2}(x+h)^{2}} \\ &=\dfrac{x^{2}-x^{2}-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \\ &=\dfrac{-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \end{aligned}\)frac{1}{(x+h)^{2}}-\dfrac{1}{x^{2}}}{h}\]

El denominador común para el numerador se encuentra enumerando cada factor a la potencia más alta que ocurra. De ahí que el denominador común sea\(x^{2}(x+h)^{2}\). El denominador no tiene fracciones para ser limpiado, por lo que basta multiplicar tanto el numerador como el denominador por\(x^{2}(x+h)^{2}\).

\[\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{\left(\dfrac{1}{(x+h)^{2}}-\dfrac{1}{x^{2}}\right) \color{blue}{x^{2}(x+h)^{2}}}{h \color{blue}{x^{2}(x+h)^{2}}} \\ &=\dfrac{\left(\dfrac{1}{(x+h)^{2}}\right) \color{blue}{x^{2}(x+h)^{2}}-\left(\dfrac{1}{x^{2}}\right) \color{blue}{x^{2}(x+h)^{2}}}{h \color{blue}{x^{2}(x+h)^{2}}} \\ &=\dfrac{x^{2}-(x+h)^{2}}{h x^{2}(x+h)^{2}} \end{aligned}\]

Ahora ampliaremos el numerador. No olvides usar paréntesis y distribuir ese signo menos.

\[\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{x^{2}-\left(x^{2}+2 x h+h^{2}\right)}{h x^{2}(x+h)^{2}} \\ &=\dfrac{x^{2}-x^{2}-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \\ &=\dfrac{-2 x h-h^{2}}{h x^{2}(x+h)^{2}} \end{aligned}\]

Finalmente, factor a −h fuera del numerador con la esperanza de encontrar un factor común para cancelar.

\[\begin{aligned} \dfrac{f(x+h)-f(x)}{h} &=\dfrac{-h(2 x+h)}{h x^{2}(x+h)^{2}} \\ &=\dfrac{-\not{h}(2 x+h)}{\not{h} x^{2}(x+h)^{2}} \\ &=\dfrac{-(2 x+h)}{x^{2}(x+h)^{2}} \end{aligned}\]

Ahora debemos discutir las restricciones. En la pregunta original (11), la h en el denominador no debe ser igual a cero. De ahí que h = 0 sea una restricción. En la forma simplificada final, el factor de\(x^{2}\) en el denominador es indefinido si x = 0. De ahí que x = 0 sea una restricción. Finalmente, el factor de\((x+h)^{2}\) en el denominador final es indefinido si x+h = 0, entonces x = −h es una restricción. Los denominadores restantes no proporcionan restricciones adicionales. Por lo tanto, siempre\(h \neq 0, x \neq 0,\) y\(x \neq-h\), para todas las demás combinaciones de x y h, el lado izquierdo de

\[\dfrac{f(x+h)-f(x)}{h}=\dfrac{-(2 x+h)}{x^{2}(x+h)^{2}}\]

es idéntico al lado derecho.

Veamos un ejemplo final usando la notación de funciones.

Ejemplo\(\PageIndex{4}\)

Si\[f(x)=\dfrac{x}{x+1}\] simplificar f (f (x)).

Solución

Primero evaluamos f en x, luego evaluamos f en el resultado del primer cálculo. Así, trabajamos primero la función interna para obtener

\[f(f(x))=f\left(\dfrac{x}{x+1}\right)\]

La notación f (x/ (x + 1)) nos está pidiendo reemplazar cada ocurrencia de x en la fórmula x/ (x + 1) con la expresión x/ (x + 1). ¿Confundir? Aquí hay una manera fácil de pensar en esta sustitución. Supongamos que eliminamos x de

\[f(x)=\dfrac{x}{x+1}\]

reemplazar cada aparición de x con paréntesis vacíos, lo que producirá la plantilla

\[f(\space )=\dfrac{( \space)}{( \space)+1}\]

Ahora, si se le pide que calme f (3), simplemente inserte 3 en las áreas en blanco entre paréntesis. En este caso, queremos calcular f (x/ (x+ 1)), así insertamos x/ (x+ 1) en el espacio en blanco entre cada conjunto de paréntesis en (15) para obtener

\[f\left(\dfrac{x}{x+1}\right)=\dfrac{\dfrac{x}{x+1}}{\dfrac{x}{x+1}+1}\]

Ahora tenemos una fracción compleja. El denominador común tanto para arriba como para abajo de esta fracción compleja es x + 1. Así, multiplicamos tanto el numerador como el denominador de nuestra fracción compleja por x + 1 y usamos la propiedad distributiva de la siguiente manera.

\[\dfrac{\dfrac{x}{x+1}}{\dfrac{x}{x+1}+1}=\dfrac{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}}{\left(\dfrac{x}{x+1}+1\right)\color{blue}{(x+1)}}=\dfrac{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}}{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}+(1)\color{blue}{(x+1)}}\]

Cancele y simplifique.

\[\dfrac{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}}{\left(\dfrac{x}{x+1}\right)\color{blue}{(x+1)}+(1)\color{blue}{(x+1)}}=\dfrac{x}{x+(x+1)}=\dfrac{x}{2 x+1}\]

En el denominador final, el valor x = −1/2 hace que el denominador 2x + 1 sea igual a cero. Por lo tanto, x = −1/2 es una restricción. En el cuerpo de nuestro trabajo, varias fracciones tienen denominadores de x + 1 y por lo tanto están indefinidas en x = −1. Así, x = −1 es una restricción. Ningún otro denominador agrega restricciones adicionales.

Por lo tanto, para todos los valores de x, excepto x = −1/2 y x = −1, el lado izquierdo de

\[f(f(x))=\dfrac{x}{2 x+1}\]

es idéntico al lado derecho.

Ejercicio

En los Ejercicios 1 - 6, evaluar la función en el número racional dado. Luego usa la primera o segunda técnica para simplificar fracciones complejas explicadas en la narrativa para simplificar tu respuesta.

Ejercicio\(\PageIndex{1}\)

Dado

\(f(x) = \frac{x+1}{2−x}\),

evaluar y simplificar\(f(\frac{1}{2})\).

Contestar

1

Ejercicio\(\PageIndex{2}\)

Dado

\(f(x) = \frac{2−x}{x+5}\),

evaluar y simplificar\(f(\frac{3}{2})\).

Ejercicio\(\PageIndex{3}\)

Dado

\(f(x) = \frac{2x+3}{4−x}\),

evaluar y simplificar\(f(\frac{1}{3})\).

Contestar

1

Ejercicio\(\PageIndex{4}\)

Dado

\(f(x) = \frac{3−2x}{x+5}\)

evaluar y simplificar\(f(\frac{2}{5})\)

Ejercicio\(\PageIndex{5}\)

Dado

\(f(x) = \frac{5−2x}{x+4}\),

evaluar y simplificar\(f(\frac{3}{5})\).

Contestar

\(\frac{19}{23}\)

Ejercicio\(\PageIndex{6}\)

Dado

\(f(x) = \frac{2x−9}{11−x}\),

evaluar y simplificar\(f(\frac{4}{3})\).

En los Ejercicios 7 - 46, simplificar la expresión racional compleja dada. Estado todas las re estricciones.

Ejercicio\(\PageIndex{7}\)

\(\frac{5+\frac{6}{x}}{\frac{25}{x}−\frac{36}{x^3}}\)

Contestar

Proporcionado\(x \ne 0, −\frac{6}{5}, or \frac{6}{5}\),

\(\frac{x^2}{5x−6}\).

Ejercicio\(\PageIndex{8}\)

\(\frac{7+\frac{9}{x}}{\frac{49}{x}−\frac{81}{x^3}}\)

Ejercicio\(\PageIndex{9}\)

\(\frac{\frac{7}{x−2}−\frac{5}{x−7}}{\frac{8}{x−7}+\frac{3}{x+8}}\)

Contestar

Proporcionado\(x \ne 2, 7, −8, or −\frac{43}{11}\),

\(\frac{(2x−39)(x+8)}{(11x+43)(x−2)}\)

Ejercicio\(\PageIndex{10}\)

\(\frac{\frac{9}{x+4}−\frac{7}{x−9}}{\frac{9}{x−9}+\frac{5}{x−4}}\)

Ejercicio\(\PageIndex{11}\)

\(\frac{3+\frac{7}{x}}{\frac{9}{x^2}−\frac{49}{x^4}}\)

Contestar

Proporcionado\(x \ne 0, −\frac{7}{3}, or \frac{7}{3}\),

\(\frac{x^3}{3x−7}\).

Ejercicio\(\PageIndex{12}\)

\(\frac{2−\frac{5}{x}}{\frac{4}{x^2}−\frac{25}{x^4}}\)

Ejercicio\(\PageIndex{13}\)

\(\frac{\frac{9}{x+4}+\frac{7}{x+9}}{\frac{9}{x+9}+\frac{2}{x−8}}\)

Contestar

Proporcionado\(x \ne −4, −9, 8, or \frac{54}{11}\),

\(\frac{(16x+109)(x−8)}{(11x−54)(x+4)}\)

Ejercicio\(\PageIndex{14}\)

\(\frac{\frac{4}{x−6}+\frac{9}{x−9}}{\frac{9}{x−6}+\frac{8}{x−9}}\)

Ejercicio\(\PageIndex{15}\)

\(\frac{\frac{5}{x−7}−\frac{4}{x−4}}{\frac{10}{x−4}−\frac{5}{x+2}}\)

Contestar

Proporcionado\(x \ne 7, 4, −2, or −8\),

\(\frac{x+2}{5(x−7)}\)

Ejercicio\(\PageIndex{16}\)

\(\frac{\frac{3}{x+6}+\frac{7}{x+9}}{\frac{9}{x+6}−\frac{4}{x+9}}\)

Ejercicio\(\PageIndex{17}\)

\(\frac{\frac{6}{x−3}+\frac{5}{x−8}}{\frac{9}{x−3}+\frac{7}{x−8}}\)

Contestar

Proporcionado\(x \ne 3, 8, or \frac{93}{16}\)

\(\frac{11x−63}{16x−93}\)

Ejercicio\(\PageIndex{18}\)

\(\frac{\frac{7}{x−7}−\frac{4}{x−2}}{\frac{7}{x−7}−\frac{6}{x−2}}\)

Ejercicio\(\PageIndex{19}\)

\(\frac{\frac{4}{x−2}+\frac{7}{x−7}}{\frac{5}{x−2}+\frac{2}{x−6}}\)

Contestar

Proporcionado\(x \ne 2, 7, or \frac{39}{7}\),

\(\frac{11x−42}{7x−39}\)

Ejercicio\(\PageIndex{20}\)

\(\frac{\frac{9}{x+2}−\frac{7}{x+5}}{\frac{4}{x+2}+\frac{3}{x+5}}\)

Ejercicio\(\PageIndex{21}\)

\(\frac{5+\frac{4}{x}}{\frac{25}{x}−\frac{16}{x^3}}\)

Contestar

Proporcionado\(x \ne 0, −\frac{4}{5}, or \frac{4}{5}\),

\(\frac{x^2}{5x−4}\).

Ejercicio\(\PageIndex{22}\)

\(\frac{\frac{6}{x+5}+\frac{5}{x+4}}{\frac{8}{x+5}−\frac{3}{x+4}}\)

Ejercicio\(\PageIndex{23}\)

\(\frac{\frac{9}{x−5}+\frac{8}{x+4}}{\frac{5}{x−5}−\frac{4}{x+4}}\)

Contestar

Proporcionado\(x \ne 5, −4, or −40\),

\(\frac{17x−4}{x+40}\).

Ejercicio\(\PageIndex{24}\)

\(\frac{\frac{4}{x−6}+\frac{4}{x−9}}{\frac{6}{x−6}+\frac{6}{x−9}}\)

Ejercicio\(\PageIndex{25}\)

\(\frac{\frac{6}{x+8}+\frac{5}{x−2}}{\frac{5}{x−2}−\frac{2}{x+2}}\)

Contestar

Proporcionado\(x \ne −8, 2, −2, or −\frac{14}{3}\),

\(\frac{(11x+28)(x+2)}{(3x+14)(x+8)}\).

Ejercicio\(\PageIndex{26}\)

\(\frac{\frac{7}{x+9}+\frac{9}{x−2}}{\frac{4}{x−2}+\frac{7}{x+1}}\)

Ejercicio\(\PageIndex{27}\)

\(\frac{\frac{7}{x+7}−\frac{5}{x+4}}{\frac{8}{x+7}−\frac{3}{x+4}}\)

Contestar

Proporcionado\(x \ne −7, −4, or −\frac{11}{5}\),

\(\frac{2x−7}{5x+11}\).

Ejercicio\(\PageIndex{28}\)

\(\frac{25−\frac{16}{x^2}}{5+\frac{4}{x}}\)

Ejercicio\(\PageIndex{29}\)

\(\frac{\frac{64}{x}−\frac{25}{x^3}}{8−\frac{5}{x}}\)

Contestar

Proporcionado\(x \ne 0 or \frac{5}{8}\),

\(\frac{8x+5}{x^2}\).

Ejercicio\(\PageIndex{30}\)

\(\frac{\frac{4}{x+2}+\frac{5}{x−6}}{\frac{7}{x−6}−\frac{5}{x+7}}\)

Ejercicio\(\PageIndex{31}\)

\(\frac{\frac{2}{x−6}−\frac{4}{x+9}}{\frac{3}{x−6​​​​​​​}−\frac{6}{x+9}}\)

Contestar

Proporcionado\(x \ne 6, −9, or 21\),

\(\frac{2}{3}\).

Ejercicio\(\PageIndex{32}\)

\(\frac{\frac{3}{x+6​​​​​​​}−\frac{4}{x+4}}{\frac{6}{x+6}−\frac{8}{x+4}}\)

Ejercicio\(\PageIndex{33}\)

\(\frac{\frac{9}{x^2}−\frac{64}{x^4}}{3−\frac{8}{x}}\)

Contestar

Proporcionado\(x \ne 0 or \frac{8}{3}\),

\(\frac{3x+8}{x^3}\).

Ejercicio\(\PageIndex{34}\)

\(\frac{\frac{9}{x^2}−\frac{25}{x^4}}{3−\frac{5}{x}}\)

Ejercicio\(\PageIndex{35}\)

\(\frac{\frac{4}{x−4​​​​​​​}−\frac{8}{x−7}}{\frac{4}{x−7}+\frac{2}{x+2}}\)

Contestar

Proporcionado\(x \ne 4, 7, −2, or 1\),

\(\frac{−2(x+2)}{3(x−4)}\).

Ejercicio\(\PageIndex{36}\)

\(\frac{2−\frac{7}{x}}{4−\frac{49}{x^2}}\)

Ejercicio\(\PageIndex{37}\)

\(\frac{\frac{3}{x^2+8x−9}+\frac{3}{x^2−81}}{\frac{9}{x^2−81}+\frac{9}{x^2−8x−9}}\)

Contestar

Proporcionado\(x \ne 1, −9, 9, −1, −5\),

\(\frac{(x−5)(x+1)}{3(x+5)(x−1)}\)

Ejercicio\(\PageIndex{38}\)

\(\frac{\frac{7}{x^2−5x−14}+\frac{2}{x^2−7x−18}}{\frac{5}{x^2−7x−18}+\frac{8}{x^2−6x−27}}\)

Ejercicio\(\PageIndex{39}\)

\(\frac{\frac{2}{x^2+8x+7}+\frac{5}{x^2+13x+42}}{\frac{7}{x^2+13x+42}+\frac{6}{x^2+3x−18}}\)

Contestar

Proporcionado\(x \ne −1, −7, −6, 3, −\frac{21}{13}\),

\(\frac{(7x+17)(x−3)}{(13x+21)(x+1)}\)

Ejercicio\(\PageIndex{40}\)

\(\frac{\frac{3}{x^2+5x−14}+\frac{3}{x^2−7x−98}}{\frac{3}{x^2−7x−98}+\frac{3}{x^2−15x+14}}\)

Ejercicio\(\PageIndex{41}\)

\(\frac{\frac{6}{x^2+11x+24}−\frac{6}{x^2+13+40}}{\frac{9}{x^2+13x+40}−{\frac{9}{x^2−3x−40}}\)

Contestar

Proporcionado\(x \ne −3, −8, −5, 8\),

\(\frac{−1(x−8)}{12(x+3)}\)

Ejercicio\(\PageIndex{42}\)

\(\frac{\frac{7}{x^2+19x+90}+\frac{7}{x^2+19x+90}}{\frac{9}{x^2+19x+90}+\frac{9}{x^2+7x−18}}\)

Ejercicio\(\PageIndex{43}\)

\(\frac{\frac{7}{x^2−6x+5}+\frac{7}{x^2+2x−35}}{\frac{8}{x^2+2x−35}+\frac{8}{x^2+8x+7}}\)

Contestar

Proporcionado\(x \ne 1, 5, −7, −1, 2\),

\(\frac{7(x+3)(x+1)}{8(x−2)(x−1)}\)

Ejercicio\(\PageIndex{44}\)

\(\frac{\frac{2}{x^2−4x−12​​​​​​​}−\frac{2}{x^2−x−30}}{\frac{2}{x^2−x−30}−\frac{2}{x^2−4x−45}}\)

Ejercicio\(\PageIndex{45}\)

\(\frac{\frac{4}{x^2 +6x−7​​​​​​​}−\frac{4}{x^2+2x−3}}{\frac{4}{x^2+2x−3}​−\frac{4}{x^2+5x+6}}\)

Contestar

Proporcionado\(x \ne −7, 1, −3, −2\),

\(\frac{−4(x+2)}{3(x+7)}\)

Ejercicio\(\PageIndex{46}\)

\(\frac{\frac{9}{x^2+3x−4}+\frac{8}{x^2−7x+6}}{\frac{4}{x^2−7x+6}+\frac{9}{x^2−10x+24}}\)

Ejercicio\(\PageIndex{47}\)

Dado\(f(x) = \frac{2}{x}\), simplificar

\(\frac{f(x)−f(3)}{x−3}\).

Estado todas las restricciones.

Contestar

Proporcionado\(x \ne 0, 3\),

\(\frac{−2}{3x}\)

Ejercicio\(\PageIndex{48}\)

Dado\(f(x) = \frac{5}{x}\), simplificar

\(\frac{f(x)−f(2)}{x−2}\).

Estado todas las restricciones.

Ejercicio\(\PageIndex{49}\)

Dado\(f(x) = \frac{3}{x^2}\), simplificar

\(\frac{f(x)−f(1)}{x−1}\).

Estado todas las restricciones.

Contestar

Proporcionado\(x \ne 0, 1\),

\(−\frac{3(x+1)}{x^2}\)

Ejercicio\(\PageIndex{50}\)

Dado\(f(x) = \frac{5}{x^2}\), simplificar

\(\frac{f(x)−f(2)}{x−2}\).

Estado todas las restricciones.

Ejercicio\(\PageIndex{51}\)

Dado\(f(x) = \frac{7}{x}\), simplificar

\(\frac{f(x+h)−f(x)}{h}\).

Estado todas las restricciones.

Contestar

Proporcionado\(x \ne 0, −h\), y\(h \ne 0\),

\(−\frac{7}{h(x+h)}\)

Ejercicio\(\PageIndex{52}\)

Dado\(f(x) = \frac{4}{x}\), simplificar

\(\frac{f(x+h)−f(x)}{h}\).

Estado todas las restricciones.

Ejercicio\(\PageIndex{53}\)

Dado

\(f(x) = \frac{x+1}{3−x}\),

encontrar y simplificar\(f(\frac{1}{x})\). Estado todas las restricciones.

Contestar

Proporcionado\(x \ne 0, \frac{1}{3}\),

\(\frac{x+1}{3x−1}\)

Ejercicio\(\PageIndex{54}\)

Dado

\(f(x) = \frac{2−x}{3x+4}\)

encontrar y simplificar\(f(\frac{2}{x})\). Afirma toda restricción.

Ejercicio\(\PageIndex{55}\)

Dado

\(f(x) = \frac{x+1}{2−5x}\),

encontrar y simplificar\(f(\frac{5}{x})\). Estado todas las restricciones.

Contestar

Proporcionado\(x \ne 0, \frac{25}{2}\),

\(\frac{x+5}{2x−25}\)

Ejercicio\(\PageIndex{56}\)

Dado

\(f(x) = \frac{2x−3}{4+x}\),

encontrar y simplificar\(f(\frac{1}{x})\). Estado todas las restricciones.

Ejercicio\(\PageIndex{57}\)

Dado

\(f(x) = \frac{x}{x+2}\),

encontrar y simplificar f (f (x)). Estado todas las restricciones.

Contestar

Proporcionado\(x \ne −2, −\frac{4}{3}\),

\(\frac{x}{3x+4}\)

Ejercicio\(\PageIndex{58}\)

Dado

\(f(x) = \frac{2x}{x+5}\)

encontrar y simplificar f (f (x)). Estado todas las restricciones.

​​​​​​​