1.2: Usar el lenguaje del álgebra
- Page ID
- 112447
Al final de esta sección, podrás:
- Encuentra factores, factorizaciones primos y múltiplos menos comunes
- Usar variables y símbolos algebraicos
- Simplificar las expresiones usando el orden de las operaciones
- Evaluar una expresión
- Identificar y combinar términos similares
- Traducir una frase en inglés a una expresión algebraica
Este capítulo pretende ser una breve revisión de conceptos que serán necesarios en un curso de Álgebra Intermedia. Una introducción más completa a los temas tratados en este capítulo se puede encontrar en el capítulo Álgebra elemental, Fundaciones.
Encuentre factores, factorizaciones principales y múltiplos menos comunes
A los números 2, 4, 6, 8, 10, 12 se les llama múltiplos de 2. Se puede escribir un múltiplo de 2 como producto de un número de conteo y 2.
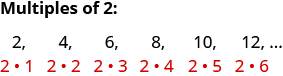
De igual manera, un múltiplo de 3 sería producto de un número de conteo y 3.
Podríamos encontrar los múltiplos de cualquier número continuando con este proceso.
| Número de conteo | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Multiplos de 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| Multiplos de 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| Multiplos de 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| Multiplos de 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| Multiplos de 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| Multiplos de 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| Multiplos de 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| Multiplos de 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
Un número es un múltiplo de\(n\) si es producto de un número de conteo y\(n\).
Otra forma de decir que 15 es un múltiplo de 3 es decir que 15 es divisible por 3. Eso quiere decir que cuando dividimos 3 en 15, obtenemos un número de conteo. De hecho,\(15÷3\) es\(5\), así\(15\) es\(5⋅3\).
Si un número\(m\) es un múltiplo de\(n\), entonces\(m\) es divisible por\(n\).
Si tuviéramos que buscar patrones en los múltiplos de los números del 2 al 9, descubriríamos las siguientes pruebas de divisibilidad:
Un número es divisible por:
- 2 si el último dígito es 0, 2, 4, 6 u 8.
- 3 si la suma de los dígitos es divisible por 3.
- 5 si el último dígito es 5 o 0.
- 6 si es divisible tanto por 2 como por 3.
- 10 si termina con 0.
Es 5.625 divisible por
- 2?
- 3?
- ¿5 o 10?
- 6?
- Responder
-
a.
\(\text{Is 5,625 divisible by 2?}\)
\( \begin{array}{ll} \text{Does it end in 0, 2, 4, 6 or 8?} & {\text{No.} \\ \text{5,625 is not divisible by 2.}} \end{array}\) - b.
\(\text{5,625 divisible by 3?}\)
\(\begin{array}{ll} {\text{What is the sum of the digits?} \\ \text{Is the sum divisible by 3?}} & {5+6+2+5=18 \\ \text{Yes.} \\ \text{5,625 is divisible by 3.}}\end{array}\) - c.
\(\text{Is 5,625 divisible by 5 or 10?}\)
\(\begin{array}{ll} \text{What is the last digit? It is 5.} & \text{5,625 is divisible by 5 but not by 10.} \end{array}\)d.\(\text{Is 5,625 divisible by 6?}\)
\(\begin{array}{ll}\text{Is it divisible by both 2 and 3?} & {\text{No, 5,625 is not divisible by 2, so 5,625 is} \\ \text{not divisible by 6.}} \end{array}\)
¿Es 4.962 divisible por a. 2? b. 3? c. 5? d. 6? e. 10?
- Responder
-
a. si b. si c. no d. si e. no
¿Es 3.765 divisible por a. 2? b. 3? c. 5? d. 6? e. 10?
- Responder
-
a. no b. si c. si d. no e. no
En matemáticas, a menudo hay varias formas de hablar de las mismas ideas. Hasta el momento, hemos visto que si\(m\) es un múltiplo de\(n\), podemos decir que\(m\) es divisible por\(n\). Por ejemplo, dado que 72 es un múltiplo de 8, decimos que 72 es divisible por 8. Dado que 72 es múltiplo de 9, decimos 72 es divisible por 9. Podemos expresarlo aún de otra manera.
Ya que\(8·9=72\), decimos que 8 y 9 son factores de 72. Cuando escribimos\(72=8·9\), decimos que hemos factorizado 72.
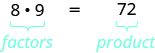
Otras formas de factorizar\(72\) son\(1·72, \; 2·36, \; 3·24, \; 4·18,\) y\(6⋅12\). El número 72 tiene muchos factores:\(1,\,2,\,3,\,4,\,6,\,8,\,9,\,12,\,18,\,24,\,36,\) y\(72\).
Si\(a\) y\(b\) están contando números, y\(a·b=m\), entonces\(a\) y\(b\) son factores de\(m\).
Algunos números, como el 72, tienen muchos factores. Otros números tienen sólo dos factores. Un número primo es un número de conteo mayor a 1 cuyos únicos factores son 1 y él mismo.
Un número primo es un número de conteo mayor que 1 cuyos únicos factores son 1 y el número en sí.
Un número compuesto es un número de conteo que no es primo. Un número compuesto tiene factores distintos a 1 y el número en sí.
Los números de conteo del 2 al 20 se listan en la tabla con sus factores. ¡Asegúrate de estar de acuerdo con la etiqueta “prime” o “composite” para cada una!
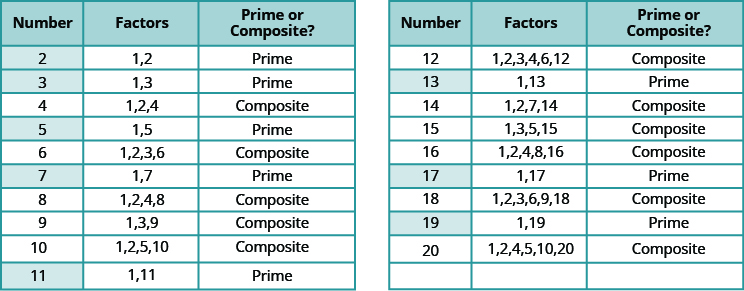
Los números primos menores a 20 son 2, 3, 5, 7, 11, 13, 17 y 19. Observe que el único número primo par es 2.
Un número compuesto se puede escribir como un producto único de primos. A esto se le llama la factorización prima del número. Encontrar la factorización prima de un número compuesto será útil en muchos temas de este curso.
La descomposición de un número primo es el producto de números primos que es igual al número.
Para encontrar la factorización prima de un número compuesto, busque dos factores cualesquiera del número y utilícelos para crear dos ramas. Si un factor es primo, esa rama está completa. Círculo que prime. De lo contrario, es fácil perder la noción de los números primos.
Si el factor no es primo, encuentra dos factores del número y continúa el proceso. Una vez que todas las ramas tienen cebos en círculo al final, la factorización se completa. El número compuesto ahora se puede escribir como un producto de números primos.
Factor 48.
- Responder
-
.jpg)
Decimos que\(2⋅2⋅2⋅2⋅3\) es la factorización prima de 48. Generalmente escribimos los primos en orden ascendente. Asegúrate de multiplicar los factores para verificar tu respuesta. \(2⋅2⋅2⋅2⋅3\)es la descomposición primo de 48. Generalmente escribimos los primos en orden ascendente. Asegúrate de multiplicar los factores para verificar tu respuesta.
Si primero factorizamos 48 de una manera diferente, por ejemplo as\(6·8\), el resultado seguiría siendo el mismo. Termina la factorización prime y verifica esto por ti mismo.
Encuentra la factorización principal de\(80\).
- Responder
-
\(2⋅2⋅2⋅2⋅5\)
Encuentra la factorización principal de\(60\).
- Responder
-
\(2⋅2⋅3⋅5\)
- Encuentra dos factores cuyo producto es el número dado, y usa estos números para crear dos ramas.
- Si un factor es primo, esa rama está completa. Da un círculo a la flor, como una hoja en el árbol.
- Si un factor no es primo, escríbelo como producto de dos factores y continúe el proceso.
- Escriba el número compuesto como el producto de todos los primos en un círculo.
Una de las razones por las que miramos los primos es utilizar estas técnicas para encontrar el múltiplo menos común de dos números. Esto será útil cuando sumemos y restemos fracciones con diferentes denominadores.
El múltiplo menos común (LCM) de dos números es el número más pequeño que es un múltiplo de ambos números.
Para encontrar el mínimo común múltiplo de dos números usaremos el Método de Factores Primos. Encontremos el MCM de 12 y 18 usando sus factores primos.
Encuentra el mínimo común múltiplo (MCM) de 12 y 18 usando el método de los factores primos.
- Responder
-
.jpg)
Observe que los factores primos de 12\((2·2·3)\) y los factores primos de 18\((2⋅3⋅3)\) están incluidos en la MCM\((2·2·3·3)\). Entonces 36 es el múltiplo menos común de 12 y 18.
Al hacer coincidir los primos comunes, cada factor primo común se usa solo una vez. De esta manera estás seguro que 36 es el múltiplo menos común.
Encuentra el LCM de 9 y 12 usando el Método de Factores Primos.
- Responder
-
36
Encuentra el LCM de 18 y 24 usando el Método de Factores Primos.
- Responder
-
72
- Escribe cada número como producto de primos.
- Enumere los números primos de cada número. Haga coincidir los primos verticalmente cuando sea posible.
- Derriba las columnas.
- Multiplicar los factores.
Usar variables y símbolos algebraicos
En álgebra, utilizamos una letra del alfabeto para representar un número cuyo valor puede cambiar. Llamamos a esto una variable y las letras comúnmente utilizadas para las variables son\(x,\,y,\,a,\,b,\) y\(c.\)
Una variable es una letra que representa un número cuyo valor puede cambiar.
Un número cuyo valor siempre permanece igual se denomina constante.
Una constante es un número cuyo valor siempre permanece igual.
Para escribir algebraicamente, necesitamos algunos símbolos de operación así como números y variables. Hay varios tipos de símbolos que vamos a utilizar. Existen cuatro operaciones aritméticas básicas: suma, resta, multiplicación y división. A continuación enumeraremos los símbolos utilizados para indicar estas operaciones.
| Operación | Notación | Decir: | El resultado es... |
|---|---|---|---|
| Adición | \(a+b\) | \(a\)más\(b\) | la suma de\(a\) y\(b\) |
| Resta | \(a−b\) | \(a\)menos\(b\) | la diferencia de\(a\) y\(b\) |
| Multiplicación | \(a⋅b,\,ab,\,(a)(b),\,(a)b,\,a(b)\) | \(a\)tiempos\(b\) | el producto de\(a\) y\(b\) |
| División | \(a÷b,\,\space a/b,\,\space\frac{a}{b},\,\space b \overline{\smash{)}a}\) | \(a\)dividido por\(b\) | el cociente de\(a\) y\(b\); \(a\) se llama dividendo, y\(b\) se llama divisor |
Cuando dos cantidades tienen el mismo valor, decimos que son iguales y las conectamos con un signo igual.
\(a=b\)se lee "\(a\)es igual a\(b\).”
El símbolo “\(=\)” se llama el signo igual.
En la recta numérica, los números se hacen más grandes a medida que van de izquierda a derecha. La línea numérica se puede utilizar para explicar los símbolos “\(<\)” y “\(>\)”.
Las expresiones\(a<b\) o se\(a>b\) pueden leer de izquierda a derecha o de derecha a izquierda, aunque en inglés solemos leer de izquierda a derecha. En general,
\[a<b \text{ is equivalent to }b>a. \text{For example, } 7<11 \text{ is equivalent to }11>7.\]
\[a>b \text{ is equivalent to }b<a. \text{For example, } 17>4 \text{ is equivalent to }4<17.\]
| Símbolos de desigualdad | Palabras |
|---|---|
| \(a\neq b\) | \(a\)no es igual a\(b\). |
| \(a<b\) | \(a\)es menor que\(b\). |
| \(a\leq b\) | \(a\)es menor o igual a\(b\). |
| \(a>b\) | \(a\)es mayor que\(b\). |
| \(a\geq b\) | \(a\)es mayor o igual a\(b\). |
Los símbolos de agrupación en álgebra son muy parecidos a las comas, dos puntos y otros signos de puntuación en inglés. Ayudan a identificar una expresión, que puede estar compuesta por un número, una variable o una combinación de números y variables usando símbolos de operación. Presentaremos ahora tres tipos de símbolos de agrupación.
\[\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\]
Aquí hay algunos ejemplos de expresiones que incluyen símbolos de agrupación. Simplificaremos expresiones como estas más adelante en esta sección.
\[8(14−8) \qquad 21−3[2+4(9−8)] \qquad 24÷ \{13−2[1(6−5)+4]\}\]
¿Cuál es la diferencia en inglés entre una frase y una oración? Una frase expresa un solo pensamiento que está incompleto por sí mismo, pero una oración hace una declaración completa. Una oración tiene un sujeto y un verbo. En álgebra, tenemos expresiones y ecuaciones.
Una expresión es un número, una variable o una combinación de números y variables que utilizan símbolos de operación.
\[\begin{array}{lll} \textbf{Expression} & \textbf{Words} & \textbf{English Phrase} \\ \mathrm{3+5} & \text{3 plus 5} & \text{the sum of three and five} \\ \mathrm{n−1} & n\text{ minus one} & \text{the difference of } n \text{ and one} \\ \mathrm{6·7} & \text{6 times 7} & \text{the product of six and seven} \\ \frac{x}{y} & x \text{ divided by }y & \text{the quotient of }x \text{ and }y \end{array} \]
Observe que las frases en inglés no forman una oración completa porque la frase no tiene verbo.
Una ecuación son dos expresiones vinculadas por un signo igual. Cuando lees las palabras que representan los símbolos en una ecuación, tienes una oración completa en inglés. El signo igual da el verbo.
Una ecuación son dos expresiones conectadas por un signo igual.
\[\begin{array}{ll} \textbf{Equation} & \textbf{English Sentence} \\ 3+5=8 & \text{The sum of three and five is equal to eight.} \\ n−1=14 & n \text{ minus one equals fourteen.} \\ 6·7=42 & \text{The product of six and seven is equal to forty-two.} \\ x=53 & x \text{ is equal to fifty-three.} \\ y+9=2y−3 & y \text{ plus nine is equal to two } y \text{ minus three.} \end{array}\]
Supongamos que necesitamos multiplicar 2 nueve veces. Podríamos escribir esto como\(2·2·2·2·2·2·2·2·2\). Esto es tedioso y puede ser difícil hacer un seguimiento de todos esos 2s, así que usamos exponentes. Escribimos\(2·2·2\) como\(\mathrm{2^3}\) y\(2·2·2·2·2·2·2·2·2\) como\(2^9\). En expresiones como\(2^3\), el 2 se llama la base y el 3 se llama el exponente. El exponente nos dice cuántas veces necesitamos multiplicar la base.
Decimos que\(2^3\) está en notación exponencial y\(2·2·2\) está en notación expandida.
\(a^n\)significa multiplicar\(n\) factores del número\(a\).
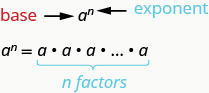
La expresión\(a^n\) se lee\(a\) al\(n^{th}\) poder.
Mientras leemos en\(a^n\) cuanto\(“a\) al\(n^{th}\) poder”, solemos leer:
\[\begin{array}{cc} a^2 & “a \text{ squared}” \\ a^3 & “a \text{ cubed}” \end{array}\]
Veremos más adelante por qué\(a^2\) y\(a^3\) tenemos nombres especiales.
La tabla muestra cómo leemos algunas expresiones con exponentes.
| Expresión | En palabras | |
|---|---|---|
| 7 2 | 7 a la segunda potencia o | 7 al cuadrado |
| 5 3 | 5 a la tercera potencia o | 5 cubos |
| 9 4 | 9 a la cuarta potencia | |
| 12 5 | 12 a la quinta potencia |
Simplificar las expresiones usando el orden de las operaciones
Simplificar una expresión significa hacer todas las matemáticas posibles. Por ejemplo, para simplificar primero\(\mathrm{4·2+1}\) multiplicaríamos\(\mathrm{4⋅2}\) para obtener 8 y luego sumar el 1 para obtener 9. Un buen hábito para desarrollar es trabajar abajo de página, escribiendo cada paso del proceso por debajo del paso anterior. El ejemplo que acabamos de describir se vería así:
\[ 4⋅2+1 \\ 8+1 \\ 9\]
Al no usar un signo igual al simplificar una expresión, puede evitar confundir expresiones con ecuaciones.
Para simplificar una expresión, realice todas las operaciones en la expresión.
Hemos introducido la mayoría de los símbolos y notación utilizados en álgebra, pero ahora necesitamos aclarar el orden de las operaciones. De lo contrario, las expresiones pueden tener diferentes significados, y pueden dar como resultado valores diferentes.
Por ejemplo, considere la expresión\(4+3⋅7\). Algunos alumnos simplifican esto obteniendo 49, sumando\(4+3\) y luego multiplicando ese resultado por 7. Otros obtienen 25, multiplicando\(3·7\) primero y luego sumando 4.
La misma expresión debería dar el mismo resultado. Por lo que los matemáticos establecieron algunos lineamientos que se llaman el orden de las operaciones.
- Paréntesis y otros símbolos de agrupación
- Simplifica todas las expresiones dentro de los paréntesis u otros símbolos de agrupación, trabajando primero en los paréntesis más internos.
- Exponentes
- Simplifica todas las expresiones con exponentes.
- Multiplicación y división
- Realiza toda la multiplicación y división en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
- Suma y resta
- Realizar todas las sumas y restas en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
Los estudiantes a menudo preguntan: “¿Cómo voy a recordar el orden?” Aquí hay una manera de ayudarte a recordar: Toma la primera letra de cada palabra clave y sustituye la tonta frase “Por favor, disculpe a mi querida tía Sally”.
\[\begin{array}{ll} \text{Parentheses} & \text{Please} \\ \text{Exponents} & \text{Excuse} \\ \text{Multiplication Division} & \text{My Dear} \\ \text{Addition Subtraction} & \text{Aunt Sally} \end{array}\]
Es bueno que “M y D oreja” vaya de la mano, ya que esto nos recuerda que m ultiplicación y d ivisión tienen igual prioridad. No siempre hacemos multiplicación antes de la división o siempre hacemos división antes de multiplicar. Los hacemos en orden de izquierda a derecha.
De igual manera, “A unt S ally” va de la mano y así nos recuerda que una ddition y una s ubtracción también tienen igual prioridad y las hacemos en orden de izquierda a derecha.
Simplificar:\(18÷6+4(5−2)\).
- Responder
-
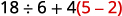
¿Paréntesis? Sí, restar primero.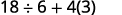 
¿Exponentes? No. ¿Multiplicación o división? Sí. Dividir primero porque multiplicamos y dividimos de izquierda a derecha.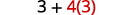 
¿Alguna otra multiplicación o división? Sí. Multiplicar. 
¿Alguna otra multiplicación de división? No. ¿Alguna suma o resta? Sí. Agregar. 
Simplificar:\(30÷5+10(3−2).\)
- Responder
-
16
Simplificar:\(70÷10+4(6−2).\)
- Responder
-
23
Cuando hay múltiples símbolos de agrupación, simplificamos primero los paréntesis más internos y trabajamos hacia afuera.
Simplificar:\(5+2^3+3[6−3(4−2)].\)
- Responder
-
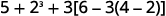
¿Hay paréntesis (u otros símbolos de agrupación)? Sí.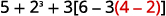 
Enfócate en los paréntesis que están dentro de los corchetes. Restar.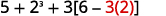 
Continuar dentro de los corchetes y multiplicar.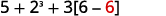 
Continuar dentro de los corchetes y restar. 
La expresión dentro de los corchetes no requiere más simplificación. ¿Hay exponentes? Sí. Simplifica los exponentes. 
¿Hay alguna multiplicación o división? Sí. Multiplicar. 
¿Hay alguna suma de resta? Sí. Agregar.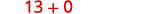 
Agregar. 
Simplificar:\(9+5^3−[4(9+3)].\)
- Responder
-
86
Simplificar:\(7^2−2[4(5+1)].\)
- Responder
-
1
Evaluar una expresión
En los últimos ejemplos, simplificamos las expresiones usando el orden de las operaciones. Ahora evaluaremos algunas expresiones, nuevamente siguiendo el orden de las operaciones. Evaluar una expresión significa encontrar el valor de la expresión cuando la variable es reemplazada por un número dado.
Evaluar una expresión significa encontrar el valor de la expresión cuando la variable es reemplazada por un número dado.
Para evaluar una expresión, sustituya ese número por la variable en la expresión y luego simplifique la expresión.
Evaluar cuándo\(x=4\): a.\(x^2\) b\(2x^2+3x+8\).\(3^x\) c.
- Responder
-
a.
b.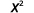
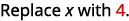
Usar definición de exponente.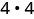 
Simplificar.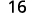 
c.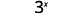
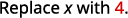
Usar definición de exponente. 
Simplificar.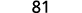 
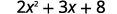
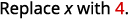
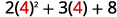
Seguir el orden de las operaciones. .jpg)
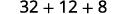
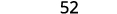
Evaluar cuándo\(x=3\), a.\(x^2\) b\(3x^2+4x+1\).\(4^x\) c.
- Responder
-
a. 9
b. 64
c. 40
Evaluar cuándo\(x=6\), a.\(x^3\) b\(6x^2−4x−7\).\(2^x\) c.
- Responder
-
a. 216
b. 64
c. 185
Identificar y combinar términos similares
Las expresiones algebraicas están compuestas por términos. Un término es una constante, o el producto de una constante y una o más variables.
Un término es una constante o producto de una constante y una o más variables.
Ejemplos de términos son\(7,\,y,\,5x^2,\,9a,\) y\(b^5\).
La constante que multiplica la variable se llama coeficiente.
El coeficiente de un término es la constante que multiplica la variable en un término.
Piense en el coeficiente como el número frente a la variable. El coeficiente del término\(3x\) es 3. Cuando escribimos\(x\), el coeficiente es 1, ya que\(x=1⋅x\).
Algunos términos comparten rasgos comunes. Cuando dos términos son constantes o tienen la misma variable y exponente, decimos que son como términos.
Mira los siguientes 6 términos. ¿Cuáles parecen tener rasgos en común?
\[5x \quad 7 \quad n^2 \quad 4 \quad 3x \quad 9n^2\]
Nosotros decimos,
\(7\)y\(4\) son como términos.
\(5x\)y\(3x\) son como términos.
\(n^2\)y\(9n^2\) son como términos.
Los términos que son constantes o tienen las mismas variables elevadas a las mismas potencias se denominan términos similares.
Si hay términos similares en una expresión, puede simplificar la expresión combinando los términos similares. Agregamos los coeficientes y mantenemos la misma variable.
\[\begin{array}{lc} \text{Simplify.} & 4x+7x+x \\ \text{Add the coefficients.} & 12x \end{array}\]
Simplificar:\(2x^2+3x+7+x^2+4x+5\).
- Responder
-
Simplificar:\(3x^2+7x+9+7x^2+9x+8\).
- Responder
-
\(10x^2+16x+17\)
Simplificar:\(4y^2+5y+2+8y^2+4y+5.\)
- Responder
-
\(12y^2+9y+7\)
- Identificar términos similares.
- Reorganice la expresión para que los términos estén juntos.
- Sumar o restar los coeficientes y mantener la misma variable para cada grupo de términos similares.
Traducir una frase en inglés a una expresión algebraica
Enumeramos muchos símbolos de operación que se utilizan en álgebra. Ahora, los usaremos para traducir frases en inglés a expresiones algebraicas. Los símbolos y variables de los que hemos hablado nos ayudarán a lograrlo. Tabla los resume.
| Operación | Frase | Expresión |
|---|---|---|
| Adición | \(a\)más\(b\)
la suma de\(a\) y\(b\) \(a\)aumentado en\(b\) \(b\)más de\(a\) el total de\(a\) y\(b\) \(b\)agregado a\(a\) |
\(a+b\) |
| Resta | \(a\)menos\(b\)
la diferencia de\(a\) y\(b\) \(a\)disminuida en\(b\) \(b\)menos de\(a\) \(b\)restado de\(a\) |
\(a−b\) |
| Multiplicación | \(a\)tiempos\(b\)
el producto de\(a\) y\(b\) dos veces\(a\) |
\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\) |
| División | \(a\)dividido por\(b\)
el cociente de\(a\) y\(b\) la proporción de\(a\) y\(b\) \(b\)dividido en\(a\) |
\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\) |
Observa de cerca estas frases usando las cuatro operaciones:
Cada frase nos dice que operemos en dos números. Busca las palabras de y y para encontrar los números.
Cada frase nos dice que operemos en dos números. Busca las palabras de y y para encontrar los números.
Traduce cada frase en inglés en una expresión algebraica:
a. la diferencia de\(14x\) y\(9\)
b. el cociente de\(8y^2\) y\(3\)c. doce más de\(y\)
d. siete menos que\(49x^2\)
- Responder
-
a. La palabra clave es diferencia, que nos dice que la operación es resta. Busca las palabras de y y t o encuentra los números para restar.
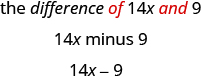
b. La palabra clave es cociente, lo que nos dice que la operación es división.
c. Las palabras clave son más que. Nos dicen que la operación es suma. Más que significa “agregado a”.
\[\text{twelve more than }y \\ \text{twelve added to }y \\ y+12\]
d. Las palabras clave son menores que. Nos dicen que restemos. Menos que significa “restado de”.
\[\text{seven less than }49x^2 \\ \text{seven subtracted from }49x^2 \\ 49x^2−7\]
Traducir la frase en inglés en una expresión algebraica:
a. la diferencia de\(14x^2\) y\(13\)
b. el cociente de\(12x\) y\(2\)
c.\(13\) más de\(z\)
d.\(18\) menos de\(8x\)
- Contestar
-
a.\(14x^2−13\) b.\(12x÷2\)
c.\(z+13\) d.\(8x−18\)
Traducir la frase en inglés en una expresión algebraica:
a. la suma de\(17y^2\) y\(19\)
b. el producto de\(7\) y\(y\)
c. Once más de\(x\)
d. Catorce menos que\(11a\)
- Contestar
-
a.\(17y^2+19\) b.\(7y\)
c.\(x+11\) d.\(11a−14\)
Observamos cuidadosamente las palabras para ayudarnos a distinguir entre multiplicar una suma y agregar un producto.
Traducir la frase en inglés en una expresión algebraica:
a. ocho veces la suma de\(x\) y\(y\)
b. la suma de ocho veces\(x\) y\(y\)
- Contestar
-
Hay dos palabras de operación: los tiempos nos dicen que nos multipliquemos y la suma nos dice que agreguemos.
a. porque estamos\(8\) multiplicando por la suma, necesitamos paréntesis alrededor de la suma de\(x\) y\(y\),\((x+y)\). Esto nos obliga a determinar primero la suma. (Recordar el orden de las operaciones.)
\[\text{eight times the sum of }x \text{ and }y \\ 8(x+y)\]
b. Para tomar una suma, buscamos las palabras de y y para ver qué se está agregando. Aquí estamos tomando la suma de ocho veces\(x\) y\(y\).
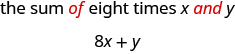
Traducir la frase en inglés en una expresión algebraica:
a. cuatro veces la suma de\(p\) y\(q\)
b. la suma de cuatro veces\(p\) y\(q\)
- Contestar
-
a.\(4(p+q)\) b.\(4p+q\)
Traducir la frase en inglés en una expresión algebraica:
a. la diferencia de dos veces\(x\) y\(8\)
b. dos veces la diferencia de\(x\) y\(8\)
- Contestar
-
a.\(2x−8\) b.\(2(x−8)\)
Más adelante en este curso, aplicaremos nuestras habilidades en álgebra para resolver aplicaciones. El primer paso será traducir una frase en inglés a una expresión algebraica. Veremos cómo hacer esto en los siguientes dos ejemplos.
La longitud de un rectángulo es 14 menos que el ancho. Dejar\(w\) representar el ancho del rectángulo. Escribe una expresión para la longitud del rectángulo.
- Contestar
-
\[\begin{array}{lc} \text{Write a phrase about the length of the rectangle.} & \text{14 less than the width} \\ \text{Substitute }w \text{ for “the width.”} & w \\ \text{Rewrite less than as subtracted from.} & \text{14 subtracted from } w \\ \text{Translate the phrase into algebra.} & w−14 \end{array}\]
La longitud de un rectángulo es 7 menos que el ancho. Dejar\(w\) representar el ancho del rectángulo. Escribe una expresión para la longitud del rectángulo.
- Contestar
-
\(w−7\)
El ancho de un rectángulo es\(6\) menor que la longitud. Dejar\(l\) representar la longitud del rectángulo. Escribe una expresión para el ancho del rectángulo.
- Contestar
-
\(l−6\)
Las expresiones en el siguiente ejemplo serán utilizadas en los problemas típicos de mezcla de monedas que veremos pronto.
June tiene dimes y cuartos en su bolso. El número de dimes es siete menos de cuatro veces el número de trimestres. Dejar\(q\) representar el número de trimestres. Escribe una expresión para el número de dimes.
- Contestar
-
\[\begin{array}{lc} \text{Write a phrase about the number of dimes.} & \text{7 less than 4 times }q \\ \text{Translate 4 times }q. & \text{7 less than 4}q \\ \text{Translate the phrase into algebra.} & 4q−7 \end{array}\]
Geoffrey tiene dimes y cuartos en el bolsillo. El número de dimes es ocho menos de cuatro veces el número de trimestres. Dejar\(q\) representar el número de trimestres. Escribe una expresión para el número de dimes.
- Contestar
-
\(4q−8\)
Lauren tiene diez y cinco dólares en su bolso. El número de dimes es de tres más de siete veces el número de nickels. Dejar\(n\) representar el número de nickels. Escribe una expresión para el número de dimes.
- Contestar
-
\(7n+3\)
Conceptos clave
- Pruebas de divisibilidad
Un número es divisible por:
2 si el último dígito es 0, 2, 4, 6 u 8.
3 si la suma de los dígitos es divisible por 3.
5 si el último dígito es 5 o 0.
6 si es divisible tanto por 2 como por 3.
10 si termina con 0. - Cómo encontrar la descomposición primo de un número compuesto.
- Encuentra dos factores cuyo producto es el número dado, y usa estos números para crear dos ramas.
- Si un factor es primo, esa rama está completa. Da un círculo a la flor, como un capullo en el árbol.
- Si un factor no es primo, escríbelo como producto de dos factores y continúe el proceso.
- Escriba el número compuesto como el producto de todos los primos en un círculo.
- Cómo Encontrar el múltiplo menos común usando el método de factores primos.
- Escribe cada número como producto de primos.
- Enumere los números primos de cada número. Haga coincidir los primos verticalmente cuando sea posible.
- Derriba las columnas.
- Multiplicar los factores.
- Símbolo de igualdad
\(a=b\) se lee “\(a\)es igual a”\(b\). El símbolo “=” se llama el signo igual. - Símbolos de desigualdad
Símbolos de desigualdad Palabras \(a≠b\) \(a\)no es igual a\(b\). \(a<b\) \(a\)es menor que\(b\). \(a≤b\) \(a\)es menor o igual a\(b\). \(a>b\) \(a\)es mayor que\(b\). \(a≥b\) \(a\)es mayor o igual a \(b\). - Agrupación de símbolos\(\begin{array}{lc} \text{Parentheses} & \mathrm{()} \\ \text{Brackets} & \mathrm{[]} \\ \text{Braces} & \mathrm{ \{ \} } \end{array}\)
- Notación exponencial\(a^n\) significa multiplicar \(a\)por sí mismo, \(n\)tiempos. La expresión a se lee \(a\)al\(n^{th}\) poder.
- Simplificar una expresión
Para simplificar una expresión, realice todas las operaciones en la expresión. - Cómo utilizar el orden de operaciones.
- Paréntesis y otros símbolos de agrupación
- Simplifica todas las expresiones dentro de los paréntesis u otros símbolos de agrupación, trabajando primero en los paréntesis más internos.
- Exponentes
- Simplifica todas las expresiones con exponentes.
- Multiplicación y división
- Realiza toda la multiplicación y división en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
- Suma y resta
- Realizar todas las sumas y restas en orden de izquierda a derecha. Estas operaciones tienen igual prioridad.
- Paréntesis y otros símbolos de agrupación
- Cómo combinar términos similares.
- Identificar términos similares.
- Reorganice la expresión para que los términos estén juntos.
- Sumar o restar los coeficientes y mantener la misma variable para cada grupo de términos similares.
Operación Frase Expresión Adición \(a\)más \(b\)
la suma de \(a\)y \(b\)
\(a\)aumentado en \(b\)
\(b\)más de\(a\)
el total de \(a\)y \(b\)
\(b\)agregado a\(a\)\(a+b\) Resta \(a\)menos \(b\)
la diferencia de\(a\) y \(b\)
\(a\)disminuyó en \(b\)
\(b\)menos de\(a\)
\(b\)restado de\(a\)\(a−b\) Multiplicación \(a\)veces \(b\)
el producto de \(a\)y \(b\)
dos veces\(a\)\(a·b,\,ab,\,a(b),\,(a)(b)\)
\(2a\)
División \(a\)dividido por \(b\)
el cociente de \(a\)y \(b\)
la proporción de \(a\)y \(b\)
\(b\)dividido en\(a\)\(a÷b,\,a/b,\,\frac{a}{b},\,b \overline{\smash{)}a}\)
Glosario
- coeficiente
- El coeficiente de un término es la constante que multiplica la variable en un término.
- número compuesto
- Un número compuesto es un número de conteo que no es primo. Tiene factores distintos al 1 y el número en sí.
- constante
- Una constante es un número cuyo valor siempre permanece igual.
- divisible por un número
- Si un número \(m\)es un múltiplo de \(n\), entonces \(m\)es divisible por \(n\).
- ecuación
- Una ecuación son dos expresiones conectadas por un signo igual.
- evaluar una expresión
- Evaluar una expresión significa encontrar el valor de la expresión cuando las variables son reemplazadas por un número dado.
- expresión
- Una expresión es un número, una variable o una combinación de números y variables que utilizan símbolos de operación.
- factores
- Si\(a·b=m\), entonces \(a\)y \(b\)son factores de \(m\).
- mínimo común múltiplo
- El múltiplo menos común (LCM) de dos números es el número más pequeño que es un múltiplo de ambos números.
- términos similares
- Los términos que son constantes o tienen las mismas variables elevadas a las mismas potencias se denominan términos similares.
- múltiplo de un número
- Un número es un múltiplo de \(n\)si es producto de un número de conteo y \(n\).
- orden de operaciones
- El orden de operaciones son pautas establecidas para simplificar una expresión.
- factorización prima
- La descomposición de un número primo es el producto de números primos que es igual al número.
- número primo
- Un número primo es un número de conteo mayor que 1 cuyos únicos factores son 1 y el número en sí.
- simplificar una expresión
- Simplificar una expresión significa hacer todas las matemáticas posibles.
- término
- Un término es una constante, o el producto de una constante y una o más variables.
- variable
- Una variable es una letra que representa un número cuyo valor puede cambiar.