1.3: Enteros
- Page ID
- 112424
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Simplificar expresiones con valor absoluto
- Sumar y restar enteros
- Multiplicar y dividir enteros
- Simplificar expresiones con enteros
- Evaluar expresiones variables con números enteros
- Traducir frases a expresiones con enteros
- Usar enteros en aplicaciones
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Álgebra elemental, Fundaciones.
Simplificar expresiones con valor absoluto
Un número negativo es un número menor que 0. Los números negativos están a la izquierda de cero en la recta numérica (Figura\(\PageIndex{1}\)).
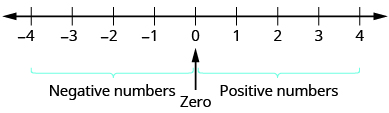
Figura\(\PageIndex{1}\). La recta numérica muestra la ubicación de los números positivos y negativos.
Es posible que hayas notado que, en la recta numérica, los números negativos son una imagen especular de los números positivos, con cero en el medio. Debido a que los números\(2\) y\(−2\) están a la misma distancia de cero, a cada uno se le llama lo opuesto al otro. Lo opuesto de\(2\) es\(−2\), y lo contrario de\(−2\) es\(2\).
Lo contrario de un número es el número que está a la misma distancia de cero en la recta numérica pero en el lado opuesto de cero.
La figura\(\PageIndex{2}\) ilustra la definición.

Figura\(\PageIndex{2}\). Lo contrario de 3 es\(−3\).
\[\begin{align} & -a \text{ means the opposite of the number }a \\ & \text{The notation} -a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
Vimos que números como 3 y −3 son opuestos porque están a la misma distancia de 0 en la recta numérica. Ambos son tres unidades de 0. La distancia entre 0 y cualquier número en la línea numérica se llama el valor absoluto de ese número.
El valor absoluto de un número es su distancia de 0 en la recta numérica.
El valor absoluto de un número\(n\) se escribe como\(|n|\) y\(|n|≥0\) para todos los números.
Los valores absolutos son siempre mayores o iguales a cero.
Por ejemplo,
\[\begin{align} & -5 \text{ is } 5 \text{ units away from 0, so } |-5|=5. \\ & 5 \text{ is }5\text{ units away from 0, so }|5|=5. \end{align}\]
La figura\(\PageIndex{3}\) ilustra esta idea.
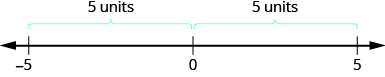
El valor absoluto de un número nunca es negativo porque la distancia no puede ser negativa. El único número con valor absoluto igual a cero es el número cero en sí porque la distancia de 0 a 0 en la línea numérica es cero unidades.
En el siguiente ejemplo, ordenaremos expresiones con valores absolutos.
Rellene\(<,\,>,\) o\(=\) para cada uno de los siguientes pares de números:
- \(\mathrm{|−5|}\_\_\mathrm{−|−5|}\_\_\mathrm{−|5|}\)
- \(\text{8__−|−8|}\)
- \(\text{−9__−|−9|}\)
- (\ text {− (−16) __|−16|}\).
- Contestar
-
a.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {|−5| \\ 5 \\ 5 \\ |−5|} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−5| \\ −5 \\ −5 \\ −|−5|} \end{array}\)
b.
\(\begin{array}{llcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {8 \\ 8 \\ 8 \\ 8} & {\_\_ \\ \_\_ \\ > \\ >} & {−|−8| \\ −8 \\ −8 \\ −|−8|} \end{array}\)
c.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−9 \\ −9 \\ −9 \\ −9} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−9| \\ −9 \\ −9 \\ −|−9|} \end{array}\)
d.
\(\begin{array}{lrcc} { \text{ } \\ \text{Simplify.} \\ \text{Order.} \\ \text{ } } & {−(−16) \\ 16 \\ 16 \\ −(−16)} & {\_\_ \\ \_\_ \\ = \\ =} & {−|−16| \\ 16 \\ 16 \\ |−16|} \end{array}\)
Rellene\(<,\,>,\) o\(=\) para cada uno de los siguientes pares de números:
ⓐ\(−9 \_\_−|−9|\) ⓑ\(2 \_\_−|−2|\) ⓒ\(−8 \_\_|−8|\) ⓓ\(−(−9) \_\_|−9|.\)
- Contestar
-
ⓐ\(>\) ⓑ\(>\) ⓒ\(<\)
ⓓ\(=\)
Rellene\(<,>,\) o\(=\) para cada uno de los siguientes pares de números:
- \(7 \_\_ −|−7|\)
- \(−(−10) \_ \_|−10|\)
- \(|−4| \_\_ −|−4|\)
- \(−1 \_\_ |−1|.\)
- Contestar
-
ⓐ\(>\) ⓑ\(=\) ⓒ\(>\)
ⓓ\(<\)
Ahora agregamos barras de valor absoluto a nuestra lista de símbolos de agrupación. Cuando usamos el orden de las operaciones, primero simplificamos dentro de las barras de valor absoluto tanto como sea posible, luego tomamos el valor absoluto del número resultante.
\[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
En el siguiente ejemplo, primero simplificamos las expresiones dentro de las barras de valores absolutos tal como lo hacemos con los paréntesis.
Simplificar:\(\mathrm{24−|19−3(6−2)|}\).
- Contestar
-
\(\begin{array}{lc} \text{} & 24−|19−3(6−2)| \\ \text{Work inside parentheses first:} & \text{} \\ \text{subtract 2 from 6.} & 24−|19−3(4)| \\ \text{Multiply 3(4).} & 24−|19−12| \\ \text{Subtract inside the absolute value bars.} & 24−|7| \\ \text{Take the absolute value.} & 24−7 \\ \text{Subtract.} & 17 \end{array}\)
Simplificar:\(19−|11−4(3−1)|\).
- Contestar
-
16
Simplificar:\(9−|8−4(7−5)|\).
- Contestar
-
9
Sumar y restar números enteros
En lo que va de nuestros ejemplos, sólo hemos utilizado los números de conteo y los números enteros.
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3… \\ \text{Whole numbers} 0,1,2,3…. \end{array}\]
Nuestro trabajo con los opuestos nos da una forma de definir los enteros. Los números enteros y sus opuestos se llaman los enteros. Los enteros son los números\(…−3,−2,−1,0,1,2,3…\)
Los números enteros y sus opuestos se llaman los enteros.
Los enteros son los números
\[…-3,-2,-1,0,1,2,3…,\]
La mayoría de los estudiantes se sienten cómodos con los hechos de suma y resta para números positivos. Pero hacer sumar o restar tanto con números positivos como negativos puede ser más desafiante.
Utilizaremos dos contadores de color para modelar la suma y resta de negativos para que puedas visualizar los procedimientos en lugar de memorizar las reglas.
Dejamos que un color (azul) represente positivo. El otro color (rojo) representará los negativos.

Si tenemos un contador positivo y otro negativo, el valor del par es cero. Forman un par neutro. El valor de este par neutro es cero.
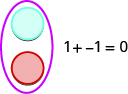
Usaremos los contadores para mostrar cómo agregar:
\[5+3 \; \; \; \; \; \; −5+(−3) \; \; \; \; \; \; −5+3 \; \; \; \; \; \; \; 5+(−3)\]
El primer ejemplo,\(5+3,\) agrega 5 positivos y 3 positivos, ambos positivos.
El segundo ejemplo,\(−5+(−3),\) agrega 5 negativos y 3 negativos, ambos negativos.
Cuando los signos son iguales, los contadores son todos del mismo color, y así los agregamos. En cada caso obtenemos 8, ya sea 8 positivos o 8 negativos.

Entonces, ¿qué pasa cuando los signos son diferentes? Vamos a agregar\(−5+3\) y\(5+(−3)\).
Cuando usamos contadores para modelar la suma de enteros positivos y negativos, es fácil ver si hay más contadores positivos o más negativos. Entonces sabemos si la suma será positiva o negativa.
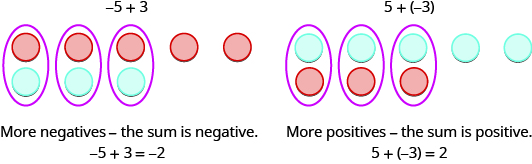
Agregar: ⓐ\(−1+(−4)\) ⓑ\(−1+5\) ⓒ\(1+(−5)\).
- Contestar
-
ⓐ
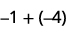

1 negativo más 4 negativos es 5 negativos 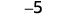
ⓑ
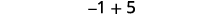

Hay más positivos, por lo que la suma es positiva. 
ⓒ
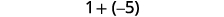

Hay más negativos, por lo que la suma es negativa. 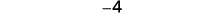
Agregar: ⓐ\(−2+(−4)\) ⓑ\(−2+4\) ⓒ\(2+(−4)\).
- Contestar
-
ⓐ\(−6\) ⓑ\(2\) ⓒ\(−2\)
Agregar: ⓐ\(−2+(−5)\) ⓑ\(−2+5\) ⓒ\(2+(−5)\).
- Contestar
-
ⓐ\(−7\) ⓑ\(3\) ⓒ\(−3\)
Seguiremos utilizando contadores para modelar la resta. Quizás cuando eras más joven, leías\(“5−3”\) como “5 quitan 3”. Cuando usas contadores, ¡puedes pensar en restar de la misma manera!
Usaremos los contadores para mostrar para restar:
\[5−3 \; \; \; \; \; \; −5−(−3) \; \; \; \; \; \; −5−3 \; \; \; \; \; \; 5−(−3) \]
El primer ejemplo\(5−3\),, restamos 3 positivos de 5 positivos y terminamos con 2 positivos.
En el segundo ejemplo,\(−5−(−3),\) restamos 3 negativos de 5 negativos y terminamos con 2 negativos.
En cada ejemplo se utilizaron contadores de un solo color, y el modelo “take away” de resta fue fácil de aplicar.
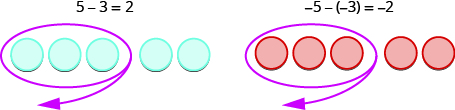
¿Qué pasa cuando tenemos que restar un número positivo y otro negativo? Tendremos que usar contadores tanto azules como rojos, así como algunos pares neutros. Si no tenemos el número de contadores necesarios para llevar, agregamos pares neutrales. Agregar un par neutro no cambia el valor. Es como cambiar trimestres a níqueles, el valor es el mismo, pero se ve diferente.
Echemos un vistazo a\(−5−3\) y\(5−(−3)\).
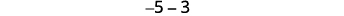 |
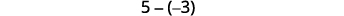 |
|
| Modele el primer número. |  |
 |
| Ahora agregamos los pares neutros necesarios. |  |
 |
| Eliminamos el número de contadores modelados por el segundo número. | 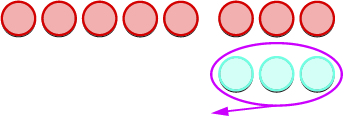 |
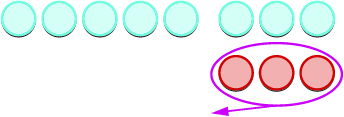 |
| Contar lo que queda. |  |
 |
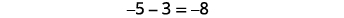 |
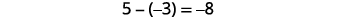 |
|
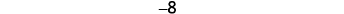 |
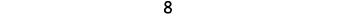 |
Restar: ⓐ\(3−1\) ⓑ\(−3−(−1)\) ⓒ\(−3−1\) ⓓ\(3−(−1)\).
- Contestar
-
ⓐ
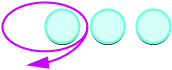
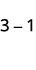
Toma 1 positivo de 3 positivos y obtén 2 positivos. 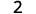
ⓑ

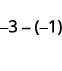
Toma 1 positivo de 3 negativos y consigue 2 negativos. 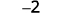
ⓒ

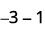
Toma 1 positivo del par neutro agregado. 
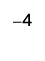
ⓓ

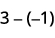
Toma 1 negativo del par neutro agregado. 

Restar: ⓐ\(6−4\) ⓑ\(−6−(−4)\) ⓒ\(−6−4\) ⓓ\(6−(−4)\).
- Contestar
-
ⓐ\(2\) ⓑ\(−2\) ⓒ\(−10\) ⓓ\(10\)
Restar: ⓐ\(7−4\) ⓑ\(−7−(−4)\) ⓒ\(−7−4\) ⓓ\(7−(−4)\).
- Contestar
-
ⓐ\(3\) ⓑ\(−3\) ⓒ\(−11\) ⓓ\(11\)
¿Te has dado cuenta de que la resta de números firmados se puede hacer sumando lo contrario? En el último ejemplo,\(−3−1\) es lo mismo que\(−3+(−1)\) y\(3−(−1)\) es lo mismo que\(3+1\). A menudo verás esta idea, la Propiedad de Resta, escrita de la siguiente manera:
\[a−b=a+(−b)\]
Restar un número es lo mismo que sumar su opuesto.
Simplifica: ⓐ\(13−8\) y\(13+(−8)\) ⓑ\(−17−9\) y\(−17+(−9)\) ⓒ\(9−(−15)\) y\(9+15\) ⓓ\(−7−(−4)\) y\(−7+4\).
- Contestar
-
ⓐ
\(\begin{array}{lccc} \text{} & 13−8 & \text{and} & 13+(−8) \\ \text{Subtract.} & 5 & \text{} & 5 \end{array}\)ⓑ
\(\begin{array}{lccc} \text{} & −17−9 & \text{and} & −17+(−9) \\ \text{Subtract.} & −26 & \text{} & −26 \end{array}\)
ⓒ
\(\begin{array}{lccc} \text{} & 9−(−15) & \text{and} & 9+15 \\ \text{Subtract.} & 24 & \text{} & 24 \end{array}\)
ⓓ
\(\begin{array}{lccc} \text{} & −7−(−4) & \text{and} & −7+4 \\ \text{Subtract.} & −3 & \text{} & −3 \end{array}\)
Simplifica: ⓐ\(21−13\) y\(21+(−13)\) ⓑ\(−11−7\) y\(−11+(−7)\) ⓒ\(6−(−13)\) y\(6+13\) ⓓ\(−5−(−1)\) y\(−5+1\).
- Contestar
-
ⓐ\(8,8\) ⓑ\(−18,−18\)
ⓒ\(19,19\) ⓓ\(−4,−4\)
Simplifica: ⓐ\(15−7\) y\(15+(−7)\) ⓑ\(−14−8\) y\(−14+(−8)\) ⓒ\(4−(−19)\) y\(4+19\) ⓓ\(−4−(−7)\) y\(−4+7\).
- Contestar
-
ⓐ\(8,8\) ⓑ\(−22,−22\)
ⓒ\(23,23\) ⓓ\(3,3\)
¿Qué sucede cuando hay más de tres enteros? Simplemente usamos el orden de las operaciones como de costumbre.
Simplificar:\(7−(−4−3)−9.\)
- Contestar
-
\(\begin{array}{lc} \text{} & 7−(−4−3)−9 \\ \text{Simplify inside the parentheses first.} & 7−(−7)−9 \\ \text{Subtract left to right.} & 14−9 \\ \text{Subtract.} & 5 \end{array}\)
Simplificar:\(8−(−3−1)−9.\)
- Contestar
-
3
Simplificar:\(12−(−9−6)−14.\)
- Contestar
-
13
Multiplicar y dividir enteros
Dado que la multiplicación es una taquigrafía matemática para la adición repetida, nuestro modelo se puede aplicar fácilmente para mostrar la multiplicación de enteros. Veamos este modelo concreto para ver qué patrones notamos. Usaremos los mismos ejemplos que usamos para sumar y restar. Aquí, estamos usando el modelo solo para ayudarnos a descubrir el patrón.
Recordamos que aba·b significa sumar a, b veces.
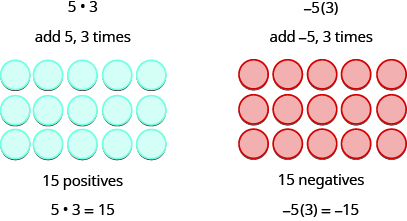
Los siguientes dos ejemplos son más interesantes. ¿Qué significa multiplicar 5 por −3? Significa restar 5,3 veces. Al mirar la resta como “quitar”, significa llevar 5, 3 veces. Pero no hay nada que quitar, así que empezamos por agregar pares neutrales en el espacio de trabajo.
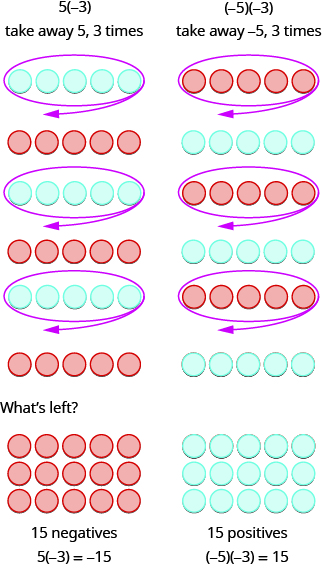
En resumen:
\[\begin{array}{ll} 5·3=15 & −5(3)=−15 \\ 5(−3)=−15 & (−5)(−3)=15 \end{array}\]
Observe que para la multiplicación de dos números firmados, cuando
\[ \text{signs are the } \textbf{same} \text{, the product is } \textbf{positive.} \\ \text{signs are } \textbf{different} \text{, the product is } \textbf{negative.} \]
¿Qué pasa con la división? La división es la operación inversa de la multiplicación. Entonces,\(15÷3=5\) porque\(15·3=15\). En palabras, esta expresión dice que 15 se pueden dividir en 3 grupos de 5 cada uno porque sumar cinco tres veces da 15. Si miras algunos ejemplos de multiplicar enteros, podrías averiguar las reglas para dividir enteros.
\[\begin{array}{lclrccl} 5·3=15 & \text{so} & 15÷3=5 & \text{ } −5(3)=−15 & \text{so} & −15÷3=−5 \\ (−5)(−3)=15 & \text{so} & 15÷(−3)=−5 & \text{ } 5(−3)=−15 & \text{so} & −15÷(−3)=5 \end{array}\]
La división sigue las mismas reglas que la multiplicación con respecto a los signos.
Para multiplicación y división de dos números firmados:
| Mismos signos | Resultado |
|---|---|
| • Dos aspectos positivos | Positivo |
| • Dos negativos | Positivo |
Si los signos son los mismos, el resultado es positivo.
| Distintas señales | Resultado |
|---|---|
| • Positivo y negativo | Negativo |
| • Negativo y positivo | Negativo |
Si los signos son diferentes, el resultado es negativo.
Multiplicar o dividir: ⓐ\(−100÷(−4)\) ⓑ\(7⋅6\) ⓒ\(4(−8)\) ⓓ\(−27÷3.\)
- Contestar
-
ⓐ
\(\begin{array}{lc} \text{} & −100÷(−4) \\ \text{Divide, with signs that are} \\ \text{the same the quotient is positive.} & 25 \end{array}\)
ⓑ
\(\begin{array} {lc} \text{} & 7·6 \\ \text{Multiply, with same signs.} & 42 \end{array}\)
ⓒ
\(\begin{array} {lc} \text{} & 4(−8) \\ \text{Multiply, with different signs.} & −32 \end{array}\)
ⓓ
\(\begin{array}{lc} \text{} & −27÷3 \\ \text{Divide, with different signs,} \\ \text{the quotient is negative.} & −9 \end{array}\)
Multiplicar o dividir: ⓐ\(−115÷(−5)\) ⓑ\(5⋅12\) ⓒ\(9(−7)\) ⓓ\(−63÷7.\)
- Contestar
-
ⓐ 23 ⓑ 60 ⓒ −63 ⓓ −9
Multiplicar o dividir: ⓐ\(−117÷(−3)\) ⓑ\(3⋅13\) ⓒ\(7(−4)\) ⓓ\(−42÷6\).
- Contestar
-
ⓐ 39 ⓑ 39 ⓒ −28 ⓓ −7
Cuando multiplicamos un número por 1, el resultado es el mismo número. Cada vez que multiplicamos un número por −1, ¡obtenemos su opuesto!
\[−1a=−a\]
Multiplicar un número por\(−1\) da su opuesto.
Simplificar expresiones con enteros
¿Qué sucede cuando hay más de dos números en una expresión? El orden de las operaciones sigue aplicándose cuando se incluyen los negativos. ¿Recuerdas por favor disculpe a mi querida tía Sally?
Vamos a probar algunos ejemplos. Simplificaremos las expresiones que utilizan las cuatro operaciones con enteros: suma, resta, multiplicación y división. Recuerda seguir el orden de las operaciones.
Simplificar: ⓐ\((−2)^4\) ⓑ\(−2^4\).
- Contestar
-
Observe la diferencia en las partes (a) y (b). En la parte (a), el exponente significa elevar lo que está entre paréntesis, la −2 a la 4ª potencia. En la parte (b), el exponente significa elevar solo la 2 a la 4ª potencia y luego tomar lo contrario.
ⓐ
\(\begin{array}{lc} \text{} & (−2)^4 \\ \text{Write in expanded form.} & (−2)(−2)(−2)(−2) \\ \text{Multiply.} & 4(−2)(−2) \\ \text{Multiply.} & −8(−2) \\ \text{Multiply.} & 16 \end{array}\)ⓑ
\(\begin{array}{lc} \text{} & −2^4 \\ \text{Write in expanded form.} & −(2·2·2·2) \\ \text{We are asked to find} & \text{} \\ \text{the opposite of }24. & \text{} \\ \text{Multiply.} & −(4·2·2) \\ \text{Multiply.} & −(8·2) \\ \text{Multiply.} & −16 \end{array}\)
Simplificar: ⓐ\((−3)^4\) ⓑ\(−3^4\).
- Contestar
-
ⓐ 81 ⓑ −81
Simplificar: ⓐ\((−7)^2\) ⓑ\(−7^2\).
- Contestar
-
ⓐ 49 ⓑ −49
El último ejemplo nos mostró la diferencia entre\((−2)^4\) y\(−2^4\). Esta distinción es importante para evitar futuros errores. El siguiente ejemplo nos recuerda multiplicar y dividir en orden de izquierda a derecha.
Simplificar: ⓐ\(8(−9)÷(−2)^3\) ⓑ\(−30÷2+(−3)(−7)\).
- Contestar
-
ⓐ
\(\begin{array}{lc} \text{} & 8(−9)÷(−2)^3 \\ \text{Exponents first.} & 8(−9)÷(−8) \\ \text{Multiply.} & −72÷(−8) \\ \text{Divide.} & 9 \end{array}\)
ⓑ
\(\begin{array}{lc} \text{} & −30÷2+(−3)(−7) \\ \text{Multiply and divide} \\ \text{left to right, so divide first.} & −15+(−3)(−7) \\ \text{Multiply.} & −15+21 \\ \text{Add.} & 6 \end{array}\)
Simplificar: ⓐ\(12(−9)÷(−3)^3\) ⓑ\(−27÷3+(−5)(−6).\)
- Contestar
-
ⓐ 4 ⓑ 21
Simplificar: ⓐ\(18(−4)÷(−2)^3\) ⓑ\(−32÷4+(−2)(−7).\)
- Contestar
-
ⓐ 9 ⓑ 6
Evaluar expresiones variables con números enteros
Recuerde que para evaluar una expresión significa sustituir un número por la variable en la expresión. Ahora podemos usar números negativos así como números positivos.
Evaluar\(4x^2−2xy+3y^2\) cuándo\(x=2,y=−1\).
- Contestar
-
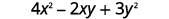
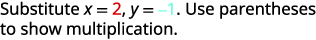
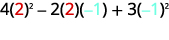
Simplifica los exponentes. 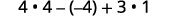
Multiplicar. 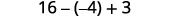
Resta. 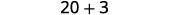
Agregar. 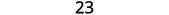
Evaluar:\(3x^2−2xy+6y^2\) cuándo\(x=1,y=−2\).
- Contestar
-
31
Evaluar:\(4x^2−xy+5y^2\) cuándo\(x=−2,y=3\).
- Contestar
-
67
Traducir frases a expresiones con números enteros
Nuestro trabajo anterior traduciendo el inglés al álgebra también se aplica a frases que incluyen números tanto positivos como negativos.
Traducir y simplificar: la suma de 8 y −12, incrementada en 3.
- Contestar
-
\(\begin{array}{lc} \text{} & \text{the } \textbf{sum } \underline{\text{of}} \; –8 \; \underline{\text{and}} −12 \text{ increased by } 3 \\ \text{Translate.} & [8+(−12)]+3 \\ \text{Simplify. Be careful not to confuse the} \; \; \; \; \; \; \; \; \; \; & (−4)+3 \\ \text{brackets with an absolute value sign.} \\ \text{Add.} & −1 \end{array}\)
Traducir y simplificar la suma de 9 y −16, incrementada en 4.
- Contestar
-
\((9+(−16))+4;−3\)
Traducir y simplificar la suma de −8 y −12, incrementada en 7.
- Contestar
-
\((−8+(−12))+7;−13\)
Usar números enteros en aplicaciones
Vamos a esbozar un plan para resolver aplicaciones. ¡Es difícil encontrar algo si no sabemos lo que estamos buscando o cómo llamarlo! Entonces, cuando resolvemos una aplicación, primero tenemos que determinar cuál es el problema que nos está pidiendo encontrar. Después escribiremos una frase que dé la información para encontrarla. Traduciremos la frase en una expresión y luego simplificaremos la expresión para obtener la respuesta. Por último, resumimos la respuesta en una oración para asegurarnos de que tenga sentido.
La temperatura en Kendallville, Indiana una mañana era de 11 grados. A media tarde, la temperatura había bajado a −9−9grados. ¿Cuál fue la diferencia en las temperaturas matutinas y vespertinas?
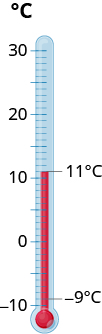
- Contestar
-






La temperatura en Anchorage, Alaska una mañana era de 15 grados. A media tarde la temperatura había bajado a 30 grados bajo cero. ¿Cuál fue la diferencia en las temperaturas matutinas y vespertinas?
- Contestar
-
La diferencia de temperaturas fue de 45 grados Fahrenheit.
La temperatura en Denver fue de −6 grados a la hora del almuerzo. Al atardecer la temperatura había bajado a −15 grados. ¿Cuál fue la diferencia en las temperaturas de la hora del almuerzo y del atardecer?
- Contestar
-
La diferencia de temperaturas fue de 9 grados.
- Lee el problema. Asegúrese de que se entiendan todas las palabras e ideas.
- Identificar lo que se nos pide encontrar.
- Escribe una frase que dé la información para encontrarla.
- Traducir la frase a una expresión.
- Simplifica la expresión.
- Contesta la pregunta con una oración completa.
Acceda a este recurso en línea para obtener instrucción adicional y práctica con números enteros.
- Restar enteros con contadores
Conceptos clave
- \[\begin{align} & −a \text{ means the opposite of the number }a \\ & \text{The notation} −a \text{ is read as “the opposite of }a \text{.”} \end{align} \]
- El valor absoluto de un número es su distancia de 0 en la recta numérica.
El valor absoluto de un número n se escribe como\(|n|\) y\(|n|≥0\) para todos los números.
Los valores absolutos son siempre mayores o iguales a cero.
- \[\begin{array}{lclc} \text{Parentheses} & () & \text{Braces} & \{ \} \\ \text{Brackets} & [] & \text{Absolute value} & ||\end{array}\]
- Propiedad de sustracción
\(a−b=a+(−b)\)
Restar un número es lo mismo que sumar su opuesto. - Para multiplicación y división de dos números firmados:
Si los signos son los mismos, el resultado es positivo.Mismos signos Resultado • Dos aspectos positivos Positivo • Dos negativos Positivo
Si los signos son diferentes, el resultado es negativo.Distintas señales Resultado • Positivo y negativo Negativo • Negativo y positivo Negativo - Multiplicación por\(−1\)
\(−1a=−a\)
Multiplicar un número por\(−1\) da su opuesto.
- Cómo Usar Enteros en Aplicaciones.
- Lee el problema. Asegúrese de que todas las palabras e ideas sean entendidas
- Identificar lo que se nos pide encontrar.
- Escribe una frase que dé la información para encontrarla.
- Traducir la frase a una expresión.
- Simplifica la expresión.
- Contesta la pregunta con una oración completa.
Glosario
- valor absoluto
- El valor absoluto de un número es su distancia desde\(0\) la línea numérica.
- enteros
- Los números enteros y sus opuestos se llaman los enteros.
- números negativos
- Los números menores que\(0\) son números negativos.
- opuesto
- Lo contrario de un número es el número que está a la misma distancia de cero en la recta numérica pero en el lado opuesto de cero.


