1.4: Fracciones
- Page ID
- 112425
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Simplificar fracciones
- Multiplicar y dividir fracciones
- Sumar y restar fracciones
- Utilizar el orden de las operaciones para simplificar las fracciones
- Evaluar expresiones variables con fracciones
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Álgebra elemental, Fundaciones.
Simplificar fracciones
Una fracción es una forma de representar partes de un todo. La fracción\(\frac{2}{3}\) representa dos de tres partes iguales (Figura\(\PageIndex{1}\)). En la fracción\(\frac{2}{3}\), al 2 se le llama numerador y al 3 se le llama denominador. La línea se llama barra de fracción.
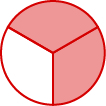
Figura\(\PageIndex{1}\): En el círculo,\(\frac{2}{3}\) del círculo está sombreado—2 de las 3 partes iguales.
Se escribe una fracción\(\dfrac{a}{b}\), donde\(b\neq 0\) y
\(a\)es el numerador y\(b\) es el denominador.
Una fracción representa partes de un todo. El denominador\(b\) es el número de partes iguales en las que se ha dividido el conjunto, y el numerador\(a\) indica cuántas partes están incluidas.
Las fracciones que tienen el mismo valor son fracciones equivalentes. Las fracciones equivalentes
La propiedad nos permite encontrar fracciones equivalentes y también simplificar fracciones.
Si\(a\),\(b\), y\(c\) son números donde\(b\neq 0,c\neq 0\),
entonces\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\) y\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
Una fracción se considera simplificada si no hay factores comunes, distintos de 1, en su numerador y denominador.
Por ejemplo,
\(\dfrac{2}{3}\)se simplifica porque no hay factores comunes de\(2\) y\(3\).
\(\dfrac{10}{15}\)no se simplifica porque\(5\) es un factor común de\(10\) y\(15\).
Simplificamos o simplificamos una fracción eliminando los factores comunes del numerador y el denominador. Una fracción no se simplifica hasta que se hayan eliminado todos los factores comunes. Si una expresión tiene fracciones, no se simplifica completamente hasta que se simplifican las fracciones.
A veces puede que no sea fácil encontrar factores comunes del numerador y denominador. Cuando esto sucede, una buena idea es facturar el numerador y el denominador en números primos. Luego divida los factores comunes usando la Propiedad de Fracciones Equivalentes.
Simplificar\(\dfrac{−315}{770}\).
- Contestar
-



Simplificar\(−\dfrac{69}{120}\).
- Contestar
-
\(−\dfrac{23}{40}\)
Simplificar\(−\dfrac{120}{192}\).
- Responder
-
\(−\dfrac{5}{8}\)
Ahora resumimos los pasos que debes seguir para simplificar fracciones.
- Reescribir el numerador y denominador para mostrar los factores comunes.
Si es necesario, factive primero el numerador y el denominador en números primos. - Simplifique el uso de la Propiedad Fracciones Equivalentes dividiendo los factores comunes.
- Multiplique cualquier factor restante.
Multiplicar y dividir fracciones
A muchas personas les resulta más fácil multiplicar y dividir fracciones que sumar y restar fracciones.
Para multiplicar fracciones, multiplicamos los numeradores y multiplicamos los denominadores.
Si\(a\),\(b\),\(c\), y\(d\) son números donde\(b≠0\), y\(d≠0\), entonces
\[\frac{a}{b}·\frac{c}{d}=\frac{ac}{bd}\]
Para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores.
Al multiplicar fracciones, las propiedades de los números positivos y negativos siguen aplicándose, por supuesto. Es una buena idea determinar el signo del producto como primer paso. En Ejemplo, vamos a multiplicar negativo y un positivo, por lo que el producto será negativo.
Al multiplicar una fracción por un entero, puede ser útil escribir el entero como una fracción. Cualquier entero, a, puede escribirse como\(\dfrac{a}{1}\). Entonces, por ejemplo,\(3=\dfrac{3}{1}\).
Multiplicar:\(−\dfrac{12}{5}(−20x).\)
- Responder
-
El primer paso es encontrar el signo del producto. Dado que los signos son los mismos, el producto es positivo.
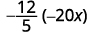
Determinar el signo del producto. Los signos son los mismos, por lo que el producto es positivo.
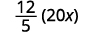
Escribe 20 x como una fracción. 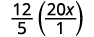
Multiplicar. 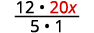
Reescribe 20 para mostrar el factor común 5 y dividirlo.
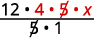
Simplificar. 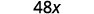
Multiplicar:\(\dfrac{1}{13}(−9a)\).
- Responder
-
\(−33a\)
Multiplicar:\(\dfrac{13}{7}(−14b)\).
- Responder
-
\(−26b\)
Ahora que sabemos multiplicar fracciones, estamos casi listos para dividirnos. Antes de que podamos hacer eso, necesitamos algo de vocabulario. El recíproco de una fracción se encuentra invirtiendo la fracción, colocando el numerador en el denominador y el denominador en el numerador. El recíproco de\(\frac{2}{3}\) es\(\frac{3}{2}\). Ya que 4 se escribe en forma de fracción como\(\frac{4}{1}\), el recíproco de 4 es\(\frac{1}{4}\).
Para dividir fracciones, multiplicamos la primera fracción por la recíproca de la segunda.
Si\(a\),\(b\),\(c\), y\(d\) son números donde\(b≠0\),\(c≠0\), y\(d≠0\), entonces
\[\frac{a}{b}÷\frac{c}{d}=\frac{a}{b}⋅\frac{d}{c}\]
Para dividir fracciones, multiplicamos la primera fracción por la recíproca de la segunda.
Tenemos que decir\(b≠0\),\(c≠0\), y\(d≠0\), para estar seguros de que no dividimos por cero!
Encuentra el cociente:\(−\dfrac{7}{18}÷(−\dfrac{14}{27}).\)
- Responder
-
\(−\dfrac{7}{18}÷(−\dfrac{14}{27})\) Para dividir, multiplicar la primera fracción por el recíproco de la segunda.
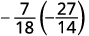
Determinar el signo del producto, y luego multiplicar.
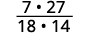
Reescritura mostrando factores comunes. 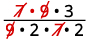
Eliminar factores comunes. 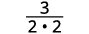
Simplificar. 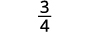
Dividir:\(−\dfrac{7}{27}÷(−\dfrac{35}{36})\).
- Responder
-
\(\dfrac{4}{15}\)
Dividir:\(−\dfrac{5}{14}÷(−\dfrac{15}{28}).\)
- Responder
-
\(\dfrac{2}{3}\)
Los numeradores o denominadores de algunas fracciones contienen fracciones en sí mismas. Una fracción en la que el numerador o el denominador es una fracción se denomina fracción compleja.
Una fracción compleja es una fracción en la que el numerador o el denominador contiene una fracción.
\[\dfrac{\frac{6}{7}}{3} \quad \dfrac{\frac{3}{4}}{\frac{5}{8}} \quad \dfrac{\frac{x}{2}}{ \frac{5}{6}}\]
Para simplificar una fracción compleja, recuerde que la barra de fracciones significa división. Por ejemplo, la fracción compleja\(\dfrac{\frac{3}{4}}{\frac{5}{8}}\) significa\(\dfrac{3}{4}÷\frac{5}{8}.\)
Simplificar:\(\dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}}\).
- Responder
-
\(\begin{array}{lc} \text{} & \dfrac{\dfrac{x}{2}}{ \dfrac{xy}{6}} \\[6pt] \text{Rewrite as division.} & \dfrac{x}{2}÷\dfrac{xy}{6} \\[6pt] \text{Multiply the first fraction by the reciprocal of the second.} & \dfrac{x}{2}·\dfrac{6}{xy} \\[6pt] \text{Multiply.} & \dfrac{x·6}{2·xy} \\[6pt] \text{Look for common factors.} & \dfrac{ \cancel{x}·3·\cancel{2}}{\cancel{2}·\cancel{x}·y} \\[6pt] \text{Divide common factors and simplify.} & \dfrac{3}{y} \end{array}\)
Simplificar:\(\dfrac{\dfrac{a}{8}}{ \dfrac{ab}{6}}\).
- Responder
-
\(\dfrac{3}{4b}\)
Simplificar:\(\dfrac{\dfrac{p}{2}}{ \dfrac{pq}{8}}\).
- Responder
-
\(\dfrac{4}{q}\)
Sumar y restar fracciones
Cuando multiplicamos fracciones, simplemente multiplicamos los numeradores y multiplicamos los denominadores directamente. Para sumar o restar fracciones, deben tener un denominador común.
Si\(a\),\(b\), y\(c\) son los números donde\(c≠0\), entonces
\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\]
Para sumar o restar fracciones, sumar o restar los numeradores y colocar el resultado sobre el denominador común.
El mínimo denominador común (LCD) de dos fracciones es el número más pequeño que se puede utilizar como denominador común de las fracciones. El LCD de las dos fracciones es el múltiplo menos común (LCM) de sus denominadores.
El mínimo común denominador (LCD) de dos fracciones es el mínimo común múltiplo (LCM) de sus denominadores.
Después de encontrar el mínimo denominador común de dos fracciones, convertimos las fracciones a fracciones equivalentes con la LCD. ¡Armando estos pasos nos permite sumar y restar fracciones porque sus denominadores serán los mismos!
Agregar:\(\dfrac{7}{12}+\dfrac{5}{18}\).
- Responder
-



Agregar:\(\dfrac{7}{12}+\dfrac{11}{15}\).
- Responder
-
\(\dfrac{79}{60}\)
Agregar:\(\dfrac{13}{15}+\dfrac{17}{20}\).
- Responder
-
\(\dfrac{103}{60}\)
- ¿Tienen un denominador común?
- Sí—vaya al paso 2.
- No: reescribe cada fracción con la pantalla LCD (mínimo denominador común).
- Encuentra la pantalla LCD.
- Cambia cada fracción en una fracción equivalente con la LCD como denominador.
- Sumar o restar las fracciones.
- Simplificar, si es posible.
Ahora tenemos las cuatro operaciones para fracciones. La tabla resume las operaciones de fracciones.
| Multiplicación de Fracciones | División de Fracciones |
|---|---|
| \(\dfrac{a}{b}⋅\dfrac{c}{d}=\dfrac{ac}{bd}\) | \(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\) |
| Multiplicar los numeradores y multiplicar los denominadores | Multiplicar la primera fracción por el recíproco de la segunda. |
| Adición de Fracciones | Resta de Fracciones |
| \(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}\) | \(\dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\) |
| Agrega los numeradores y coloca la suma sobre el denominador común. | Restar los numeradores y colocar la diferencia sobre el denominador común. |
|
Para multiplicar o dividir fracciones, NO se necesita una pantalla LCD. Para sumar o restar fracciones, se necesita una pantalla LCD. |
|
Al iniciar un ejercicio, siempre identifique la operación y luego recuerde los métodos necesarios para esa operación.
Simplificar: ⓐ\(\dfrac{5x}{6}−\dfrac{3}{10}\) ⓑ\(\dfrac{5x}{6}·\dfrac{3}{10}\).
- Responder
-
Primero pregunta: “¿Cuál es la operación?” Identificar la operación determinará si necesitamos o no un denominador común. Recuerden, necesitamos un denominador común para sumar o restar, pero no para multiplicar o dividir.
ⓐ
\ (\ begin {array} {lc}\ text {¿Cuál es la operación? La operación es resta.}\\ [6pt]\ text {¿Las fracciones tienen un denominador común? No.} &\ dfrac {5x} {6} −\ dfrac {3} {10}\\ [6pt]\ text {Encuentra la pantalla LCD de} 6\ text {y} 10 &\ text {La LCD es 30.}\\ [6pt] {\ begin {align*} 6 & =2·3\ [6pt]
\;\;\ subrayado {\;\;\; 10\;\;\;\;} &\ subrayado {=2·5\;\;\;\;}\;\;\ [6pt]
\ texto {LCD} & =2·3·5\\ [6 pt]
\ text {LCD} & =30\ end {align*}}\\ [6pt]\\\
\\ text {Reescribe cada fracción como fracción equivalente con la LCD.} &\ dfrac {5x·5} {6·5} −\ dfrac {3·3} {10·3}\\ [6pt]
\ text {} &\ dfrac {25x} {30} −\ dfrac {9} {30}\\ [6pt]
\ text {Restar los numeradores y colocar el}\\ [6pt]
\ text {diferencia sobre el común denominadores.} &\ dfrac {25x−9} {30}\\ [6pt]\\\\
\ text {Simplifica, si es posible.No hay factores comunes.}\\ [6pt]
\ text {La fracción se simplifica.} \ end {array}\)ⓑ
\(\begin{array}{lc} \text{What is the operation? Multiplication.} & \dfrac{25x}{6}·\dfrac{3}{10} \\ \text{To multiply fractions,multiply the numerators} \\ \text{and multiply the denominators.} & \dfrac{25x·3}{6·10} \\ \text{Rewrite, showing common factors.} \\ \text{Remove common factors.} & \dfrac{\cancel{5} x · \cancel{3}}{2·\cancel{3}·2·\cancel{5}} \\ \text{Simplify.} & \dfrac{x}{4} \end{array}\)
Observe, necesitábamos una pantalla LCD para agregar\(\dfrac{25x}{6}−\dfrac{3}{10}\), pero no para multiplicar\(\dfrac{25x}{6}⋅\dfrac{3}{10}\).
Simplificar: ⓐ\(\dfrac{3a}{4}−\dfrac{8}{9}\) ⓑ\(\dfrac{3a}{4}·\dfrac{8}{9}\).
- Responder
-
ⓐ\(\dfrac{27a−32}{36}\) ⓑ\(\dfrac{2a}{3}\)
Simplificar: ⓐ\(\dfrac{4k}{5}−\dfrac{1}{6}\) ⓑ\(\dfrac{4k}{5}⋅\dfrac{1}{6}\).
- Responder
-
ⓐ\(\dfrac{24k−5}{30}\) ⓑ\(\dfrac{2k}{15}\)
Utilizar el orden de operaciones para simplificar fracciones
La barra de fracción en una fracción actúa como símbolo de agrupación. El orden de las operaciones nos dice entonces que simplifiquemos el numerador y luego el denominador. Entonces dividimos.
- Simplifica la expresión en el numerador. Simplifica la expresión en el denominador.
- Simplifica la fracción.
¿A dónde va el signo negativo en una fracción? Por lo general, el signo negativo está frente a la fracción, pero a veces verá una fracción con un numerador negativo, o a veces con un denominador negativo. Recuerda que las fracciones representan división. Cuando el numerador y el denominador tienen signos diferentes, el cociente es negativo.
\[\dfrac{−1}{3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{negative}}{\text{positive}}=\text{negative}\]
\[\dfrac{1}{−3}=−\dfrac{1}{3} \; \; \; \; \; \; \dfrac{\text{positive}}{\text{negative}}=\text{negative}\]
Para cualquier número positivo\(a\) y\(b\),
\[\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\]
Simplificar:\(\dfrac{4(−3)+6(−2)}{−3(2)−2}\).
- Responder
-
La barra de fracciones actúa como un símbolo de agrupación. Así que simplifica completamente el numerador y el denominador por separado.
\(\begin{array}{lc} \text{} & \dfrac{4(−3)+6(−2)}{−3(2)−2} \\[5pt] \text{Multiply.} & \dfrac{−12+(−12)}{−6−2} \\[5pt] \text{Simplify.} & \dfrac{−24}{−8} \\[5pt] \text{Divide.} & 3 \end{array}\)
Simplificar:\(\dfrac{8(−2)+4(−3)}{−5(2)+3}\).
- Responder
-
4
Simplificar:\(\dfrac{7(−1)+9(−3)}{−5(3)−2}\).
- Responder
-
2
Ahora veremos fracciones complejas donde el numerador o denominador contiene una expresión que se puede simplificar. Entonces primero debemos simplificar completamente el numerador y el denominador por separado usando el orden de las operaciones. Luego dividimos el numerador por el denominador ya que la barra de fracción significa división.
Simplificar:\(\dfrac{\left(\frac{1}{2}\right)^2}{4+3^2}\).
- Responder
-
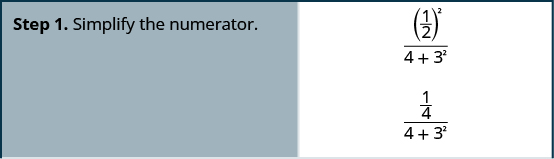


Simplificar:\(\dfrac{\left(\frac{1}{3}\right)^2}{2^3+2}\).
- Responder
-
\(\frac{1}{90}\)
Simplificar:\(\dfrac{1+4^2}{\left(\frac{1}{4}\right)^2}\).
- Responder
-
272
- Simplifica el numerador.
- Simplifica el denominador.
- Divide el numerador por el denominador. Simplificar si es posible.
Simplificar:\(\dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}}\).
- Responder
-
Puede ayudar poner paréntesis alrededor del numerador y el denominador.
\(\begin{array}{lc}\text{} & \dfrac{\dfrac{1}{2}+\dfrac{2}{3}}{\dfrac{3}{4}−\dfrac{1}{6}} \\[6pt] \text{Simplify the numerator }(LCD=6)\text{ and } \\[6pt] \text{simplify the denominator }(LCD=12). & \dfrac{\left(\dfrac{3}{6}+\dfrac{4}{6}\right)}{\left(\dfrac{9}{12}−\dfrac{2}{12}\right)} \\[6pt] \text{Simplify.} & \left(\dfrac{7}{6}\right)\left(\dfrac{7}{12}\right) \\[6pt] \text{Divide the numerator by the denominator.} & \dfrac{7}{6}÷\dfrac{7}{12} \\[6pt] \text{Simplify.} & \dfrac{7}{6}⋅\dfrac{12}{7} \\[6pt] \text{Divide out common factors.} & \dfrac{\cancel{7}⋅\cancel{6}⋅2}{ \cancel{6}⋅\cancel{7}⋅1} \\[6pt] \text{Simplify.} & 2 \end{array}\)
Simplificar:\( \dfrac{\dfrac{1}{3}+\dfrac{1}{2}}{ \dfrac{3}{4}−\dfrac{1}{3}}\).
- Responder
-
2
Simplificar:\(\dfrac{\dfrac{2}{3}−\dfrac{1}{2}}{ \dfrac{1}{4}+\dfrac{1}{3}}\).
- Responder
-
\(\frac{2}{7}\)
Evaluar expresiones variables con fracciones
Hemos evaluado expresiones antes, pero ahora podemos evaluar expresiones con fracciones. Recuerde, para evaluar una expresión, sustituimos el valor de la variable en la expresión y luego simplificamos.
Evaluar\(2x^2y\) cuándo\(x=\frac{1}{4}\) y\(y=−\frac{2}{3}\).
- Responder
-
Sustituir los valores en la expresión.
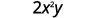
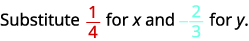
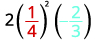
Simplifique primero los exponentes. 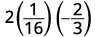
Multiplicar; dividir los factores comunes. Observe que escribimos 16 como 2242·2·4 para que sea fácil eliminar factores comunes. 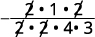
Simplificar. 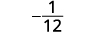
Evaluar\(3ab^2\) cuándo\(a=−\frac{2}{3}\) y\(b=−\frac{1}{2}\).
- Responder
-
\(−\dfrac{1}{2}\)
Evaluar\(4c^3d\) cuándo\(c=−\frac{1}{2}\) y\(d=−\frac{4}{3}\).
- Responder
-
\(\dfrac{2}{3}\)
Acceda a este recurso en línea para obtener instrucción adicional y práctica con fracciones.
- Sumando fracciones con denominadores diferentes
Conceptos clave
- Si\(a\),\(b\), y\(c\) son los números donde\(b≠0,c≠0\), entonces
\(\dfrac{a}{b}=\dfrac{a·c}{b·c}\)y\(\dfrac{a·c}{b·c}=\dfrac{a}{b}.\)
- Como simplificar una fracción.
- Reescribir el numerador y denominador para mostrar los factores comunes.
Si es necesario, factive primero el numerador y el denominador en números primos. - Simplifique el uso de la Propiedad Fracciones Equivalentes dividiendo los factores comunes.
- Multiplique cualquier factor restante.
- Reescribir el numerador y denominador para mostrar los factores comunes.
- Si\(a\),\(b\),\(c\), y\(d\) son números donde\(b≠0\), y\(d≠0\), entonces
\(\dfrac{a}{b}·\dfrac{c}{d}=\dfrac{ac}{bd}\)
Para multiplicar fracciones, multiplicar los numeradores y multiplicar los denominadores.
- Si\(a\),\(b\),\(c\), y\(d\) son números donde\(b≠0\),\(c≠0\), y\(d≠0\), entonces
\(\dfrac{a}{b}÷\dfrac{c}{d}=\dfrac{a}{b}⋅\dfrac{d}{c}\)
Para dividir fracciones, multiplicamos la primera fracción por la recíproca de la segunda.
- Si\(a\),\(b\), y\(c\) son los números donde\(c≠0\), entonces
\(\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \text{ and } \dfrac{a}{c}−\dfrac{b}{c}=\dfrac{a−b}{c}\)
Para sumar o restar fracciones, sumar o restar los numeradores y colocar el resultado sobre el denominador común.
- Cómo sumar o restar fracciones.
- ¿Tienen un denominador común?
- Sí—vaya al paso 2.
- No: reescribe cada fracción con la pantalla LCD (mínimo denominador común).
- Encuentra la pantalla LCD.
- Cambia cada fracción en una fracción equivalente con la LCD como denominador.
- Sumar o restar las fracciones.
- Simplificar, si es posible.
- ¿Tienen un denominador común?
- Como simplificar una expresión con una barra de fracciones.
- Simplifica la expresión en el numerador. Simplifica la expresión en el denominador.
- Simplifica la fracción.
- Para cualquier número positivo\(a\) y\(b\),
\(\dfrac{−a}{b}=\dfrac{a}{−b}=−\dfrac{a}{b}\)
- Cómo simplificar fracciones complejas.
- Simplifica el numerador.
- Simplifica el denominador.
- Divide el numerador por el denominador. Simplificar si es posible.
Glosario
- fracción compleja
- Una fracción en la que el numerador o el denominador es una fracción se denomina fracción compleja.
- denominador
- En una fracción, escrita\(\dfrac{a}{b}\), donde\(b≠0\), el denominador\(b\) es el número de partes iguales en las que se ha dividido el conjunto.
- fracciones equivalentes
- Las fracciones equivalentes son fracciones que tienen el mismo valor.
- fracción
- Se escribe una fracción\(\dfrac{a}{b}\), donde\(b≠0\), y a es el numerador y\(b\) es el denominador. Una fracción representa partes de un todo.
- mínimo común denominador
- El mínimo común denominador (LCD) de dos fracciones es el mínimo común múltiplo (LCM) de sus denominadores.
- numerador
- En una fracción, escrita\(\dfrac{a}{b}\), donde\(b≠0\), el numerador a indica cuántas partes se incluyen.
- recíproco
- El recíproco de una fracción se encuentra invirtiendo la fracción, colocando el numerador en el denominador y el denominador en el numerador.


