1.3E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112434

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Simplificar expresiones con valor absoluto

En los siguientes ejercicios, rellene$<,>,$ o$=$ para cada uno de los siguientes pares de números.

1. ⓐ$|−7| \text{ ___ }−|−7|$

ⓑ$6 \text{ ___ }−|−6|$

ⓒ$|−11|\text{ ___ }−11$

ⓓ$−(−13)\text{ ___ }−|−13|$

Responder: ⓐ$>$ ⓑ$>$ ⓒ$>$ ⓓ$>$

2. ⓐ$−|−9| \text{ ___ } |−9|$

ⓑ$−8 \text{ ___ } |−8| $

ⓒ$|−1| \text{ ___ } −1 $

ⓓ$−(−14) \text{ ___ } −|−14|$

3. ⓐ$−|2| \text{ ___ }−|−2|$

ⓑ$−12 \text{ ___ }−|−12|$

ⓒ$|−3| \text{ ___ }−3$

ⓓ$|−19| \text{ ___ }−(−19) $

Responder: ⓐ$=$ ⓑ$=$ ⓒ$>$ ⓓ$=$

4. ⓐ$−|−4| \text{ ___ } −|4| $

ⓑ$5 \text{ ___ } −|−5| $

ⓒ$ −|−10| \text{ ___ } −10 $

ⓓ$−|−0| \text{ ___ } −(−0) $

En los siguientes ejercicios, simplifique.

5. $|15−7|−|14−6|$

Responder: 0

6. $|17−8|−|13−4|$

7. $18−|2(8−3)|$

Responder: 8

8. $15−|3(8−5)|$

9. $18−|12−4(4−1)+3|$

Responder: 15

10. $27−|19+4(3−1)−7|$

11. $10−3|9−3(3−1)|$

Responder: 1

12. $13−2|11−2(5−2)|$

Sumar y restar números enteros

En los siguientes ejercicios, simplifique cada expresión.

13. ⓐ$−7+(−4)$

ⓑ$−7+4$

ⓒ$7+(−4).$

Responder: ⓐ$−11$ ⓑ$−3$ ⓒ$3$

14. ⓐ$−5+(−9)$

ⓑ$−5+9$

ⓒ$5+(−9)$

15. $48+(−16)$

Responder: 32

16. $34+(−19)$

17. $−14+(−12)+4$

Responder: $-22$

18. $−17+(−18)+6$

19. $19+2(−3+8)$

Responder: $29$

20. $24+3(−5+9)$

21. ⓐ$13−7$

ⓑ$−13−(−7)$

ⓒ$−13−7$

ⓓ$13−(−7)$

Contestar: ⓐ 6 ⓑ −6 ⓒ −20 ⓓ 20

22. ⓐ$15−8$

ⓑ$−15−(−8)$

ⓒ$−15−8$

ⓓ$15−(−8)$

23. $−17−42$

Contestar: $-59$

24. $−58−(−67)$

25. $−14−(−27)+9$

Contestar: 22

26. $64+(−17)−9$

27. ⓐ$44−28$ ⓑ$44+(−28)$

Contestar: ⓐ 16 ⓑ 16

28. ⓐ$35−16$ ⓑ$35+(−16)$

29. ⓐ$27−(−18)$ ⓑ$27+18$

Contestar: ⓐ 45 ⓑ 45

30. ⓐ$46−(−37)$ ⓑ$46+37$

31. $(2−7)−(3−8)$

Contestar: 0

32. $(1−8)−(2−9)$

33. $−(6−8)−(2−4)$

Contestar: 4

34. $−(4−5)−(7−8)$

35. $25−[10−(3−12)]$

Contestar: 6

36. $32−[5−(15−20)]$

Multiplicar y dividir enteros

En los siguientes ejercicios, multiplique o divida.

37. ⓐ$−4⋅8$

ⓑ$13(−5)$

ⓒ$−24÷6$

ⓓ$−52÷(−4)$

Contestar: ⓐ$−32$ ⓑ$−65$ ⓒ$−4$ ⓓ$13$

38. ⓐ$−3⋅9$

ⓑ$9(−7)$

ⓒ$35÷(−7)$

ⓓ$−84÷(−6)$

39. ⓐ$−28÷7$

ⓑ$−180÷15$

ⓒ$3(−13)$

ⓓ$−1(−14)$

Contestar: ⓐ$−4$ ⓑ$−12$ ⓒ$−39$ ⓓ$14$

40. ⓐ$−36÷4$

ⓑ$−192÷12$

ⓒ$9(−7)$

ⓓ$−1(−19)$

Simplificar y evaluar expresiones con números enteros

En los siguientes ejercicios, simplifique cada expresión.

41. ⓐ$(−2)^6$ ⓑ$−2^6$

Contestar: ⓐ$64$ ⓑ$−64$

42. ⓐ$(−3)^5$ ⓑ$−3^5$

43. $5(−6)+7(−2)−3$

Contestar: $−47$

44. $8(−4)+5(−4)−6$

45. $−3(−5)(6)$

Contestar: $90$

46. $−4(−6)(3)$

47. $(8−11)(9−12)$

Contestar: $9$

48. $(6−11)(8−13)$

49. $26−3(2−7)$

Contestar: $41$

50. $23−2(4−6)$

51. $65÷(−5)+(−28)÷(−7)$

Contestar: $-9$

52. $52÷(−4)+(−32)÷(−8)$

53. $9−2[3−8(−2)]$

Contestar: $-29$

54. $11−3[7−4(−2)]$

55. $8−|2−4(4−1)+3|$

Contestar: $1$

56. $7−|5−3(4−1)−6|$

57. $9−3|2(2−6)−(3−7)|$

Contestar: $-3$

58. $5−2|2(1−4)−(2−5)|$

59. $(−3)^2−24÷(8−2)$

Contestar: $5$

60. $(−4)^2−32÷(12−4)$

En los siguientes ejercicios, evalúe cada expresión.

61. $y+(−14)$cuando ⓐ$y=−33$ ⓑ$y=30$

Contestar: ⓐ$−47$ ⓑ$16$

62. $x+(−21)$cuando ⓐ$x=−27$ ⓑ$x=44$

63. $(x+y)^2$cuándo$x=−3$ y$y=14$

Contestar: $121$

64. $(y+z)^2$cuándo$y=−3$ y$z=15$

65. $9a−2b−8$cuándo$a=−6$ y$b=−3$

Contestar: $-56$

66. $7m−4n−2$cuándo$m=−4$ y$n=−9$

67. $3x^2−4xy+2y^2$cuándo$x=−2$ y$y=−3$

Contestar: $6$

68. $4x^2−xy+3y^2$cuándo$x=−3$ y$y=−2$

Traducir frases en inglés a expresiones algebraicas

En los siguientes ejercicios, traduzca a una expresión algebraica y simplifique si es posible.

69. la suma de 3 y −15, incrementada en 7

Contestar: $(3+(−15))+7;−5$

70. la suma de$−8$ y$−9$, incrementada en$23$

71. ⓐ la diferencia de$10$ y$−18$

ⓑ restar$11$ de$−25$

Contestar

ⓐ$10−(−18);28$

ⓑ$−25−11;−36$

72. ⓐ la diferencia de$−5$ y$−30$

ⓑ restar$−6$ de$−13$

73. el cociente de$−6$ y la suma de$a$ y$b$

Contestar: $\dfrac{−6}{a+b}$

74. el producto de$−13$ y la diferencia de$c$ y$d$

Usar números enteros en aplicaciones

En los siguientes ejercicios, resuelve.

75. Temperatura El 15 de enero, la alta temperatura en Anaheim, California, fue$84°$. Ese mismo día, la alta temperatura en Embarrass, Minnesota, fue$−12°$. ¿Cuál fue la diferencia entre la temperatura en Anaheim y la temperatura en Embarrass?

Contestar: $96^\circ$

76. Temperatura El 21 de enero, la alta temperatura en Palm Springs, California, era$89°$, y la alta temperatura en Whitefield, New Hampshire, fue$−31°$. ¿Cuál fue la diferencia entre la temperatura en Palm Springs y la temperatura en Whitefield?

77. Futbol En el primer down, los Chargers tenían el balón en su línea de 25 yardas. En las siguientes tres bajas, perdieron 6 yardas, ganaron 10 yardas y perdieron 8 yardas. ¿Cuál era la línea de yarda al final de la cuarta bajada?

Contestar: 21

78. Futbol En el primer down, los Steelers tenían el balón en su línea de 30 yardas. En las siguientes tres bajadas, ganaron 9 yardas, perdieron 14 yardas y perdieron 2 yardas. ¿Cuál era la línea de yarda al final de la cuarta bajada?

79. Cuenta corriente Mayra tiene 124 dólares en su cuenta corriente. Ella escribe un cheque por 152 dólares. ¿Cuál es el nuevo saldo en su cuenta corriente?

Contestar: $−\$ 28$

80. Cuenta corriente Reymonte tiene saldo$−$49$ en su cuenta corriente. Deposita 281 dólares en la cuenta. ¿Cuál es el nuevo saldo?

Ejercicios de escritura

81. Explique por qué la suma de −8 y 2 es negativa, pero la suma de 8 y −2 es positiva.

Contestar: Las respuestas variarán.

82. Da un ejemplo de tu experiencia de vida de sumar dos números negativos.

83. En sus propias palabras, establezca las reglas para multiplicar y dividir enteros.

Contestar: Las respuestas variarán.

84. ¿Por qué es$−4^3=(−4)^3$?

Autocomprobación

ⓐ Después de completar los EJEMPLOS, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

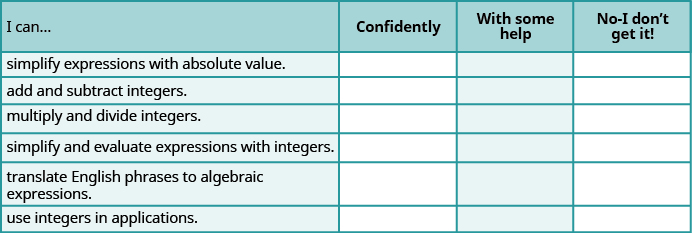
$Esta tabla tiene 4 columnas, 6 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna puedo, con confianza, con algo de ayuda y no, no la entiendo. La primera columna tiene las siguientes declaraciones: simplificar expresiones con valor absoluto, sumar y restar enteros, multiplicar y dividir enteros, simplificar y evaluar expresiones con enteros, traducir frases en inglés a expresiones algebraicas, usar enteros en aplicaciones. Las columnas restantes están en blanco.$

ⓑ Después de revisar esta lista de verificación, ¿qué harás para tener confianza en todos los objetivos?

Search

Text Color

Text Size

Margin Size

Font Type