1.5: Decimales
- Page ID
- 112484
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Decimales redondos
- Sumar y restar decimales
- Multiplicar y dividir decimales
- Convertir decimales, fracciones y porcentajes
- Simplifica expresiones con raíces cuadradas
- Identificar números enteros, números racionales, números irracionales y números reales
- Localizar fracciones y decimales en la recta numérica
Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Álgebra elemental, Fundaciones.
Decimales Redondos
Los decimales son otra forma de escribir fracciones cuyos denominadores son poderes de diez.
\[\begin{array}{rcll} 0.1 & = & \dfrac{1}{10} & \text{is “one tenth”} \\ 0.01 & = & \dfrac{1}{100} & \text{is “one hundredth”} \\ 0.001 & = & \dfrac{1}{1000} & \text{is “one thousandth”} \\ 0.0001 & = & \dfrac{1}{10,000} & \text{is “one ten-thousandth”} \end{array}\]
Al igual que en números enteros, cada dígito de un decimal corresponde al valor posicional basado en las potencias de diez. La figura muestra los nombres de los valores posicionales a la izquierda y derecha del punto decimal.
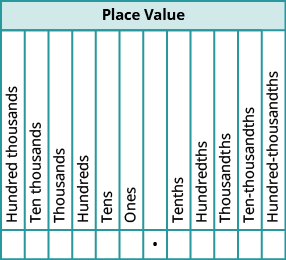
Cuando trabajamos con decimales, a menudo es necesario redondear el número al valor posicional requerido más cercano. Resumimos aquí los pasos para redondear un decimal.
- Localice el valor posicional dado y márquelo con una flecha.
- Subrayar el dígito a la derecha del valor posicional.
- ¿El dígito subrayado es mayor o igual a 5?
- Sí: suma 1 al dígito en el valor posicional dado.
- No: no cambie el dígito en el valor posicional dado
- Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo.
Redondear\(18.379\) al ⓐ centésimo ⓑ décimo ⓒ número entero más cercano.
- Contestar
-
Redonda\(18.379.\)
ⓐ a la centésima más cercana
Localiza el lugar centésimas con una flecha. 
Subrayar el dígito a la derecha del valor posicional dado. 
Debido a que 9 es mayor o igual a 5, agregue 1 al 7. 
Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo. 
Observe que los dígitos eliminados NO fueron reemplazados por ceros. 
ⓑ a la décima más cercana
Localiza el décimo lugar con una flecha. 
Subrayar el dígito a la derecha del valor posicional dado. 
Debido a que 7 es mayor o igual a 5, agregue 1 al 3. 
Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo. 
Observe que los dígitos eliminados NO fueron reemplazados por ceros. 
ⓒ al número entero más cercano
Localiza el lugar con una flecha. 
Subrayar el dígito a la derecha del valor posicional dado. 
Dado que 3 no es mayor ni igual a 5, no agregue 1 al 8. 
Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo. 

Redondear\(6.582\) al ⓐ centésimo ⓑ décimo ⓒ número entero más cercano.
- Contestar
-
ⓐ\(6.58\) ⓑ\(6.6\) ⓒ\(7\)
Redondear\(15.2175\) a la ⓐ milésima ⓑ centésima ⓒ décima más cercana.
- Contestar
-
ⓐ\(15.218\) ⓑ\(15.22\)
ⓒ\(15.2\)
Sumar y restar decimales
Para sumar o restar decimales, alineamos los puntos decimales. Al alinear los puntos decimales de esta manera, podemos sumar o restar los valores posicionales correspondientes. Luego sumamos o restamos los números como si fueran números enteros y luego colocamos el punto decimal en la suma.
- Determinar el signo de la suma o diferencia.
- Escribe los números para que los decimales se alineen verticalmente.
- Utilice ceros como marcadores de posición, según sea necesario.
- Sumar o restar los números como si fueran números enteros. Luego coloque el punto
decimal en la respuesta debajo de los puntos decimales en los números dados. - Escriba la suma o diferencia con el signo correspondiente.
Sumar o restar: ⓐ\(−23.5−41.38\) ⓑ\(14.65−20.\)
- Contestar
-
ⓐ
\(\begin{array}{ll} \text{} & −23.5−41.38 \\ \\ \\ {\text{The difference will be negative. To subtract, we add the} \\ \text{numerals. Write the numbers so the decimal points line} \\ \text{up vertically.}} & { \; \; 23.5 \\ \underline{+41.38}} \\ \\ \\ { \text{Put 0 as a placeholder after the 5 in 23.5.} \\ \text{Remember, } \frac{5}{10}=\frac{50}{100} \text{ so } 0.5=0.50.} & { \; \; 23.50 \\ \underline{+41.38}} \\ \\ \\ {\text{Add the numbers as if they were whole numbers.} \\ \text{Then place the decimal point in the sum.}} & {\; \; 23.50 \\ \underline{+41.38} \\ \; \; 64.88 } \\ \\ \\ \text{ Write the result with the correct sign.} & 64.88−23.5−41.38=−64.88 \end{array}\)
ⓑ
\(\begin{array}{ll} \text{} & 14.65−20 \\ \\ \\ {\text{The difference will be negative. To subtract, we} \\ \text{subtract 14.65 from 20.}} \\ \\ \\ {\text{Write the numbers so the decimal points line up} \\ \text{vertically.}} & { \; \; 20 \\ \underline{−14.65}} \\ \\ \\ {\text{Remember, 20 is a whole number, so place the} \\ \text{decimal point after the 0.}} \\ \\ \\ \text{Put in zeros to the right as placeholders.} & { \; \; 20.00 \\ \underline{−14.65}} \\ \\ \\ \text{Subtract and place the decimal point in the answer.} & {\begin{array}{lcccc} {} & 9 & {} & 9 & {} \\ 1 & \cancel{10} & {} & \cancel{10} & 10 \\ 2 & 0 & . & 0 & 0 \\ −1 & 4 & . & 6 & 5 \end{array} \\ \text{______________________} \\ \begin{array}{lcccc} {\; \; \; \; \; \; \; \; \; } & 5 & . & 3 & 5 \end{array}} \\ \\ \\ \text{Write the result with the correct sign.} & 14.65−20=−5.35 \end{array} \)
Sumar o restar: ⓐ\(−4.8−11.69\) ⓑ\(9.58−10\).
- Contestar
-
ⓐ\(−16.49\) ⓑ\(−0.42\)
Sumar o restar: ⓐ\(−5.123−18.47\) ⓑ\(37.42−50\).
- Contestar
-
ⓐ\(−23.593\) ⓑ\(−12.58\)
Multiplicar y dividir decimales
Cuando multiplicamos decimales firmados, primero determinamos el signo del producto y luego multiplicamos como si los números fueran ambos positivos. Multiplicamos los números ignorando temporalmente el punto decimal y luego contamos el número de puntos decimales en los factores y esa suma nos dice el número de decimales en el producto. Por último, escribimos el producto con el letrero correspondiente.
- Determinar el signo del producto.
- Escribe en formato vertical, alineando los números de la derecha. Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales.
- Coloque el punto decimal. El número de decimales en el producto es la suma
del número de decimales en los factores. - Escriba el producto con el letrero correspondiente.
Multiplicar:\((−3.9)(4.075)\).
- Contestar
-
\((−3.9)(4.075)\) Los signos son diferentes. El producto
será negativo.El producto será negativo. Escribe en formato vertical, alineando los
números de la derecha.
Multiplicar. 
Suma el número de decimales en
los factores (1 + 3). Coloque el punto decimal a 4 lugares de la derecha.

Los signos son los diferentes, por lo que el producto es negativo. \((−3.9)(4.075)=−15.8925\)
Multiplicar:\(−4.5(6.107)\).
- Contestar
-
\(−27.4815\)
Multiplicar:\(−10.79(8.12)\).
- Contestar
-
\(−87.6148\)
A menudo, sobre todo en las ciencias, multiplicarás decimales por potencias de 10 (10, 100, 1000, etc). Si multiplica algunos productos en papel, puede notar un patrón que relaciona el número de ceros en la potencia de 10 al número de decimales movemos el punto decimal a la derecha para obtener el producto.
- Mueve el punto decimal hacia la derecha el mismo número de lugares que el
número de ceros en la potencia de 10. - Agrega ceros al final del número según sea necesario.
Multiplicar: 5.63 por ⓐ 10 ⓑ 100 ⓒ 1000.
- Contestar
-
Al observar el número de ceros en el múltiplo de diez, vemos el número de lugares que necesitamos para mover el decimal a la derecha.
ⓐ
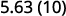
Hay 1 cero en 10, así que mueve el punto decimal 1 lugar a la derecha. 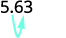
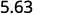
ⓑ
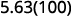
Hay 2 ceros en 100, así que mueve el punto decimal 2 lugares hacia la derecha. 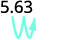

ⓒ
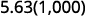
Hay 3 ceros en 1,000, así que mueve el punto decimal 3 lugar a la derecha. 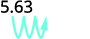
Se debe agregar un cero al final. 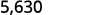
Multiplica 2.58 por ⓐ 10 ⓑ 100 ⓒ 1000.
- Contestar
-
ⓐ 25.8 ⓑ 258 ⓒ 2,580
Multiplica 14.2 por ⓐ 10 ⓑ 100 ⓒ 1000.
- Contestar
-
ⓐ 142 ⓑ 1,420 ⓒ 14,200
Al igual que con la multiplicación, la división de decimales firmados es muy parecida a dividir números enteros. Sólo tenemos que averiguar dónde se debe colocar el punto decimal y el signo del cociente. Al dividir decimales firmados, primero determinar el signo del cociente y luego dividir como si los números fueran ambos positivos. Por último, escribir el cociente con el signo correspondiente.
Revisamos la notación y el vocabulario para la división:

Escribiremos los pasos a seguir al dividir decimales para facilitar la referencia.
- Determinar el signo del cociente.
- Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. “Mueve” el punto decimal en el dividendo el mismo número de lugares, agregando ceros según sea necesario.
- Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.
- Escriba el cociente con el signo correspondiente.
Dividir:\(−25.65÷(−0.06)\).
- Contestar
-
Recuerda, puedes “mover” los decimales en el divisor y dividendo debido a la Propiedad de Fracciones Equivalentes.
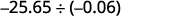
Los signos son los mismos. El cociente es positivo. Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. “Mover” el punto decimal en el dividendo el mismo número de lugares. 
Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo. 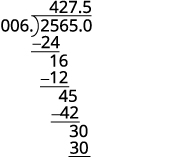
Escriba el cociente con el signo correspondiente. 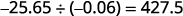
Dividir:\(−23.492÷(−0.04)\).
- Contestar
-
\(587.3\)
Dividir:\(−4.11÷(−0.12)\).
- Contestar
-
\(34.25\)
Convertir decimales, fracciones y porcentajes
En nuestro trabajo, muchas veces es necesario cambiar la forma de un número. Es posible que tengamos que cambiar fracciones a decimales o decimales a porcentaje.
Convertimos decimales en fracciones identificando el valor posicional del último dígito (más a la derecha). En el decimal 0.03. el 3 está en el lugar de centésimas, por lo que 100 es el denominador de la fracción equivalente a 0.03.
\[0.03=\dfrac{3}{100}\]
Los pasos a seguir para convertir un decimal a una fracción se resumen en el cuadro de procedimiento.
- Para convertir un decimal a una fracción propia, determine el valor posicional del dígito final.
- Escribe la fracción.
- numerador—los “números” a la derecha del punto decimal
- denominador—el valor posicional correspondiente al dígito final
- Para convertir una fracción a decimal, divida el numerador de la fracción por el denominador de la fracción.
Escribe: ⓐ\(0.374\) como fracción ⓑ\(−\frac{5}{8}\) como decimal.
- Contestar
-
ⓐ
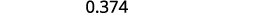
Determinar el valor posicional del dígito final. 
Escribe la fracción para 0.374: El numerador es 374. El denominador es 1,000. 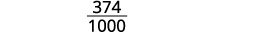
Simplifica la fracción. 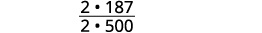
Dividir los factores comunes. 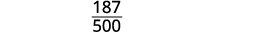
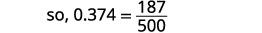
ⓑ Dado que una barra de fracción significa división, comenzamos por escribir la fracción\(\frac{5}{8}\) como\(8\sqrt{5}\). Ahora divide.
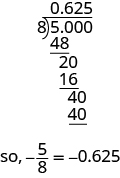
Escribe: ⓐ\(0.234\) como fracción ⓑ\(−\frac{7}{8}\) como decimal.
- Contestar
-
ⓐ\(\frac{117}{500}\) ⓑ\(−0.875\)
Escribe: ⓐ\(0.024\) como fracción ⓑ\(−\frac{3}{8}\) como decimal.
- Contestar
-
ⓐ\(\frac{3}{125}\) ⓑ\(−0.375\)
Un por ciento es una relación cuyo denominador es 100. Porcentaje de medias por cien. Utilizamos el símbolo de porcentaje,%, para mostrar el porcentaje. Dado que un porcentaje es una relación, se puede expresar fácilmente como una fracción. Porcentaje medio por 100, por lo que el denominador de la fracción es 100. Luego cambiamos la fracción a un decimal dividiendo el numerador por el denominador. Después de hacer esto muchas veces, es posible que veas el patrón.
Para convertir un número porcentual a un número decimal, movemos el punto decimal dos lugares hacia la izquierda.
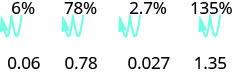
Para convertir un decimal a un por ciento, recuerde que por ciento significa por cien. Si cambiamos el decimal a una fracción cuyo denominador es 100, es fácil cambiar esa fracción a un porcentaje. Después de muchas conversiones, es posible que reconozcas el patrón.
Para convertir un decimal a un porcentaje, movemos el punto decimal dos lugares a la derecha y luego agregamos el signo de porcentaje.
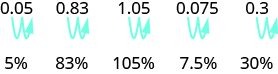
- Para convertir un porcentaje a un decimal, mueva el punto decimal dos lugares a la izquierda después de eliminar el signo de porcentaje.
- Para convertir un decimal a un porcentaje, mueva el punto decimal dos lugares a la derecha y luego agregue el signo de porcentaje.
Convertir cada uno:
ⓐ por ciento a decimal: 62%, 135% y 13.7%.
ⓑ decimal a un porcentaje: 0.51, 1.25 y 0.093.
- Contestar
-
ⓐ
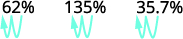
Mueve el punto decimal dos lugares hacia la izquierda. 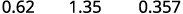
ⓑ
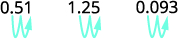
Mueve el punto decimal dos lugares a la derecha. 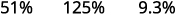
Convertir cada uno:
ⓐ por ciento a un decimal: 9%, 87% y 3.9%.
ⓑ decimal a un porcentaje: 0.17, 1.75 y 0.0825.
- Contestar
-
ⓐ 0.09, 0.87, 0.039 ⓑ 17%, 175%, 8.25%
Convertir cada uno:
ⓐ por ciento a un decimal: 3%, 91% y 8.3%.
ⓑ decimal a un porcentaje: 0.41, 2.25 y 0.0925.
- Contestar
-
ⓐ 0.03, 0.91, 0.083 ⓑ 41%, 225%, 9.25%
Simplifique expresiones con raíces cuadradas
Recuerda que cuando un número\(n\) se multiplica por sí mismo, lo escribimos\(n^2\) y leemos “\(n\)al cuadrado”. El resultado se llama el cuadrado de un número n. Por ejemplo,\(\frac{8}{2}\) se lee “8 cuadrados” y 64 se llama el cuadrado de 8. De igual manera, 121 es el cuadrado de 11 porque\(11^2\) es 121. Será útil aprender a reconocer los números cuadrados perfectos.
Si\(n^2=m\), entonces m es el cuadrado de n.
¿Y los cuadrados de los números negativos? Sabemos que cuando los signos de dos números son iguales, su producto es positivo. Por lo que el cuadrado de cualquier número negativo también es positivo.
\[(−3)^2=9 \; \; \; \; \; \; \; \; \; (−8)^2=64 \; \; \; \; \; \; \; \; \; (−11)^2=121 \; \; \; \; \; \; \; \; \; (−15)^2=225\]
Porque\(10^2=100\), decimos 100 es el cuadrado de 10. También decimos que 10 es una raíz cuadrada de 100. Un número cuyo cuadrado es m se llama raíz cuadrada de un número m.
Si\(n^2=m\), entonces n es una raíz cuadrada de m.
Observe\((−10)^2=100\) también, por lo que −10 también es una raíz cuadrada de 100. Por lo tanto, tanto 10 como −10 son raíces cuadradas de 100. Entonces, cada número positivo tiene dos raíces cuadradas, una positiva y otra negativa. El signo radical,\(\sqrt{m}\), denota la raíz cuadrada positiva. La raíz cuadrada positiva se llama raíz cuadrada principal. Cuando usamos el signo radical eso siempre significa que queremos la raíz cuadrada principal.
\(\sqrt{m}\)se lee “la raíz cuadrada de mm.”
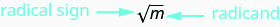
Si\(m=n^2\), entonces\(\sqrt{m}=n\), para\(n≥0\).
La raíz cuadrada de m,\(\sqrt{m}\), es el número positivo cuyo cuadrado es m.
Sabemos que cada número positivo tiene dos raíces cuadradas y el signo radical indica el positivo. Escribimos\(\sqrt{100}=10\). Si queremos encontrar la raíz cuadrada negativa de un número, colocamos un negativo frente al signo radical. Por ejemplo,\(−\sqrt{100}=−10\). Leemos\(−\sqrt{100}\) como “lo contrario de la raíz cuadrada principal de 10”.
Simplifica: ⓐ\(\sqrt{25}\) ⓑ\(\sqrt{121}\) ⓒ\(−\sqrt{144}\).
- Contestar
-
ⓐ
\(\begin{array}{ll} \text{} & \sqrt{25} \\ \text{Since }5^2=25 & 5 \end{array}\)ⓑ
\(\begin{array}{ll} \text{} & \sqrt{121} \\ \text{Since }11^2=121 & 11 \end{array}\)
ⓒ
\(\begin{array}{ll} {} & −\sqrt{144} \\ \text{The negative is in front of} & −12 \\ \text{the radical sign.} \end{array}\)
Simplificar: ⓐ\(\sqrt{36}\) ⓑ\(\sqrt{169}\) ⓒ\(−\sqrt{225}\)
- Contestar
-
ⓐ 6 ⓑ 13 ⓒ −15
Simplificar: ⓐ\(\sqrt{16}\) ⓑ\(\sqrt{196}\) ⓒ\(−\sqrt{100}\)
- Contestar
-
ⓐ 4 ⓑ 14 ⓒ −10
Identificar números enteros, números racionales, números irracionales y números reales
Ya hemos descrito los números como números de conteo s, números enteros y enteros. ¿Cuál es la diferencia entre estos tipos de números? La diferencia podría confundirse con la resta. ¿Qué tal preguntar cómo distinguimos entre este tipo de números?
\[\begin{array}{ll} \text{Counting numbers} & 1,2,3,4,….. \\ \text{Whole numbers} & 0,1,2,3,4,…. \\ \text{Integers} & ….−3,−2,−1,0,1,2,3,…. \end{array}\]
¿Qué tipo de números obtendríamos si empezáramos con todos los enteros y luego incluimos todas las fracciones? Los números que tendríamos forman el conjunto de números racionales. Un número racional es un número que se puede escribir como una relación de dos enteros.
En general, cualquier decimal que termine después de un número de dígitos (como 7.3 o −1.2684) es un número racional. Podemos usar el valor posicional del último dígito como denominador al escribir el decimal como fracción. El decimal para\(\frac{1}{3}\) es el número\(0.\overline{3}\). La barra sobre el 3 indica que el número 3 se repite infinitamente. Continuamente tiene un significado importante en el cálculo. El (los) número (s) debajo de la barra se llama bloque repetitivo y se repite continuamente.
Dado que todos los enteros se pueden escribir como una fracción cuyo denominador es 1, los enteros (y así también el conteo y los números enteros. son números racionales.
Cada número racional se puede escribir tanto como una relación de enteros\(\frac{p}{q}\), donde p y q son enteros y\(q≠0\), y como un decimal que se detiene o repite.
Un número racional es un número de la forma\(\frac{p}{q}\), donde p y q son números enteros y\(q≠0\).
Su forma decimal se detiene o se repite.
¿Hay decimales que no se detienen ni repiten? ¡Sí! El número ππ (la letra griega pi, pronunciada “pie”), que es muy importante para describir los círculos, tiene una forma decimal que no se detiene ni se repite. Utilizamos tres puntos (...) para indicar que el decimal no se detiene ni se repite.
\[π=3.141592654...\]
La raíz cuadrada de un número que no es un cuadrado perfecto es un decimal que no se detiene ni se repite.
Un número cuya forma decimal no se detiene ni se repite no se puede escribir como una fracción de enteros. A esto lo llamamos un número irracional.
Un número irracional es un número que no se puede escribir como la relación de dos enteros.
Su forma decimal no se detiene y no se repite.
Resumamos un método que podemos usar para determinar si un número es racional o irracional.
Si la forma decimal de un número
- repite o detiene, el número es un número racional.
- no se repite y no se detiene, el número es un número irracional.
Hemos visto que todos los números de conteo son números enteros, todos los números enteros son números enteros, y todos los enteros son números racionales. Los números irracionales son números cuya forma decimal no se detiene y no se repite. Cuando armamos los números racionales y los números irracionales, obtenemos el conjunto de números reales s.
Un número real es un número que es racional o irracional.
Posteriormente en este curso introduciremos números más allá de los números reales. La figura ilustra cómo encajan los conjuntos de números que hemos usado hasta ahora.
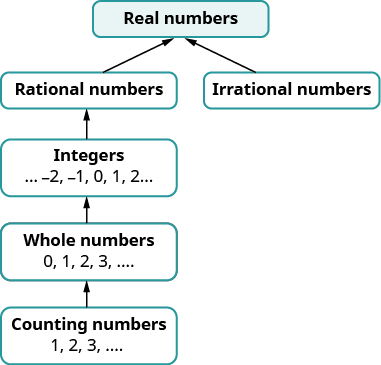
¿Te parece extraño el término “números reales”? ¿Hay números que no sean “reales” y, de ser así, ¿cuáles podrían ser? ¿Podemos simplificar\(−\sqrt{25}\)? ¿Hay un número cuyo cuadrado es\(−25\)?
\[()^2=−25?\]
Ninguno de los números que hemos tratado hasta ahora tiene un cuadrado que sea\(−25\). ¿Por qué? Cualquier número positivo al cuadrado es positivo. Cualquier número negativo al cuadrado es positivo. Entonces decimos que no hay un número real igual a\(\sqrt{−25}\). La raíz cuadrada de un número negativo no es un número real.
Dados los números\(−7,\frac{14}{5},8,\sqrt{5},5.9,−\sqrt{64}\), enumere los ⓐ números enteros ⓑ enteros ⓒ números racionales ⓓ números irracionales ⓔ números reales.
- Contestar
-
ⓐ Recuerda, los números enteros son\(0,1,2,3,…,\) así que 8 es el único número entero dado.
ⓑ Los enteros son los números enteros y sus opuestos (que incluye 0). Así que el número entero 8 es un número entero, y −7 es lo opuesto a un número entero así que también es un número entero. También, fíjese que 64 es el cuadrado de 8 así\(−\sqrt{64}=−8\). Entonces los enteros son\(−7,8,\) y\(−\sqrt{64}\).
ⓒ Ya que todos los enteros son racionales, entonces\(−7,8,\) y\(−\sqrt{64}\) son racionales. Los números racionales también incluyen fracciones y decimales que se repiten o se detienen, así\(\frac{14}{5}\) y\(5.9\) son racionales. Entonces la lista de números racionales es\(−7,\frac{14}{5},8,5.9,\) y\(−\sqrt{64}\).
ⓓ Recuerda que 5 no es un cuadrado perfecto, por lo que\(\sqrt{5}\) es irracional.
ⓔ Todos los números listados son números reales.
Teniendo en cuenta la\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49},\) lista de números los ⓐ números enteros ⓑ enteros ⓒ números racionales
ⓓ números irracionales ⓔ números reales.
- Contestar
-
ⓐ\(4,\sqrt{49}\) ⓑ\(−3,4,\sqrt{49}\)
ⓒ\(−3,0.\overline{3},\frac{9}{5},4,\sqrt{49}\) ⓓ\(−\sqrt{2}\)ⓔ\(−3,−\sqrt{2},0.\overline{3},\frac{9}{5},4,\sqrt{49}\)
Los números dados\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...,\) enumeran los ⓐ números enteros ⓑ enteros ⓒ números racionales ⓓ números irracionales ⓔ números reales.
- Contestar
-
ⓐ\(6,\sqrt{121}\)
ⓑ\(−\sqrt{25},−1,6,\sqrt{121}\)
ⓒ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121}\)
ⓓ\(2.041975...\)
ⓔ\(−\sqrt{25},−\frac{3}{8},−1,6,\sqrt{121},2.041975...\)
Localizar fracciones y decimales en la línea numérica
Ahora queremos incluir fracciones y decimales en la recta numérica. Empecemos con fracciones y localicemos\(\frac{1}{5},−\frac{4}{5},3,\frac{7}{4},−\frac{9}{2},−5\) y\(\frac{8}{3}\) en la recta numérica.
Empezaremos con los números enteros 3 y −5 porque son los más fáciles de trazar. Ver Figura.
Las fracciones propias listadas son\(\frac{1}{5}\) y\(−\frac{4}{5}.\) Sabemos que la fracción propiamente dicha\(\frac{1}{5}\) tiene un valor menor a uno y así se ubicaría entre 0 y 1. El denominador es 5, por lo que dividimos la unidad de 0 a 1 en 5 partes iguales\(\frac{1}{5},\frac{2}{5},\frac{3}{5},\frac{4}{5}\). Trazar\(\frac{1}{5}\).
Del mismo modo,\(−\frac{4}{5}\) se encuentra entre 0 y −1. Después de dividir la unidad en 5 partes iguales trazamos\(−\frac{4}{5}\).
Por último, mira las fracciones impropias\(\frac{7}{4},\frac{9}{2},\frac{8}{3}\). Localizar estos puntos puede ser más fácil si cambias cada uno de ellos a un número mixto.
\[\dfrac{7}{4}=1\dfrac{3}{4} \; \; \; \; \; \; \; \; \; −\dfrac{9}{2}=−4\dfrac{1}{2} \; \; \; \; \; \; \; \; \; \dfrac{8}{3}=2\dfrac{2}{3}\]
La figura muestra la recta numérica con todos los puntos trazados.

Localice y etiquete lo siguiente en una recta numérica:\(4,\frac{3}{4},−\frac{1}{4},−3,\frac{6}{5},−\frac{5}{2},\) y\(\frac{7}{3}\).
- Contestar
-
Localizar y trazar los enteros,\(4,−3.\)
Localice\(\frac{3}{4}\) primero la fracción adecuada. La fracción\(\frac{3}{4}\) está entre 0 y 1. Divide la distancia entre 0 y 1 en cuatro partes iguales, luego trazamos\(\frac{3}{4}\). Del mismo modo parcela\(−\frac{1}{4}\).
Ahora localice las fracciones impropias\(\frac{6}{5},−\frac{5}{2},\) y\(\frac{7}{3}\). Es más fácil trazarlos si los convertimos a números mixtos y luego los trazamos como se describió anteriormente:\(\frac{6}{5}=1\frac{1}{5},−\frac{5}{2}=−2\frac{1}{2},\frac{7}{3}=2\frac{1}{3}\).

Localice y etiquete lo siguiente en una recta numérica:\(−1,\frac{1}{3},\frac{6}{5},−\frac{7}{4},\frac{9}{2},5,−\frac{8}{3}\).
- Contestar
-
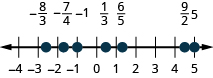
Localice y etiquete lo siguiente en una recta numérica:\(−2,\frac{2}{3},\frac{7}{5},−\frac{7}{4},\frac{7}{2},3,−\frac{7}{3}\).
- Contestar
-
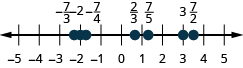
Dado que los decimales son formas de fracciones, ubicar decimales en la recta numérica es similar a ubicar fracciones en la recta numérica.
Localizar en la recta numérica: ⓐ 0.4 ⓑ −0.74.
- Contestar
-
ⓐ El número decimal 0.4 es equivalente a\(\frac{4}{10}\), una fracción propia, por lo que 0.4 se ubica entre 0 y 1. En una recta numérica, divida el intervalo entre 0 y 1 en 10 partes iguales. Ahora etiquetar las partes 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0. Escribimos 0 como 0.0 y 1 como 1.0, para que los números estén consistentemente en décimas. Por último, marque 0.4 en la recta numérica.

ⓑ El decimal\(−0.74\) es equivalente a\(−\frac{74}{100}\), por lo que se ubica entre 0 y .−1. En una recta numérica, marque y etiquete las centésimas en el intervalo entre 0 y −1.

Localizar en la línea numérica: ⓐ\(0.6\) ⓑ\(−0.25.\)
- Contestar
-
ⓐ

ⓑ
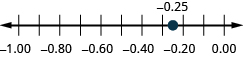
Localice en la recta numérica: ⓐ 0.90.9 ⓑ −0.75.−0.75.
- Contestar
-
ⓐ

ⓑ
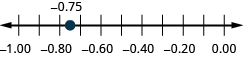
Acceda a este recurso en línea para obtener instrucción adicional y práctica con decimales.
- Conceptos básicos de aritmética: dividir decimales
Conceptos clave
- Cómo redondear decimales.
- Localice el valor posicional dado y márquelo con una flecha.
- Subrayar el dígito a la derecha del valor posicional.
- ¿El dígito subrayado es mayor o igual a 5?
- Sí: suma 1 al dígito en el valor posicional dado.
- No: no cambie el dígito en el valor posicional dado
- Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo.
- Cómo sumar o restar decimales.
- Determinar el signo de la suma o diferencia.
- Escribe los números para que los decimales se alineen verticalmente.
- Utilice ceros como marcadores de posición, según sea necesario.
- Sumar o restar los números como si fueran números enteros. Luego coloque el punto decimal en la respuesta debajo de los puntos decimales en los números dados.
- Escribe la suma o diferencia con el signo correspondiente
- Cómo multiplicar decimales.
- Determinar el signo del producto.
- Escribe en formato vertical, alineando los números de la derecha. Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales.
- Coloque el punto decimal. El número de decimales en el producto es la suma del número de decimales en los factores.
- Escriba el producto con el letrero correspondiente.
- Cómo multiplicar un decimal por una potencia de diez.
- Mueve el punto decimal hacia la derecha el mismo número de lugares que el número de ceros en la potencia de 10.
- Agrega ceros al final del número según sea necesario.
- Cómo dividir decimales.
- Determinar el signo del cociente.
- Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. “Mueve” el punto decimal en el dividendo el mismo número de lugares, agregando ceros según sea necesario.
- Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.
- Escriba el cociente con el signo correspondiente.
- Cómo convertir un decimal en una fracción propia y una fracción en un decimal.
- Para convertir un decimal a una fracción propia, determine el valor posicional del dígito final.
- Escribe la fracción.
- numerador—los “números” a la derecha del punto decimal
- denominador—el valor posicional correspondiente al dígito final
- Para convertir una fracción a decimal, divida el numerador de la fracción por el denominador de la fracción.
- Cómo convertir un porcentaje a un decimal y un decimal a un porcentaje.
- Para convertir un porcentaje a un decimal, mueva el punto decimal dos lugares a la izquierda después de eliminar el signo de porcentaje.
- Para convertir un decimal a un porcentaje, mueva el punto decimal dos lugares a la derecha y luego agregue el signo de porcentaje.
- Notación de raíz cuadrada\(\sqrt{m}\) se lee “la raíz cuadrada de m.” Si\(m=n^2\), entonces\(\sqrt{m}=n\), para\(n≥0\). La raíz cuadrada de m,\(\sqrt{m}\), es el número positivo cuyo cuadrado es m.
- Racional o Irracional Si la forma decimal de un número
- repite o detiene, el número es un número racional.
- no se repite y no se detiene, el número es un número irracional.
- Números reales
.jpg)
Figura 4.
Glosario
- número irracional
- Un número irracional es un número que no se puede escribir como la relación de dos enteros. Su forma decimal no se detiene y no se repite.
- por ciento
- Un por ciento es una relación cuyo denominador es 100.
- raíz cuadrada principal
- La raíz cuadrada positiva se llama raíz cuadrada principal.
- número racional
- Un número racional es un número de la forma\(\frac{p}{q}\), donde p y q son números enteros y\(q≠0\). Su forma decimal se detiene o se repite.
- número real
- Un número real es un número que es racional o irracional.
- cuadrado de un número
- Si\(n^2=m\), entonces m es el cuadrado de n.
- raíz cuadrada de un número
- Si\(n^2=m\), entonces n es una raíz cuadrada de m.


