1.5E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112492

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

La práctica hace la perfección

Decimales Redondos

En los siguientes ejercicios, redondear cada número al número entero ⓐ centésima ⓑ décima ⓒ más cercana.

1. $5.781$

Contestar: ⓐ$5.78$ ⓑ$5.8$ ⓒ$6$

2. $1.638$

3. $0.299$

Contestar: ⓐ$0.30$ ⓑ$0.3$ ⓒ$0$

4. $0.697$

5. $63.479$

Contestar: ⓐ$63.48$ ⓑ$63.5$ ⓒ$63$

6. $84.281$

Sumar y restar decimales

En los siguientes ejercicios, sumar o restar.

7. $−16.53−24.38$

Contestar: $−40.91$

8. $−19.47−32.58$

9. $−38.69+31.47$

Contestar: $−7.22$

10. $−29.83+19.76$

11. $72.5-100$

Contestar: $-27.5$

12. $86.2-100$

13. $91.75−(−10.462)$

Contestar: $02.212$

14. $94.69−(−12.678)$

15. $55.01−3.7$

Contestar: $51.31$

16. $59.08−4.6$

17. $2.51−7.4$

Contestar: $−4.89$

18. $3.84−6.1$

Multiplicar y dividir decimales

En los siguientes ejercicios, multiplicar.

19. $94.69−(−12.678)$

Contestar: $−11.653$

20. $(−8.5)(1.69)$

21. $(−5.18)(−65.23)$

Contestar: $337.8914$

22. $(−9.16)(−68.34)$

23. $(0.06)(21.75)$

Contestar: $1.305$

24. $(0.08)(52.45)$

25. $(9.24)(10)$

Contestar: $92.4$

26. $(6.531)(10)$

27. $(0.025)(100)$

Contestar: $2.5$

28. $(0.037)(100)$

29. $(55.2)(1000)$

Contestar: $55200$

30. $(99.4)(1000)$

En los siguientes ejercicios, divide. Dinero redondo respuestas monetarias al centavo más cercano.

31. $$117.25÷48$

Contestar: $$2.44$

32. $$109.24÷36$

33. $1.44÷(−0.3)$

Contestar: $−4.8$

34. $−1.15÷(−0.05)$

35. $5.2÷2.5$

Contestar: $2.08$

36. $14÷0.35$

Convertir decimales, fracciones y porcentajes

En los siguientes ejercicios, escribe cada decimal como fracción.

37. $0.04$

Contestar: $\frac{1}{25}$

38. $1.464$

39. $0.095$

Contestar: $\frac{19}{200}$

40. $−0.375$

En los siguientes ejercicios, convierte cada fracción a un decimal.

41. $\frac{17}{20}$

Contestar: $0.85$

42. $\frac{17}{4}$

43. $−\frac{310}{25}$

Contestar: $−12.4$

44. $−\frac{18}{11}$

En los siguientes ejercicios, convertir cada porcentaje a un decimal.

45. $71 \%$

Contestar: $0.71$

46. $150 \%$

47. $39.3 \% $

Contestar: $0.393$

48. $7.8 \% $

En los siguientes ejercicios, convertir cada decimal a un porcentaje.

49. $1.56$

Contestar: $156 \% $

50. $3$

51. $0.0625$

Contestar: $6.25 \% $

52. $2.254$

Simplifique las expresiones con raíces cuadradas

En los siguientes ejercicios, simplifique.

53. $\sqrt{64}$

Contestar: $8$

54. $\sqrt{169}$

55. $\sqrt{144}$

Contestar: $12$

56. $−\sqrt{4}$

57. $−\sqrt{100}$

Contestar: $−10$

58. $−\sqrt{121}$

Identificar números enteros, números racionales, números irracionales y números reales

En los siguientes ejercicios, enumere los ⓐ números enteros, ⓑ enteros, ⓒ números racionales, ⓓ números irracionales, ⓔ números reales para cada conjunto de números.

59. $−8,0,1.95286...,\frac{12}{5},\sqrt{36},9$

Contestar: ⓐ Números enteros:$0,\sqrt{36},9$
ⓑ Números enteros:$−8,0,\sqrt{36},9$
ⓒ Números racionales:$−8,0,\sqrt{36},9$
ⓓ Números irracionales:$1.95286...,$
ⓔ Números reales:$−8,0,1.95286...,\frac{12}{5},\sqrt{36},9$

60. $−9,−3\frac{4}{9},−\sqrt{9},0.40 \overline{9},\frac{11}{6},7$

61. $−\sqrt{100},−7,−\frac{8}{3},−1,0.77,3\frac{1}{4}$

Contestar: ⓐ Números enteros: ninguno
ⓑ Números enteros:$−\sqrt{100},−7,−1$
ⓒ Números racionales:$−\sqrt{100},−7,−\frac{8}{3},−1,0.77,3\frac{1}{4}$
ⓓ Números irracionales: ninguno
ⓔ Números reales:$−\sqrt{100},−7,−\frac{8}{3},−1,0.77,3\frac{1}{4}$

62. $−6,−\frac{5}{2},0,0. \overline{714285},2\frac{1}{5},\sqrt{14}$

Localizar fracciones y decimales en la línea numérica

En los siguientes ejercicios, ubique los números en una recta numérica.

63. $\frac{3}{10},\frac{7}{2},\frac{11}{6},4$

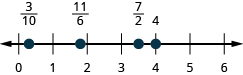
Contestar: $La figura muestra una línea numérica con números que van del 0 al 6. Se resaltan algunos valores. De izquierda a derecha, estos son: 3 por 10, 11 por 6, 7 por 2 y 4.$

64. $\frac{7}{10},\frac{5}{2},\frac{13}{8},3$

65. $\frac{3}{4},−\frac{3}{4},1\frac{2}{3},−1\frac{2}{3},\frac{5}{2},−\frac{5}{2}$

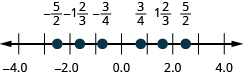
Contestar: $La figura muestra una línea numérica con números que van de menos 4 a 4. Se resaltan algunos valores. De izquierda a derecha, estos son: menos 5 por 2, menos 1 y dos tercios, menos 3 por 4, 3 por 4, 1 y dos tercios, y 5 por 2.$

66. $\frac{2}{5},−\frac{2}{5},1\frac{3}{4},−1\frac{3}{4},\frac{8}{3},−\frac{8}{3}$

67. ⓐ$0.8$ ⓑ$−1.25$

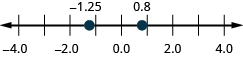
Contestar: $La figura muestra una línea numérica con números que van de menos 4 a 4. Se resaltan dos valores. Uno está entre menos 2 y menos 1. El otro está entre 0 y 1.$

68. ⓐ$−0.9$ ⓑ$−2.75$

69. ⓐ$−1.6$ ⓑ$3.25$

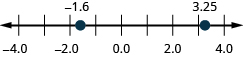
Contestar: $La figura muestra una línea numérica con números que van de menos 4 a 4. Se resaltan dos valores. Uno está entre menos 2 y menos 1. El otro está entre 3 y 4.$

70. ⓐ$3.1$ ⓑ$−3.65$

Ejercicios de escritura

71. ¿Cómo te ayuda saber sobre el dinero estadounidense a aprender sobre los decimales?

Contestar: Las respuestas variarán.

72. Cuando los Szetos vendieron su casa, el precio de venta era del 500% de lo que habían pagado por la casa hace 30 años. Explique lo que significa 500% en este contexto.Szetos vendieron su casa, el precio de venta era del 500% de lo que habían pagado por la casa hace 30 años. Explique lo que significa 500% en este contexto.

73. En sus propias palabras, explique la diferencia entre un número racional y un número irracional.

Contestar: Las respuestas variarán.

74. Explicar cómo los conjuntos de números (contar, enteros, enteros, racionales, irracionales, reales) se relacionan entre sí.

Autocomprobación

ⓐ Usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

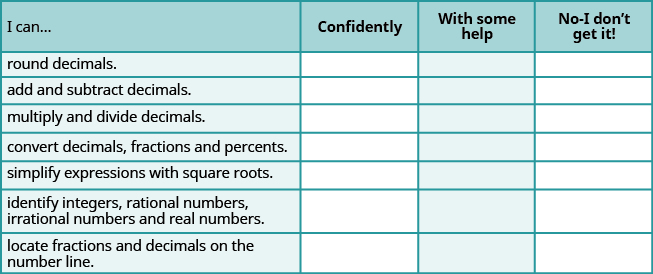
$Esta tabla tiene 4 columnas, 6 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna: Puedo, con confianza, con algo de ayuda y no, no lo consigo. Las declaraciones en la primera columna son: redondear decimales, sumar y restar decimales, multiplicar y dividir decimales, convertir decimales, fracciones y porcentajes, simplificar expresiones con raíces cuadradas, identificar enteros, números racionales, números irracionales y números reales, ubicar fracciones y decimales en el número línea. Las columnas restantes están en blanco.$

ⓑ En una escala del 1-10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?

Search

Text Color

Text Size

Margin Size

Font Type