2.2E: Usar una Estrategia General para Resolver Ecuaciones Lineales (Ejercicios)

Última actualización
Guardar como PDF

Page ID: 112725

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

La práctica hace la perfección

Resolver ecuaciones usando la estrategia general

En los siguientes ejercicios, determinar si los valores dados son soluciones a la ecuación.

1. $6y+10=12y$

a.$y=\frac{5}{3}$

b.$y=−\frac{1}{2}$

Responder: a. si
b. no

2. $4x+9=8x$

a.$x=−\frac{7}{8}$

b.$x=\frac{9}{4}$

3. $8u−1=6u$

a.$u=−\frac{1}{2}$

b.$u=\frac{1}{2}$

Responder: a. no
b. si

4. $9v−2=3v$

a.$v=−\frac{1}{3}$

b.$v=\frac{1}{3}$

En los siguientes ejercicios, resuelve cada ecuación lineal.

5. $15(y−9)=−60$

Responder: $y=5$

6. $−16(3n+4)=32$

7. $−(w−12)=30$

Responder: $w=−18$

8. $−(t−19)=28$

9. $51+5(4−q)=56$

Responder: $q=3$

10. $−6+6(5−k)=15$

11. $3(10−2x)+54=0$

Responder: $x=14$

12. $−2(11−7x)+54=4$

13. $\frac{2}{3}(9c−3)=22$

Responder: $c=4$

14. $\frac{3}{5}(10x−5)=27$

15. $\frac{1}{5}(15c+10)=c+7$

Responder: $c=\frac{5}{2}$

16. $\frac{1}{4}(20d+12)=d+7$

17. $3(4n−1)−2=8n+3$

Responder: $n=2$

18. $9(2m−3)−8=4m+7$

19. $12+2(5−3y)=−9(y−1)−2$

Responder: $y=−5$

20. $−15+4(2−5y)=−7(y−4)+4$

21. $5+6(3s−5)=−3+2(8s−1)$

Responder: $s=10$

22. $−12+8(x−5)=−4+3(5x−2)$

23. $4(p−4)−(p+7)=5(p−3)$

Responder: $p=−4$

24. $3(a−2)−(a+6)=4(a−1)$

25. $4[5−8(4c−3)]=12(1−13c)−8$

Responder: $c=−4$

26. $5[9−2(6d−1)]=11(4−10d)−139$

27. $3[−9+8(4h−3)]=2(5−12h)−19$

Responder: $h=\frac{3}{4}$

28. $3[−14+2(15k−6)]=8(3−5k)−24$

29. $5[2(m+4)+8(m−7)]=2[3(5+m)−(21−3m)]$

Responder: $m=6$

30. $10[5(n+1)+4(n−1)]=11[7(5+n)−(25−3n)]$

Clasificar ecuaciones

En los siguientes ejercicios, clasifique cada ecuación como una ecuación condicional, una identidad o una contradicción para luego declarar la solución.

31. $23z+19=3(5z−9)+8z+46$

Responder: identidad; todos los números reales

32. $15y+32=2(10y−7)−5y+46$

33. $18(5j−1)+29=47$

Responder: ecuación condicional;$j=\frac{2}{5}$

34. $24(3d−4)+100=52$

35. $22(3m−4)=8(2m+9)$

Responder: ecuación condicional;$m=165$

36. $30(2n−1)=5(10n+8)$

37. $7v+42=11(3v+8)−2(13v−1)$

Responder: contradicción; no hay solución

38. $18u−51=9(4u+5)−6(3u−10)$

39. $45(3y−2)=9(15y−6)$

Responder: contradicción; no hay solución

40. $60(2x−1)=15(8x+5)$

41. $9(14d+9)+4d=13(10d+6)+3$

Responder: identidad; todos los números reales

42. $11(8c+5)−8c=2(40c+25)+5$

Resolver ecuaciones con coeficientes de fracción o decimales

En los siguientes ejercicios, resuelve cada ecuación con coeficientes de fracción.

43. $\frac{1}{4}x−\frac{1}{2}=−\frac{3}{4}$

Responder: $x=−1$

44. $\frac{3}{4}x−\frac{1}{2}=\frac{1}{4}$

45. $\frac{5}{6}y−\frac{2}{3}=−\frac{3}{2}$

Responder: $y=−1$

46. $\frac{5}{6}y−\frac{1}{3}=−\frac{7}{6}$

47. $\frac{1}{2}a+\frac{3}{8}=\frac{3}{4}$

Responder: $a=\frac{3}{4}$

48. $\frac{5}{8}b+\frac{1}{2}=−\frac{3}{4}$

49. $2=\frac{1}{3}x−\frac{1}{2}x+\frac{2}{3}x$

Responder: $x=4$

50. $2=\frac{3}{5}x−\frac{1}{3}x+\frac{2}{5}x$

51. $\frac{1}{3}w+\frac{5}{4}=w−\frac{1}{4}$

Responder: $w=\frac{9}{4}$

52. $\frac{1}{2}a−\frac{1}{4}=\frac{1}{6}a+\frac{1}{12}$

53. $\frac{1}{3}b+\frac{1}{5}=\frac{2}{5}b−\frac{3}{5}$

Responder: $b=12$

54. $\frac{1}{3}x+\frac{2}{5}=\frac{1}{5}x−\frac{2}{5}$

55. $\frac{1}{4}(p−7)=\frac{1}{3}(p+5)$

Responder: $p=−41$

56. $\frac{1}{5}(q+3)=\frac{1}{2}(q−3)$

57. $\frac{1}{2}(x+4)=\frac{3}{4}$

Responder: $x=−\frac{5}{2}$

58. $\frac{1}{3}(x+5)=\frac{5}{6}$

59. $\dfrac{4n+8}{4}=\dfrac{n}{3}$

Responder: $n=−3$

60. $\dfrac{3p+6}{3}=\dfrac{p}{2}$

61. $\dfrac{3x+4}{2}+1=\dfrac{5x+10}{8}$

Responder: $x=−2$

62. $\dfrac{10y−2}{3}+3=\dfrac{10y+1}{9}$

63. $\dfrac{7u−1}{4}−1=\dfrac{4u+8}{5}$

Responder: $u=3$

64. $\dfrac{3v−6}{2}+5=\dfrac{11v−4}{5}$

En los siguientes ejercicios, resuelve cada ecuación con coeficientes decimales.

65. $0.4x+0.6=0.5x−1.2$

Responder: $x=18$

66. $0.7x+0.4=0.6x+2.4$

67. $0.9x−1.25=0.75x+1.75$

Responder: $x=20$

68. $1.2x−0.91=0.8x+2.29$

69. $0.05n+0.10(n+8)=2.15$

Responder: $n=9$

70. $0.05n+0.10(n+7)=3.55$

71. $0.10d+0.25(d+5)=4.05$

Responder: $d=8$

72. $0.10d+0.25(d+7)=5.25$

Matemáticas cotidianas

73. Esgrima Micah tiene 74 pies de esgrima para hacer correr a un perro en su patio. Quiere que el largo sea 2.5 pies más que el ancho. Encuentra la longitud, L, resolviendo la ecuación$2L+2(L−2.5)=74$.

Responder: $L=19.75$pies

74. Sellos Paula compró sellos de 49 centavos y sellos de 21 centavos por valor de 22.82 dólares. El número de sellos de 21 centavos fue ocho menos que el número de sellos de 49 centavos. Resuelve la ecuación$0.49s+0.21 (s−8) =22.82$ para s, para encontrar el número de sellos de 49 centavos que Paula compró.

Ejercicios de escritura

75. Usando sus propias palabras, enumere los pasos en la estrategia general para resolver ecuaciones lineales.

Responder: Las respuestas variarán.

76. Explique por qué debe simplificar ambos lados de una ecuación tanto como sea posible antes de recopilar los términos variables a un lado y los términos constantes al otro lado.

77. ¿Cuál es el primer paso que das al resolver la ecuación$3−7(y−4)=38?$ ¿Por qué es este tu primer paso?

Responder: Las respuestas variarán.

78. Si una ecuación tiene varias fracciones, ¿cómo la multiplicación de ambos lados por la LCD facilita su resolución?

79. Si una ecuación tiene fracciones solo en un lado, ¿por qué hay que multiplicar ambos lados de la ecuación por la LCD?

Responder: Las respuestas variarán.

80. Para la ecuación$0.35x+2.1=3.85$, ¿cómo se borra el decimal?

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

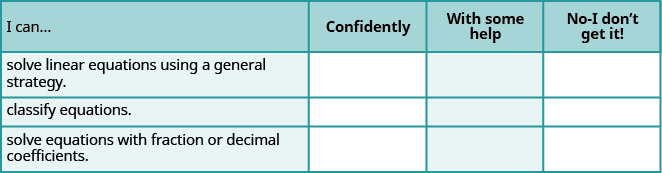
$Esta tabla tiene cuatro columnas y cuatro filas. La primera fila es un encabezado y etiqueta a cada columna, “Puedo...”, “Con confianza”, “Con algo de ayuda” y “¡No-I don't get it!” En la fila 2, lo que puedo fue resolver ecuaciones lineales usando una estrategia general. En la fila 3, el yo puedo fue clasificar ecuaciones. En la fila 4, lo que puedo era resolver ecuaciones con coeficientes fraccionarios o decimales.$

b. Si la mayoría de sus cheques fueron:

... con confianza. ¡Felicidades! Has logrado los objetivos en esta sección. Reflexiona sobre las habilidades de estudio que usaste para que puedas seguir usándolas. ¿Qué hiciste para confiar en tu capacidad para hacer estas cosas? Ser específico.

... con alguna ayuda. Esto debe abordarse rápidamente porque los temas que no dominas se convierten en baches en tu camino hacia el éxito. En matemáticas cada tema se basa en trabajos anteriores. Es importante asegurarse de tener una base sólida antes de seguir adelante. ¿A quién puedes pedir ayuda? Tus compañeros de clase e instructor son buenos recursos. ¿Hay algún lugar en el campus donde estén disponibles los tutores de matemáticas? ¿Se pueden mejorar tus habilidades de estudio?

... no - ¡No lo consigo! Esta es una señal de advertencia y no debes ignorarla. Debería obtener ayuda de inmediato o rápidamente se verá abrumado. Consulte a su instructor lo antes posible para discutir su situación. Juntos pueden idear un plan para obtener la ayuda que necesita.