2.4E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112726

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Resolver una fórmula para una variable específica

En los siguientes ejercicios, resuelva la fórmula dada para la variable especificada.

1. Resuelve la fórmula$C=πd$ para$d$.

Contestar: $d=\dfrac{C}{π}$

2. Resuelve la fórmula$C=πd$ para$π$.

3. Resuelve la fórmula$V=LWH$ para$L$.

Contestar: $L=\dfrac{V}{WH}$

4. Resuelve la fórmula$V=LWH$ para$H$.

5. Resuelve la fórmula$A=\frac{1}{2}bh$ para$b$.

Contestar: $b=\dfrac{2A}{h}$

6. Resuelve la fórmula$A=\frac{1}{2}bh$ para$h$.

7. Resuelve la fórmula

$A=\frac{1}{2}d_1d_2$para$d_1$.

Contestar: $d_1=\dfrac{2A}{d_2}$

8. Resuelve la fórmula

$A=\frac{1}{2}d_1d_2$para$d_2.$

9. Resuelve la fórmula

$A=\frac{1}{2}h(b_1+b_2)$para$b_1$.

Contestar: $b_1=\dfrac{2A}{h}−b_2$

10. Resuelve la fórmula

$A=\frac{1}{2}h(b_1+b_2)$para$b_2$.

11. Resuelve la fórmula

$h=54t+\frac{1}{2}at^2$para$a$.

Contestar: $a=\dfrac{2h−108t}{t^2}$

12. Resuelve la fórmula

$h=48t+\frac{1}{2}at^2$para$a$.

13. Resolver$180=a+b+c$ para$a$.

Contestar: $a=180−b−c$

14. Resolver$180=a+b+c$ for$c$.

15. Resuelve la fórmula

$A=\frac{1}{2}pI+B$para$p$.

Contestar: $p=\dfrac{2A−2B}{I}$

16. Resuelve la fórmula

$A=\frac{1}{2}pI+B$para$I$.

17. Resuelve la fórmula

$P=2L+2W$para$L$.

Contestar: $L=\dfrac{P−2W}{2}$

18. Resuelve la fórmula

$P=2L+2W$para$W$.

En los siguientes ejercicios, resuelve para la fórmula para$y$.

19. Resuelve la fórmula

$8x+y=15$para$y$.

Contestar: $y=15−8x$

20. Resuelve la fórmula

$9x+y=13$para$y$.

21. Resuelve la fórmula

$−4x+y=−6$para$y$.

Contestar: $y=−6+4x$

22. Resuelve la fórmula

$−5x+y=−1$para$y$.

23. Resuelve la fórmula

$x−y=−4$para$y$.

Contestar: $y=4+x$

24. Resuelve la fórmula

$x−y=−3$para$y$.

25. Resuelve la fórmula

$4x+3y=7$para$y$.

Contestar: $y=\frac{7−4x}{3}$

26. Resuelve la fórmula

$3x+2y=11$para$y$.

27. Resuelve la fórmula

$2x+3y=12$para$y$.

Contestar: $y=\frac{12−2x}{3}$

28. Resuelve la fórmula

$5x+2y=10$para$y$.

29. Resuelve la fórmula

$3x−2y=18$para$y$.

Contestar: $y=\frac{18−3x}{−2}$

30. Resuelve la fórmula

$4x−3y=12$para$y$.

Uso de fórmulas para resolver aplicaciones de geometría

En los siguientes ejercicios, resuelve usando una fórmula de geometría.

31. Una bandera triangular tiene un área de 0.75 pies cuadrados y una altura de 1.5 pies. ¿Cuál es su base?

Contestar: 1 pie

32. Una ventana triangular tiene un área de 24 pies cuadrados y una altura de seis pies. ¿Cuál es su base?

33. ¿Cuál es la base de un triángulo con área 207 pulgadas cuadradas y altura 18 pulgadas?

Contestar: 23 pulgadas

34. ¿Cuál es la altura de un triángulo con área 893 pulgadas cuadradas y base 38 pulgadas?

35. Los dos ángulos más pequeños de un triángulo rectángulo tienen medidas iguales. Encuentra las medidas de los tres ángulos.

Contestar: $45°,\; 45°,\; 90°$

36. La medida del ángulo más pequeño de un triángulo rectángulo es$20°$ menor que la medida del siguiente ángulo mayor. Encuentra las medidas de los tres ángulos.

37. Los ángulos en un triángulo son tales que un ángulo es el doble del ángulo más pequeño, mientras que el tercer ángulo es tres veces más grande que el ángulo más pequeño. Encuentra las medidas de los tres ángulos.

Contestar: $30°,\; 60°,\; 90°$

38. Los ángulos en un triángulo son tales que un ángulo es$20$ más que el ángulo más pequeño, mientras que el tercer ángulo es tres veces más grande que el ángulo más pequeño. Encuentra las medidas de los tres ángulos.

En los siguientes ejercicios, utilice el Teorema de Pitágoras para encontrar la longitud de la hipotenusa.

39.
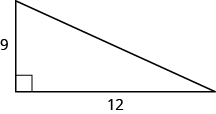
$La figura es un triángulo rectángulo con lados 9 unidades y 12 unidades.$

Contestar: $15$

40.
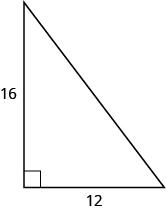
$La figura es un triángulo rectángulo con lados de 16 unidades y 12 unidades.$

41.
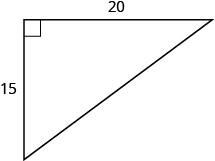
$La figura es un triángulo rectángulo con lados de 15 unidades y 20 unidades.$

Contestar: $25$

42.
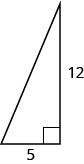
$La figura es un triángulo rectángulo con lados 5 unidades y 12 unidades.$

En los siguientes ejercicios, usa el Teorema de Pitágoras para encontrar la longitud de la pierna desconocida. Redondear a la décima más cercana si es necesario.

43.
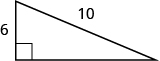
$La figura es un triángulo rectángulo con lados 6 unidades y 10 unidades.$

Contestar: $8$

44.
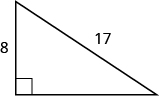
$La figura es un triángulo rectángulo con un lado que es de 8 unidades y una hipotenusa que es de 17 unidades.$

45.
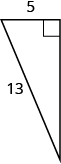
$La figura es un triángulo rectángulo con un lado que es de 5 unidades y una hipotenusa que es de 13 unidades.$

Contestar: $12$

46.
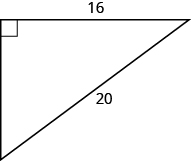
$La figura es un triángulo rectángulo con un lado que es de 16 unidades y una hipotenusa que es de 20 unidades.$

47.
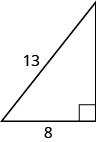
$La figura es un triángulo rectángulo con un lado que es de 8 unidades y una hipotenusa que es de 13 unidades.$

Contestar: $10.2$

48.
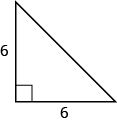
$La figura es un triángulo rectángulo con lados que son ambos 6 unidades.$

49.
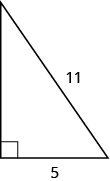
$La figura es un triángulo rectángulo con lados que son 5 unidades y 11 unidades.$

Contestar: $9.8$

50.
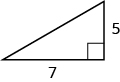
$La figura es un triángulo rectángulo con lados que son 5 unidades y 7 unidades.$

En los siguientes ejercicios, resuelve usando una fórmula de geometría.

51. El ancho de un rectángulo es siete metros menos que la longitud. El perímetro es de$58$ metros. Encuentra el largo y ancho.

Contestar: $18$metros,$11$ metros

52. La longitud de un rectángulo es ocho pies más que el ancho. El perímetro es$60$ pies. Encuentra el largo y ancho.

53. El ancho del rectángulo es$0.7$ metros menor que la longitud. El perímetro de un rectángulo es de$52.6$ metros. Encuentra las dimensiones del rectángulo.

Contestar: $13.5$m,$12.8$ m

54. La longitud del rectángulo es$1.1$ metros menor que el ancho. El perímetro de un rectángulo es de$49.4$ metros. Encuentra las dimensiones del rectángulo.

55. El perímetro de un rectángulo de$150$ pies. La longitud del rectángulo es el doble del ancho. Encuentra el largo y ancho del rectángulo.

Contestar: $25$ft,$50$ ft

56. La longitud del rectángulo es tres veces la anchura. El perímetro de un rectángulo es$72$ pies. Encuentra el largo y ancho del rectángulo.

57. La longitud del rectángulo es de tres metros menos del doble del ancho. El perímetro de un rectángulo es de$36$ metros. Encuentra las dimensiones del rectángulo.

Contestar: $7$m,$11$ m

58. La longitud de un rectángulo es de cinco pulgadas más del doble de ancho. El perímetro es$34$ inches. Find the length and width.

59. El perímetro de un triángulo es de$39$ pies. Un lado del triángulo es un pie más largo que el segundo lado. El tercer lado es dos pies más largo que el segundo lado. Encuentra la longitud de cada lado.

Contestar: $12$$13$pies,$14$ pies

60. El perímetro de un triángulo es de$35$ pies. Un lado del triángulo es cinco pies más largo que el segundo lado. El tercer lado es tres pies más largo que el segundo lado. Encuentra la longitud de cada lado.

61. Un lado de un triángulo es el doble del lado más pequeño. El tercer lado es cinco pies más que el lado más corto. El perímetro es$17$ pies. Encuentra las longitudes de los tres lados.

Contestar: $3$$6$pies,$8$ pies

62. Un lado de un triángulo es tres veces el lado más pequeño. El tercer lado es tres pies más que el lado más corto. El perímetro es$13$ pies. Encuentra las longitudes de los tres lados.

63. El perímetro de un campo rectangular es de$560$ yardas. El largo es$40$ yardas más que el ancho. Encuentra el largo y ancho del campo.

Contestar: $120$$160$yd

64. El perímetro de un atrio rectangular es$160$ pies. El largo es$16$ pies más que el ancho. Encuentra el largo y ancho del atrio.

65. Un estacionamiento rectangular tiene$250$ pies perimetrales. La longitud es de cinco pies más del doble del ancho. Encuentra el largo y ancho del estacionamiento.

Contestar: $40$ft,$85$ ft

66. Una alfombra rectangular tiene$240$ pulgadas perimetrales. El largo es$12$ pulgadas más del doble de ancho. Encuentra el largo y ancho de la alfombra.

En los siguientes ejercicios, resuelve. Respuestas aproximadas a la décima más cercana, si es necesario.

67. Se adjuntará una cadena de luces de$13$ pie a la parte superior de un poste$12$ de pie para una exhibición navideña como se muestra. ¿A qué distancia de la base del poste se debe anclar el extremo de la cadena de luces?

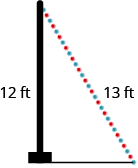
$La figura es una ilustración que muestra una cadena de luces de 13 pies unidas diagonalmente a la parte superior de un poste de 12 pies.$

Contestar: $5$pies

68. Pam quiere poner una pancarta en diagonal en la puerta de su cochera, como se muestra, para felicitar a su hijo por su graduación universitaria. La puerta del garaje es de$12$ pies de alto y$16$ pies de ancho. ¿Cuánto tiempo debe ser la pancarta para que se ajuste a la puerta del garaje?

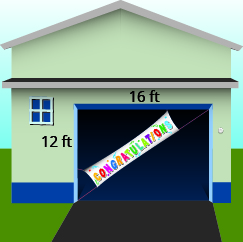
$La figura es una ilustración de una pancarta colocada diagonalmente a través de una puerta de garaje que mide 12 pies de alto y 16 pies de ancho.$

69. Chi planea poner un camino diagonal de adoquines a través de su jardín de flores como se muestra. El jardín de flores es un cuadrado con$10$ pies laterales. ¿Cuál será la longitud del camino?

$La figura es una ilustración de un camino diagonal de piedras a través de un jardín cuadrado con lados de 10 pies.$

Contestar: $14.1$pies

70. Brian tomó$20$ prestada una escalera de extensión de pie para usarla cuando pinta su casa. Si pone la base de la escalera a seis pies de la casa como se muestra, ¿a qué distancia llegará la parte superior de la escalera?

$La figura es una ilustración de una casa que tiene una escalera contra ella. La escalera mide 20 pies. Su base está posicionada a 6 pies de la casa.$

Matemáticas cotidianas

71. Conversión de temperatura Mientras estaba de gira por Grecia, Tatyana vio que la temperatura era$40°$ centígrados. Resuelve$F$ en la fórmula$C=\frac{5}{9}(F−32)$ para encontrar la temperatura Fahrenheit.

Contestar: $104°$F

72. Convirtiendo temperatura Yon estaba de visita por Estados Unidos y vio que la temperatura en Seattle un día era de$50°$ Fahrenheit. Resuelve$C$ en la fórmula$F=\frac{9}{5}C+32$ para encontrar la temperatura Celsius

73. Christa quiere poner una cerca alrededor de su cantero triangular. Los lados del cantero son seis pies, ocho pies y$10$ pies. ¿Cuántos pies de esgrima necesitará para encerrar su cantero?

Contestar: $24$ft

74. José acaba de retirar el juego infantil de su patio trasero para hacer espacio para un jardín rectangular. Quiere poner una barda alrededor del jardín para mantener al perro fuera. Tiene un rollo de barda de$50$ -pie en su cochera que planea usar. Para caber en el patio trasero, el ancho del jardín debe ser$10$ pies. ¿Cuánto tiempo puede hacer el otro lado?

Ejercicios de escritura

75. Si necesitas poner baldosas en el piso de tu cocina, ¿necesitas conocer el perímetro o el área de la cocina? Explica tu razonamiento.

Contestar: Las respuestas variarán.

76. Si necesitas poner una barda alrededor de tu patio trasero, ¿necesitas conocer el perímetro o el área del patio trasero? Explica tu razonamiento.

77. Mira las dos figuras a continuación.

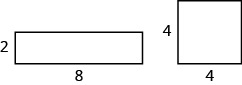
$Una figura de un rectángulo con un ancho que es de 2 unidades y una longitud que es de 8 unidades y un cuadrado con lados que son 4 unidades.$

a. ¿Qué figura parece que tiene el área más grande? ¿Cuál parece que tiene el perímetro más grande?

b. Ahora calcule el área y perímetro de cada figura. ¿Cuál tiene el área más grande? ¿Cuál tiene el perímetro más grande?

c. ¿Los resultados de la parte b) fueron los mismos que sus respuestas en la parte (a)? ¿Eso te sorprende?

Contestar

a. Las respuestas variarán. b. Las áreas son las mismas. El$2×8$ rectángulo tiene un perímetro mayor que el$4×4$ cuadrado.

c. Las respuestas variarán.

78. Escribe un problema de palabra de geometría que se relacione con tu experiencia de vida, luego resolverlo y explicar todos tus pasos.

Autocomprobación

a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

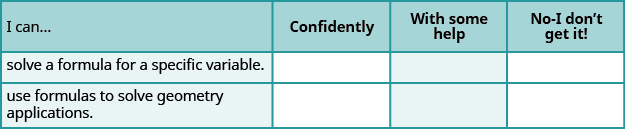
$Esta tabla tiene cuatro columnas y tres filas. La primera fila es un encabezado y etiqueta a cada columna, “Puedo...”, “Con confianza”, “Con algo de ayuda” y “¡No-I don't get it!” En la fila 2, el yo puedo fue resolver una fórmula para una variable específica. En la fila 3, el I can fue usar fórmulas para resolver aplicaciones de geometría.$

b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?