2.5E: Ejercicios

Última actualización
Guardar como PDF

Page ID: 112765

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

La práctica hace la perfección

Solucionar problemas verbales de monedas

En los siguientes ejercicios, resuelve cada problema de palabras de moneda.

1. Michaela tiene $2.05 en monedas de diez centavos y cinco centavos en su monedero. Tiene siete monedas de diez centavos más que de cinco centavos. ¿Cuántas monedas de cada tipo tiene?

Contestar: nueve nickels, 16 dimes

2. Liliana tiene $2.10 en monedas de cinco centavos y cuartos en su mochila. Tiene 12 monedas más de cinco centavos que cuartos. ¿Cuántas monedas de cada tipo tiene?

3. En un cajón de efectivo hay $125 en billetes de $5 y $10. El número de billetes de $10 es el doble que el número de billetes de $5. ¿Cuántos de cada tipo de factura hay en el cajón?

Contestar: diez billetes de $10, cinco billetes de $5

4. Sumanta tiene 175 dólares en billetes de 5 dólares y 10 dólares en su cajón. El número de billetes de $5 es tres veces el número de billetes de $10. ¿Cuántos de cada uno hay en el cajón?

5. Chi tiene $11.30 en monedas de diez centavos y trimestres. El número de monedas de diez centavos es tres veces más que tres veces el número de trimestres. ¿Cuántos de cada uno hay?

Contestar: 63 dimes, 20 trimestres

6. Alison tiene $9.70 en monedas de diez centavos y trimestres. El número de trimestres es ocho más de cuatro veces el número de monedas de diez centavos. ¿Cuántas de cada moneda tiene?

7. Mukul tiene 3.75 dólares en cuartos, monedas de diez centavos y cinco centavos en el bolsillo. Tiene cinco monedas de diez centavos más que cuartos y nueve centavos más que cuartos. ¿Cuántas de cada moneda hay en su bolsillo?

Contestar: 16 nickels, 12 dimes, siete cuartos

8. Viña tiene $4.70 en cuartos, monedas de diez centavos y cinco centavos en su bolso. Tiene ocho monedas de diez centavos más que cuartos y seis monedas más de cinco centavos que cuartos. ¿Cuántas de cada moneda hay en su bolso?

Resolver problemas verbales de boletos y sellos

En los siguientes ejercicios, resuelve cada problema de palabra de boleto o sello.

9. El primer día de un torneo de waterpolo el valor total de los boletos vendidos fue de $17,610. Los pases de un día se venden por $20 y los pases de torneo se venden por $30. El número de pases de torneo vendidos fue 37 más que el número de pases de día vendidos. ¿Cuántos pases de día y cuántos pases de torneo se vendieron?

Contestar: 330 pases diarios, 367 pases para torneos

10. En el cine, el valor total de los boletos vendidos fue de $2,612.50. Los boletos para adultos se venden por $10 cada uno y los boletos para mayores/niños se venden por $7.50 cada uno El número de boletos mayores/niños vendidos fue de 25 menos del doble del número de boletos de adultos vendidos. ¿Cuántos boletos para adultos mayores y niños y cuántos boletos de adultos se vendieron?

11. Julie fue a la oficina de correos y compró tanto sellos de $0.41 como postales de $0.26. Ella gastó $51.40. El número de sellos fue de 20 más del doble del número de postales. ¿Cuántos de cada uno compró?

Contestar: 40 postales, 100 sellos

12. Jason fue a la oficina de correos y compró tanto $0.41 sellos como $0.26 postales y gastó $10.28 El número de sellos fue cuatro más del doble que el número de postales. ¿Cuántos de cada uno compró?

13. Hilda tiene $210 por valor de $10 y $12 acciones en acciones. El número de acciones de $10 es cinco más del doble del número de acciones de $12. ¿Cuántas de cada tipo de acciones tiene?

Contestar: 15 $10 acciones, cinco $12 acciones

14. Mario invirtió $475 en acciones de $45 y $25. El número de acciones de $25 fue cinco menos que tres veces el número de acciones de $45. ¿Cuántas de cada tipo de acción compró?

15. En la pista de hielo se vendieron 95 boletos para la sesión de patinaje vespertino, por un total de 828 dólares. Los boletos de admisión general cuestan $10 cada uno y los boletos juveniles cuestan $8 cada uno. ¿Cuántos boletos de admisión general y cuántos boletos juveniles se vendieron?

Contestar: 34 general, 61 jóvenes

16. Para la hora del espectáculo de las 7:30 se vendieron 140 boletos de cine. Los recibos de los boletos para adultos de $13 y los boletos senior de $10 sumaron $1,664. ¿Cuántos boletos para adultos y cuántos boletos para adultos se vendieron?

17. En la taquilla se vendieron 360 entradas para un concierto en la universidad. Los ingresos totales fueron de $4,170. Los boletos de admisión general cuestan $15 y los boletos de estudiante cuestan $10. ¿Cuántos de cada tipo de boleto se vendió?

Contestar: 114 general, 246 alumno

18. El sábado pasado, la taquilla del museo vendió 281 boletos por un total de $3,954. Los boletos para adultos cuestan $15 y los boletos para estudiantes cuestan $12. ¿Cuántos de cada tipo de boleto se vendió?

Solucionar problemas verbales de mezcla

En los siguientes ejercicios, resuelve cada problema de mezcla de palabras.

19. Macario está haciendo 12 libras de mezcla de nueces con nueces de macadamia y almendras. Las nueces de macadamia cuestan $9 por libra y las almendras cuestan $5.25 por libra. ¿Cuántas libras de nueces de macadamia y cuántas libras de almendras debe usar Macario para que la mezcla cueste $6.50 por libra para hacer?

Contestar: Cuatro libras de nueces de macadamia, ocho libras de almendras

20. Carmen quiere enlosar el piso de su casa. Necesitará 1,000 pies cuadrados de azulejo. Hará la mayor parte del piso con una baldosa que cuesta $1.50 por pie cuadrado,

21. Riley planea plantar un césped en su patio. Necesitará nueve libras de semilla de pasto. Quiere mezclar semilla Bermuda que cuesta $4.80 por libra con semilla de Festuca que cuesta $3.50 por libra. ¿Cuánto de cada semilla debe comprar para que el costo general sea de $4.02 por libra?

Contestar: 3.63.6 lbs Semilla Bermuda, 5.45.4 lbs Semilla Festuca

22. A Vartan le pagaron 25.000 dólares por una aplicación de celular que escribió y quiere invertirla para ahorrar para la educación de su hijo. Quiere poner parte del dinero en un bono que paga 4% de interés anual y el resto en acciones que pagan 9% de interés anual. Si quiere ganar 7.4% de interés anual sobre el monto total, ¿cuánto dinero debe invertir en cada cuenta?

23. Vern vendió su Ford Mustang 1964 por 55,000 dólares y quiere invertir el dinero para ganarle 5.8% de interés al año. Pondrá parte del dinero en el Fondo A que gana 3% anual y el resto en Fondo B que gana 10% anual. ¿Cuánto debería invertir en cada fondo si quiere ganar 5.8% de interés anual sobre el monto total?

Contestar: 33,000 dólares en Fondo A, 22,000 dólares en Fondo B

24. Dominic paga 7% de interés sobre su préstamo universitario de $15,000 y 12% de interés sobre su préstamo de automóvil de $11,000. ¿Qué tasa de interés promedio paga sobre el total de 26 mil dólares que debe? (Redondee su respuesta al décimo por ciento más cercano.)

25. Liam pidió prestado un total de 35.000 dólares para pagar la universidad. Él paga a sus padres el 3% de interés sobre los $8,000 que les pidió prestados y paga al banco 6.8% sobre el resto. ¿Qué tasa de interés promedio paga sobre el total de 35 mil dólares? (Redondee su respuesta al décimo por ciento más cercano.)

Contestar: $5.9%$

Resolver aplicaciones de movimiento uniforme

En los siguientes ejercicios, resuelve.

26. Lilah se muda de Portland a Seattle. Le toma tres horas ir en tren. Mason sale de la estación de tren en Portland y conduce a la estación de tren en Seattle con todas las cajas de Lilah en su automóvil. Le toma 2.4 horas llegar a Seattle, conduciendo a 15 millas por hora más rápido que la velocidad del tren. Encuentra la velocidad de Mason y la velocidad del tren.

27. Kathy y Cheryl están caminando en una recaudación de fondos. Kathy completa el curso en 4.8 horas y Cheryl lo completa en ocho horas. Kathy camina dos millas por hora más rápido que Cheryl. Encuentra la velocidad de Kathy y la velocidad de Cheryl.

Contestar: Kathy 5 mph, Cheryl 3 mph

28. Dos autobuses van de Sacramento a San Diego. El autobús express realiza el viaje en 6.8 horas y el autobús local tarda 10.2 horas para el viaje. La velocidad del autobús expreso es 25 mph más rápida que la velocidad del autobús local. Encuentra la velocidad de ambos autobuses.

29. Un jet comercial y un avión privado vuelan de Denver a Phoenix. El avión comercial tarda 1.6 horas para el vuelo, y el avión privado tarda 2.6 horas. La velocidad del jet comercial es 210 millas por hora más rápida que la velocidad del avión privado. Encuentra la velocidad de ambos aviones a las 10 mph más cercanas.

Contestar: comerciales 540 mph, avión privado 330 mph

30. Saúl condujo su camioneta tres horas desde Dallas hacia Kansas City y se detuvo en una parada de camiones para ir a cenar. En la parada de camiones conoció a Erwin, quien había conducido cuatro horas desde Kansas City hacia Dallas. La distancia entre Dallas y Kansas City es de 542 millas, y la velocidad de Erwin fue ocho millas por hora más lenta que la velocidad de Saúl. Encuentra la velocidad de los dos camioneros.

31. Charlie y Violet se reunieron para almorzar en un restaurante entre Memphis y Nueva Orleans. Charlie había salido de Memphis y condujo 4.8 horas con dirección a Nueva Orleans. Violet había salido de Nueva Orleans y condujo dos horas hacia Memphis, a una velocidad 10 millas por hora más rápida que la velocidad de Charlie. La distancia entre Memphis y Nueva Orleans es de 394 millas. Encuentra la velocidad de los dos pilotos.

Contestar: Violeta 65 mph, Charlie 55 mph

32. Las hermanas Helen y Anne viven a 332 millas de distancia. Para el Día de Acción de Gracias, se conocieron en la casa de su otra hermana a medio camino entre sus casas. Helen condujo 3.2 horas y Anne manejó 2.8 horas. La velocidad promedio de Helen fue cuatro millas por hora más rápida que la de Anne. Encuentra la velocidad promedio de Helen y la velocidad promedio de Anne.

33. Ethan y Leo comienzan a andar en bicicleta en los extremos opuestos de un carril bici de 65 millas. Después de que Ethan haya montado 1.5 horas y Leo haya montado dos horas, se encuentran en el camino. La velocidad de Ethan es seis millas por hora más rápida que la velocidad de Leo. Encuentra la velocidad de los dos ciclistas.

Contestar: Ethan 22 mph, Leo 16 mph

34. Elvira y Aletheia viven a 3.1 millas de distancia en la misma calle. Están en un grupo de estudio que se reúne en una cafetería entre sus casas. Elvira tardó media hora y Aletheia dos tercios de hora en caminar hasta la cafetería. La velocidad de Aletheia es 0.6 millas por hora más lenta que la velocidad de Elvira. Encuentra ambas velocidades para caminar de mujeres.

35. DaMarcus y Fabián viven a 23 millas de distancia y juegan futbol en un parque entre sus casas. DaMarcus montó su bicicleta durante tres cuartos de hora y Fabián montó su bicicleta durante media hora para llegar al parque. La velocidad de Fabián fue seis millas por hora más rápida que la velocidad de DaMarcus. Encuentra la velocidad de ambos futbolistas.

Contestar: DaMarcus 16 mph, Fabián 22 mph

36. Cindy y Richard dejan su dormitorio en Charleston al mismo tiempo. Cindy monta su bicicleta hacia el norte a una velocidad de 18 millas por hora. Richard monta su bicicleta hacia el sur a una velocidad de 14 millas por hora. ¿Cuánto tiempo les llevará estar a 96 millas de distancia?

37. Matt y Chris dejan la casa de su tío en Phoenix al mismo tiempo. Matt conduce hacia el oeste por la I-60 a una velocidad de 76 millas por hora. Chris conduce hacia el este por la I-60 a una velocidad de 82 millas por hora. ¿Cuántas horas les llevará estar a 632 millas de distancia?

Contestar: cuatro horas

38. Dos autobuses salen de Billings al mismo tiempo. El autobús de Seattle se dirige hacia el oeste por la I-90 a una velocidad de 73 millas por hora, mientras que el autobús de Chicago se dirige hacia el este a una velocidad de 79 millas por hora. ¿Cuántas horas les llevará estar a 532 millas de distancia?

39. Dos embarcaciones salen del mismo muelle en El Cairo al mismo tiempo. Uno se dirige al norte por el río Mississippi mientras que el otro se dirige hacia el sur. El barco en dirección norte recorre cuatro millas por hora. El barco con dirección sur recorre ocho millas por hora. ¿Cuánto tiempo les llevará estar a 54 millas de distancia?

Contestar: 4.5 horas

40. Lorena recorre el camino alrededor del parque en 30 minutos. Si trota, le toma 20 minutos. Su velocidad de trote es 1.5 millas por hora más rápida que su velocidad para caminar. Encuentra la velocidad de caminar y trotar de Lorena

41. Julian monta su bicicleta cuesta arriba durante 45 minutos, luego se da la vuelta y vuelve cuesta abajo. Le toma 15 minutos volver a donde empezó. Su velocidad cuesta arriba es 3.2 millas por hora más lenta que su velocidad cuesta abajo. Encuentra la velocidad cuesta arriba y cuesta abajo de Julian.

Contestar

$1.6$mph cuesta arriba,$4.8$ mph cuesta abajo

42. Cassius conduce su bote aguas arriba durante 45 minutos. Le toma 30 minutos regresar río abajo. Su velocidad que va aguas arriba es tres millas por hora más lenta que su velocidad que va aguas abajo. Encuentra sus velocidades aguas arriba y aguas abajo.

43. Darline tarda 20 minutos en conducir para trabajar en semáforo. Llegar a casa, cuando hay mucho tráfico, le toma 36 minutos. Su velocidad en el tráfico ligero es 24 millas por hora más rápida que su velocidad en el tráfico pesado. Encuentra su velocidad en el tráfico ligero y en el tráfico pesado.

Contestar: tráfico ligero 54 mph, tráfico pesado 30 mph

44. A la 1:30, Marlon salió de su casa para ir a la playa, a una distancia de 7.6 millas. Montó su patineta hasta las 2:15, y luego caminó el resto del camino. Llegó a la playa a las 3:00. La velocidad de Marlon en su patineta es 2.5 veces su velocidad de caminar. Encuentra su velocidad al andar en patineta y al caminar.

45. Aarón salió a las 9:15 para conducir a su cabaña de montaña a 108 millas de distancia. Condujo por la autopista hasta las 10:45 y luego condujo por una carretera de montaña. Llegó a las 11:05. Su velocidad en la autopista era tres veces su velocidad en la carretera de montaña. Encuentra la velocidad de Aaron en la autopista y en la carretera de montaña.

Contestar: autopista 72 mph, carretera de montaña 24 mph

46. Marisol salió de Los Ángeles a las 2:30 para conducir a Santa Bárbara, a una distancia de 95 millas. El tráfico era pesado hasta las 3:20. Ella manejó el resto del camino con un tráfico muy ligero y llegó a las 4:20. Su velocidad en el tráfico pesado era 40 millas por hora más lenta que su velocidad en el tráfico ligero. Encuentra su velocidad en el tráfico pesado y en el tráfico ligero.

47. Lizette está entrenando para un maratón. A las 7:00 salió de su casa y corrió hasta las 8:15 después caminó hasta las 11:15. Ella recorrió una distancia total de 19 millas. Su velocidad de carrera era cinco millas por hora más rápida que su velocidad de caminar. Encuéntrala corriendo y caminando velocidades.

Contestar: corriendo ocho mph, caminando tres mph

Matemáticas cotidianas

48. John salió de su casa en Irvine a las 8:35 a.m. para conducir a una reunión en Los Ángeles, a 45 millas de distancia. Llegó a la reunión a las 9:50 horas. A las 5:30 de la noche salió de la reunión y condujo a su casa. Llegó a su casa a las 7:18 p.m.

ⓐ ¿Cuál fue su velocidad promedio en el viaje de Irvine a Los Ángeles?

ⓑ ¿Cuál fue su velocidad promedio en el viaje de Los Ángeles a Irvine?

49. Sarah quiere llegar a la boda de su amiga a las 3:00. La distancia de la casa de Sarah a la boda es de 95 millas. Basado en los patrones de tráfico habituales, Sarah predice que puede conducir las primeras 15 millas a 60 millas por hora, las siguientes 10 millas a 30 millas por hora y el resto del viaje a 70 millas por hora.

ⓐ ¿Cuánto tardará Sarah en conducir las primeras 15 millas?

ⓑ ¿Cuánto tiempo tardará Sarah en conducir las siguientes 10 millas?

ⓓ ¿A qué hora debería salir Sarah de su casa?

Ejercicios de escritura

50. Supongamos que tiene seis cuartos, nueve centavos y cuatro centavos. Explica cómo encuentras el valor total de todas las monedas.

51. ¿Te resulta útil usar una mesa a la hora de resolver problemas de monedas? ¿Por qué o por qué no?

Contestar: Las respuestas variarán.

52. En la tabla utilizada para resolver problemas de monedas, una columna está etiquetada como “número” y otra columna está etiquetada como “valor”. ¿Cuál es la diferencia entre el “número” y el “valor”?

53. Al resolver un problema de movimiento uniforme, ¿cómo te ayuda dibujar un diagrama de la situación?

Contestar: Las respuestas variarán.

Autocomprobación

ⓐ Después de completar los ejercicios, usa esta lista de verificación para evaluar tu dominio de los objetivos de esta sección.

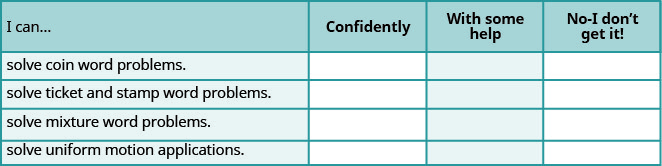
$Esta tabla tiene cuatro columnas y cinco filas. La primera fila es un encabezado y etiqueta a cada columna, “Puedo...”, “Con confianza”, “Con algo de ayuda” y “¡No-I don't get it!” En la fila 2, el yo puedo fue resolver problemas verbales de monedas. En la fila 3, el yo puedo fue usar fórmulas para resolver problemas de boletos y estampar palabras. En la fila 4, el yo puedo fue resolver problemas verbales de mezcla. En la fila 5, lo que puedo fue resolver aplicaciones de movimiento uniforme.$

ⓑ En una escala del 1-10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?