5.4: Multiplicar polinomios
- Page ID
- 112369
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Multiplicar monomios
- Multiplicar un polinomio por un monomio
- Multiplicar un binomio por un binomio
- Multiplicar un polinomio por un polinomio
- Multiplicar productos especiales
- Multiplicar funciones polinómicas
Antes de comenzar, toma este cuestionario de preparación.
Multiplicar monomios
Estamos listos para realizar operaciones en polinomios. Dado que los monomios son expresiones algebraicas, podemos usar las propiedades de los exponentes para multiplicar los monomios.
Multiplicar:
- \((3x^2)(−4x^3)\)
- \(\left(\frac{5}{6}x^3y\right)(12xy^2).\)
- Contestar a
-
\(\begin{array} {ll} {} &{(3x^2)(−4x^3)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{3·(−4)·x^2·x^3} \\ {\text{}} &{−12x^5} \\ \end{array} \)
- Respuesta b
-
\(\begin{array} {ll} {} &{\left(\frac{5}{6}x^3y\right)(12xy^2)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{\frac{5}{6}·12·x^3·x·y·y^2} \\ {\text{Multiply.}} &{10x^4y^3} \\ \end{array} \)
Multiplicar:
- \((5y^7)(−7y^4)\)
- \((25a^4b^3)(15ab^3)\)
- Contestar a
-
\(−35y^{11}\)
- Respuesta b
-
\(375 a^5b^6\)
Multiplicar:
- \((−6b^4)(−9b^5)\)
- \((23r^5s)(12r^6s^7).\)
- Contestar a
-
\(54b^9\)
- Respuesta b
-
\(276 r^{11}s^8\)
Multiplicar un polinomio por un monomio
Multiplicar un polinomio por un monomio es realmente solo aplicar la Propiedad Distributiva.
Multiplicar:
- \(−2y(4y^2+3y−5)\)
- \(3x^3y(x^2−8xy+y^2)\).
- Contestar a
-
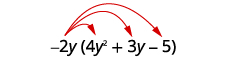
Distribuir. 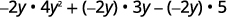
Multiplicar. 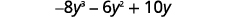
- Respuesta b
-
\(\begin{array} {ll} {} &{3x^3y(x^2−8xy+y^2)} \\ {\text{Distribute.}} &{3x^3y⋅x^2+(3x^3y)⋅(−8xy)+(3x^3y)⋅y^2} \\ {\text{Multiply.}} &{3x^5y−24x^4y^2+3x^3y^3} \\ \end{array} \)
Multiplicar:
- \(-3y(5y^2+8y^{7})\)
- \(4x^2y^2(3x^2−5xy+3y^2)\)
- Contestar a
-
\(−15y^3−24y^8\)
- Respuesta b
-
\(12x^4y^2−20x^3y^3+12x^2y^4\)
Multiplicar:
- \(4x^2(2x^2−3x+5)\)
- \(−6a^3b(3a^2−2ab+6b^2)\)
- Contestar a
-
\(8x^4−12x^3+20x^2\)
- Respuesta b
-
\(−18a^5b+12a^4b^2−36a^3b^3\)
Multiplicar un Binomio por un Binomio
Al igual que hay diferentes formas de representar la multiplicación de números, existen varios métodos que se pueden utilizar para multiplicar un binomio por un binomio. Comenzaremos por usar la Propiedad Distributiva.
Multiplicar:
- \((y+5)(y+8)\)
- \((4y+3)(2y−5)\).
- Responder
-
ⓐ
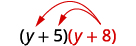
Distribuir\((y+8)\). 
Distribuir de nuevo. 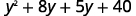
Combina términos similares. 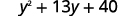
ⓑ
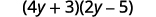
Distribuir. 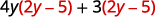
Distribuir de nuevo. 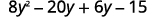
Combina términos similares. 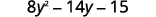
Multiplicar:
- \((x+8)(x+9)\)
- \((3c+4)(5c−2)\).
- Contestar a
-
\(x^2+17x+72\)
- Respuesta b
-
\(15c^2+14c−8\)
Multiplicar:
- \((5x+9)(4x+3)\)
- \((5y+2)(6y−3)\).
- Contestar a
-
\(20x^2+51x+27\)
- Respuesta b
-
\(30y^2−3y−6\)
Si multiplica binomios con la suficiente frecuencia, puede notar un patrón. Observe que el primer término en el resultado es producto de los primeros términos en cada binomio. El segundo y tercer término son producto de multiplicar los dos términos externos y luego los dos términos internos. Y el último término resulta de multiplicar los dos últimos términos,
Abreviamos “Primero, Exterior, Interior, Último” como FOIL. Las letras significan 'Primero, Exterior, Interior, Último'. Usamos esto como otro método de multiplicar binomios. La palabra FOIL es fácil de recordar y asegura que encontremos los cuatro productos.
Multipliquemos\((x+3)(x+7)\) usando ambos métodos.

A continuación resumimos los pasos del método FOIL. El método FOIL solo se aplica a multiplicar binomios, ¡no a otros polinomios!

Cuando multiplicas por el método FOIL, dibujar las líneas ayudará a que tu cerebro se concentre en el patrón y facilitará su aplicación.
Ahora haremos un ejemplo donde usamos el patrón FOIL para multiplicar dos binomios.
Multiplicar:
- \((y−7)(y+4)\)
- \((4x+3)(2x−5)\).
- Responder
-
a.

b.

Multiplicar:
- \((x−7)(x+5)\)
- \((3x+7)(5x−2)\).
- Responder
-
a.\(x^2−2x−35\)
b.\(15x^2+29x−14\)
Multiplicar:
- \((b−3)(b+6)\)
- \((4y+5)(4y−10)\).
- Responder
-
a.\(b^2+3b−18\)
b.\(16y^2−20y−50\)
Los productos finales en el último ejemplo fueron trinomios porque podíamos combinar los dos términos medios. No siempre es así.
Multiplicar:
- \((n^2+4)(n−1)\)
- \((3pq+5)(6pq−11)\).
- Responder
-
a.
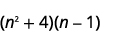
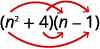
Paso 1. Multiplicar los primeros términos. 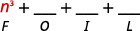
Paso 2. Multiplicar los términos externos. 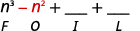
Paso 3. Multiplicar los términos internos. 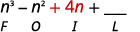
Paso 4. Multiplicar los últimos términos. 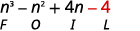
Paso 5. Combina términos similares, no hay ninguno. 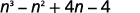
b.
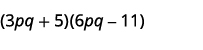
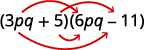
Paso 1. Multiplicar los primeros términos. 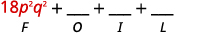
Paso 2. Multiplicar los términos externos. 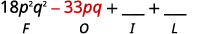
Paso 3. Multiplicar los términos internos. 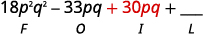
Paso 4. Multiplicar los últimos términos. 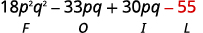
Paso 5. Combina términos similares. 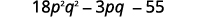
Multiplicar:
- \((x^2+6)(x−8)\)
- \((2ab+5)(4ab−4)\).
- Responder
-
a.\(x^3−8x^2+6x−48\)
b.\(8a^2b^2+12ab−20\)
Multiplicar:
- \((y^2+7)(y−9)\)
- \((2xy+3)(4xy−5)\).
- Responder
-
a.\(y^3−9y^2+7y−63\)
b.\(8x^2y^2+2xy−15\)
El método FOIL suele ser el método más rápido para multiplicar dos binomios, pero solo funciona para binomios. Puede utilizar la Propiedad Distributiva para encontrar el producto de cualquiera de dos polinomios. Otro método que funciona para todos los polinomios es el Método Vertical. Es muy parecido al método que usas para multiplicar números enteros. Observe con atención este ejemplo de multiplicar números de dos dígitos.

Ahora aplicaremos este mismo método para multiplicar dos binomios.
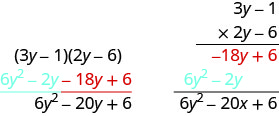
Multiplicar usando el Método Vertical:\((3y−1)(2y−6)\).
- Responder
-
No importa qué binomio vaya en la parte superior.
\ (\ begin {align*} & &\ quad\;\;\; 3y - 1\\ [4pt]
& & &\ subrayado {\ quad\ veces\; 2y-6}\\ [4pt]
&\ text {Multiplicar} 3y-1\ texto {por} -6. & &\ quad -18y + 6 & &\ texto {producto parcial}\\ [4pt]
&\ texto {Multiplicar} 3y-1\ texto {por} 2y. & &\ subrayado {6y^2 - 2y} &\ text {producto parcial}\\ [4pt]
&\ text {Agregar términos similares.} & & 6y^2 - 20y + 6\ end {alinear*}\)Observe que los productos parciales son los mismos que los términos en el método FOIL.
Multiplicar usando el Método Vertical:\((5m−7)(3m−6)\).
- Responder
-
\(15m^2−51m+42\)
Multiplicar usando el Método Vertical:\((6b−5)(7b−3)\).
- Responder
-
\(42b^2−53b+15\)
Ahora hemos utilizado tres métodos para multiplicar binomios. Asegúrate de practicar cada método, y trata de decidir cuál prefieres. Los métodos se enumeran aquí todos juntos, para ayudarte a recordarlos.
Para multiplicar binomios, utilice el:
- Propiedad distributiva
- Método FOIL
- Método Vertical
Multiplicar un polinomio por un polinomio
Hemos multiplicado los monomios por monomios, los monomios por los polinomios y los binomios por los binomios. Ahora estamos listos para multiplicar un polinomio por un polinomio. Recuerde, FOIL no funcionará en este caso, pero podemos usar ya sea la Propiedad Distributiva o el Método Vertical.
Multiplicar\((b+3)(2b^2−5b+8)\) usando ⓐ la Propiedad Distributiva y ⓑ el Método Vertical.
- Responder
-
a.
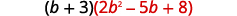
Distribuir. 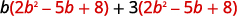
Multiplicar. 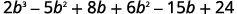
Combina términos similares. 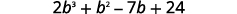
b. Es más fácil poner el polinomio con menos términos en la parte inferior porque obtenemos menos productos parciales de esta manera.
Multiplicar\((2b^2−5b+8)\) por 3.
Multiplicar\((2b^2−5b+8)\) por\(b\).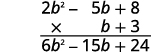
Agregar términos similares. 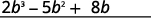
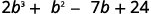
Multiplicar\((y−3)(y^2−5y+2)\) usando ⓐ la Propiedad Distributiva y ⓑ el Método Vertical.
- Responder
-
a.\(y^3−8y^2+17y−6\)
b.\(y^3−8y^2+17y−6\)
Multiplicar\((x+4)(2x^2−3x+5)\) usando a) la Propiedad Distributiva y b) El Método Vertical.
- Responder
-
a. y b.\(2x^3+5x^2−7x+20\)
Ahora hemos visto dos métodos que puedes usar para multiplicar un polinomio por un polinomio. Después de practicar cada método, probablemente encontrarás que prefieres una forma sobre la otra. Enumeramos ambos métodos que se enumeran aquí, para una fácil referencia.
Para multiplicar un trinomio por un binomio, use el:
- Propiedad distributiva
- Método Vertical
Multiplicar productos especiales
A los matemáticos les gusta buscar patrones que faciliten su trabajo. Un buen ejemplo de esto es la cuadratura de binomios. Si bien siempre puedes obtener el producto escribiendo el binomio dos veces y multiplicándolos, hay menos trabajo por hacer si aprendes a usar un patrón. Empecemos por mirar tres ejemplos y buscar un patrón.
Mira estos resultados. ¿Ves algún patrón?
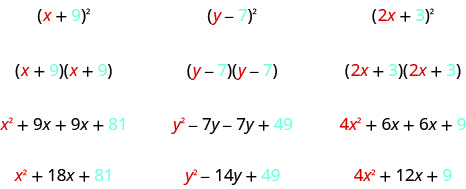
¿Qué pasa con el número de términos? En cada ejemplo cuadrábamos un binomio y el resultado fue un trinomio.
\[(a+b)^2=\text{___}+\text{___}+\text{___} \nonumber\]
Ahora mira el primer término en cada resultado. ¿De dónde vino?
El primer término es producto de los primeros términos de cada binomio. Como los binomios son idénticos, ¡es solo el cuadrado del primer término!
\[(a+b)^2=a^2+\text{___}+\text{___} \nonumber\]
Para obtener el primer término del producto, cuadrar el primer término.
¿De dónde vino el último término? Mira los ejemplos y encuentra el patrón.
El último término es producto de los últimos términos, que es el cuadrado del último término.
\[(a+b)^2=\text{___}+\text{___}+b^2 \nonumber\]
Para obtener el último término del producto, cuadrar el último término.
Por último, mira el término medio. Observe que vino de agregar los términos “exterior” e “interno”, ¡que son ambos iguales! Entonces el término medio es el doble del producto de los dos términos del binomio.
\[(a+b)^2=\text{___}+2ab+\text{___} \nonumber\]
\[(a−b)^2=\text{___}−2ab+\text{___} \nonumber\]
Para obtener el término medio del producto, multiplique los términos y duplique su producto.
Poniéndolo todo junto:
Si a y b son números reales,

Para cuadrar un binomio, cuadrar el primer término, cuadrar el último término, duplicar su producto.
Multiplicar: a.\((x+5)^2\) b\((2x−3y)^2\).
- Responder
-
a.
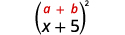
Cuadrado el primer término. 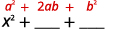
Cuadrarse el último término. 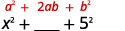
Duplique su producto. 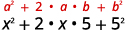
Simplificar. 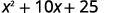
b.
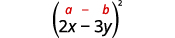
Usa el patrón. 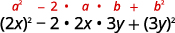
Simplificar. 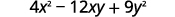
Multiplicar: a.\((x+9)^2\) b\((2c−d)^2\).
- Responder
-
a.\(x^2+18x+81\)
b.\(4c^2−4cd+d^2\)
Multiplicar: a.\((y+11)^2\) b\((4x−5y)^2\).
- Responder
-
a.\(y^2+22y+121\)
b.\(16x^2−40xy+25y^2\)
Acabamos de ver un patrón para cuadrar binomios que podemos usar para facilitar la multiplicación de algunos binomios. De igual manera, existe un patrón para otro producto de binomios. Pero antes de llegar a ello, necesitamos introducir algo de vocabulario.
Un par de binomios que tienen cada uno el mismo primer término y el mismo último término, pero uno es una suma y uno es una diferencia se llama par conjugado y es de la forma\((a−b)\),\((a+b)\).
Un par conjugado es dos binomios de la forma
\[(a−b), (a+b). \nonumber\]
El par de binomios tienen cada uno el mismo primer término y el mismo último término, pero un binomio es una suma y el otro es una diferencia.
Hay un patrón agradable para encontrar el producto de los conjugados. Podrías, por supuesto, simplemente FOIL para obtener el producto, pero usar el patrón facilita tu trabajo. Busquemos el patrón usando FOIL para multiplicar algunos pares conjugados.
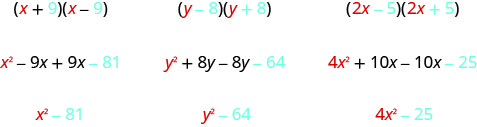
¿Qué observas de los productos?
¡El producto de los dos binomios también es un binomio! La mayoría de los productos resultantes de FOIL han sido trinomios.
Cada primer término es producto de los primeros términos de los binomios, y como son idénticos es el cuadrado del primer término.
\[(a+b)(a−b)=a^2−\text{___} \nonumber\]
Para obtener el primer término, cuadrar el primer término.
El último término vino de multiplicar los últimos términos, el cuadrado del último término.
\[(a+b)(a−b)=a^2−b^2 \nonumber\]
Para obtener el último término, cuadrar el último término.
¿Por qué no hay término medio? Observe los dos términos medios que obtiene de FOIL combinan a 0 en cada caso, el resultado de una suma y una resta.
El producto de los conjugados es siempre de la forma\(a^2−b^2\). A esto se le llama diferencia de cuadrados.
Esto lleva al patrón:
Si a y b son números reales,

El producto se llama diferencia de cuadrados.
Para multiplicar conjugados, cuadrar el primer término, cuadrar el último término, escribirlo como una diferencia de cuadrados.
Multiplicar usando el producto del patrón de conjugados: a.\((2x+5)(2x−5)\) b\((5m−9n)(5m+9n)\).
- Responder
-
a.
¿Los binomios son conjugados? 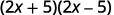
Es el producto de los conjugados. 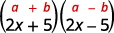
Cuadrado el primer término, 2x.2x. 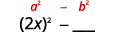
Cuadrarse el último término, 5.5. 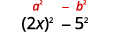
Simplificar. El producto es una diferencia de cuadrados. 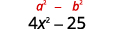
b.
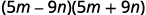
Esto se ajusta al patrón. 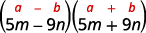
Usa el patrón. 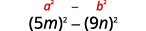
Simplificar. 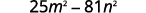
Multiplicar: a.\((6x+5)(6x−5)\) b\((4p−7q)(4p+7q)\).
- Responder
-
a.\(36x^2−25\)
b.\(16p^2−49q^2\)
Multiplicar: a.\((2x+7)(2x−7)\) b\((3x−y)(3x+y)\).
- Responder
-
a.\(4x^2−49\) b.\(9x^2−y^2\)
Acabamos de desarrollar patrones especiales de productos para Cuadrados Binomiales y para el Producto de Conjugados. Los productos se ven similares, por lo que es importante reconocer cuándo es apropiado usar cada uno de estos patrones y notar en qué se diferencian. Observe los dos patrones juntos y anote sus similitudes y diferencias.
| Cuadrados Binomiales | Producto de Conjugados |
|---|---|
| \((a+b)^2=a^2+2ab+b^2\) | \((a−b)(a+b)=a^2−b^2\) |
| \((a−b)^2=a^2−2ab+b^2\) | |
| • Al cuadrado de un binomio | • Multiplicar conjugados |
| • El producto es un trinomio | • El producto es un binomio. |
| • Los términos internos y externos con FOIL son los mismos. | • Los términos internos y externos con FOIL son opuestos. |
| • El término medio es el doble del producto de los términos | • No hay término medio. |
Elige el patrón adecuado y úsalo para encontrar el producto:
a.\((2x−3)(2x+3)\) b.\((8x-5)^2\) c.\((6m+7)^2\) d\((5x−6)(6x+5)\).
- Responder
-
a.\((2x−3)(2x+3)\)
Estos son conjugados. Tienen los mismos primeros números, y los mismos últimos números, y un binomio es una suma y el otro es una diferencia. Se ajusta al patrón Producto de Conconjugados.
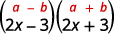
Usa el patrón. 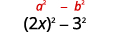
Simplificar. 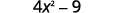
b.\((8x−5)^2\)
Se nos pide cuadrar un binomio. Se ajusta al patrón de cuadrados binomiales.
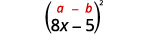
Usa el patrón. 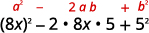
Simplificar. 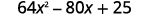
c.\((6m+7)^2\)
Nuevamente, cuadraremos un binomio así que usaremos el patrón de cuadrados binomiales.
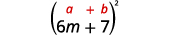
Usa el patrón. 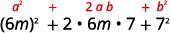
Simplificar. 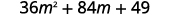
d.\((5x−6)(6x+5)\)
Este producto no se ajusta a los patrones, por lo que usaremos FOIL.
\(\begin{array} {ll} {} &{(5x−6)(6x+5)} \\ {\text{Use FOIL.}} & {30x^2+25x−36x−30} \\ {\text{Simplify.}} & {30x^2−11x−30} \\ \end{array}\)
Elige el patrón adecuado y úsalo para encontrar el producto:
a.\((9b−2)(2b+9)\) b.\((9p−4)^2\) c.\((7y+1)^2\) d\((4r−3)(4r+3)\).
- Responder
-
a. FOIL;\(18b^2+77b−18\)
b. Cuadrados Binomiales;\(81p^2−72p+16\)
c. Cuadrados Binomiales;\(49y^2+14y+1\)
d. Producto de Conjugados;\(16r^2−9\)
Elige el patrón adecuado y úsalo para encontrar el producto:
a.\((6x+7)^2\) b.\((3x−4)(3x+4)\) c.\((2x−5)(5x−2)\) d\((6n−1)^2\).
- Responder
-
a. Cuadrados Binomiales;\(36x^2+84x+49\) b. Producto de Conconjugados;\(9x^2−16\) c. Lámina;\(10x^2−29x+10\) d. Cuadrados Binomiales;\(36n^2−12n+1\)
Multiplicar funciones polinomiales
Así como los polinomios se pueden multiplicar, las funciones polinómicas también se pueden multiplicar.
Para funciones\(f(x)\) y\(g(x)\),
\[(f·g)(x)=f(x)·g(x)\]
Para funciones\(f(x)=x+2\) y\(g(x)=x^2−3x−4\), encuentre:
- \((f·g)(x)\)
- \((f·g)(2)\).
- Responder
-
a.
\(\begin{array} {ll} {} &{(f·g)(x)=f(x)·g(x)} \\ {\text{Substitute for } f(x) \text{ and } g(x)} &{(f·g)(x)=(x+2)(x^2−3x−4)} \\ {\text{Multiply the polynomials.}} &{(f·g)(x)=x(x^2−3x−4)+2(x^2−3x−4)} \\ {\text{Distribute.}} &{(f·g)(x)=x3−3x^2−4x+2x^2−6x−8} \\ {\text{Combine like terms.}} &{(f·g)(x)=x3−x^2−10x−8} \\ \end{array}\)
b. en la parte a. encontramos\((f·g)(x)\) y ahora se les pide encontrar\((f·g)(2)\).
\(\begin{array} {ll} {} &{(f·g)(x)=x^3−x^2−10x−8} \\ {\text{To find }(f·g)(2), \text{ substitute } x=2.} &{(f·g)(2)=2^3−2^2−10·2−8} \\ {} &{(f·g)(2)=8−4−20−8} \\ {} &{(f·g)(2)=−24} \\ \end{array}\)
Para funciones\(f(x)=x−5\) y\(g(x)=x^2−2x+3\), encontrar
- \((f·g)(x)\)
- \((f·g)(2)\).
- Contestar a
-
\((f·g)(x)=x^3−7x^2+13x−15\)
- Respuesta b
-
\((f·g)(2)=−9\)
Para funciones\(f(x)=x−7\) y\(g(x)=x^2+8x+4\), encontrar
- \((f·g)(x)\)
- \((f·g)(2)\).
- Contestar a
-
\((f·g)(x)=x^3+x^2−52x−28\)
- Contestar a
-
\((f·g)(2)=−120\)
Acceda a este recurso en línea para obtener instrucción y práctica adicionales con polinomios multiplicadores.
- Introducción a productos especiales de binomios
Conceptos clave
- Cómo utilizar el método FOIL para multiplicar dos binomios.
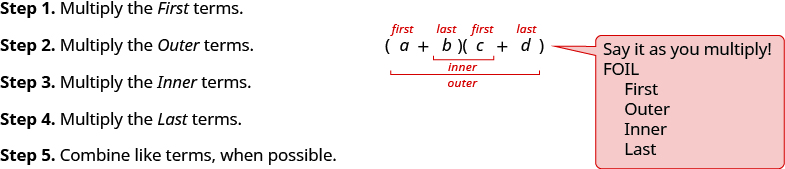
- Multiplicar dos binomios: Para multiplicar binomios, use el:
- Propiedad distributiva
- Método FOIL
- Multiplicar un polinomio por un polinomio: Para multiplicar un trinomio por un binomio, use el:
- Propiedad distributiva
- Método Vertical
- Patrón de cuadrados binomiales
Si a y b son números reales,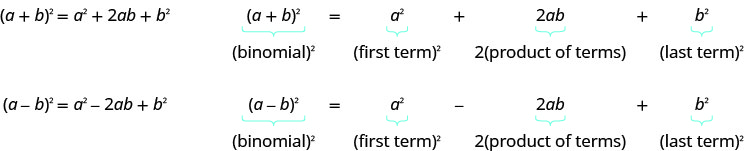
- Producto de Conjugados Patrón
Si a, b son números reales
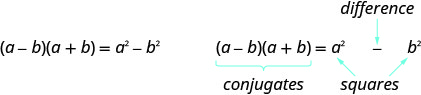
El producto se llama diferencia de cuadrados.
Para multiplicar conjugados, cuadrar el primer término, cuadrar el último término, escribirlo como una diferencia de cuadrados. - Comparación de los patrones de productos especiales
Cuadrados Binomiales Producto de Conconjugados \((a+b)^2=a^2+2ab+b^2\) \((a−b)^2=a^2−2ab+b^2\) \((a−b)(a+b)=a^2−b^2\) • Al cuadrado de un binomio • Multiplicar conjugados • El producto es un trinomio • El producto es un binomio. • Los términos internos y externos con FOIL son los mismos. • Los términos internos y externos con FOIL son opuestos. • El término medio es el doble del producto de los términos • No hay término medio. - Multiplicación de Funciones Polinómicas:
- Para funciones\(f(x)\) y\(g(x)\),
\[(f⋅g)(x)=f(x)⋅g(x) \nonumber\]
- Para funciones\(f(x)\) y\(g(x)\),
Glosario
- par conjugado
- Un par conjugado es dos binomios de la forma\((a−b)\) y\((a+b)\). El par de binomios tienen cada uno el mismo primer término y el mismo último término, pero un binomio es una suma y el otro es una diferencia.


