11.4: Elipses
- Page ID
- 112797
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Grafica una elipse con el centro en el origen
- Encuentra la ecuación de una elipse con el centro en el origen
- Graficar una elipse con el centro no en el origen
- Resolver aplicación con elipses
Antes de comenzar, toma este cuestionario de preparación.
- Gráfica\(y=(x-1)^{2}-2\) usando transformaciones.
Si te perdiste este problema, revisa el Ejemplo 9.57. - Completa el cuadrado:\(x^{2}-8 x=8\).
Si te perdiste este problema, revisa el Ejemplo 9.12. - Escribir en forma estándar. \(y=2 x^{2}-12 x+14\)
Si te perdiste este problema, revisa el Ejemplo 9.59.
Grafica una elipse con el centro en el origen
La siguiente sección cónica que veremos es una elipse. Definimos una elipse como todos los puntos en un plano donde la suma de las distancias desde dos puntos fijos es constante. Cada uno de los puntos dados se llama foco de la elipse.
Una elipse son todos los puntos de un plano donde la suma de las distancias desde dos puntos fijos es constante. Cada uno de los puntos fijos se llama foco de la elipse.
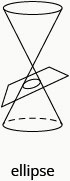
Podemos dibujar una elipse tomando alguna longitud fija de cuerda flexible y uniendo los extremos a dos tachuelas. Usamos una pluma para tirar de la cuerda tensa y girarla alrededor de las dos tachuelas. La cifra que resulta es una elipse.
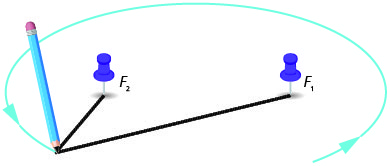
Una línea dibujada a través de los focos intersecta la elipse en dos puntos. Cada punto se llama un vértice de la elipse. El segmento que conecta los vértices se denomina eje mayor. El punto medio del segmento se llama el centro de la elipse. Un segmento perpendicular al eje mayor que pasa por el centro e intersecta la elipse en dos puntos se denomina eje menor.
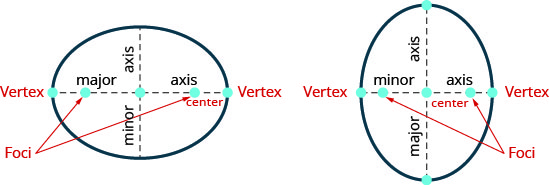
Mencionamos anteriormente que nuestro objetivo es conectar la geometría de una cónica con el álgebra. Colocar la elipse en un sistema de coordenadas rectangulares nos da esa oportunidad. En la figura, colocamos la elipse de manera que los focos\(((−c,0),(c,0))\) estén en el\(x\) eje -y el centro sea el origen.
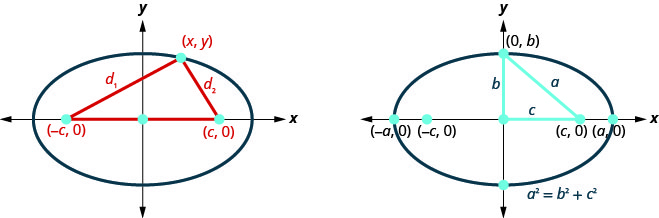
La definición establece que la suma de la distancia desde los focos a un punto\((x,y)\) es constante. Entonces\(d_{1}+d_{2}\) es una constante a la que llamaremos\(2a\) así,\(d_{1}+d_{2}=2 a\). Usaremos la fórmula de distancia para llevarnos a una fórmula algebraica para una elipse.
\(d_{1} \quad+\quad \quad d_{2} \quad=\quad 2 a\)
Usa la fórmula de distancia para encontrar\(d_{1},d_{2}\).
\(\sqrt{(x-(-c))^{2}+(y-0)^{2}}+\sqrt{(x-c)^{2}+(y-0)^{2}}=2 a\)
Después de eliminar radicales y simplificar, obtenemos:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}-c^{2}}=1\)
Para simplificar la ecuación de la elipse,\(a^{2}−c^{2}=b^{2}\) dejamos.Entonces, la ecuación de una elipse centrada en el origen en forma estándar es:
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Para graficar la elipse, será útil conocer las intercepciones. Encontraremos las\(x\) -intercepciones e\(y\) -intercepciones usando la fórmula.
\(y\)-intercepta
Vamos\(x=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{0^{2}}{a^{2}}+\frac{y^{2}}{a^{2}} &=1 \\ \frac{y^{2}}{b^{2}} &=1 \\ y^{2} &=b^{2} \\ y &=\pm b \end{aligned}\)
Los\(y\) -interceptos son\((0,b)\) y\((0, -b)\).
\(x\)-intercepta
Vamos\(y=0\).
\(\begin{aligned} \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}}+\frac{0^{2}}{b^{2}} &=1 \\ \frac{x^{2}}{a^{2}} &=1 \\ x^{2} &=a^{2} \\ x &=\pm a \end{aligned}\)
Los\(x\) -interceptos son\((a,0)\) y\((-a,0)\).
Forma estándar de la ecuación una elipse con centro\((0,0)\)
La forma estándar de la ecuación de una elipse con centro\((0,0)\), es
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Los\(x\) -interceptos son\((a,0)\) y\((−a,0)\).
Los\(y\) -interceptos son\((0,b)\) y\((0,−b)\).
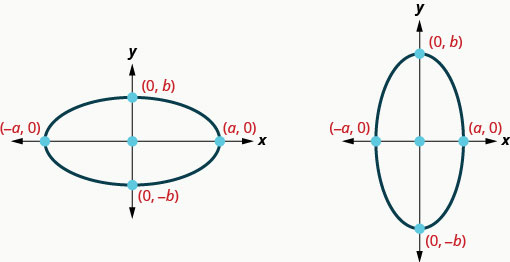
Observe que cuando el eje mayor es horizontal, el valor de\(a\) será mayor que el valor de\(b\) y cuando el eje mayor sea vertical, el valor de\(b\) será mayor que el valor de\(a\). Utilizaremos esta información para graficar una elipse centrada en el origen.
Elipse con centro\((0,0)\)
| \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\) | \(a>b\) | \(b>a\) |
|---|---|---|
| Eje mayor | en el\(x\) eje -. | en el\(y\) eje |
| \(x\)-intercepta | \((-a, 0),(a, 0)\) | |
| \(y\)-intercepta | \((0,-b),(0, b)\) |
Gráfica:\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\).
Solución:
| Paso 1. Escribe la ecuación en forma estándar. | Está en forma estándar. | \(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) |
| Paso 2. Determinar si el eje mayor es horizontal o vertical. | Ya que\(9>4\) y\(9\) está en el\(y^{2}\) término, el eje mayor es vertical. | El eje mayor es vertical. |
| Paso 3. Encuentra los puntos finales del eje mayor. |
Los puntos finales serán los\(y\) -interceptos. Desde\(b^{2}=9\) entonces\(b=\pm 3\). Los puntos finales del eje mayor son\((0,3),(0,-3)\). |
Los puntos finales del eje mayor son\((0,3),(0,-3)\). |
| Paso 4. Encuentra los extremos del eje menor. | Los puntos finales serán los\(x\) -interceptos.
Desde\(a^{2}=4\) entonces\(a=\pm 2\). Los puntos finales del eje mayor son\((2,0),(-2,0)\). |
Los puntos finales del eje mayor son\((2,0),(-2,0)\). |
| Paso 5. Esboza la elipse. | .png) |
Gráfica:\(\frac{x^{2}}{4}+\frac{y^{2}}{16}=1\).
- Contestar
-
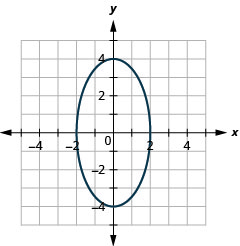
Figura 11.3.7
Gráfica:\(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\).
- Contestar
-
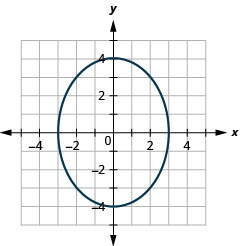
Figura 11.3.8
Resumimos los pasos para referencia.
CÓMO GRAPAR UNA ELIPSE CON CENTRO\((0,0)\).
- Escribe la ecuación en forma estándar.
- Determinar si el eje mayor es horizontal o vertical.
- Encuentra los puntos finales del eje mayor.
- Encontrar los puntos finales del eje menor
- Esboza la elipse.
A veces nuestra ecuación primero tendrá que ser puesta en forma estándar.
Gráfica\(x^{2}+4 y^{2}=16\).
Solución:
| Reconocemos esto como la ecuación de una elipse ya que tanto los\(x\)\(y\) términos como son cuadrados y tienen coeficientes diferentes. |
\(x^{2}+4 y^{2}=16\) |
| Para obtener la ecuación en forma estándar, divida ambos lados por\(16\) para que la ecuación sea igual a\(1\). |
\(\frac{x^{2}}{16}+\frac{4 y^{2}}{16}=\frac{16}{16}\) |
| Simplificar. | \(\frac{x^{2}}{16}+\frac{y^{2}}{4}=1\) |
| La ecuación está en forma estándar. La elipse está centrada en el origen. |
El centro es\((0,0)\). |
| Ya que\(16>4\) y\(16\) está en el\(x^{2}\) término, el eje mayor es horizontal. |
|
| \(a^{2}=16, a=\pm 4\) \(b^{2}=4, \quad b=\pm 2\) |
Los vértices son\((4,0),(−4,0)\). Los extremos del eje menor son \((0,2),(0,−2)\). |
| Esbozar la parábola. | 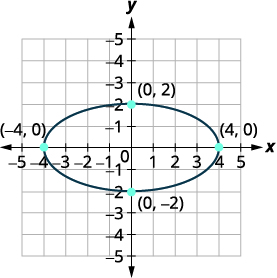 |
Gráfica\(9 x^{2}+16 y^{2}=144\).
- Contestar
-
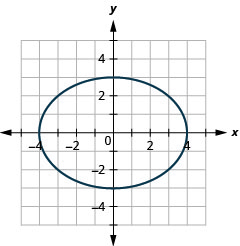
Figura 11.3.10
Gráfica\(16 x^{2}+25 y^{2}=400\).
- Contestar
-
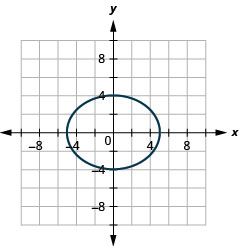
Figura 11.3.11
Encuentra la ecuación de una elipse con el centro en el origen
Si se nos da la gráfica de una elipse, podemos encontrar la ecuación de la elipse.
Encuentra la ecuación de la elipse mostrada.
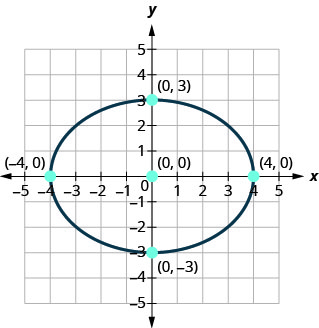
Solución:
Reconocemos esto como una elipse que se centra en el origen.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Ya que el eje mayor es horizontal y la distancia desde el centro hasta el vértice es\(4\), sabemos\(a=4\) y así\(a^{2}=16\).
\(\frac{x^{2}}{16}+\frac{y^{2}}{b^{2}}=1\)
El eje menor es vertical y la distancia desde el centro a la elipse es\(3\), sabemos\(b=3\) y así\(b^{2}=9\).
\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\)
Encuentra la ecuación de la elipse mostrada.
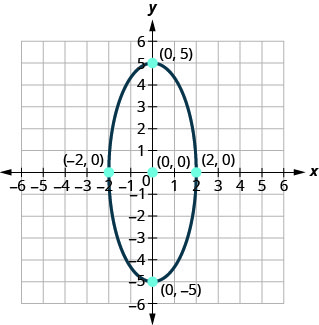
- Contestar
-
\(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
Encuentra la ecuación de la elipse mostrada.
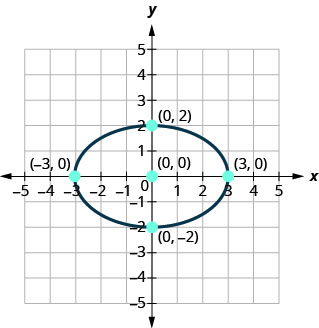
- Contestar
-
\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\)
Grafica una elipse con el centro no en el origen
Las elipses que hemos mirado hasta ahora han sido todas centradas en el origen. Ahora veremos elipses cuyo centro es\((h,k)\).
La ecuación es\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) y cuándo\(a>b\), el eje mayor es horizontal por lo que la distancia desde el centro al vértice es\(a\). Cuando\(b>a\), el eje mayor es vertical por lo que la distancia desde el centro al vértice es\(b\).
Forma estándar de la ecuación una elipse con centro\((h,k)\)
La forma estándar de la ecuación de una elipse con centro\((h,k)\), es
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
Cuando\(a>b\), el eje mayor es horizontal por lo que la distancia desde el centro al vértice es\(a\).
Cuando\(b>a\), el eje mayor es vertical por lo que la distancia desde el centro al vértice es\(b\).
Gráfica:\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\).
Solución:
| La ecuación está en forma estándar,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). | \(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) |
| La elipse está centrada en\((h,k)\). | El centro es\((3,1)\). |
| Ya que\(9>4\) y\(9\) está en el\(x^{2}\) término, el eje mayor es horizontal. | |
| \(a^{2}=9, a=\pm 3\) \(b^{2}=4, b=\pm 2\) |
La distancia desde el centro a los vértices es\(3\). La distancia desde el centro hasta los extremos del eje menor es\(2\). |
| Esboza la elipse. | 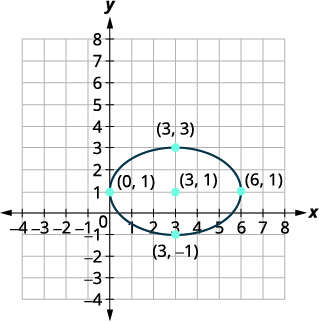 |
Gráfica:\(\frac{(x+3)^{2}}{4}+\frac{(y-5)^{2}}{16}=1\).
- Contestar
-
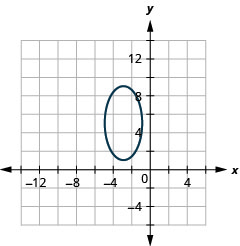
Figura 11.3.16
Gráfica:\(\frac{(x-1)^{2}}{25}+\frac{(y+3)^{2}}{16}=1\).
- Contestar
-
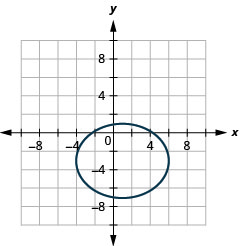
Figura 11.3.17
Si miramos las ecuaciones de\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\) y\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\), vemos que ambas son elipses con\(a=3\) y\(b=2\). Por lo que tendrán el mismo tamaño y forma. Son diferentes en que no tienen el mismo centro.
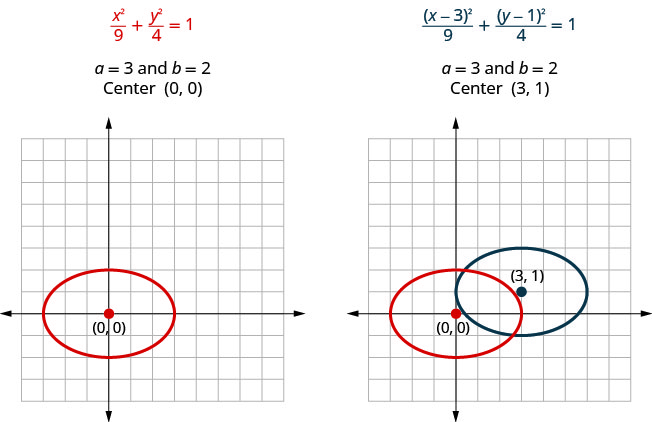
Observe en la gráfica anterior que podríamos haber graficado\(\frac{(x-3)^{2}}{9}+\frac{(y-1)^{2}}{4}=1\) por traducciones. Trasladamos la elipse original a las\(3\) unidades correctas y luego subimos\(1\) la unidad.
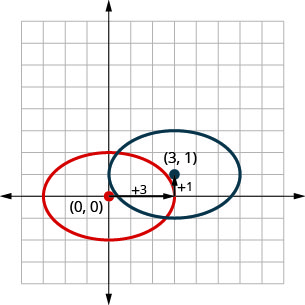
En el siguiente ejemplo usaremos el método de traducción para graficar la elipse.
Gráfica\(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) por traducción.
Solución:
Esta elipse tendrá el mismo tamaño y forma que\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) cuyo centro es\((0,0)\). Primero graficamos esta elipse.
| El centro es\((0,0)\). | Centro\((0,0)\) |
| Ya que\(16>9\), el eje mayor es horizontal. | |
| \(a^{2}=16, a=\pm 4\) \(b^{2}=9, \quad b=\pm 3\) |
Los vértices son\((4,0),(−4,0)\). Los extremos del eje menor son \((0,3),(0,−3)\). |
| Esboza la elipse. | 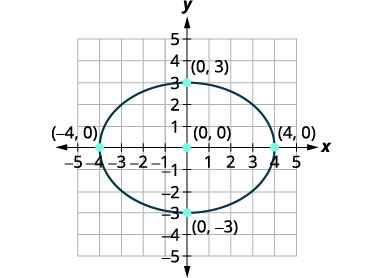 |
| La ecuación original está en forma estándar,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\). | \(\frac{(x-(-4))^{2}}{16}+\frac{(y-6)^{2}}{9}=1\) |
| La elipse está centrada en\((h,k)\). | El centro es\((-4,6)\). |
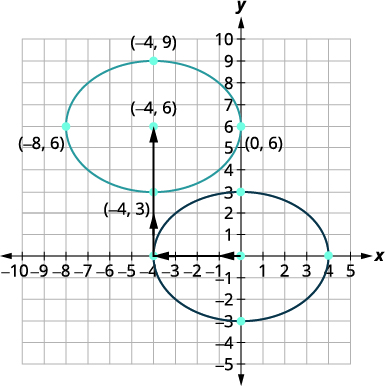
| Traducimos la gráfica de\(\frac{x^{2}}{16}+\frac{y^{2}}{9}=1\) cuatro unidades a la izquierda y luego hacia arriba\(6\) unidades. Verificar que el centro sea\((−4,6)\). La nueva elipse es la elipse cuya ecuación es \(\frac{(x+4)^{2}}{16}+\frac{(y-6)^{2}}{9}=1\). |
 |
Gráfica\(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{4}=1\) por traducción.
- Contestar
-
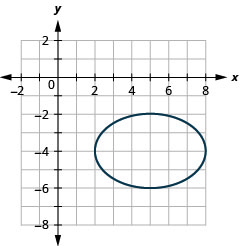
Figura 11.3.22
Gráfica\(\frac{(x+6)^{2}}{16}+\frac{(y+2)^{2}}{25}=1\) por traducción.
- Contestar
-
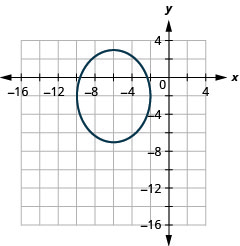
Figura 11.3.23
Cuando una ecuación tiene tanto a como a\(y^{2}\) con coeficientes diferentes, verificamos que es una elipsis poniéndola en forma estándar.\(x^{2}\) Entonces podremos graficar la ecuación.
Escribe la ecuación\(x^{2}+4 y^{2}-4 x+24 y+24=0\) en forma estándar y grafica.
Solución:
Ponemos la ecuación en forma estándar completando los cuadrados en ambos\(x\) y\(y\).
| \(x^{2}+4 y^{2}-4 x+24 y+24=0\) | |
| Reescribir agrupando los\(x\) términos y\(y\) términos. | 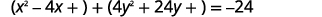 |
| Hacer los coeficientes de\(x^{2}\) e\(y^{2}\) iguales\(1\). | 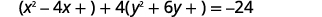 |
| Completa los cuadrados. | 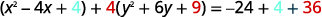 |
| Escribir como cuadrados binomiales. | 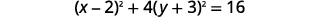 |
| Dividir ambos lados por\(16\) para\(1\) ponerse a la derecha. | 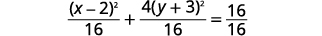 |
| Simplificar. | 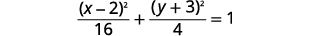 |
| La ecuación está en forma estándar,\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\) | 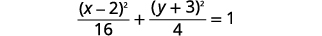 |
| La elipse está centrada en\((h,k)\). | El centro es\((2,-3)\). |
|
Ya que\(16>4\) y\(16\) está en el\(x^{2}\) término, el eje mayor es horizontal. \(a^{2}=16, a=\pm 4\) |
La distancia desde el centro a los vértices es\(4\). La distancia desde el centro hasta los extremos del eje menor es\(2\). |
| Esboza la elipse. | 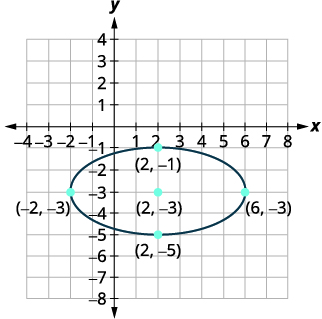 |
- Escribe la ecuación\(6 x^{2}+4 y^{2}+12 x-32 y+34=0\) en forma estándar y
- Gráfica.
- Contestar
-
- \(\frac{(x+1)^{2}}{6}+\frac{(y-4)^{2}}{9}=1\)
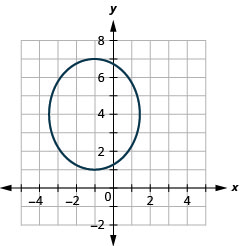
Figura 11.3.32
- Escribe la ecuación\(4 x^{2}+y^{2}-16 x-6 y+9=0\) en forma estándar y
- Gráfica.
- Contestar
-
- \(\frac{(x-2)^{2}}{4}+\frac{(y-3)^{2}}{16}=1\)
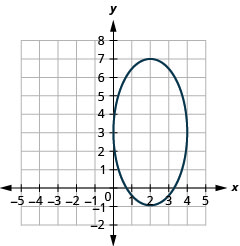
Figura 11.3.33
Resolver aplicación con elipses
Las órbitas de los planetas alrededor del sol siguen caminos elípticos.
Plutón (un planeta enano) se mueve en una órbita elíptica alrededor del Sol. Lo más cercano que Plutón llega al Sol son aproximadamente unidades\(30\) astronómicas (AU) y la más alejada es aproximadamente\(50\) AU. El Sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica de Plutón.
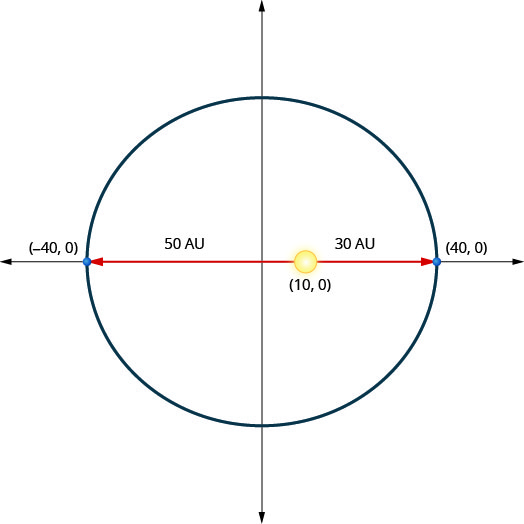
Solución:
Reconocemos esto como una elipse que se centra en el origen.
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Ya que el eje mayor es horizontal y la distancia desde el centro hasta el vértice es\(40\), sabemos\(a=40\) y así\(a^{2}=1600\).
\(\frac{x^{2}}{1600}+\frac{y^{2}}{b^{2}}=1\)
El eje menor es vertical pero no se dan los puntos finales.Para encontrar\(b\) usaremos la ubicación del Sol. Ya que el Sol es un foco de la elipse en el punto\((10,0)\), lo sabemos\(c=10\). Usa esto para resolver para\(b^{2}\).
\(b^{2}=a^{2}-c^{2}\)
\(b^{2}=40^{2}-10^{2}\)
\(b^{2}=1600-100\)
\(b^{2}=1500\)
Sustituir\(a^{2}\) y\(b^{2}\) en la forma estándar de la elipse.
\(\frac{x^{2}}{1600}+\frac{y^{2}}{1500}=1\)
Un planeta se mueve en órbita elíptica alrededor de su sol. Lo más cerca que el planeta se acerca al sol es aproximadamente\(20\) AU y el más lejano es aproximadamente\(30\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del planeta.
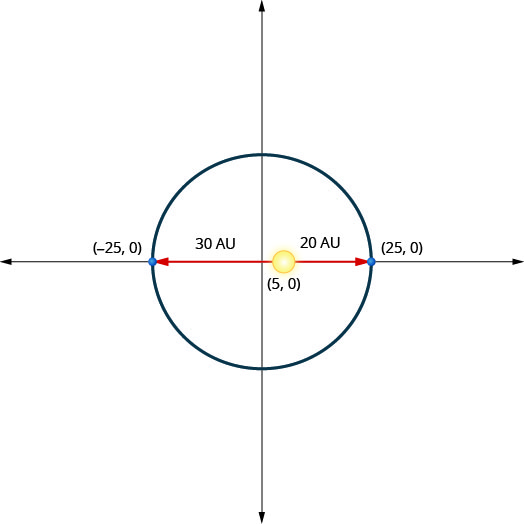
- Contestar
-
\(\frac{x^{2}}{625}+\frac{y^{2}}{600}=1\)
Un planeta se mueve en órbita elíptica alrededor de su sol. Lo más cerca que el planeta se acerca al sol es aproximadamente\(20\) AU y el más lejano es aproximadamente\(50\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del planeta.
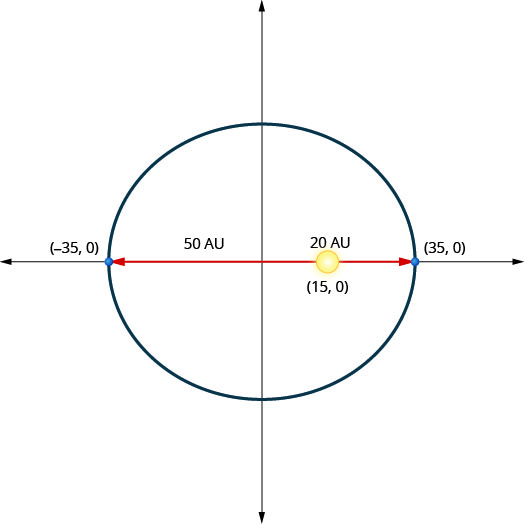
- Contestar
-
\(\frac{x^{2}}{1225}+\frac{y^{2}}{1000}=1\)
Acceda a estos recursos en línea para obtener instrucciones adicionales y practique con elipses.
- Secciones Cónicas: Elipses Gráficas Parte 1
- Secciones Cónicas: Gráficas Elipses Parte 2
- Ecuación para elipse a partir de gráfico
Conceptos clave
- Elipse: Una elipse es todos los puntos en un plano donde la suma de las distancias desde dos puntos fijos es constante. Cada uno de los puntos fijos se llama foco de la elipse.
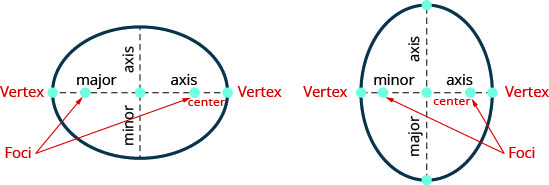
Figura 11.3.37
- Si dibujamos una línea a través de los focos, la elipse se cruza en dos puntos, cada uno se llama un vértice de la elipse.
El segmento que conecta los vértices se denomina eje mayor.
El punto medio del segmento se llama el centro de la elipse.
Un segmento perpendicular al eje mayor que pasa por el centro e intersecta la elipse en dos puntos se denomina eje menor. - Forma estándar de la ecuación una elipse con centro\((0,0)\): La forma estándar de la ecuación de una elipse con centro\((0,0)\), es
\(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1\)
Los\(x\) -interceptos son\((a,0)\) y\((−a,0)\).
Los\(y\) -interceptos son\((0,b)\) y\((0,−b)\). - Cómo hacer una elipse con centro\((0,0)\)
- Escribe la ecuación en forma estándar.
- Determinar si el eje mayor es horizontal o vertical.
- Encuentra los puntos finales del eje mayor.
- Encontrar los puntos finales del eje menor
- Esboza la elipse.
- Forma estándar de la ecuación una elipse con centro\((h,k)\): La forma estándar de la ecuación de una elipse con centro\((h,k)\), es
\(\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1\)
Cuando\(a>b\), el eje mayor es horizontal por lo que la distancia desde el centro al vértice es\(a\).
Cuando\(b>a\), el eje mayor es vertical por lo que la distancia desde el centro al vértice es\(b\).
Glosario
- elipse
- Una elipse son todos los puntos de un plano donde la suma de las distancias desde dos puntos fijos es constante.


