Saltar al contenido principal
LibreTexts Español

11.4E: Ejercicios

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    112802

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)

    La práctica hace la perfección

    Ejercicio\(\PageIndex{15}\) Graph an Ellipse with Center at the Origin

    En los siguientes ejercicios, grafica cada elipse.

    1. \(\frac{x^{2}}{4}+\frac{y^{2}}{25}=1\)
    2. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    3. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    4. \(\frac{x^{2}}{16}+\frac{y^{2}}{36}=1\)
    5. \(\frac{x^{2}}{36}+\frac{y^{2}}{16}=1\)
    6. \(\frac{x^{2}}{25}+\frac{y^{2}}{9}=1\)
    7. \(x^{2}+\frac{y^{2}}{4}=1\)
    8. \(\frac{x^{2}}{9}+y^{2}=1\)
    9. \(4 x^{2}+25 y^{2}=100\)
    10. \(16 x^{2}+9 y^{2}=144\)
    11. \(16 x^{2}+36 y^{2}=576\)
    12. \(9 x^{2}+25 y^{2}=225\)
    Contestar

    1.

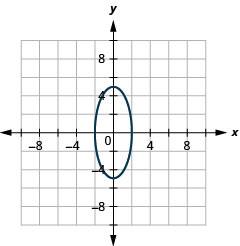
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 5) y (0, negativo 5) y extremos de eje menor (2, 0) y (negativo 2, 0).
    Figura 11.3.38

    3.

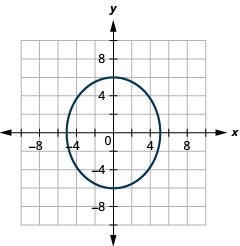
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 6) y (0, 6 negativo) y extremos de eje menor (5, 0) y (negativo 5, 0).
    Figura 11.3.39

    5.

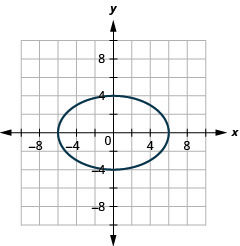
    Esta gráfica muestra una elipse con centro (0, 0), vértices (6, 0) y (negativo 6, 0) y extremos de eje menor (0, 4) y (0, negativo 4).
    Figura 11.3.40

    7.

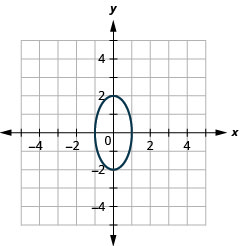
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 2) y (0, negativo 2) y extremos de eje menor (1, 0) y (negativo 1, 0).
    Figura 11.3.41

    9.

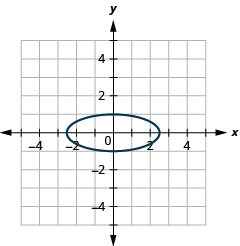
    Esta gráfica muestra una elipse con centro (0, 0), vértices (5, 0) y (negativo 5, 0) y puntos finales de eje menor (0, 2) y (0, negativo 2).
    Figura 11.3.42

    11.

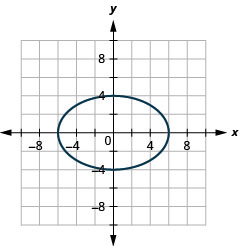
    Esta gráfica muestra una elipse con centro (0, 0), vértices (6, 0) y (negativo 6, 0) y extremos de eje menor (0, 4) y (0, negativo 4).
    Figura 11.3.43
    Ejercicio\(\PageIndex{16}\) Find the Equation of an Ellipse with Center at the Origin

    En los siguientes ejercicios, encuentra la ecuación de la elipse que se muestra en la gráfica.

    1.

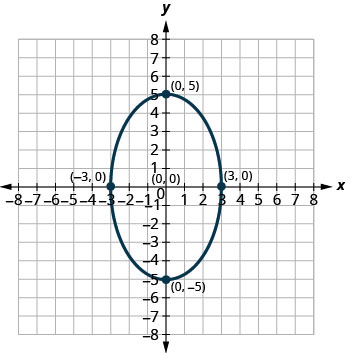
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 5) y (0, negativo 5) y puntos finales de eje menor (negativos 3, 0) y (3, 0).
    Figura 11.3.44

    2.

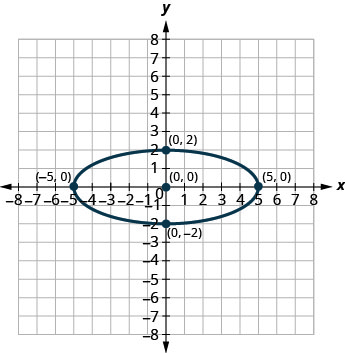
    Esta gráfica muestra una elipse con centro (0, 0), vértices (5, 0) y (negativo 5, 0) y puntos finales de eje menor (0, 2) y (0, negativo 2).
    Figura 11.3.45

    3.

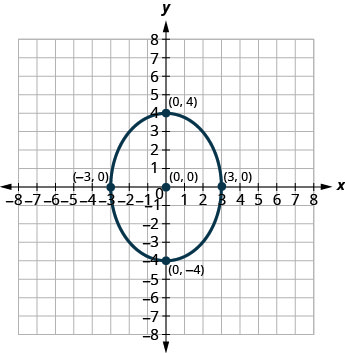
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 4) y (0, negativo 4) y extremos de eje menor (negativos 3, 0) y (3, 0).
    Figura 11.3.46

    4.

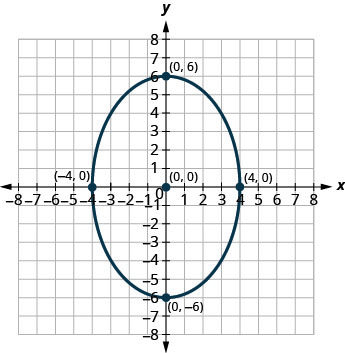
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 6) y (0, 6 negativo) y extremos de eje menor (negativos 4, 0) y (4, 0).
    Figura 11.3.47
    Contestar

    1. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)

    3. \(\frac{x^{2}}{9}+\frac{y^{2}}{16}=1\)

    Ejercicio\(\PageIndex{17}\) Graph an Ellipse with Center Not at the Origin

    En los siguientes ejercicios, grafica cada elipse.

    1. \(\frac{(x+1)^{2}}{4}+\frac{(y+6)^{2}}{25}=1\)
    2. \(\frac{(x-3)^{2}}{25}+\frac{(y+2)^{2}}{9}=1\)
    3. \(\frac{(x+4)^{2}}{4}+\frac{(y-2)^{2}}{9}=1\)
    4. \(\frac{(x-4)^{2}}{9}+\frac{(y-1)^{2}}{16}=1\)
    Contestar

    1.

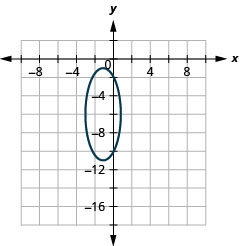
    Esta gráfica muestra una elipse con centro (negativo 1, negativo 6, vértices (negativo 1, negativo 1) y (negativo 1, negativo 11) y puntos finales de eje menor (negativo 3, negativo 6) y (1, negativo 6).
    Figura 11.3.48

    3.

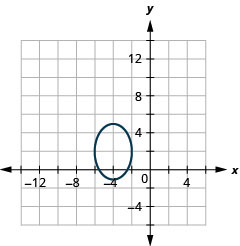
    Esta gráfica muestra una elipse con centro (negativo 4, 2, vértices (negativo 4, 5) y (negativo 4, negativo 1) y puntos finales de eje menor (3, 1) y (negativo 6, 2) y (negativo 2, 2).
    Figura 11.3.49
    Ejercicio\(\PageIndex{18}\) Graph an Ellipse with Center Not at the Origin

    En los siguientes ejercicios, grafica cada ecuación por traducción.

    1. \(\frac{(x-3)^{2}}{4}+\frac{(y-7)^{2}}{25}=1\)
    2. \(\frac{(x+6)^{2}}{16}+\frac{(y+5)^{2}}{4}=1\)
    3. \(\frac{(x-5)^{2}}{9}+\frac{(y+4)^{2}}{25}=1\)
    4. \(\frac{(x+5)^{2}}{36}+\frac{(y-3)^{2}}{16}=1\)
    Contestar

    1.

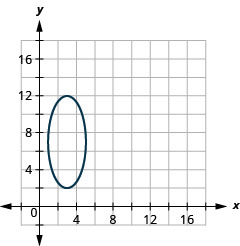
    Esta gráfica muestra una elipse con centro (3, 7), vértices (3, 2) y (3, 12), y extremos de eje menor (1, 7) y (5, 7).
    Figura 11.3.50

    3.

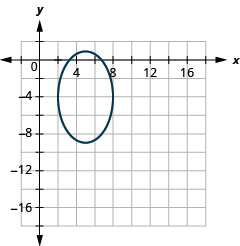
    Esta gráfica muestra una elipse con centro (5, negativo 4), vértices (5, 1) y (5, negativo 9) y extremos de eje menor (2, negativo 4) y (8, negativo 4).
    Figura 11.3.51
    Ejercicio\(\PageIndex{19}\) Graph an Ellipse with Center Not at the Origin

    En los siguientes ejercicios,

    1. Escribe la ecuación en forma estándar y
    2. Gráfica.
    1. \(25 x^{2}+9 y^{2}-100 x-54 y-44=0\)
    2. \(4 x^{2}+25 y^{2}+8 x+100 y+4=0\)
    3. \(4 x^{2}+25 y^{2}-24 x-64=0\)
    4. \(9 x^{2}+4 y^{2}+56 y+160=0\)
    Contestar

    1.

    1. \(\frac{(x-2)^{2}}{9}+\frac{(y-3)^{2}}{25}=1\)
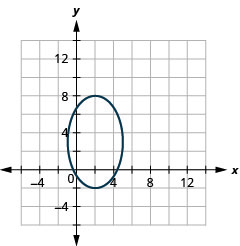
    Esta gráfica muestra una elipse con centro (2, 3), vértices (2, negativo 2) y (2, 8) y puntos finales de eje menor (negativos 1, 3) y (5, 3).
    Figura 11.3.52

    3.

    1. \(\frac{y^{2}}{4}+\frac{(x-3)^{2}}{25}=1\)
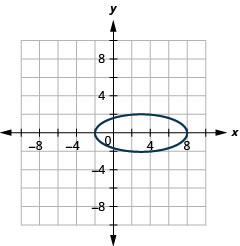
    Esta gráfica muestra una elipse con centro (3, 0), vértices (negativo 2, 0) y (8, 0) y puntos finales de eje menor (3, 2) y (3, negativo 2).
    Figura 11.3.53
    Ejercicio\(\PageIndex{20}\) Graph an Ellipse with Center Not at the Origin

    En los siguientes ejercicios, grafica la ecuación.

    1. \(x=-2(y-1)^{2}+2\)
    2. \(x^{2}+y^{2}=49\)
    3. \((x+5)^{2}+(y+2)^{2}=4\)
    4. \(y=-x^{2}+8 x-15\)
    5. \(\frac{(x+3)^{2}}{16}+\frac{(y+1)^{2}}{4}=1\)
    6. \((x-2)^{2}+(y-3)^{2}=9\)
    7. \(\frac{x^{2}}{25}+\frac{y^{2}}{36}=1\)
    8. \(x=4(y+1)^{2}-4\)
    9. \(x^{2}+y^{2}=64\)
    10. \(\frac{x^{2}}{9}+\frac{y^{2}}{25}=1\)
    11. \(y=6 x^{2}+2 x-1\)
    12. \(\frac{(x-2)^{2}}{9}+\frac{(y+3)^{2}}{25}=1\)
    Contestar

    1.

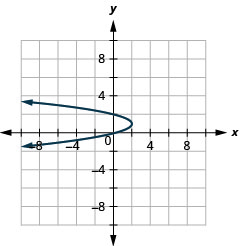
    Esta gráfica muestra una parábola con vértice (2, 1) e intercepciones y (0, 0) y (2, 0).
    Figura 11.3.54

    3.

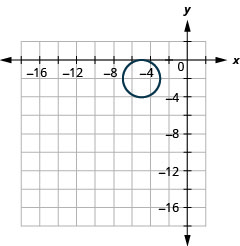
    Esta gráfica muestra un círculo con centro (negativo 5, negativo 2) y un radio de 2 unidades.
    Figura 11.3.55

    5.

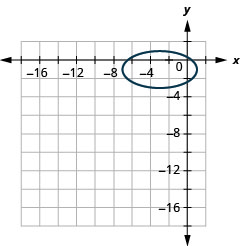
    Esta gráfica muestra una elipse con centro (negativo 3, negativo 1), vértices (1, negativo 1) y (negativo 7, negativo 1) y puntos finales de eje menor (negativo 3, 1) y (negativo 3, negativo 3).
    Figura 11.3.56

    7.

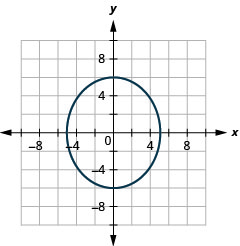
    Esta gráfica muestra una elipse con centro (0, 0), vértices (0, 6) y (0, 6 negativo) y extremos de eje menor (negativos 5, 0) y (5, 0).
    Figura 11.3.57

    9.

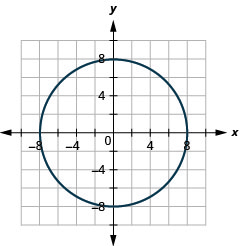
    Esta gráfica muestra círculo con centro (0, 0) y con radio 8 unidades.
    Figura 11.3.58

    11.

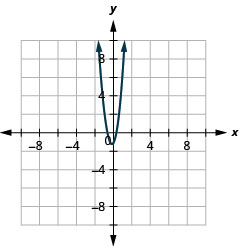
    Esta gráfica muestra la parábola de apertura ascendente. Su vértice tiene un valor x ligeramente menor que 0 y un valor y ligeramente menor que menos 1. Un punto en él está aproximadamente en (negativo 1, 3).
    Figura 11.3.59
    Ejercicio\(\PageIndex{21}\) Solve Application with Ellipses

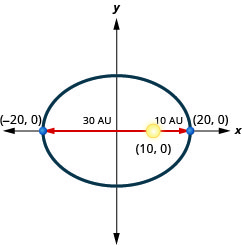
    1. Un planeta se mueve en órbita elíptica alrededor de su sol. Lo más cerca que el planeta se acerca al sol es aproximadamente\(10\) AU y el más lejano es aproximadamente\(30\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del planeta.

    Esta gráfica muestra una elipse con centro (0, 0), vértices (negativo 20, 0) y (20, 0). El sol se muestra en el punto (10, 0), que está a 30 unidades del vértice izquierdo y 10 unidades del vértice derecho.
    Figura 11.3.60

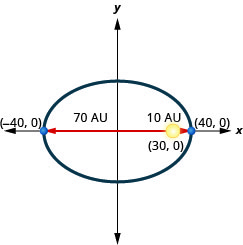
    2. Un planeta se mueve en órbita elíptica alrededor de su sol. Lo más cerca que el planeta se acerca al sol es aproximadamente\(10\) AU y el más lejano es aproximadamente\(70\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del planeta.

    Esta gráfica muestra una elipse con centro (0, 0), vértices (negativo 40, 0) y (40, 0). El sol se muestra en el punto (30, 0), que está a 70 unidades desde el vértice izquierdo y 10 unidades desde el vértice derecho.
    Figura 11.3.61

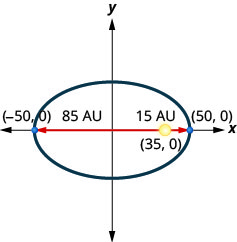
    3. Un cometa se mueve en órbita elíptica alrededor de un sol. Lo más cerca que el cometa llega al sol es aproximadamente\(15\) AU y el más alejado es aproximadamente\(85\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del cometa.

    Esta gráfica muestra una elipse con centro (0, 0), vértices (negativo 50, 0) y (50, 0). El sol se muestra en el punto (35, 0), que está a 85 unidades del vértice izquierdo y 15 unidades del vértice derecho.
    Figura 11.3.62

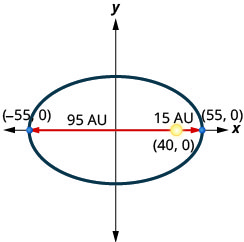
    4. Un cometa se mueve en órbita elíptica alrededor de un sol. Lo más cerca que el cometa llega al sol es aproximadamente\(15\) AU y el más alejado es aproximadamente\(95\) AU. El sol es uno de los focos de la órbita elíptica. Dejando que la elipse se centre en el origen y etiquetando los ejes en AU, la órbita se verá como la figura de abajo. Usa la gráfica para escribir una ecuación para la órbita elíptica del cometa.

    Esta gráfica muestra una elipse con centro (0, 0), vértices (negativo 55, 0) y (55, 0). El sol se muestra en el punto (40, 0), que está a 95 unidades del vértice izquierdo y 15 unidades del vértice derecho.
    Figura 11.3.63
    Contestar

    1. \(\frac{x^{2}}{400}+\frac{y^{2}}{300}=1\)

    3. \(\frac{x^{2}}{2500}+\frac{y^{2}}{1275}=1\)

    Ejercicio\(\PageIndex{22}\) Writing Exercises
    1. En tus propias palabras, define una elipse y escribe la ecuación de una elipse centrada en el origen en forma estándar. Dibuja un boceto de la elipse etiquetando el centro, vértices y ejes mayor y menor.
    2. Explica con tus propias palabras cómo obtener los ejes de la ecuación en forma estándar.
    3. Comparar y contrastar las gráficas de las ecuaciones\(\frac{x^{2}}{4}+\frac{y^{2}}{9}=1\) y\(\frac{x^{2}}{9}+\frac{y^{2}}{4}=1\).
    4. Explica con tus propias palabras, la diferencia entre un vértice y un foco de la elipse.
    Contestar

    1. Las respuestas pueden variar

    3. Las respuestas pueden variar

    Autocomprobación

    a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

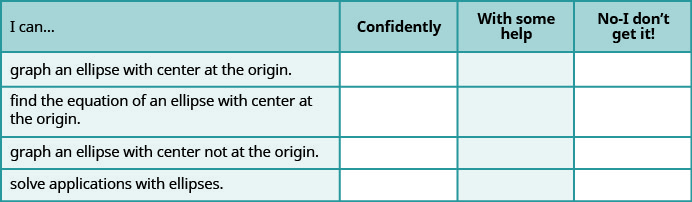
    Esta tabla tiene 4 columnas 4 filas y una fila de cabecera. La fila de encabezado etiqueta cada columna puedo, con confianza, con algo de ayuda y no, no lo consigo™ no lo consigo. Las primeras columnas tienen las siguientes declaraciones: graficar una elipse con centro en el origen, encontrar la ecuación de una elipse con centro en el origen, graficar una elipse con centro no en el origen, resolver aplicaciones con elipses. Las columnas restantes están en blanco.
    Figura 11.3.64

    b. ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?

    This page titled 11.4E: Ejercicios is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.