4.5: Combinar polinomios usando suma y resta
( \newcommand{\kernel}{\mathrm{null}\,}\)
Términos de Me Gusta
Términos de Me Gusta
Los términos cuyas partes variables, incluyendo los exponentes, son idénticos se denominan términos similares. Como términos es un nombre apropiado ya que los términos con partes variables idénticas y diferentes coeficientes numéricos representan diferentes cantidades de la misma cantidad. Siempre y cuando estemos tratando con cantidades del mismo tipo podemos combinarlas usando suma y resta.
Una expresión algebraica se puede simplificar combinando términos similares.
Conjunto de Muestras A
Combina los términos similares.
6 casas + 4 casas = 10 casas. 6 y 4 son del mismo tipo dan 10 de ese tipo.
6 casas + 4 casas+ 2 moteles = 10 casas + 2 moteles. 6 y 4 del mismo tipo dan 10 de ese tipo. Así, tenemos 10 de un tipo y 2 de otro tipo.
Supongamos que dejamos que lax letra represente “casa”. Entonces,6x+4x=10x. 6 y 4 del mismo tipo dan 10 de ese tipo.
Supongamos que dejamosx representar “casa” yy representar “motel”.
6x + 4x + 2y = 10x + 2y
Conjunto de práctica A
Los términos similares con el mismo coeficiente numérico representan cantidades iguales de la misma cantidad.
Términos similares con diferentes coeficientes numéricos representan
- Contestar
-
diferentes cantidades de la misma cantidad
Combinando términos similares
Dado que los términos similares representan cantidades de la misma cantidad, pueden combinarse, es decir, se pueden sumar términos similares.
Simplifica cada uno de los siguientes polinomios combinando términos similares.
2x + 5x + 3x.
2xHay, luego 5 más, luego 3 más. Esto hace un total de iof10x.
7x + 8y - 3x.
De7x's, perdemos3x. Esto hace. Los4x8y's representan una cantidad diferente a losx's y por lo tanto no se combinarán con ellos.
7x + 8y - 3x = 4x + 8y.
4a^3 - 2a^2 + 8a^3 + a^2 - 2a^3.
4a^3, 8a^3, y-2a^3 representan cantidades del mismo tipo.
4a^3 + 8a^3 - 2a^3 = 10a^3.
-2a^2ya^2 representan cantidades del mismo tipo.
-2a^2 + a^2 = -a^2.
Por lo tanto,
4a^3 - 2a^2 + 8a^3 + a^2 - 2a^3 = 10a^3 - a^2.
Set de práctica B
Simplifica cada una de las siguientes expresiones.
4y + 7y
- Contestar
-
11y
3x + 6x + 11x
- Contestar
-
20x
5a + 2b + 4a - b - 7b
- Contestar
-
9a - 6b
10x^3 - 4x^3 + 3x^2 - 12x^3 + 5x^2 + 2x + x^3 + 8x
- Contestar
-
-5x^3 + 8x^2 + 10x
2a^5 - a^5 + 1 - 4ab - 9 + 9ab - 2 - 3 - a^5.
- Contestar
-
5ab - 13.
Simplificación de expresiones que contienen paréntesis
Simplificación de expresiones que contienen paréntesis
Cuando aparecen paréntesis en las expresiones, deben eliminarse antes de que la expresión pueda simplificarse. Los paréntesis se pueden eliminar usando la propiedad distributiva.
Propiedad distributiva
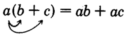
Conjunto de Muestras C
Simplifique cada una de las siguientes expresiones usando la propiedad distributiva y combinando términos similares.
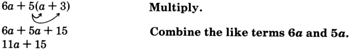
4x + 9(x^2 - 6x - 2) + 5Eliminar paréntesis.
4x + 9x^2 - 54x - 18 + 5Combina términos similares.
-50x + 9x^2 - 13
Por convención, los términos en una expresión se colocan en orden descendente con el término de grado más alto apareciendo primero. Los términos numéricos se colocan en el extremo derecho de la expresión. La propiedad conmutativa de adición nos permite cambiar el orden de los términos.
9x^2 - 50x - 13
2+2[5+4(1+a)]
Elimine primero el conjunto de paréntesis más interno
2+2[5+4+4a]
Por el orden de las operaciones, simplificar dentro de los paréntesis antes de multiplicar (por el 2)
2 + 2[9 + 4a]Quite este conjunto de paréntesis.
2 + 18 + 8aCombina términos similares.
20 + 8aEscribir en orden descendente.
8a + 20
x(x−3)+6x(2x+3)
Usa la regla para multiplicar poderes con la misma base.
x^2 - 3x + 12x^2 + 18xCombina términos similares.
13x^2 + 15x
Set de práctica C
Simplifique cada una de las siguientes expresiones usando la propiedad distributiva y combinando términos similares.
4(x+6)+3(2+x+3x^2)-2x^2
- Contestar
-
7x^2+7x+30
7(x+x^3)-4x^3-x+1+4(x^2-2x^3+7)
- Contestar
-
-5x^3+4x^2+6x+29
5(a+2)+6a-7+(8+4)(a+3a+2)
- Contestar
-
59a+27
x(x+3)+4x^2+2x
- Contestar
-
5x^2+5x
a^3(a^2+a+5)+a(a^4+3a^2+4)+1
- Contestar
-
2a^5+a^4+8a^3+4a+1
2[8-3(x-3)]
- Contestar
-
-6x+34
x^2+3x+7[x+4x^2+3(x+x^2)]
- Contestar
-
50x^2+31x
Ejercicios
Para los siguientes problemas, simplifique cada una de las expresiones algebraicas.
x+3x
- Contestar
-
4x
4x + 7x
9a + 12a
- Contestar
-
21a
5m - 3m
10x - 7x
- Contestar
-
3x
7y - 9y
6k - 11k
- Contestar
-
-5k
3a+5a+2a
9y+10y+2y
- Contestar
-
21y
5m−7m−2m
h−3h−5h
- Contestar
-
-7h
a+8a+3a
7ab+4ab
- Contestar
-
11ab
8ax+2ax+6ax
3a^2 + 6a^2 + 2a^2
- Contestar
-
11a^2
14a^2b + 4a^2b + 19a^2b
10y - 15y
- Contestar
-
-5y
7ab−9ab+4ab
210ab^4 + 412ab^4 + 100a^4b(Mira de cerca a los exponentes.)
- Contestar
-
622ab^4 + 100a^4b
5x^2y^0 + 3x^2y + 2x^2y + 1, y \not = 0(Mira de cerca a los exponentes.)
8w^2 - 12w^2 - 3w^2
- Contestar
-
-7w^2
6xy−3xy+7xy−18xy
7x^3 - 2x^2 - 10x + 1 - 5x^2 - 3x^3 - 12 + x
- Contestar
-
4x^3 - 7x^2 - 9x - 11
21y−15x+40xy−6−11y+7−12x−xy
1x+1y−1x−1y+x−y
- Contestar
-
x-y
5x^2 - 3x - 7 + 2x^2 - x
-2z + 15z + 4z^3 + z^2 - 6z^2 + z
- Contestar
-
2z^3 - 5z^2 + 16z
18x^2y - 14x^2y - 20x^2y
-9w^5 - 9w^4 - 9w^5 + 10w^4
- Contestar
-
-18w^5 + w^4
2x^4 + 4x^3 - 8x^2 + 12x - 1 - 7x^3 - 1x^4 - 6x + 2
17d^3r + 3d^3r - 5d^3r + 6d^2r + d^3r - 30d^2r + 3 - 7 + 2
- Contestar
-
16d^3r - 24d^2r - 2
a^0 + 2a^0 - 4a^0, a \not = 0
4x^0 + 3x^0 - 5x^0 + 7x^0 - x^0, x \not = 0
- Contestar
-
8
2a^3b^2c + 3a^2b^2c^0 + 4a^2b^2 - a^3b^2c, c \not = 0
3z−6z+8z
- Contestar
-
5z
3z^2 - z + 3z^3
6x^3 + 12x + 5
- Contestar
-
6x^3 + 12x + 5
3(x+5)+2x
7(a+2)+4
- Contestar
-
7a+18
y+5(y+6)
2b+6(3−5b)
- Contestar
-
−28b+18
5a−7c+3(a−c)
8x−3x+4(2x+5)+3(6x−4)
- Contestar
-
31x+8
2z+4ab+5z−ab+12(1−ab−z)
(a+5)4+6a−20
- Contestar
-
10a
(4a+5b−2)3+3(4a+5b−2)
(10x + 3y^2)4 + 4(10x + 3y^2)
- Contestar
-
80x + 24y^2
2(x−6)+5
1(3x+15)+2x−12
- Contestar
-
5x+3
1(2 + 9a + 4a^2) + a^2 - 11a
1(2x - 6b + 6a^2b + 8b^2) + 1(5x + 2b - 3a^2b
- Contestar
-
3a^2b + 8b^2 - 4b + 7x
Después de observar los siguientes problemas, ¿se puede hacer una conjetura sobre1(a+b)?
1(a+b) =
Usando el resultado del problema 52, es correcto escribir
(a+b)=a+b?
- Contestar
-
si
3(2a + 2a^2) + 8(3a + 3a^2)
x(x + 2) + 2(x^2 + 3x - 4
- Contestar
-
3x^2 + 8x - 8
A(A+7) + 4(A^2 + 3a + 1)
b(2b^3 + 5b^2 + b + 6) - 6b^2 - 4b + 2
- Contestar
-
2b^4 + 5b^3 - 5b^2 + 2b + 2
4a−a(a+5)
x - 3x(x^2 - 7x - 1)
- Contestar
-
-3x^3 + 21x^2 + 4x
ab(a - 5) - 4a^2b + 2ab - 2
xy(3xy + 2x - 5y) - 2x^2y^2 - 5x^2y + 4xy^2
- Contestar
-
x^2y^2 - 3x^2y - xy^2
3h[2h+5(h+2)]
2k[5k+3(1+7k)]
- Contestar
-
52k^2 + 6k
8a[2a−4ab+9(a−5−ab)]
6{m + 5n[n + 3(n-1)] + 2n^2} - 4n^2 - 9m
- Contestar
-
128n^2 - 90n - 3m
5[4(r−2s)−3r−5s]+12s
8{9[b - 2a + 6c(c + 4) - 4c^2] + 4a + b} - 3b
- Contestar
-
144c^2 - 112a + 77b + 1728c
5[4(6x−3)+x]−2x−25x+4
3xy^2(4xy + 5y) + 2xy^3 + 6x^2y^3 + 4y^3 - 12xy^3
- Contestar
-
18x^2y^3 + 5xy^3 + 4y^3
9a^3b^7(a^3b^5-2a^2b^2+6) - 2a(a^2b^7 - 5a^5b^{12} + 3a^4b^9) - a^3b^7
−8(3a+2)
- Contestar
-
−24a−16
−4(2x−3y)
-4xy^2[7xy - 6(5-xy^2) + 3(-xy + 1) +1]
- Contestar
-
-24x^2y^4 - 16x^2y^3 + 104xy^2
Ejercicios para la revisión
Simplificar(\dfrac{x^{10}y^8z^2}{x^2y^6})^3
Encuentra el valor de\dfrac{-3(4-9)-6(-3)-1}{2^3}
- Contestar
-
4
Escribe la expresión\dfrac{42x^2y^5z^3}{21x^4y^7} para que no aparezca ningún denominador.
Cuantos(2a+5) hay en3x(2a+5)
- Contestar
-
3x
Simplificar3(5n + 6m^2) - 2(3n + 4m^2)


