3.6: Líneas paralelas y perpendiculares
- Page ID
- 110110
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Determinar las pendientes de líneas paralelas y perpendiculares.
- Encuentra ecuaciones de líneas paralelas y perpendiculares
Definición de Paralelo y perpendicular
Las líneas paralelas son líneas en el mismo plano que nunca se cruzan. Dos líneas no verticales en un mismo plano, con pendientes\(m_{1}\) y\(m_{2}\), son paralelas si sus pendientes son iguales,\(m_{1}=m_{2}\). Considera las siguientes dos líneas:
Considera sus gráficas correspondientes:
.png)
Figura\(\PageIndex{1}\)
Ambas líneas tienen pendiente\(m=\frac{3}{4}\) y por lo tanto son paralelas.
Las líneas perpendiculares son líneas en el mismo plano que se cruzan en ángulos rectos (\(90\)grados). Dos líneas no verticales en un mismo plano, con pendientes\(m_{1}\) y\(m_{2}\), son perpendiculares si el producto de sus pendientes es\(−1: m1⋅m2=−1\). Podemos resolver\(m_{1}\) y obtener\(m_{1}=\frac{−1}{m_{2}}\). De esta forma, vemos que las líneas perpendiculares tienen pendientes que son recíprocas negativas, u recíprocas opuestas. Por ejemplo, si se le da una pendiente
\(m=-\frac{5}{8}\)
entonces la pendiente de una línea perpendicular es el recíproco opuesto:
\(m_{\perp}=\frac{8}{5}\)
La notación matemática\(m_{⊥}\) dice “\(m\)perpendicular”. Podemos verificar que dos pendientes produzcan líneas perpendiculares si su producto es\(−1\).
\(m\cdot m_{\perp}=-\frac{5}{8}\cdot\frac{8}{5}=-\frac{40}{40}=-1\quad\color{Cerulean}{\checkmark}\)
Geométricamente, observamos que si una línea tiene una pendiente positiva, entonces cualquier línea perpendicular tendrá una pendiente negativa. Además, se intercambian la subida y la carrera entre dos líneas perpendiculares.
.png)
Figura\(\PageIndex{2}\)
Las líneas perpendiculares tienen pendientes que son recíprocas opuestas, así que recuerda encontrar lo recíproco y cambiar el signo. En otras palabras,
Si\(m=\frac{a}{b}\), entonces\(m_{\perp}=-\frac{b}{a}\)
Determinar la pendiente de una línea perpendicular se puede realizar mentalmente. Algunos ejemplos siguen
| Pendiente dada | Pendiente de línea perpendicular |
|---|---|
| \(m=\frac{1}{2}\) | \(m_{\perp}=-2\) |
| \(m=-\frac{3}{4}\) | \(m_{\perp}=\frac{4}{3}\) |
| \(m=3\) | \(m_{\perp}=-\frac{1}{3}\) |
| \(m=-4\) | \(m_{\perp}=\frac{1}{4}\) |
Ejemplo\(\PageIndex{1}\)
Determinar la pendiente de una línea paralela a\(y=−5x+3\).
Solución:
Dado que la línea dada está en forma de pendiente-intersección, podemos ver que su pendiente es\(m=−5\). Así la pendiente de cualquier línea paralela a la línea dada debe ser la misma,\(m_{∥}=−5\). La notación matemática\(m_{∥}\) dice “\(m\)paralelo”.
Respuesta:
\(m_{∥}=−5\)
Ejemplo\(\PageIndex{2}\)
Determinar la pendiente de una línea perpendicular a\(3x−7y=21\).
Solución:
Primero, resolver\(y\) y expresar la línea en forma de pendiente-intercepción.
En esta forma, podemos ver que la pendiente de la línea dada es\(m=\frac{3}{7}\), y así\(m_{⊥}=−\frac{7}{3}\).
Respuesta:
\(m_{⊥}=−\frac{7}{3}\)
Ejercicio\(\PageIndex{1}\)
Encuentra la pendiente de la línea perpendicular a\(15x+5y=20\).
- Contestar
-
\(m_{\perp}=\frac{1}{3}\)
Encontrar ecuaciones de líneas paralelas y perpendiculares
Hemos visto que la gráfica de una línea está completamente determinada por dos puntos o un punto y su pendiente. A menudo se le pedirá que encuentre la ecuación de una línea dada alguna relación geométrica, por ejemplo, si la línea es paralela o perpendicular a otra línea.
Ejemplo\(\PageIndex{3}\)
Encuentra la ecuación de la línea que pasa a través\((6, −1)\) y paralela a\(y=\frac{1}{2}x+2\)
Solución
Aquí la línea dada tiene pendiente\(m=\frac{1}{2}\), y la pendiente de una línea paralela es\(m_{∥}=\frac{1}{2}\). Como se le da un punto y la pendiente, utilice la forma de punto-pendiente de una línea para determinar la ecuación.
\(\begin{array}{cc}{\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(6,-1)}&{m_{\parallel}=\frac{1}{2}} \end{array}\)
Respuesta:
\(y=\frac{1}{2}x-4\)
Es importante tener una comprensión geométrica de esta cuestión. Se nos pidió encontrar la ecuación de una línea paralela a otra línea que pasaba por cierto punto.
.png)
Figura\(\PageIndex{3}\)
A través del punto\((6, −1)\) encontramos una línea paralela,\(y=\frac{1}{2}x−4\), mostrada discontinua. Observe que la pendiente es la misma que la línea dada, pero la\(y\) -intercepción es diferente. Si tenemos en cuenta la interpretación geométrica, entonces será más fácil recordar el proceso necesario para resolver el problema.
Ejemplo\(\PageIndex{4}\)
Encuentra la ecuación de la línea que pasa a través\((−1, −5)\) y perpendicular a\(y=−\frac{1}{4}x+2\).
Solución:
La línea dada tiene pendiente\(m=−\frac{1}{4}\), y por lo tanto\(m_{⊥}=+\frac{4}{1}=4\). Sustituya esta pendiente y el punto dado en forma de pendiente puntual.
\(\begin{array}{cc} {\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(-1,-5)}&{m_{\perp}=4}\end{array}\)
Respuesta:
\(y=4x-1\)
Geométricamente, vemos que la línea\(y=4x−1\), que se muestra discontinua abajo, pasa a través\((−1, −5)\) y es perpendicular a la línea dada.
.png)
Figura\(\PageIndex{4}\)
No siempre ocurre que la línea dada esté en forma de pendiente-intercepción. Muchas veces hay que realizar pasos adicionales para determinar la pendiente. Los pasos generales para encontrar la ecuación de una línea se describen en el siguiente ejemplo.
Ejemplo\(\PageIndex{5}\)
Encuentra la ecuación de la línea que pasa a través\((8, −2)\) y perpendicular a\(6x+3y=1\).
Solución:
Paso 1: Encuentra la pendiente\(m\). Primero, encuentra la pendiente de la línea dada. Para ello, resuelva\(y\) para cambiar forma estándar a forma pendiente-interceptar,\(y=mx+b\).
\(\begin{aligned} 6x+3y&=1 \\ 6x+3y\color{Cerulean}{-6x}&=1\color{Cerulean}{-6x} \\ 3y&=-6x+1 \\ \frac{3y}{\color{Cerulean}{3}}&=\frac{-6x+1}{\color{Cerulean}{3}} \\ y&=\frac{-6x}{3}+\frac{1}{3}\\y&=-2x+\frac{1}{3} \end{aligned}\)
En esta forma, se puede ver que la pendiente es\(m=−2=−\frac{2}{1}\), y así\(m_{⊥}=\frac{−1}{−2}=+\frac{1}{2}\).
Paso 2: Sustituye la pendiente que encontraste y el punto dado en la forma de punto-pendiente de una ecuación por una línea. En este caso, la pendiente es\(m_{⊥}=\frac{1}{2}\) y el punto dado es\((8, −2)\).
\(\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-(-2)&=\frac{1}{2}(x-8) \end{aligned}\)
Paso 3: Resolver para\(y\).
Respuesta:
\(y=\frac{1}{2}x−6\)
Ejemplo\(\PageIndex{6}\)
Encuentra la ecuación de la línea que pasa a través\((\frac{7}{2}, 1)\) y paralela a\(2x+14y=7\).
Solución:
Encuentra la pendiente\(m\) resolviendo para\(y\).
\(\begin{aligned} 2x+14y&=7 \\ 2x+14y\color{Cerulean}{-2x}&=7\color{Cerulean}{-2x} \\ 14y&=-2x+7 \\ \frac{14y}{\color{Cerulean}{14}}&=\frac{-2x+7}{\color{Cerulean}{14}} \\ y&=\frac{-2x}{14}+\frac{7}{14} \\ y&=-\frac{1}{7}x+\frac{1}{2} \end{aligned}\)
La línea dada tiene la pendiente\(m=−\frac{1}{7}\), y así\(m_{∥}=−\frac{1}{7}\). Utilizamos esto y el punto\((\frac{7}{2}, 1)\) en forma de punto-pendiente.
\(\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-1&=-\frac{1}{7}\left(x-\frac{7}{2} \right) \\ y-1&=-\frac{1}{7}x+\frac{1}{2} \\ y-1\color{Cerulean}{+1}&=-\frac{1}{7}x+\frac{1}{2}\color{Cerulean}{+1} \\ y&=-\frac{1}{7}x+\frac{1}{2}+\color{Cerulean}{\frac{2}{2}} \\ y&=-\frac{1}{7}x+\frac{3}{2} \end{aligned}\)
Respuesta:
\(y=-\frac{1}{7}x+\frac{3}{2}\)
Ejercicio\(\PageIndex{2}\)
Encuentra la ecuación de la línea perpendicular a\(x−3y=9\) y que pasa por ella\((−\frac{1}{2}, 2)\).
- Contestar
-
\(y=-3x+\frac{1}{2}\)
Al encontrar una ecuación de una línea perpendicular a una línea horizontal o vertical, lo mejor es considerar la interpretación geométrica.
Ejemplo\(\PageIndex{7}\)
Encuentra la ecuación de la línea que pasa a través\((−3, −2)\) y perpendicular a\(y=4\).
Solución:
Reconocemos que\(y=4\) es una línea horizontal y queremos encontrar una línea perpendicular que pase por ella\((−3, −2)\).
.png)
Figura\(\PageIndex{5}\)
Si dibujamos la línea perpendicular a la línea horizontal dada, el resultado es una línea vertical.
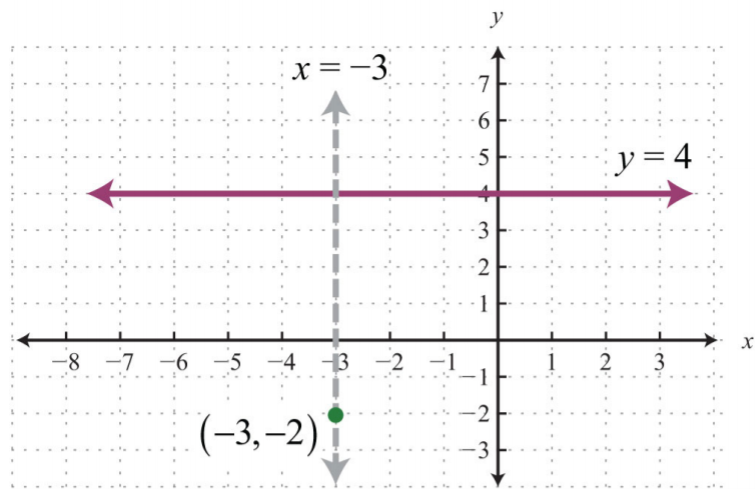.png)
Figura\(\PageIndex{6}\)
Parecen ecuaciones de líneas verticales\(x=k\). Ya que debe pasar\((−3, −2)\), concluimos que esa\(x=−3\) es la ecuación. Todas las soluciones de pares ordenadas de una línea vertical deben compartir la misma\(x\) coordenada.
Respuesta:
\(x=−3\)
Podemos reescribir la ecuación de cualquier línea horizontal,\(y=k\), en forma pendiente-intercepción de la siguiente manera:
\(y=0x+k\)
Escrito en esta forma, vemos que la pendiente es\(m=0=\frac{0}{1}\). Si tratamos de encontrar la pendiente de una línea perpendicular encontrando el recíproco opuesto, nos encontramos con un problema:\(m_{⊥}=−\frac{1}{0}\), que no está definido. Es por ello que nos encargamos de restringir la definición a dos líneas no verticales. Recuerda que las líneas horizontales son perpendiculares a las verticales.
Claves para llevar
- Las líneas paralelas tienen la misma pendiente.
- Las líneas perpendiculares tienen pendientes que son recíprocas opuestas. En otras palabras, si\(m=\frac{a}{b}\), entonces\(m_{⊥}=−\frac{b}{a}\).
- Para encontrar una ecuación de una línea, primero use la información dada para determinar la pendiente. Luego usa la pendiente y un punto en la línea para encontrar la ecuación usando la forma de punto-pendiente.
- Las líneas horizontales y verticales son perpendiculares entre sí.
Ejercicio\(\PageIndex{3}\) Parallel and Perpendicular Lines
Determinar la pendiente de líneas paralelas y perpendiculares.
- \(y=−\frac{3}{4}x+8\)
- \(y=\frac{1}{2}x−3\)
- \(y=4x+4\)
- \(y=−3x+7\)
- \(y=−\frac{5}{8}x−12\)
- \(y=\frac{7}{3}x+\frac{3}{2}\)
- \(y=9x−25\)
- \(y=−10x+15\)
- \(y=5\)
- \(x=−12\)
- \(x−y=0\)
- \(x+y=0\)
- \(4x+3y=0\)
- \(3x−5y=10\)
- \(−2x+7y=14\)
- \(−x−y=\frac{1}{5}\)
- \(\frac{1}{2}x−\frac{1}{3}y=−1\)
- \(−\frac{2}{3}x+\frac{4}{5}y=8\)
- \(2x−\frac{1}{5}y=\frac{1}{10}\)
- \(−\frac{4}{5}x−2y=7\)
- Contestar
-
1. \(m_{∥}=−\frac{3}{4}\)y\(m_{⊥}=\frac{4}{3}\)
3. \(m_{∥}=4\)y\(m_{⊥}=−\frac{1}{4}\)
5. \(m_{∥}=−\frac{5}{8}\)y\(m_{⊥}=\frac{8}{5}\)
7. \(m_{∥}=9\)y\(m_{⊥}=−\frac{1}{9}\)
9. \(m_{∥}=0\)y\(m_{⊥}\) undefined
11. \(m_{∥}=1\)y\(m_{⊥}=−1\)
13. \(m_{∥}=−\frac{4}{3}\)y\(m_{⊥}=\frac{3}{4}\)
15. \(m_{∥}=\frac{2}{7}\)y\(m_{⊥}=−\frac{7}{2}\)
17. \(m_{∥}=\frac{3}{2}\)y\(m_{⊥}=−\frac{2}{3}\)
19. \(m_{∥}=10\)y\(m_{⊥}=−\frac{1}{10}\)
Ejercicio\(\PageIndex{4}\) Parallel and Perpendicular Lines
Determina si las líneas son paralelas, perpendiculares o ninguna.
- \(\left\{\begin{aligned}y&=\frac{2}{3}x+3\\y&=\frac{2}{3}x−3\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=\frac{3}{4}x−1\\y&=\frac{4}{3}x+3\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=−2x+1\\ y&=\frac{1}{2}x+8\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=3x−\frac{1}{2}\\ y&=3x+2\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=5\\x&=−2\end{aligned}\right.\)
- \(\left\{\begin{aligned}y&=7\\y&=−\frac{1}{7}\end{aligned}\right.\)
- \(\left\{\begin{aligned}3x−5y&=15\\ 5x+3y&=9\end{aligned}\right.\)
- \(\left\{\begin{aligned}x−y&=7\\3x+3y&=2\end{aligned}\right.\)
- \(\left\{\begin{aligned}2x−6y&=4\\−x+3y&=−2 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−4x+2y&=3\\6x−3y&=−3 \end{aligned}\right.\)
- \(\left\{\begin{aligned}x+3y&=9\\2x+3y&=6 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y−10&=0\\x−10&=0 \end{aligned}\right.\)
- \(\left\{\begin{aligned}y+2&=0\\2y−10&=0 \end{aligned}\right.\)
- \(\left\{\begin{aligned}3x+2y&=6\\2x+3y&=6 \end{aligned}\right.\)
- \(\left\{\begin{aligned}−5x+4y&=20\\10x−8y&=16 \end{aligned}\right.\)
- \(\left\{\begin{aligned}\frac{1}{2}x−\frac{1}{3}y&=1\\\frac{1}{6}x+\frac{1}{4}y&=−2\end{aligned}\right.\)
- Contestar
-
1. Paralelo
3. perpendiculares
5. perpendiculares
7. perpendiculares
9. Paralelo
11. Tampoco
13. Paralelo
15. Paralelo
Ejercicio\(\PageIndex{5}\) Equations in Point-Slope Form
Encuentra la ecuación de la línea
- Paralelo\(y=\frac{1}{2}x+2\) y de paso\((6, −1)\).
- Paralelo\(y=−\frac{3}{4}x−3\) y de paso\((−8, 2)\).
- Perpendicular a\(y=3x−1\) y de paso\((−3, 2)\).
- Perpendicular a\(y=−\frac{1}{3}x+2\) y de paso\((4, −3)\).
- Perpendicular a\(y=−2\) y de paso\((−1, 5)\).
- Perpendicular a\(x=\frac{1}{5}\) y de paso\((5, −3)\).
- Paralelo\(y=3\) y de paso\((2, 4)\).
- Paralelo\(x=2\) y pasando por (7, −3)\).
- Perpendicular a\(y=x\) y de paso\((7, −13)\).
- Perpendicular a\(y=2x+9\) y de paso\((3, −1)\).
- Paralelo\(y=\frac{1}{4}x−5\) y de paso\((−2, 1)\).
- Paralelo\(y=−\frac{3}{4}x+1\) y de paso\((4, \frac{1}{4})\).
- Paralelo\(2x−3y=6\) y de paso\((6, −2)\).
- Paralelo\(−x+y=4\) y de paso\((9, 7)\).
- Perpendicular a\(5x−3y=18\) y de paso\((−9, 10)\).
- Perpendicular a\(x−y=11\) y de paso\((6, −8)\).
- Paralelo\(\frac{1}{5}x−\frac{1}{3}y=2\) y de paso\((−15, 6)\).
- Paralelo\(−10x−\frac{5}{7}y=12\) y de paso\((−1, \frac{1}{2})\).
- Perpendicular a\(\frac{1}{2}x−\frac{1}{3}y=1\) y de paso\((−10, 3)\).
- Perpendicular a\(−5x+y=−1\) y de paso\((−4, 0)\).
- Paralelo\(x+4y=8\) y de paso\((−1, −2)\).
- Paralelo\(7x−5y=35\) y de paso\((2, −3)\).
- Perpendicular a\(6x+3y=1\) y de paso\((8, −2)\).
- Perpendicular a\(−4x−5y=1\) y de paso\((−1, −1)\).
- Paralelo\(−5x−2y=4\) y de paso\((\frac{1}{5}, −\frac{1}{4})\).
- Paralelo\(6x−\frac{3}{2}y=9\) y de paso\((\frac{1}{3}, \frac{2}{3})\).
- Perpendicular a\(y−3=0\) y de paso\((−6, 12)\).
- Perpendicular a\(x+7=0\) y de paso\((5, −10)\).
- Contestar
-
1. \(y=\frac{1}{2}x−4\)
3. \(y=−\frac{1}{3}x+1\)
5. \(x=−1\)
7. \(y=4\)
9. \(y=−x−6\)
11. \(y=\frac{1}{4}x+\frac{3}{2}\)
13. \(y=\frac{2}{3}x−6\)
15. \(y=−\frac{3}{5}x+\frac{23}{5}\)
17. \(y=\frac{3}{5}x+15\)
19. \(y=−\frac{2}{3}x−\frac{11}{3}\)
21. \(y=−\frac{1}{4}x−\frac{9}{4}\)
23. \(y=\frac{1}{2}x−6\)
25. \(y=−\frac{5}{2}x+\frac{1}{4}\)
27. \(x=−6\)


