5.2: Introducción a los polinomios
- Page ID
- 110073
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Identificar un polinomio y determinar su grado.
- Evaluar un polinomio para valores dados de las variables.
- Evaluar un polinomio usando notación de función.
Definiciones
Un polinomio es una expresión algebraica especial con términos que consisten en coeficientes numéricos reales y factores variables con exponentes de números enteros.
\(\color{Cerulean}{Examples\:of\:polynomials:}\)
\(3x^{2}\quad 7xy+5\quad \frac{3}{2}x^{3}+3x^{2}-\frac{1}{2}x+1\quad 6x^{2}y-4xy^{3}-4xy^{3}+7\)
Los polinomios no tienen variables en el denominador de ningún término.
\(\color{Cerulean}{Examples\:that\:are\:not\:polynomials:}\)
\(\frac{2x^{2}}{y} \quad 5\sqrt{x}+5\quad 5x^{2}+3x^{-2}+7\quad \frac{2}{x}-\frac{5}{y}=3\)
El grado de un término en un polinomio se define como el exponente de la variable, o si hay más de una variable en el término, el grado es la suma de sus exponentes. Recordemos eso\(x^{0}=1\); cualquier término constante puede escribirse como producto de\(x^{0}\) y en sí mismo. De ahí que el grado de un término constante sea\(0\).
| Término | Titulación |
|---|---|
| \(3x^{2}\) | \(2\) |
| \(6x^{2}y\) | \(2+1=3\) |
| \(7a^{2}b^{3}\) | \(2+3=5\) |
| \(8\) | \(0\), ya que\(8=8x^{0}\) |
| \(2x\) | \(1\), ya que\(x=x^{1}\) |
El grado de un polinomio es el grado más grande de todos sus términos.
| Polinomio | Titulación |
|---|---|
| \(4x^{5}-3x^{3}+2x-1\) | \(5\) |
| \(6x^{2}y-5xy^{3}+7\) | \(4\), porque\(5xy^{3}\) tiene grado\(4\). |
| \(12x+54\) | \(1\), porque\(x=x^{1}\) |
Clasificamos los polinomios por el número de términos y el grado de la siguiente manera:
| Expresión | Clasificación | Titulación |
|---|---|---|
| \(5x^{7}\) | Monomial (un término) | \(7\) |
| \(8x^{6}-1\) | Binomial (dos términos) | \(6\) |
| \(-3x^{2}+x-1\) | Trinomio (tres términos) | \(2\) |
| \(5x^{3}-2x^{2}+3x-6\) | Polinomio (muchos términos) | \(3\) |
En este texto, llamaremos polinomios con cuatro o más términos simplemente polinomios.
Ejemplo\(\PageIndex{1}\)
Clasificar y declarar el grado:
\(7x^{2}−4x^{5}−1\).
Solución:
Aquí hay tres términos. El exponente variable más alto es\(5\). Por lo tanto, se trata de un trinomio de grado\(5\).
Respuesta:
Trinomio; grado\(5\)
Ejemplo\(\PageIndex{2}\)
Clasificar y declarar el grado:
\(12a^{5}bc^{3}\).
Solución:
Dado que la expresión consiste únicamente en multiplicación, es un término, un monomio. La parte variable se puede escribir como\(a^{5}b^{1}c^{3}\); de ahí su grado es\(5+1+3=9\).
Respuesta:
Monomio; grado\(9\)
Ejemplo\(\PageIndex{3}\)
Clasificar y declarar el grado:
\(4x^{2}y−6xy^{4}+5x^{3}y^{3}+4\).
Solución:
El término\(4x^{2}y\) tiene grado\(3\);\(−6xy^{4}\) tiene grado\(5; 5x^{3}y^{3}\) tiene grado\(6\); y el término constante\(4\) tiene grado\(0\). Por lo tanto, el polinomio tiene\(4\) términos con grado\(6\).
Respuesta:
Polinomio; grado\(6\)
De particular interés son los polinomios con una variable, donde cada término es de la forma\(a_{n}x^{n}\). Aquí\(a_{n}\) hay cualquier número real y\(n\) es cualquier número entero. Tales polinomios tienen la forma estándar
\[a_{n}x^{n}+a_{n-1}x^{n-1}+...+a_{1}x+a_{0}\]
Normalmente, organizamos términos de polinomios en orden descendente en función del grado de cada término. El coeficiente principal es el coeficiente de la variable con mayor potencia, en este caso,\(a_{n}\).
Ejemplo\(\PageIndex{4}\)
Escriba en forma estándar:
\(3x−4x^{2}+5x^{3}+7−2x^{4}\).
Solución:
Dado que los términos están separados por adición, escriba lo siguiente:
\(\begin{aligned} & 3x-4x^{2}+5x^{3}+7-2x^{4} \\ &=3x+(-4x^{2})+5x^{3}+7+(-2x^{4}) \end{aligned}\)
De esta forma, podemos ver que la resta en el original corresponde a coeficientes negativos. Debido a que la suma es conmutativa, podemos escribir los términos en orden descendente en función del grado de cada término de la siguiente manera:
\(\begin{aligned} &=(-2x^{4})+5x^{3}+(-4x^{2})+3x+7 \\ &=-2x^{4}+5x^{3}-4x^{2}+3x+7 \end{aligned}\)
Respuesta:
\(-2x^{4}+5x^{3}-4x^{2}+3x+7\)
Podemos clasificar adicionalmente polinomios con una variable por su grado de la siguiente manera:
| Polinomio | Nombre |
|---|---|
| \(5\) | Constante (grado\(0\)) |
| \(2x+1\) | Lineal (grado\(1\)) |
| \(3x^{2}+5x-3\) | Cuadrático (grado\(2\)) |
| \(x^{3}+x^{2}+x+1\) | Cúbico (grado\(3\)) |
| \(7x^{4}+3x^{3}-7x+8\) | Polinomio de cuarto grado |
En este texto, llamamos a cualquier polinomio de grado\(n≥4\) un polinomio de\(n\) grado th-grado. Es decir, si el grado lo es\(4\), llamamos al polinomio un polinomio de cuarto grado. Si el grado es\(5\), lo llamamos polinomio de quinto grado, y así sucesivamente.
Evaluación de polinomios
Dados los valores para las variables en un polinomio, podemos sustituir y simplificar usando el orden de las operaciones.
Ejemplo\(\PageIndex{5}\)
Evaluar:
\(3x−1\), donde\(x=−\frac{3}{2}\).
Solución:
Primero, reemplace la variable por paréntesis y luego sustituya el valor dado.
Respuesta:
\(-\frac{11}{2}\)
Ejemplo\(\PageIndex{6}\)
Evaluar:
\(3x^{2}+2x−1\), donde\(x=−1\).
Solución:
Respuesta:
\(0\)
Ejemplo\(\PageIndex{7}\)
Evaluar:
\(−2a^{2}b+ab^{2}−7\), donde\(a=3\) y\(b=−2\).
Solución:
Respuesta:
\(41\)
Ejemplo\(\PageIndex{8}\)
El volumen de una esfera en unidades cúbicas viene dado por la fórmula\(V=\frac{4}{3}πr^{3}\), donde\(r\) está el radio. Calcular el volumen de una esfera con\(r=\frac{3}{2}\) metros de radio.
.png)
Solución:
\(\begin{aligned} V&=\frac{4}{3}\pi r^{3} \\ &=\frac{4}{3}\pi \left( \frac{3}{2} \right)^{3} \\ &=\frac{4}{3}\pi \frac{3^{3}}{2^{3}} \\ &=\frac{\color{Cerulean}{\stackrel{1}{\cancel{\color{black}{4}}}}}{\color{Cerulean}{\stackrel{\cancel{\color{black}{3}}}{1}}} \pi \frac{\color{Cerulean}{\stackrel{9}{\cancel{\color{black}{27}}}}}{\color{Cerulean}{\stackrel{\cancel{\color{black}{8}}}{2}}} \\ &=\frac{9}{2} \pi \end{aligned}\)
Respuesta:
\(\frac{9}{2}\pi\)metros cúbicos
Ejercicio\(\PageIndex{1}\)
Evaluar:
\(x^{3}−x^{2}+4x−2\), donde\(x=−3\).
- Contestar
-
\(-50\)
Funciones polinomiales
Las funciones polinómicas con una variable son funciones que se pueden escribir en la forma
\[f(x) = a_{n}x^{n} + a_{n-1}x^{n-1} + ... + a_{0}\],
donde\(a_{n}\) está cualquier número real y\(n\) es cualquier número entero. A continuación se enumeran algunos ejemplos de las diferentes clases de funciones polinómicas:
| Función polinomial | Nombre |
|---|---|
| \(f(x)=5\) | Función constante (grado\(0\)) |
| \(f(x)=-2x+1\) | Función lineal (grado\(1\)) |
| \(f(x)=5x^{2}+4x-3\) | Función cuadrática (grado\(2\)) |
| \(f(x)=x^{3}-1\) | Función cúbica (grado\(3\)) |
| \(f(x)=4x^{5}+3x^{4}-7\) | Función polinomial |
Dado que no hay restricciones en los valores para\(x\), el dominio de cualquier función polinómica consiste en todos los números reales.
Ejemplo\(\PageIndex{9}\)
Calcular:
\(f(5)\), dado\(f(x)=−2x^{2}+5x+10\).
Solución:
Recordemos que la notación de la función\(f(5)\) indica que debemos evaluar la función cuando\(x=5\). Reemplazar cada instancia de la variable\(x\) con el valor\(5\).
Respuesta:
\(f(5)=-15\)
Ejemplo\(\PageIndex{10}\)
Calcular:
\(f(−1)\), dado\(f(x)=−x^{3}+2x^{2}−4x+1\).
Solución:
Reemplace la variable\(x\) por\(−1\).
\(\begin{aligned} f(\color{OliveGreen}{-1}\color{black}{)} &=-(\color{OliveGreen}{-1}\color{black}{)^{3}+2(}\color{OliveGreen}{-1}\color{black}{)^{2}-4(}\color{OliveGreen}{-1}\color{black}{)+1} \\ &=-(-1)+2\cdot 1 +4+1 \\ &=1+2+4+1 \\ &=8 \end{aligned}\)
Respuesta:
\(f(-1)=8\)
Ejercicio\(\PageIndex{2}\)
Dado\(g(x)=x^{3}−2x^{2}−x−4\), calcular\(g(−1)\).
- Contestar
-
\(g(−1)=−6\)
Claves para llevar
- Los polinomios son expresiones algebraicas especiales donde los términos son productos de números reales y variables con exponentes de números enteros.
- El grado de un polinomio con una variable es el mayor exponente de la variable que se encuentra en cualquier término.
- Los términos de un polinomio se ordenan típicamente en orden descendente en función del grado de cada término.
- Al evaluar un polinomio, es una buena práctica reemplazar todas las variables por paréntesis y luego sustituir los valores apropiados.
- Todos los polinomios son funciones.
Ejercicio\(\PageIndex{3}\) Definitions
Clasificar el polinomio dado como lineal, cuadrático o cúbico.
- \(2x+1\)
- \(x^{2}+7x+2\)
- \(2−3x^{2}+x\)
- \(4x\)
- \(x^{2}−x^{3}+x+1\)
- \(5−10x^{3}\)
- Contestar
-
1. Lineal
3. Cuadrático
5. Cúbico
Ejercicio\(\PageIndex{4}\) Definitions
Clasificar el polinomio dado como monomio, binomio o trinomio y declarar el grado.
- \(x^{3}−1\)
- \(x^{2}y^{2}\)
- \(x−x^{5}+1\)
- \(x^{2}+3x−1\)
- \(5ab^{4}\)
- \(13x−12\)
- \(−5x^{3}+2x+1\)
- \(8x^{2}−9\)
- \(4x^{5}−5x^{3}+6x\)
- \(8x^{4}−x^{5}+2x−3\)
- \(9x+7\)
- \(x^{5}+x^{4}+x^{3}+x^{2}−x+1\)
- \(6x−1+5x^{4}−8\)
- \(4x−3x^{2}+3\)
- \(7\)
- \(x^{2}\)
- \(4x^{2}y−3x^{3}y^{3}+xy^{3}\)
- \(a^{3}b^{2}−6ab\)
- \(a^{3}b^{3}\)
- \(x^{2}y−y^{2}x\)
- \(xy−3\)
- \(a^{5}bc^{2}+3a^{9}−5a^{4}b^{3}c\)
- \(−3x^{10}y^{2}z−xy^{12}z+9x^{13}+30\)
- \(7x^{0}\)
- Contestar
-
1. Binomial; grado\(3\)
3. Trinomio; grado\(5\)
5. Monomio; grado\(5\)
7. Trinomio; grado\(3\)
9. Trinomio; grado\(5\)
11. Binomial; grado\(1\)
13. No es un polinomio
15. Monomio; grado\(0\)
17. Trinomio; grado\(6\)
19. Monomio; grado\(6\)
21. Binomial; grado\(2\)
23. Polinomio; grado\(14\)
Ejercicio\(\PageIndex{5}\) Definitions
Escribe los siguientes polinomios en forma estándar.
- \(1−6x+7x^{2}\)
- \(x−9x^{2}−8\)
- \(7−x^{3}+x^{7}−x^{2}+x−5x^{5}\)
- \(a^{3}−a^{9}+6a^{5}−a+3−a^{4}\)
- Contestar
-
1. \(7x^{2}−6x+1\)
3. \(x^{7}−5x^{5}−x^{3}−x^{2}+x+7\)
Ejercicio\(\PageIndex{6}\) Evaluating Polynomials
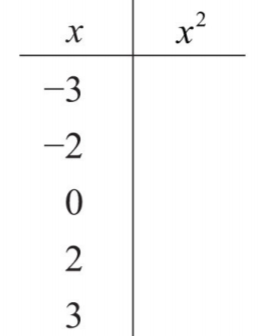
- Rellena la siguiente tabla:
.png)
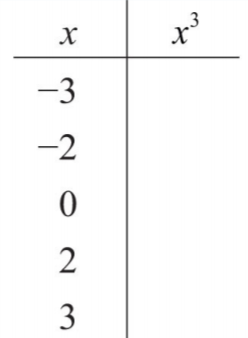
Figura\(\PageIndex{2}\) - Rellena la siguiente tabla:
.png)
Figura\(\PageIndex{3}\)
- Contestar
-
1.
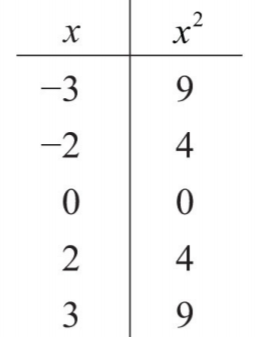.png)
Figura\(\PageIndex{4}\)
Ejercicio\(\PageIndex{7}\) Evaluating Polynomials
Evaluar.
- \(2x−3\), donde\(x=3\)
- \(x^{2}−3x+5\), donde\(x=−2\)
- \(−12x+13\), donde\(x=−13\)
- \(−x^{2}+5x−1\), donde\(x=−12\)
- \(−2x^{2}+3x−5\), donde\(x=0\)
- \(8x^{5}−27x^{3}+81x−17\), donde\(x=0\)
- \(y^{3}−2y+1\), donde\(y=−2\)
- \(y^{4}+2y^{2}−32\), donde\(y=2\)
- \(a^{3}+2a^{2}+a−3\), donde\(a=−3\)
- \(x^{3}−x^{2}\), donde\(x=5\)
- \(34x^{2}−12x+36\), donde\(x=−23\)
- \(58x^{2}−14x+12\), donde\(x=4\)
- \(x^{2}y+xy^{2}\), dónde\(x=2\) y\(y=−3\)
- \(2a^{5}b−ab^{4}+a^{2}b^{2}\), dónde\(a=−1\) y\(b=−2\)
- \(a^{2}−b^{2}\), dónde\(a=5\) y\(b=−6\)
- \(a^{2}−b^{2}\), dónde\(a=34\) y\(b=−14\)
- \(a^{3}−b^{3}\), dónde\(a=−2\) y\(b=3\)
- \(a^{3}+b^{3}\), dónde\(a=5\) y\(b=−5\)
- Contestar
-
1. \(3\)
3. \(\frac{1}{2}\)
5. \(−5\)
7. \(−3\)
9. \(−15\)
11. \(\frac{7}{6}\)
13. \(6\)
15. \(−11\)
17. \(−35\)
Ejercicio\(\PageIndex{8}\) Evaluating Polynomials
Para cada problema, evalúe\(b^{2}−4ac\), dados los siguientes valores.
- \(a=−1, b=2\), y\(c=−1\)
- \(a=2, b=−2\), y\(c=12\)
- \(a=3, b=−5, c=0\)
- \(a=1, b=0\), y\(c=−4\)
- \(a=14, b=−4\), y\(c=2\)
- \(a=1, b=5\), y\(c=6\)
- Contestar
-
1. \(0\)
3. \(25\)
5. \(14\)
Ejercicio\(\PageIndex{9}\) Evaluating Polynomials
El volumen de una esfera en unidades cúbicas viene dado por la fórmula\(V=\frac{4}{3}πr^{3}\), donde\(r\) está el radio. Para cada problema, calcule el volumen de una esfera dados los siguientes radios.
- \(r = 3\)centímetros
- \(r = 1\)centímetro
- \(r = \frac{1}{2}\)pies
- \(r = \frac{3}{2}\)pies
- \(r = 0.15\)en
- \(r = 1.3\)pulgadas
- Contestar
-
1. \(36π\)centímetros cúbicos
3. \(\frac{π}{6}\)pies cúbicos
5. \(0.014\)pulgadas cúbicas
Ejercicio\(\PageIndex{10}\) Evaluating Polynomials
La altura en pies de un proyectil lanzado verticalmente desde el suelo con una velocidad inicial\(v_{0}\) en pies por segundo viene dada por la fórmula\(h=−16t^{2}+v_{0}t\), donde\(t\) representa el tiempo en segundos. Para cada problema, calcule la altura del proyectil dada la siguiente velocidad y tiempos iniciales.
- \(v_{0}=64\)pies/segundo, a veces\(t = 0, 1, 2, 3, 4\) segundos
- \(v_{0}=80\)pies/segundo, a veces\(t = 0, 1, 2, 2.5, 3, 4, 5\) segundos
- Contestar
-
1.
Tiempo Altura \(t=0\)segundos \(h=0\)pies \(t=1\)segundo \(h=48\)pies \(t=2\)segundos \(h=64\)pies \(t=3\)segundos \(h=48\)pies \(t=4\)segundos \(h=0\)pies Mesa\(\PageIndex{6}\)
Ejercicio\(\PageIndex{11}\) Evaluating Polynomials
La distancia de parada de un automóvil, tomando en cuenta un tiempo promedio de reacción, se puede estimar con la fórmula\(d=0.05v^{2}+1.5\), donde\(d\) está en pies y\(v\) es la velocidad en millas por hora. Para cada problema, calcule la distancia de parada de un automóvil que viaja a las velocidades dadas.
- \(20\)millas por hora
- \(40\)millas por hora
- \(80\)millas por hora
- \(100\)millas por hora
- Contestar
-
1. \(21.5\)pies
3. \(321.5\)pies
Ejercicio\(\PageIndex{12}\) Polynomial Functions
Dada la función lineal\(f(x)=\frac{2}{3}x+6\), evaluar cada una de las siguientes.
- \(f(−6)\)
- \(f(−3)\)
- \(f(0)\)
- \(f(3)\)
- Encuentra\(x\) cuándo\(f(x)=10\).
- Encuentra\(x\) cuándo\(f(x)=−4\).
- Contestar
-
1. \(2\)
3. \(6\)
5. \(x=6\)
Ejercicio\(\PageIndex{13}\) Polynomial Functions
Dada la función cuadrática\(f(x)=2x^{2}−3x+5\), evaluar cada una de las siguientes.
- \(f(−2)\)
- \(f(−1)\)
- \(f(0)\)
- \(f(2)\)
- Contestar
-
1. \(19\)
3. \(5\)
Ejercicio\(\PageIndex{14}\) Polynomial Functions
Dada la función cúbica\(g(x)=x^{3}−x^{2}+x−1\), evalúe cada una de las siguientes.
- \(g(−2)\)
- \(g(−1)\)
- \(g(0)\)
- \(g(1)\)
- Contestar
-
1. \(-15\)
3. \(-1\)
Ejercicio\(\PageIndex{15}\) Polynomial Functions
La altura en pies de un proyectil lanzado verticalmente desde el suelo con una velocidad inicial de\(128\) pies por segundo viene dada por la función\(h(t)=−16t^{2}+128t\), donde\(t\) está en segundos. Calcular e interpretar lo siguiente.
- \(h(0)\)
- \(h(12) \)
- \(h(1) \)
- \(h(3) \)
- \(h(4) \)
- \(h(5) \)
- \(h(7) \)
- \(h(8)\)
- Contestar
-
1. El proyectil se lanza desde el suelo.
3. El proyectil se encuentra a\(112\) pies sobre el suelo\(1\) segundo después del lanzamiento.
5. El proyectil se encuentra a\(256\) pies sobre el suelo\(4\) segundos después del lanzamiento.
7. El proyectil se encuentra a\(112\) pies sobre el suelo\(7\) segundos después del lanzamiento.
Ejercicio\(\PageIndex{16}\) Discussion Board Topics
- Encuentra y comparte algunas gráficas de funciones polinómicas.
- Explica cómo convertir pies por segundo en millas por hora.
- Encontrar y compartir los nombres de polinomios de cuarto grado, quinto grado y superior.
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar


