8.2: Simplificar expresiones radicales
- Page ID
- 110116
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Simplifica las expresiones radicales usando la regla de producto y cociente para radicales.
- Usa fórmulas que involucren radicales.
- Evaluar las funciones dadas de raíz cuadrada y raíz cúbica.
Simplificación de expresiones radicales
Una expresión algebraica que contiene radicales se llama expresión radical. Utilizamos las reglas de producto y cociente para simplificarlos.
Ejemplo\(\PageIndex{1}\)
Simplificar:
\(\sqrt[3]{8 y^{3}}\)
Solución:
Usa el hecho de que\(\sqrt[n]{a^{n}}=a\) cuando n es impar.
\(\begin{aligned} \sqrt[3]{8 y^{3}} &=\sqrt[3]{2^{3} \cdot y^{3}} \qquad\quad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.}\\ &=\sqrt[3]{2^{3}} \cdot \sqrt[3]{y^{3}}\quad\:\:\:\color{Cerulean}{Simplify.} \\ &=2 y \end{aligned}\)
Respuesta:
\(2y\)
Ejemplo\(\PageIndex{2}\)
Simplificar:
\(\sqrt{9 x^{2}}\)
Solución:
La raíz cuadrada tiene índice 2; usa el hecho de que\(\sqrt[n]{a^{n}}=a\) cuando n es par.
\(\begin{aligned} \sqrt{9 x^{2}} &=\sqrt{3^{2} x^{2}}\qquad\quad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.} \\ &=\sqrt{3^{2}} \cdot \sqrt{x^{2}}\quad\:\color{Cerulean}{Simplify.} \\ &=3|x| \end{aligned}\)
Dado que x es una variable, puede representar un número negativo. Por lo tanto, debemos asegurarnos de que el resultado sea positivo al incluir el operador de valor absoluto.
Respuesta:
\(3|x|\)
Nota
Por lo general, en este punto los textos de álgebra iniciales señalan que todas las variables se supone que son positivas. Si este es el caso, entonces x en el ejemplo anterior es positivo y no se necesita el operador de valor absoluto. El ejemplo se puede simplificar de la siguiente manera:
\(\sqrt{9x^{2}}=\sqrt{3^{2}x^{2}}=\sqrt{3^{2}}\cdot\sqrt{x^{2}}=3x\)
En esta sección, asumiremos que todas las variables son positivas. Esto nos permite enfocarnos en el cálculo de las raíces n th sin los tecnicismos asociados con el problema principal de raíz n th. Por esta razón, utilizaremos la siguiente propiedad para el resto de la sección:
\(\sqrt[n]{a^{n}}=a\), si la raíz\(a≥0\) n
Al simplificar expresiones radicales, busque factores con potencias que coincidan con el índice.
Ejemplo\(\PageIndex{3}\)
Simplificar:
\(\sqrt{18x^{3}y^{4}}\)
Solución:
Comience por determinar los factores cuadrados de\(18, x^{3}\), y\(y^{4}\).
\( \ \begin{aligned} 18 &=2 \cdot \color{Cerulean}{3^{2}} \\ x^{3} &=\color{Cerulean}{x^{2}}\color{black}{ \cdot} x \\ y^{4} &=\color{Cerulean}{\left(y^{2}\right)^{2}} \end{aligned} \ \qquad\color{Cerulean}{Square\:factors}\)
Haga estas sustituciones y luego aplique la regla del producto para los radicales y simplifique.
\(\begin{aligned} \sqrt{18 x^{3} y^{4}} &=\sqrt{\color{Cerulean}{2}\color{black}{ \cdot} 3^{2} \cdot x^{2} \cdot \color{Cerulean}{x}\color{black}{ \cdot}\left(y^{2}\right)^{2}}\qquad\qquad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.} \\ &=\sqrt{3^{2}} \cdot \sqrt{x^{2}} \cdot \sqrt{\left(y^{2}\right)^{2}} \cdot \color{black}{\sqrt{\color{Cerulean}{2 x}}}\quad\color{Cerulean}{Simplify.} \\ &=3 \cdot x \cdot y^{2} \cdot \sqrt{2 x} \\ &=3 x y^{2} \sqrt{2 x} \end{aligned}\)
Respuesta:
\(3 x y^{2} \sqrt{2 x}\)
Ejemplo\(\PageIndex{4}\)
Simplificar:
\(\sqrt{4a^{5}b^{6}}\)
Solución:
Comience por determinar los factores cuadrados de\(4, a^{5}\), y\(b^{6}\).
\(\begin{array}{l}{4=\color{Cerulean}{2^{2}}} \\ {a^{5}=a^{2} \cdot a^{2} \cdot a=\color{Cerulean}{\left(a^{2}\right)^{2}}\color{black}{ \cdot} a} \\ {b^{6}=b^{3} \cdot b^{3}=\color{Cerulean}{\left(b^{3}\right)^{2}}}\end{array} \qquad\color{Cerulean}{Square\:factors}\)
Haga estas sustituciones y luego aplique la regla del producto para los radicales y simplifique.
\(\begin{aligned} \sqrt{\frac{4 a^{5}}{b^{6}}} &=\sqrt{\frac{2^{2}\left(a^{2}\right)^{2} \cdot a}{\left(b^{3}\right)^{2}}}\qquad\qquad\color{Cerulean}{Apply\:the\:product\:and\:quotient\:rule\:for\:radicals.} \\ &=\frac{\sqrt{2^{2}} \cdot \sqrt{\left(a^{2}\right)^{2}} \cdot \sqrt{a}}{\sqrt{\left(b^{3}\right)^{2}}}\quad\color{Cerulean}{Simplify.} \\ &=\frac{2 a^{2} \sqrt{a}}{b^{3}} \end{aligned}\)
Respuesta:
\(\frac{2 a^{2} \sqrt{a}}{b^{3}}\)
Ejemplo\(\PageIndex{5}\)
Simplificar:
\(\sqrt[3]{80x^{5}y^{7}}\)
Solución:
Comience por determinar los factores cúbicos de\(80, x^{5}\), y\(y^{7}\).
\(\begin{array}{l}{80=2^{4} \cdot 5=\color{Cerulean}{2^{3}}\color{black}{ \cdot} 2 \cdot 5} \\ {x^{5}=\color{Cerulean}{x^{3}}\color{black}{ \cdot} x^{2}} \\ {y^{7}=y^{6} \cdot y=\color{Cerulean}{\left(y^{2}\right)^{3}}\color{black}{ \cdot} y}\end{array} \qquad\color{Cerulean}{Cubic\:factors}\)
Haga estas sustituciones y luego aplique la regla del producto para los radicales y simplifique.
\(\begin{aligned} \sqrt[3]{80 x^{5} y^{7}} &=\sqrt[3]{\color{Cerulean}{2^{3}}\color{black}{ \cdot} 2 \cdot 5 \cdot \color{Cerulean}{x^{3}}\color{black}{ \cdot} x^{2} \cdot\color{Cerulean}{\left(y^{2}\right)^{3}}\color{black}{ \cdot} y} \qquad\qquad\qquad\color{Cerulean}{Apply\:the\:product\:rule\:for\:radicals.}\\ &=\color{black}{\sqrt[3]{\color{Cerulean}{2^{3}}}} \cdot \color{black}{\sqrt[3]{\color{Cerulean}{x^{3}}}} \cdot \color{black}{\sqrt[3]{\color{Cerulean}{\left(y^{2}\right)^{3}}}} \cdot \sqrt[3]{2 \cdot 5 \cdot x^{2} \cdot y} \quad\:\:\color{Cerulean}{Simplify.} \\ &=2 \cdot x \cdot y^{2} \cdot \sqrt[3]{10 x^{2} y} \\ &=2 x y^{2} \sqrt[3]{10 x^{2} y} \end{aligned}\)
Respuesta:
\(2 x y^{2} \sqrt[3]{10 x^{2} y}\)
Ejemplo\(\PageIndex{6}\)
Simplificar:
\(\sqrt[3]{9x^{6}y^{3}z^{9}}\)
Solución:
El coeficiente\(9=3^{2}\) y por lo tanto no tiene ningún factor cubo perfecto. Se dejará como el único radical restante porque todos los demás factores son cubos, como se ilustra a continuación:
\(\begin{aligned} x^{6} &=\left(x^{2}\right)^{3} \\ y^{3} &=(y)^{3} \\ z^{9} &=\left(z^{3}\right)^{3} \end{aligned}\qquad \color{Cerulean}{Cubic\:factors}\)
Reemplazar las variables con estos equivalentes, aplicar la regla de producto y cociente para radicales, y luego simplificar.
\(\begin{aligned} \sqrt[3]{\frac{9 x^{6}}{y^{3} z^{9}}} &=\sqrt[3]{\frac{3^{2} \cdot\left(x^{2}\right)^{3}}{y^{3} \cdot\left(z^{3}\right)^{3}}} \\ &=\frac{\sqrt[3]{3^{2}} \cdot \sqrt[3]{\left(x^{2}\right)^{3}}}{\sqrt[3]{y^{3}} \cdot \sqrt[3]{\left(z^{3}\right)^{3}}} \\ &=\frac{\sqrt[3]{3^{2}} \cdot x^{2}}{y \cdot z^{3}} \\ &=\frac{\sqrt[3]{9} \cdot x^{2}}{y \cdot z^{3}} \end{aligned}\)
Respuesta:
\(\frac{\sqrt[3]{9} \cdot x^{2}}{y \cdot z^{3}}\)
Ejemplo\(\PageIndex{7}\)
Simplificar:
\(\sqrt[4]{81a^{4}b^{5}}\)
Solución:
Determinar todos los factores que se pueden escribir como poderes perfectos de 4. Aquí es importante verlo\(b^{5}=b^{4}⋅b\). De ahí que el factor\(b\) quede dentro del radical.
\(\begin{aligned} \sqrt[4]{81 a^{4} b^{5}} &=\sqrt[4]{3^{4} \cdot a^{4} \cdot b^{4} \cdot b} \\ &=\sqrt[4]{3^{4}} \cdot \sqrt[4]{a^{4}} \cdot \sqrt[4]{b^{4}} \cdot \sqrt[4]{b} \\ &=3 \cdot a \cdot b \cdot \sqrt[4]{b} \end{aligned}\)
Respuesta:
\(3ab\sqrt[4]{b}\)
Ejemplo\(\PageIndex{8}\)
Simplificar:
Solución:
Observe que la variable factor x no puede escribirse como una potencia de 5 y así quedará dentro del radical. Además, para\(y^{6}=y^{5}⋅y\); el factor y se dejará dentro del radical también.
Respuesta:
\(-2yz\sqrt[5]{x^{3}y}\)
Ejercicio\(\PageIndex{1}\)
Simplificar:
\(\sqrt{192x^{6}y^{7}z^{12}}\)
(Supongamos que todas las variables son positivas.)
- Contestar
-
\(8x^{3}y^{3}z^{6}\sqrt{3y}\)
Nota
Para simplificar fácilmente una raíz n ésima, podemos dividir las potencias por el índice.
\(\sqrt{a^{6}}=a^{3}\), que es\(a^{6÷2}= a^{3}\)\(\sqrt[3]{b^{6}}=b^{2}\), que es\(b^{6÷3}=b^{2}\)\(\sqrt[6]{c^{6}}=c\), que es\(c^{6÷6}=c^{1}\)
Si el índice no divide en la potencia de manera uniforme, entonces podemos usar el cociente y el resto para simplificar. Por ejemplo,
\(\sqrt{a^{5}}=a^{2}⋅\sqrt{a}\), que es\(a^{5÷2}=a^{2}_{r\:1}\)\(\sqrt[3]{b^{5}}=b⋅\sqrt[3]{b^{2}}\), que es\(b^{5÷3}=b^{1}_{r\:2}\)\(\sqrt[5]{c^{14}}=c^{2}⋅\sqrt[5]{c^{4}}\), que es\(c^{14÷5}=c^{2}_{r\:4}\)
El cociente es el exponente del factor fuera del radical, y el resto es el exponente del factor que queda dentro del radical.
Fórmulas que involucran radicales
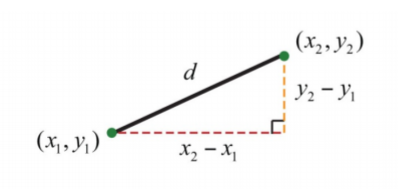
A continuación revisamos la fórmula de distancia. Teniendo en cuenta dos puntos\((x_{1}, y_{1})\) y\((x_{2}, y_{2})\),
.png)
La distancia, d, entre ellos viene dada por la siguiente fórmula:
Fórmula de distancia:
\[d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}\]
Recordemos que esta fórmula se derivó del teorema de Pitágoras.
Ejemplo\(\PageIndex{9}\)
Calcular la distancia entre\((−4, 7)\) y\((2, 1)\).
Solución:
Utilice la fórmula de distancia con los siguientes puntos.
\(\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\left(x_{2}, y_{2}\right)} \\ {(\color{Cerulean}{-4}\color{black}{,}\color{OliveGreen}{7}\color{black}{)}} & {(\color{Cerulean}{2}\color{black}{,}\color{OliveGreen}{1}\color{black}{)}}\end{array}\)
Es una buena práctica incluir la fórmula en su forma general antes de sustituir valores por las variables; esto mejora la legibilidad y reduce la probabilidad de cometer errores.
\(\begin{aligned} d &=\sqrt{\left(x_{2}-x_{1}\right)^{2}+\left(y_{2}-y_{1}\right)^{2}} \\ &=\sqrt{(\color{Cerulean}{2}\color{black}{-}(\color{Cerulean}{-4}\color{black}{)})^{2}+(\color{OliveGreen}{1}\color{black}{-}\color{OliveGreen}{7}\color{black}{)}^{2}} \\ &=\sqrt{(2+4)^{2}+(1-7)^{2}} \\ &=\sqrt{(6)^{2}+(-6)^{2}} \\ &=\sqrt{72} \\ &=\sqrt{36 \cdot 2} \\ &=6 \sqrt{2} \end{aligned}\)
Respuesta:
\(6\sqrt{2}\)unidades
Ejemplo\(\PageIndex{10}\)
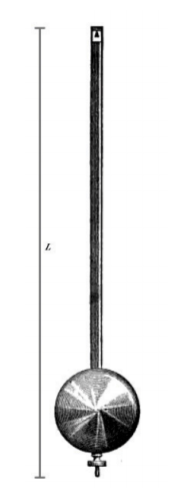
El periodo, T, de un péndulo en segundos viene dado por la fórmula
\[T=2 \pi \sqrt{\frac{L}{32}}\]
donde L representa la longitud del péndulo en pies. Si la longitud de un péndulo mide 6 pies, entonces calcula el período redondeado a la décima de segundo más cercana.
.png)
Solución:
Sustituye 6 por L y luego simplifica.
\(\begin{aligned} T &=2 \pi \sqrt{\frac{L}{32}} \\ &=2 \pi \sqrt{\frac{6}{32}}\quad\color{Cerulean}{Reduce.} \\ &=2 \pi \sqrt{\frac{3}{16}} \quad\color{Cerulean}{Apply\:the\:quotient\:rule\:for\:radicals.}\\ &=2 \pi \frac{\sqrt{3}}{\sqrt{16}} \quad\color{Cerulean}{Simplify.}\\ &=\frac{2 \pi \sqrt{3}}{4}\quad\:\:\:\color{Cerulean}{Use\:a\:calculator.} \\ & \approx 2.7 \end{aligned}\)
Respuesta:
El periodo es de aproximadamente 2.7 segundos.
Funciones Raíz Cuadrada y Raíz Cube
Comenzamos con la función de raíz cuadrada:
\(f(x)=\sqrt{x}\)
Sabemos que la raíz cuadrada no es un número real cuando el radicando x es negativo. Por lo tanto, concluimos que el dominio consiste en todos los números reales mayores o iguales a 0. Aquí elegimos 0 y algunos valores positivos para x, calculamos los valores y correspondientes y trazamos los pares ordenados resultantes.
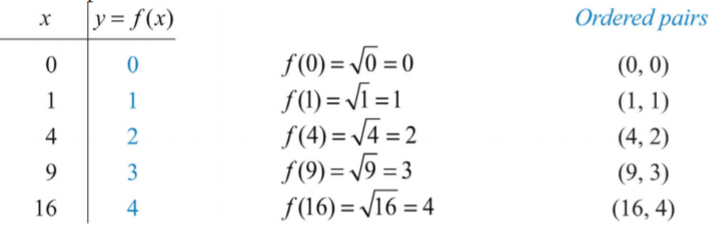.png)
Después de trazar los puntos, podemos entonces bosquejar la gráfica de la función de raíz cuadrada.
.png)
Ejemplo\(\PageIndex{11}\)
Dada la función\(f(x)=\sqrt{x+2}\), encuentra f (−2), f (2) y f (6).
Solución:
Reemplazar x con cada uno de los valores dados.
\(f(x)=\sqrt{x+2}\)
\(\begin{aligned} f(\color{OliveGreen}{-2}\color{black}{)} &=\sqrt{\color{OliveGreen}{-2}\color{black}{+}2}=\sqrt{0}=0 \\ f(\color{OliveGreen}{2}\color{black}{)} &=\sqrt{\color{OliveGreen}{2}\color{black}{+}2}=\sqrt{4}=2 \\ f(\color{OliveGreen}{6}\color{black}{)} &=\sqrt{\color{OliveGreen}{6}\color{black}{+}2}=\sqrt{8}=\sqrt{4 \cdot 2}=2 \sqrt{2} \end{aligned}\)
Respuesta:
\(f(−2)=0, f(2)=2\), y\(f(6)=2\sqrt{2}\)
A continuación, considere la función de raíz cubo:
\(f(x)=\sqrt[3]{x}\)
Dado que la raíz cubo podría ser negativa o positiva, concluimos que el dominio consiste en todos los números reales. Para la integridad, elija algunos valores positivos y negativos para x, así como 0, y luego calcule los valores y correspondientes
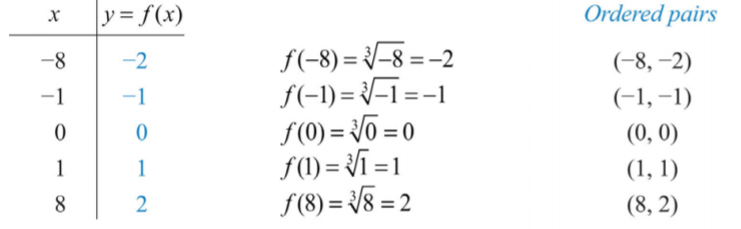.png)
Trace los puntos y dibuje la gráfica de la función de raíz cúbica.
.png)
Ejemplo\(\PageIndex{12}\)
Dada la función\(g(x)=\sqrt[3]{x-1}\), encuentra g (−7), g (0) y g (55).
Solución:
Reemplazar x con cada uno de los valores dados.
\(g(x)=\sqrt[3]{x-1}\)
Respuesta:
\(g(−7)=−2, g(0)=−1\), y\(g(55)=3\sqrt[3]{2}\)
Claves para llevar
- Al principio del álgebra, normalmente asumimos que todas las expresiones variables dentro del radical son positivas. Esto nos permite enfocarnos en simplificar los radicales sin los problemas técnicos asociados con la raíz n principal.
- Para simplificar las expresiones radicales, busque factores del radicando con potencias que coincidan con el índice. Si se encuentran, pueden simplificarse aplicando las reglas de producto y cociente para radicales, así como la propiedad\(\sqrt[n]{a^{n}}=a\), donde\(a\) es positiva.
Ejercicio\(\PageIndex{2}\) simplifying radical expressions
Simplificar. (Supongamos que todas las variables representan números positivos.)
- \(\sqrt{36a^{2}}\)
- \(\sqrt{121b^{2}}\)
- \(\sqrt{x^{2}y^{2}}\)
- \(\sqrt{25x^{2}y^{2}z^{2}}\)
- \(\sqrt{180x^{3}}\)
- \(\sqrt{150y^{3}}\)
- \(\sqrt{49a^{3}b^{2}}\)
- \(\sqrt{4a^{4}b^{3}c}\)
- \(\sqrt{45x^{5}y^{3}}\)
- \(\sqrt{50x^{6}y^{4}}\)
- \(\sqrt{64r^{2}s^{6}t^{5}}\)
- \(\sqrt{144r^{8}s^{6}t^{2}}\)
- \(\sqrt{(x + 1 )^{2}}\)
- \(\sqrt{( 2 x + 3 )^{2}}\)
- \(\sqrt{4 ( 3 x − 1 )^{2}}\)
- \(\sqrt{9 ( 2 x + 3 )^{2}}\)
- \(\sqrt{9x^{3}5y^{2}}\)
- \(\sqrt{4x^{5}9y^{4}}\)
- \(\sqrt{m^{7}36 n^{4}}\)
- \(\sqrt{147 m^{9}n^{6}}\)
- \(\sqrt{2 r^{2}s^{5}25t^{4}}\)
- \(\sqrt{36 r^{5} s^{2} t^{6}}\)
- \(\sqrt[3]{27 a^{ 3}}\)
- \(\sqrt[3]{125 b^{3}}\)
- \(\sqrt[3]{250 x^{4}y^{3}}\)
- \(\sqrt[3]{162 a^{3} b^{5}}\)
- \(\sqrt[3]{64 x^{3}y^{6} z^{9}}\)
- \(\sqrt[3]{216 x^{12}y^{3}}\)
- \(\sqrt[3]{8 x^{3}y^{4}}\)
- \(\sqrt[3]{27 x^{5}y^{3}}\)
- \(\sqrt[3]{a^{4} b^{5} c^{6}}\)
- \(\sqrt[3]{a^{7} b^{5} c^{3}}\)
- \(\sqrt[3]{8 x^{4}27y^{3}}\)
- \(\sqrt[3]{x^{5}125y^{6}}\)
- \(\sqrt[3]{360 r^{5} s^{12} t^{13}}\)
- \(\sqrt[3]{540r^{3}s^{2}t^{9}}\)
- \(\sqrt[4]{81x^{4}}\)
- \(\sqrt[4]{x^{4}y^{4}}\)
- \(\sqrt[4]{16x^{4}y^{8}}\)
- \(\sqrt[4]{81x^{12}y^{4}}\)
- \(\sqrt[4]{a^{4}b^{5}c^{6}}\)
- \(\sqrt[4]{54a^{6}c^{8}}\)
- \(\sqrt[4]{128x^{6}}\)
- \(\sqrt[4]{243y^{7}}\)
- \(\sqrt[5]{32m^{10}n^{5}}\)
- \(\sqrt[5]{37m^{9}n^{10}}\)
- \(-3\sqrt{4x^{2}}\)
- \(7\sqrt{9y^{2}}\)
- \(-5\sqrt{x4x^{2}y}\)
- \(−3\sqrt{y^{16}x^{3}y^{2}}\)
- \(12ab\sqrt{a^{5}b^{3}}\)
- \(6a^{2}b^{9}\sqrt{a^{7}b^{2}}\)
- \(2x\sqrt[3]{8x^{6}}\)
- \(−5x^{2}\sqrt[3]{27x^{3}}\)
- \(2ab\sqrt[3]{−8a^{4}b^{5}}\)
- \(5a^{2}b\sqrt[3]{−27a^{3}b^{3}}\)
- Contestar
-
1. \(6a\)
3. \(xy\)
5. \(6x \sqrt{5x}\)
7. \(7ab\sqrt{a}\)
9. \(3x^{2}y\sqrt{5xy}\)
11. \(8rs^{3}t^{2}\sqrt{t}\)
13. \(x+1\)
15. \(2(3x−1)\)
17. \(3xy\sqrt{5x}\)
19. \(6n^{2}m^{3}\sqrt{m}\)
21. \(5\sqrt{2s}rt^{2}s^{2}\)
23. \(3a\)
25. \(5xy\sqrt[3]{2x}\)
27. \(4xy^{2}z^{3}\)
29. \(2xy\sqrt[3]{y}\)
31. \(abc^{2}\sqrt[3]{ab^{2}}\)
33. \(6yx\sqrt[3]{x}\)
35. \(2rs^{4}t^{4}\sqrt[3]{45r^{2}t}\)
37. \(3x\)
39. \(2xy^{2}\)
41. \(abc\sqrt[4]{bc^{2}}\)
43. \(2x\sqrt[4]{8x^{2}}\)
45. \(2^{m}2^{n}\)
47. \(−6x\)
49. \(−10 x\sqrt{xy}\)
51. \(12 a^{3} b^{2}\sqrt{ab}\)
53. \(4x^{3}\)
55. \(− 4 a^{ 2} b^{ 2}\sqrt[3]{ab^{2}}\)
Ejercicio\(\PageIndex{3}\) simplifying radical expressions
Reescribe lo siguiente como una expresión radical con coeficiente 1.
- \(5\sqrt{2x}\)
- \(2\sqrt{3y}\)
- \(2x\sqrt{3}\)
- \(3y\sqrt{2}\)
- \(ab\sqrt{10a}\)
- \(2ab\sqrt{2a}\)
- \(m^{2}n\sqrt{mn}\)
- \(2m^{2}n^{3}\sqrt{3n}\)
- \(5\sqrt[3]{2x}\)
- \(3\sqrt[3]{5y}\)
- \(2x\sqrt[3]{3}\)
- \(3y\sqrt[3]{2}\)
- Contestar
-
1. \(\sqrt{50 x}\)
3. \(\sqrt{12 x^{2}}\)
5. \(\sqrt{10 a^{3} b^{2}}\)
7. \(\sqrt{m^{5} n^{3}}\)
9. \(\sqrt[3]{250 x}\)
11. \(\sqrt[3]{24 x^{3}}\)
Ejercicio\(\PageIndex{4}\) simplifying radical expressions
Supongamos que la variable podría representar cualquier número real y luego simplificar.
- \(\sqrt{4x^{2}}\)
- \(\sqrt{25y^{2}}\)
- \(\sqrt[3]{8y^{3}}\)
- \(\sqrt[3]{125a^{3}}\)
- \(\sqrt[4]{64x^{4}}\)
- \(\sqrt[4]{81y^{4}}\)
- \(\sqrt{36a^{4}}\)
- \(\sqrt{100a^{8}}\)
- \(\sqrt{4a^{6}}\)
- \(\sqrt{a^{10}}\)
- \(\sqrt{18a^{4}b^{5}}\)
- \(\sqrt{48a^{5}b^{3}}\)
- \(\sqrt[6]{128x^{6}y^{8}}\)
- \(\sqrt[6]{a^{6}b^{7}c^{8}}\)
- Contestar
-
1. \(2 | x | \)
3. \(2y \)
5. \(2 | x | \)
7. \(6 a^{2}\)
9. \(2| a^{3}|\)
11. \(3 a^{2} b^{2}\sqrt{2 b}\)
13. \(2 |xy |\sqrt[6]{ 2y^{2}}\)
Ejercicio\(\PageIndex{5}\) formulas involving radicals
Las intercepciones y para cualquier gráfica tendrán la forma (0, y), donde y es un número real. Por lo tanto, para encontrar y -intercepciones, establezca x = 0 y resuelva para y. Encuentra las intercepciones y para lo siguiente.
- \(y=\sqrt{x+4}−1\)
- \(y=\sqrt{x+1}−3\)
- \(y=\sqrt[3]{x−1}+2\)
- \(y=\sqrt[3]{x+1}−3\)
- Contestar
-
1. \((0, 1)\)
3. \((0, 1)\)
Ejercicio\(\PageIndex{6}\) formulas involving radicals
Usa la fórmula de distancia para calcular la distancia entre los dos puntos dados.
- \((5, −7)\)y\((3, −8)\)
- \((−9, 7)\)y\((−8, 4)\)
- \((−3, −4)\)y\((3, −6)\)
- \((−5, −2)\)y\((1, −6)\)
- \((−1, 1)\)y\((−4, 10)\)
- \((8, −3)\)y\((2, −12)\)
- Contestar
-
1. \(\sqrt{5}\)
3. \(2\sqrt{10}\)
5. \(3\sqrt{10}\)
Ejercicio\(\PageIndex{7}\) formulas involving radicals
Factorice el radicando y luego simplifique. (Supongamos que todas las expresiones son positivas.)
- \(\sqrt{x^{2}−6x+9}\)
- \(\sqrt{x^{2}−10x+25}\)
- \(\sqrt{4x^{2}+12x+9}\)
- \(\sqrt{9x^{2}+6x+1}\)
- La velocidad de un vehículo antes de que se aplicaran los frenos se puede estimar por la longitud de las marcas de derrape dejadas en la carretera. En pavimento seco, la velocidad, v, en millas por hora se puede estimar por la fórmula\(v=\sqrt{5d}\), donde d representa la longitud de las marcas de derrape en pies. Estime la velocidad de un vehículo antes de aplicar los frenos sobre pavimento seco si las marcas de derrape dejadas miden 36 pies.
- El radio, r, de una esfera se puede calcular usando la fórmula\(r=\sqrt[3]{\frac{3 V}{4 \pi}}\), donde V representa el volumen de la esfera. ¿Cuál es el radio de una esfera si el volumen es de centímetros\(36π\) cúbicos?
- Contestar
-
1. \(x − 3\)
3. \(2 x + 3\)
5. \(30\)millas por hora
Ejercicio\(\PageIndex{8}\) formulas involving radicals
El periodo, T, de un péndulo en segundos viene dado por la fórmula
\(T=2 \pi \sqrt{\frac{L}{32}}\)
donde L representa la longitud en pies. Calcular el periodo, dadas las siguientes duraciones. Dar el valor exacto y el valor aproximado redondeado a la décima de segundo más cercana.
- 8 pies
- 32 pies
- 1/2 pie
- 1/8 pie
- Contestar
-
1. \(π≈3.1\)segundos
3. \(\frac{π}{4} ≈0.8\)segundos
Ejercicio\(\PageIndex{9}\) formulas involving radicals
El tiempo, t, en segundos que un objeto está en caída libre viene dado por la fórmula
\(s=16\cdot t^{2}\)
donde s representa la distancia que ha caído en pies. Calcula el tiempo que tarda un objeto en caer, dadas las siguientes distancias. Dar el valor exacto y el valor aproximado redondeado a la décima de segundo más cercana.
- 48 pies
- 80 pies
- 192 pies
- 288 pies
- Contestar
-
1. \(\sqrt{3} ≈1.7\)segundos
3. \(2\sqrt{3} \approx 3.5\)segundos
Ejercicio\(\PageIndex{10}\) radical functions
Dada la función, calcula lo siguiente.
- \(f(x)=\sqrt{x−1}\), encontrar f (1), f (2) y f (5)
- \(f(x)=\sqrt{x+5}\), encontrar f (−5), f (−1) y f (20)
- \(f(x)=\sqrt{x}+3\), encontrar f (0), f (1) y f (16)
- \(f(x)=\sqrt{x}−5\), encontrar f (0), f (1) y f (25)
- \(g(x)=\sqrt[3]{x}\), encontrar g (−1), g (0) y g (1)
- \(g(x)=\sqrt[3]{x+7}\), encontrar g (−15), g (−7) y g (20)
- \(g(x)=\sqrt[3]{x}−2\), encontrar g (−1), g (0) y g (8)
- \(g(x)=\(\sqrt[3]{x−1}+2\), encontrar g (0), g (2) y g (9)
- Contestar
-
1. \(f(1)=0, f(2)=1\), y\(f(5)=2\)
3. \(f(0)=3, f(1)=4\), y\(f(16)=7\)
5. \(g(−1)=−1, g(0)=0\), y\(g(1)=1\)
7. \(g(−1)=−3, g(0)=−2\), y\(g(8)=0\)
Ejercicio\(\PageIndex{11}\) radical functions
Para cada función, rellene la tabla.
- \(f(x)=\sqrt{x+1}\)
.png)
Figura\(\PageIndex{7}\) - \(f(x)=\sqrt{x−2}\)
.png)
Figura\(\PageIndex{8}\) - \(f(x)=\sqrt[3]{x}+1\)
.png)
Figura\(\PageIndex{9}\) - \(f(x)=\sqrt[3]{x+2}\)
.png)
Figura\(\PageIndex{10}\)
- Contestar
-
1.
.png)
Figura\(\PageIndex{11}\) 3.
.png)
Figura\(\PageIndex{12}\)
Ejercicio\(\PageIndex{12}\) discussion board
- Dar un valor para x tal que\(\sqrt{x^{2}}≠x\). Explique por qué es importante asumir que las variables representan números positivos.
- Investigar y discutir los logros de Christoph Rudolff. ¿Por qué se le atribuye?
- Investigar y discutir los métodos utilizados para calcular raíces cuadradas antes del uso común de las calculadoras electrónicas.
- ¿Qué es un surd y de dónde viene la palabra?
- Contestar
-
1. Las respuestas pueden variar
3. Las respuestas pueden variar


