2.1: Relaciones, Gráficas y Funciones

Última actualización
Guardar como PDF

Page ID: 109885

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Objetivos de aprendizaje

Declarar el dominio y el rango de una relación.
Identificar una función.
Usar notación de función

Gráficas, Relaciones, Dominio y Rango

El sistema de coordenadas rectangulares ¹ consta de dos líneas numéricas reales que se cruzan en ángulo recto. La línea numérica horizontal se llama eje x ², y la línea numérica vertical se llama eje y ³. Estas dos líneas numéricas definen una superficie plana llamada plano ⁴, y cada punto en este plano está asociado con un par ordenado ⁵ de números reales$(x, y)$. El primer número se llama la$x$ coordenada -y el segundo número se llama la$y$ coordenada -. La intersección de los dos ejes se conoce como el origen ⁶, que corresponde al punto$(0, 0)$.

Los$y$ ejes$x$ - y -rompen el plano en cuatro regiones llamadas cuadrantes ⁷, nombradas usando los números romanos I, II, III y IV, como se muestra en la imagen. El par ordenado$(x, y)$ representa la posición de los puntos relativos al origen. Por ejemplo, el par ordenado$(−4, 3)$ representa las$4$ unidades de posición a la izquierda del origen, y$3$ las unidades arriba en el segundo cuadrante.

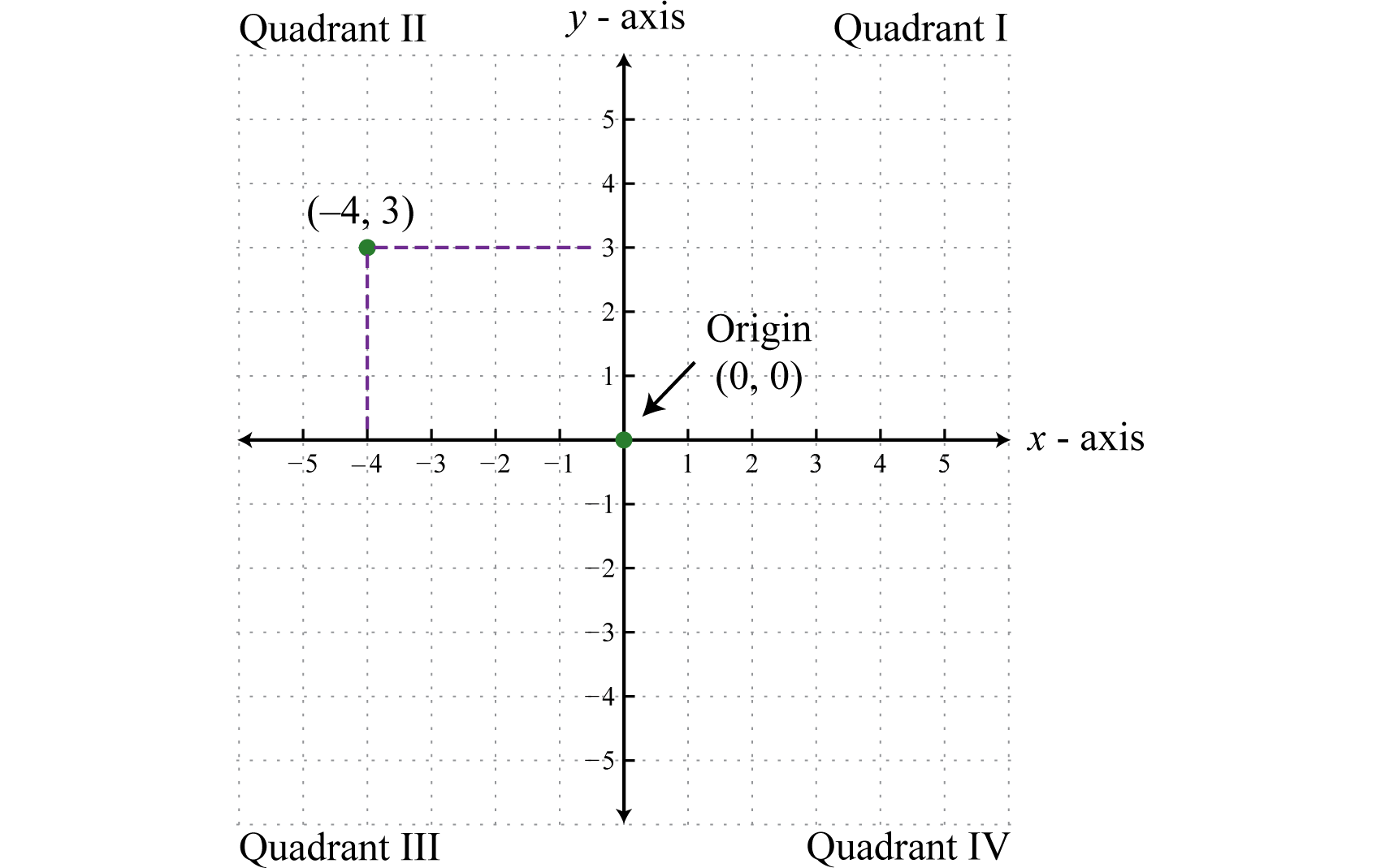
Este sistema suele llamarse sistema de coordenadas cartesianas ⁸, llamado así por el matemático francés René Descartes (1596—1650).

A continuación, definimos una relación ⁹ como cualquier conjunto de pares ordenados. En el contexto del álgebra, las relaciones de interés son conjuntos de pares ordenados$(x, y)$ en el plano de coordenadas rectangulares. Normalmente, las coordenadas están relacionadas por una regla expresada usando una ecuación algebraica. Por ejemplo, tanto las ecuaciones$y = |x| − 2$ algebraicas como$x = |y| + 1$ definir las relaciones entre$x$ y$y$. A continuación se presentan algunos números enteros que satisfacen ambas ecuaciones:

Aquí se obtienen dos relaciones que constan de siete soluciones de pares ordenados:

$y=|x|−2 has solutions \{(−3,1),(−2,0),(−1,−1),(0,−2),(1,−1),(2,0),(3,1)\}$

$and$

$x=|y|+1 has solutions \{(4,−3),(3,−2),(2,−1),(1,0),(2,1),(3,2),(4,3)\}$

Podemos mostrar visualmente cualquier relación de este tipo en un plano de coordenadas trazando los puntos.

Los conjuntos de soluciones de cada ecuación formarán una relación que consiste en infinitamente muchos pares ordenados. Podemos usar las soluciones de pares ordenados dadas para estimar todos los demás pares ordenados dibujando una línea a través de los puntos dados. Aquí ponemos una flecha en los extremos de nuestras líneas para indicar que este conjunto de pares ordenados continúa sin límites.

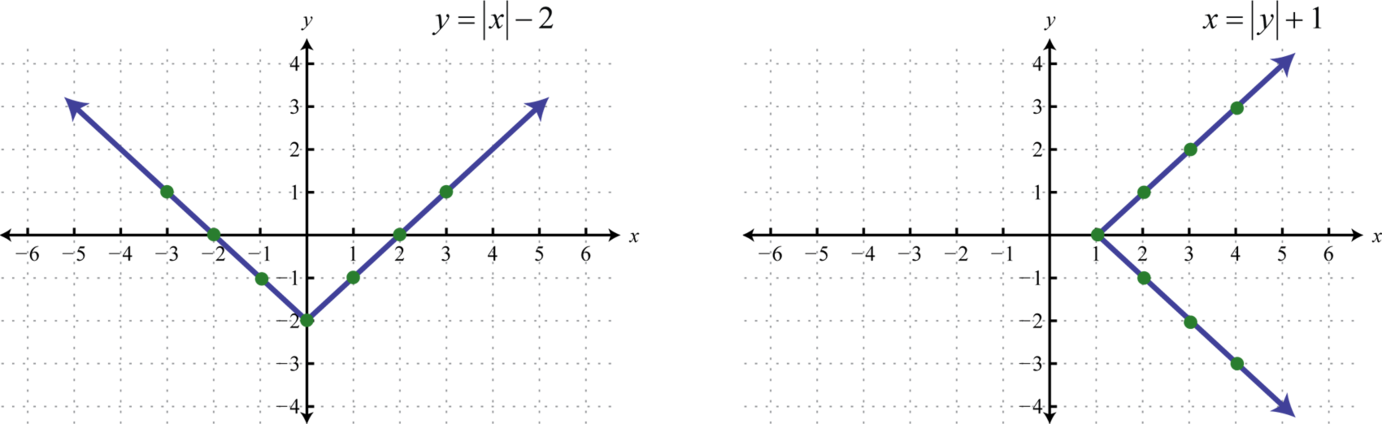
La representación de una relación en un plano de coordenadas rectangular, como se ilustra anteriormente, se denomina gráfica ¹⁰. Cualquier curva graficada en un plano de coordenadas rectangular representa un conjunto de pares ordenados y, por lo tanto, define una relación.

El conjunto que consiste en todos los primeros componentes de una relación, en este caso los valores x, se denomina dominio ¹¹. Y el conjunto que consiste en todos los segundos componentes de una relación, en este caso los valores y, se denomina rango ¹² (o codominio ¹³). A menudo, podemos determinar el dominio y el rango de una relación si se nos da su gráfica.

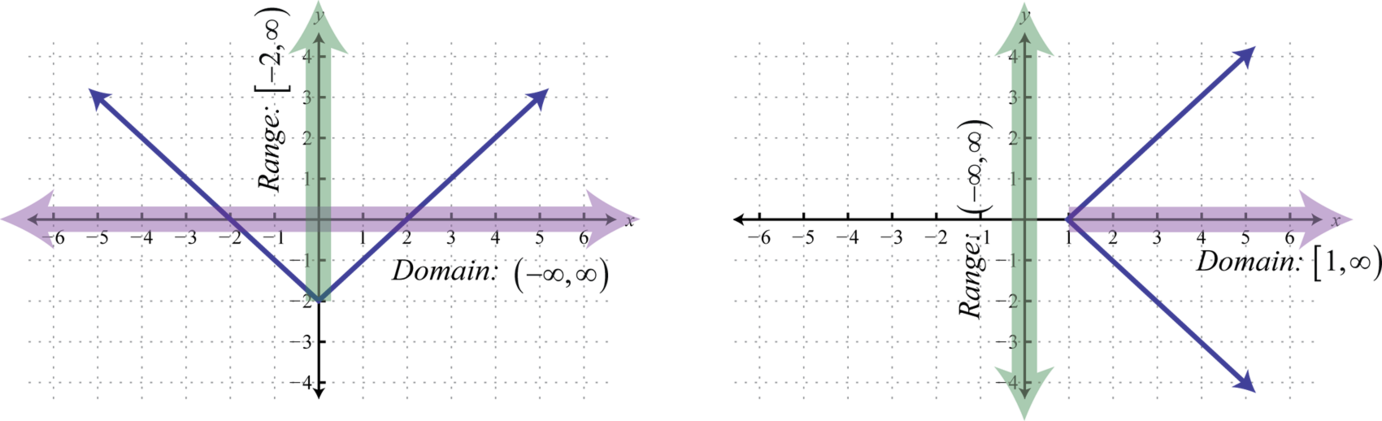
Aquí podemos ver que la gráfica de$y=|x|−2$ tiene un dominio que consiste en todos los números reales$ℝ=(−∞,∞)$,, y un rango de todos los valores y mayores o iguales a$−2, [−2,∞)$. El dominio de la gráfica de$x=|y|+1$ consiste en todos los x -valores mayores o iguales a$1, [1,∞)$, y el rango consiste en todos los números reales,$ℝ=(−∞,∞)$.

Ejemplo$\PageIndex{1}$:

Determine el dominio y el rango de la siguiente relación:

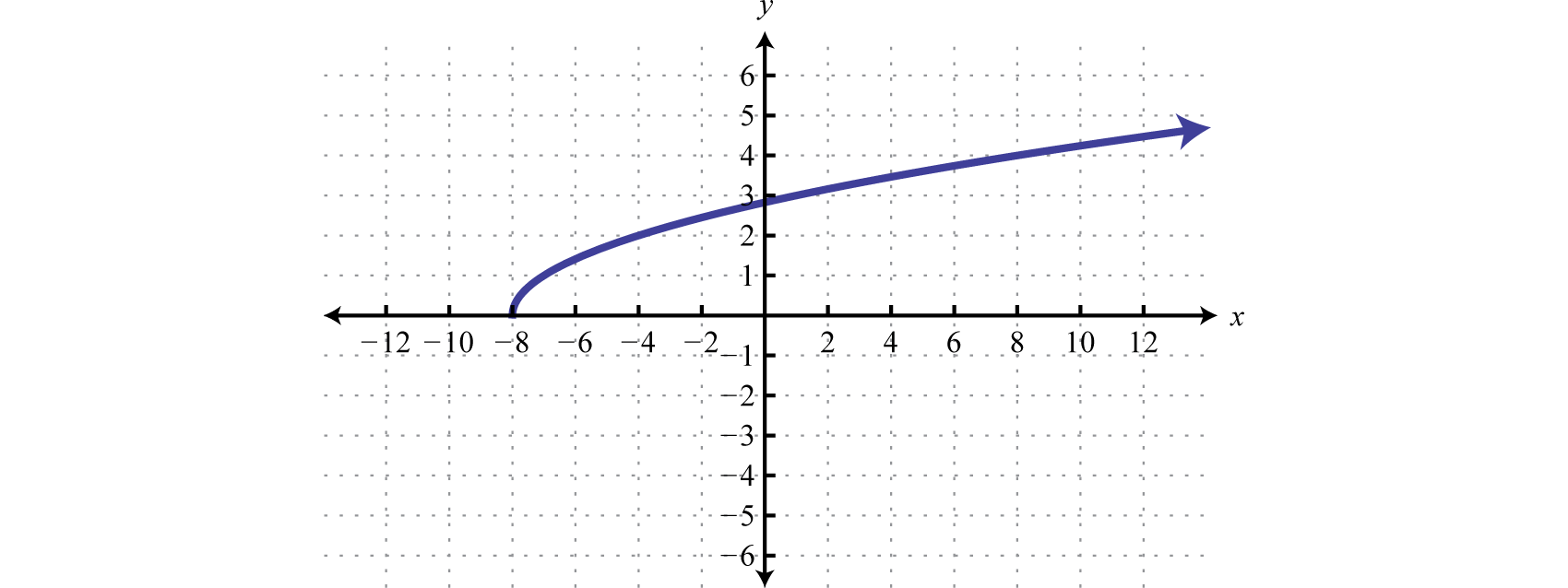
Solución

El$x$ valor mínimo representado en la gráfica es que$−8$ todos los demás son mayores. Por lo tanto, el dominio consiste en todos$x$ los -valores en el intervalo$[−8,∞)$. El$y$ valor mínimo representado en la gráfica es$0$; así, el rango es$[0,∞)$.

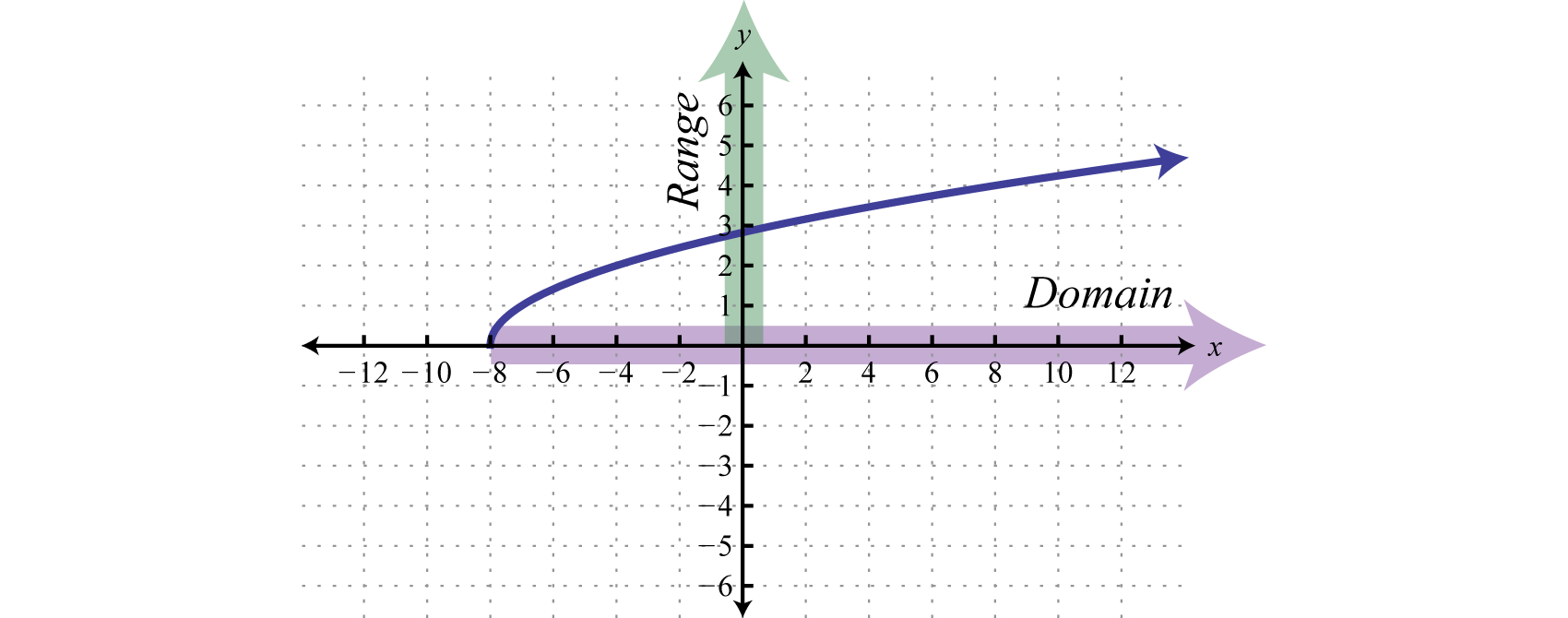
Respuesta:

Dominio:$[−8,∞)$; rango:$[0,∞)$

Funciones

De especial interés son las relaciones donde cada$x$ -valor corresponde exactamente a un$y$ -valor. Una relación con esta propiedad se llama función ¹⁴.

Ejemplo$\PageIndex{2}$:

Determine el dominio y rango de la siguiente relación y establezca si es una función o no:$\{(−1, 4), (0, 7), (2, 3), (3, 3), (4, −2)\}$

Solución

Aquí separamos el dominio (valores x), y el rango (valores y), y representamos la correspondencia entre los valores con flechas.

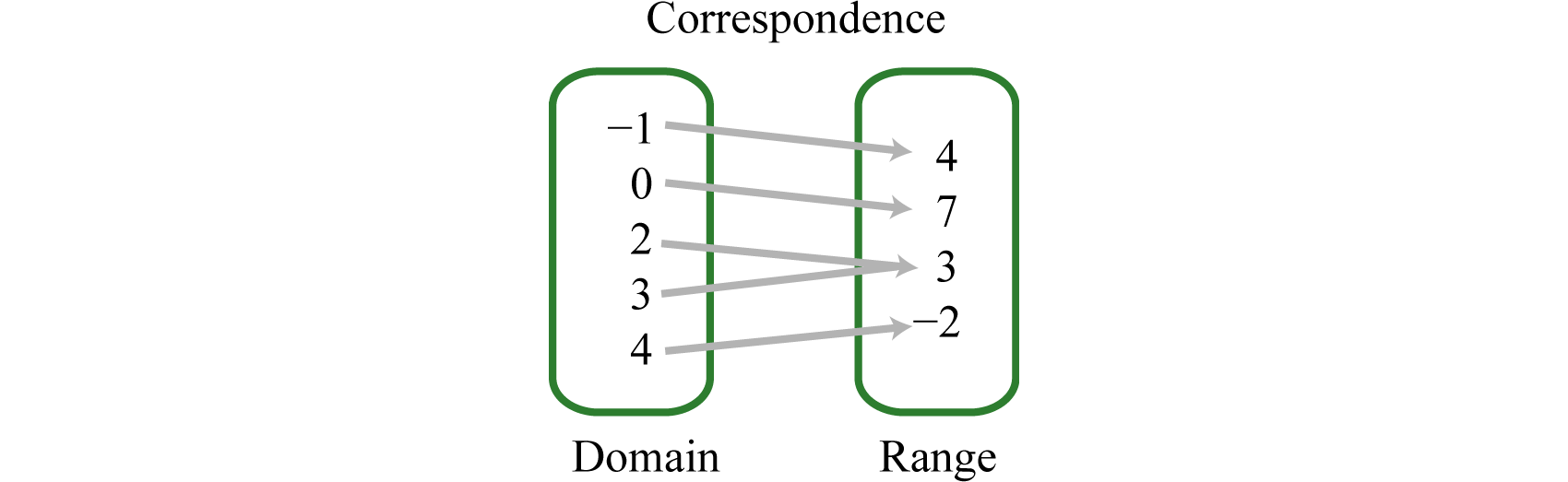
La relación es una función porque cada valor x corresponde exactamente a un valor y.

Respuesta:

El dominio es$\{−1, 0, 2, 3, 4\}$ y el rango es$\{−2, 3, 4, 7\}$. La relación es una función.

Ejemplo$\PageIndex{3}$:

Determine el dominio y rango de la siguiente relación y establezca si es una función o no:$\{(−4, −3), (−2, 6), (0, 3), (3, 5), (3, 7)\}$

Solución

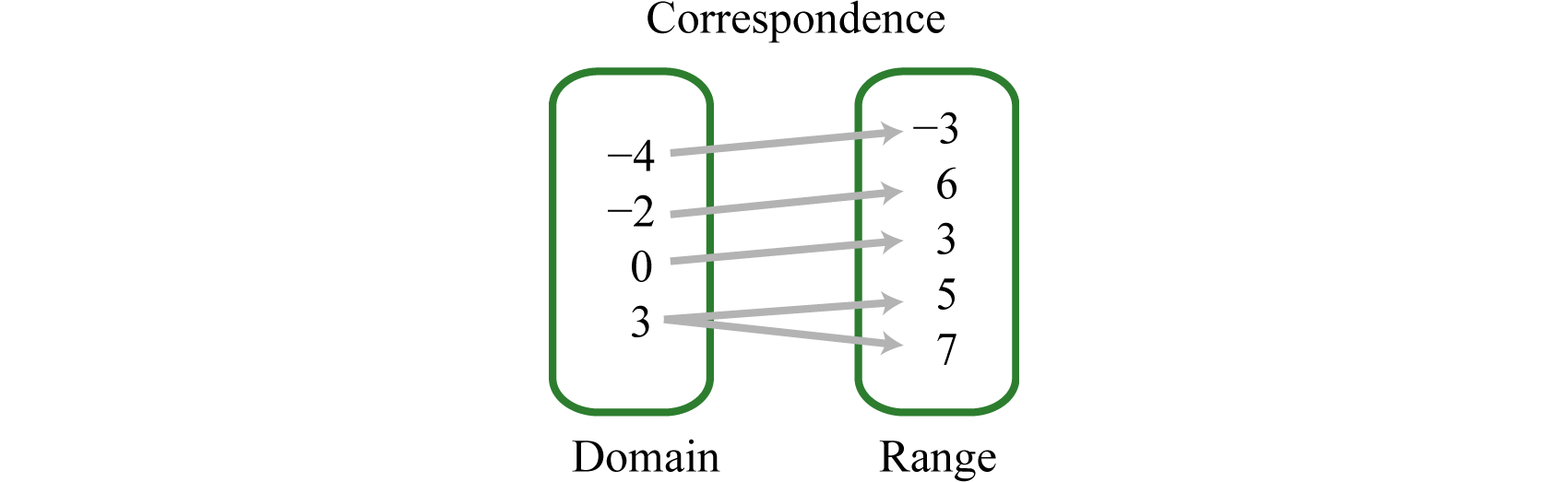
La relación dada no es una función porque el$x$ -value$3$ corresponde a dos$y$ -valores. También podemos reconocer funciones como relaciones donde no se repiten$x$ valores.

Respuesta:

El dominio es$\{−4, −2, 0, 3\}$ y el rango es$\{−3, 3, 5, 6, 7\}$. Esta relación no es una función.

Considerar las relaciones que consisten en las siete soluciones de pares ordenados a$y = |x| − 2 $ y$x = |y| + 1$. La correspondencia entre el dominio y el rango de cada uno se puede representar de la siguiente manera:

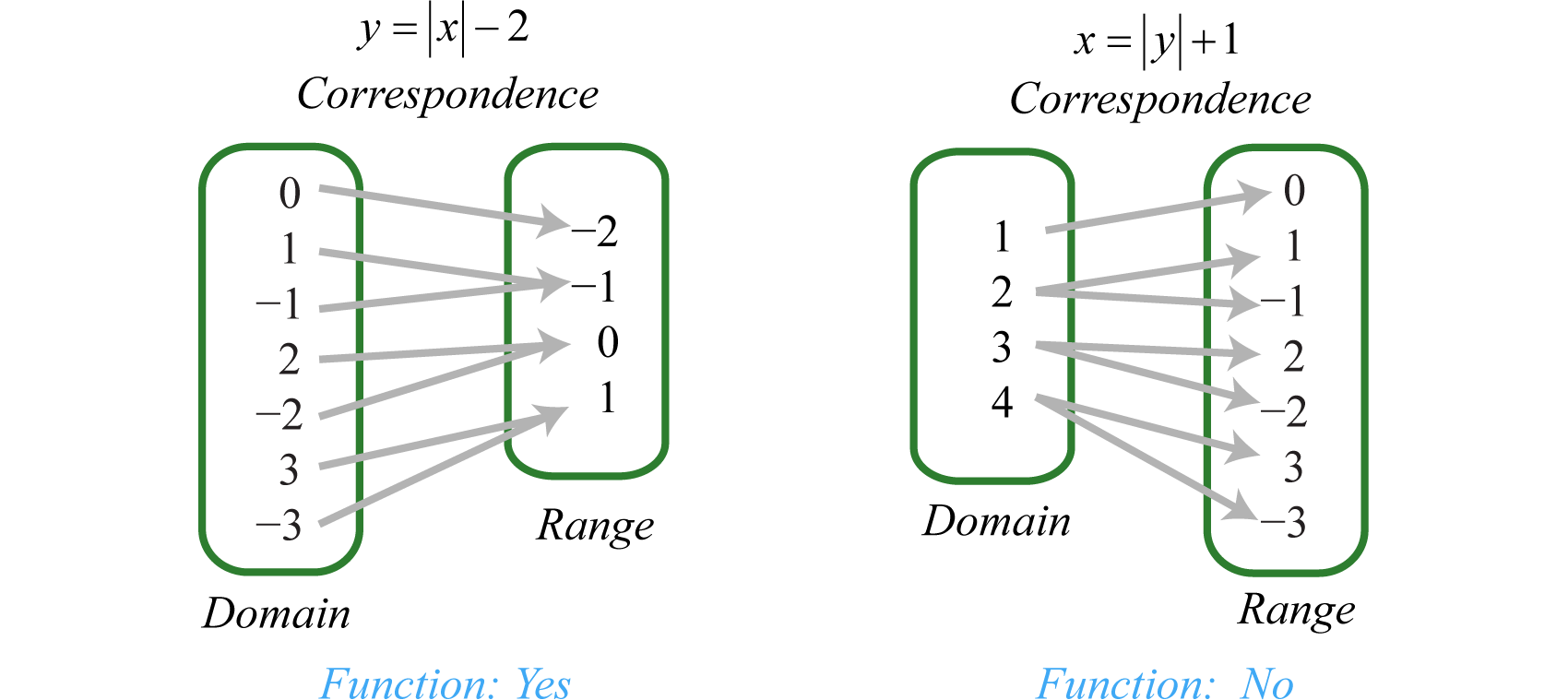
Observe que cada elemento en el dominio del conjunto de soluciones de$y = |x| − 2$ corresponde a un solo elemento en el rango; es una función. Las soluciones para$x = |y| + 1$, por otro lado, tener valores en el dominio que corresponden a dos elementos en el rango. En particular, el valor x$4$ corresponde a dos valores$−3$ y y$3$. Por lo tanto,$x = |y| + 1$ no define una función.

Podemos identificar visualmente funciones por sus gráficas usando la prueba de línea vertical ¹⁵. Si alguna línea vertical cruza la gráfica más de una vez, entonces la gráfica no representa una función.

La línea vertical representa un valor en el dominio, y el número de intersecciones con la gráfica representa el número de valores a los que corresponde. Como podemos ver, cualquier línea vertical cruzará la gráfica de una$y=|x|−2$ sola vez; por lo tanto, es una función. Una línea vertical puede cruzar la gráfica de$x=|y|+1$ más de una vez; por lo tanto, no es una función. Como se muestra en la imagen, el$x$ valor$3$ -corresponde a más de un$y$ valor.

Ejemplo$\PageIndex{1}$:

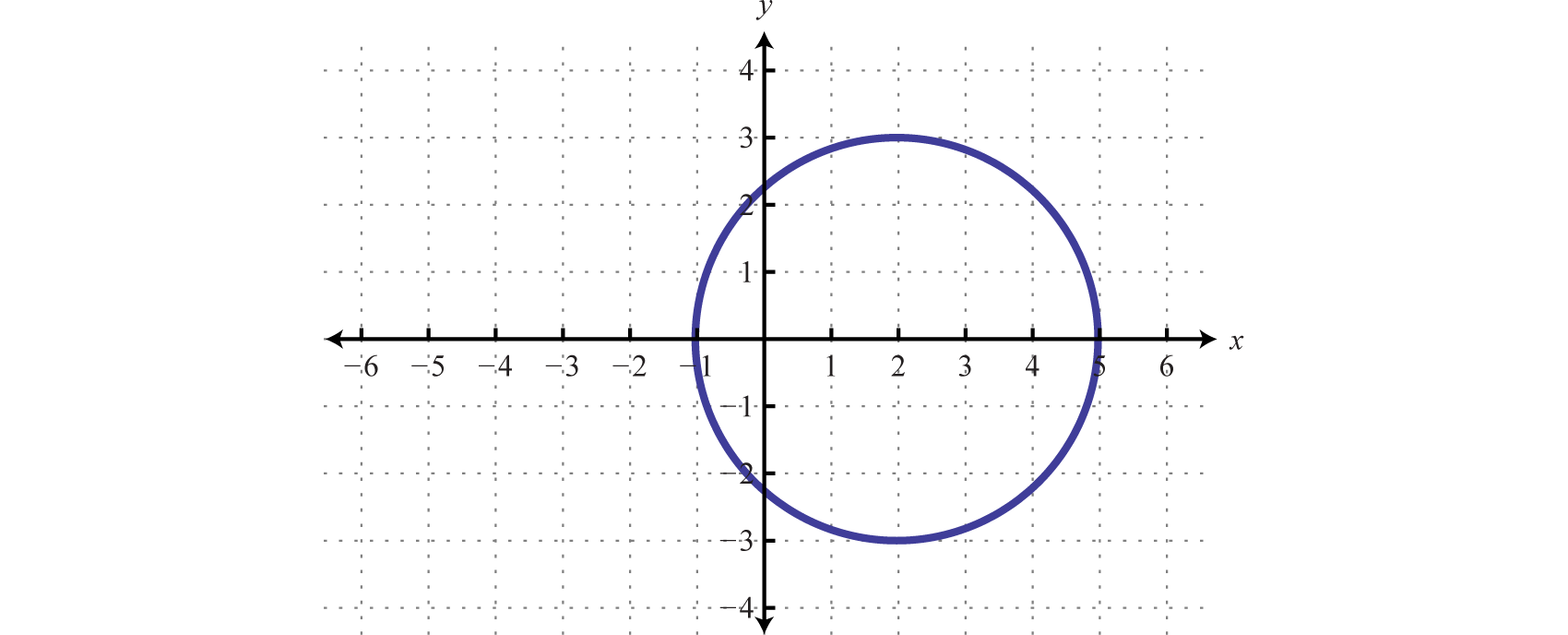
Dada la gráfica, indique el dominio y el rango y determine si representa o no una función:

Solución

De la gráfica podemos ver que el$x$ valor mínimo es$−1$ y el$x$ valor máximo es$5$. De ahí que el dominio esté formado por todos los números reales en el conjunto de$[−1,5]$. El$y$ valor máximo es$3$ y el mínimo es$−3$; por lo tanto, el rango consiste en$y$ -valores en el intervalo$[−3,3]$.

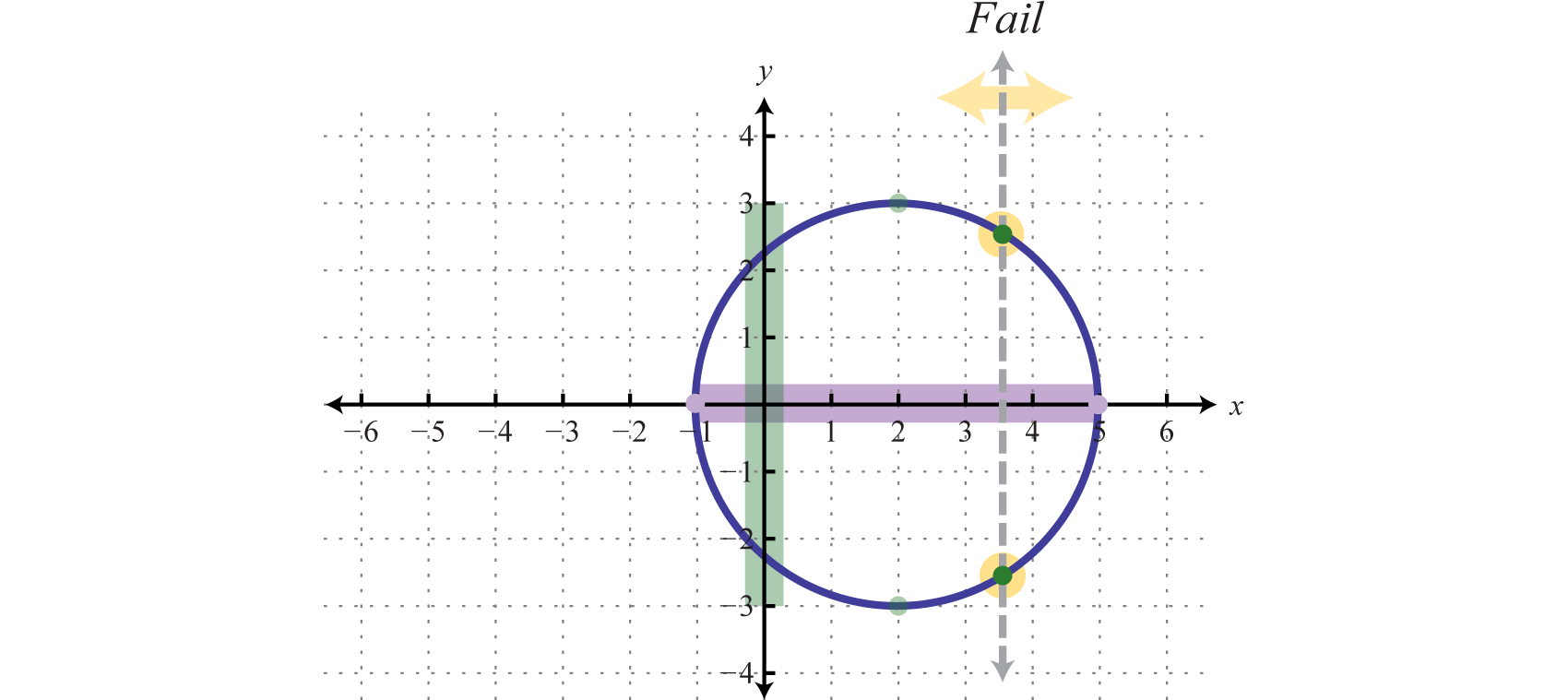
Además, dado que podemos encontrar una línea vertical que intersecta la gráfica más de una vez, concluimos que la gráfica no es una función. Hay muchos$x$ -valores en el dominio que corresponden a dos$y$ -valores.

Respuesta:

Dominio:$[−1,5]$; rango:$[−3,3]$; función: no

Ejercicio$\PageIndex{1}$

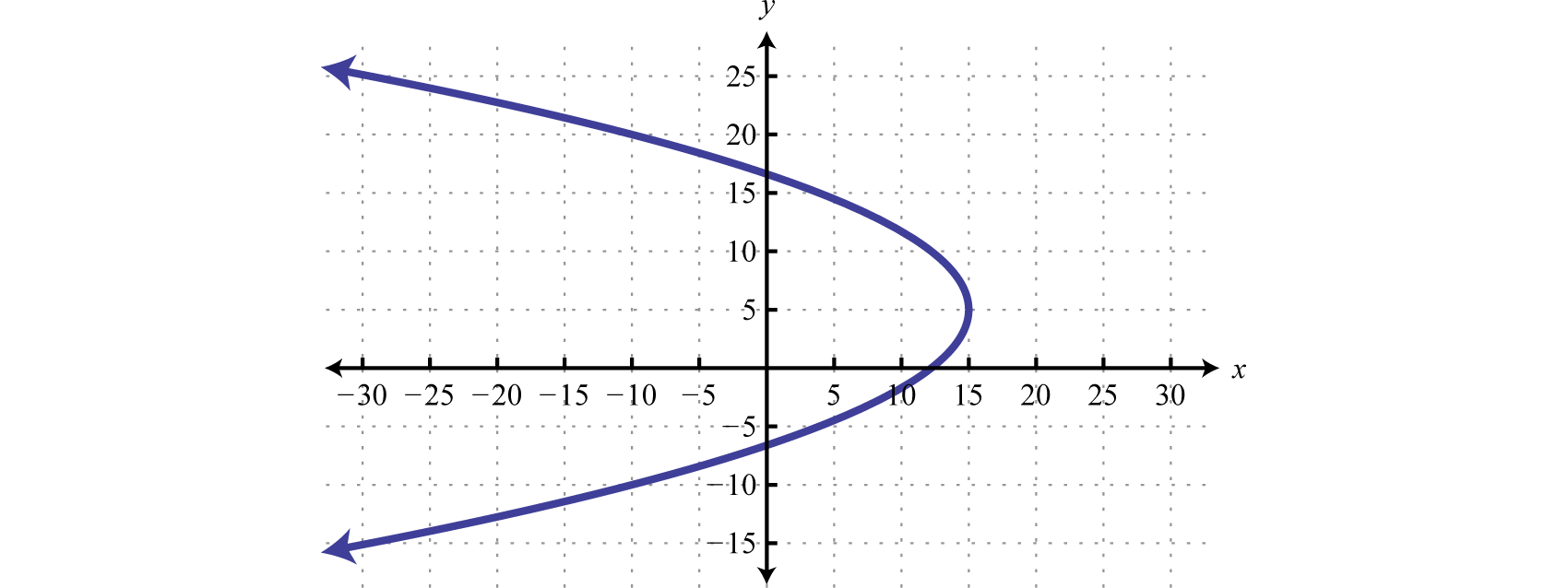
Dada la gráfica, determinar el dominio y el rango y declarar si es o no una función:

Contestar

Dominio:$(−∞,15]$; rango:$ℝ$; función: no

www.youtube.com/v/uetvdkjvsx8

Notación de funciones

Con la definición de una función viene notación especial. Si consideramos que cada valor x es la entrada que produce exactamente una salida, entonces podemos usar la notación de función ¹⁶:

$f ( x ) = y$

La notación$f(x)$ dice, “f de x” y no debe confundirse con la multiplicación. El álgebra frecuentemente involucra funciones, por lo que la notación se vuelve útil al realizar tareas comunes. Aquí$f$ está el nombre de la función, y$f (x)$ denota el valor en el rango asociado con el valor x en el dominio. Las funciones a menudo se nombran con letras diferentes; algunos nombres comunes para las funciones son$f, g, h, C$, y$R$. Hemos determinado que el conjunto de soluciones a$y = |x| − 2$ es una función; por lo tanto, usando la notación de funciones podemos escribir:

$\begin{aligned} y & = | x | - 2 \\ \color{Cerulean}{\downarrow} & \\ f ( x ) & = | x | - 2 \end{aligned}$

Es importante señalar que$y$ y$f(x)$ se utilizan indistintamente. Esta notación se utiliza de la siguiente manera:

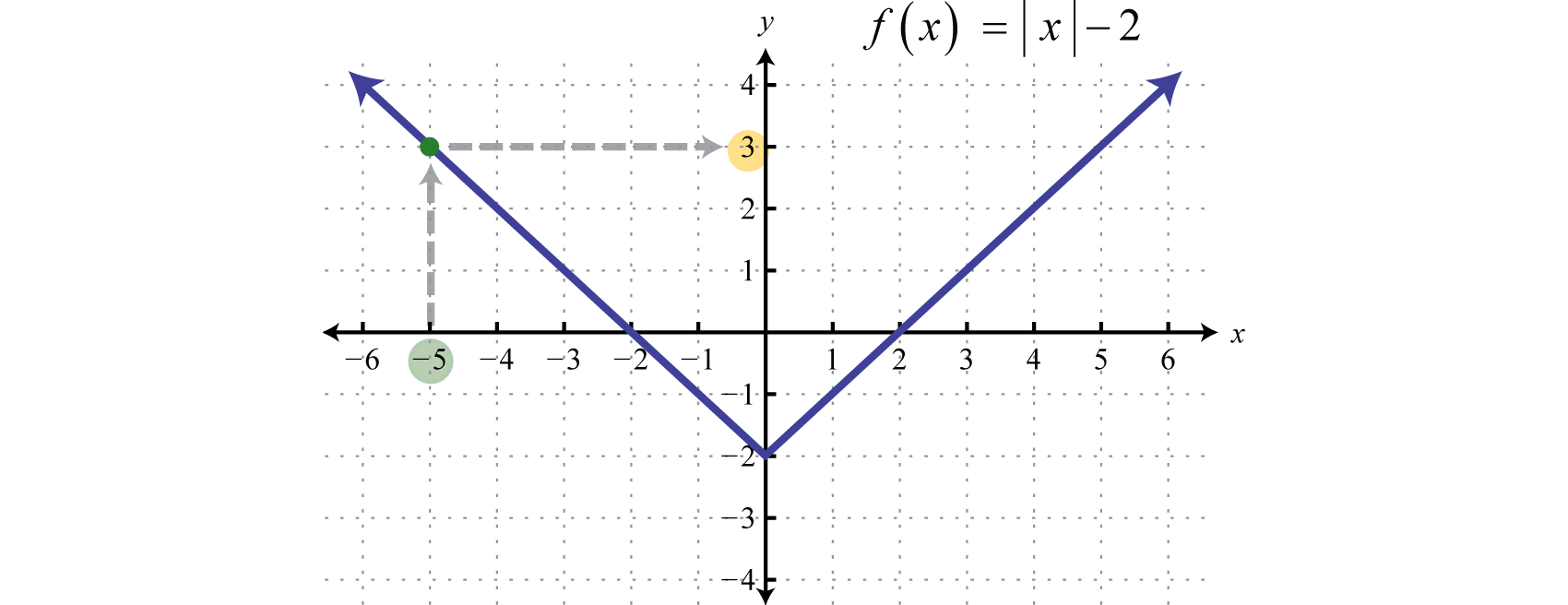
$\begin{array} { l } { f ( x )\:\: =\:\:\: | x | - 2 } \\ { \:\:\:\:\:\downarrow \quad\quad\quad \downarrow } \\ { f ( \color{Cerulean}{- 5}\color{Black}{ )} = | \color{Cerulean}{- 5}\color{Black}{ |} - 2 = 5 - 2 = 3 } \end{array}$

Aquí la notación compacta$f(−5) = 3$ indica que donde$x = −5$ (la entrada), la función da como resultado$y = 3$ (la salida). En otras palabras, reemplace la variable con el valor dado dentro de los paréntesis.

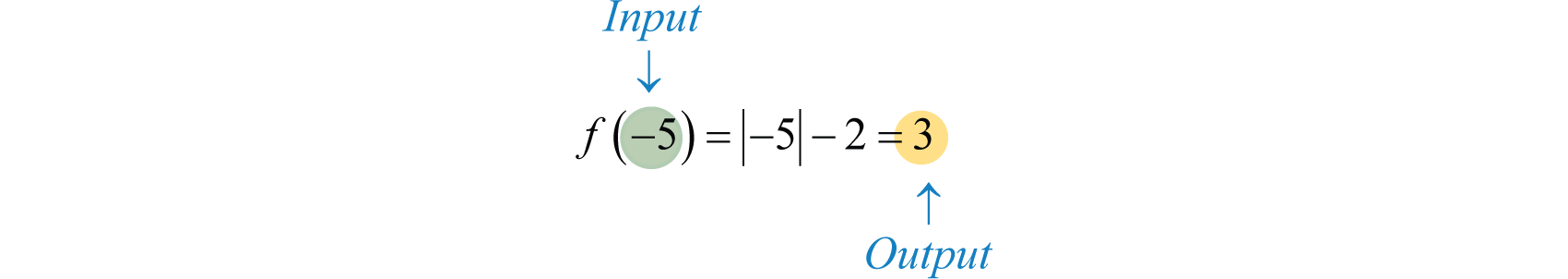
Las funciones se definen de forma compacta por una ecuación algebraica, como$f (x) = |x| − 2$. Dados los valores para$x$ en el dominio, podemos calcular rápidamente los valores correspondientes en el rango. Como hemos visto, las funciones también se expresan mediante gráficas. En este caso, interpretamos de la$f(−5) = 3$ siguiente manera:

La notación de funciones agiliza la tarea de evaluar. Por ejemplo, utilice la función$h$ definida por$h (x) = \frac{1}{2} x − 3$ para evaluar$x$ los valores -en el conjunto$\{−2, 0, 7\}$.

$\begin{array} { c } { h ( \color{Cerulean}{- 2}\color{Black}{ )} = \frac { 1 } { 2 } ( \color{Cerulean}{- 2}\color{Black}{ )} - 3 = - 1 - 3 = - 4 } \\ { h ( \color{Cerulean}{0}\color{Black}{ )} = \frac { 1 } { 2 } ( \color{Cerulean}{0}\color{Black}{ )} - 3 = 0 - 3 = - 3 } \\ { h ( \color{Cerulean}{7}\color{Black}{ )} = \frac { 1 } { 2 } ( \color{Cerulean}{7}\color{Black}{ )} - 3 = \frac { 7 } { 2 } - 3 = \frac { 1 } { 2 } } \end{array}$

Dada cualquier función definida por$h(x) = y$, el valor$x$ se llama el argumento de la función ¹⁷. El argumento puede ser cualquier expresión algebraica. Por ejemplo:

$\begin{aligned} h ( \color{Cerulean}{4 a ^ { 3 }}\color{Black}{ )} & = \frac { 1 } { 2 } ( \color{Cerulean}{4 a ^ { 3 } }\color{Black}{)} - 3 = 2 a ^ { 3 } - 3 \\ h ( \color{Cerulean}{2 x - 1}\color{Black}{ )} & = \frac { 1 } { 2 } ( \color{Cerulean}{2 x - 1}\color{Black}{ )} - 3 = x - \frac { 1 } { 2 } - 3 = x - \frac { 7 } { 2 } \end{aligned}$

Ejemplo$\PageIndex{5}$:

Dado$g ( x ) = x ^ { 2 }$, encontrar$g (−2), g ( \frac{1}{2} )$, y$g (x + h)$.

Solución

Recordemos que al evaluar, es una buena práctica comenzar reemplazando las variables por paréntesis y luego sustituir los valores apropiados. Esto ayuda con el orden de las operaciones a la hora de simplificar las expresiones.

$\begin{aligned} g ( \color{Cerulean}{- 2}\color{Black}{ )} & = ( \color{Cerulean}{- 2}\color{Black}{ )} ^ { 2 } = 4 \\ g ( \color{Cerulean}{\frac { 1 } { 2 }}\color{Black}{)} & = ( \color{Cerulean}{\frac { 1 } { 2 }} \color{Black}{)} ^ { 2 } = \frac { 1 } { 4 } \\ g (\color{Cerulean}{ x + h}\color{Black}{ )} & = ( \color{Cerulean}{x + h}\color{Black}{ )} ^ { 2 } = x ^ { 2 } + 2 x h + h ^ { 2 } \end{aligned}$

Respuesta:

$g (−2) = 4,\: g ( \frac{1}{2} ) = \frac{1}{4} ,\: g (x + h) = x^{2} + 2xh + h^{2}$

En este punto, es importante señalar que, en general,$f (x + h) ≠ f (x) + f (h)$. El ejemplo anterior, donde$g (x) = x^{2}$, ilustra esto muy bien

$\begin{array} { l } { g ( x + h ) \neq g ( x ) + g ( h ) } \\ { ( x + h ) ^ { 2 } \neq x ^ { 2 } + h ^ { 2 } } \end{array}$

Ejemplo$\PageIndex{6}$:

Dado$f ( x ) = \sqrt { 2 x + 4 }$, encontrar$f (−2), f (0)$, y$f \left( \frac { 1 } { 2 } a ^ { 2 } - 2 \right)$.

Solución

$\begin{aligned} f ( \color{Cerulean}{- 2}\color{Black}{ )} & = \sqrt { 2 ( \color{Cerulean}{- 2}\color{Black}{ )} + 4 } = \sqrt { - 4 + 4 } = \sqrt { 0 } = 0 \\ f ( \color{Cerulean}{0}\color{Black}{ )} & = \sqrt { 2 ( \color{Cerulean}{0}\color{Black}{ )} + 4 } = \sqrt { 0 + 4 } = \sqrt { 4 } = 2 \\ f ( \color{Cerulean}{\frac { 1 } { 2 } a ^ { 2 } - 2}\color{Black}{ )} & = \sqrt { 2( \color{Cerulean}{ \frac { 1 } { 2 } a ^ { 2 } - 2}\color{Black}{)} + 4 } = \sqrt { a ^ { 2 } - 4 + 4 } = \sqrt { a ^ { 2 } } = | a | \end{aligned}$

Respuesta:

$f (−2) = 0,\: f (0) = 2,\: f \left( \frac { 1 } { 2 } a ^ { 2 } - 2 \right)= |a|$

Ejemplo$\PageIndex{7}$:

Dada la gráfica de$g(x)$, encontrar$g(−8), g(0)$, y$g(8)$.

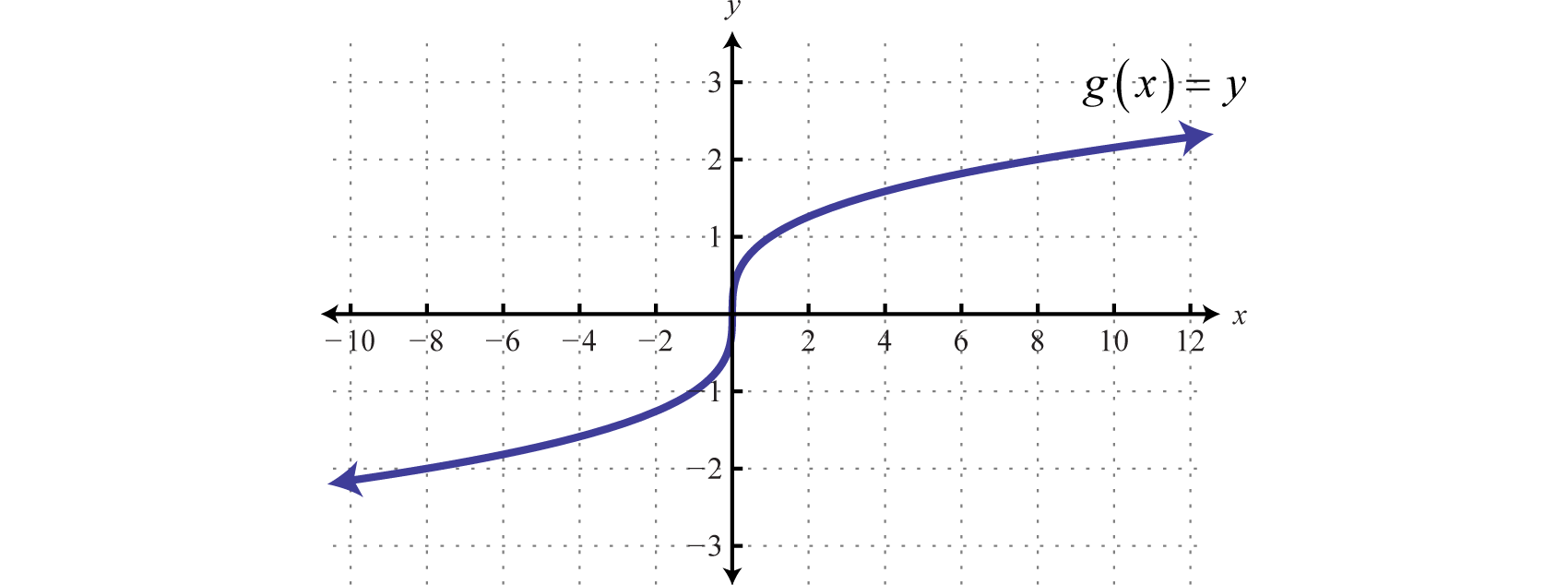
Solución

Utilice la gráfica para encontrar los$y$ valores -correspondientes donde$x = −8, 0$, y$8$.

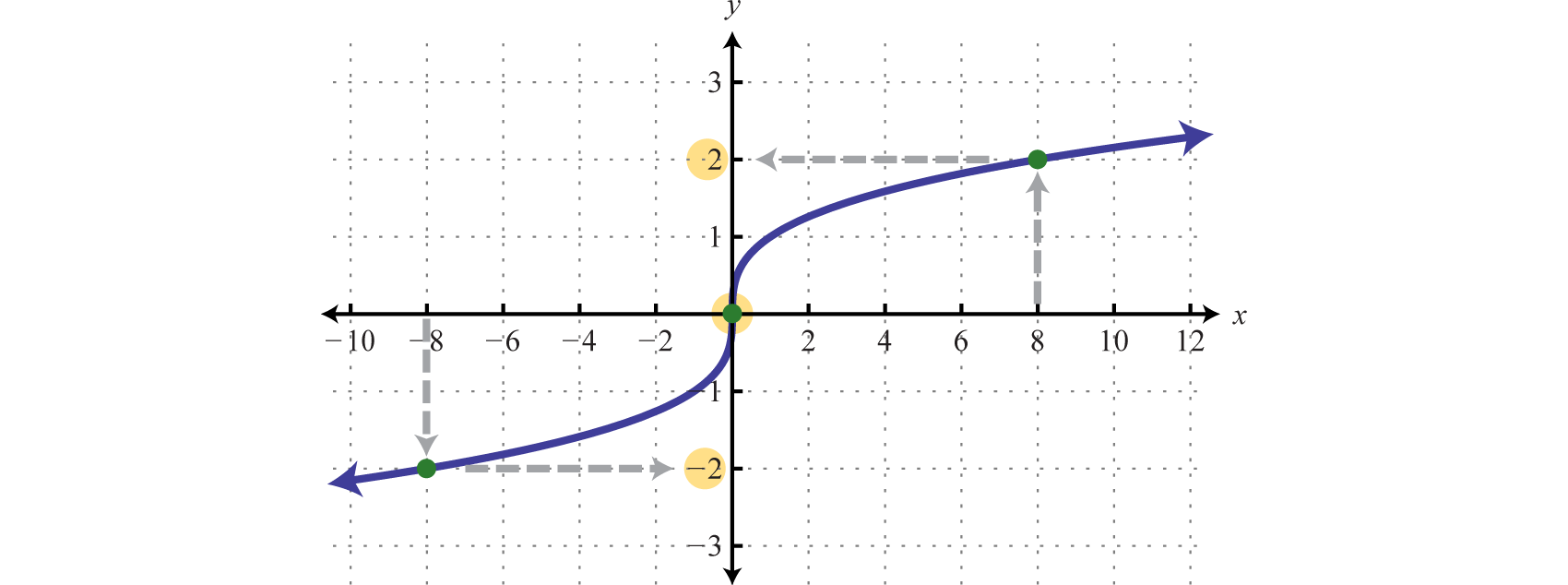
Respuesta:

$g(−8)=−2,\: g(0)=0,\: g(8)=2$

A veces se da la salida y se nos pide que encontremos la entrada.

Ejemplo$\PageIndex{8}$:

Dado$f (x) = 5x + 7$, encuentra$x$ dónde$f (x) = 27$.

Solución

En este ejemplo, se da la salida y se nos pide encontrar la entrada. Sustituir$f (x)$ con$27$ y resolver.

$\begin{array} { c } { f ( x ) = 5 x + 7 }\\\color{Cerulean}{\downarrow}\quad\quad\quad\:\:\: \\ { 27 = 5 x + 7 } \\ { 20 = 5 x } \\ { 4 = x } \end{array}$

Por lo tanto,$f (4) = 27$. Como cheque, podemos evaluar$f (4) = 5 (4) + 7 = 27$.

Respuesta:

$x = 4$

Ejemplo$\PageIndex{9}$:

Dada la gráfica de$g$, encuentra$x$ dónde$g(x)=2$.

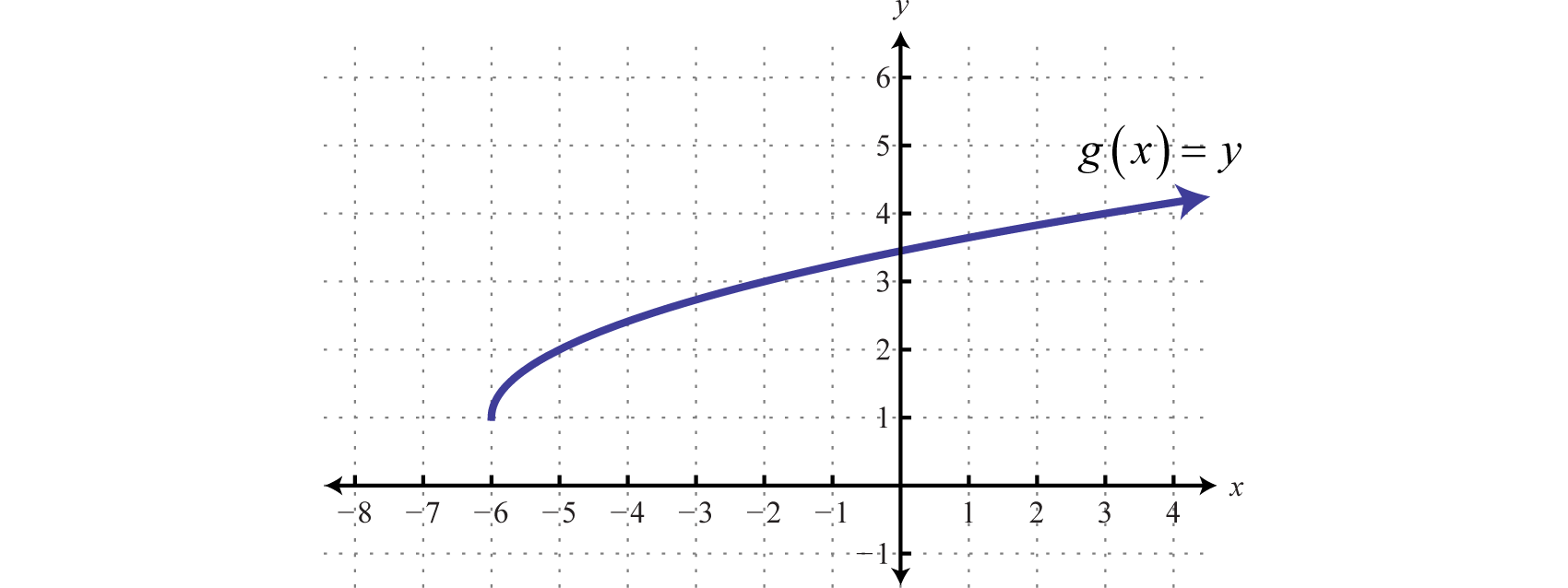
Solución

Aquí se nos pide encontrar el valor x dado un valor y particular. Comenzamos con 2 en el eje y y luego leemos el valor x correspondiente.

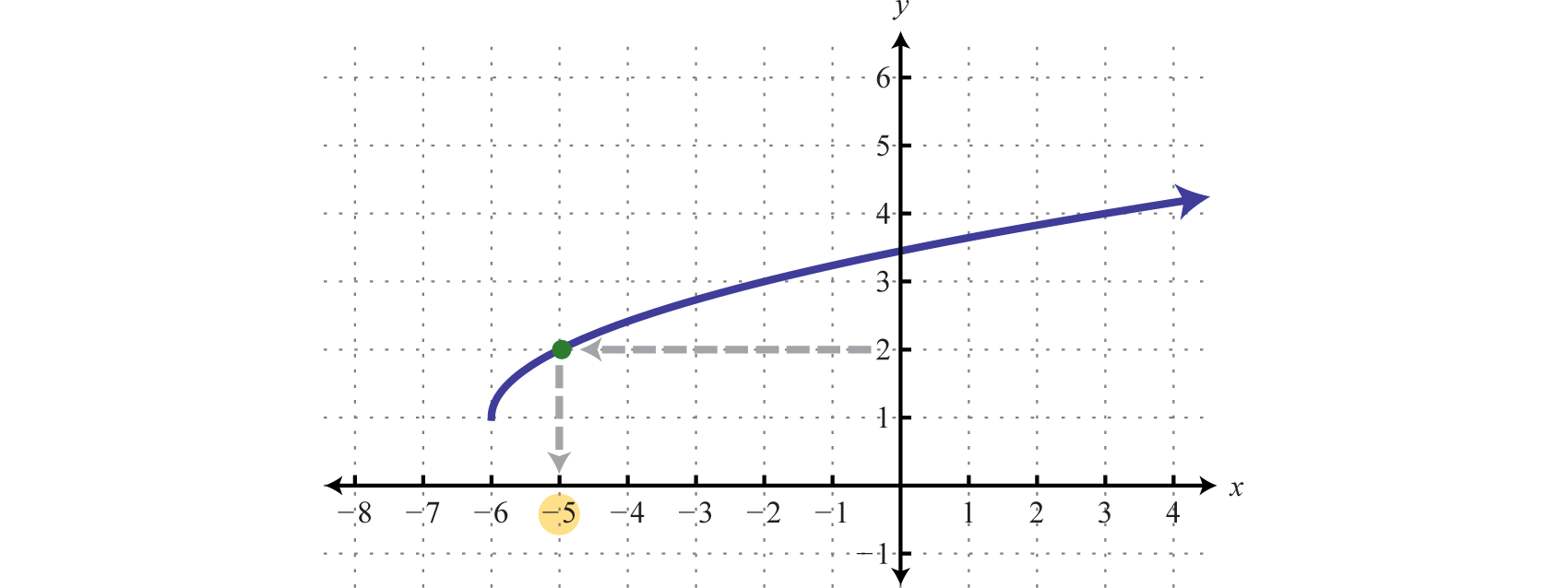
Podemos ver que$g(x)=2$ donde$x=−5$; en otras palabras,$g(−5)=2$.

Respuesta:

$ x=−5$

Ejercicio$\PageIndex{2}$

Dada la gráfica de$h$, encontrar$x$ dónde$h(x)=-4$

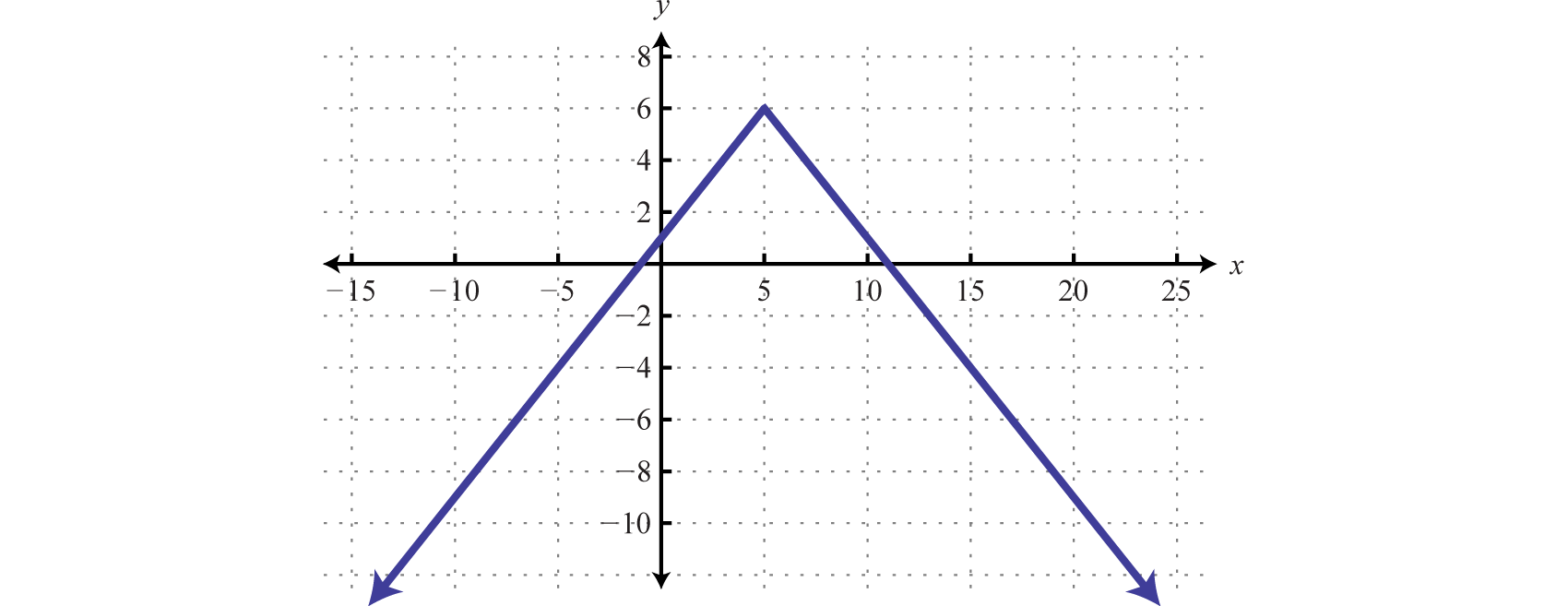
Contestar

$x=-15$y$x=15$

www.youtube.com/v/ntvyMlfpqws

Claves para llevar

Una relación es cualquier conjunto de pares ordenados. No obstante, en este curso, estaremos trabajando con conjuntos de pares ordenados$(x, y)$ en el sistema de coordenadas rectangulares. El conjunto de$x$ valores define el dominio y el conjunto de$y$ -valores define el rango.
Las relaciones especiales donde cada$x$ -valor (entrada) corresponde exactamente a un$y$ -valor (salida) se llaman funciones.
Podemos determinar fácilmente si una ecuación representa o no una función realizando la prueba de línea vertical en su gráfica. Si alguna línea vertical cruza la gráfica más de una vez, entonces la gráfica no representa una función.
Si una ecuación algebraica define una función, entonces podemos usar la notación$f (x) = y$. La notación$f (x)$ se lee “f de x” y no debe confundirse con la multiplicación. Al trabajar con funciones, es importante recordarlo$y$ y$f (x)$ se usan indistintamente.
Si se le pide encontrar$f(a)$, sustituimos el argumento por$a$ la variable y luego simplificamos. El argumento podría ser una expresión algebraica.
Si se le pide encontrar$x$ dónde$f(x) = a$, establecemos la función igual a$a$ y luego resolvemos para$x$.

Ejercicio$\PageIndex{3}$

Determinar el dominio y el rango y establecer si la relación es una función o no.

$\{ ( 3,1 ) , ( 5,2 ) , ( 7,3 ) , ( 9,4 ) , ( 12,4 ) \}$
$\{ ( 2,0 ) , ( 4,3 ) , ( 6,6 ) , ( 8,6 ) , ( 10,9 ) \}$
$\{ ( 7,5 ) , ( 8,6 ) , ( 10,7 ) , ( 10,8 ) , ( 15,9 ) \}$
$\{ ( 1,1 ) , ( 2,1 ) , ( 3,1 ) , ( 4,1 ) , ( 5,1 ) \}$
$\{ ( 5,0 ) , ( 5,2 ) , ( 5,4 ) , ( 5,6 ) , ( 5,8 ) \}$
$\{ ( - 3,1 ) , ( - 2,2 ) , ( - 1,3 ) , ( 0,4 ) , ( 0,5 ) \}$

10.

11.

12.

13.

14.

15.

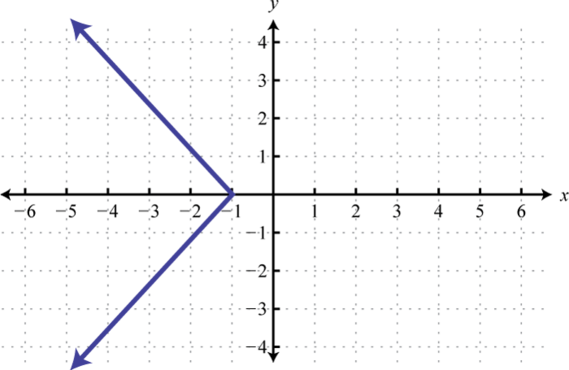
16.

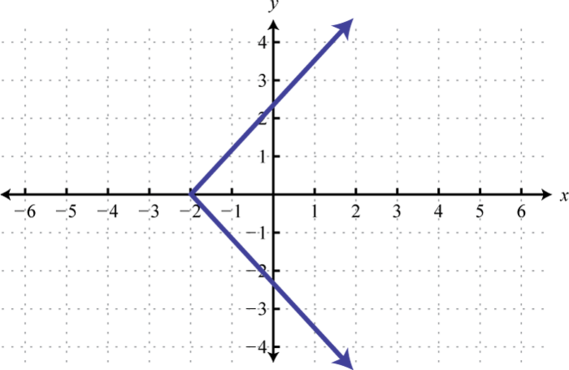
17.

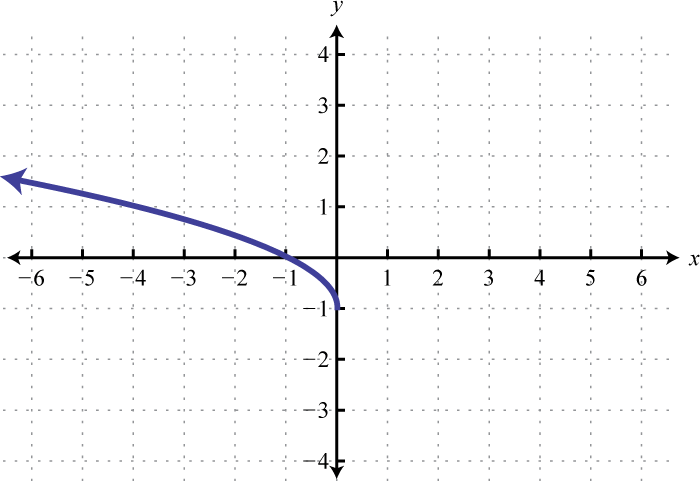
18.

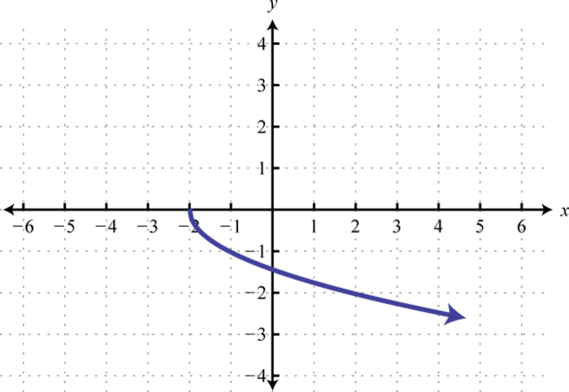
19.

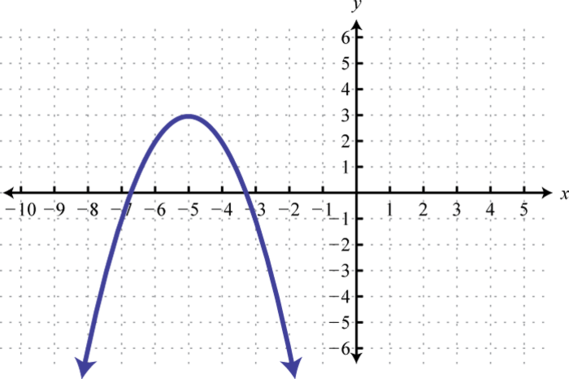
20.

21.

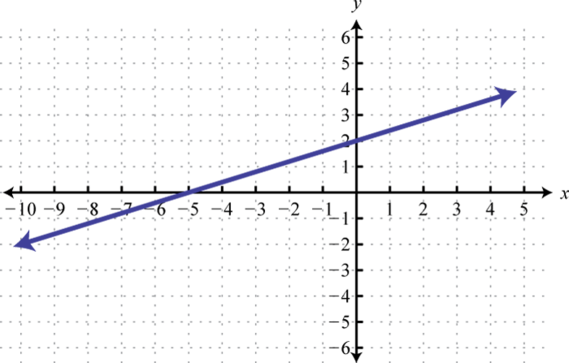
22.

23.

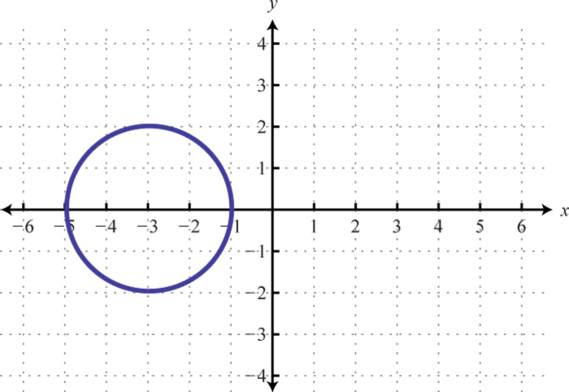
24.

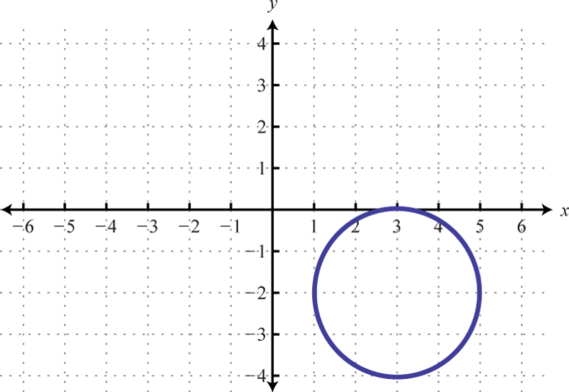
25.

26.

27.

28.

29.

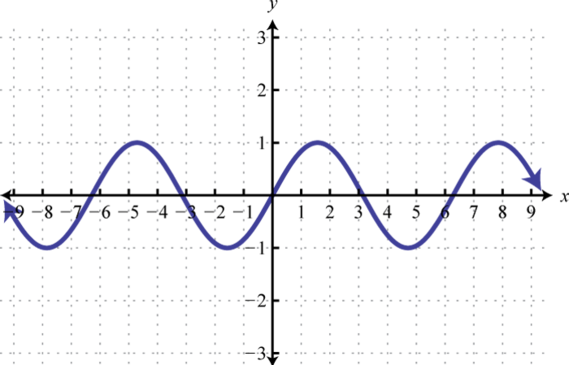
30.

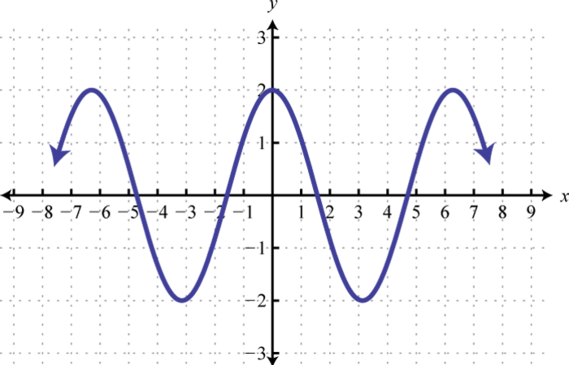
31.

32.

33.

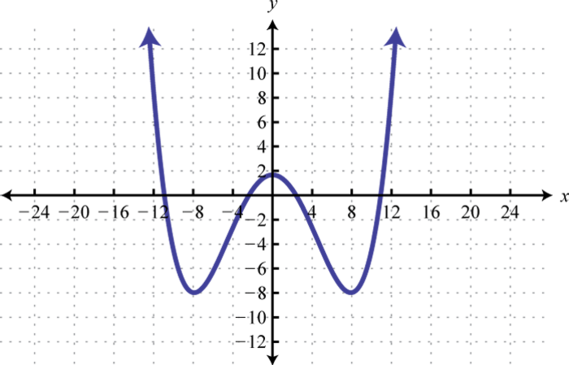
34.

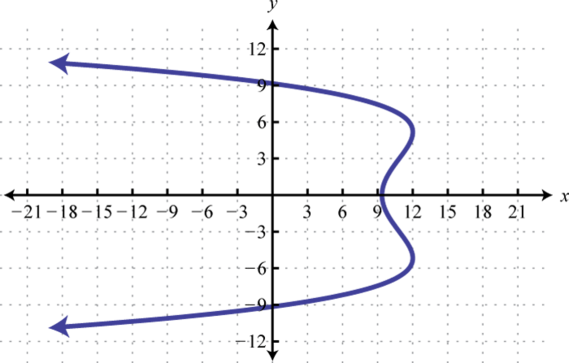
Contestar

1. Dominio:$\{ 3,5,7,9,12 \}$; rango:$\{ 1,2,3,4 \}$; función: sí

3. Dominio:$\{ 7,8,10,15 \}$; rango:$\{ 5,6,7,8,9 \}$; función: no

5. Dominio:$\{5\}$; rango:$\{ 0,2,4,6,8 \}$; función: no

7. Dominio:$\{ - 4 , - 1,0,2,3 \}$; rango:$\{ 1,2,3 \}$; función: sí

9. Dominio:$\{−1, 0, 1, 2\}$; rango:$\{0, 1, 2, 3, 4\}$; función: no

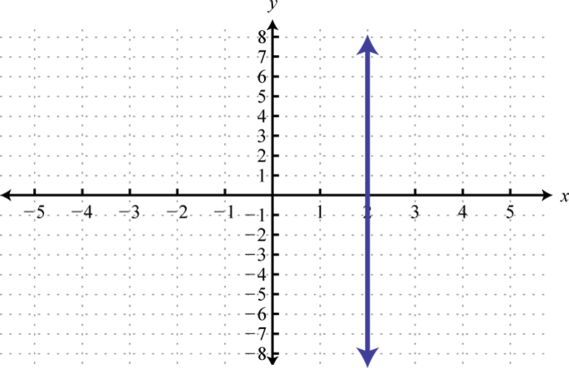
11. Dominio:$\{−2\}$; rango:$\{−4, −2, 0, 2, 4\}$; función: no

13. Dominio:$ℝ$; rango:$[−2, ∞)$; función: sí

15. Dominio:$(−∞, −1]$; rango:$ℝ$; función: no

17. Dominio:$(−∞, 0]$; rango:$[−1, ∞)$; función: sí

19. Dominio:$ℝ$; rango:$(−∞, 3]$; función: sí

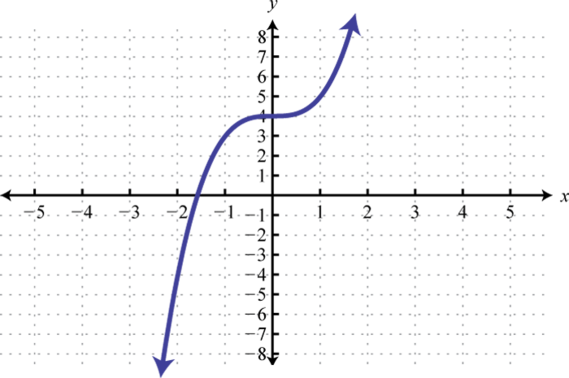
21. Dominio:$ℝ$; rango:$ℝ$; función: sí

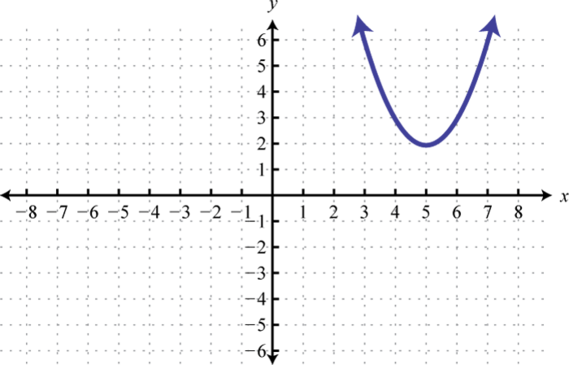
23. Dominio:$[−5, −1]$; rango:$[−2, 2]$; función: no

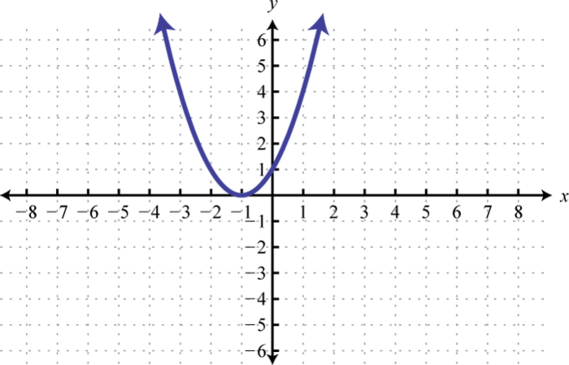
25. Dominio:$ℝ$; rango:$[0, ∞]$; función: sí

27. Dominio:$ℝ$; rango:$ℝ$; función: sí

29. Dominio:$ℝ$; rango:$[−1, 1]$; función: sí

31. Dominio:$[−8, 8]$; rango:$[−3, 3]$; función: no

33. Dominio:$ℝ$; rango:$[−8, ∞]$; función: sí

Ejercicio$\PageIndex{4}$

Evaluar.

$g ( x ) = | x - 5 | \text { find } g ( - 5 ) , g ( 0 ) , \text { and } g ( 5 )$
$g ( x ) = | x | - 5 ; \text { find } g ( - 5 ) , g ( 0 ) , \text { and } g ( 5 )$
$g ( x ) = | 2 x - 3 | ; \text { find } g ( - 1 ) , g ( 0 ) , \text { and } g \left( \frac { 3 } { 2 } \right)$
$g ( x ) = 3 - | 2 x | ; \text { find } g ( - 3 ) , g ( 0 ) , \text { and } g ( 3 )$
$f ( x ) = 2 x - 3 ; \text { find } f ( - 2 ) , f ( 0 ) , \text { and } f ( x - 3 )$
$f ( x ) = 5 x - 1 ; \text { find } f ( - 2 ) , f ( 0 ) , \text { and } f ( x + 1 )$
$g ( x ) = \frac { 2 } { 3 } x + 1 ; \text { find } g ( - 3 ) , g ( 0 ) , \text { and } f ( 9 x + 6 )$
$g ( x ) = - \frac { 3 } { 4 } x - \frac { 1 } { 2 } ; \text { find } g ( - 4 ) , g ( 0 ) , \text { and } g ( 6 x - 2 )$
$g ( x ) = x ^ { 2 } ; \text { find } g ( - 5 ) , g ( \sqrt { 3 } ) , \text { and } g ( x - 5 )$
$g ( x ) = x ^ { 2 } + 1 ; \text { find } g ( - 1 ) , g ( \sqrt { 6 } ) , \text { and } g ( 2 x - 1 )$
$f ( x ) = x ^ { 2 } - x - 2 ; \text { find } f ( 0 ) , f ( 2 ) , \text { and } f ( x + 2 )$
$f ( x ) = - 2 x ^ { 2 } + x - 4 ; \text { find } f ( - 2 ) , f \left( \frac { 1 } { 2 } \right) , \text { and } f ( x - 3 )$
$h ( t ) = - 16 t ^ { 2 } + 32 ; \text { find } h \left( \frac { 1 } { 4 } \right) , h \left( \frac { 1 } { 2 } \right) , \text { and } h ( 2 a - 1 )$
$h ( t ) = - 16 t ^ { 2 } + 32 ; \text { find } h ( 0 ) , h ( \sqrt { 2 } ) , h ( 2 a + 1 )$
$f ( x ) = \sqrt { x + 1 } - 2 \text { find } f ( - 1 ) , f ( 0 ) , f ( x - 1 )$
$f ( x ) = \sqrt { x - 3 } + 1 ; \text { find } f ( 12 ) , f ( 3 ) , f ( x + 3 )$
$g ( x ) = \sqrt { x + 8 } ; \text { find } g ( 0 ) , g ( - 8 ) , \text { and } g ( x - 8 )$
$g ( x ) = \sqrt { 3 x - 1 } ; \text { find } g \left( \frac { 1 } { 3 } \right) , g \left( \frac { 5 } { 3 } \right) , \text { and } g \left( \frac { 1 } { 3 } a ^ { 2 } + \frac { 1 } { 3 } \right)$
$f ( x ) = x ^ { 3 } + 1 ; \text { find } f ( - 1 ) , f ( 0 ) , f \left( a ^ { 2 } \right)$
$f ( x ) = x ^ { 3 } - 8 ; \text { find } f ( 2 ) , f ( 0 ) , f \left( a ^ { 3 } \right)$

Contestar

1. $g ( - 5 ) = 10 , g ( 0 ) = 5 , g ( 5 ) = 0$

3. $g ( - 1 ) = 5 , g ( 0 ) = 3 , g \left( \frac { 3 } { 2 } \right) = 0$

5. $f ( - 2 ) = - 7 , f ( 0 ) = - 3 , f ( x - 3 ) = 2 x - 9$

7. $g ( - 3 ) = - 1 , g ( 0 ) = 1 , g ( 9 x + 6 ) = 6 x + 5$

9. $g ( - 5 ) = 25 , g ( \sqrt { 3 } ) = 3 , g ( x - 5 ) = x ^ { 2 } - 10 x + 25$

11. $f ( 0 ) = - 2 , f ( 2 ) = 0 , f ( x + 2 ) = x ^ { 2 } + 3 x$

13. $h \left( \frac { 1 } { 4 } \right) = 31 , h \left( \frac { 1 } { 2 } \right) = 28 , h ( 2 a - 1 ) = - 64 a ^ { 2 } + 64 a + 16$

15. $f ( - 1 ) = - 2 , f ( 0 ) = - 1 , f ( x - 1 ) = \sqrt { x } - 2$

17. $g ( 0 ) = 2 \sqrt { 2 } , g ( - 8 ) = 0 , g \left( a ^ { 2 } - 8 \right) = | a |$

19. $f ( - 1 ) = 0 , f ( 0 ) = 1 , f \left( a ^ { 2 } \right) = a ^ { 6 } + 1$

Ejercicio$\PageIndex{5}$

Dada la función find$f(x+h)$.

$f ( x ) = 3 x - 1$
$f ( x ) = - 5 x + 2$
$f ( x ) = x ^ { 2 } + x + 1$
$f ( x ) = 2 x ^ { 2 } - x - 1$
$f ( x ) = x ^ { 3 }$
$f ( x ) = 2 x ^ { 3 } - 1$

Contestar

1. $f ( x + h ) = 3 x + 3 h - 1$

3. $f ( x + h ) = x ^ { 2 } + 2 x h + h ^ { 2 } + x + h + 1$

5. $f ( x + h ) = x ^ { 3 } + 3 h x ^ { 2 } + 3 h ^ { 2 } x + h ^ { 3 }$

Ejercicio$\PageIndex{6}$

Encontrar$x$ dada la función.

$f ( x ) = 2 x - 3 ; \text { find } x \text { where } f ( x ) = 25$
$f ( x ) = 7 - 3 x ; \text { find } x \text { where } f ( x ) = - 27$
$f ( x ) = 2 x + 5 ; \text { find } x \text { where } f ( x ) = 0$
$f ( x ) = - 2 x + 1 ; \text { find } x \text { where } f ( x ) = 0$
$g ( x ) = 6 x + 2 ; \text { find } x \text { where } g ( x ) = 5$
$g ( x ) = 4 x + 5 ; \text { find } x \text { where } g ( x ) = 2$
$h ( x ) = \frac { 2 } { 3 } x - \frac { 1 } { 2 } ; \text { find } x \text { where } h ( x ) = \frac { 1 } { 6 }$
$h ( x ) = \frac { 5 } { 4 } x + \frac { 1 } { 3 } ; \text { find } x \text { where } h ( x ) = \frac { 1 } { 2 }$
El valor de un auto nuevo en dólares viene dado por la función$V(t) = −1,800t + 22,000$ donde$t$ representa la antigüedad del automóvil en años. Utilice la función para determinar el valor del automóvil cuando tenga$4$ años de antigüedad. ¿Cuál era el valor del auto nuevo?
El ingreso mensual en dólares de un vendedor de autos comisionado viene dado por la función$I(n) = 350n + 1,450$ donde$n$ representa el número de autos vendidos en el mes. Utilice la función para determinar los ingresos del vendedor si vende$3$ autos este mes. ¿Cuáles son sus ingresos si no vende ningún auto en un mes?

Contestar

1. $x=14$

3. $x=-\frac{5}{2}$

5. $x=\frac{1}{2}$

7. $x=1$

9. Nuevo:$$22,000$;$4$ años:$$14,800$

Ejercicio$\PageIndex{7}$

Dada la gráfica de la función$f$, encuentra los valores de la función.

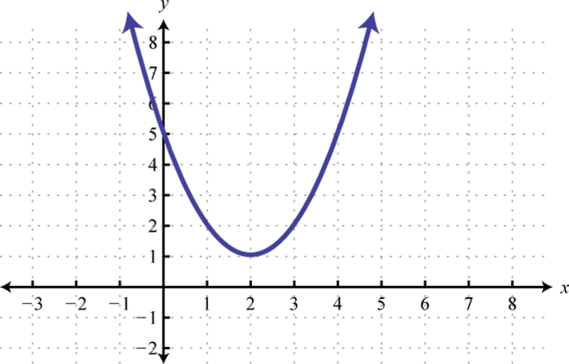
Encontrar$f ( 0 ) , f ( 2 )$, y$f ( 4 )$.

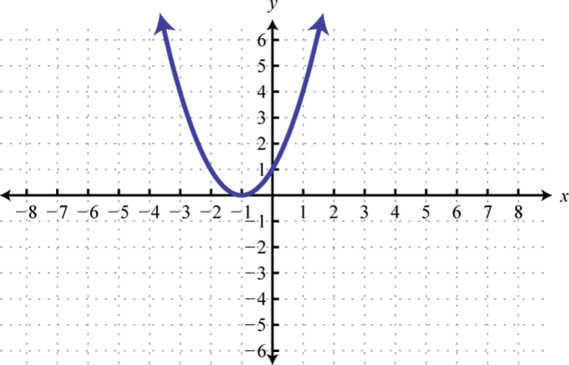
2. Encontrar$f(-1), f(0)$, y$f(1)$.

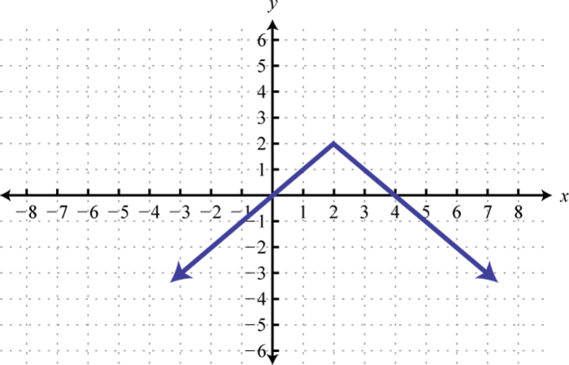
3. Encontrar$f (0), f (2)$, y$f (4)$.

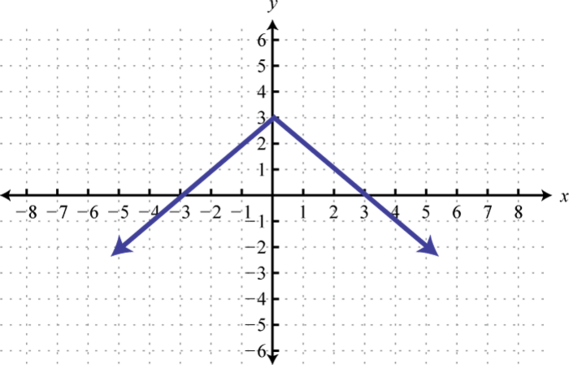
4. Encontrar$f (−3), f (0)$, y$f (3)$.

5. Encontrar$f (−4), f (0)$, y$f (2)$. \

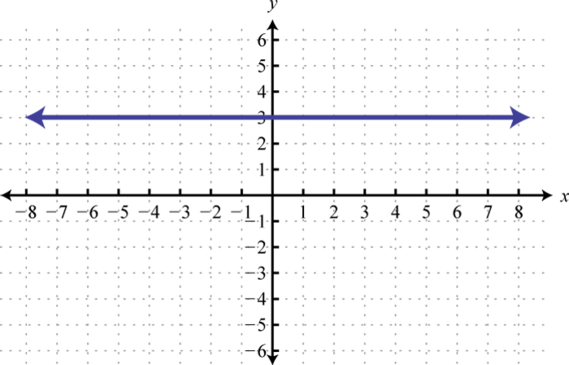
6. Encontrar$f (−6), f (0)$, y$f (6)$.

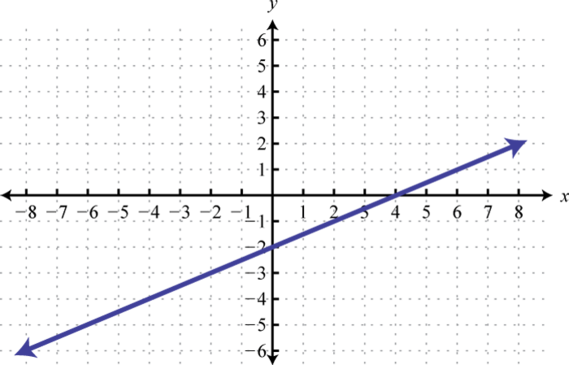
7. Encontrar$f (−2), f (2)$, y$f (7)$.

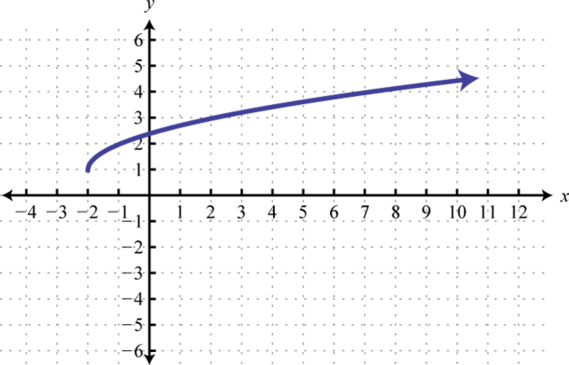
8. Encontrar$f (0), f (5)$, y$f (9)$.

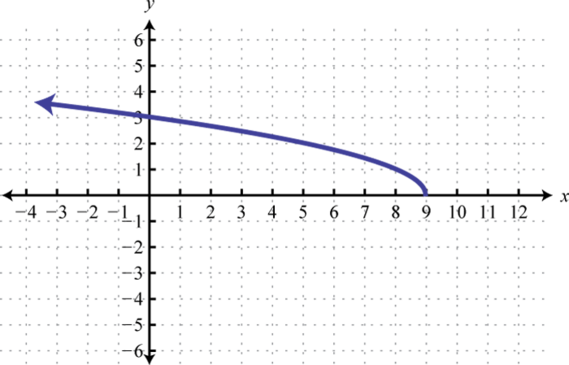
9. Encontrar$f (−8), f (0)$, y$f (8)$.

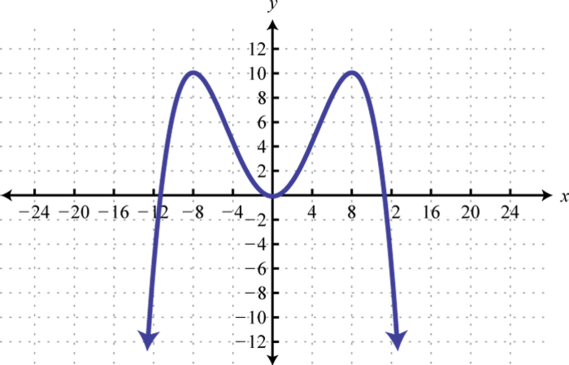
10. Encontrar$f (−12), f (0)$, y$f (12)$.

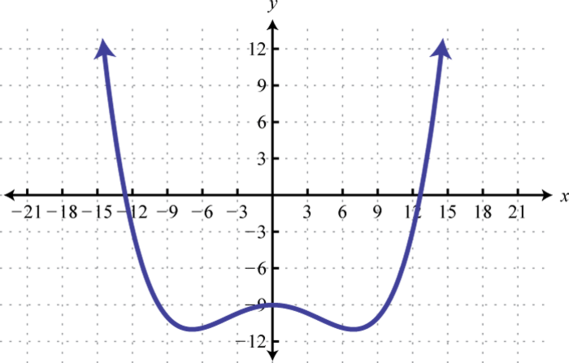
Contestar

1. $f (0) = 5, f (2) = 1, f (4) = 5$

3. $f (0) = 0, f (2) = 2, f (4) = 0$

5. $f (−4) = 3, f (0) = 3, f (2) = 3$

7. $f (−2) = 1, f (2) = 3, f (7) = 4$

9. $f (−8) = 10, f (0) = 0, f (8) = 10$

Ejercicio$\PageIndex{8}$

Dada la gráfica de una función$g$, encuentra los$x$ -valores:

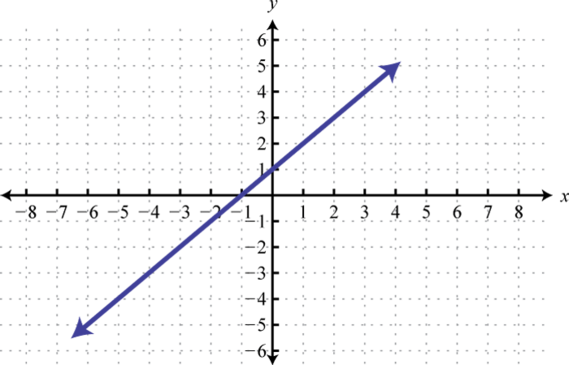
Encuentra$x$ dónde$g (x) = 3, g (x) = 0$, y$g (x) = −2$.

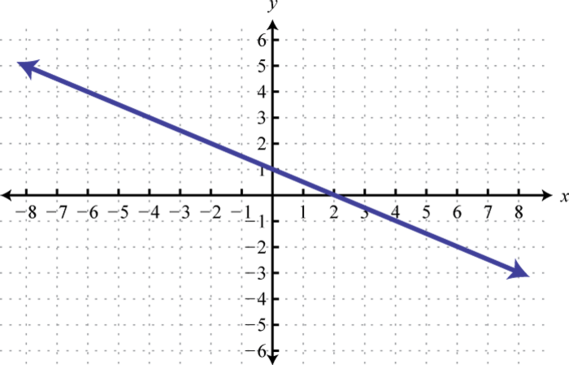
2. Encuentra$x$ dónde$g (x) = 0, g (x) = 1$, y$g (x) = 4$.

3. Encuentra$x$ dónde$g (x) = −5, g (x) = 0$, y$g (x) = 10$.

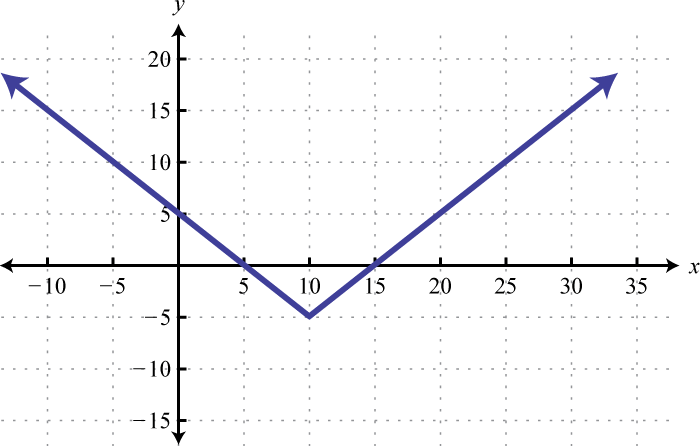
4. Encuentra$x$ dónde$g (x) = 0, g (x) = 10$, y$g (x) = 15$.

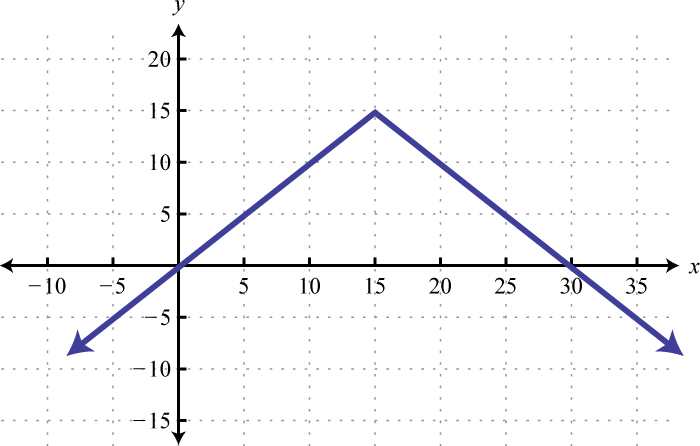
5. Encuentra$x$ dónde$g (x) = −5, g (x) = −4$, y$g (x) = 4$. \

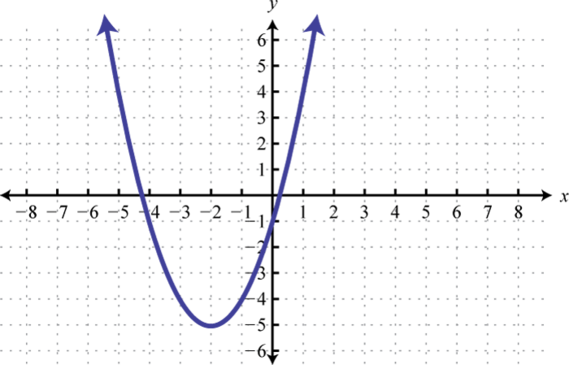
6. Encuentra$x$ dónde$g (x) = 1, g (x) = 0$, y$g (x) = −3$.

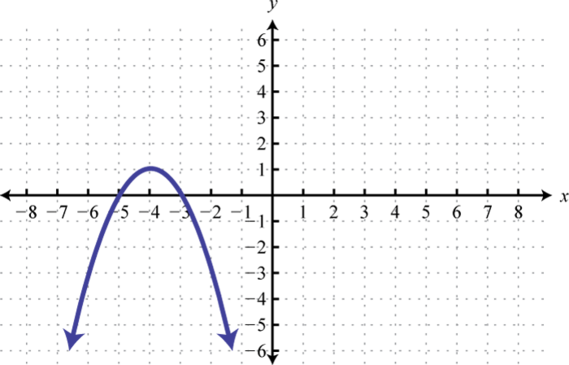
7. Encuentra$x$ dónde$g (x) = −4, g (x) = 3$, y$g (x) = 4$.

8. Encuentra$x$ dónde$g (x) = −5, g (x) = −4$, y$g (x) = 4$.

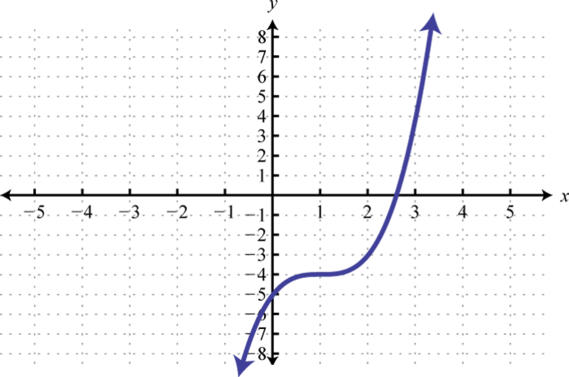
9. Encuentra$x$ dónde$g (x) = −10$ y$g (x) = 5$.

10. Encuentra$x$ dónde$g(x)=2$.

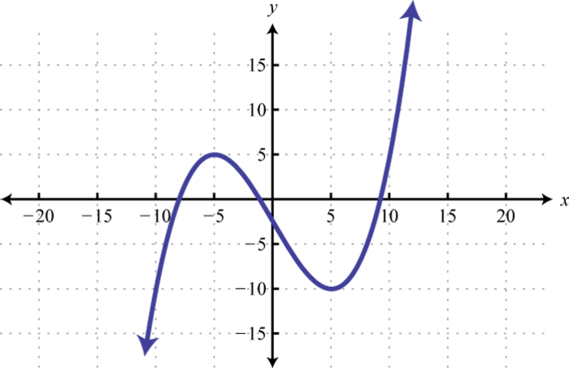
El valor de un determinado automóvil en dólares depende del número de años desde que se compró en$1970$ según la siguiente función:

11. ¿Cuál era el valor del auto cuando era nuevo en$1970$?

12. ¿En qué año estaba en un mínimo el valor del auto?

13. ¿Cuál era el valor del auto en$2005$?

14. ¿En qué años se valoró el auto$$4,000$?

Contestar

1. $g (−4) = 3, g (2) = 0$, y$g (6) = −2$.

3. $g (10) = −5, g (5) = 0$y$g (15) = 0 , g (−5) = 10$ y$g (25) = 10$

5. $g (−2) = −5, g (−3) = −4$y$g (−1) = −4 , g (−5) = 4$ y$g (1) = 4$

7. $g (−2) = −4, g (−1) = 3, g (0) = 4$

9. $g (−10) = −10$y$g (5) = −10 ; g (−5) = 5$ y$g (10) = 5$

11. $$5,000$

13. $$10,000$

Ejercicio$\PageIndex{9}$

Dada la función lineal definida por$f(x)=2x-5$, simplificar lo siguiente.

$f ( 5 ) - f ( 3 )$
$f ( 0 ) - f ( 7 )$
$f ( x + 2 ) - f ( 2 )$
$f ( x + 7 ) - f ( 7 )$
$f ( x + h ) - f ( x )$
$\frac { f ( x + h ) - f ( x ) } { h }$
Simplificar$\frac { c ( x + h ) - c ( x ) } { h }$ dado$c ( x ) = 3 x + 1$.
Simplificar$\frac { p ( x + h ) - p ( x ) } { h }$ dado$p ( x ) = 7 x - 3$.
Simplificar$\frac { g ( x + h ) - g ( x ) } { h }$ dado$g ( x ) = m x + b$.
Simplificar$\frac { q ( x + h ) - q ( x ) } { h }$ dado$q ( x ) = a x$.

Contestar

1. $4$

3. $2x$

5. $2h$

7. $3$

9. $m$

Ejercicio$\PageIndex{10}$

¿A quién se le atribuye la introducción de la notación$y = f (x)$? Proporcionar un breve resumen de su vida y logros.
Explique a un estudiante principiante de álgebra qué es la prueba de línea vertical y por qué funciona.
Investigar y discutir la vida y aportes de René Descartes.
Realizar una búsqueda en Internet para la prueba de línea vertical, funciones y funciones de evaluación. Comparte un enlace a una página que creas que otros pueden encontrar útil.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

¹ Un sistema con dos líneas numéricas en ángulo recto especificando puntos en un plano usando pares ordenados$(x, y)$.

² La línea numérica horizontal utilizada como referencia en un sistema de coordenadas rectangulares.

³ La recta numérica vertical utilizada como referencia en un sistema de coordenadas rectangulares.

⁴ La superficie plana definida por$x$ - y$y$ -ejes.

⁵ Pares$(x, y)$ que identifican la posición relativa al origen en un plano de coordenadas rectangulares.

⁶ El punto donde se cruzan$y$ los ejes$x$ - y -denotado por$(0, 0)$.

⁷ Las cuatro regiones de un plano de coordenadas rectangulares, parcialmente delimitadas por los$y$ ejes$x$ - y -y numeradas usando los números romanos I, II, III y IV.

⁸ Término utilizado en honor a René Descartes al referirse al sistema de coordenadas rectangulares.

⁹ Cualquier conjunto de pares ordenados.

¹⁰ Una representación visual de una relación en un plano de coordenadas rectangulares.

¹¹ El conjunto que consiste en todos los primeros componentes de una relación. Para las relaciones que constan de puntos en el plano, el dominio es el conjunto de todos los$x$ -valores.

¹² El conjunto que consiste en todos los segundos componentes de una relación. Para las relaciones que constan de puntos en el plano, el rango es el conjunto de todos los$y$ -valores.

¹³ Se usa al hacer referencia al rango.

¹⁴ Una relación donde cada elemento del dominio corresponde exactamente a un elemento en el rango.

¹⁵ Si alguna línea vertical cruza la gráfica más de una vez, entonces la gráfica no representa una función.

¹⁶ La notación$f (x) = y$, que dice “$f$de$x$ es igual a”$y$. Dada una función,$y$ y se$f (x)$ puede usar indistintamente.

¹⁷ El valor o expresión algebraica utilizada como entrada cuando se utiliza la notación de funciones.