2.2: Funciones lineales y sus gráficas
- Page ID
- 109893
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Grafica una línea trazando puntos.
- Determinar la pendiente de una línea.
- Identificar y graficar una función lineal usando la pendiente y\(y\) -interceptar.
- Interpretar soluciones a ecuaciones lineales y desigualdades gráficamente.
Una revisión de las líneas gráficas
Recordemos que el conjunto de todas las soluciones a una ecuación lineal se puede representar en un plano de coordenadas rectangulares utilizando una línea recta a través de al menos dos puntos; esta línea se llama su gráfica. Por ejemplo, para graficar la ecuación lineal primero\(8x + 4y = 12\) resolveríamos para\(y\).
\(\begin{aligned} 8 x + 4 y & = 12 \quad\quad\quad\quad \color{Cerulean}{Subtract\: 8x\: on\: both\: sides.} \\ 4 y & = - 8 x + 12 \quad \color{Cerulean}{Divide\: both\: sides\: by\: 4.} \\ y & = \frac { - 8 x + 12 } { 4 }\quad \color{Cerulean}{Simplify.} \\ y & = \frac { - 8 x } { 4 } + \frac { 12 } { 4 } \\ y & = - 2 x + 3 \end{aligned}\)
Escrito en esta forma, podemos ver que\(y\) depende de\(x\); en otras palabras,\(x\) es la variable independiente 18 y\(y\) es la variable dependiente 19. Elija al menos dos\(x\) -valores y encuentre los\(y\) valores -correspondientes. Es una buena práctica elegir cero, algunos números negativos, así como algunos números positivos. Aquí elegiremos cinco\(x\) valores, determinaremos los\(y\) valores correspondientes y luego formaremos un conjunto representativo de soluciones de pares ordenados.
| \(x\) | \(y\) | \(y=-2x+3\) | Soluciones |
|---|---|---|---|
| \ (x\) ">
\(−2\) |
\ (y\) ">
\(7\) |
\ (y=-2x+3\) ">
\(y=−2(\color{Cerulean}{−2}\color{Black}{)}+3=4+3=7\) |
\((−2, 7)\) |
| \ (x\) ">
\(−1\) |
\ (y\) ">
\(5\) |
\ (y=-2x+3\) ">
\(y=−2(\color{Cerulean}{−1}\color{Black}{)}+3=2+3=5\) |
\((−1, 5)\) |
| \ (x\) ">
\(0\) |
\ (y\) ">
\(3\) |
\ (y=-2x+3\) ">
\(y=−2(\color{Cerulean}{0}\color{Black}{)}+3=0+3=3\) |
\((0, 3)\) |
| \ (x\) ">
\(4\) |
\ (y\) ">
\(−5\) |
\ (y=-2x+3\) ">
\(y=−2(\color{Cerulean}{4}\color{Black}{)}+3=−8+3=−5\) |
\((4, −5)\) |
| \ (x\) ">
\(6\) |
\ (y\) ">
\(−9\) |
\ (y=-2x+3\) ">
\(y=−2(\color{Cerulean}{6}\color{Black}{)}+3=−12+3=−9\) |
\((6, −9)\) |
Traza los puntos y dibuja una línea a través de los puntos con una recta. Asegúrese de agregar flechas en cualquiera de los extremos para indicar que la gráfica se extiende indefinidamente.
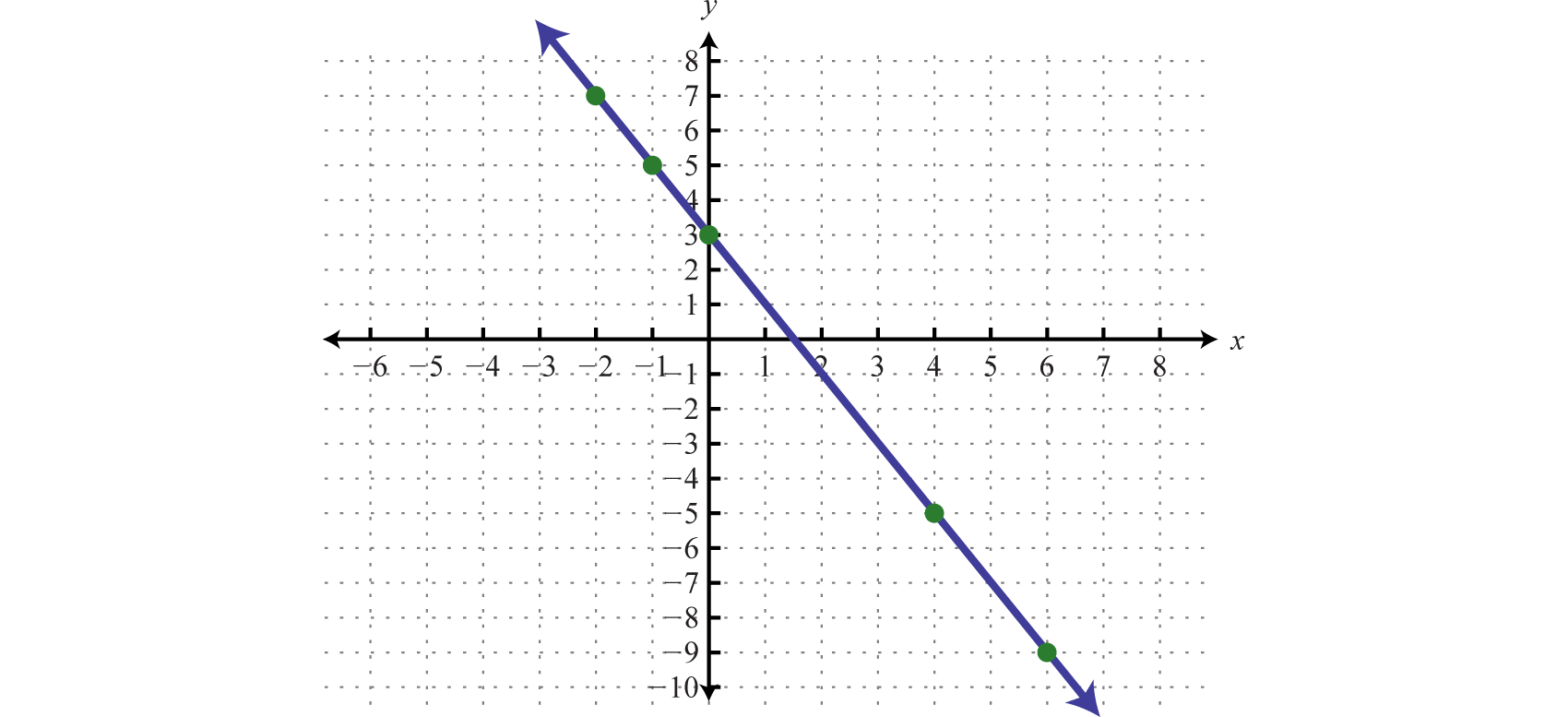
La línea resultante representa todas las soluciones a\(8x+4y=12\), de las cuales hay infinitamente muchas. El proceso anterior describe la técnica para graficar conocida como puntos de trazado 20. Esta técnica será utilizada para graficar funciones más complicadas a medida que avancemos en este curso.
La inclinación de cualquier inclinación se puede medir como la relación entre el cambio vertical y el cambio horizontal. Por ejemplo, un\(5\)% de inclinación puede escribirse como\(\frac{5}{100}\), lo que significa que por cada\(100\) pie adelante, la altura aumenta\(5\) los pies.

En matemáticas, llamamos a la pendiente de una línea la pendiente 21, denotada por la letra m. El cambio vertical se llama subida 22 y el cambio horizontal se llama carrera 23. Dados dos puntos cualesquiera\((x1, y1)\) y\((x2, y2)\), podemos obtener la subida y correr restando las coordenadas correspondientes.

Esto nos lleva a la fórmula de pendiente 24. Dados dos puntos cualesquiera\((x1, y1)\) y\((x2, y2)\), la pendiente viene dada por:
\(\color{Cerulean}{Slope} \:\:\:\color{Black}{m} = \frac {rise} {run} = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } = \frac { \Delta y } { \Delta x } \quad \begin{array} { l l } { \color{Cerulean} { \gets\:\: Change\: in\: } y } \\ { \color{Cerulean} {\gets\:\: Change\: in\: } x } \end{array}\)
La letra griega delta (\(Δ\)) se utiliza a menudo para describir el cambio en una cantidad. Por lo tanto, la pendiente a veces se describe usando la notación\(\frac{Δy}{Δx}\), que representa el cambio en\(y\) dividido por el cambio en\(x\).
Ejemplo\(\PageIndex{1}\):
Encuentra la pendiente de la línea que pasa por\((−3, −5)\) y\((2, 1)\).
Solución
Dado\((−3, −5)\) y\((2, 1)\), calcular la diferencia de los\(y\) -valores divididos por la diferencia de los valores x. Tenga cuidado de ser consistente al restar las coordenadas:
\(\begin{array} { l l } { \left( x _ { 1 } , y _ { 1 } \right) } & { \left( x _ { 2 } , y _ { 2 } \right) } \\ { ( - 3 , - 5 ) } & { ( 2,1 ) } \end{array}\)
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { 1 - ( - 5 ) } { 2 - ( - 3 ) } \\ & = \frac { 1 + 5 } { 2 + 3 } \\ & = \frac { 6 } { 5 } \end{aligned}\)
No importa qué punto consideres el primero y el segundo. No obstante, debido a que la resta no es conmutativa, se debe tener cuidado de restar las coordenadas del primer punto de las coordenadas del segundo punto en el mismo orden. Por ejemplo, obtenemos el mismo resultado si aplicamos la fórmula de pendiente con los puntos cambiados:
\(\begin{array} { l } { \left( x _ { 1 } , y _ { 1 } \right) \quad \left( x _ { 2 } , y _ { 2 } \right) } \\ { ( 2,1 ) \quad ( - 3 , - 5 ) } \end{array}\)
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { - 5 - 1 } { - 3 - 2 } \\ & = \frac { - 6 } { - 5 } \\ & = \frac { 6 } { 5 } \end{aligned}\)
Respuesta:
\(m=\frac{6}{5}\)
Verificar que la pendiente sea\(\frac{6}{5}\) graficando la línea descrita en el ejemplo anterior.
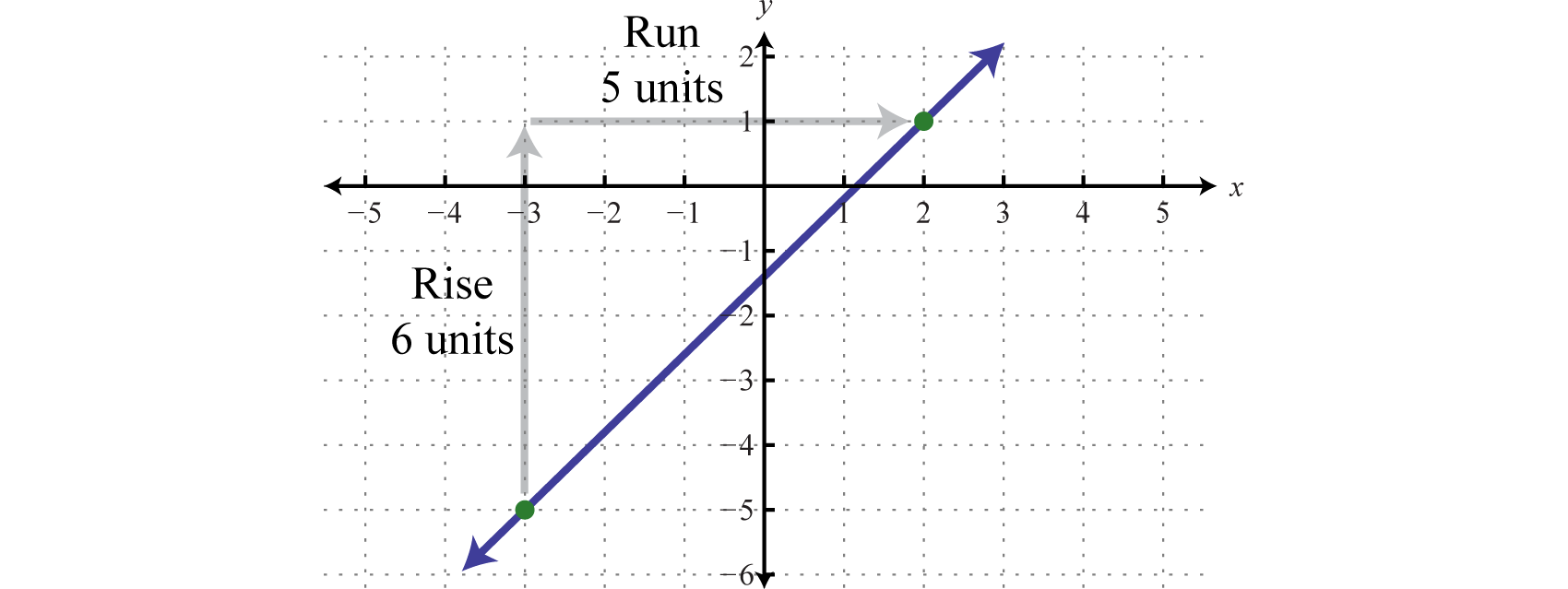
Ciertamente la gráfica es opcional; la belleza de la fórmula de pendiente es que, dados dos puntos cualesquiera, podemos obtener la pendiente utilizando únicamente álgebra.
Ejemplo\(\PageIndex{2}\):
Encuentra el\(y\) -valor para el cual se encuentra la pendiente de la línea que pasa por\((6, −3)\) y\((−9, y)\)\(−\frac{2}{3}\).
Solución
Sustituya la información dada en la fórmula de pendiente.
\(\begin{array} { l l } { \text { Slope } } & { \left( x _ { 1 } , y _ { 1 } \right) } & { \left( x _ { 2 } , y _ { 2 } \right) } \\ { m = - \frac { 2 } { 3 } } & { ( 6 , - 3 ) } & { ( - 9 , y ) } \end{array}\)
\(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ - \frac { 2 } { 3 } & = \frac { y - ( - 3 ) } { - 9 - 6 } \\ - \frac { 2 } { 3 } & = \frac { y + 3 } { - 15 } \end{aligned}\)
Después de sustituir en la información dada, la única variable que queda es\(y\). Resolver.
\(\begin{aligned} \color{Cerulean}{- 15}\color{Black}{ \left( - \frac { 2 } { 3 } \right)} & = \color{Cerulean}{- 15}\color{Black}{ \left( - \frac { y + 3 } { 15 } \right)} \\ 10 & = y + 3 \\ 7 & = y \end{aligned}\)
Respuesta:
\(y=7\)
Hay cuatro casos geométricos para el valor de la pendiente.

Al leer la gráfica de izquierda a derecha, las líneas con pendiente ascendente tienen pendientes positivas y las líneas con pendiente descendente tienen pendientes negativas. Los otros dos casos involucran líneas horizontales y verticales. Recordemos que si\(k\) es un número real tenemos
\(\begin{array} { l } { y = k \color{Cerulean} { Horizontal line } } \\ { x = k \color{Cerulean} { Vertical line } } \end{array}\)
Por ejemplo, si\(y=2\) graficamos obtenemos una línea horizontal, y si\(x=−4\) graficamos obtenemos una línea vertical.
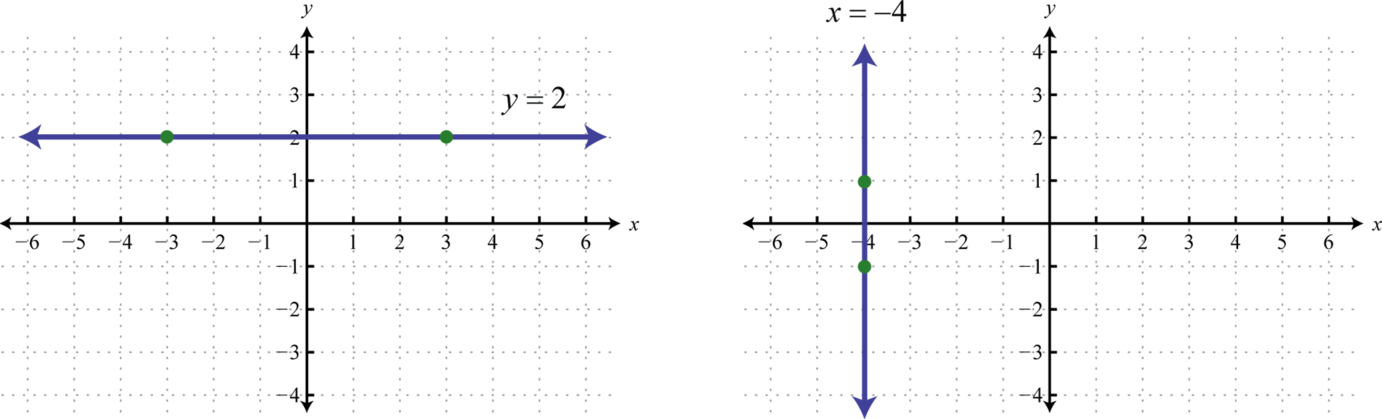
A partir de las gráficas podemos determinar dos puntos y calcular la pendiente usando la fórmula de pendiente.
| Línea Horizontal | Línea Vertical |
|---|---|
|
\(\begin{array} { l l } { \left( x _ { 1 } , y _ { 1 } \right) } & { \left( x _ { 2 } , y _ { 2 } \right) } \\ { ( - 3,2 ) } & { ( 3,2 ) } \end{array}\) \(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { 2 - ( 2 ) } { 3 - ( - 3 ) } \\ & = \frac { 2 - 2 } { 3 + 3 } \\ & = \frac { 0 } { 6 } = 0 \end{aligned}\) |
\(\begin{array} { c c } { \left( x _ { 1 } , y _ { 1 } \right) } & { \left( x _ { 2 } , y _ { 2 } \right) } \\ { ( - 4 , - 1 ) } & { ( - 4,1 ) } \end{array}\) \(\begin{aligned} m & = \frac { y _ { 2 } - y _ { 1 } } { x _ { 2 } - x _ { 1 } } \\ & = \frac { 1 - ( - 1 ) } { - 4 - ( - 4 ) } \\ & = \frac { 1 + 1 } { - 4 + 4 } \\ & = \frac { 2 } { 0 } \quad\quad\quad\quad \color{Cerulean} { Undefined } \end{aligned}\) |
Observe que los puntos de la línea horizontal comparten los mismos\(y\) valores. Por lo tanto, la subida es cero y de ahí la pendiente es cero. Los puntos en la línea vertical comparten los mismos\(x\) valores. En consecuencia, la carrera es cero, lo que lleva a una pendiente indefinida. En general,

Funciones Lineales
Dada cualquier ecuación lineal en forma estándar 25,\(ax + by = c\), podemos resolver\(y\) para obtener la forma pendiente-intercepción 26,\(y = mx + b\). Por ejemplo,
\(\begin{aligned} 3 x - 4 y & = 8\quad\quad\quad\color{Cerulean}{\gets \:\:Standard\: form} \\ - 4 y & = - 3 x + 8 \\ y & = \frac { - 3 x + 8 } { - 4 } \\ y & = \frac { - 3 x } { - 4 } + \frac { 8 } { - 4 } \\ y & = \frac { 3 } { 4 } x - 2 \quad\color{Cerulean} {\gets\:\: Slope-lntercept\: Form } \end{aligned}\)
Donde\(x=0\), podemos ver eso\(y=−2\) y así\((0,−2)\) es una solución de par ordenado. Este es el punto donde la gráfica cruza el\(y\) eje -eje y se llama la \(y\)-intercepción 27. Podemos utilizar este punto y la pendiente como medio para graficar rápidamente una línea. Por ejemplo, para graficar\(y=\frac{3}{4}x−2\), comience en la\(y\) intersección\((0,−2)\) y marque la pendiente para encontrar un segundo punto. Luego usa estos puntos para graficar la línea de la siguiente manera:
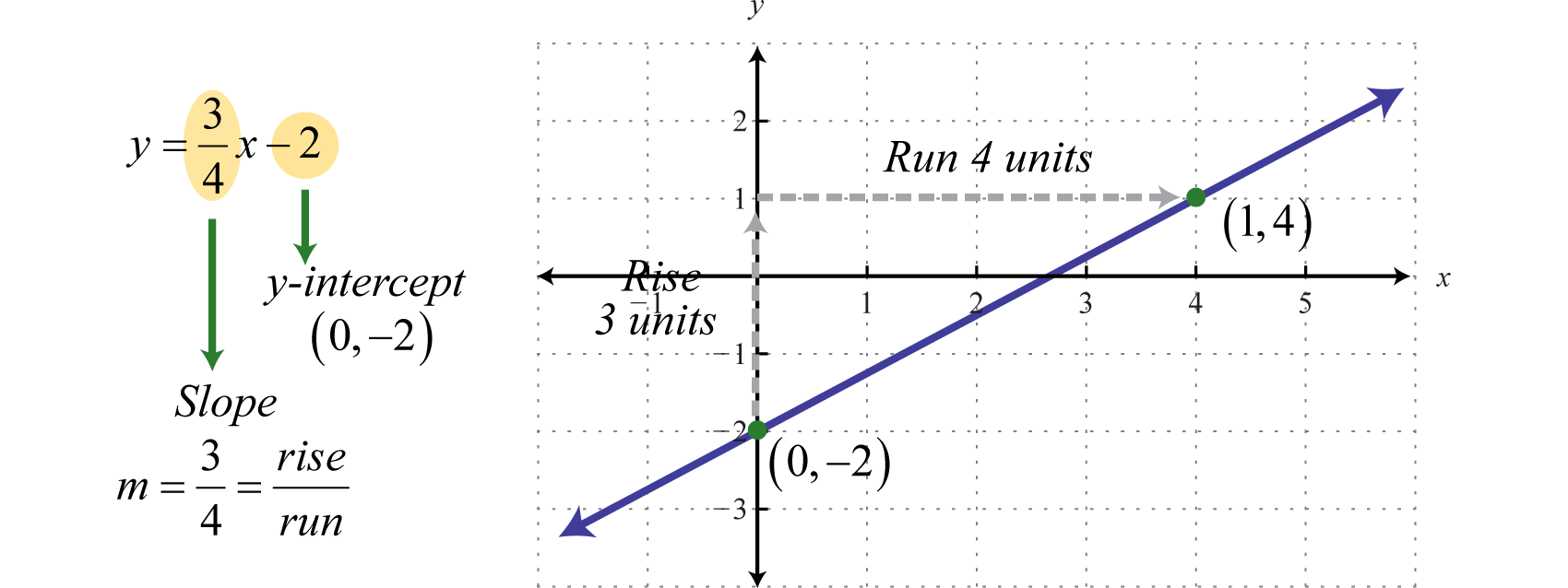
La prueba de línea vertical indica que esta gráfica representa una función. Además, el dominio y el rango están formados por todos los números reales.
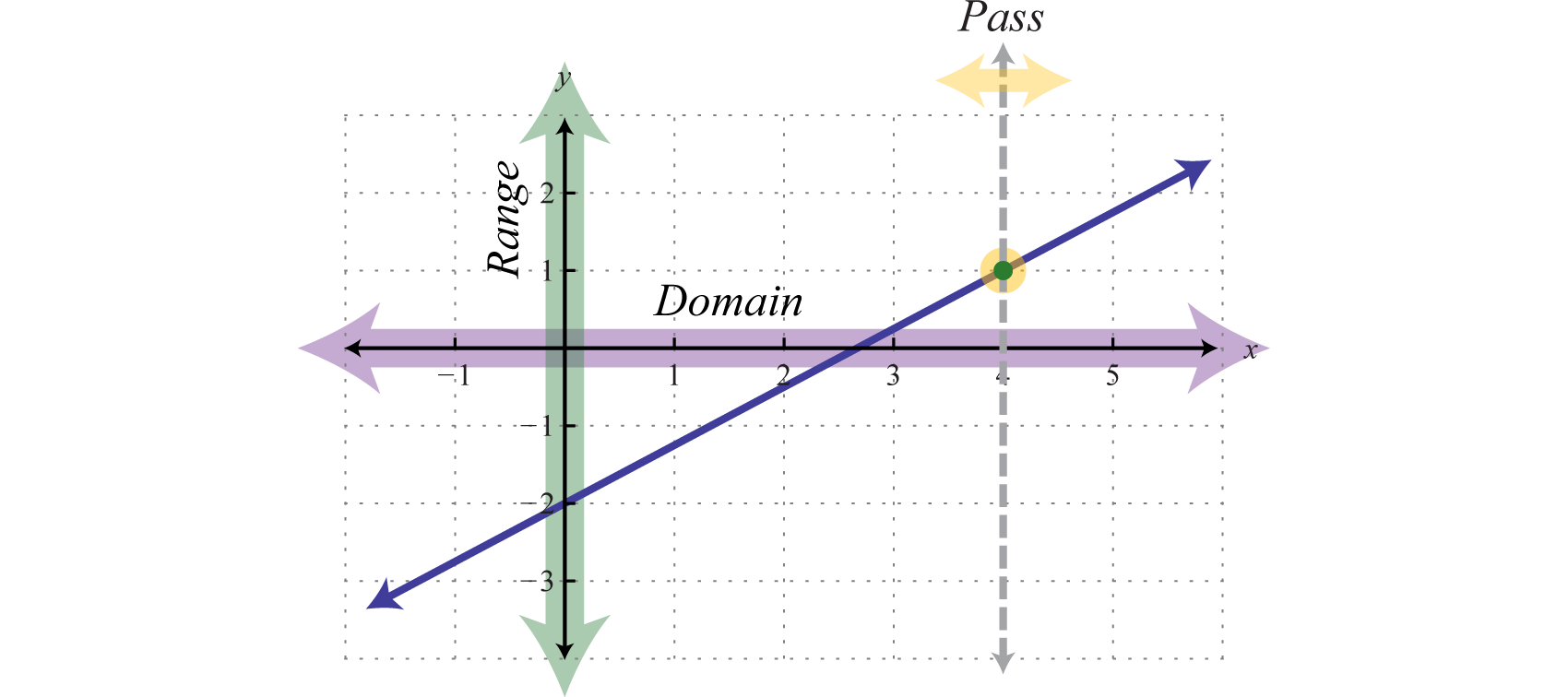
En general, una función lineal 28 es una función que se puede escribir en la forma
\(f ( x ) = m x + b\:\:\color{Cerulean}{Linear\:Function}\)
donde la pendiente\(m\) y\(b\) representar cualquier número real. Porque\(y = f (x)\), podemos usar\(y\) e\(f (x)\) indistintamente, y las soluciones de par ordenadas en la gráfica se\((x, y)\) pueden escribir en la forma\((x, f (x))\).
\(( x , y ) \quad \color{Cerulean}{\Leftrightarrow} \quad \color{Black}{(} x , f ( x ) )\)
Sabemos que cualquier\(y\) -intercepción tendrá un\(x\) -valor igual a cero. Por lo tanto, la\(y\) intersección se puede expresar como el par ordenado.\((0, f (0))\) Para funciones lineales,
\(\begin{aligned} f ( \color{Cerulean}{0}\color{Black}{ )} & = m ( \color{Cerulean}{0}\color{Black}{ )} + b \\ & = b \end{aligned}\)
De ahí que la\(y\) -intercepción de cualquier función lineal\((0, b)\) es.Para encontrar la intersección x 29, el punto donde la función se cruza con el\(x\) eje -, encontramos\(x\) dónde\(y = 0\) o\(f (x) = 0\).
Ejemplo\(\PageIndex{3}\):
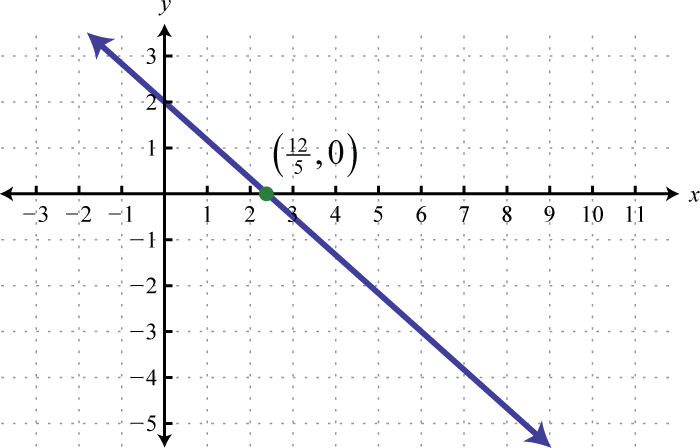
Grafica la función lineal\(f(x)=−\frac{5}{3}x+6\) y etiqueta la\(x\) -intercepción.
Solución
A partir de la función, vemos que\(f(0)=6\) (o\(b=6\)) y así la\(y\) -intercepción es\((0, 6)\). También, podemos ver que la pendiente\(m=−\frac{5}{3}=−\frac{5}{3}=\frac{rise}{run}\). A partir de la\(y\) -intercepción, marcar un segundo punto abajo\(5\) unidades y unidades\(3\) derechas. Dibuja la línea que pasa por estos dos puntos con una recta.
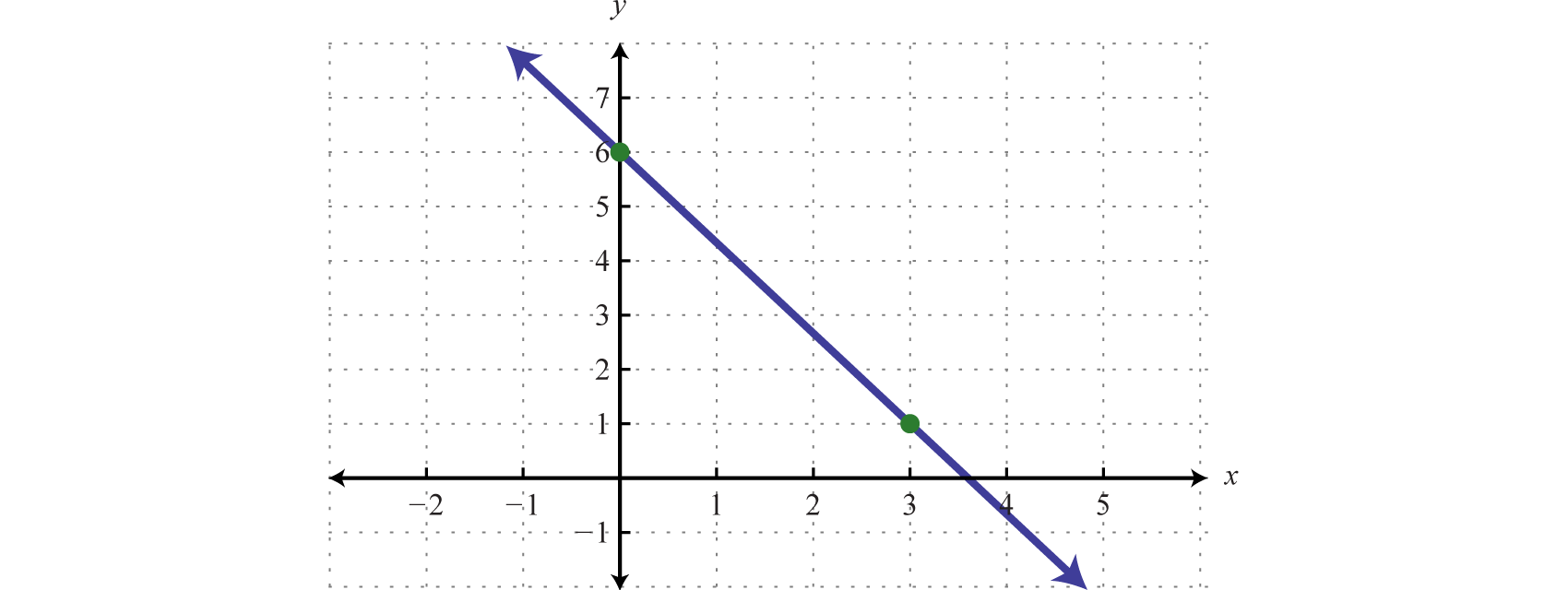
Para determinar la\(x\) -intercepción, busque el\(x\) -valor donde la función es igual a cero. En otras palabras, determinar\(x\) dónde\(f(x)=0\).
\(\begin{aligned} f ( x ) & = - \frac { 5 } { 3 } x + 6 \\ 0 & = - \frac { 5 } { 3 } x + 6 \\ \frac { 5 } { 3 } x & = 6 \\ \left( \color{Cerulean}{\frac { 3 } { 5 }} \right) \frac { 5 } { 3 } x & = \left( \color{Cerulean}{\frac { 3 } { 5 }} \right) 6 \\ x & = \frac { 18 } { 5 } = 3 \frac { 3 } { 5 } \end{aligned}\)
Por lo tanto, la\(x\) -intercepción es\((\frac{18}{5},0)\). La regla general es etiquetar todos los puntos importantes que no se puedan leer claramente de la gráfica.
Respuesta:
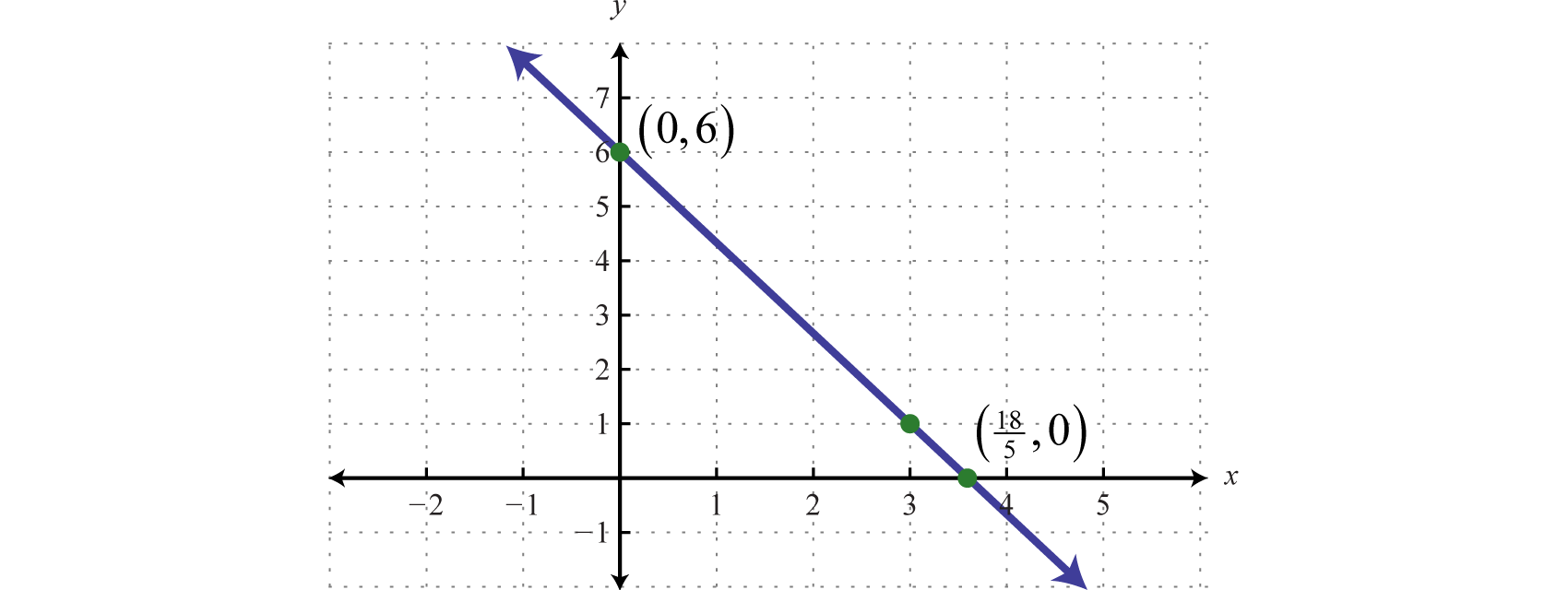
Ejemplo\(\PageIndex{4}\):
Determine una función lineal que defina la gráfica dada y encuentre la\(x\) -intercepción.
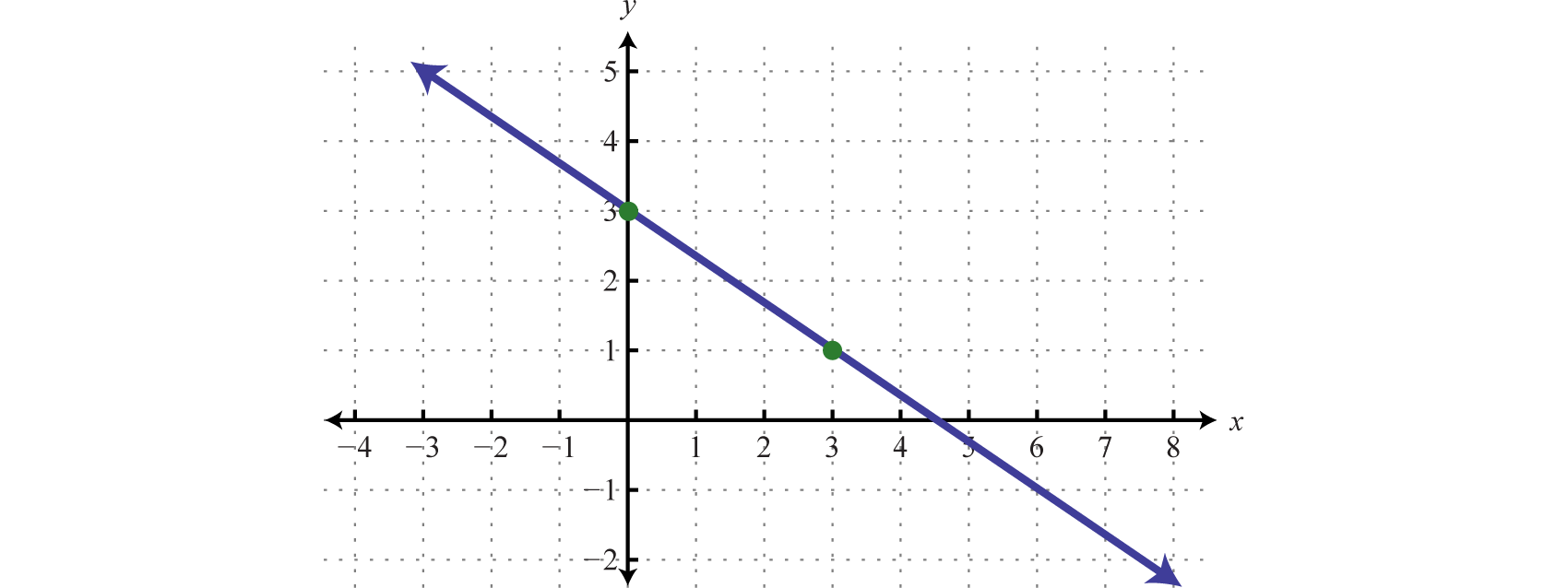
Solución
Comenzamos leyendo la pendiente de la gráfica. En este caso, se dan dos puntos y podemos ver que,
\(m = \frac { r i s e } { r u n } = \frac { - 2 } { 3 }\)
Además, la\(y\) -intercepción es\((0, 3)\) y por lo tanto\(b=3\). Podemos sustituir en la ecuación cualquier función lineal.
\(\begin{array} { c } { g ( x ) = m x + b } \\ \quad\quad\quad\color{Cerulean}{\downarrow\quad\quad\downarrow} \\ { g ( x ) = - \frac { 2 } { 3 } x + 3 } \end{array}\)
Para encontrar la\(x\) -intercepción, nos fijamos\(g(x)=0\) y resolvemos para\(x\).
\(\begin{aligned} g ( x ) & = - \frac { 2 } { 3 } x + 3 \\ 0 & = - \frac { 2 } { 3 } x + 3 \\ \frac { 2 } { 3 } x & = 3 \\ \left( \color{Cerulean}{\frac { 3 } { 2 }} \right) \frac { 2 } { 3 } x & = \left( \color{Cerulean}{\frac { 3 } { 2 }} \right) 3 \\ x & = \frac { 9 } { 2 } = 4 \frac { 1 } { 2 } \end{aligned}\)
Respuesta:
\(g(x)=−\frac{2}{3}x+3\);\(x\) -interceptar:\((\frac{9}{2},0)\)
A continuación, considere líneas horizontales y verticales. Utilice la prueba de línea vertical para ver que cualquier línea horizontal representa una función, y que una línea vertical no.
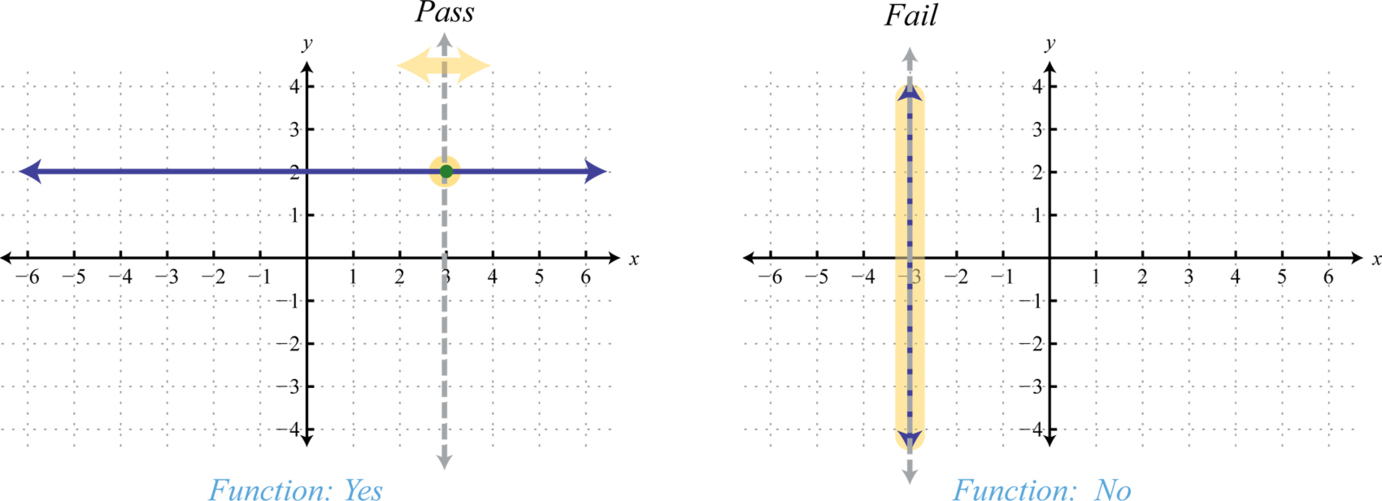
Dada cualquier línea horizontal, la prueba de línea vertical muestra que cada\(x\) -valor en el dominio corresponde exactamente a un\(y\) -valor en el rango; es una función. Una línea vertical, por otro lado, falla la prueba de línea vertical; no es una función. Una línea vertical representa un conjunto de pares ordenados donde todos los elementos del dominio son iguales. Esto viola el requisito de que las funciones deben asociar exactamente un elemento en el rango a cada elemento en el dominio. Resumimos de la siguiente manera:
| Línea Horizontal | Línea Vertical | |
|---|---|---|
| Ecuación: | \(y=2\) | \(x=-3\) |
| \(x\)-interceptar: | Ninguno | \((-3,0)\) |
| \(y\)-interceptar: | \((0,2)\) | Ninguno |
| Dominio: | \(( - \infty , \infty )\) | \(\{ - 3 \}\) |
| Rango: | \(\{ 2 \}\) | \(( - \infty , \infty )\) |
| Función: | Sí | No |
Una línea horizontal a menudo se llama función constante. Dado cualquier número real\(c\),
\(f ( x ) = c\:\:\:\color{Cerulean}{Constant\: Function}\)
Ejemplo\(\PageIndex{5}\):
Grafique la función constante\(g(x)=−2\) y establezca el dominio y el rango.
Solución
Aquí se nos da una función constante que es equivalente a\(y=−2\). Esto define una línea horizontal a través\((0,−2)\).
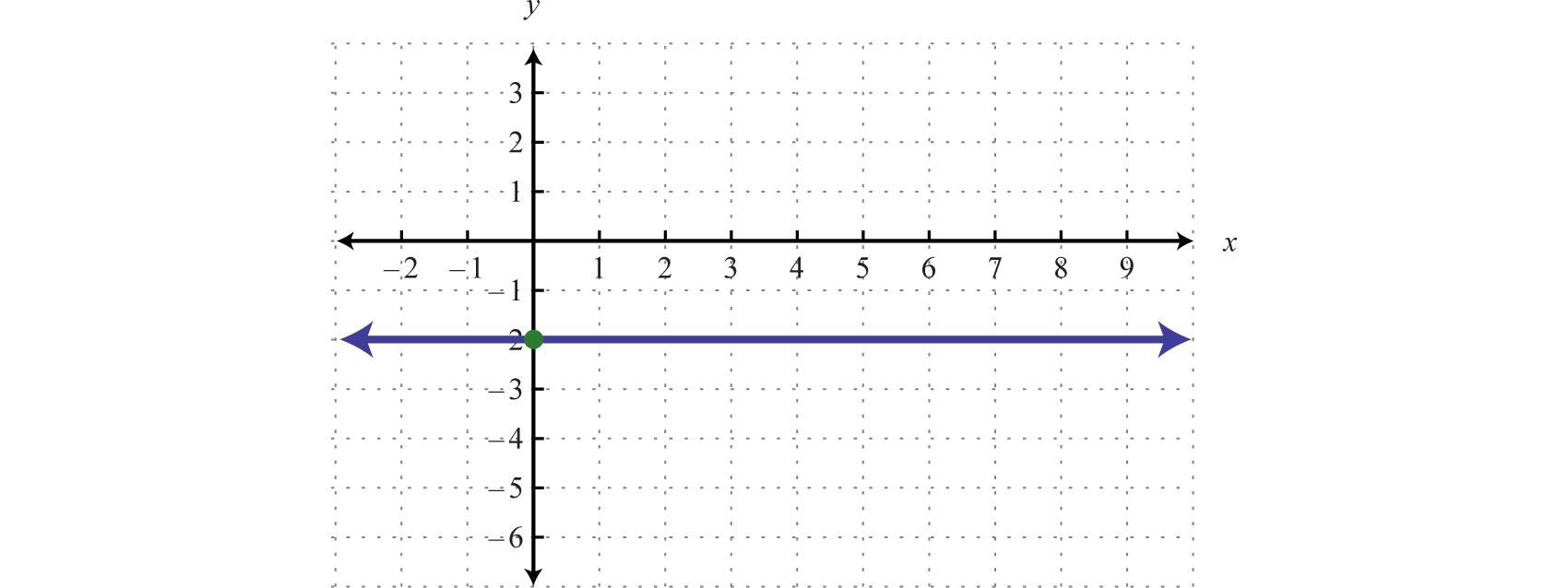
Respuesta:
Dominio:\(ℝ\); rango:\(\{−2\}\)
Ejercicio\(\PageIndex{1}\)
Grafica\(f(x)=3x−2\) y etiqueta la\(x\) -intercepción.
- Contestar
-
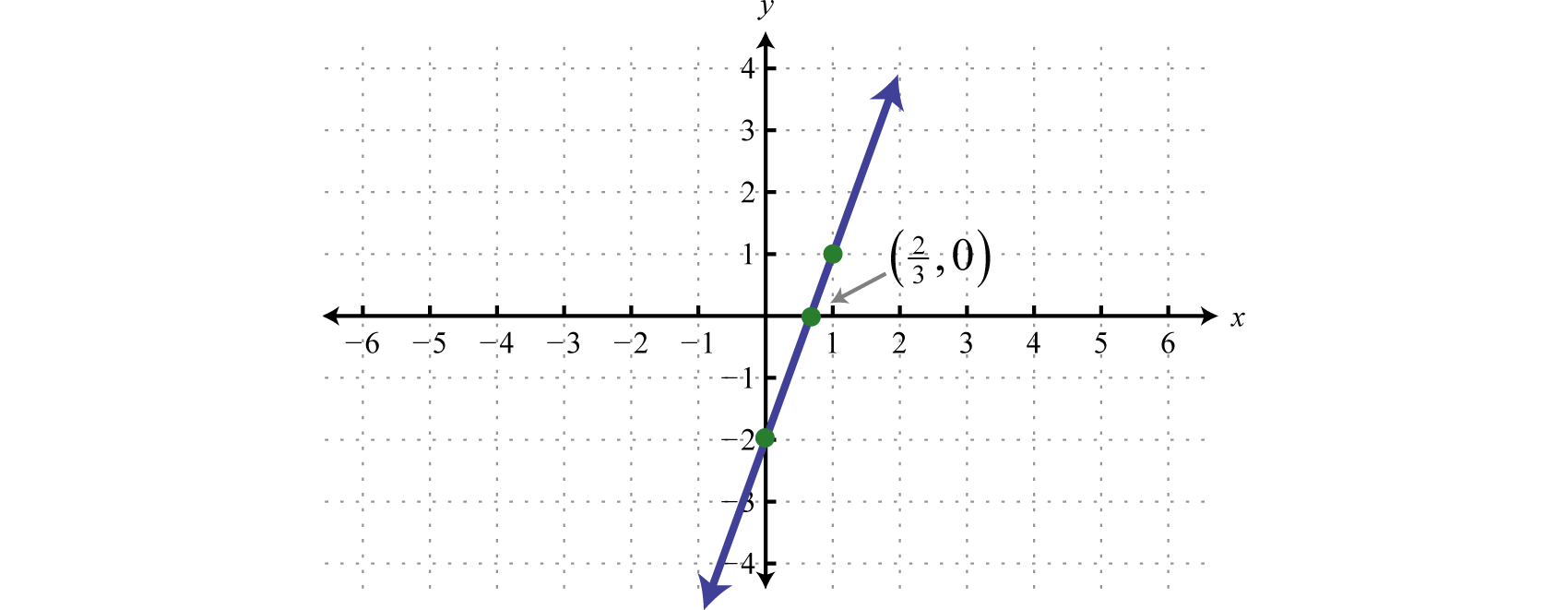
Figura\(\PageIndex{15}\) www.youtube.com/v/iyeppmpamla
Ecuaciones lineales y desigualdades: una interpretación gráfica
Podemos utilizar las ideas de esta sección para desarrollar una comprensión geométrica de lo que significa resolver ecuaciones de la forma\(f (x) = g (x)\), dónde\(f\) y\(g\) son funciones lineales. Usando álgebra, podemos resolver la ecuación lineal de la\(\frac{1}{2} x + 1 = 3\) siguiente manera:
\(\begin{aligned} \frac { 1 } { 2 } x + 1 & = 3 \\ \frac { 1 } { 2 } x & = 2 \\ (\color{Cerulean}{ 2 }\color{Black}{)} \frac { 1 } { 2 } x & = ( \color{Cerulean}{2}\color{Black}{)} 2 \\ x & = 4 \end{aligned}\)
La solución a esta ecuación es\(x = 4\). Geométricamente, este es el\(x\) -valor de la intersección de las dos gráficas\(f (x) = \frac{1}{2} x + 1\) y\(g (x) = 3\). La idea es graficar las funciones lineales a cada lado de la ecuación y determinar dónde coinciden las gráficas.
Ejemplo\(\PageIndex{6}\):
Gráfica\(f(x)=\frac{1}{2}x+1\) y\(g(x)=3\) sobre el mismo conjunto de ejes y determina dónde\(f(x)=g(x)\).
Solución
Aquí\(f\) hay una función lineal con pendiente\(\frac{1}{2}\) e\(y\) -intercepción\((0,1)\). La función\(g\) es una función constante y representa una línea horizontal. Grafica ambas funciones en el mismo conjunto de ejes.
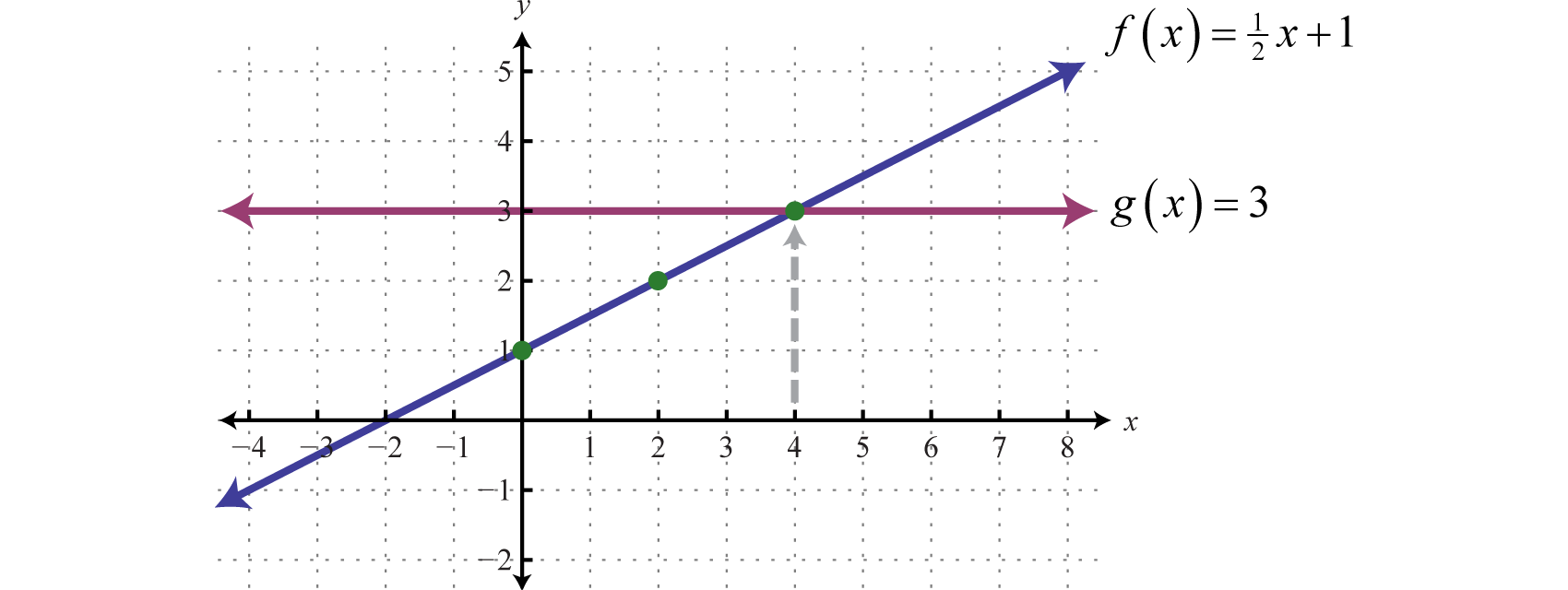
De la gráfica podemos ver que\(f(x)=g(x)\) dónde\(x=4\). En otras palabras,\(\frac{1}{2}x+1=3\) dónde\(x=4\).
Respuesta:
\(x = 4\)
Podemos extender un poco más la interpretación geométrica para resolver las desigualdades. Por ejemplo, podemos resolver la desigualdad lineal\(\frac{1}{2} x + 1 ≥ 3\), utilizando álgebra, de la siguiente manera:
\(\begin{array} { c } { \frac { 1 } { 2 } x + 1 \geq 3 } \\ { \quad \frac { 1 } { 2 } x \geq 2 } \\ ({ \color{Cerulean}{ 2}\color{Black}{)} \frac { 1 } { 2 } x \geq ( \color{Cerulean}{2}\color{Black}{ )} 2 } \\ { x \geq 4 } \end{array}\)
El conjunto de soluciones consiste en todos los números reales mayores o iguales a\(4\). Geométricamente, estos son los\(x\) -valores para los que la gráfica\(f (x) = 1 2 x + 1\) se encuentra por encima de la gráfica de\(g (x) = 3\).
Ejemplo\(\PageIndex{7}\):
Gráfica\(f(x)=\frac{1}{2}x+1\) y\(g(x)=3\) sobre el mismo conjunto de ejes y determina dónde\(f(x)≥g(x)\).
Solución
En la gráfica podemos ver esta sombreada.
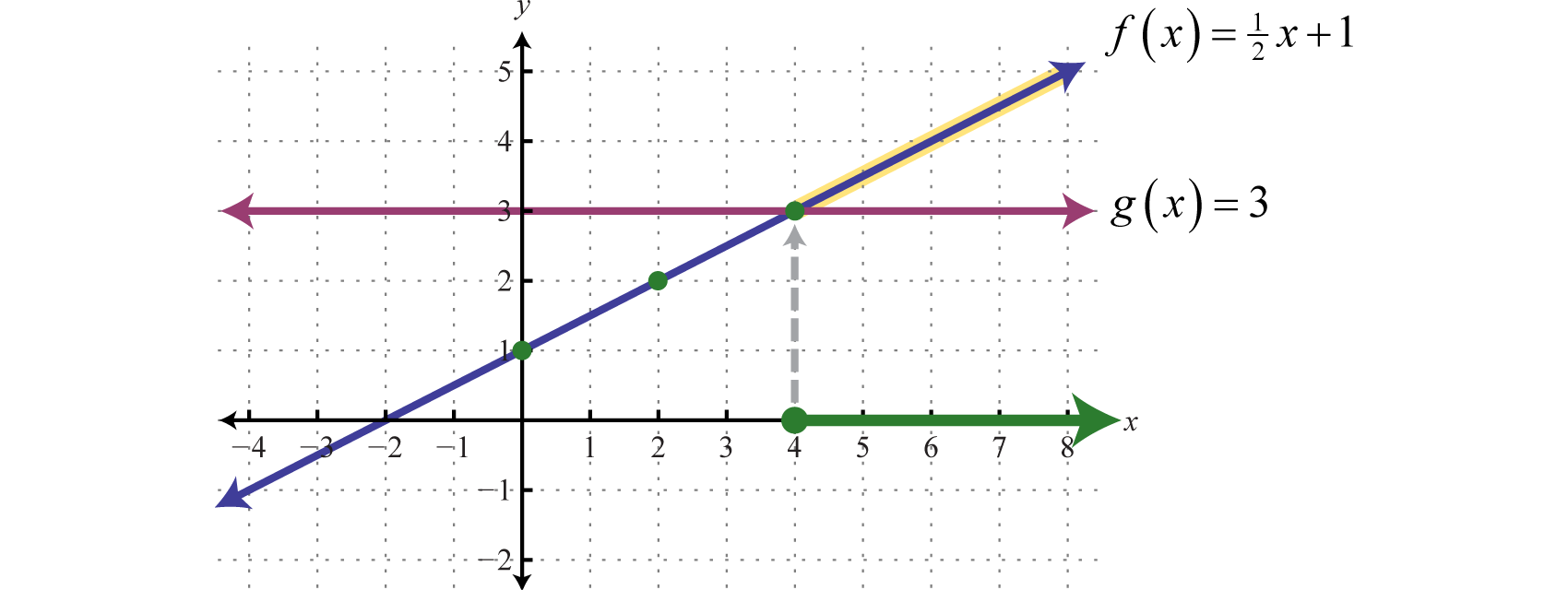
De la gráfica podemos ver eso\(f(x)≥g(x)\) o\(\frac{1}{2}x+1≥3\) dónde\(x≥4\).
Respuesta:
Los\(x\) -valores que resuelven la desigualdad, en notación de intervalos, son\([4,∞)\).
Claves para llevar
- Podemos graficar líneas trazando puntos. Elija algunos valores para\(x\), encuentre los\(y\) valores correspondientes y luego grafique las soluciones de pares ordenados resultantes. Dibuja una línea a través de los puntos con una recta para completar la gráfica.
- Dados dos puntos cualesquiera en una línea, podemos calcular la pendiente algebraicamente usando la fórmula de pendiente,\(m = \frac{rise}{run} = \frac{y_{2}−y_{1}}{x_{2}−x_{1}} = \frac{Δy}{Δx}\).
- Utilice la forma pendiente-intercepción\(y = mx + b\) para esbozar rápidamente la gráfica de una línea. Desde la\(y\) -intercepción\((0, b)\), marque la pendiente para determinar un segundo punto. Dado que dos puntos determinan una línea, dibuja una línea a través de estos dos puntos con una recta para completar la gráfica.
- Las funciones lineales tienen la forma\(f (x) = mx + b\), donde la pendiente\(m\) y\(b\) son números reales. Para encontrar la\(x\) -intercepción, si existe, establecer\(f (x) = 0\: \) y resolver para\(x\).
- Ya que\(y = f (x)\) podemos usar\(y\) e\(f (x)\) indistintamente. Cualquier punto en la gráfica de una función se puede expresar usando notación de función\((x, f (x))\).
Ejercicio\(\PageIndex{2}\)
Encuentra cinco soluciones de pares ordenados y grafica.
- \(y = 3x − 6\)
- \(y = 2x − 4\)
- \(y = −5x + 15\)
- \(y = −3x + 18\)
- \(y = \frac{1}{2} x + 8\)
- \(y = \frac{2}{3} x + 2\)
- \(y = −\frac{3}{5} x + 1\)
- \(y = −\frac{3}{2} x + 4\)
- \(y = \frac{1}{4} x\)
- \(y = −\frac{2}{5} x\)
- \(y = 10\)
- \(x = −1\)
- \(6x + 3y = 18\)
- \(8x − 2y = 16\)
- \(−2x + 4y = 8\)
- \(−x + 3y = 18\)
- \(\frac{1}{2} x − \frac{1}{5} y = 1\)
- \(\frac{1}{6} x − \frac{2}{3} y = 2\)
- \(x + y = 0\)
- \(−x + y = 0\)
- Contestar
-
1.

Figura\(\PageIndex{18}\) 3.
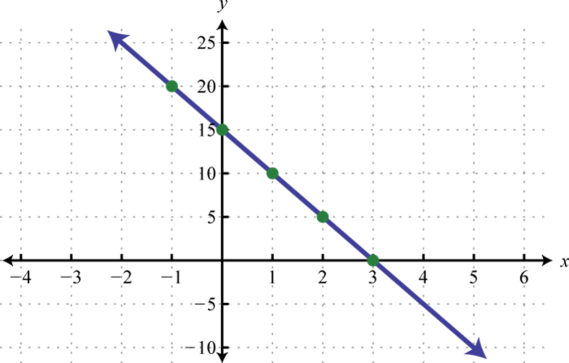
Figura\(\PageIndex{19}\) 5.
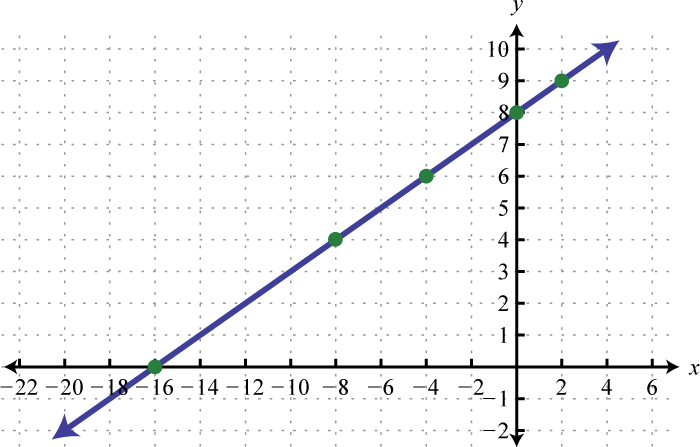
Figura\(\PageIndex{20}\) 7.
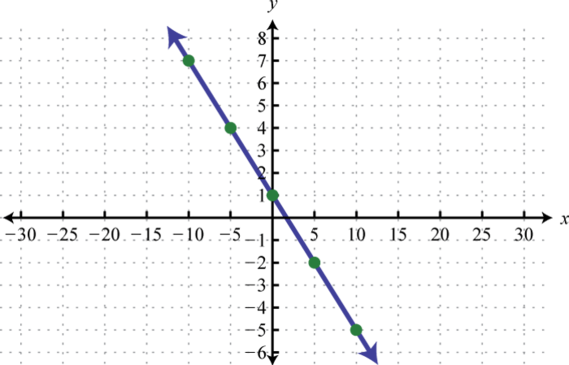
Figura\(\PageIndex{21}\) 9.
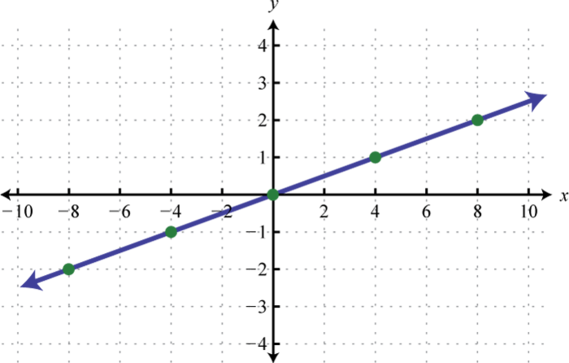
Figura\(\PageIndex{22}\) 11.
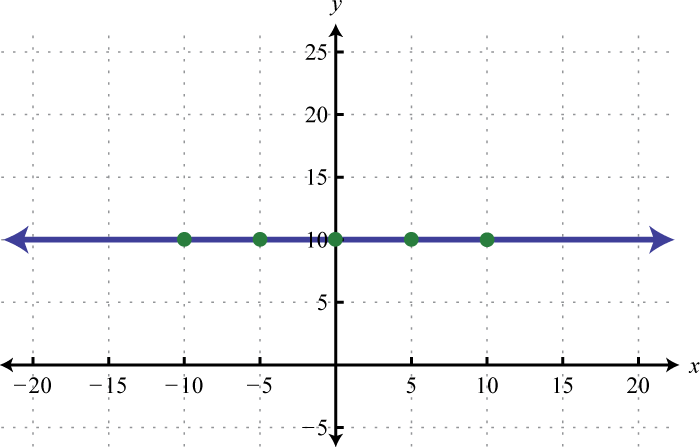
Figura\(\PageIndex{23}\) 13.
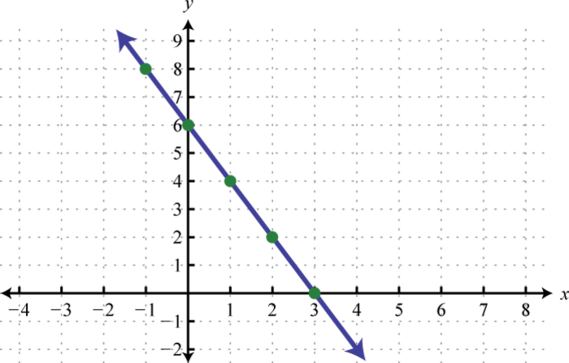
Figura\(\PageIndex{24}\) 15.
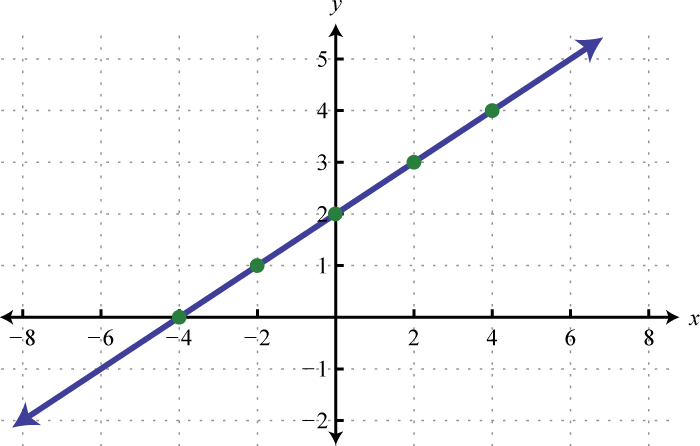
Figura\(\PageIndex{25}\) 17.
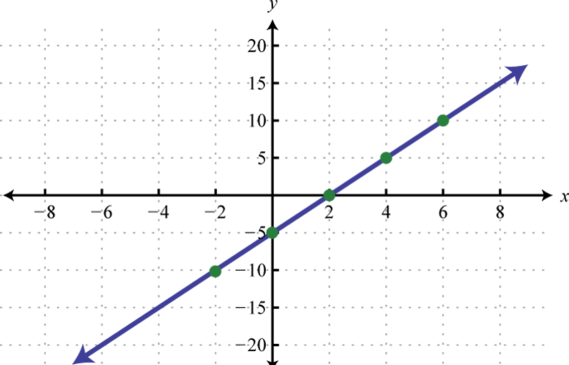
Figura\(\PageIndex{26}\) 19.
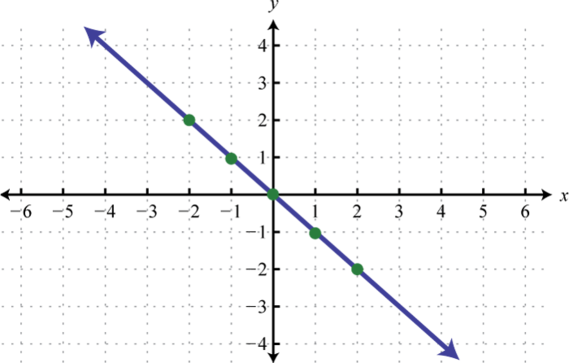
Figura\(\PageIndex{27}\)
Ejercicio\(\PageIndex{3}\)
Encuentra la pendiente de la línea que pasa por los puntos dados.
- \((-2, -4)\)y\((1, -1)\)
- \((-3,0)\)y\((3, -4)\)
- \((-\frac{5}{2}, \frac{1}{4})\)y\((-\frac{1}{2}, \frac{5}{4})\)
- \((-4, -3)\)y\((-2, -3)\)
- \((9, -5)\)y\((9, -6)\)
- \((\frac{1}{2}, -1)\)y\((-1, -\frac{3}{2})\)
- Contestar
-
1. \(1\)
3. \(\frac{1}{2}\)
5. Sin definir
Ejercicio\(\PageIndex{4}\)
Encuentra el\(y\) -valor para el cual la pendiente de la línea que pasa por puntos dados tiene la pendiente dada.
- \(m = \frac { 3 } { 2 } ; ( 6,10 ) , ( - 4 , y )\)
- \(m = - \frac { 1 } { 3 } ; ( - 6,4 ) , ( 9 , y )\)
- \(m = - 4 ; ( - 2,5 ) , ( - 1 , y )\)
- \(m = 3 ; ( 1 , - 2 ) , ( - 2 , y )\)
- \(m = \frac { 1 } { 5 } ; ( 1 , y ) , \left( 6 , \frac { 1 } { 5 } \right)\)
- \(m = - \frac { 3 } { 4 } ; ( - 1 , y ) , ( - 4,5 )\)
- Contestar
-
1. \(y=-5\)
3. \(y=1\)
5. \(y=-\frac{4}{5}\)
Ejercicio\(\PageIndex{5}\)
Dada la gráfica, determinar la pendiente.
1.
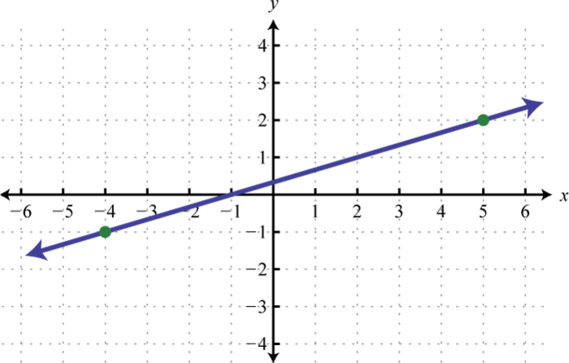
2.
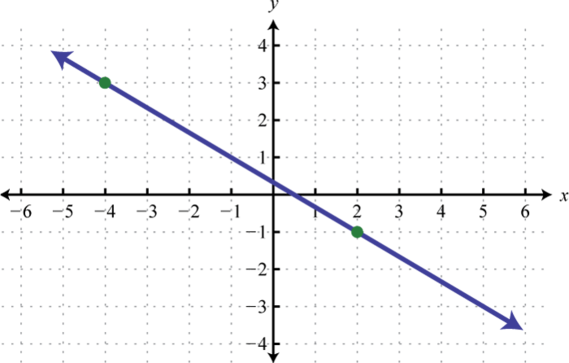
3.
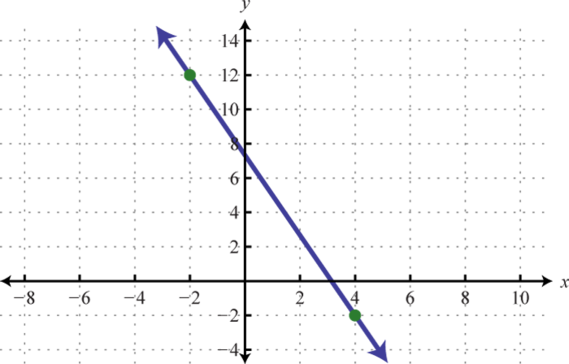
4.
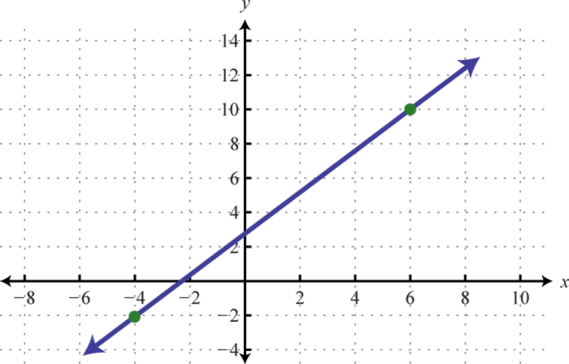
5.
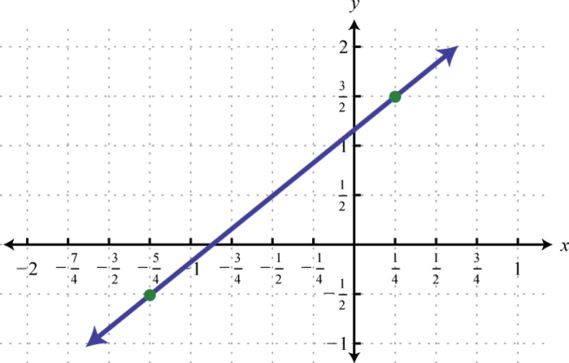
6.
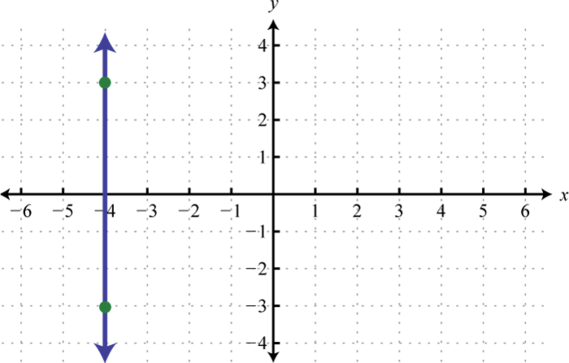
7.
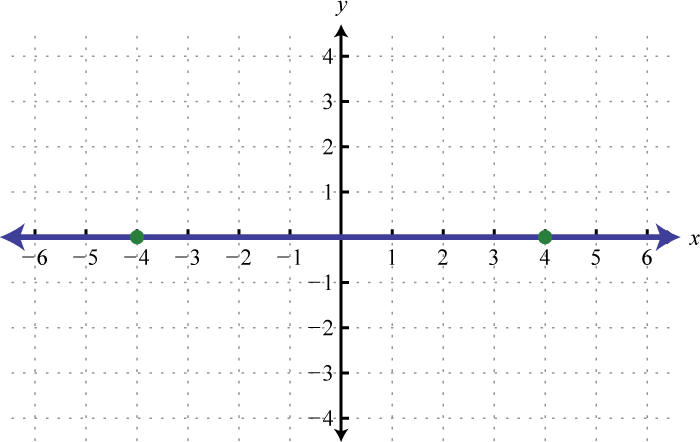
8.
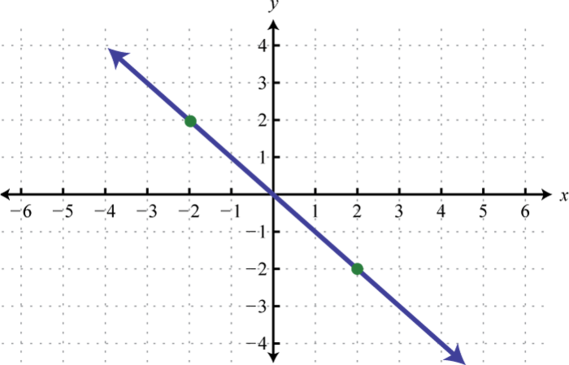
- Contestar
-
1. \(m = \frac { 1 } { 3 }\)
3. \(m = - \frac { 7 } { 3 }\)
5. \(m = \frac { 4 } { 3 }\)
7. \(m=0\)
Ejercicio\(\PageIndex{6}\)
\(x\)Encuentra las\(y\) intercepciones y utilízalas para graficar las siguientes funciones.
- \(6x − 3y = 18\)
- \(8x − 2y = 8\)
- \(−x + 12y = 6\)
- \(−2x − 6y = 8\)
- \(x − 2y = 5\)
- \(−x + 3y = 1\)
- \(2x + 3y = 2\)
- \(5x − 4y = 2\)
- \(9x − 4y = 30\)
- \(−8x + 3y = 28\)
- \(\frac{1}{3} x + \frac{1}{2} y = −3\)
- \(\frac{1}{4} x − \frac{1}{3} y = 3\)
- \(\frac{7}{9} x − \frac{2}{3} y = \frac{14}{3}\)
- \(\frac{1}{8} x − \frac{1}{6} y = −\frac{3}{2}\)
- \(−\frac{1}{6} x + \frac{2}{9} y = \frac{4}{3}\)
- \(\frac{2}{15} x + \frac{1}{6} y = \frac{4}{3}\)
- \(y = −\frac{1}{4} x + \frac{1}{2}\)
- \(y = \frac{3}{8} x −\frac{3}{2}\)
- \(y = \frac{2}{3} x + \frac{1}{2}\)
- \(y = \frac{4}{5} x + 1\)
- Contestar
-
1.
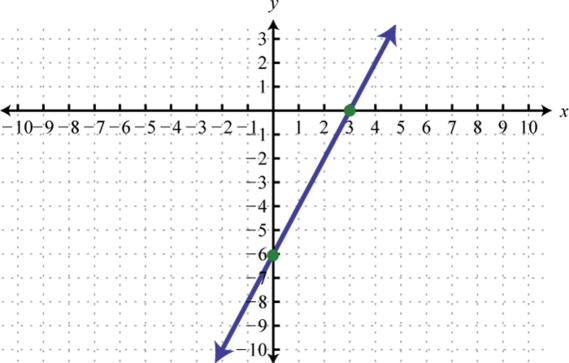
Figura\(\PageIndex{36}\) 3.
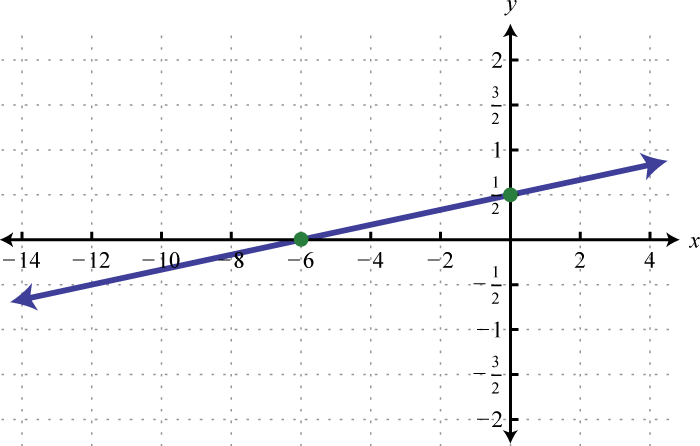
Figura\(\PageIndex{37}\) 5.
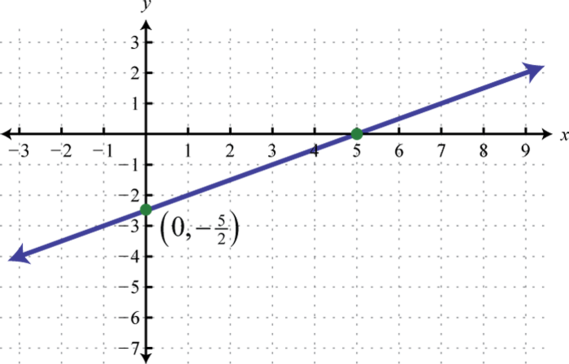
Figura\(\PageIndex{38}\) 7.
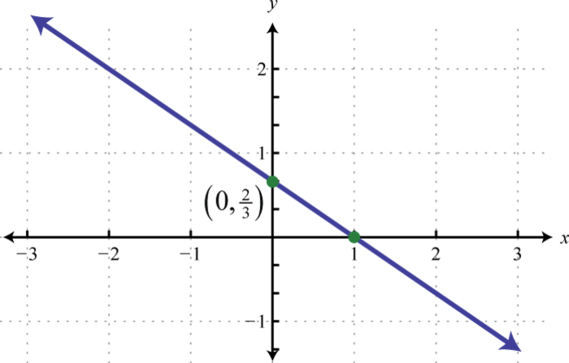
Figura\(\PageIndex{39}\) 9.
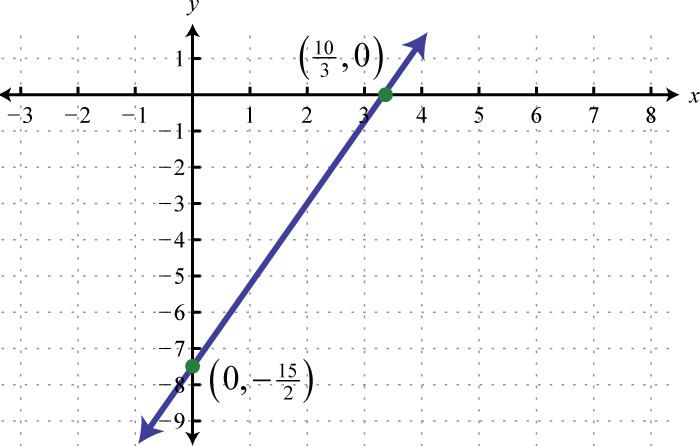
Figura\(\PageIndex{40}\) 11.
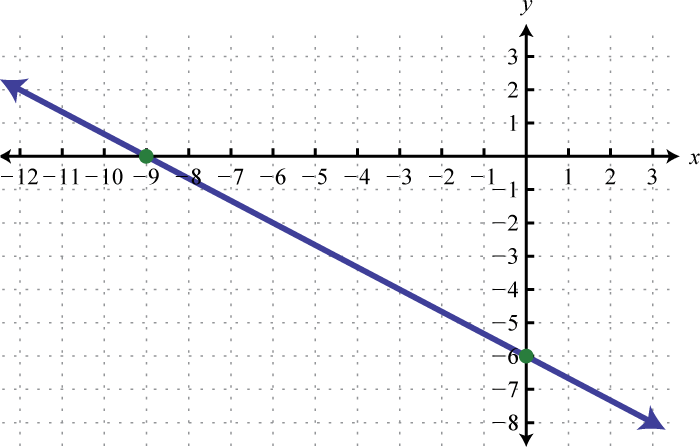
Figura\(\PageIndex{41}\) 13.
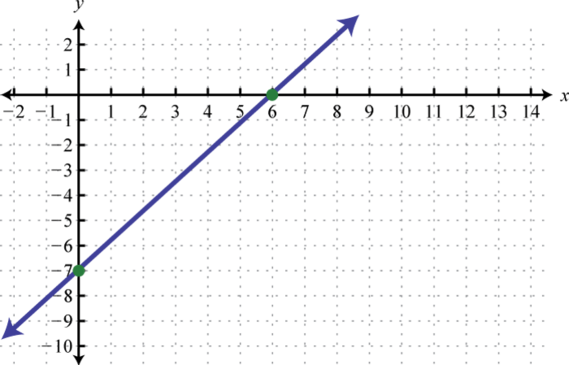
Figura\(\PageIndex{42}\) 15.
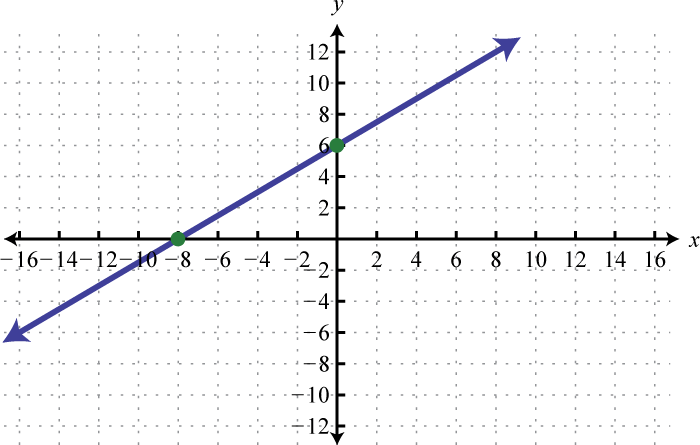
Figura\(\PageIndex{43}\) 17.
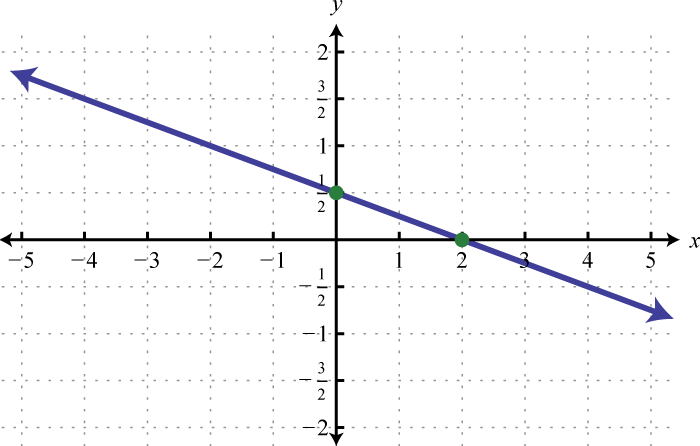
Figura\(\PageIndex{44}\) 19.
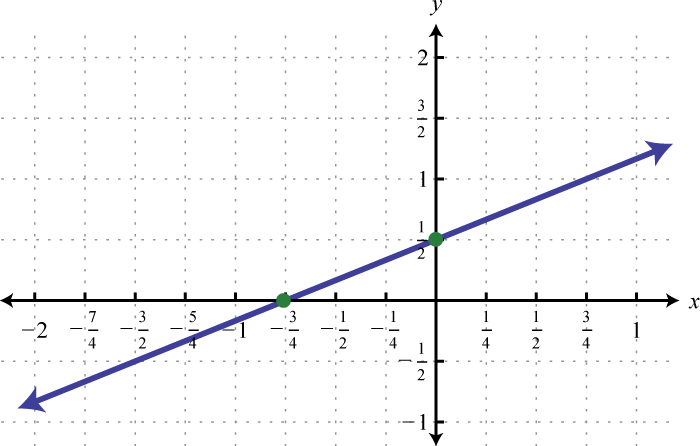
Figura\(\PageIndex{45}\)
Ejercicio\(\PageIndex{7}\)
Grafica la función lineal y etiqueta la\(x\) -intercepción.
- \(f (x) = −5x + 15\)
- \(f (x) = −2x + 6\)
- \(f (x) = −x − 2\)
- \(f (x) = x + 3\)
- \(f (x) = \frac{1}{3} x + 2\)
- \(f (x) = \frac{5}{2} x + 10\)
- \(f (x) = \frac{5}{3} x + 2\)
- \(f (x) = \frac{2}{5} x − 3\)
- \(f (x) = −\frac{5}{6} x + 2\)
- \(f (x) = −\frac{4}{3} x + 3\)
- \(f (x) = 2x\)
- \(f (x) = 3\)
- Contestar
-
1.
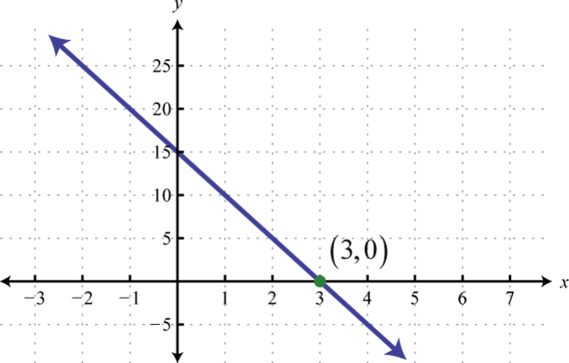
Figura\(\PageIndex{46}\) 3.
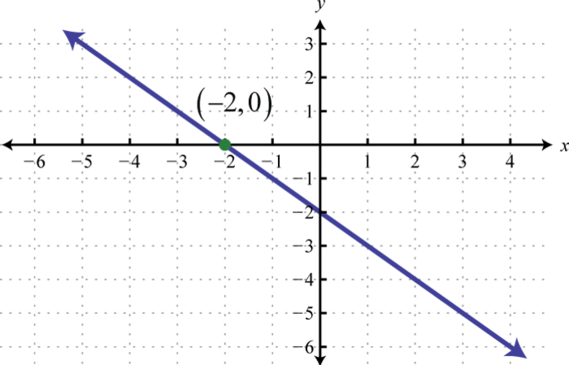
Figura\(\PageIndex{47}\) 5.
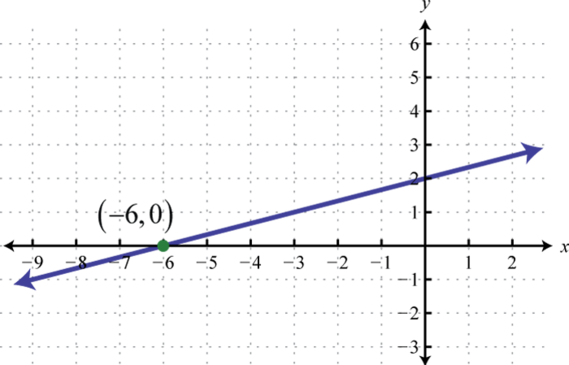
Figura\(\PageIndex{48}\) 7.
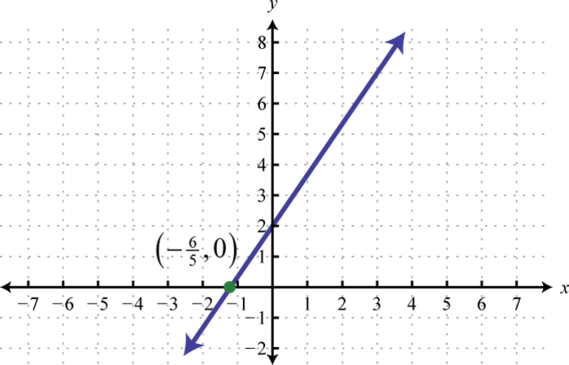
Figura\(\PageIndex{49}\) 9.
Figura\(\PageIndex{50}\) 11.
Figura\(\PageIndex{51}\)
Ejercicio\(\PageIndex{8}\)
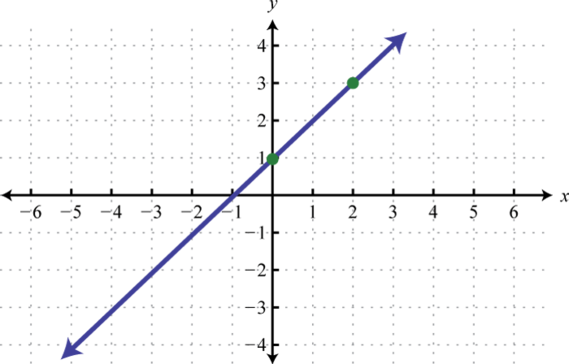
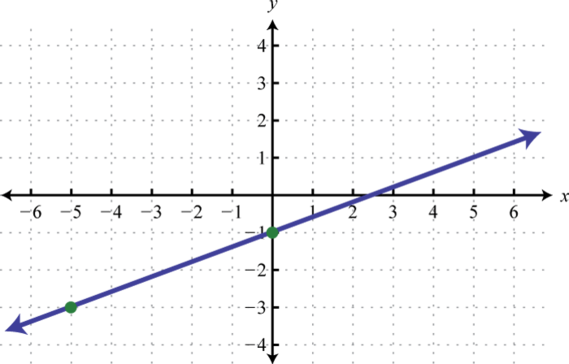
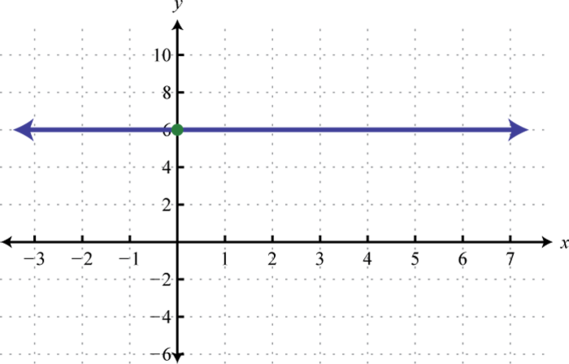
Determine la función lineal que define la gráfica dada y encuentre la\(x\) -intercepción.
1.
2.
3.
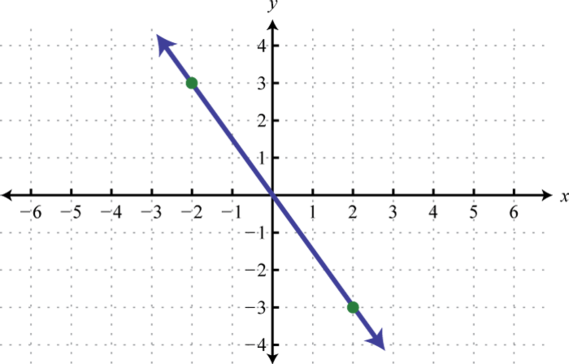
4.
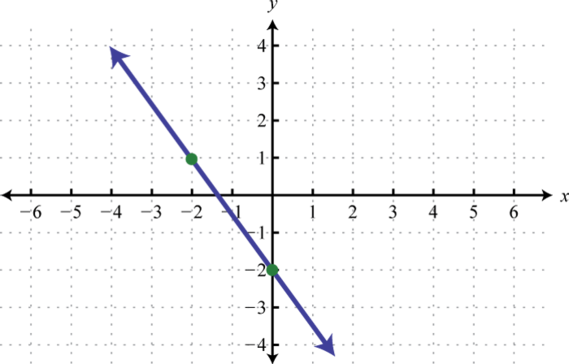
5.

6.
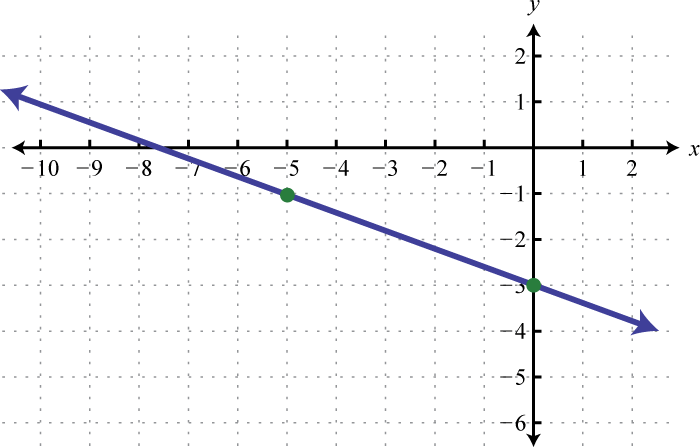
7.
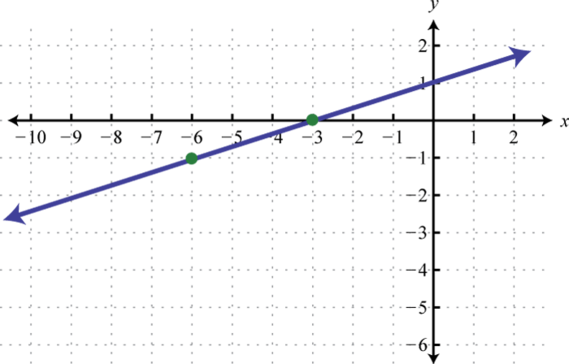
8.
- Contestar
-
1. \(f (x) = x + 1; (−1, 0)\)
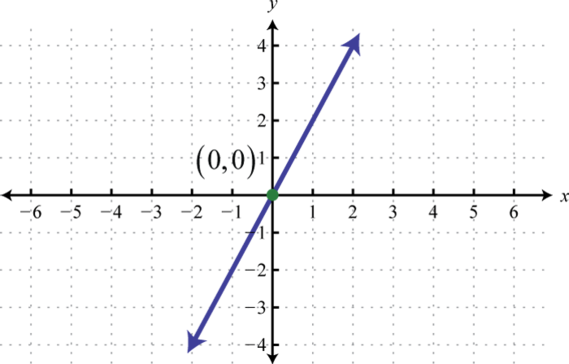
3. \(f (x) = −\frac{3}{2} x; (0, 0)\)
5. \(f (x) = −9;\)ninguno
7. \(f (x) = \frac{1}{3} x + 1; (−3, 0)\)
Ejercicio\(\PageIndex{9}\)
Grafica las funciones\(f\) y\(g\) en el mismo conjunto de ejes y determina dónde\(f(x)=g(x)\). Verifica algebraicamente tu respuesta.
- \(f (x) = \frac{1}{2} x − 3, g (x) = 1\)
- \(f (x) = \frac{1}{3} x + 2, g (x) = −1\)
- \(f (x) = 3x − 2 , g (x) = −5\)
- \(f (x) = x + 2, g (x) = −3\)
- \(f (x) = −\frac{2}{3} x + 4, g (x) = 2\)
- \(f (x) = −\frac{5}{2} x + 6, g (x) = 1\)
- \(f (x) = 3x − 2 , g (x) = −2x + 3\)
- \(f (x) = −x + 6, g (x) = x + 2\)
- \(f (x) = −\frac{1}{3} x, g (x) = −\frac{2}{3} x + 1\)
- \(f (x) = \frac{2}{3} x − 1, g (x) = −\frac{4}{3} x − 3\)
- Contestar
-
1. \(x = 8\)
3. \(x = −1\)
5. \(x = 3\)
7. \(x = 1\)
9. \(x = 3\)
Ejercicio\(\PageIndex{10}\)
Grafica las funciones\(f\) y\(g\) en el mismo conjunto de ejes y determina dónde\(f(x)\geq g(x)\). Verifica algebraicamente tu respuesta.
- \(f (x) = 3x + 7 , g (x) = 1\)
- \(f (x) = 5x − 3 , g (x) = 2\)
- \(f (x) = \frac{2}{3} x − 3, g (x) = −3\)
- \(f (x) = \frac{3}{4} x + 2, g (x) = −1\)
- \(f (x) = −x + 1, g (x) = −3\)
- \(f (x) = −4x + 4 , g (x) = 8\)
- \(f (x) = x − 2, g (x) = −x + 4\)
- \(f (x) = 4x − 5 , g (x) = x + 1\)
- Contestar
-
1. \([ - 2 , \infty )\)
3. \([ 0 , \infty )\)
5. \(( - \infty , 4 ]\)
7. \([ 3 , \infty )\)
Ejercicio\(\PageIndex{11}\)
Grafica las funciones\(f\) y\(g\) en el mismo conjunto de ejes y determina dónde\(f(x)<g(x)\). Verifica algebraicamente tu respuesta.
- \(f (x) = x + 5, g (x) = −1\)
- \(f (x) = 3x − 3 , g (x) = 6\)
- \(f (x) = −\frac{4}{5} x, g (x) = −8\)
- \(f (x) = −\frac{3}{2} x + 6, g (x) = −3\)
- \(f (x) = \frac{1}{4} x + 1, g (x) = 0\)
- \(f (x) = \frac{3}{5} x − 6, g (x) = 0\)
- \(f (x) = \frac{1}{3} x + 2, g (x) = − \frac{1}{3} x\)
- \(f (x) = \frac{3}{2} x + 3, g (x) = −\frac{3}{2} x − 3\)
- Contestar
-
1. \(( - \infty , - 6 )\)
3. \(( 10 , \infty )\)
5. \(( - \infty , - 4 )\)
7. \(( - \infty , - 3 )\)
Ejercicio\(\PageIndex{12}\)
- ¿Todas las funciones lineales tienen\(y\) -intercepciones? ¿Todas las funciones lineales tienen\(x\) -intercepciones? Explique.
- ¿Puede una función tener más\(y\) de una intercepción? Explique.
- ¿Cómo muestra la prueba de línea vertical que una línea vertical no es una función?
- Contestar
-
1. La respuesta puede variar
3. La respuesta puede variar
Notas al pie
18 La variable que determina los valores de otras variables. Por lo general, pensamos en el\(x\) -valor de un par ordenado\((x, y)\) como la variable independiente.
19 La variable cuyo valor está determinado por el valor de la variable independiente. Por lo general, pensamos en el\(y\) -valor de un par ordenado\((x, y)\) como la variable dependiente.
20 Una forma de determinar una gráfica utilizando un número finito de soluciones representativas de pares ordenados.
21 La inclinación de una línea medida como la relación entre el cambio vertical y el cambio horizontal, a menudo denominado “subida sobre carrera”.
22 El cambio vertical entre dos puntos cualesquiera en una línea.
23 El cambio horizontal entre dos puntos cualesquiera en una línea.
24 La pendiente de la línea a través de los puntos\((x1, y1)\) y\((x2, y2)\) viene dada por la fórmula\(m = \frac{y2−y1}{x2−x1}\).
25 Cualquier línea no vertical se puede escribir en forma estándar\(ax + by = c\).
26 Cualquier línea no vertical se puede escribir en la forma\(y = mx + b\), donde\(m\) está la pendiente y\((0, b)\) es la\(y\) intersección.
27 El punto (o puntos) donde una gráfica cruza el eje y, expresado como un par ordenado\((0, y)\).
28 Cualquier función que pueda escribirse en la forma f (x) = mx + b
29 El punto (o puntos) donde una gráfica se cruza con el eje x, expresado como un par ordenado (x, 0).


