1.2: Clases Básicas de Funciones

Objetivos de aprendizaje

• Calcular la pendiente de una función lineal e interpretar su significado.
• Reconocer el grado de un polinomio.
• Encontrar las raíces de un polinomio cuadrático.
• Describir las gráficas de funciones polinómicas pares e impares básicas.
• Identificar una función racional.
• Describir las gráficas de poder y funciones raíz.
• Explicar la diferencia entre funciones algebraicas y trascendentales.
• Grafique una función definida por partes.
• Esboce la gráfica de una función que ha sido desplazada, estirada o reflejada desde su posición inicial de gráfico.

Hemos estudiado las características generales de las funciones, así que ahora examinemos algunas clases específicas de funciones. Comenzamos revisando las propiedades básicas de las funciones lineales y cuadráticas, y luego generalizamos para incluir polinomios de mayor grado. Al combinar funciones raíz con polinomios, podemos definir funciones algebraicas generales y distinguirlas de las funciones trascendentales que examinamos más adelante en este capítulo. Terminamos la sección con ejemplos de funciones definidas por partes y echamos un vistazo a cómo esbozar la gráfica de una función que ha sido desplazada, estirada o reflejada desde su forma inicial.

Funciones lineales y pendiente

El tipo de función más fácil de considerar es una función lineal. Las funciones lineales tienen la forma\(f(x)=ax+b\), donde\(a\) y\(b\) son constantes. En la Figura\(\PageIndex{1}\), vemos ejemplos de funciones lineales cuando a es positivo, negativo y cero. Tenga en cuenta que si\(a>0\), la gráfica de la línea se eleva a medida que\(x\) aumenta. En otras palabras,\(f(x)=ax+b\) está aumentando en\((−∞, ∞)\). Si\(a<0\), la gráfica de la línea cae a medida que\(x\) aumenta. En este caso,\(f(x)=ax+b\) está disminuyendo el\((−∞, ∞)\). Si\(a=0\), la línea es horizontal.

Figura\(\PageIndex{1}\): Estas funciones lineales están aumentando o disminuyendo\((∞, ∞)\) y una función es una línea horizontal.

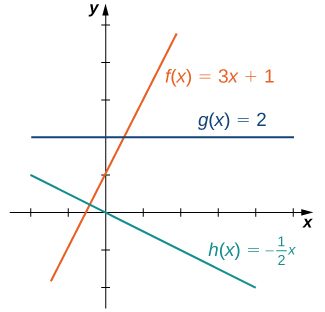
Como sugiere la Figura\(\PageIndex{1}\), la gráfica de cualquier función lineal es una línea. Una de las características distintivas de una línea es su pendiente. La pendiente es el cambio en\(y\) para cada cambio de unidad en\(x\). La pendiente mide tanto la inclinación como la dirección de una línea. Si la pendiente es positiva, la línea apunta hacia arriba cuando se mueve de izquierda a derecha. Si la pendiente es negativa, la línea apunta hacia abajo cuando se mueve de izquierda a derecha. Si la pendiente es cero, la línea es horizontal. Para calcular la pendiente de una línea, necesitamos determinar la relación del cambio en\(y\) versus el cambio en\(x\). Para ello, elegimos dos puntos cualquiera\((x_1,y_1)\) y\((x_2,y_2)\) en la línea y calculamos\(\dfrac{y_2−y_1}{x_2−x_1}\). En la Figura\(\PageIndex{2}\), vemos que esta relación es independiente de los puntos elegidos.

Figura\(\PageIndex{2}\): Para cualquier función lineal, la pendiente\((y_2−y_1)/(x_2−x_1)\) es independiente de la elección de los puntos\((x_1,y_1)\) y\((x_2,y_2)\) en la línea.

Definición: Pendiente de una función lineal

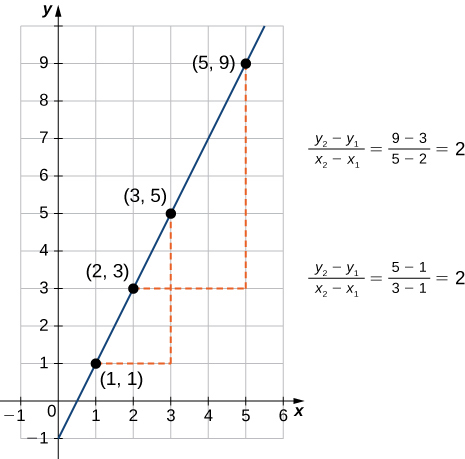
Considere el\(L\) paso de línea por puntos\((x_1,y_1)\) y\((x_2,y_2)\). Dejar\(Δy=y_2−y_1\) y\(Δx=x_2−x_1\) denotar los cambios en\(y\) y\(x\), respectivamente. La pendiente de la línea es

\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{Δy}{Δx} \nonumber \]

Ahora examinamos la relación entre pendiente y la fórmula para una función lineal. Considera la función lineal dada por la fórmula\(f(x)=ax+b\). Como se discutió anteriormente, sabemos que la gráfica de una función lineal viene dada por una línea. Podemos usar nuestra definición de pendiente para calcular la pendiente de esta línea. Como se muestra, podemos determinar la pendiente calculando\((y_2−y_1)/(x_2−x_1)\) para cualquier punto\((x_1,y_1)\) y\((x_2,y_2)\) en la línea. Evaluando la función\(f\) en\(x=0\), vemos que\((0,b)\) es un punto en esta línea. Evaluando esta función en\(x=1\), vemos que también\((1,a+b)\) es un punto en esta línea. Por lo tanto, la pendiente de esta línea es

\[\dfrac{(a+b)−b}{1−0}=a. \nonumber \]

Hemos demostrado que el coeficiente\(a\) es la pendiente de la línea. Podemos concluir que la fórmula\(f(x)=ax+b\) describe una línea con pendiente\(a\). Además, debido a que esta línea cruza el\(y\) eje -eje en el punto\((0,b)\), vemos que la\(y\) -intercepción para esta función lineal es\((0,b)\). Concluimos que la fórmula nos\(f(x)=ax+b\) dice la pendiente,\(a\), y la\(y\) -intercepción,\((0,b)\), para esta línea. Como a menudo usamos el símbolo\(m\) para denotar la pendiente de una línea, podemos escribir

\[\underbrace{f(x)=mx+b}_{\text{slope-intercept form}} \nonumber \]

para denotar la forma pendiente-intercepción de una función lineal.

A veces es conveniente expresar una función lineal de diferentes maneras. Por ejemplo, supongamos que la gráfica de una función lineal pasa por el punto\((x_1,y_1)\) y la pendiente de la línea es\(m\). Dado que cualquier otro punto\((x,f(x))\) en la gráfica de\(f\) debe satisfacer la ecuación

\[m=\dfrac{f(x)−y_1}{x−x_1}, \nonumber \]

esta función lineal se puede expresar escribiendo

\[\underbrace{f(x)−y_1=m(x−x_1)}_{\text{point-slope equation}}. \nonumber \]

Llamamos a esta ecuación la ecuación de punto-pendiente para esa función lineal.

Dado que cada línea no vertical es la gráfica de una función lineal, los puntos en una línea no vertical se pueden describir usando las ecuaciones de pendiente-intersección o punto-pendiente. Sin embargo, una línea vertical no representa la gráfica de una función y no puede expresarse en ninguna de estas formas. En cambio, una línea vertical es descrita por la ecuación\(x=k\) para alguna constante\(k\). Como ni la forma pendiente-intersección ni la forma punto-pendiente permiten líneas verticales, usamos la notación

\[\underbrace{ax+by=c}_{\text{standard form}}, \nonumber \]

donde ambos no\(a,b\) son cero, para denotar la forma estándar de una línea.

Definición: Ecuación de Punto-Pendiente, Forma de Inclinación-Intercepción y Forma Estándar de la Ecuación de una Línea

Considera una línea que pasa por el punto\((x_1,y_1)\) con pendiente\(m\). La ecuación

\[y−y_1=m(x−x_1) \nonumber \]

es la ecuación de punto-pendiente para esa línea.

Considerar una línea con pendiente\(m\) e\(y\) -interceptar\((0,b).\) La ecuación

\[y=mx+b \nonumber \]

es una ecuación para esa línea en forma de pendiente-intercepción.

La forma estándar de una línea viene dada por la ecuación

\[ax+by=c, \nonumber \]

donde\(a\) y ambos no\(b\) son cero. Esta forma es más general porque permite una línea vertical,\(x=k\).

Ejemplo\(\PageIndex{1}\): Finding the Slope and Equations of Lines

Considera la línea que pasa por los puntos\((11,−4)\) y\((−4,5)\), como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Encontrar la ecuación de una función lineal con una gráfica que es una línea entre dos puntos dados.

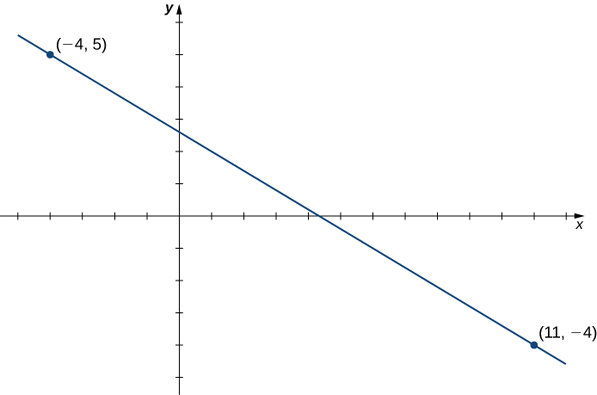
1. Encuentra la pendiente de la línea.
2. Encuentra una ecuación para esta función lineal en forma de punto-pendiente.
3. Encuentra una ecuación para esta función lineal en forma de pendiente-intercepción.

Solución

1. La pendiente de la línea es

\[m=\dfrac{y_2−y_1}{x_2−x_1}=\dfrac{5−(−4)}{−4−11}=−\dfrac{9}{15}=−\dfrac{3}{5}. \nonumber \]

2. Para encontrar una ecuación para la función lineal en forma de punto-pendiente, utilice la pendiente\(m=−3/5\) y elija cualquier punto de la línea. Si elegimos el punto\((11,−4)\), obtenemos la ecuación

\[f(x)+4=−\dfrac{3}{5}(x−11). \nonumber \]

3. Para encontrar una ecuación para la función lineal en forma pendiente-intersección, resuelva la ecuación en la parte b. para\(f(x)\). Cuando hacemos esto, obtenemos la ecuación

\[f(x)=−\dfrac{3}{5}x+\dfrac{13}{5}. \nonumber \]

Ejercicio\(\PageIndex{1}\)

Considera la línea que pasa por puntos\((−3,2)\) y\((1,4)\).

1. Encuentra la pendiente de la línea.
2. Encuentra una ecuación de esa línea en forma de punto-pendiente.
3. Encuentra una ecuación de esa línea en forma de pendiente-intercepción.

Pista

La pendiente\(m=Δy/Δx\).

Contestar a

\(m=1/2\).

Respuesta b

La forma punto-pendiente es\(y−4=\dfrac{1}{2}(x−1)\).

Respuesta c

La forma pendiente-intercepción es\(y=\dfrac{1}{2}x+\dfrac{7}{2}\).

Ejemplo\(\PageIndex{2}\):

Jessica sale de su casa a las 5:50 a.m. y va a correr de 9 millas. Ella regresa a su casa a las 7:08 a.m. Responde las siguientes preguntas, asumiendo que Jessica corre a un ritmo constante.

1. Describir la distancia\(D\) (en millas) que Jessica recorre como una función lineal de su tiempo de ejecución\(t\) (en minutos).
2. Esbozar una gráfica de\(D\).
3. Interpretar el significado de la pendiente.

Solución

a. en su momento\(t=0\), Jessica está en su casa, entonces\(D(0)=0\). A tiempo\(t=78\) minutos, Jessica ha terminado de correr\(9\) mi, entonces\(D(78)=9\). La pendiente de la función lineal es

\[m=\dfrac{9−0}{78−0}=\dfrac{3}{26}.\nonumber \]

El\(y\) -intercept es\((0,0)\), así que la ecuación para esta función lineal es

\[D(t)=\dfrac{3}{26}t. \nonumber \]

b. para graficar\(D\), utilizar el hecho de que la gráfica pasa por el origen y tiene pendiente\(m=3/26.\)

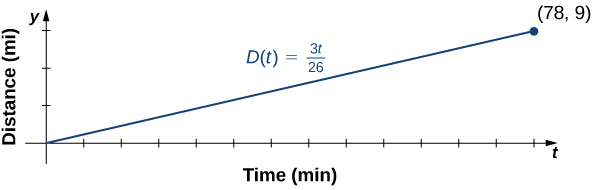
c. La pendiente\(m=3/26≈0.115\) describe la distancia (en millas) que Jessica recorre por minuto, o su velocidad promedio.

Polinomios

Una función lineal es un tipo especial de una clase de funciones más general: polinomios. Una función polinómica es cualquier función que se pueda escribir en la forma

\[f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0 \nonumber \]

para algunos enteros\(n≥0\) y constantes\(a_n,a_{n−1},…,a_0\), donde\(a_n≠0\). En el caso cuando\(n=0\), permitimos\(a_0=0\); si\(a_0=0\), la función\(f(x)=0\) se llama la función cero. El valor\(n\) se llama el grado del polinomio; la constante\(a_n\) se llama el coeficiente principal. Una función lineal de la forma\(f(x)=mx+b\) es un polinomio de grado 1 si\(m≠0\) y grado 0 si\(m=0\). Un polinomio de grado 0 también se llama función constante. Una función polinómica de grado 2 se denomina función cuadrática. En particular, una función cuadrática tiene la forma

\[f(x)=ax^2+bx+c, \nonumber \]

donde\(a≠0\). Una función polinómica de grado\(3\) se llama función cúbica.

Funciones de alimentación

Algunas funciones polinómicas son funciones de potencia. Una función de potencia es cualquier función de la forma\(f(x)=ax^b\), donde\(a\) y\(b\) son los números reales. El exponente en una función de potencia puede ser cualquier número real, pero aquí consideramos el caso cuando el exponente es un entero positivo. (Consideramos otros casos más adelante.) Si el exponente es un entero positivo, entonces\(f(x)=ax^n\) es un polinomio. Si\(n\) es par, entonces\(f(x)=ax^n\) es una función par porque\(f(−x)=a(−x)^n=ax^n\) si\(n\) es par. Si\(n\) es impar, entonces\(f(x)=ax^n\) es una función impar porque\(f(−x)=a(−x)^n=−ax^n\) if\(n\) es impar (Figura\(\PageIndex{4}\)).

Figura\(\PageIndex{4}\): (a) Para cualquier entero par\(n\),\(f(x)=ax^n\) es una función par. (b) Para cualquier entero impar\(n\),\(f(x)=ax^n\) es una función impar.

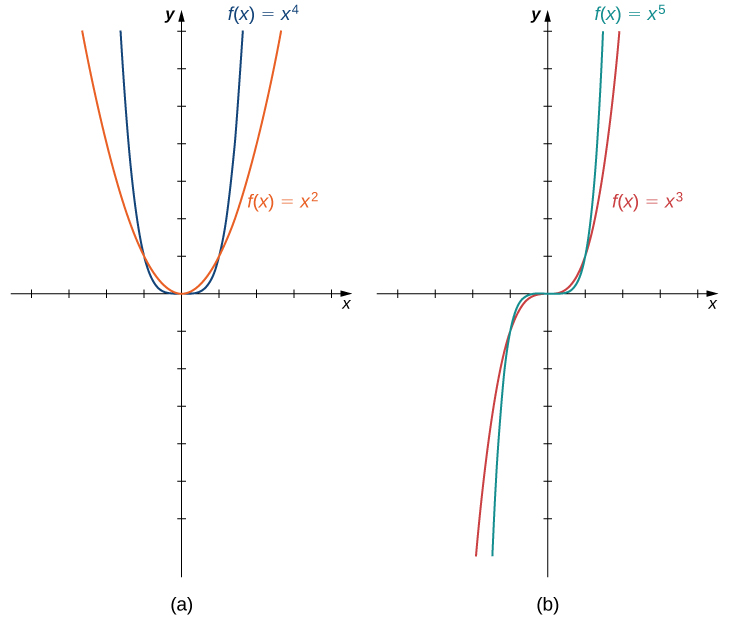
Comportamiento en el Infinito

Para determinar el comportamiento de una función a\(f\) medida que las entradas se acercan al infinito, observamos los valores\(f(x)\) como las entradas,\(x\), se hacen más grandes. Para algunas funciones, los valores de\(f(x)\) acercarse a un número finito. Por ejemplo, para la función\(f(x)=2+1/x\), los valores\(1/x\) se acercan cada vez más a cero para todos los valores de a\(x\) medida que se hacen cada vez más grandes. Para esta función, decimos “\(f(x)\)se acerca a dos como\(x\) va al infinito”, y escribimos\(f(x)→2\) como\(x→∞\). La línea\(y=2\) es una asíntota horizontal para la función\(f(x)=2+1/x\) porque la gráfica de la función se acerca a la línea a medida que\(x\) se hace más grande.

Para otras funciones, es\(f(x)\) posible que los valores no se acerquen a un número finito, sino que se hagan más grandes para todos los valores de a\(x\) medida que se hacen mayores. En ese caso, decimos “\(f(x)\)se acerca al infinito como\(x\) se acerca al infinito”, y escribimos\(f(x)→∞\) como\(x→∞\). Por ejemplo, para la función\(f(x)=3x^2\), las salidas\(f(x)\) se hacen más grandes a medida que las entradas se\(x\) hacen más grandes. Podemos concluir que la función se\(f(x)=3x^2\) acerca al infinito como\(x\) se acerca al infinito, y escribimos\(3x^2→∞\) como\(x→∞\). El comportamiento como\(x→−∞\) y el significado de\(f(x)→−∞\) como\(x→∞\) o\(x→−∞\) puede definirse de manera similar. Podemos describir lo que sucede con los valores de\(f(x)\) como\(x→∞\) y\(x→−∞\) como el comportamiento final de la función.

Para entender el comportamiento final de las funciones polinómicas, podemos enfocarnos en funciones cuadráticas y cúbicas. El comportamiento de polinomios de mayor grado se puede analizar de manera similar. Considera una función cuadrática\(f(x)=ax^2+bx+c\). Si\(a>0\), los valores\(f(x)→∞\) como\(x→±∞\). Si\(a<0\), los valores\(f(x)→−∞\) como\(x→±∞\). Dado que la gráfica de una función cuadrática es una parábola, la parábola se abre hacia arriba si\(a>0\).; la parábola se abre hacia abajo si\(a<0\) (Figura\(\PageIndex{5a}\)).

Consideremos ahora una función cúbica\(f(x)=ax^3+bx^2+cx+d\). Si\(a>0\), entonces\(f(x)→∞\) como\(x→∞\) y\(f(x)→−∞\) como\(x→−∞\). Si\(a<0\), entonces\(f(x)→−∞\) como\(x→∞\) y\(f(x)→∞\) como\(x→−∞\). Como podemos ver en ambas gráficas, el término principal del polinomio determina el comportamiento final (Figura\(\PageIndex{5b}\)).

Figura\(\PageIndex{5}\): (a) Para una función cuadrática, si el coeficiente inicial\(a>0\), la parábola se abre hacia arriba. Si\(a<0\), la parábola se abre hacia abajo. (b) Para una función cúbica\(f\), si el coeficiente principal\(a>0\), los valores\(f(x)→∞\) as\(x→∞\) y los valores\(f(x)→−∞\) as\(x→−∞\). Si el coeficiente principal\(a<0\), lo contrario es cierto.

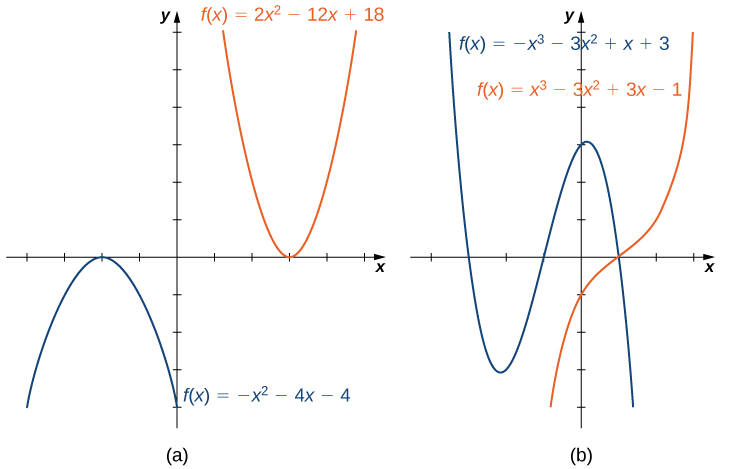
Ceros de funciones polinómicas

Otra característica de la gráfica de una función polinómica es donde se cruza con el\(x\) eje -eje. Para determinar dónde una función\(f\) se cruza con el\(x\) eje -eje, necesitamos resolver la ecuación\(f(x)=0\) para\(x\). En el caso de la función lineal\(f(x)=mx+b\), la\(x\) -intercepción se da resolviendo la ecuación\(mx+b=0\). En este caso, vemos que la\(x\) -intercepción viene dada por\((−b/m,0)\). En el caso de una función cuadrática, encontrar la (s)\(x\) intersección (s) requiere encontrar los ceros de una ecuación cuadrática:\(ax^2+bx+c=0\). En algunos casos, es fácil factorizar el polinomio\(ax^2+bx+c\) para encontrar los ceros. Si no, hacemos uso de la fórmula cuadrática.

La fórmula cuadrática

Considerar la ecuación cuadrática

\[ax^2+bx+c=0, \nonumber \]

donde\(a≠0\). Las soluciones de esta ecuación vienen dadas por la fórmula cuadrática

\[x=\dfrac{−b±\sqrt{b^2−4ac}}{2a}. \label{quad} \]

Si el discriminante\(b^2−4ac>0\), la Ecuación\ ref {quad} nos dice que hay dos números reales que satisfacen la ecuación cuadrática. Si\(b^2−4ac=0\), esta fórmula nos dice que sólo hay una solución, y es un número real. Si\(b^2−4ac<0\), ningún número real satisface la ecuación cuadrática.

En el caso de polinomios de mayor grado, puede ser más complicado determinar dónde la gráfica se cruza con el\(x\) eje -eje. En algunos casos, es posible encontrar las\(x\) -intercepciones factorizando el polinomio para encontrar sus ceros. En otros casos, es imposible calcular los valores exactos de las\(x\) -intercepciones. Sin embargo, como vemos más adelante en el texto, en casos como este, podemos utilizar herramientas analíticas para aproximar (en un grado muy alto) dónde se encuentran las\(x\) -intercepciones. Aquí nos enfocamos en las gráficas de polinomios para los cuales podemos calcular sus ceros explícitamente.

Ejemplo\(\PageIndex{3}\): Graphing Polynomial Functions

Para las siguientes funciones,

1. \(f(x)=−2x^2+4x−1\)
2. \(f(x)=x^3−3x^2−4x\)

1. describir el comportamiento de\(f(x)\) como\(x→±∞\),
2. encontrar todos los ceros de\(f\), y
3. bosquejar una gráfica de\(f\).

Solución

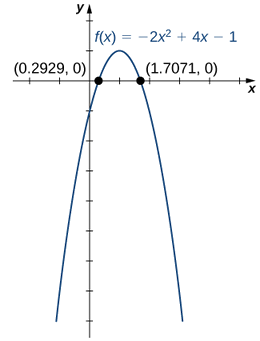
1. La función\(f(x)=−2x^2+4x−1\) es una función cuadrática.

1. Porque\(a=−2<0\), como\(x→±∞,f(x)→−∞.\)

2. Para encontrar los ceros de\(f\), usa la fórmula cuadrática. Los ceros son

\(x=\dfrac{−4±\sqrt{4^2−4(−2)(−1)}}{2(−2)}=\dfrac{−4±\sqrt{8}}{−4}=\dfrac{−4±2\sqrt{2}}{−4}=\dfrac{2±\sqrt{2}}{2}.\)

3. Para bosquejar la gráfica de\(f\), usa la información de tus respuestas anteriores y combínala con el hecho de que la gráfica es una parábola que se abre hacia abajo.

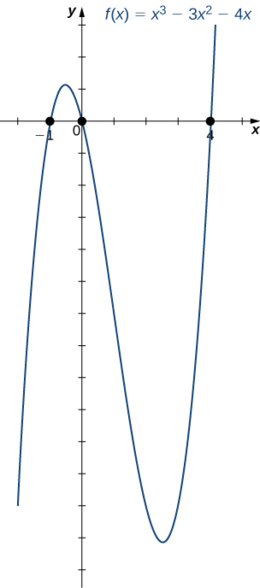
2. La función\(f(x)=x^3−3x^2−4x\) es una función cúbica.

1. Porque\(a=1>0\), como\(x→∞\),\(f(x)→∞\). Como\(x→−∞\),\(f(x)→−∞\).

2. Para encontrar los ceros de\(f\), necesitamos factorial el polinomio. Primero, cuando tenemos\(x\) en cuenta todos los términos, encontramos

\(f(x)=x(x^2−3x−4).\)

Entonces, cuando facteamos la función cuadrática\(x^2−3x−4\), encontramos

\(f(x)=x(x−4)(x+1).\)

Por lo tanto, los ceros de\(f\) son\(x=0,4,−1\).

3. Combinando los resultados de las partes i. y ii., dibujar un boceto aproximado de\(f\).

Ejercicio\(\PageIndex{2}\)

Considera la función cuadrática\(f(x)=3x^2−6x+2.\) Encuentra los ceros de\(f\). ¿La parábola se abre hacia arriba o hacia abajo?

Pista

Usa la fórmula cuadrática.

Contestar

Los ceros son\(x=1±\sqrt{3}/3\). La parábola se abre hacia arriba.

Modelos matemáticos

Una gran variedad de situaciones del mundo real se pueden describir utilizando modelos matemáticos. Un modelo matemático es un método para simular situaciones de la vida real con ecuaciones matemáticas. Físicos, ingenieros, economistas y otros investigadores desarrollan modelos combinando la observación con datos cuantitativos para desarrollar ecuaciones, funciones, gráficas y otras herramientas matemáticas para describir el comportamiento de varios sistemas con precisión. Los modelos son útiles porque ayudan a predecir resultados futuros. Ejemplos de modelos matemáticos incluyen el estudio de la dinámica poblacional, investigaciones de patrones climáticos y predicciones de ventas de productos.

Como ejemplo, consideremos un modelo matemático que una empresa podría utilizar para describir sus ingresos por la venta de un artículo en particular. El monto de ingresos que recibe\(R\) una empresa por la venta de\(n\) artículos vendidos a un precio de\(p\) dólares por artículo se describe en la ecuación\(R=p⋅n\). A la compañía le interesa cómo cambian las ventas a medida que cambia el precio del artículo. Supongamos que los datos de la Tabla\(\PageIndex{1}\) muestran el número de unidades que una empresa vende en función del precio por artículo.

Tabla\(\PageIndex{1}\): Número de unidades vendidas\(n\) (en miles) en función del precio por unidad\(p\) (en dólares)

\(p\)	6	8	10	12	14
\(n\)	19.4	18.5	16.2	13.8	12.2

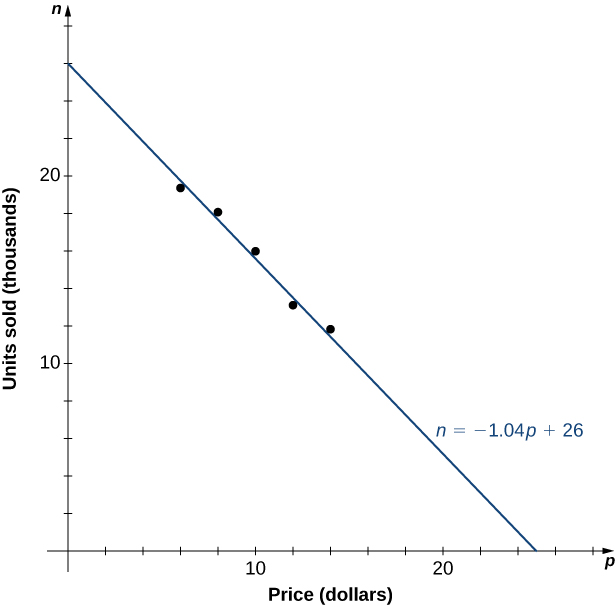
En la Figura\(\PageIndex{6}\), vemos en la gráfica el número de unidades vendidas (en miles) en función del precio (en dólares). Observamos a partir de la forma de la gráfica que el número de unidades vendidas es probablemente una función lineal del precio por artículo, y los datos pueden aproximarse estrechamente por la función lineal\(n= −1.04p+26\) para\(0≤p≤25\), donde\(n\) predice el número de unidades vendidas en miles. Usando esta función lineal, los ingresos (en miles de dólares) pueden ser estimados por la función cuadrática

\[R(p)=p⋅ (−1.04p+26)=−1.04p^2+26p \text{ for }0≤p≤25. \nonumber \]

En Ejemplo\(\PageIndex{4}\), utilizamos esta función cuadrática para predecir la cantidad de ingresos que recibe la compañía dependiendo del precio que cobra la compañía por artículo. Tenga en cuenta que no podemos concluir definitivamente el número real de unidades vendidas por valores de\(p\), para los cuales no se recogen datos. Sin embargo, dados los otros valores de datos y la gráfica mostrada, parece razonable que el número de unidades vendidas (en miles) si el precio cobrado es\(p\) dólares pueda estar cerca de los valores pronosticados por la función lineal\(n=−1.04p+26.\)

Figura\(\PageIndex{6}\): Los datos recopilados para el número de artículos vendidos en función del precio son aproximadamente lineales. Utilizamos la función lineal\(n=−1.04p+26\) para estimar esta función.

Ejemplo\(\PageIndex{4}\): Maximizing Revenue

Una empresa está interesada en predecir la cantidad de ingresos que recibirá dependiendo del precio que cobre por un artículo en particular. Utilizando los datos de Table\(\PageIndex{1}\), la compañía llega a la siguiente función cuadrática para modelar\(R\) los ingresos en función del precio por artículo\(p:\)

\[R(p)=p⋅(−1.04p+26)=−1.04p^2+26p \nonumber \]

para\(0≤p≤25\).

1. Predecir los ingresos si la compañía vende el artículo a un precio de\(p=$5\) y\(p=$17\).
2. Encuentra los ceros de esta función e interpreta el significado de los ceros.
3. Esbozar una gráfica de\(R\).
4. Utilice la gráfica para determinar el valor de\(p\) que maximiza los ingresos. Encuentra los ingresos máximos.

Solución

a. Evaluando la función de ingresos en\(p=5\) y\(p=17\), podemos concluir que

\(R(5)=−1.04(5)^2+26(5)=104,\text{ so revenue}=$104,000;\)

\(R(17)=−1.04(17)^2+26(17)=141.44,\text{ so revenue}=$141,440.\)

b. Los ceros de esta función se pueden encontrar resolviendo la ecuación\(−1.04p^2+26p=0\). Cuando facetamos la expresión cuadrática, obtenemos\(p(−1.04p+26)=0\). Las soluciones a esta ecuación vienen dadas por\(p=0,25\). Para estos valores de\(p\), los ingresos son cero. Cuando\(p=$0\), los ingresos son cero porque la empresa está regalando su mercancía de forma gratuita. Cuando\(p=$25\), los ingresos son cero porque el precio es demasiado alto, y nadie va a comprar ningún artículo.

c. Sabiendo que la función es cuadrática, también sabemos que la gráfica es una parábola. Dado que el coeficiente principal es negativo, la parábola se abre a la baja. Una propiedad de las parábolas es que son simétricas alrededor del eje de simetría, por lo que dado que los ceros están en\(p=0\) y\(p=25\), la parábola debe ser simétrica alrededor de la línea a medio camino entre ellos, o\(p=12.5\).

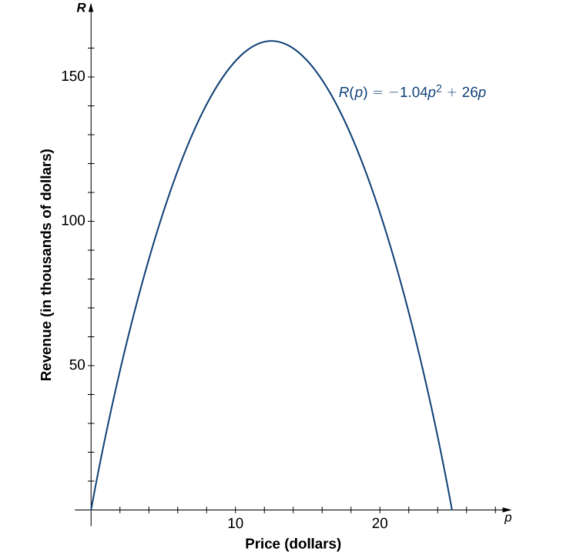
d. La función es una parábola con ceros a\(p=0\) y\(p=25\), y es simétrica respecto a la línea\(p=12.5\), por lo que el ingreso máximo se produce a un precio de\(p=$12.50\) por artículo. A ese precio, los ingresos son\(R(p)=−1.04(12.5)^2+26(12.5)=$162,500.\)

Funciones algebraicas

Al permitir cocientes y potencias fraccionarias en funciones polinómicas, creamos una clase más grande de funciones. Una función algebraica es aquella que implica suma, resta, multiplicación, división, poderes racionales y raíces. Dos tipos de funciones algebraicas son las funciones racionales y las funciones raíz.

Así como los números racionales son cocientes de enteros, las funciones racionales son cocientes de polinomios. En particular, una función racional es cualquier función de la forma\(f(x)=p(x)/q(x)\), donde\(p(x)\) y\(q(x)\) son polinomios. Por ejemplo,

\(f(x)=\dfrac{3x−1}{5x+2}\)y\(g(x)=\dfrac{4}{x^2+1}\)

son funciones racionales. Una función raíz es una función de potencia de la forma\(f(x)=x^{1/n}\), donde\(n\) es un entero positivo mayor que uno. Por ejemplo,\(f(x)=x^{1/2}=\sqrt{x}\) es la función de raíz cuadrada y\(g(x)=x^{1/3}=\sqrt[3]{x}\) es la función de raíz cúbica. Al permitir composiciones de funciones raíz y funciones racionales, podemos crear otras funciones algebraicas. Por ejemplo,\(f(x)=\sqrt{4−x^2}\) es una función algebraica.

Ejemplo\(\PageIndex{5}\): Finding Domain and Range for Algebraic Functions

Para cada una de las siguientes funciones, encuentra el dominio y el rango.

1. \(f(x)=\dfrac{3x−1}{5x+2}\)
2. \(f(x)=\sqrt{4−x^2}\)

Solución

1. No es posible dividir por cero, por lo que el dominio es el conjunto de números reales\(x\) tales que\(x≠−2/5\). Para encontrar el rango, necesitamos encontrar los valores\(y\) para los que existe un número real\(x\) tal que

\(y=\dfrac{3x−1}{5x+2}\)

Cuando multiplicamos ambos lados de esta ecuación por\(5x+2\), vemos que\(x\) debe satisfacer la ecuación

\(5xy+2y=3x−1.\)

A partir de esta ecuación, podemos ver que\(x\) debe satisfacer

\(2y+1=x(3−5y).\)

Si y=\(3/5\), esta ecuación no tiene solución. Por otra parte, siempre y cuando\(y≠3/5\),

\(x=\dfrac{2y+1}{3−5y}\)

satisface esta ecuación. Podemos concluir que el rango de\(f\) es\(\{y\,|\,y≠3/5\}\).

2. Para encontrar el dominio de\(f\), necesitamos\(4−x^2≥0\). Cuando facetamos, escribimos\(4−x^2=(2−x)(2+x)≥0\). Esta desigualdad se mantiene si y sólo si ambos términos son positivos o ambos términos son negativos. Para que ambos términos sean positivos, necesitamos encontrar\(x\) tal que

\(2−x≥0\)y\(2+x≥0.\)

Estas dos desigualdades se reducen a\(2≥x\) y\(x≥−2\). Por lo tanto, el conjunto\(\{x\,|\,−2≤x≤2\}\) debe ser parte del dominio. Para que ambos términos sean negativos, necesitamos

\(2−x≤0\)y\(2+x\le 0.\)

Estas dos desigualdades también reducen a\(2≤x\) y\(x\le −2\). No hay valores de\(x\) que satisfagan ambas desigualdades. Así, podemos concluir que el dominio de esta función es\(\{x\,|\,−2≤x≤2\}.\)

Si\(−2≤x≤2\), entonces\(0≤4−x^2≤4\). Por lo tanto\(0≤\sqrt{4−x2}≤2\),, y el rango de\(f\) es\(\{y\,|\,0≤y≤2\}.\)

Ejercicio\(\PageIndex{3}\)

Encuentra el dominio y el rango para la función\(f(x)=(5x+2)/(2x−1).\)

Pista

El denominador no puede ser cero. Resuelve la ecuación\(y=(5x+2)/(2x−1)\)\(x\) para encontrar el rango.

Responder

El dominio es el conjunto de números reales\(x\) tales que\(x≠1/2\). El rango es el conjunto\(\{y\,|\,y≠5/2\}\).

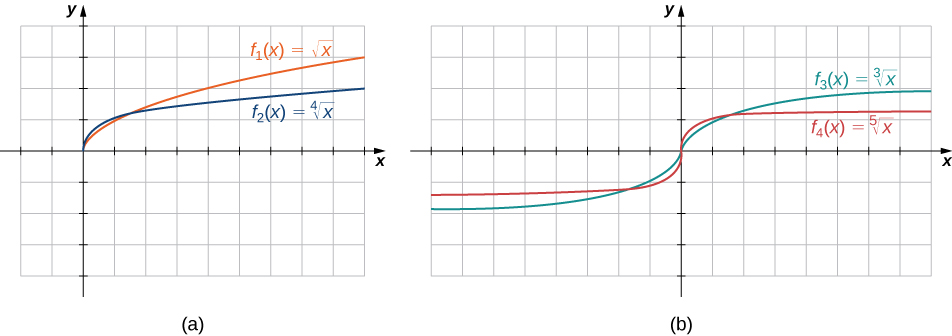
Las funciones raíz\(f(x)=x^{1/n}\) tienen características definitorias dependiendo de si\(n\) es impar o par. Para todos los enteros pares\(n≥2\), el dominio de\(f(x)=x^{1/n}\) es el intervalo\([0,∞)\). Para todos los enteros impares\(n≥1\), el dominio de\(f(x)=x^{1/n}\) es el conjunto de todos los números reales. Dado que\(x^{1/n}=(−x)^{1/n}\) para los enteros impares\(n\),\(f(x)=x^{1/n}\) es una función impar si\(n\) es impar. Consulte las gráficas de funciones raíz para diferentes valores de\(n\) en la Figura\(\PageIndex{7}\).

Figura\(\PageIndex{7}\): (a) Si\(n\) es par, el dominio de\(f(x)=\sqrt[n]{x}\) is\([0,∞)\). (b) Si\(n\) es impar, el dominio de\(f(x)=\sqrt[n]{x}\) is\((−∞,∞)\) y la función\(f(x)=\sqrt[n]{x}\) es una función impar.

Ejemplo\(\PageIndex{6}\): Finding Domains for Algebraic Functions

Para cada una de las siguientes funciones, determinar el dominio de la función.

1. \(f(x)=\dfrac{3}{x^2−1}\)
2. \(f(x)=\dfrac{2x+5}{3x^2+4}\)
3. \(f(x)=\sqrt{4−3x}\)
4. \(f(x)=\sqrt[3]{2x−1}\)

Solución

1. No se puede dividir por cero, por lo que el dominio es el conjunto de valores\(x\) tales que\(x^2−1≠0\). Por lo tanto, el dominio es\(\{x\,|\,x≠±1\}\).
2. Es necesario determinar los valores de\(x\) para los cuales el denominador es cero. Ya que\(3x^2+4≥4\) para todos los números reales\(x\), el denominador nunca es cero. Por lo tanto, el dominio es\((−∞,∞).\)
3. Dado que la raíz cuadrada de un número negativo no es un número real, el dominio es el conjunto de valores\(x\) para los cuales\(4−3x≥0\). Por lo tanto, el dominio es\(\{x\,|\,x≤4/3\}.\)
4. La raíz cúbica se define para todos los números reales, por lo que el dominio es el intervalo\((−∞, ∞).\)

Ejercicio\(\PageIndex{4}\)

Encuentra el dominio para cada una de las siguientes funciones:\(f(x)=(5−2x)/(x^2+2)\) y\(g(x)=\sqrt{5x−1}\).

Pista

Determinar los valores de\(x\) cuando la expresión en el denominador de\(f\) es distinta de cero, y encontrar los valores de\(x\) cuando la expresión dentro del radical de no\(g\) es negativa.

Responder

El dominio de\(f\) es\((−∞, ∞)\). El dominio de\(g\) es\(\{x\,|\,x≥1/5\}.\)

Funciones trascendentales

Hasta el momento, hemos discutido las funciones algebraicas. Algunas funciones, sin embargo, no pueden ser descritas por operaciones algebraicas básicas. Estas funciones son conocidas como funciones trascendentales porque se dice que “trascienden”, o van más allá, del álgebra. Las funciones trascendentales más comunes son las funciones trigonométricas, exponenciales y logarítmicas. Una función trigonométrica relaciona las proporciones de dos lados de un triángulo rectángulo. Ellos son\(\sin x, \cos x, \tan x, \cot x, \sec x,\text{ and }\csc x.\) (Se discuten las funciones trigonométricas más adelante en el capítulo.) Una función exponencial es una función de la forma\(f(x)=b^x\), donde la base\(b>0,\, b≠1\). Una función logarítmica es una función de la forma\(f(x)=\log_b(x)\) para alguna constante\(b>0,\,b≠1,\) donde\(\log_b(x)=y\) si y solo si\(b^y=x\). (También discutimos las funciones exponenciales y logarítmicas más adelante en el capítulo.)

Ejemplo\(\PageIndex{7}\): Classifying Algebraic and Transcendental Functions

Clasificar cada una de las siguientes funciones, a. a c., como algebraicas o trascendentales.

1. \(f(x)=\dfrac{\sqrt{x^3+1}}{4x+2}\)
2. \(f(x)=2^{x^2}\)
3. \( f(x)=\sin(2x)\)

Solución

1. Dado que esta función implica únicamente operaciones algebraicas básicas, es una función algebraica.
2. Esta función no puede escribirse como una fórmula que involucra únicamente operaciones algebraicas básicas, por lo que es trascendental. (Tenga en cuenta que las funciones algebraicas solo pueden tener poderes que son números racionales.)
3. Al igual que en la parte b, esta función no puede escribirse usando una fórmula que involucre únicamente operaciones algebraicas básicas; por lo tanto, esta función es trascendental.

Ejercicio\(\PageIndex{5}\):

¿Es\(f(x)=x/2\) una función algebraica o trascendental?

Responder

Algebraico

Funciones definidas por piezas

A veces una función se define por diferentes fórmulas en diferentes partes de su dominio. Una función con esta propiedad se conoce como una función definida por partes. La función de valor absoluto es un ejemplo de una función definida por partes porque la fórmula cambia con el signo de\(x\):

\[f(x)=\begin{cases}−x, & \text{if } x<0\\x, & \text{if } x≥0\end{cases}. \nonumber \]

Otras funciones definidas por partes pueden ser representadas por fórmulas completamente diferentes, dependiendo de la parte del dominio en la que caiga un punto. Para graficar una función definida por partes, graficamos cada parte de la función en su respectivo dominio, en el mismo sistema de coordenadas. Si la fórmula para una función es diferente para\(x<a\) y\(x>a\), debemos prestar especial atención a lo que sucede\(x=a\) cuando graficamos la función. A veces la gráfica necesita incluir un círculo abierto o cerrado para indicar el valor de la función at\(x=a\). Esto lo examinamos en el siguiente ejemplo.

Ejemplo\(\PageIndex{8}\): Graphing a Piecewise-Defined Function

Esboce un gráfico de la siguiente función definida por partes:

\[f(x)=\begin{cases}x+3, & \text{if } x<1\\(x−2)^2, & \text{if } x≥1\end{cases} \nonumber \]

Solución

Grafica la función lineal\(y=x+3\) en el intervalo\((−∞,1)\) y grafica la función cuadrática\(y=(x−2)^2\) en el intervalo\([1,∞)\). Ya que el valor de la función at\(x=1\) viene dado por la fórmula\(f(x)=(x−2)^2\), vemos eso\(f(1)=1\). Para indicarlo en la gráfica, dibujamos un círculo cerrado en el punto\((1,1)\). El valor de la función viene dado por\(f(x)=x+3\) para todos\(x<1\), pero no en\(x=1\). Para indicarlo en la gráfica, dibujamos un círculo abierto en\((1,4)\).

= 1” .La función tiene x intercepta en (-3, 0) y (2, 0) y una intersección y en (0, 3)." src="https://math.libretexts.org/@api/dek...5976625651.png">

Figura\(\PageIndex{8}\): Esta función definida por partes es lineal para\(x<1\) y cuadrática para\(x≥1.\)

2) Esbozar un gráfico de la función

\(f(x)=\begin{cases}2−x, & \text{if } x≤2\\x+2, & \text{if } x>2\end{cases}.\)

Solución:

2.La función tiene una intercepción x en (2, 0) y una intercepción y en (0, 2)." src="https://math.libretexts.org/@api/dek...8509006001.png">

Ejemplo\(\PageIndex{9}\): Parking Fees Described by a Piecewise-Defined Function

En una gran ciudad, a los conductores se les cobran tarifas variables por estacionar en una cochera de estacionamiento. Se les cobra $10 por la primera hora o cualquier parte de la primera hora y $2 adicionales por cada hora o parte de la misma hasta un máximo de $30 por día. El garaje de estacionamiento está abierto de 6 a.m. a 12 de la medianoche.

1. Escriba una función definida por partes que describa el costo\(C\) para estacionar en el estacionamiento en función de las horas estacionadas\(x\).
2. Esbozar un gráfico de esta función\(C(x).\)

Solución

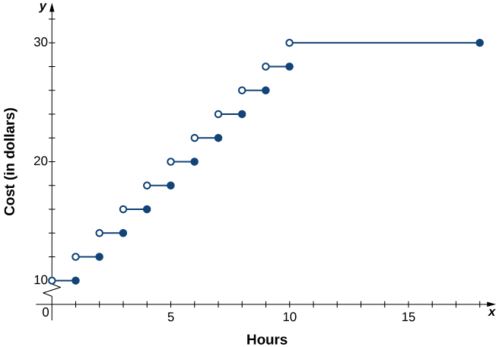
1.Dado que la cochera de estacionamiento está abierta 18 horas todos los días, el dominio para esta función es\(\{x\,|\,0<x≤18\}\). El costo para estacionar un automóvil en este estacionamiento se puede describir por partes por la función

\[C(x)=\begin{cases}10, & \text{for } 0<x≤1\\12, & \text{for } 1<x≤2\\14, & \text{for } 2<x≤3\\16, & \text{for } 3<x≤4\\ ⋮\\30, & \text{for } 10<x≤18\end{cases}. \nonumber \]

2.La gráfica de la función consta de varios segmentos de línea horizontales.

Ejercicio\(\PageIndex{6}\)

El costo de enviar una carta es una función del peso de la carta. Supongamos que el costo de enviar una carta es\(49¢\) por la primera onza y\(21¢\) por cada onza adicional. Escribir una función definida por partes describiendo el costo\(C\) como una función del peso\(x\) para\(0<x≤3\), donde\(C\) se mide en centavos y\(x\) se mide en onzas.

Pista

La función definida por partes es constante en los intervalos\((0,1],\,(1,2],\,….\)

Responder

\[C(x)=\begin{cases}49, 0<x≤1\\70, 1<x≤2\\91, 2<x≤3\end{cases} \nonumber \]

Transformaciones de funciones

Hemos visto varios casos en los que hemos sumado, restado o multiplicado constantes para formar variaciones de funciones simples. En el ejemplo anterior, por ejemplo, restamos 2 del argumento de la función\(y=x^2\) para obtener la función\(f(x)=(x−2)^2\). Esta resta representa un desplazamiento de la función\(y=x^2\) dos unidades hacia la derecha. Un desplazamiento, horizontal o verticalmente, es un tipo de transformación de una función. Otras transformaciones incluyen escalados horizontales y verticales, y reflexiones sobre los ejes.

Se produce un desplazamiento vertical de una función si sumamos o restamos la misma constante a cada salida\(y\). Para\(c>0\), la gráfica de\(f(x)+c\) es un desplazamiento de la gráfica de\(c\) unidades\(f(x)\) ascendentes, mientras que la gráfica de\(f(x)−c\) es un desplazamiento de la gráfica de\(c\) unidades\(f(x)\) descendentes. Por ejemplo, la gráfica de la función\(f(x)=x^3+4\) es la gráfica de\(4\) unidades\(y=x^3\) desplazadas hacia arriba; la gráfica de la función\(f(x)=x^3−4\) es la gráfica de\(4\) unidades\(y=x^3\) desplazadas hacia abajo (Figura\(\PageIndex{9}\)).

Figura\(\PageIndex{9}\): (a) Para\(c>0\), la gráfica de\(y=f(x)+c\) es un desplazamiento vertical hacia arriba\(c\) unidades de la gráfica de\(y=f(x)\). (b) Para\(c>0\), la gráfica de\(y=f(x)−c\) es un desplazamiento vertical hacia abajo c unidades de la gráfica de\(y=f(x)\).

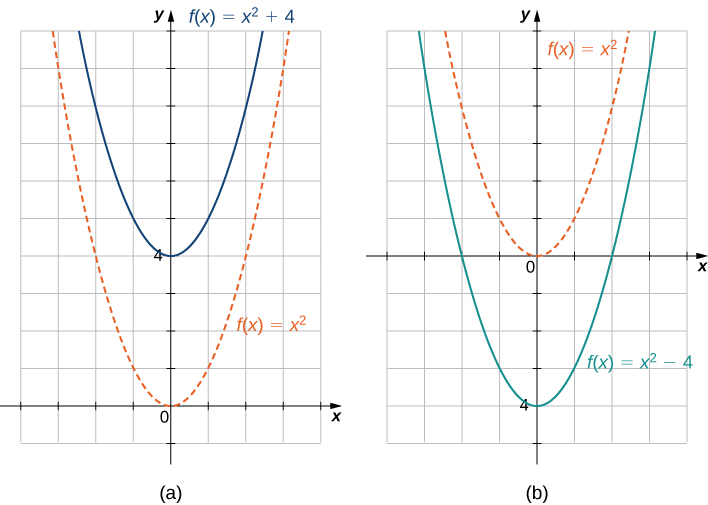
Se produce un desplazamiento horizontal de una función si sumamos o restamos la misma constante a cada entrada\(x\). Para\(c>0\), la gráfica de\(f(x+c)\) es un desplazamiento de la gráfica de\(f(x)\) a las\(c\) unidades de la izquierda; la gráfica de\(f(x−c)\) es un desplazamiento de la gráfica de\(f(x)\) a las\(c\) unidades de la derecha. ¿Por qué la gráfica se desplaza a la izquierda cuando se suma una constante y se desplaza a la derecha al restar una constante? Para responder a esta pregunta, veamos un ejemplo.

Considere la función\(f(x)=|x+3|\) y evalúe esta función en\(x−3\). Desde\(f(x−3)=|x|\) y\(x−3<x\), la gráfica de\(f(x)=|x+3|\) es la gráfica de\(3\) unidades\(y=|x|\) desplazadas a la izquierda. De igual manera, la gráfica de\(f(x)=|x−3|\) es la gráfica de\(3\) unidades\(y=|x|\) desplazadas a la derecha (Figura\(\PageIndex{10}\)).

Figura\(\PageIndex{10}\): (a) Para\(c>0\), la gráfica de\(y=f(x+c)\) es un desplazamiento horizontal a la izquierda\(c\) unidades de la gráfica de\(y=f(x)\). (b) Para\(c>0\), la gráfica de\(y=f(x−c)\) es un desplazamiento horizontal a la derecha\(c\) unidades de la gráfica de\(y=f(x).\)

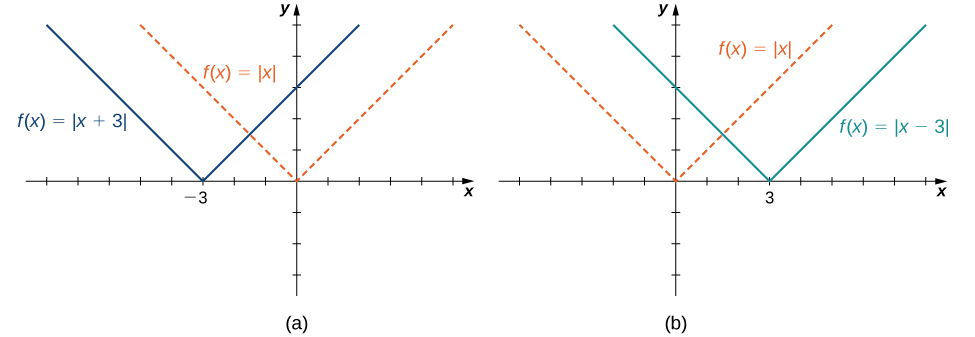
Un escalado vertical de una gráfica ocurre si multiplicamos todas las salidas\(y\) de una función por la misma constante positiva. Para\(c>0\), la gráfica de la función\(cf(x)\) es la gráfica de\(f(x)\) escalado verticalmente por un factor de\(c\). Si\(c>1\), los valores de las salidas para la función\(cf(x)\) son mayores que los valores de las salidas para la función\(f(x)\); por lo tanto, la gráfica se ha estirado verticalmente. Si\(0<c<1\), entonces las salidas de la función\(cf(x)\) son más pequeñas, por lo que la gráfica ha sido comprimida. Por ejemplo, la gráfica de la función\(f(x)=3x^2\) es la gráfica de\(y=x^2\) estirada verticalmente por un factor de 3, mientras que la gráfica de\(f(x)=x^2/3\) es la gráfica de\(y=x^2\) comprimida verticalmente por un factor de\(3\) (Figura\(\PageIndex{11b}\)).

Figura\(\PageIndex{11}\): (a) Si\(c>1\), la gráfica de\(y=cf(x)\) es un estiramiento vertical de la gráfica de\(y=f(x)\). (b) Si\(0<c<1\), la gráfica de\(y=cf(x)\) es una compresión vertical de la gráfica de\(y=f(x)\).

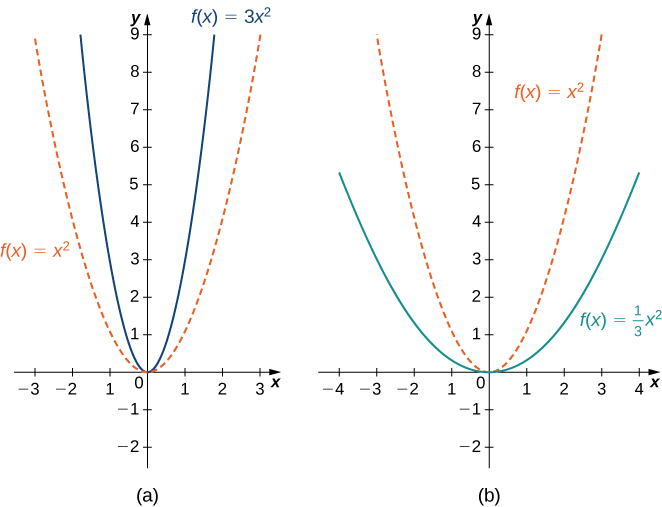
El escalado horizontal de una función ocurre si multiplicamos las entradas\(x\) por la misma constante positiva. Para\(c>0\), la gráfica de la función\(f(cx)\) es la gráfica de\(f(x)\) escalado horizontalmente por un factor de\(c\). Si\(c>1\), la gráfica de\(f(cx)\) es la gráfica de\(f(x)\) comprimida horizontalmente. Si\(0<c<1\), la gráfica de\(f(cx)\) es la gráfica de\(f(x)\) estirada horizontalmente. Por ejemplo, considere la función\(f(x)=\sqrt{2x}\) y evalúe\(f\) en\(x/2\). Ya que\(f(x/2)=\sqrt{x}\), la gráfica de\(f(x)=\sqrt{2x}\) es la gráfica de\(y=\sqrt{x}\) comprimida horizontalmente. La gráfica de\(y=\sqrt{x/2}\) es un tramo horizontal de la gráfica de\(y=\sqrt{x}\) (Figura\(\PageIndex{12}\)).

Figura\(\PageIndex{12}\): (a) Si\(c>1\), la gráfica de\(y=f(cx)\) es una compresión horizontal de la gráfica de\(y=f(x)\). (b) Si\(0<c<1\), la gráfica de\(y=f(cx)\) es un tramo horizontal de la gráfica de\(y=f(x)\).

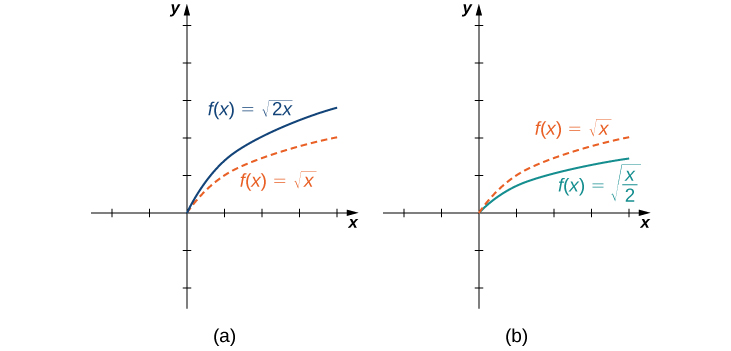
Hemos explorado lo que sucede con la gráfica de una función\(f\) cuando multiplicamos\(f\) por una constante\(c>0\) para obtener una nueva función\(cf(x)\). También hemos discutido qué sucede con la gráfica de una función\(f\) cuando multiplicamos la variable independiente\(x\) por\(c>0\) para obtener una nueva función\(f(cx)\). Sin embargo, no hemos abordado lo que le sucede a la gráfica de la función si la constante\(c\) es negativa. Si tenemos una constante\(c<0\), podemos escribir\(c\) como un número positivo multiplicado por\(−1\); pero, qué tipo de transformación obtenemos cuando multiplicamos la función o su argumento por\(−1?\) Cuando multiplicamos todas las salidas por\(−1\), obtenemos una reflexión sobre el\(x\) eje -eje. Cuando multiplicamos todas las entradas por\(−1\), obtenemos una reflexión sobre el\(y\) eje -eje. Por ejemplo, la gráfica de\(f(x)=−(x^3+1)\) es la gráfica de\(y=(x^3+1)\) reflejada alrededor del\(x\) eje -. La gráfica de\(f(x)=(−x)^3+1\) es la gráfica de\(y=x^3+1\) reflejada alrededor del\(y\) eje -( Figura\(\PageIndex{13}\)).

Figura\(\PageIndex{13}\): (a) La gráfica de\(y=−f(x)\) es la gráfica de\(y=f(x)\) reflejado alrededor del\(x\) eje. (b) La gráfica de\(y=f(−x)\) es la gráfica de\(y=f(x)\) reflejada alrededor del\(y\) eje.

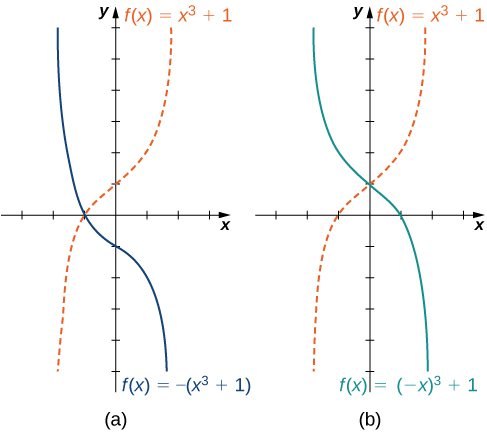
Si la gráfica de una función consiste en más de una transformación de otra gráfica, es importante transformar la gráfica en el orden correcto. Dada una función\(f(x)\), la gráfica de la función relacionada se\(y=cf(a(x+b))+d\) puede obtener a partir de la gráfica de\(y=f(x)\) realizando las transformaciones en el siguiente orden.

• Desplazamiento horizontal de la gráfica de\(y=f(x)\). Si\(b>0\), desplace a la izquierda. Si\(b<0\) desplace a la derecha.
• Escalado horizontal de la gráfica de\(y=f(x+b)\) por un factor de\(|a|\). Si\(a<0\), refleje la gráfica sobre el\(y\) eje -eje.
• Escalado vertical de la gráfica de\(y=f(a(x+b))\) por un factor de\(|c|\). Si\(c<0\), refleje la gráfica sobre el\(x\) eje -eje.
• Desplazamiento vertical de la gráfica de\(y=cf(a(x+b))\). Si\(d>0\), cambiar hacia arriba. Si\(d<0\), cambiar hacia abajo.

Podemos resumir las diferentes transformaciones y sus efectos relacionados en la gráfica de una función en la siguiente tabla.

Transformación de\(f (c>0)\)	Efecto de la gráfica de\(f\)
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x)+c\)	\ (f\)” style="text-align:center; vertical-align:middle; "\(c\)>Unidades de desplazamiento vertical hacia arriba
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x)-c\)	\ (f\)” style="text-align:center; vertical-align:middle; "\(c\)>Unidades de desplazamiento vertical hacia abajo
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x+c)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Desplazar a la izquierda por\(c\) unidades
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(x-c)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Desplazar a la derecha por\(c\) unidades
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(cf(x)\)	\ (f\)” style="vertical-align:middle; "> Estiramiento vertical si\(c>1\); compresión vertical si\(0<c<1\)
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(cx)\)	\ (f\)” style="vertical-align:middle; "> Estiramiento horizontal si\(0<c<1\); compresión horizontal si\(c>1\)
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(-f(x)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Reflexión sobre el\(x\) eje
\ (f (c>0)\)” style="text-align:center; vertical-align:middle; ">\(f(-x)\)	\ (f\)” style="text-align:center; vertical-align:middle; ">Reflexión sobre el\(y\) eje

Ejemplo\(\PageIndex{10}\): Transforming a Function

Para cada una de las siguientes funciones, a. y b., esbozar una gráfica utilizando una secuencia de transformaciones de una función bien conocida.

1. \(f(x)=−|x+2|−3\)
2. \(f(x)=\sqrt[3]{x}+1\)

Solución

1.Comenzando con la gráfica de\(y=|x|\), desplaza\(2\) las unidades hacia la izquierda, reflexiona sobre el\(x\) eje y luego desplaza\(3\) las unidades hacia abajo.

Figura\(\PageIndex{14}\): La función\(f(x)=−|x+2|−3\) puede ser vista como una secuencia de tres transformaciones de la función\(y=|x|\).

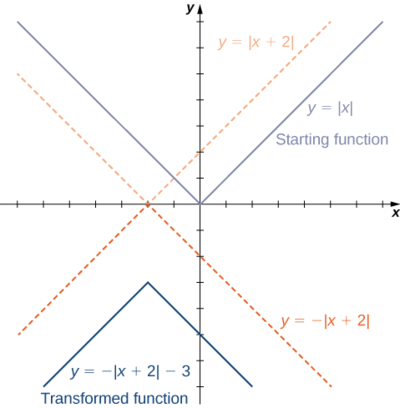
2. Comenzando con la gráfica de\(y=sqrt{x},\) reflejar alrededor del\(y\) eje -eje, estirar la gráfica verticalmente por un factor de 3, y mover hacia arriba 1 unidad.

Figura\(\PageIndex{15}\): La función\(f(x)=\sqrt[3]{x}+1\) puede ser vista como una secuencia de tres transformaciones de la función\(y=\sqrt{x}\).

Ejercicio\(\PageIndex{7}\)

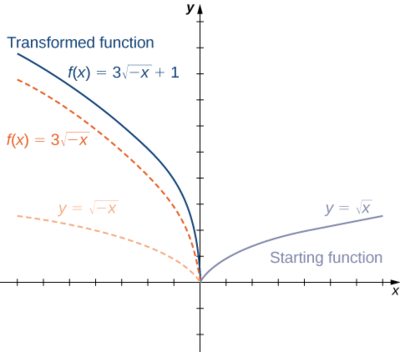
Describir cómo se\(f(x)=−(x+1)^2−4\) puede graficar la función usando la gráfica de\(y=x^2\) y una secuencia de transformaciones

Responder

Desplace la gráfica\(y=x^2\) hacia la izquierda 1 unidad, reflexione sobre el\(x\) eje -y luego desplace hacia abajo 4 unidades.

Conceptos clave

• La función power\(f(x)=x^n\) es una función par si n es par y\(n≠0\), y es una función impar si\(n\) es impar.
• La función raíz\(f(x)=x^{1/n}\) tiene el dominio\([0,∞)\) si n es par y el dominio\((−∞,∞)\) if\(n\) es impar. Si\(n\) es impar, entonces\(f(x)=x^{1/n}\) es una función impar.
• El dominio de la función racional\(f(x)=p(x)/q(x)\), donde\(p(x)\) y\(q(x)\) son funciones polinómicas, es el conjunto de\(x\) tal que\(q(x)≠0\).
• Las funciones que involucran las operaciones básicas de suma, resta, multiplicación, división y poderes son funciones algebraicas. Todas las demás funciones son trascendentales. Las funciones trigonométricas, exponenciales y logarítmicas son ejemplos de funciones trascendentales.
• Una función polinómica\(f\) con grado\(n≥1\) satisface\(f(x)→±∞\) como\(x→±∞\). El signo de la salida como\(x→∞\) depende únicamente del signo del coeficiente principal y de si\(n\) es par o impar.
• Los desplazamientos verticales y horizontales, los escalamientos verticales y horizontales y las reflexiones sobre los\(y\) ejes\(x\) - y -son ejemplos de transformaciones de funciones.

Ecuaciones Clave

• Ecuación de pendiente puntual de una línea\[y−y_1=m(x−x_1)\nonumber \]
• Forma pendiente-intercepción de una línea\[y=mx+b\nonumber \]
• Forma estándar de una línea\[ax+by=c\nonumber \]
• Función polinomial\[f(x)=a_n{x^n}+a_{n−1}x^{n−1}+⋯+a_1x+a_0\nonumber \]

Glosario

función algebraica

una función que involucra cualquier combinación de solo las operaciones básicas de suma, resta, multiplicación, división, potencias y raíces aplicadas a una variable de entrada\(x\)

función cúbica

un polinomio de grado 3; es decir, una función de la forma\(f(x)=ax^3+bx^2+cx+d\), donde\(a≠0\)

grado

para una función polinómica, el valor del exponente más grande de cualquier término

función lineal

una función que se puede escribir en la forma\(f(x)=mx+b\)

función logarítmica

una función de la forma\(f(x)=\log_b(x)\) para alguna base\(b>0,\,b≠1\) tal que\(y=\log_b(x)\) si y solo si\(b^y=x\)

modelo matemático

Un método para simular situaciones de la vida real con ecuaciones matemáticas

función definida por partes

una función que se define de manera diferente en diferentes partes de su dominio

ecuación de punto-pendiente

ecuación de una función lineal que indica su pendiente y un punto en la gráfica de la función

función polinomial

una función de la forma\(f(x)=a_nx^n+a_{n−1}x^{n−1}+…+a_1x+a_0\)

función de potencia

una función de la forma\(f(x)=x^n\) para cualquier entero positivo\(n≥1\)

función cuadrática

un polinomio de grado 2; es decir, una función de la forma\(f(x)=ax^2+bx+c\) donde\(a≠0\)

función racional

una función de la forma\(f(x)=p(x)/q(x)\), donde\(p(x)\) y\(q(x)\) son polinomios

función raíz

una función de la forma\(f(x)=x^{1/n}\) para cualquier entero\(n≥2\)

pendiente

el cambio en\(y\) para cada unidad cambio en\(x\)

forma pendiente-intercepción

ecuación de una función lineal que indica su pendiente e\(y\) -intercepción

función trascendental

una función que no puede expresarse mediante una combinación de operaciones aritméticas básicas

transformación de una función

un cambio, escalado o reflejo de una función