5.6: Resolver ecuaciones radicales

Objetivos de aprendizaje

• Resolver ecuaciones que involucran raíces cuadradas.
• Resuelve ecuaciones que involucran raíces cúbicas.

Ecuaciones Radales

Una ecuación radical ²² es cualquier ecuación que contiene uno o más radicales con una variable en el radicando. A continuación se presentan algunos ejemplos de ecuaciones radicales, todas las cuales se resolverán en esta sección:

Mesa$\PageIndex{1}$

$\sqrt { 2 x - 1 } = 3$

$\sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 = 0$

$\sqrt { x + 2 } - \sqrt { x } = 1$

Comenzamos con la propiedad de cuadratura de igualdad ²³; dados números reales$a$ y$b$, tenemos los siguientes:

$\text{If}\:\:\:a = b , \text { then } a ^ { 2 } = b ^ { 2 }$

En otras palabras, la igualdad se mantiene si cuadramos ambos lados de una ecuación.

$\begin{aligned} - 3 = - 3 \Rightarrow ( - 3 ) ^ { 2 } & = ( - 3 ) ^ { 2 } \\ 9 & = 9\:\:\color{Cerulean}{✓} \end{aligned}$

Lo contrario, en cambio, no es necesariamente cierto,

$\begin{aligned} 9 &= 9 \\ ( - 3 ) ^ { 2 } &= ( 3 ) ^ { 2 } \Rightarrow - 3 \neq 3\:\:\color{red}{✗} \end{aligned}$

Esto es importante porque usaremos esta propiedad para resolver ecuaciones radicales. Consideremos una ecuación radical muy simple que pueda resolverse mediante inspección,

$\sqrt { x } = 5$

Aquí podemos ver que$x = 25$ es una solución. Para resolver esta ecuación algebraicamente, hacer uso de la propiedad de cuadratura de igualdad y el hecho de que$( \sqrt { a } ) ^ { 2 } = \sqrt { a ^ { 2 } } = a$ cuando$a$ es no negativo. Elimine la raíz cuadrada al cuadrar ambos lados de la ecuación de la siguiente manera:

$\begin{aligned} \color{Cerulean}{(}\color{black}{ \sqrt { x } }\color{Cerulean}{) ^ { 2 }} & \color{black}{=}\color{Cerulean}{ (}\color{black}{ 5}\color{Cerulean}{ ) ^ { 2 }} \\ x & = 25 \end{aligned}$

Como cheque, podemos ver eso$\sqrt{25}=5$ como se esperaba. Debido a que lo contrario de la propiedad cuadrangular de la igualdad no es necesariamente cierto, las soluciones a la ecuación cuadrada pueden no ser soluciones a la original. De ahí que al cuadrar ambos lados de una ecuación se introduce la posibilidad de soluciones extrañas ²⁴, que son soluciones que no resuelven la ecuación original. Por ejemplo,

$\sqrt { x } = - 5$

Esta ecuación claramente no tiene una solución numérica real. Sin embargo, cuadrar ambos lados nos da una solución:

$\begin{aligned} \color{Cerulean}{(}\color{black}{ \sqrt { x } }\color{Cerulean}{) ^ { 2 }} & \color{black}{=}\color{Cerulean}{ (}\color{black}{ -5}\color{Cerulean}{ ) ^ { 2 }} \\ x & = 25 \end{aligned}$

Como cheque, podemos ver eso$\sqrt { 25 } \neq - 5$. Por esta razón, debemos verificar las respuestas que resultan de cuadrar ambos lados de una ecuación.

Ejemplo$\PageIndex{1}$:

Resolver:$\sqrt { 3 x + 1 } = 4$.

Solución

Podemos eliminar la raíz cuadrada aplicando la propiedad de cuadratura de igualdad.

$\begin{aligned} \sqrt { 3 x + 1 } & = 4 \\ ( \sqrt { 3 x + 1 } ) ^ { 2 } & = ( 4 ) ^ { 2 }\quad\color{Cerulean}{Square \:both\:sides.} \\ 3 x + 1 & = 16 \quad\:\:\:\color{Cerulean}{Solve.}\\ 3 x & = 15 \\ x & = 5 \end{aligned}$

A continuación, debemos verificar.

$\begin{aligned} \sqrt { 3 (\color{OliveGreen}{ 5}\color{black}{ )} + 1 } & = 4 \\ \sqrt { 15 + 1 } & = 4 \\ \sqrt { 16 } & = 4 \\ 4 & = 4\:\:\color{Cerulean}{✓} \end{aligned}$

Respuesta:

La solución es$5$.

Hay una interpretación geométrica al ejemplo anterior. Grafica la función definida por$f ( x ) = \sqrt { 3 x + 1 }$ y determina dónde se cruza con la gráfica definida por$g (x) = 4$.

Figura$\PageIndex{1}$

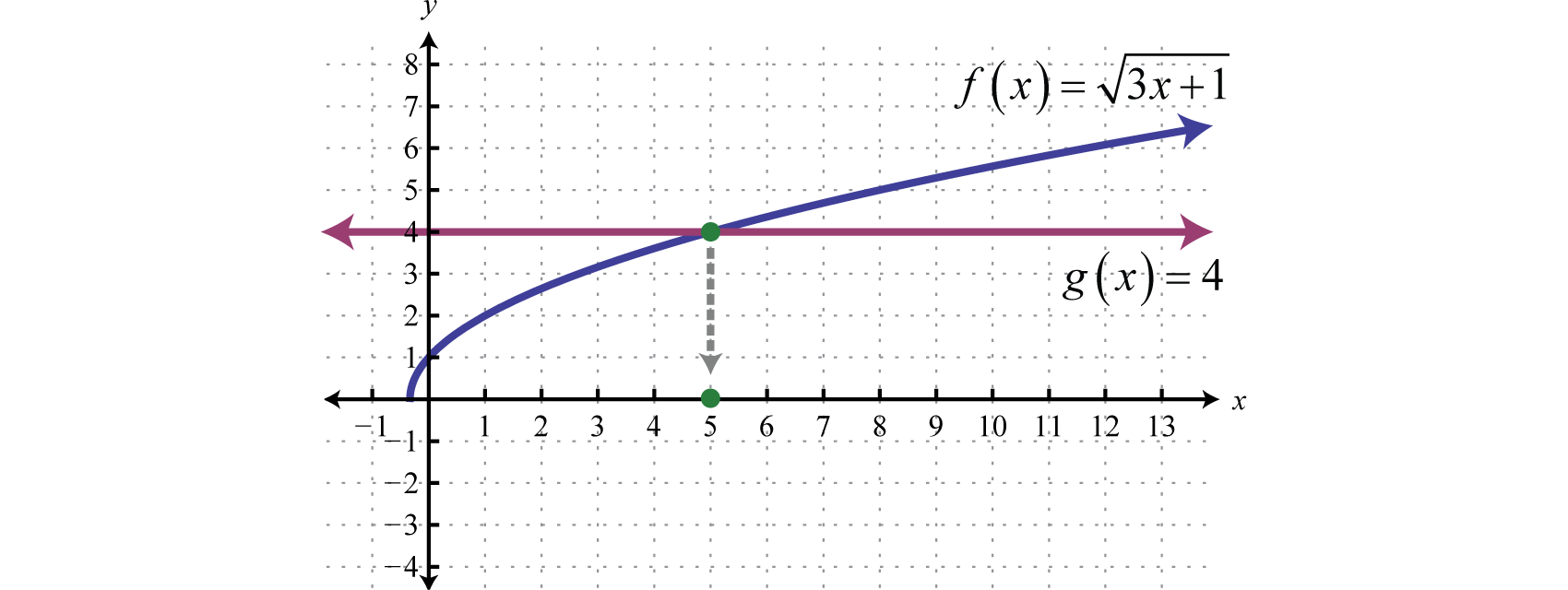
Como se ilustra,$f ( x ) = g ( x )$ dónde$x=5$.

Ejemplo$\PageIndex{2}$:

Resolver:$\sqrt { x - 3 } = x - 5$.

Solución

Comience por cuadrar ambos lados de la ecuación.

$\begin{aligned} \sqrt { x - 3 } &= x - 5 \\ ( \sqrt { x - 3 } ) ^ { 2 } &= ( x - 5 ) ^ { 2 }\quad\quad\quad\color{Cerulean}{Square\:both\:sides.} \\ x - 3 &= x ^ { 2 } - 10 x + 25 \end{aligned}$

La ecuación cuadrática resultante se puede resolver factorizando.

$\begin{aligned} x - 3 & = x ^ { 2 } - 10 x + 25 \\ 0 & = x ^ { 2 } - 11 x + 28 \\ 0 & = ( x - 4 ) ( x - 7 ) \end{aligned}$

$\begin{array} { r l } { x - 4 = 0 } & { \text { or } \quad x - 7 = 0 } \\ { x = 4 } & \quad\quad\quad\quad\:{ x = 7 } \end{array}$

Verificar las soluciones después de cuadrar ambos lados de una ecuación no es opcional. Utilice la ecuación original al realizar la comprobación.

Mesa$\PageIndex{2}$

$\color{Cerulean}{Check} \color{black}{x=4}$	$\color{Cerulean}{Check} \color{black}{x=7}$
$\begin{aligned} \sqrt { x - 3 } & = x - 5 \\ \sqrt { \color{Cerulean}{4}\color{black}{ -} 3 } & = \color{Cerulean}{4}\color{black}{ -} 5 \\ \sqrt { 1 } & = - 1 \\ 1 & = - 1 \quad \color{red}{✗} \end{aligned}$	$\begin{aligned} \sqrt { x - 3 } & = x - 5 \\ \sqrt { \color{Cerulean}{7}\color{black}{ -} 3 } & = \color{Cerulean}{7}\color{black}{ -} 5 \\ \sqrt { 4 } & = 2 \\ 2 & = 2\quad\color{Cerulean}{✓} \end{aligned}$

Después de verificar, se puede ver que$x = 4$ es una solución extraña; no resuelve la ecuación radical original. No tenga en cuenta esa respuesta. Esto deja$x = 7$ como única solución.

Respuesta:

La solución es$7$.

Geométricamente podemos ver que$f ( x ) = \sqrt { x + 3 }$ es igual a$g (x) = x − 5$ donde$x = 7$.

Figura$\PageIndex{2}$

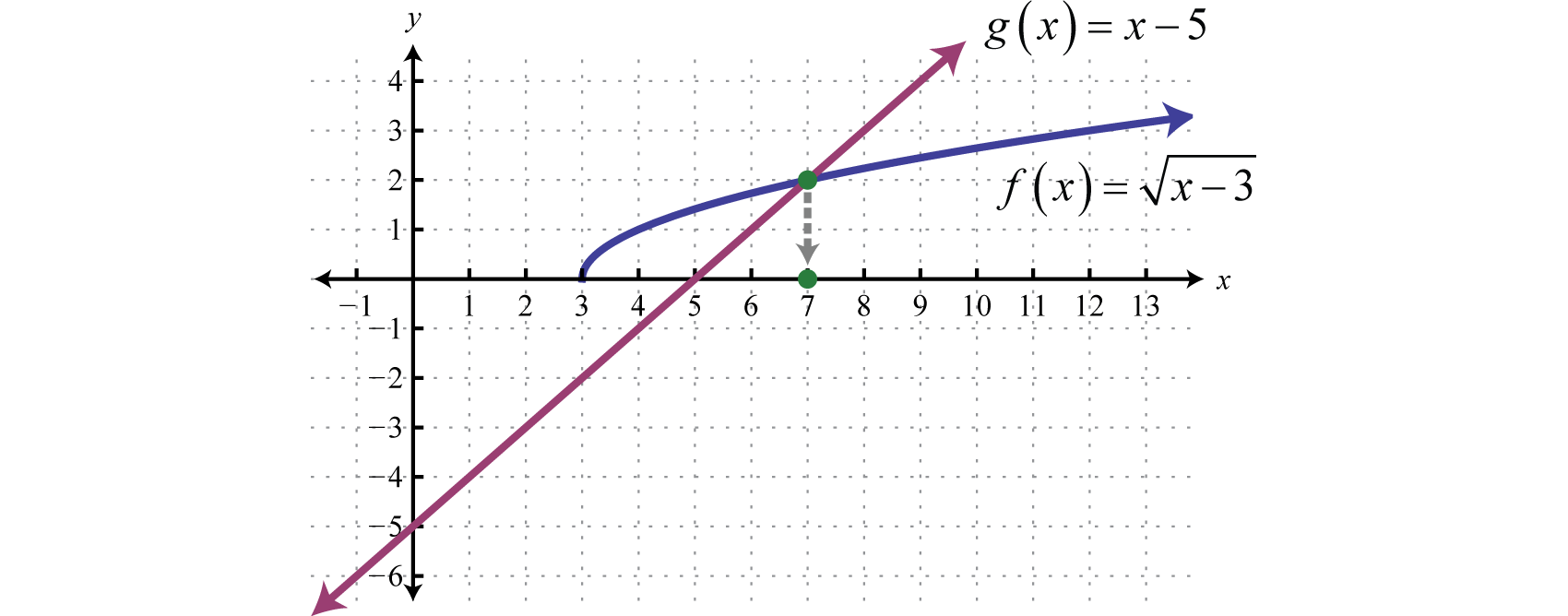
En los dos ejemplos anteriores, observe que el radical está aislado en un lado de la ecuación. Por lo general, este no es el caso. Los pasos para resolver ecuaciones radicales que involucran raíces cuadradas se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{3}$:

Resolver:$\sqrt { 2 x - 1 } + 2 = x$.

Solución

Paso 1: Aislar la raíz cuadrada. Comience restando 2 de ambos lados de la ecuación.

$\begin{aligned} \sqrt { 2 x - 1 } + 2 &= x \\ \sqrt { 2 x - 1 } &= x - 2 \end{aligned}$

Paso 2: Cuadrar ambos lados. Al cuadrar ambos lados se elimina la raíz cuadrada.

$\begin{aligned} ( \sqrt { 2 x - 1 } ) ^ { 2 } &= ( x - 2 ) ^ { 2 } \\ 2 x - 1 &= x ^ { 2 } - 4 x + 4 \end{aligned}$

Paso 3: Resolver la ecuación resultante. Aquí nos quedamos con una ecuación cuadrática que se puede resolver factorizando.

$\begin{aligned} 2 x - 1 & = x ^ { 2 } - 4 x + 4 \\ 0 & = x ^ { 2 } - 6 x + 5 \\ 0 & = ( x - 1 ) ( x - 5 ) \end{aligned}$

$\begin{array} { r l } { x - 1 = 0 } & { \text { or } \quad x - 5 = 0 } \\ { x = 1 } & \quad\quad\quad\quad{ x = 5 } \end{array}$

Paso 4: Verifique las soluciones en la ecuación original. Al cuadrar ambos lados se introduce la posibilidad de soluciones extrañas; de ahí que se requiera la verificación.

Mesa$\PageIndex{3}$

$\color{Cerulean}{Check} \color{black}{x=1}$	$\color{Cerulean}{Check} \color{black}{x=5}$
$\begin{aligned} \sqrt { 2 x - 1 } + 2 & = x \\ \sqrt { 2 ( \color{Cerulean}{1}\color{black}{ )} - 1 } + 2 & = \color{Cerulean}{1} \\ \sqrt { 1 } + 2 & = 1 \\ 1 + 2 & = 1 \\ 3 & = 1 \:\:\color{red}{✗}\end{aligned}$	$\begin{aligned} \sqrt { 2 x - 1 } + 2 & = x \\ \sqrt { 2 ( \color{Cerulean}{5}\color{black}{ )} - 1 } + 2 & = \color{Cerulean}{5} \\ \sqrt { 9 } + 2 & = 5 \\ 3 + 2 & = 5 \\ 5 & = 5\:\:\color{Cerulean}{✓} \end{aligned}$

Después de verificar, podemos ver que$x = 1$ es una solución extraña; no resuelve la ecuación radical original. Esto deja$x = 5$ como única solución.

Respuesta:

La solución es$5$.

A veces hay más de una solución a una ecuación radical.

Ejemplo$\PageIndex{4}$:

Resolver:$2 \sqrt { 2 x + 5 } - x = 4$.

Solución

Comience aislando el término con el radical.

$\begin{aligned} 2 \sqrt { 2 x + 5 } - x &= 4 \quad\quad\color{Cerulean}{Add\:x\:to\:both\:sides.} \\ 2 \sqrt { 2 x + 5 } &= x + 4 \end{aligned}$

A pesar de que el término del lado izquierdo tiene un coeficiente, seguimos considerándolo aislado. Recordemos que los términos están separados por operadores de suma o resta.

$\begin{aligned} 2 \sqrt { 2 x + 5 } & = x + 4 \\ ( 2 \sqrt { 2 x + 5 } ) ^ { 2 } & = ( x + 4 ) ^ { 2 } \quad\quad\quad\color{Cerulean}{Square\:both\:sides.}\\ 4 ( 2 x + 5 ) & = x ^ { 2 } + 8 x + 16 \end{aligned}$

Resolver la ecuación cuadrática resultante.

$\begin{aligned} 4 ( 2 x + 5 ) & = x ^ { 2 } + 8 x + 16 \\ 8 x + 20 & = x ^ { 2 } + 8 x + 16 \\ 0 & = x ^ { 2 } - 4 \\ 0 & = ( x + 2 ) ( x - 2 ) \end{aligned}$

$\begin{array} { r l } { x + 2 = 0 } & { \text { or } x - 2 = 0 } \\ { x = - 2 } & \quad\quad\quad\:{ x = 2 } \end{array}$

Ya que cuadramos ambos lados, debemos verificar nuestras soluciones.

Mesa$\PageIndex{4}$

$\color{Cerulean}{Check} \color{black}{x=-2}$	$\color{Cerulean}{Check} \color{black}{x=2}$
$\begin{array} { r } { 2 \sqrt { 2 x + 5 } - x = 4 } \\ { 2 \sqrt { 2 ( \color{Cerulean}{- 2}\color{black}{ )} + 5 } - ( \color{Cerulean}{- 2}\color{black}{ )} = 4 } \\ { 2 \sqrt { - 4 + 5 } + 2 = 4 } \\ { 2 \sqrt { 1 } + 2 = 4 } \\ { 2 + 2 = 4 } \\ { 4 = 4 }\:\:\color{Cerulean}{✓} \end{array}$	$\begin{aligned} 2 \sqrt { 2 x + 5 } - x & = 4 \\ 2 \sqrt { 2 (\color{Cerulean}{ 2}\color{black}{ )} + 5 } - ( \color{Cerulean}{2}\color{black}{ )} & = 4 \\ 2 \sqrt { 4 + 5 } - 2 & = 4 \\ 2 \sqrt { 9 } - 2 & = 4 \\ 6 - 2 & = 4 \\ 4 & = 4 \:\:\color{Cerulean}{✓}\end{aligned}$

Después de verificar, podemos ver que ambas son soluciones a la ecuación original.

Respuesta:

Las soluciones son$\pm 2$.

A veces ambas soluciones posibles son extrañas.

Ejemplo$\PageIndex{5}$:

Resolver:$\sqrt { 4 - 11 x } - x + 2 = 0$.

Solución

Comience aislando al radical.

$\begin{aligned} \sqrt { 4 - 11 x } - x + 2 & = 0\quad\quad\quad\quad\quad\color{Cerulean}{Isolate\:the\:radical.} \\ \sqrt { 4 - 11 x } & = x - 2 \\ ( \sqrt { 4 - 11 x } ) ^ { 2 } & = ( x - 2 ) ^ { 2 }\quad\quad\color{Cerulean}{Square\:both\:sides.} \\ 4 - 11 x & = x ^ { 2 } - 4 x + 4\:\:\color{Cerulean}{Solve.} \\ 0 & = x ^ { 2 } + 7 x \\ 0 & = x ( x + 7 ) \end{aligned}$

$\begin{aligned} x = 0 \text { or } x + 7 & = 0 \\ x & = - 7 \end{aligned}$

Ya que cuadramos ambos lados, debemos verificar nuestras soluciones.

Mesa$\PageIndex{5}$

$\color{Cerulean}{Check} \color{black}{x=0}$	$\color{Cerulean}{Check} \color{black}{x=-7}$
$\begin{aligned} \sqrt { 4 - 11 x } - x + 2 & = 0 \\ \sqrt { 4 - 11 ( \color{Cerulean}{0}\color{black}{ )} } -\color{Cerulean}{ 0}\color{black}{ +} 2 & = 0 \\ \sqrt { 4 } + 2 & = 0 \\ 2 + 2 & = 0 \\ 4 & = 0 \:\:\color{red}{✗} \end{aligned}$	$\begin{aligned} \sqrt { 4 - 11 x } - x + 2 &=0 \\ \sqrt { 4 - 11 ( \color{Cerulean}{- 7}\color{black}{ )} } - ( \color{Cerulean}{- 7}\color{black}{ )} + 2 &=0 \\ \sqrt { 4 + 77 } + 7 + 2 &=0 \\ \sqrt { 81 } + 9 &=0 \\ 9 + 9 &=0 \\ 18 &=0 \:\:\color{red}{✗} \end{aligned}$

Dado que ambas soluciones posibles son extrañas, la ecuación no tiene solución.

Respuesta:

Sin solución,$\emptyset$

La propiedad de cuadratura de igualdad se extiende a cualquier potencia entera positiva$n$. Dados los números reales$a$ y$b$, tenemos los siguientes:

$\text{If}\:\:\:a = b , \text { then } a ^ { n } = b ^ { n }$

A esto se le suele referir como la propiedad de poder de la igualdad ²⁵. Utilice esta propiedad, junto con el hecho de que$( \sqrt [ n ] { a } ) ^ { n } = \sqrt [ n ] { a ^ { n } } = a$, cuando no$a$ es negativo, para resolver ecuaciones radicales con índices mayores que$2$.

Ejemplo$\PageIndex{6}$:

Resolver$\sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 = 0$.

Solución

Aísle el radical, y luego cubo ambos lados de la ecuación.

$\begin{aligned} \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 & = 0\quad\quad\color{Cerulean}{Isolate\:the\:radical.} \\ \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } & = 2 \\ \left( \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } \right) ^ { 3 } & = ( 2 ) ^ { 3 }\quad\color{Cerulean}{Cube\:both\:sides.} \\ 4 x ^ { 2 } + 7 & = 8 \quad\quad\color{Cerulean}{Solve.}\\ 4 x ^ { 2 } - 1 & = 0 \\ ( 2 x + 1 ) ( 2 x - 1 ) & = 0 \end{aligned}$

$\begin{array} { r l } { 2 x + 1 = 0 } & { \text { or } \quad 2 x - 1 = 0 } \\ { 2 x = - 1 } &\quad\quad\quad\quad\: { 2 x = 1 } \\ { x = - \frac { 1 } { 2 } } &\quad\quad\quad\quad\:\:\; { x = \frac { 1 } { 2 } } \end{array}$

Cheque.

Mesa$\PageIndex{6}$

$\color{Cerulean}{Check} \color{black}{x=-\frac{1}{2}}$	$\color{Cerulean}{Check} \color{black}{x=\frac{1}{2}}$
$\begin{aligned} \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \left( \color{Cerulean}{- \frac { 1 } { 2} } \right) ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \cdot \frac { 1 } { 4 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 8 } - 2 & = 0 \\ 2- 2 & = 0 \\ 0 & = 0\:\:\color{Cerulean}{✓} \end{aligned}$	$\begin{aligned} \sqrt [ 3 ] { 4 x ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \left( \color{Cerulean}{\frac { 1 } { 2} } \right) ^ { 2 } + 7 } - 2 & = 0 \\ \sqrt [ 3 ] { 4 \cdot \frac { 1 } { 4 } + 7 } - 2 & = 0 \\ \sqrt[3]{1+7}-2 &=0 \\ \sqrt [ 3 ] { 8 } - 2 & = 0 \\ 2 - 2 & = 0 \\ 0 & = 0\:\:\color{Cerulean}{✓} \end{aligned}$

Respuesta:

Las soluciones son$\pm \frac { 1 } { 2 }$.

Ejercicio$\PageIndex{1}$

$x - 3 \sqrt { 3 x + 1 } = 3$

Contestar

La solución es$33$.

www.youtube.com/v/kr6x0qjbtbs

Puede darse el caso de que la ecuación tenga más de un término que consiste en expresiones radicales.

Ejemplo$\PageIndex{7}$:

Resolver:$\sqrt { 5 x - 3 } = \sqrt { 4 x - 1 }$.

Solución

Ambos radicales se consideran aislados en lados separados de la ecuación.

$\begin{aligned} \sqrt { 5 x - 3 } & = \sqrt { 4 x - 1 } \\ ( \sqrt { 5 x - 3 } ) ^ { 2 } & = ( \sqrt { 4 x - 1 } ) ^ { 2 } \quad\color{Cerulean}{Square\:both\:sides.}\\ 5 x - 3 & = 4 x - 1 \quad\quad\quad\color{Cerulean}{Solve.}\\ x & = 2 \end{aligned}$

Cheque$x=2$.

$\begin{aligned} \sqrt { 5 x - 3 } & = \sqrt { 4 x - 1 } \\ \sqrt { 5 ( \color{OliveGreen}{2}\color{black}{ )} - 3 } & = \sqrt { 4 ( \color{OliveGreen}{2}\color{black}{ )} - 1 } \\ \sqrt { 10 - 3 } & = \sqrt { 8 - 1 } \\ \sqrt { 7 } & = \sqrt { 7 }\:\:\color{Cerulean}{✓} \end{aligned}$

Respuesta:

La solución es$2$.

Ejemplo$\PageIndex{8}$:

Resolver:$\sqrt [ 3 ] { x ^ { 2 } + x - 14 } = \sqrt [ 3 ] { x + 50 }$.

Solución

Elimina los radicales al cubicar ambos lados.

$\begin{aligned} \sqrt [ 3 ] { x ^ { 2 } + x - 14 } & = \sqrt [ 3 ] { x + 50 } \\ \left( \sqrt [ 3 ] { x ^ { 2 } + x - 14 } \right) ^ { 3 } & = ( \sqrt [ 3 ] { x + 50 } ) ^ { 3 }\quad\color{Cerulean}{Cube\:both\:sides.} \\ x ^ { 2 } + x - 14 & = x + 50 \quad\quad\quad\color{Cerulean}{Solve.}\\ x ^ { 2 } - 64 & = 0 \\ ( x + 8 ) ( x - 8 ) & = 0 \end{aligned}$

$\begin{array} { r l } { x + 8 = 0 } & { \text { or } \quad x - 8 = 0 } \\ { x = - 8 } & \quad\quad\quad\quad{ x = 8 } \end{array}$

Cheque.

Mesa$\PageIndex{7}$

$\color{Cerulean}{Check} \color{black}{x=-8}$

$\color{Cerulean}{Check} \color{black}{x=8}$

$\begin{aligned} \sqrt [ 3 ] { x ^ { 2 } + x - 14 } & = \sqrt [ 3 ] { x + 50 } \\ \sqrt [ 3 ] { ( \color{Cerulean}{- 8}\color{black}{ )} ^ { 2 } + ( \color{Cerulean}{- 8}\color{black}{ )} - 14 } & = \sqrt [ 3 ] { ( \color{Cerulean}{- 8}\color{black}{ )} + 50 } \\ \sqrt [ 3 ] { 64 - 8 - 14 } & = \sqrt [ 3 ] { 42 } \\ \sqrt [ 3 ] { 42 } & = \sqrt [ 3 ] { 42 Table \(\PageIndex{7}$}\:\:\ color {cerúleo} {✓}\ final {alineado}\)

\ (\ begin {alineado}\ sqrt [3] {x ^ {2} + x - 14} & =\ sqrt [3] {x + 50}\\\ sqrt [3] {(\ color {cerúleo} {8}\ color {negro} {)} ^ {2} + (\ color {cerúleo} {8}\ color {negro} {)} - 14} & =\ sqrt [3] {(\ color {cerúleo} {8}\ color {negro} {)} + 50}\\\ sqrt [3] {64 + 8 - 14} & =\ sqrt [3] ] {58}\\\ sqrt [3] {58} & =\ sqrt [3] {58}\:\ color {cerúleo} {✓}\ final {alineado}\

Respuesta:

Las soluciones son$\pm 8$.

Puede que no sea posible aislar un radical en ambos lados de la ecuación. Cuando este es el caso, aísle los radicales, uno a la vez, y aplique la propiedad de cuadratura de igualdad varias veces hasta que solo quede un polinomio.

Ejemplo$\PageIndex{9}$:

Resolver:$\sqrt { x + 2 } - \sqrt { x } = 1$

Solución

Comience aislando uno de los radicales. En este caso,$\sqrt { x }$ sumar a ambos lados de la ecuación.

$\begin{aligned} \sqrt { x + 2 } - \sqrt { x } & = 1 \\ \sqrt { x + 2 } & = \sqrt { x } + 1 \end{aligned}$

A continuación, cuadrar ambos lados. Tenga cuidado de aplicar la propiedad distributiva al lado derecho.

$\begin{aligned} ( \sqrt { x + 2 } ) ^ { 2 } & = ( \sqrt { x } + 1 ) ^ { 2 } \\ x + 2 & = ( \sqrt { x } + 1 ) ( \sqrt { x } + 1 ) \\ x + 2 & = \sqrt { x ^ { 2 } } + \sqrt { x } + \sqrt { x } + 1 \\ x + 2 & = x + 2 \sqrt { x } + 1 \end{aligned}$

En este punto tenemos un término que contiene un radical. Aíslalo y vuelve a cuadrar ambos lados.

$\begin{aligned} x + 2 & = x + 2 \sqrt { x } + 1 \\ 1 & = 2 \sqrt { x } \\ ( 1 ) ^ { 2 } & = ( 2 \sqrt { x } ) ^ { 2 } \\ 1 & = 4 x \\ \frac { 1 } { 4 } & = x \end{aligned}$

Verifica si$x = \frac { 1 } { 4 }$ satisface la ecuación original$\sqrt { x + 2 } - \sqrt { x } = 1$

$\begin{array} { r } { \sqrt { \color{OliveGreen}{\frac { 1 } { 4 }}\color{black}{ +} 2 } - \sqrt { \color{OliveGreen}{\frac { 1 } { 4 }} } \color{black}{=} 1 } \\ { \sqrt { \frac { 9 } { 4 } } - \frac { 1 } { 2 } = 1 } \\ { \frac { 3 } { 2 } - \frac { 1 } { 2 } = 1 } \\ { \frac { 2 } { 2 } = 1 } \\ { 1 = 1 }\color{Cerulean}{✓} \end{array}$

Contestar

La solución es$\frac { 1 } { 4 }$.

Porque$( A + B ) ^ { 2 } \neq A ^ { 2 } + B ^ { 2 }$, no podemos simplemente cuadrar cada término. Por ejemplo, es incorrecto cuadrar cada término de la siguiente manera.

$\color{Cerulean}{(}\color{black}{ \sqrt { x + 2 }}\color{Cerulean}{ ) ^ { 2 } }\color{black}{-}\color{Cerulean}{ (}\color{black}{ \sqrt { x }}\color{Cerulean}{ ) ^ { 2 }}\color{black}{ =}\color{Cerulean}{ (}\color{black}{ 1}\color{Cerulean}{ ) ^ { 2 }}\\\color{red}{Incorrect!}$

Este es un error común y lleva a un resultado incorrecto. Al cuadrar ambos lados de una ecuación con múltiples términos, debemos tener cuidado de aplicar la propiedad distributiva.

Ejemplo$\PageIndex{10}$:

Resolver:$\sqrt { 2 x + 10 } - \sqrt { x + 6 } = 1$

Solución

Comience aislando uno de los radicales. En este caso,$\sqrt{x+6}$ sumar a ambos lados de la ecuación.

$\begin{aligned} \sqrt { 2 x + 10 } - \sqrt { x + 6 } &= 1 \\ \sqrt { 2 x + 10 } & = \sqrt { x + 6 } + 1 \end{aligned}$

A continuación, cuadrar ambos lados. Tenga cuidado de aplicar la propiedad distributiva al lado derecho.

$\begin{aligned} ( \sqrt { 2 x + 10 } ) ^ { 2 } & = ( \sqrt { x + 6 } + 1 ) ^ { 2 } \\ 2 x + 10 & = x + 6 + 2 \sqrt { x + 6 } + 1 \\ 2 x + 10 & = x + 7 + 2 \sqrt { x + 6 } \end{aligned}$

En este punto tenemos un término que contiene un radical. Aíslalo y vuelve a cuadrar ambos lados.

$\begin{aligned} 2 x + 10 & = x + 7 + 2 \sqrt { x + 6 } \\ x + 3 & = 2 \sqrt { x + 6 } \\ ( x + 3 ) ^ { 2 } & = ( 2 \sqrt { x + 6 } ) ^ { 2 } \\ x ^ { 2 } + 6 x + 9 & = 4 ( x + 6 ) \\ x ^ { 2 } + 6 x + 9 & = 4 x + 24 \\ x ^ { 2 } + 2 x - 15 & = 0 \\ (x - 3 ) ( x + 5 ) & = 0 \end{aligned}$

$\begin{array} { r l } { x - 3 = 0 } & { \text { or } \quad x + 5 = 0 } \\ { x = 3 } & \quad\quad\quad\quad\:{ x = - 5 } \end{array}$

Cheque.

Mesa$\PageIndex{8}$

$\color{Cerulean}{Check} \color{black}{x=3}$	$\color{Cerulean}{Check} \color{black}{x=-5}$
$\begin{aligned} \sqrt { 2 x + 10 } - \sqrt { x + 6 } & = 1 \\ \sqrt { 2 ( \color{Cerulean}{3}\color{black}{ )} + 10 } - \sqrt { \color{Cerulean}{3}\color{black}{ +} 6 } & = 1 \\ \sqrt { 16 } - \sqrt { 9 } & = 1 \\ 4 - 3 & = 1 \\ 1 & = 1\:\:\color{Cerulean}{✓} \end{aligned}$	$\begin{aligned} \sqrt { 2 x + 10 } - \sqrt { x + 6 } &= 1 \\ \sqrt { 2 (\color{Cerulean}{ - 5}\color{black}{ )} + 10 } - \sqrt { \color{Cerulean}{- 5}\color{black}{ +} 6 } &=1 \\ \sqrt { 0 } - \sqrt { 1 }& =1 \\ 0 - 1 &=1 \\ - 1 &=1\:\:\color{red}{✗} \end{aligned}$

Contestar

La solución es$3$.

Ejercicio$\PageIndex{2}$

Resolver:$\sqrt { 4 x + 21 } - \sqrt { 2 x + 22 } = 1$

Contestar

La solución es$7$.

www.youtube.com/v/btmeqwpsmayo

Claves para llevar

• Resuelve ecuaciones que involucran raíces cuadradas aislando primero el radical y luego cuadrando ambos lados. Al cuadrar una raíz cuadrada se elimina el radical, dejándonos con una ecuación que se puede resolver utilizando las técnicas aprendidas anteriormente en nuestro estudio del álgebra.
• Al cuadrar ambos lados de una ecuación se introduce la posibilidad de soluciones extrañas. Por ello, debes verificar tus soluciones en la ecuación original.
• Resolver ecuaciones que involucran las raíces$n$ th aislando primero el radical y luego elevando ambos lados al$n$ th poder. Esto elimina el radical y da como resultado una ecuación que puede resolverse con técnicas que ya hayas dominado.
• Cuando más de un término radical esté presente en una ecuación, aislarlos uno a la vez, y aplique la propiedad de poder de la igualdad varias veces hasta que solo quede un polinomio.

Ejercicio$\PageIndex{3}$

Resolver

1. $\sqrt { x } = 7$
2. $\sqrt { x } = 4$
3. $\sqrt { x } + 8 = 9$
4. $\sqrt { x } - 4 = 5$
5. $\sqrt { x } + 7 = 4$
6. $\sqrt { x } + 3 = 1$
7. $5 \sqrt { x } - 1 = 0$
8. $3 \sqrt { x } - 2 = 0$
9. $\sqrt { 3 x + 1 } = 2$
10. $\sqrt { 5 x - 4 } = 4$
11. $\sqrt { 7 x + 4 } + 6 = 11$
12. $\sqrt { 3 x - 5 } + 9 = 14$
13. $2 \sqrt { x - 1 } - 3 = 0$
14. $3 \sqrt { x + 1 } - 2 = 0$
15. $\sqrt { x + 1 } = \sqrt { x } + 1$
16. $\sqrt { 2 x - 1 } = \sqrt { 2 x } - 1$
17. $\sqrt { 4 x - 1 } = 2 \sqrt { x } - 1$
18. $\sqrt { 4 x - 11 } = 2 \sqrt { x } - 1$
19. $\sqrt { x + 8 } = \sqrt { x } - 4$
20. $\sqrt { 25 x - 1 } = 5 \sqrt { x } + 1$
21. $\sqrt [ 3 ] { x } = 3$
22. $\sqrt [ 3 ] { x } = - 4$
23. $\sqrt [ 3 ] { 2 x + 9 } = 3$
24. $\sqrt [ 3 ] { 4 x - 11 } = 1$
25. $\sqrt [ 3 ] { 5 x + 7 } + 3 = 1$
26. $\sqrt [ 3 ] { 3 x - 6 } + 5 = 2$
27. $4 - 2 \sqrt [ 3 ] { x + 2 } = 0$
28. $6 - 3 \sqrt [ 3 ] { 2 x - 3 } = 0$
29. $\sqrt [ 5 ] { 3 ( x + 10 ) } = 2$
30. $\sqrt [ 5 ] { 4 x + 3 } + 5 = 4$
31. $\sqrt { 8 x + 11 } = 3 \sqrt { x + 1 }$
32. $2 \sqrt { 3 x - 4 } = \sqrt { 2 ( 3 x + 1 ) }$
33. $\sqrt { 2 ( x + 10 ) } = \sqrt { 7 x - 15 }$
34. $\sqrt { 5 ( x - 4 ) } = \sqrt { x + 4 }$
35. $\sqrt [ 3 ] { 5 x - 2 } = \sqrt [ 3 ] { 4 x }$
36. $\sqrt [ 3 ] { 9 ( x - 1 ) } = \sqrt [ 3 ] { 3 ( x + 7 ) }$
37. $\sqrt [ 3 ] { 3 x + 1 } = \sqrt [ 3 ] { 2 ( x - 1 ) }$
38. $\sqrt [ 3 ] { 9 x } = \sqrt [ 3 ] { 3 ( x - 6 ) }$
39. $\sqrt [ 5 ] { 3 x - 5 } = \sqrt [ 5 ] { 2 x + 8 }$
40. $\sqrt [ 5 ] { x + 3 } = \sqrt [ 5 ] { 2 x + 5 }$
41. $\sqrt { 4 x + 21 } = x$
42. $\sqrt { 8 x + 9 } = x$
43. $\sqrt { 4 ( 2 x - 3 ) } = x$
44. $\sqrt { 3 ( 4 x - 9 ) } = x$
45. $2 \sqrt { x - 1 } = x$
46. $3 \sqrt { 2 x - 9 } = x$
47. $\sqrt { 9 x + 9 } = x + 1$
48. $\sqrt { 3 x + 10 } = x + 4$
49. $\sqrt { x - 1 } = x - 3$
50. $\sqrt { 2 x - 5 } = x - 4$
51. $\sqrt { 16 - 3 x } = x - 6$
52. $\sqrt { 7 - 3 x } = x - 3$
53. $3 \sqrt { 2 x + 10 } = x + 9$
54. $2 \sqrt { 2 x + 5 } = x + 4$
55. $3 \sqrt { x - 1 } - 1 = x$
56. $2 \sqrt { 2 x + 2 } - 1 = x$
57. $\sqrt { 10 x + 41 } - 5 = x$
58. $\sqrt { 6 ( x + 3 ) } - 3 = x$
59. $\sqrt { 8 x ^ { 2 } - 4 x + 1 } = 2 x$
60. $\sqrt { 18 x ^ { 2 } - 6 x + 1 } = 3 x$
61. $5 \sqrt { x + 2 } = x + 8$
62. $4 \sqrt { 2 ( x + 1 ) } = x + 7$
63. $\sqrt { x ^ { 2 } - 25 } = x$
64. $\sqrt { x ^ { 2 } + 9 } = x$
65. $3 + \sqrt { 6 x - 11 } = x$
66. $2 + \sqrt { 9 x - 8 } = x$
67. $\sqrt { 4 x + 25 } - x = 7$
68. $\sqrt { 8 x + 73 } - x = 10$
69. $2 \sqrt { 4 x + 3 } - 3 = 2 x$
70. $2 \sqrt { 6 x + 3 } - 3 = 3 x$
71. $2 x - 4 = \sqrt { 14 - 10 x }$
72. $3 x - 6 = \sqrt { 33 - 24 x }$
73. $\sqrt [ 3 ] { x ^ { 2 } - 24 } = 1$
74. $\sqrt [ 3 ] { x ^ { 2 } - 54 } = 3$
75. $\sqrt [ 3 ] { x ^ { 2 } + 6 x } + 1 = 4$
76. $\sqrt [ 3 ] { x ^ { 2 } + 2 x } + 5 = 7$
77. $\sqrt [ 3 ] { 25 x ^ { 2 } - 10 x - 7 } = - 2$
78. $\sqrt [ 3 ] { 9 x ^ { 2 } - 12 x - 23 } = - 3$
79. $\sqrt [ 3 ] { 4 x ^ { 2 } - 1 } - 2 = 0$
80. $4 \sqrt [ 3 ] { x ^ { 2 } } - 1 = 0$
81. $\sqrt [ 5 ] { x ( 2 x + 1 ) } - 1 = 0$
82. $\sqrt [ 5 ] { 3 x ^ { 2 } - 20 x } - 2 = 0$
83. $\sqrt { 2 x ^ { 2 } - 15 x + 25 } = \sqrt { ( x + 5 ) ( x - 5 ) }$
84. $\sqrt { x ^ { 2 } - 4 x + 4 } = \sqrt { x ( 5 - x ) }$
85. $\sqrt [ 3 ] { 2 \left( x ^ { 2 } + 3 x - 20 \right) } = \sqrt [ 3 ] { ( x + 3 ) ^ { 2 } }$
86. $\sqrt [ 3 ] { 3 x ^ { 2 } + 3 x + 40 } = \sqrt [ 3 ] { ( x - 5 ) ^ { 2 } }$
87. $\sqrt { 2 x - 5 } + \sqrt { 2 x } = 5$
88. $\sqrt { 4 x + 13 } - 2 \sqrt { x } = 3$
89. $\sqrt { 8 x + 17 } - 2 \sqrt { 2 - x } = 3$
90. $\sqrt { 3 x - 6 } - \sqrt { 2 x - 3 } = 1$
91. $\sqrt { 2 ( x - 2 ) } - \sqrt { x - 1 } = 1$
92. $\sqrt { 2 x + 5 } - \sqrt { x + 3 } = 2$
93. $\sqrt { 2 ( x + 1 ) } - \sqrt { 3 x + 4 } - 1 = 0$
94. $\sqrt { 6 - 5 x } + \sqrt { 3 - 3 x } - 1 = 0$
95. $\sqrt { x - 2 } - 1 = \sqrt { 2 ( x - 3 ) }$
96. $\sqrt { 14 - 11 x } + \sqrt { 7 - 9 x } = 1$
97. $\sqrt { x + 1 } = \sqrt { 3 } - \sqrt { 2 - x }$
98. $\sqrt { 2 x + 9 } - \sqrt { x + 1 } = 2$
99. $x ^ { 1 / 2 } - 10 = 0$
100. $x ^ { 1 / 2 } - 6 = 0$
101. $x ^ { 1 / 3 } + 2 = 0$
102. $x ^ { 1 / 3 } + 4 = 0$
103. $( x - 1 ) ^ { 1 / 2 } - 3 = 0$
104. $( x + 2 ) ^ { 1 / 2 } - 6 = 0$
105. $( 2 x - 1 ) ^ { 1 / 3 } + 3 = 0$
106. $( 3 x - 1 ) ^ { 1 / 3 } - 2 = 0$
107. $( 4 x + 15 ) ^ { 1 / 2 } - 2 x = 0$
108. $( 3 x + 2 ) ^ { 1 / 2 } - 3 x = 0$
109. $( 2 x + 12 ) ^ { 1 / 2 } - x = 6$
110. $( 4 x + 36 ) ^ { 1 / 2 } - x = 9$
111. $2 ( 5 x + 26 ) ^ { 1 / 2 } = x + 10$
112. $3 ( x - 1 ) ^ { 1 / 2 } = x + 1$
113. $x ^ { 1 / 2 } + ( 3 x - 2 ) ^ { 1 / 2 } = 2$
114. $( 6 x + 1 ) ^ { 1 / 2 } - ( 3 x ) ^ { 1 / 2 } = 1$
115. $( 3 x + 7 ) ^ { 1 / 2 } + ( x + 3 ) ^ { 1 / 2 } - 2 = 0$
116. $( 3 x ) ^ { 1 / 2 } + ( x + 1 ) ^ { 1 / 2 } - 5 = 0$

Contestar

1. $49$

3. $1$

5. $Ø$

7. $\frac{1}{25}$

9. $1$

11. $3$

13. $\frac{13}{4}$

15. $0$

17. $\frac{1}{4}$

19. $Ø$

21. $27$

23. $9$

25. $−3$

27. $6$

29. $\frac{2}{3}$

31. $2$

33. $7$

35. $2$

37. $−3$

39. $13$

41. $7$

43. $2, 6$

45. $2$

47. $−1, 8$

49. $5$

51. $Ø$

53. $−3, 3$

55. $2, 5$

57. $−4, 4$

59. $\frac{1}{2}$

61. $2, 7$

63. $Ø$

65. $10$

67. $−6, −4$

69. $−\frac{1}{2}, \frac{3}{2}$

71. $Ø$

73. $−5, 5$

75. $−9, 3$

77. $\frac{1}{5}$

79. $− \frac{3}{2} ,\frac{ 3}{2}$

81. $−1, \frac{1}{2}$

83. $5, 10$

85. $−7, 7$

87. $\frac{9}{2}$

89. $1$

91. $10$

93. $Ø$

95. $3$

97. $1, 2$

99. $100$

101. $−8$

103. $10$

105. $−13$

107. $\frac{5}{2}$

109. $−6, −4$

111. $−2, 2$

113. $1$

115. $−2$

Ejercicio$\PageIndex{4}$

Determinar las raíces de las funciones dadas. Recordemos que una raíz es un valor en el dominio que resulta en cero. En otras palabras, encuentra$x$ dónde$f (x) = 0$.

1. $f ( x ) = \sqrt { x + 5 } - 2$
2. $f ( x ) = \sqrt { 2 x - 3 } - 1$
3. $f ( x ) = 2 \sqrt { x + 2 } - 8$
4. $f ( x ) = 3 \sqrt { x - 7 } - 6$
5. $f ( x ) = \sqrt [ 3 ] { x + 1 } + 2$
6. $f ( x ) = 2 \sqrt [ 3 ] { x - 1 } + 6$

Contestar

1. $−1$

3. $14$

5. $−9$

Ejercicio$\PageIndex{5}$

Resolver para la variable indicada.

1. Resolver para$\mathrm { P } : r = \sqrt { P } - 1$
2. Resolver para$x : y = \sqrt { x - h } + k$
3. Resolver para$s : t = \sqrt { \frac { 2 s } { g } }$
4. Resolver para$\mathrm { L } : T = 2 \pi \sqrt { \frac { L } { 32 } }$
5. Resolver para$\mathrm { R } : I = \sqrt { \frac { P } { R } }$
6. Resolver para$h : r = \sqrt { \frac { 3 V } { \pi h } }$
7. Resolver para$V : r = \sqrt [ 3 ] { \frac { 3 V } { 4 \pi } }$
8. Resolver para$c : a = \sqrt [ 3 ] { \frac { b ^ { 2 } \pi } { 2 c } }$
9. La raíz cuadrada de$1$ menos de dos veces un número es igual a$2$ menor que el número. Encuentra el número.
10. La raíz cuadrada de$4$ menos de dos veces un número es igual a$6$ menor que el número. Encuentra el número.
11. La raíz cuadrada de dos veces un número es igual a la mitad de ese número. Encuentra el número.
12. La raíz cuadrada de dos veces un número es igual a un tercio de ese número. Encuentra el número.
13. La distancia$d$ en millas que una persona puede ver un objeto en el horizonte viene dada por la fórmula$d = \frac { \sqrt { 6 h } } { 2 }$ donde$h$ representa la altura en pies de los ojos de la persona sobre el nivel del mar. ¿Qué tan altos deben estar los ojos de una persona para ver un objeto a$5$ kilómetros de distancia?
14. La corriente$I$ medida en amperios viene dada por la fórmula$I = \sqrt { \frac { P } { R } }$ donde$P$ se mide el consumo de energía en vatios y$R$ es la resistencia medida en ohmios. Si una bombilla requiere$1/2$ amperios de corriente y usa$60$ vatios de potencia, entonces ¿cuál es la resistencia a través de la bombilla?

Contestar

1. $P = ( r + 1 ) ^ { 2 }$

3. $s = \frac { g t ^ { 2 } } { 2 }$

5. $R = \frac { P } { I ^ { 2 } }$

7. $V = \frac { 4 \pi r ^ { 3 } } { 3 }$

9. $5$

11. $0,8$

13. $16 \frac { 2 } { 3 }$pies

Ejercicio$\PageIndex{6}$

El período de un péndulo$T$ en segundos viene dado por la fórmula

$T = 2 \pi \sqrt { \frac { L } { 32 } }$

donde$L$ representa la longitud en pies. Calcular la longitud de un péndulo dado el periodo. Dar el valor exacto y el valor aproximado redondeado a la décima de pie más cercana.

1. $1$segundo
2. $2$segundos
3. $\frac{1}{2}$segundo
4. $\frac{1}{3}$segundo

Contestar

1. $\frac { 8 } { \pi ^ { 2 } }$pies;$0.8$ pies

3. $\frac { 2 } { \pi ^ { 2 } }$pies;$0.2$ pies

Ejercicio$\PageIndex{7}$

El tiempo$t$ en segundos, un objeto está en caída libre viene dado por la fórmula

$t = \frac { \sqrt { s } } { 4 }$

donde$s$ representa la distancia que ha caído, en pies. Calcula la distancia que caerá un objeto dada la cantidad de tiempo.

1. $1$segundo
2. $2$segundos
3. $\frac{1}{2}$segundo
4. $\frac{1}{4}$segundo

Contestar

1. $16$pies

3. $4$pies

Ejercicio$\PageIndex{9}$

1. Discutir razones por las que a veces obtenemos soluciones extrañas a la hora de resolver ecuaciones radicales. ¿Alguna vez hay alguna condición en la que no sea necesario verificar soluciones extrañas? ¿Por qué o por qué no?
2. Si una ecuación tiene múltiples términos, explique por qué cuadrar todos ellos es incorrecto. Dé un ejemplo.

Contestar

1. La respuesta puede variar

Notas al pie

²² Cualquier ecuación que contenga uno o más radicales con una variable en el radicando.

²³ Dados números reales$a$ y$b$, dónde$a = b$, entonces$a^{2} = b^{2}$.

²⁴ Una solución debidamente encontrada que no resuelve la ecuación original. \

²⁵ Dado cualquier número entero positivo$n$ y números reales$a$ y$b$ dónde$a = b$, entonces$a ^ { n } = b ^ { n }$.