8.4: Hipérbolas

Objetivos de aprendizaje

• Graficar una hipérbola en forma estándar.
• Determinar la ecuación de una hipérbola dada su gráfica.
• Reescribir la ecuación de una hipérbola en forma estándar.
• Identificar una sección cónica dada su ecuación.

La hipérbola en forma estándar

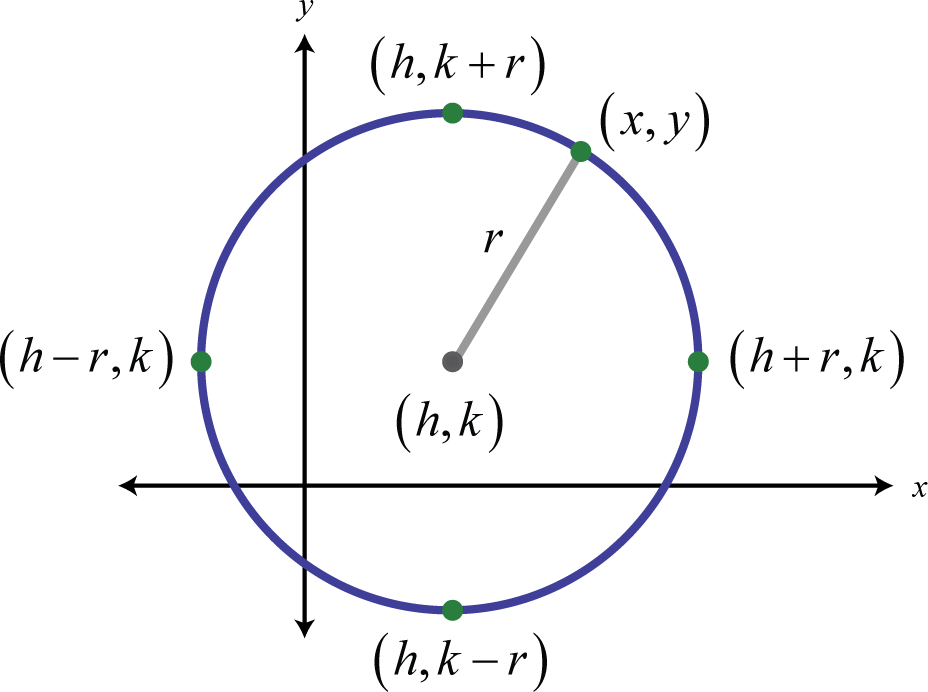
Una hipérbola ²³ es el conjunto de puntos en un plano cuyas distancias desde dos puntos fijos, llamados focos, tiene una diferencia absoluta que es igual a una constante positiva. En otras palabras, si los puntos$F_{1}$ y$F_{2}$ son los focos y$d$ se da alguna constante positiva entonces$(x,y)$ es un punto en la hipérbola si$d=\left|d_{1}-d_{2}\right|$ como se muestra a continuación:

Figura$\PageIndex{1}$

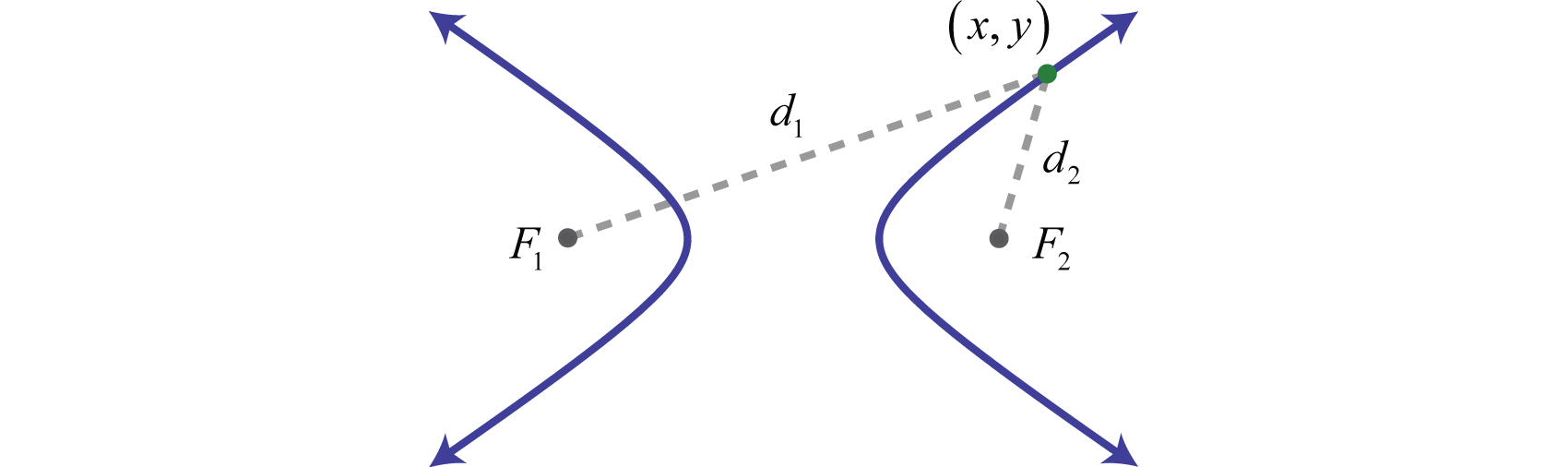
Además, una hipérbola está formada por la intersección de un cono con un plano oblicuo que cruza la base. Consta de dos curvas separadas, llamadas ramas ²⁴. Los puntos en las ramas separadas de la gráfica donde la distancia es mínima se denominan vértices ²⁵. El punto medio entre los vértices de una hipérbola es su centro. A diferencia de una parábola, una hipérbola es asintótica a ciertas líneas dibujadas a través del centro. En esta sección, nos centraremos en graficar hipérbolas que se abren a izquierda y derecha o hacia arriba y hacia abajo.

Figura$\PageIndex{2}$

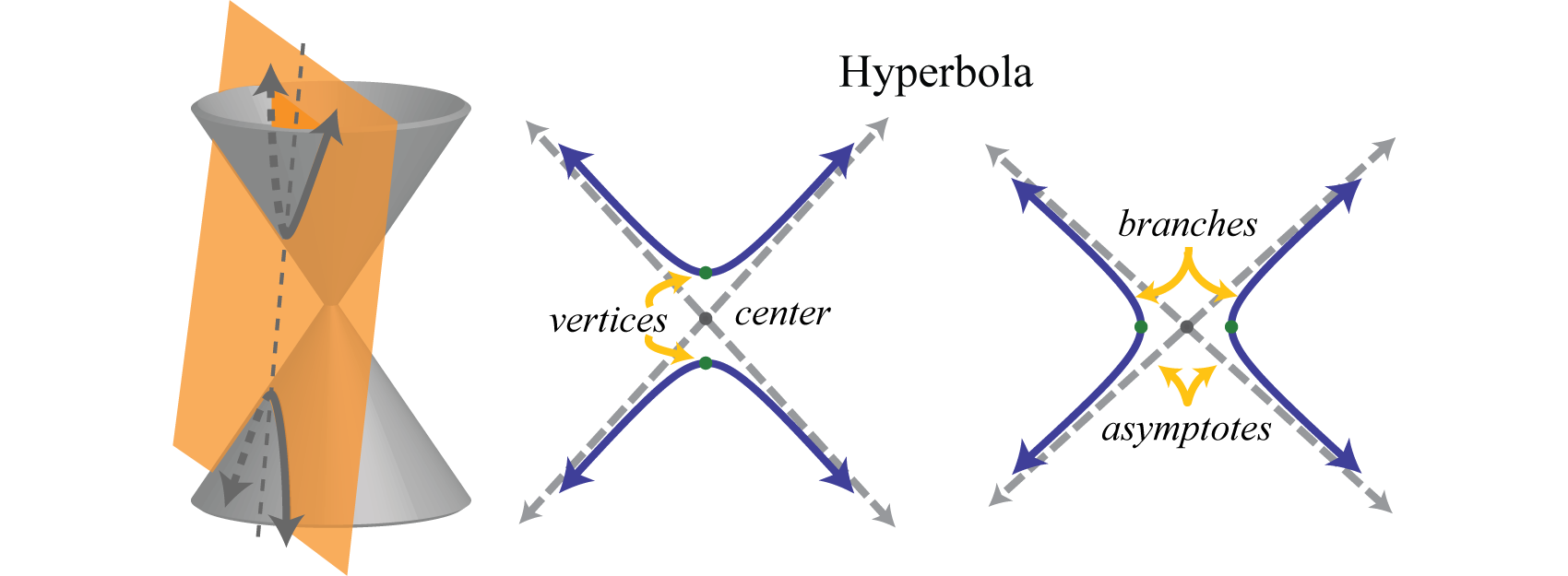
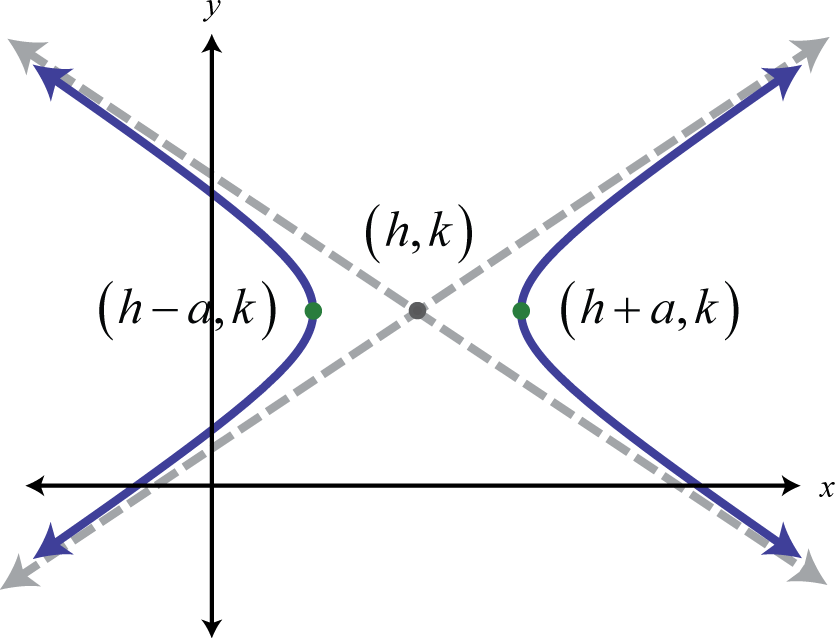
Las asíntotas se dibujan discontinuas ya que no forman parte de la gráfica; simplemente indican el comportamiento final de la gráfica. La ecuación de una hipérbola que se abre a la izquierda y a la derecha en forma estándar ²⁶ sigue:

$$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1 \nonumber$$

Figura$\PageIndex{3}$

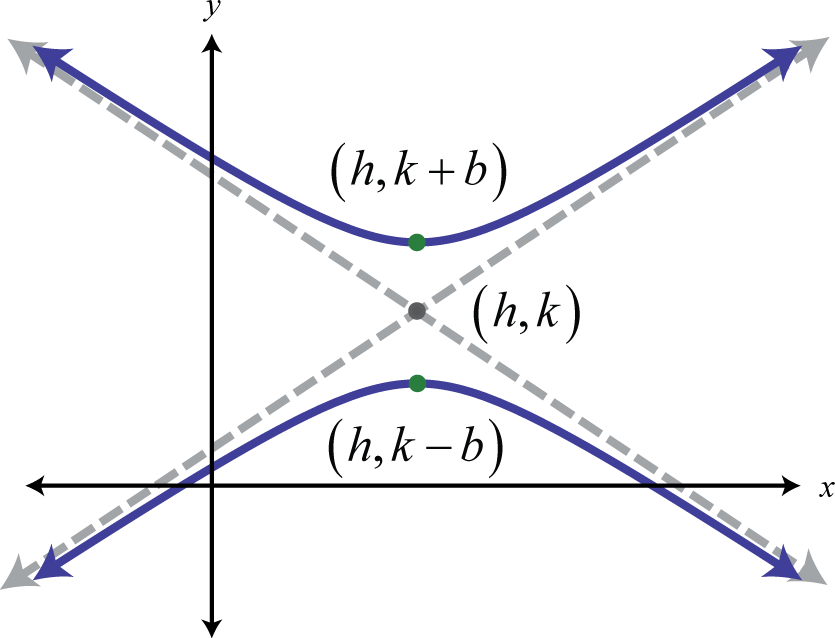
Aquí está el centro$(h,k)$ y los vértices están$(h±a,k)$. La ecuación de una hipérbola que se abre hacia arriba y hacia abajo en la forma estándar ²⁷ sigue:

$$\frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}}=1 \nonumber$$

Figura$\PageIndex{4}$

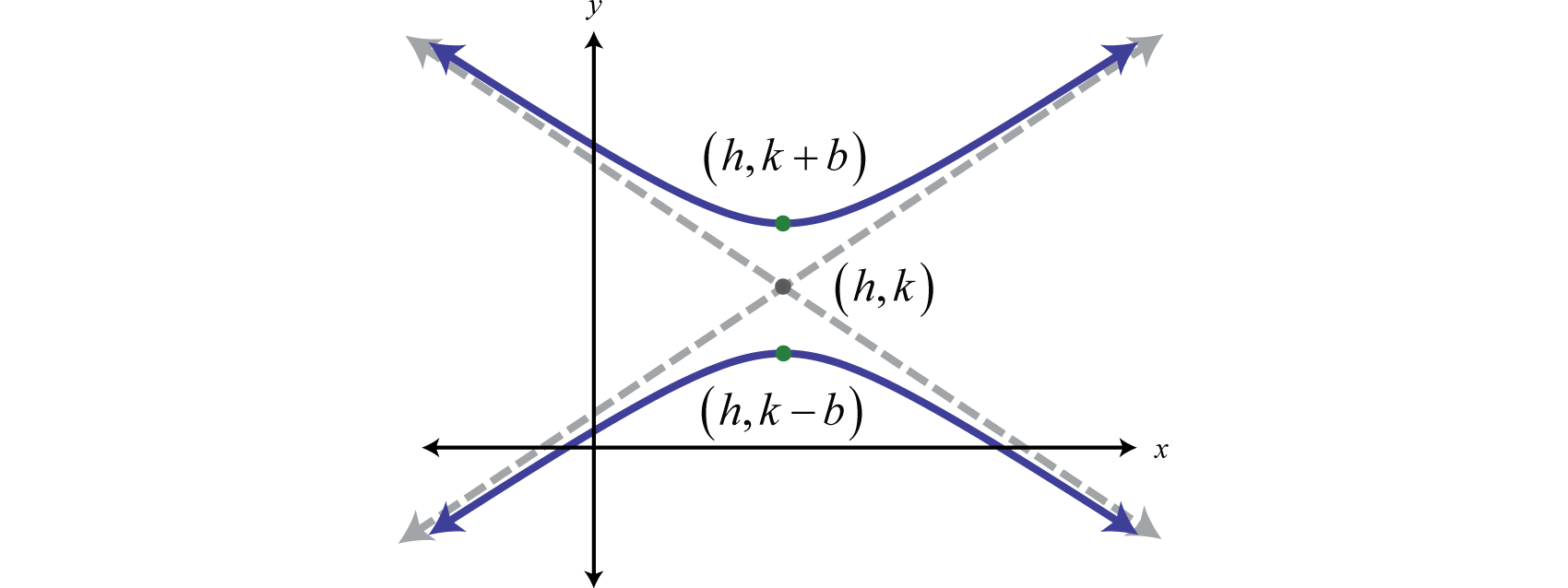
Aquí está el centro$(h,k)$ y los vértices están$(h,k±b)$.

Las asíntotas son esenciales para determinar la forma de cualquier hipérbola. Dada la forma estándar, las asíntotas son líneas que pasan por el centro$(h,k)$ con pendiente$m=\pm \frac{b}{a}$. Para bosquejar fácilmente las asíntotas hacemos uso de dos segmentos de línea especiales a través del centro usando$a$ y$b$. Dada cualquier hipérbola, el eje transversal ²⁸ es el segmento lineal formado por sus vértices. El eje conjugado ²⁹ es el segmento lineal a través del centro perpendicular al eje transversal como se muestra a continuación:

Figura$\PageIndex{5}$

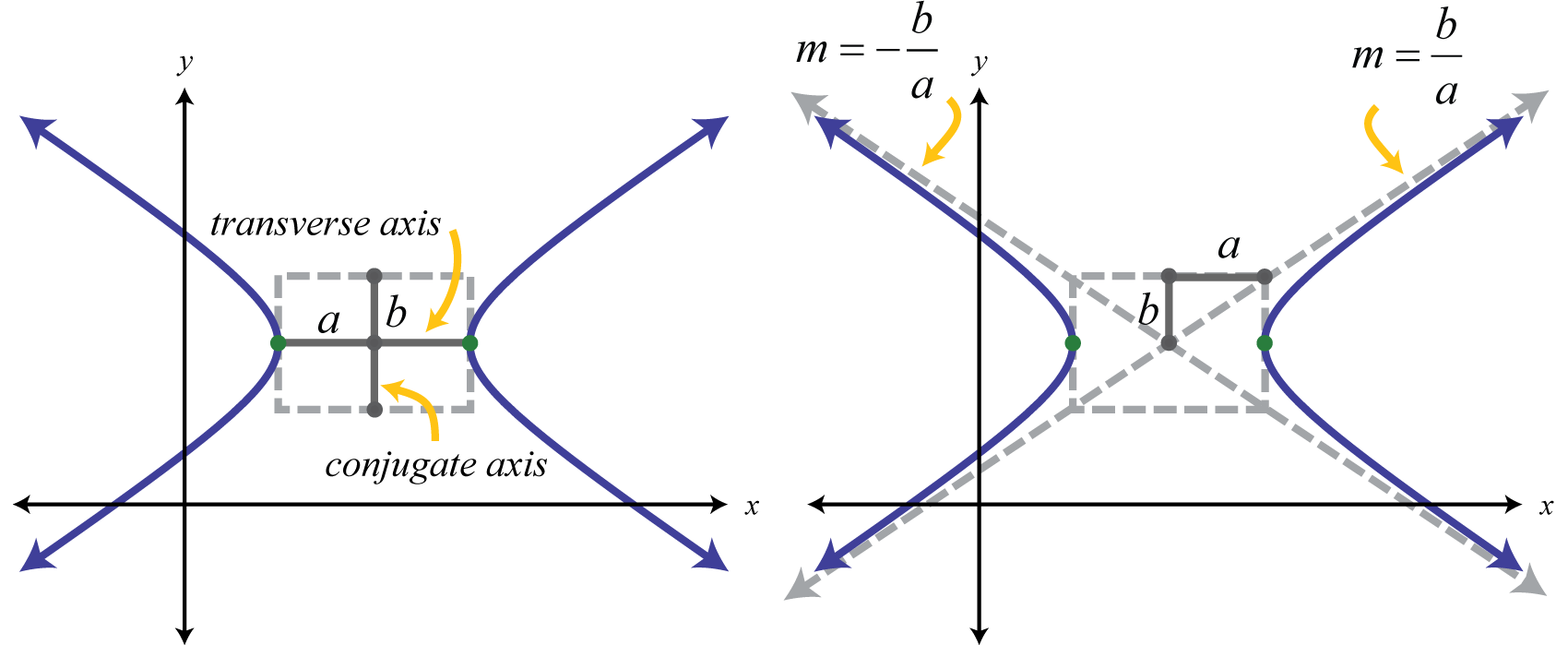
El rectángulo definido por los ejes transversal y conjugado se denomina rectángulo fundamental ³⁰. Las líneas que atraviesan las esquinas de este rectángulo tienen pendientes$m=\pm \frac{b}{a}$. Estas líneas son las asíntotas que definen la forma de la hipérbola. Por lo tanto, dada la forma estándar, muchas de las propiedades de una hipérbola son evidentes.

Mesa$\PageIndex{1}$

Ecuación	Centro	$a$	$b$	Abre
$\frac{(x-3)^{2}}{25}-\frac{(y-5)^{2}}{16}=1$	$(3,5)$	\ (a\) ">$a=5$	\ (b\) ">$b=4$	Izquierda y derecha
$\frac{(y-2)^{2}}{36}-\frac{(x+1)^{2}}{9}=1$	$(-1,2)$	\ (a\) ">$a=3$	\ (b\) ">$b=6$	Al alza y a la baja
$\frac{(y+2)^{2}}{3}-(x-5)^{2}=1$	$(5,-2)$	\ (a\) ">$a=1$	\ (b\) ">$b=\sqrt{3}$	Al alza y a la baja
$\frac{x^{2}}{49}-\frac{(y+4)^{2}}{8}=1$	$(0,-4)$	\ (a\) ">$a=7$	\ (b\) ">$b=2 \sqrt{2}$	Izquierda y derecha

La gráfica de una hipérbola está completamente determinada por su centro, vértices y asíntotas.

Ejemplo$\PageIndex{1}$:

Gráfica:$\frac{(x-5)^{2}}{9}-\frac{(y-4)^{2}}{4}=1$.

Solución:

En este caso, la expresión que implica$x$ tiene un coeficiente inicial positivo; por lo tanto, la hipérbola se abre a izquierda y derecha. Aquí$a=\sqrt{9}=3$ y$b=\sqrt{4}=2$. Desde el centro$(5,4)$, marcar puntos$3$ unidades izquierda y derecha así como$2$ unidades arriba y abajo. Conecte estos puntos con un rectángulo de la siguiente manera:

Figura$\PageIndex{6}$

Las líneas que atraviesan las esquinas de este rectángulo definen las asíntotas.

Figura$\PageIndex{7}$

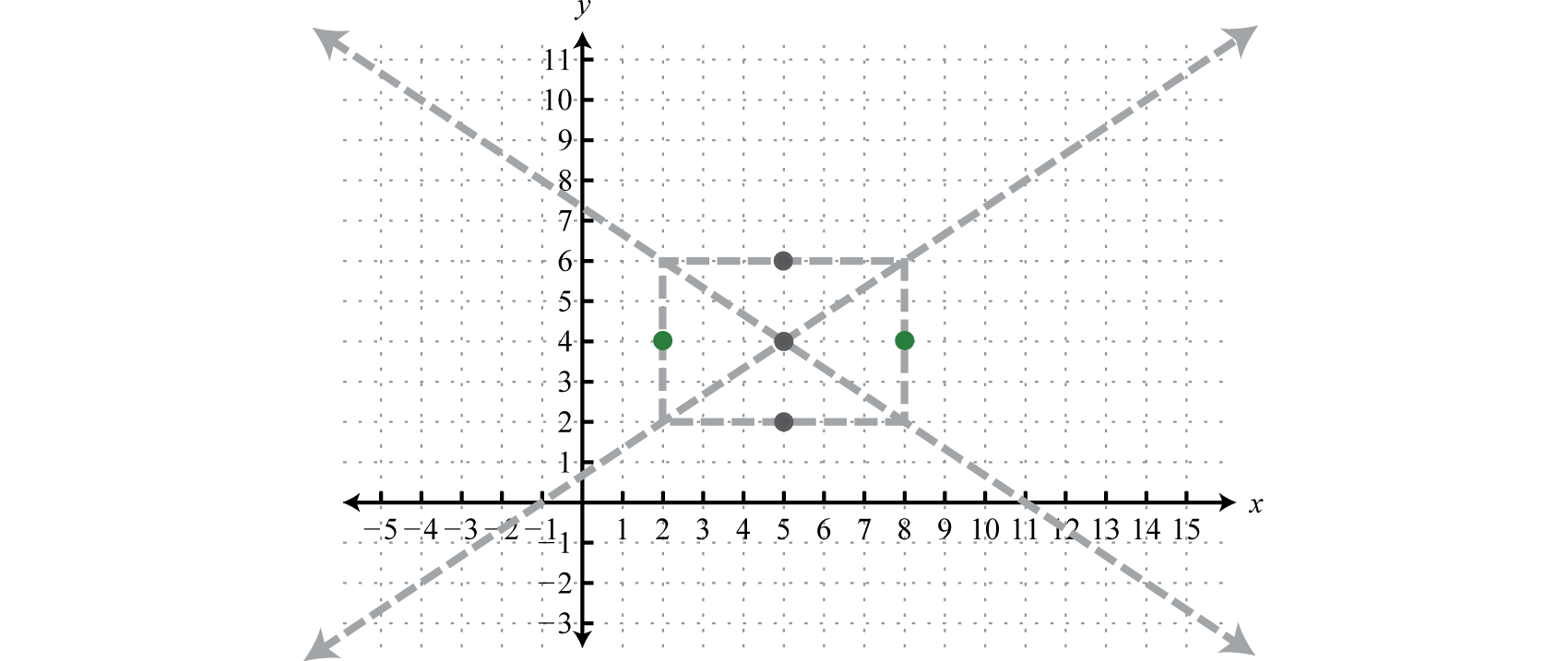
Utilice estas líneas discontinuas como guía para graficar la hipérbola abriendo izquierda y derecha pasando por los vértices.

Contestar

Figura$\PageIndex{8}$

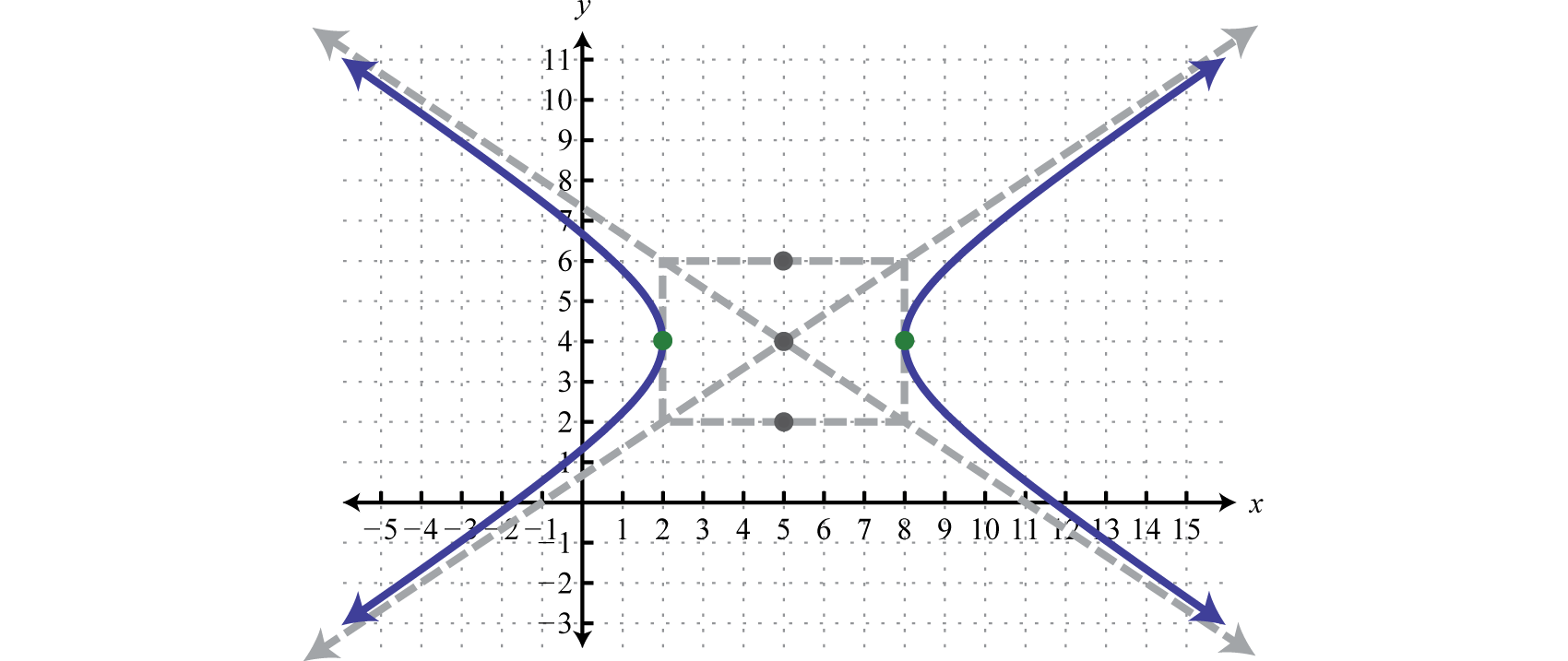
Ejemplo$\PageIndex{2}$:

Gráfica:$\frac{(y-2)^{2}}{4}-\frac{(x+1)^{2}}{36}=1$.

Solución

En este caso, la expresión que implica$y$ tiene un coeficiente inicial positivo; por lo tanto, la hipérbola se abre hacia arriba y hacia abajo. Aquí$a=\sqrt{36}=6$ y$b=\sqrt{4}=2$. Desde el centro$(−1,2)$ marca puntos$6$ unidades izquierda y derecha así como$2$ unidades arriba y abajo. Conecta estos puntos con un rectángulo. Las líneas que atraviesan las esquinas de este rectángulo definen las asíntotas.

Figura$\PageIndex{9}$

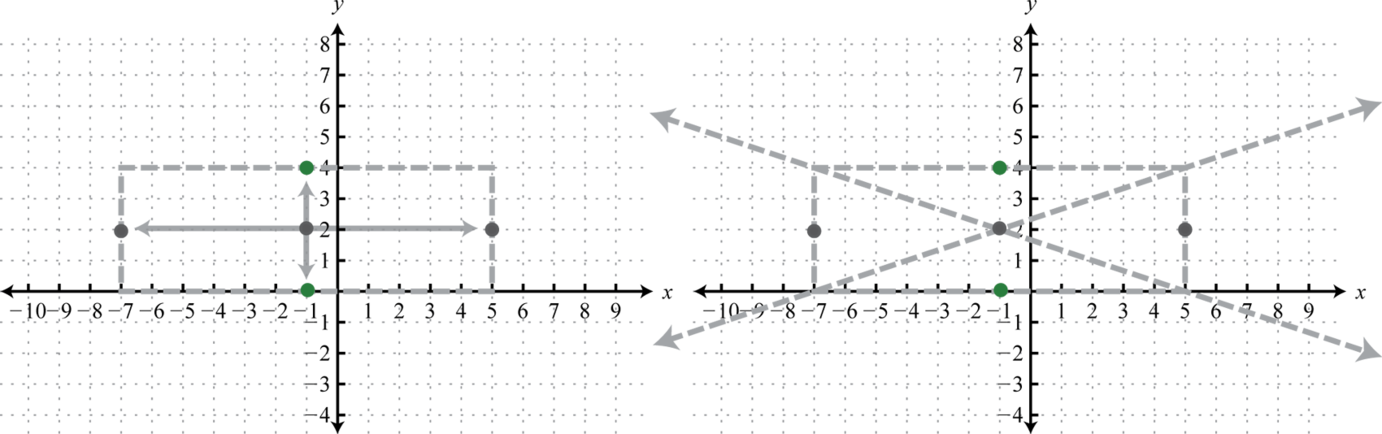
Utilice estas líneas discontinuas como guía para graficar la apertura de la hipérbola hacia arriba y hacia abajo pasando por los vértices.

Respuesta:

Figura$\PageIndex{10}$

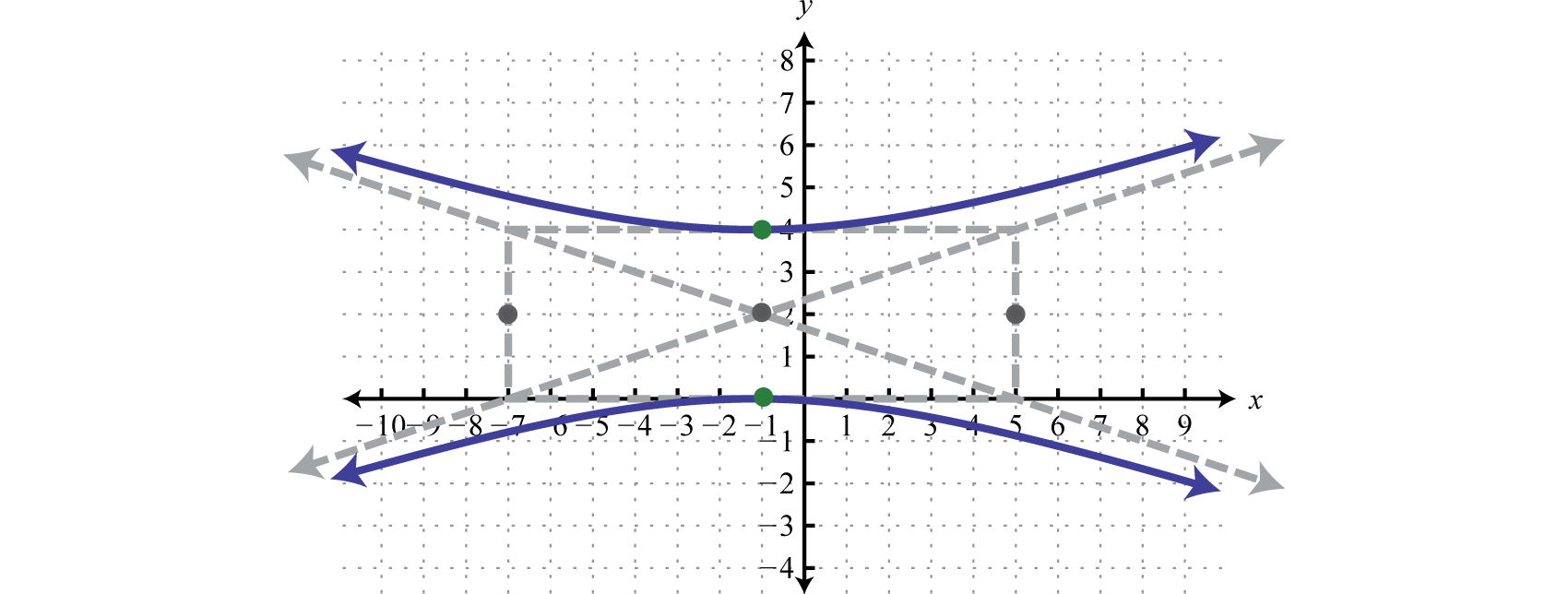
Nota

Cuando se le da una hipérbola abriendo hacia arriba y hacia abajo, como en el ejemplo anterior, es un error común intercambiar los valores para el centro,$h$ y$k$. Este es el caso porque la cantidad que involucra la variable$y$ suele aparecer primero en forma estándar. Tenga cuidado de que el$y$ -valor del centro provenga de la cantidad que implica la variable$y$ y que el$x$ -valor del centro se obtenga de la cantidad que involucra la variable$x$.

Al igual que con cualquier gráfica, nos interesa encontrar las$x$ -y$y$ -intercepciones.

Ejemplo$\PageIndex{3}$:

Encuentra las intercepciones:$\frac{(y-2)^{2}}{4}-\frac{(x+1)^{2}}{36}=1$.

Solución

Para encontrar el conjunto de$x$ -intercepciones$y=0$ y resolver para$x$.

$$\begin{align*} \frac{(\color{Cerulean}{0}\color{black}{-}2)^{2}}{4}-\frac{(x+1)^{2}}{36} &=1 \\[4pt] 1-\frac{(x+1)^{2}}{36} &=1 \\[4pt] -\frac{(x+1)^{2}}{36} &=0 \\[4pt] (x+1)^{2} &=0 \\[4pt] x+1 &=0 \\[4pt] x &=-1 \end{align*}$$

Por lo tanto sólo hay una$x$ -intercepción,$(−1,0)$. Para encontrar el conjunto$y$ -intercepción$x=0$ y resolver para$y$.

$$\begin{align*} \frac{(y-2)^{2}}{4}-\frac{(\color{Cerulean}{0}\color{black}{+}1)^{2}}{36} &=1 \\[4pt] \frac{(y-2)^{2}}{4}-\frac{1}{36} &=1 \\[4pt] \frac{(y-2)^{2}}{4} &=\frac{37}{36} \\[4pt] \frac{(y-2)}{2} &=\frac{\sqrt{37}}{36} \\[4pt] y-2 &=\pm \frac{\sqrt{37}}{3} \\[4pt] y &=2 \pm \frac{\sqrt{37}}{3}=\frac{6 \pm \sqrt{37}}{3} \end{align*}$$

Por lo tanto hay dos$y$ -intercepciones,$\left(0, \frac{6-\sqrt{37}}{3}\right) \approx(0,-0.03)$ y$\left(0, \frac{6+\sqrt{37}}{3}\right) \approx(0,4.03)$ .Tómese un momento para compararlas con el boceto de la gráfica en el ejemplo anterior.

Respuesta:

$x$-interceptar:$(−1,0)$;$y$ -intercepta:$\left(0, \frac{6-\sqrt{37}}{3}\right)$ y$\left(0, \frac{6+\sqrt{37}}{3}\right)$.

Considerar la hipérbola centrada en el origen,

$$9 x^{2}-5 y^{2}=45\nonumber$$

La forma estándar requiere que un lado sea igual a$1$. En este caso, podemos obtener forma estándar dividiendo ambos lados por$45$.

$$\begin{align*} \frac{9 x^{2}-5 y^{2}}{45} &=\frac{45}{45} \\[4pt] \frac{9 x^{2}}{45}-\frac{5 y^{2}}{45} &=\frac{45}{45} \\[4pt] \frac{x^{2}}{5}-\frac{y^{2}}{9} &=1 \end{align*}$$

Esto se puede escribir de la siguiente manera:

$$\frac{(x-0)^{2}}{5}-\frac{(y-0)^{2}}{9}=1\nonumber$$

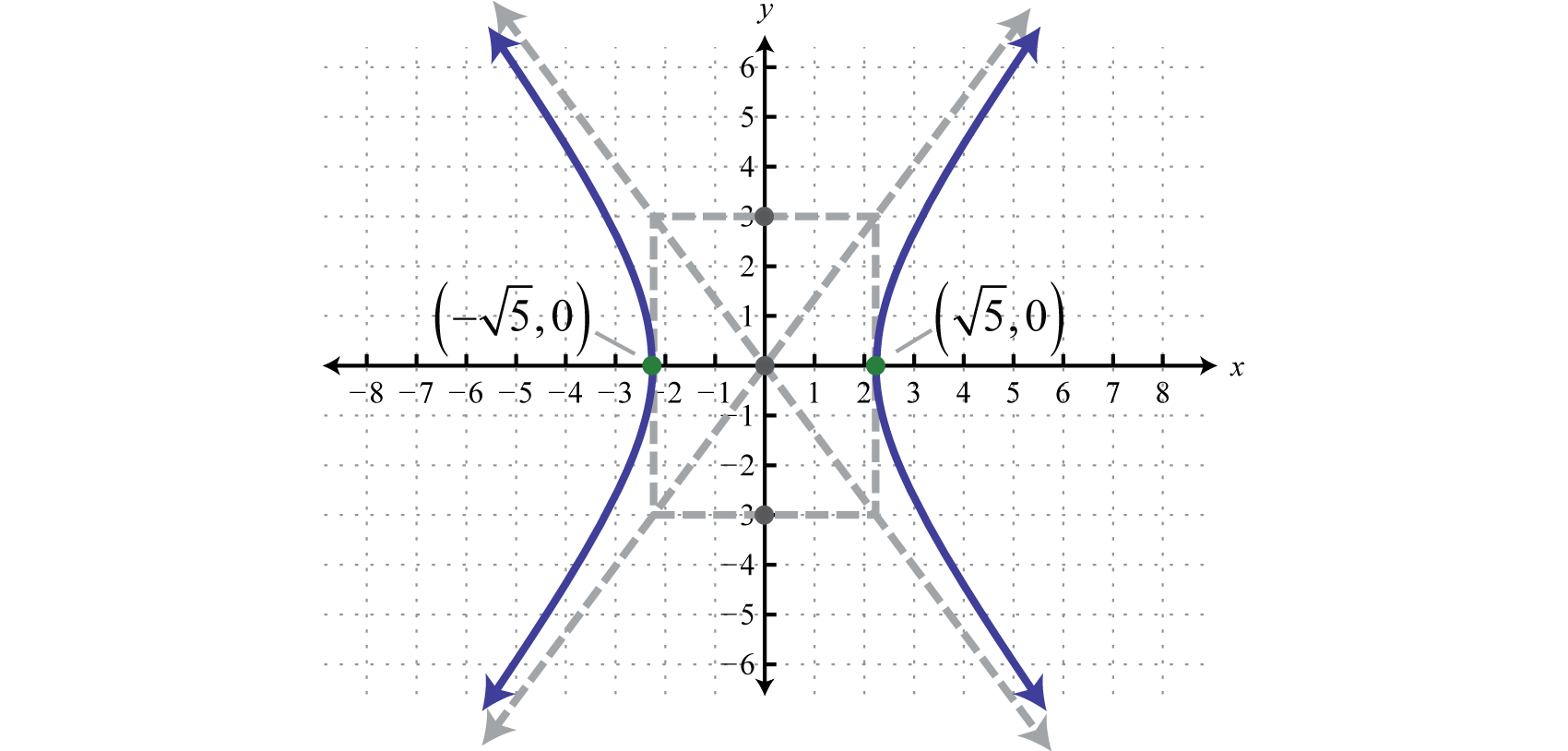
En esta forma, es claro que el centro es$(0,0)$,$a=\sqrt{5}$, y$b=3$. A continuación se muestra la gráfica.

Figura$\PageIndex{11}$

Ejercicio$\PageIndex{1}$:

Gráfica:$\frac{y^{2}}{25}-\frac{(x-5)^{2}}{9}=1$:

Respuesta:

Figura$\PageIndex{12}$

www.youtube.com/v/dc2vw_iit1q

La hipérbola en forma general

Hemos visto que la gráfica de una hipérbola está completamente determinada por su centro, vértices y asíntotas; que se puede leer de su ecuación en forma estándar. Sin embargo, la ecuación no siempre se da en forma estándar. La ecuación de una hipérbola en forma general ³¹ sigue:

$\begin{array}{l}{p x^{2}-q y^{2}+c x+d y+e=0\quad \color{Cerulean} { Hyperbola \:opens\: left\: and\: right.}} \\[4pt] {q y^{2}-p x^{2}+c x+d y+e=0\quad \color{Cerulean} { Hyperbola \:opens\: upward\: and\: downward.}}\end{array}$

donde$p,q>0$. Los pasos para graficar una hipérbola dada su ecuación en forma general se describen en el siguiente ejemplo.

Ejemplo$\PageIndex{4}$:

Gráfica:$4 x^{2}-9 y^{2}+32 x-54 y-53=0$.

Solución

Comience por reescribir la ecuación en forma estándar.

Paso 1: Agrupar los términos con las mismas variables y mover la constante hacia el lado derecho. Factor para que el coeficiente principal de cada agrupación sea$1$.

$\begin{aligned} 4 x^{2}-9 y^{2}+32 x-54 y-53 &=0 \\[4pt] \left(4 x^{2}+32 x+\_\_\_\right )+\left(-9 y^{2}-54 y+\_\_\_\right)&=53 \\[4pt] 4\left(x^{2}+8x+\_\_\_ \right)-9\left(y^{2}+6y+\_\_\_ \right)&=53 \end{aligned}$

Paso 2: Completar el cuadrado para cada agrupación. En este caso, para los términos que impliquen$x$ uso$\left(\frac{8}{2}\right)^{2}=4^{2}=16$ y para los términos que impliquen$y$ uso$\left(\frac{6}{2}\right)^{2}=(3)^{2}=9$. El factor frente a cada agrupación afecta el valor utilizado para equilibrar la ecuación de la derecha,

$4\color{black}{\left(x^{2}+8 x\color{Cerulean}{+16}\right)-}9\color{black}{\left(y^{2}+6 y\color{OliveGreen}{+9}\right)=}53\color{Cerulean}{+64}\color{OliveGreen}{-81}$

Debido a la propiedad distributiva, agregar$16$ dentro de la primera agrupación equivale a agregar$4⋅16=64$. De igual manera, agregar$9$ dentro de la segunda agrupación equivale a sumar$−9⋅9=−81$. Ahora factor y luego dividir para obtener$1$ en el lado derecho.

$\begin{aligned} 4(x+4)^{2}-9(y+3)^{2} &=36 \\[4pt] \frac{4(x+4)^{2}-9(y+3)^{2}}{\color{Cerulean}{36}} &\color{black}{=}\frac{36}{\color{Cerulean}{36}} \\[4pt] \frac{4(x+4)^{2}}{36}-\frac{9(y+3)^{2}}{36} &=\frac{36}{36} \\[4pt] \frac{(x+4)^{2}}{9}-\frac{(y+3)^{2}}{4} &=1 \end{aligned}$

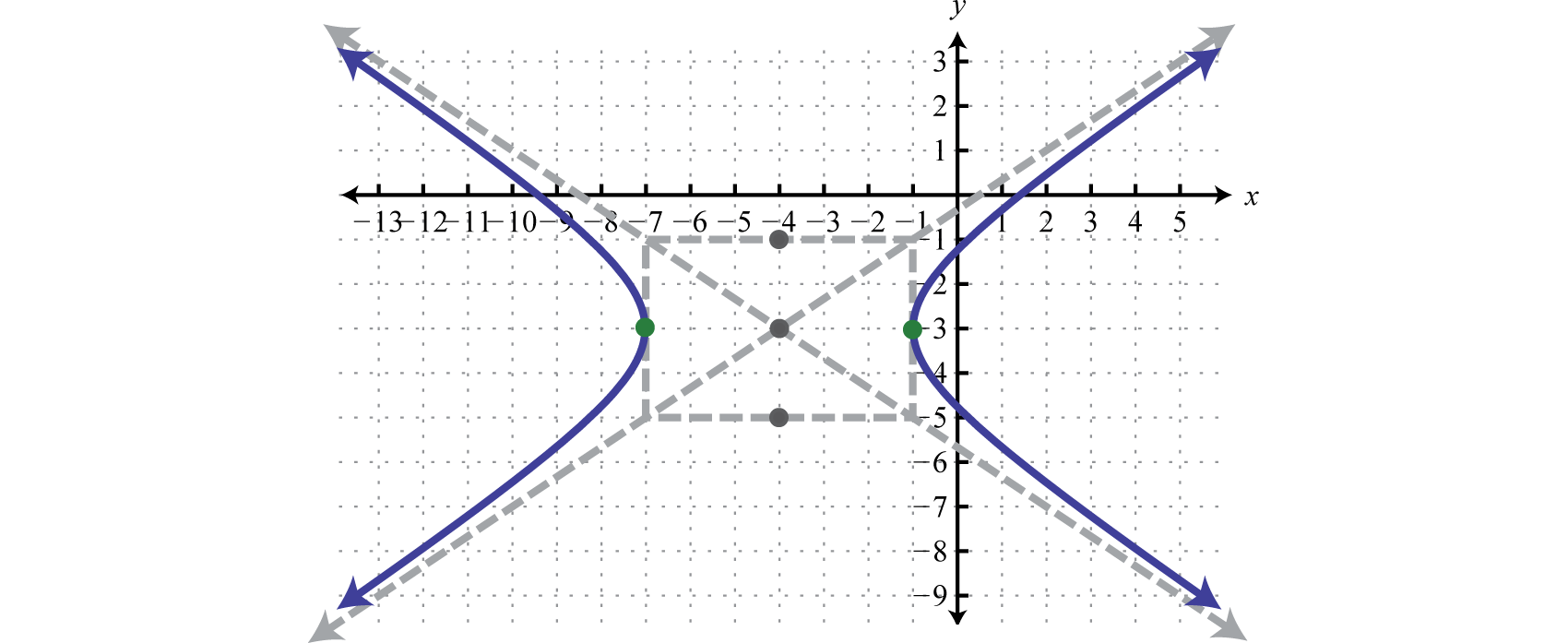
Paso 3: Determine el centro, a y b, y luego use esta información para bosquejar la gráfica. En este caso, el centro es$(−4,−3)$,$a=\sqrt{9}=3$, y$b=\sqrt{4}=2$. Debido a que el coeficiente principal de la expresión implicada$x$ es positivo y el coeficiente de la expresión implicada$y$ es negativo, graficamos una hipérbola que se abre a izquierda y derecha.

Respuesta:

Figura$\PageIndex{13}$

Ejercicio$\PageIndex{2}$:

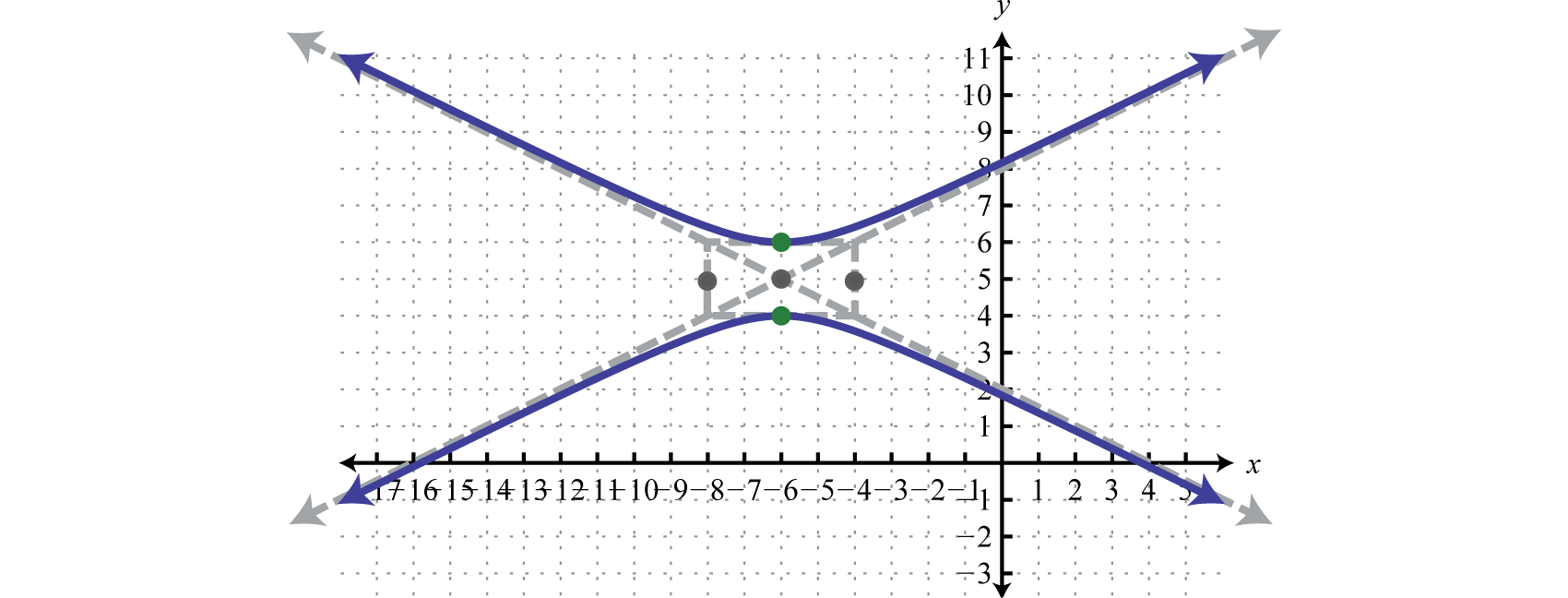
Gráfica:$4 y^{2}-x^{2}-40 y-12 x+60=0$.

Respuesta:

Figura$\PageIndex{14}$

www.youtube.com/V/S4F6iZlgVHS

Identificación de las Secciones Cónicas

En esta sección, el reto es identificar una sección cónica dada su ecuación en forma general. Para distinguir entre las secciones cónicas, utilice los exponentes y coeficientes. Si la ecuación es cuadrática en una sola variable y lineal en la otra, entonces su gráfica será una parábola.

Mesa$\PageIndex{2}$

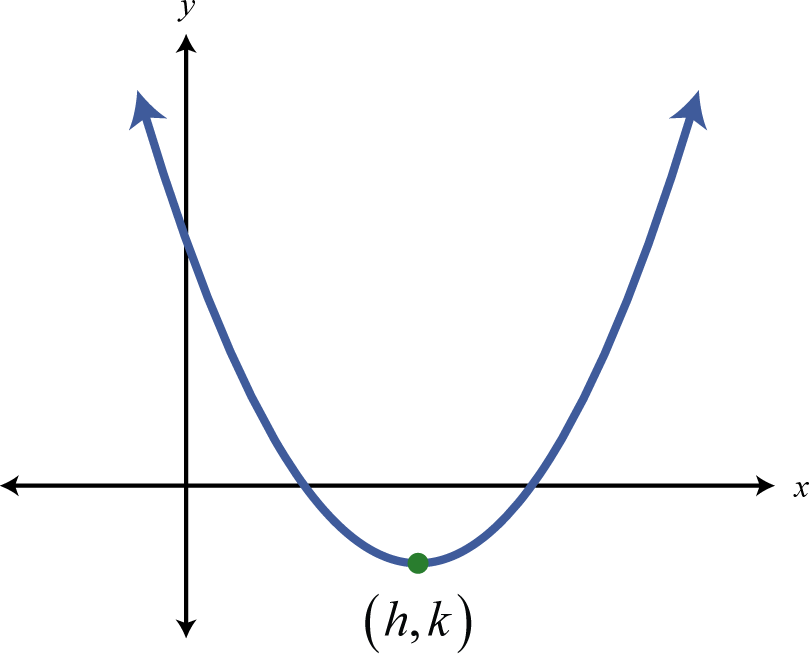
Parábola:$a>0$
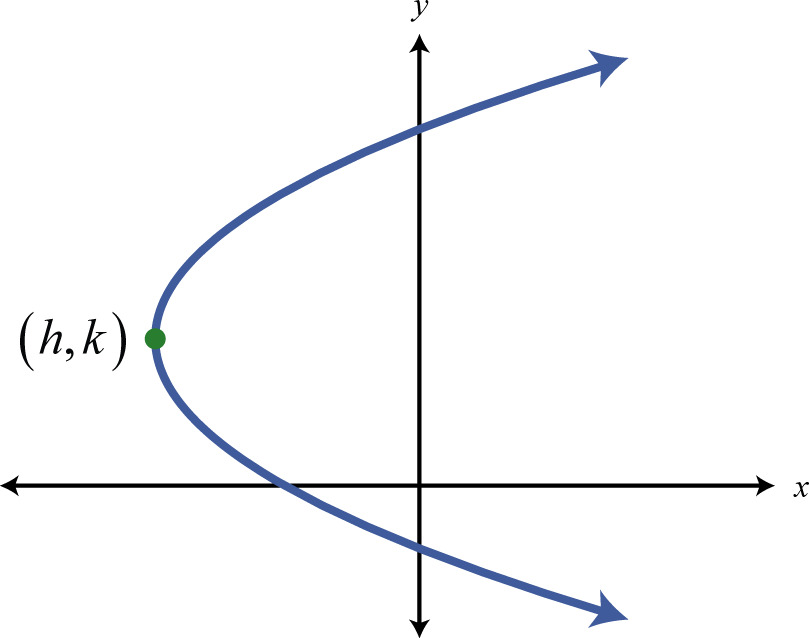
\ (a>0\) ">$y=a(x-h)^{2}+k$ $y=a x^{2}+b x+c$	$x=a(y-k)^{2}+h$ $x=a y^{2}+b y+c$
\ (a>0\) "> Figura$\PageIndex{15}$	Figura$\PageIndex{16}$

Mesa$\PageIndex{3}$

Parábola:$a<0$
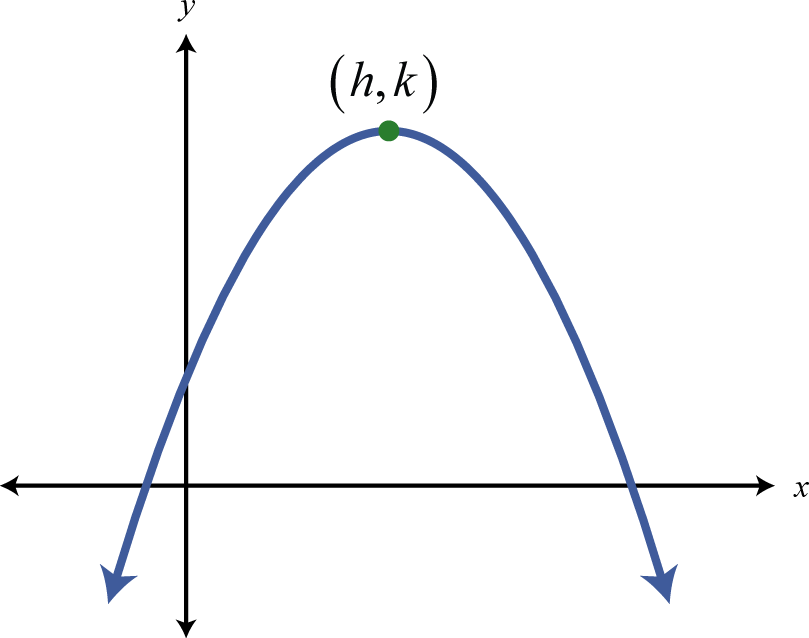
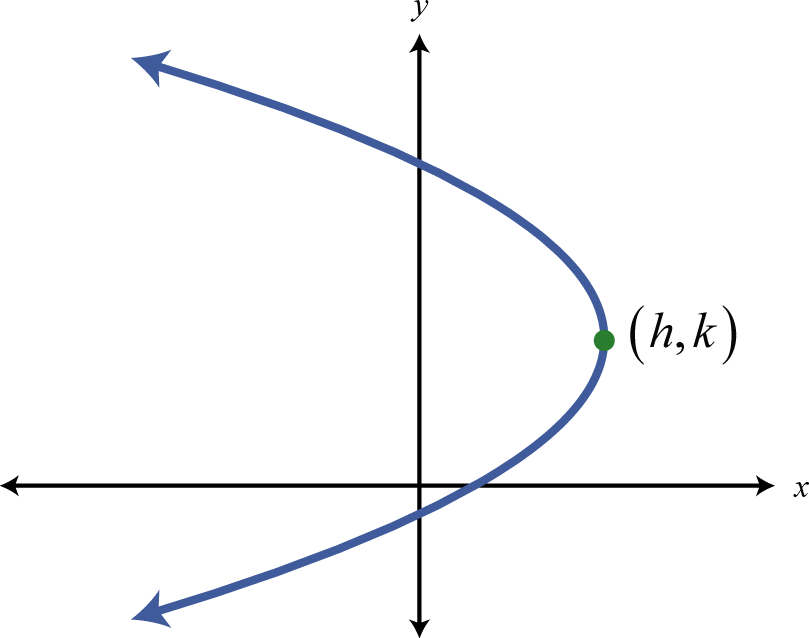
\ (a<0\) ">$y=a(x-h)^{2}+k$ $y=a x^{2}+b x+c$	$x=a(y-k)^{2}+h$ $x=a y^{2}+b y+c$
\ (a<0\) "> Figura$\PageIndex{17}$	Figura$\PageIndex{18}$

Si la ecuación es cuadrática en ambas variables, donde los coeficientes de los términos cuadrados son los mismos, entonces su gráfica será un círculo.

Mesa$\PageIndex{4}$

Círculo:
$\begin{aligned}(x-h)^{2}+(y-k)^{2} &=r^{2} \\[4pt] x^{2}+y^{2}+c x+d y+e &=0 \end{aligned}$	Figura$\PageIndex{19}$

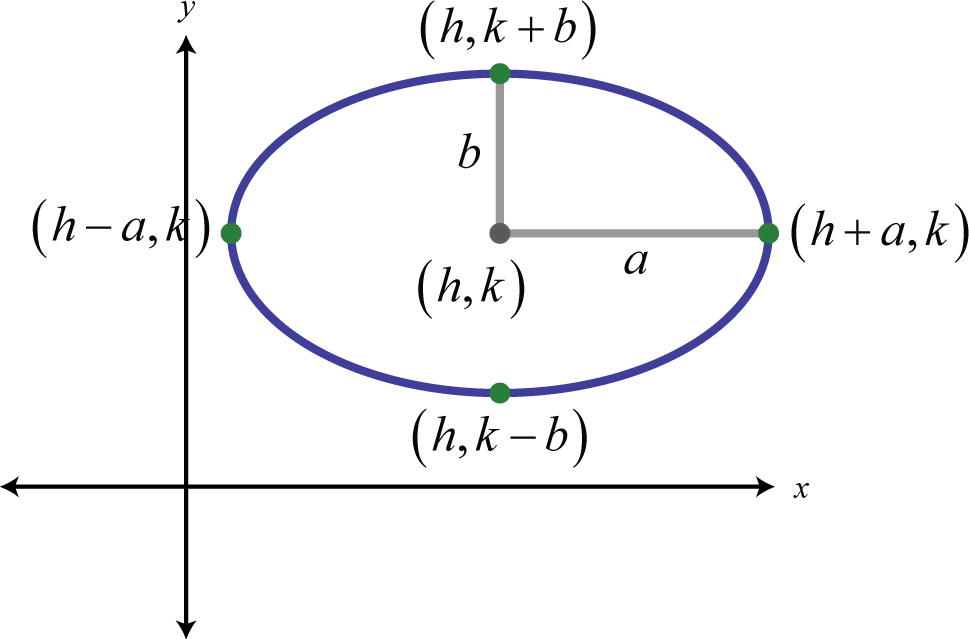
Si la ecuación es cuadrática en ambas variables donde los coeficientes de los términos cuadrados son diferentes pero tienen el mismo signo, entonces su gráfica será una elipse.

Mesa$\PageIndex{5}$

Elipse:$a, b>0$ y$p, q>0$
\ (a, b>0\) y$p, q>0$ “>$\frac{(x-h)^{2}}{a^{2}}+\frac{(y-k)^{2}}{b^{2}}=1$ $p x^{2}+q y^{2}+c x+d y+e=0$	Figura$\PageIndex{20}$

Si la ecuación es cuadrática en ambas variables donde los coeficientes de los términos cuadrados tienen signos diferentes, entonces su gráfica será una hipérbola.

Mesa$\PageIndex{6}$

Hipérbola:$a, b>0$ y$p, q>0$
$\begin{aligned} \frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}} &=1 \\[4pt] p x^{2}-q y^{2}+c x+d y+e &=0 \end{aligned}$	$\begin{aligned} \frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}} &=1 \\[4pt] q y^{2}-p x^{2}+c x+d y+e &=0 \end{aligned}$
Figura$\PageIndex{21}$	Figura$\PageIndex{22}$

Ejemplo$\PageIndex{5}$:

Identificar la gráfica de cada ecuación como una parábola, círculo, elipse o hipérbola.

1. $4 x^{2}+4 y^{2}-1=0$
2. $3 x^{2}-2 y^{2}-12=0$
3. $x-y^{2}-6 y+11=0$

Solución

1. La ecuación es cuadrática en ambas$x$ y$y$ donde los coeficientes iniciales para ambas variables es el mismo,$4$.

$\begin{aligned} 4 x^{2}+4 y^{2}-1 &=0 \\[4pt] 4 x^{2}+4 y^{2} &=1 \\[4pt] x^{2}+y^{2} &=\frac{1}{4} \end{aligned}$

Esta es una ecuación de un círculo centrado en el origen con radio$1/2$.

2. La ecuación es cuadrática en ambas$x$ y$y$ donde los coeficientes principales para ambas variables tienen signos diferentes.

$3 x^{2}-2 y^{2}-12=0$
$\frac{3 x^{2}-2 y^{2}}{12}=\frac{12}{12}$
$\frac{x^{2}}{4}-\frac{y^{2}}{6}=1$

Esta es una ecuación de una hipérbola que se abre a izquierda y derecha centrada en el origen.

3. La ecuación es cuadrática en$y$ solo.

$\begin{aligned} x-y^{2}+6 y-11 &=0 \\[4pt] x &=y^{2}-6 y+\quad+11 \\[4pt] x &=\color{black}{\left(y^{2}-6 y\color{Cerulean}{+9}\right)+}11\color{Cerulean}{-9} \\[4pt] x &=(y-3)^{2}+2 \end{aligned}$

Esta es una ecuación de una parábola que se abre a la derecha con vértice$(2,3)$.

Respuesta:

1. Círculo

2. Hipérbola

3. Parábola

Claves para llevar

• La gráfica de una hipérbola está completamente determinada por su centro, vértices y asíntotas.
• El centro, los vértices y las asíntotas son evidentes si la ecuación de una hipérbola se da en forma estándar:$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$ o$\frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}}=1$.
• Para graficar una hipérbola, marcar puntos$a$ unidades izquierda y derecha desde el centro y puntos$b$ unidades arriba y abajo desde el centro. Usa estos puntos para dibujar el rectángulo fundamental; las líneas que atraviesan las esquinas de este rectángulo son las asíntotas. Si el coeficiente de$x^{2}$ es positivo, dibuja las ramas de la hipérbola abriendo izquierda y derecha a través de los puntos determinados por$a$. Si el coeficiente de$y^{2}$ es positivo, dibuja las ramas de la hipérbola abriéndose hacia arriba y hacia abajo a través de los puntos determinados por$b$.
• La orientación del eje transversal depende del coeficiente de$x^{2}$ y$y^{2}$.
• Si la ecuación de una hipérbola se da en forma general$p x^{2}-q y^{2}+c x+d y+e=0$ o$q y^{2}-p x^{2}+c x+d y+e=0$ dónde$p,q>0$, agrupe los términos con las mismas variables, y complete el cuadrado para ambas agrupaciones para obtener la forma estándar.
• Reconocemos la ecuación de una hipérbola si es cuadrática en ambas$x$ y$y$ donde los coeficientes de los términos cuadrados son de signo opuesto.

Ejercicio$\PageIndex{3}$

Dada la ecuación de una hipérbola en forma estándar, determinar su centro, en qué dirección se abre la gráfica, y los vértices.

1. $\frac{(x-6)^{2}}{16}-\frac{(y+4)^{2}}{9}=1$
2. $\frac{(y-3)^{2}}{25}-\frac{(x+1)^{2}}{64}=1$
3. $\frac{(y+9)^{2}}{5}-x^{2}=1$
4. $\frac{(x-5)^{2}}{12}-y^{2}=1$
5. $4(y+10)^{2}-25(x+1)^{2}=100$
6. $9(x-1)^{2}-5(y+10)^{2}=45$

Contestar

1. Centro:$(6,-4) ; a=4 ; b=3$; abre izquierda y derecha; vértices:$(2, −4), (10, −4)$

3. Centro:$(0,-9) ; a=1, b=\sqrt{5}$; se abre hacia arriba y hacia abajo; vértices:$(0,-9-\sqrt{5}),(0,-9+\sqrt{5})$

5. Centro:$(−1, −10); a = 2, b = 5$; se abre hacia arriba y hacia abajo; vértices:$(−1, −15) , (−1, −5)$

Ejercicio$\PageIndex{4}$

Determinar la forma estándar para la ecuación de una hipérbola dada la siguiente información.

1. El centro$(2,7), a=6, b=3,$ se abre a izquierda y derecha.
2. El centro$(-9,1), a=7, b=2,$ se abre hacia arriba y hacia abajo.
3. El centro$(10,-3), a=\sqrt{7}, b=5 \sqrt{2},$ se abre hacia arriba y hacia abajo.
4. El centro$(-7,-2), a=3 \sqrt{3}, b=\sqrt{5},$ se abre a izquierda y derecha.
5. El centro$(0,-8), a=\sqrt{2} b=1,$ se abre hacia arriba y hacia abajo.
6. El centro$(0,0), a=2 \sqrt{6}, b=4,$ se abre a izquierda y derecha.

Contestar

1. $\frac{(x-2)^{2}}{36}-\frac{(y-7)^{2}}{9}=1$

3. $\frac{(y+3)^{2}}{50}-\frac{(x-10)^{2}}{7}=1$

5. $\frac{(y+8)^{2}}{1}-\frac{x^{2}}{2}=1$

Ejercicio$\PageIndex{5}$

Gráfica.

1. $\frac{(x-3)^{2}}{9}-\frac{(y+1)^{2}}{16}=1$
2. $\frac{(x+3)^{2}}{4}-\frac{(y-1)^{2}}{25}=1$
3. $\frac{(x-2)^{2}}{16}-\frac{(y+3)^{2}}{1}=1$
4. $\frac{(y+2)^{2}}{9}-\frac{(x+2)^{2}}{36}=1$
5. $\frac{(y-1)^{2}}{4}-\frac{(x-2)^{2}}{16}=1$
6. $(y+2)^{2}-\frac{(x+3)^{2}}{9}=1$
7. $4(x+3)^{2}-9(y-3)^{2}=36$
8. $16 x^{2}-4(y-1)^{2}=64$
9. $4(y-1)^{2}-25 x^{2}=100$
10. $9 y^{2}-16 x^{2}=144$
11. $\frac{(x-2)^{2}}{12}-\frac{(y-4)^{2}}{9}=1$
12. $\frac{(x+2)^{2}}{4}-\frac{(y-1)^{2}}{8}=1$
13. $\frac{(y+1)^{2}}{5}-\frac{(x-3)^{2}}{2}=1$
14. $\frac{(y-4)^{2}}{3}-\frac{(x+6)^{2}}{18}=1$
15. $4 x^{2}-3(y-3)^{2}=12$
16. $7(x+1)^{2}-2 y^{2}=14$
17. $6 y^{2}-3 x^{2}=18$
18. $10 x^{2}-3 y^{2}=30$

Contestar

1.

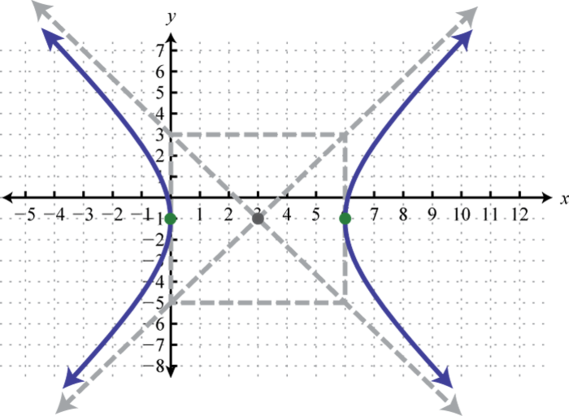
Figura$\PageIndex{23}$

3.

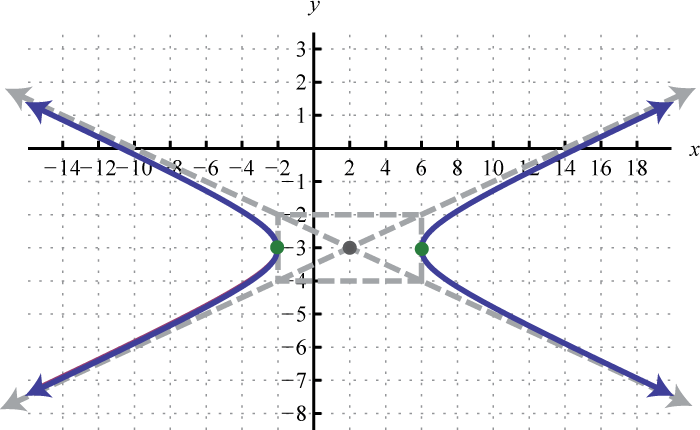
Figura$\PageIndex{24}$

5.

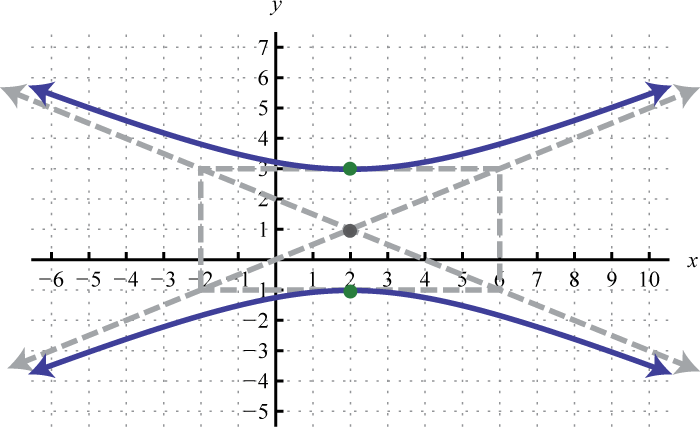
Figura$\PageIndex{25}$

7.

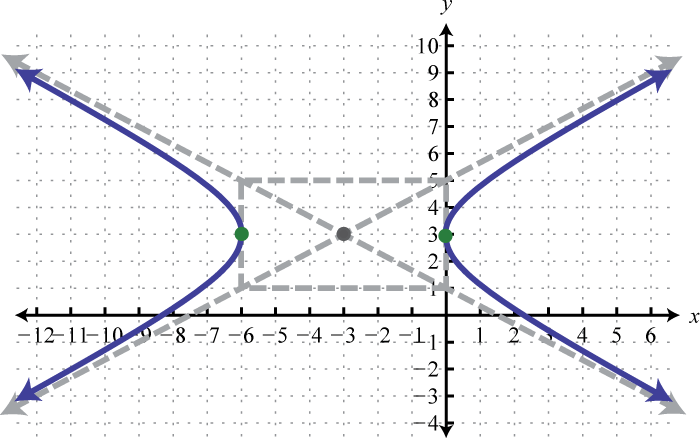
Figura$\PageIndex{26}$

9.

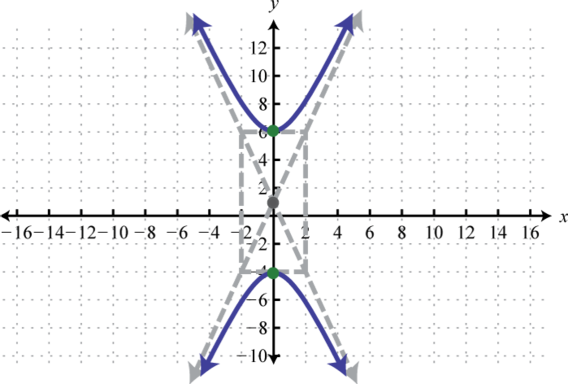
Figura$\PageIndex{27}$

11.

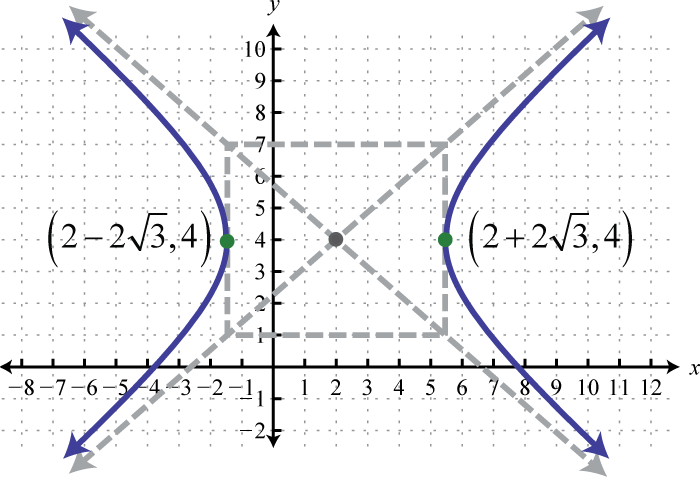
Figura$\PageIndex{28}$

13.

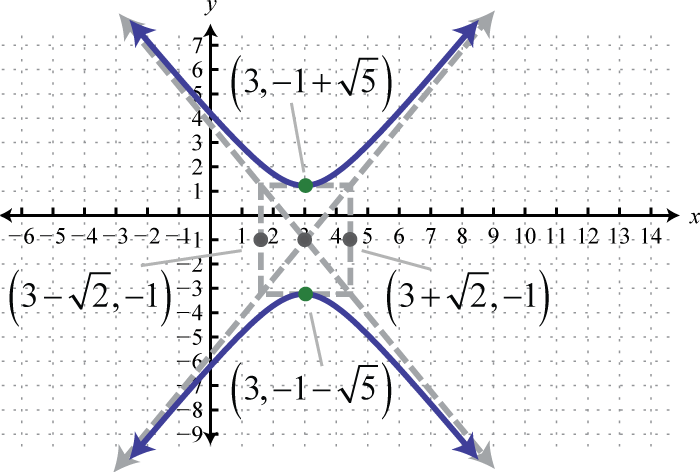
Figura$\PageIndex{29}$

15.

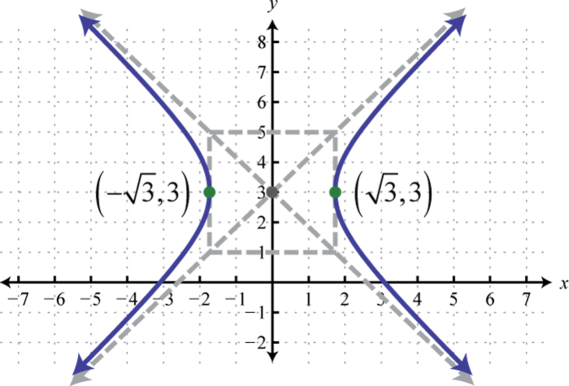
Figura$\PageIndex{30}$

17.

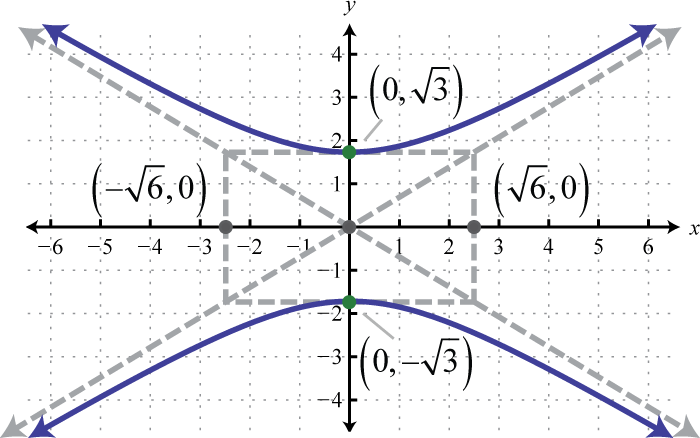
Figura$\PageIndex{31}$

Ejercicio$\PageIndex{6}$

Encuentra las$x$ - y$y$ -intercepciones.

1. $\frac{(x-1)^{2}}{9}-\frac{(y-4)^{2}}{4}=1$
2. $\frac{(x+4)^{2}}{16}-\frac{(y-3)^{2}}{9}=1$
3. $\frac{(y-1)^{2}}{4}-\frac{(x+1)^{2}}{36}=1$
4. $\frac{(y+2)^{2}}{4}-\frac{(x-1)^{2}}{16}=1$
5. $2 x^{2}-3(y-1)^{2}=12$
6. $6(x-5)^{2}-2 y^{2}=12$
7. $36 x^{2}-2 y^{2}=9$
8. $6 y^{2}-4 x^{2}=2$
9. Encuentra la ecuación de la hipérbola con vértices$(±2, 3)$ y un eje conjugado que mide$12$ unidades.
10. Encuentra la ecuación de la hipérbola con vértices$(4, 7)$$(4, 3)$ y un eje conjugado que mide$6$ unidades.

Contestar

1. $x$-intercepta:$(1 \pm 3 \sqrt{5}, 0)$$y$ -intercepta: ninguna

3. $x$-intercepta: ninguno$y$ -intercepta:$\left(0, \frac{3 \pm \sqrt{37}}{3}\right)$

5. $x$-intercepta:$\left(\pm \frac{\sqrt{30}}{2}, 0\right)$$y$ -intercepta: ninguna

7. $x$-intercepta:$\left(\pm \frac{1}{2}, 0\right)$$y$ -intercepta: ninguna

9. $\frac{x^{2}}{4}-\frac{(y-3)^{2}}{36}=1$

Ejercicio$\PageIndex{7}$

Reescribir en forma estándar y gráfica.

1. $4 x^{2}-9 y^{2}+16 x+54 y-101=0$
2. $9 x^{2}-25 y^{2}-18 x-100 y-316=0$
3. $4 y^{2}-16 x^{2}-64 x+8 y-124=0$
4. $9 y^{2}-4 x^{2}-24 x-72 y+72=0$
5. $y^{2}-36 x^{2}-72 x-12 y-36=0$
6. $9 y^{2}-x^{2}+8 x-36 y+11=0$
7. $36 x^{2}-4 y^{2}+24 y-180=0$
8. $x^{2}-25 y^{2}-2 x-24=0$
9. $25 x^{2}-64 y^{2}+200 x+640 y-2,800=0$
10. $49 y^{2}-4 x^{2}+40 x+490 y+929=0$
11. $3 x^{2}-2 y^{2}+24 x+8 y+34=0$
12. $4 x^{2}-8 y^{2}-24 x+80 y-196=0$
13. $3 y^{2}-x^{2}-2 x-6 y-16=0$
14. $12 y^{2}-5 x^{2}+40 x+48 y-92=0$
15. $4 x^{2}-16 y^{2}+12 x+16 y-11=0$
16. $4 x^{2}-y^{2}-4 x-2 y-16=0$
17. $4 y^{2}-36 x^{2}+108 x-117=0$
18. $4 x^{2}-9 y^{2}+8 x+6 y-33=0$

Contestar

1. $\frac{(x+2)^{2}}{9}-\frac{(y-3)^{2}}{4}=1$;

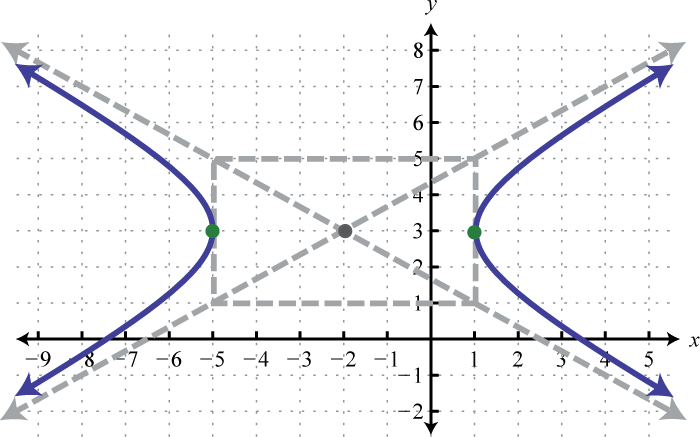
Figura$\PageIndex{32}$

3. $\frac{(y+1)^{2}}{16}-\frac{(x+2)^{2}}{4}=1$;

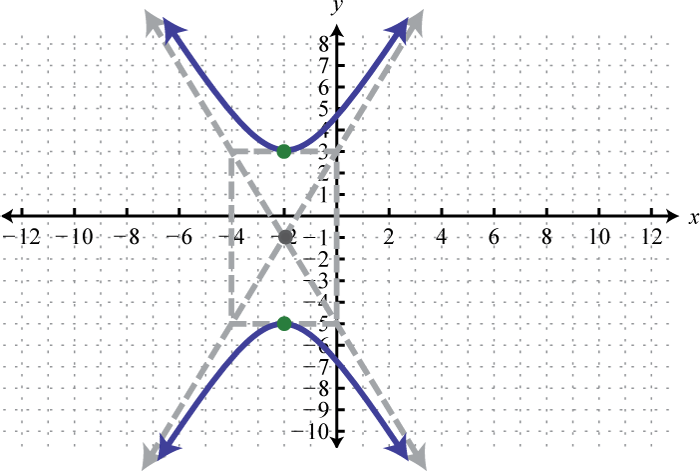
Figura$\PageIndex{33}$

5. $\frac{(y-6)^{2}}{36}-(x+1)^{2}=1$;

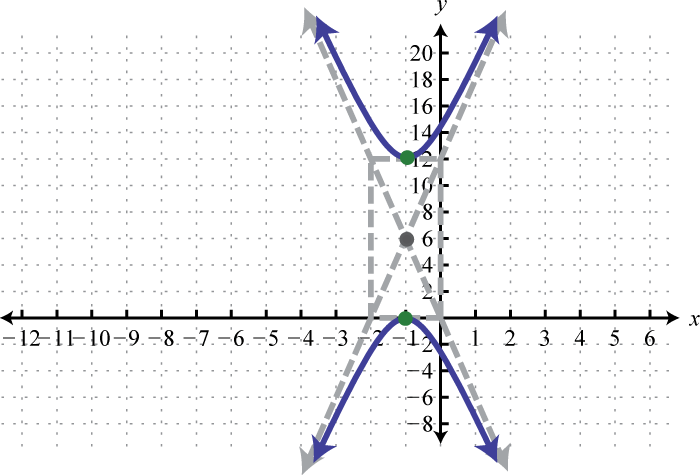
Figura$\PageIndex{34}$

7. $\frac{x^{2}}{4}-\frac{(y-3)^{2}}{36}=1$;

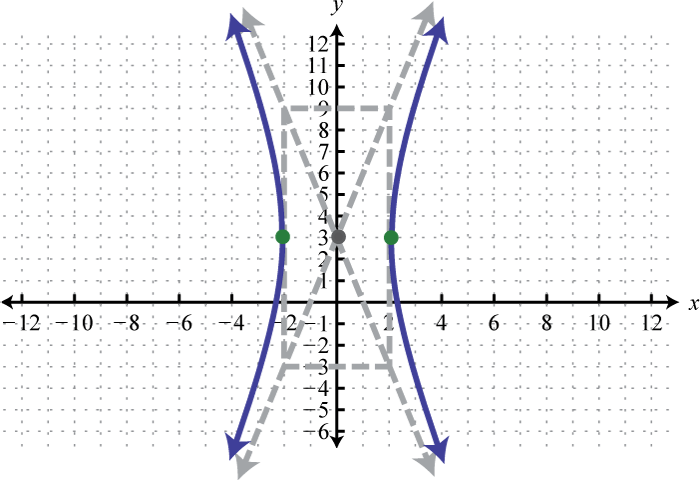
Figura$\PageIndex{35}$

9. $\frac{(x+4)^{2}}{64}-\frac{(y-5)^{2}}{25}=1$;

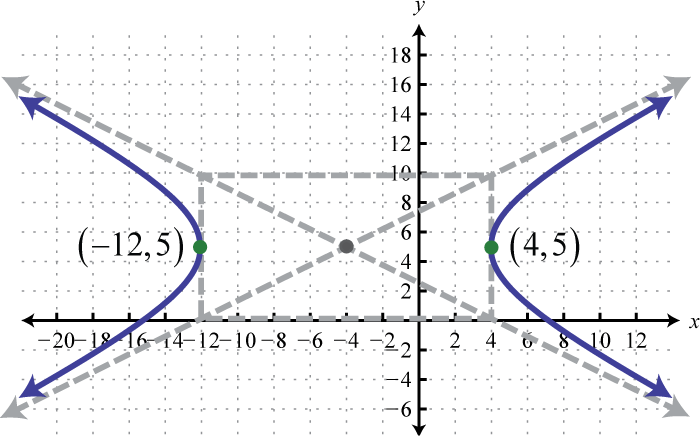
Figura$\PageIndex{36}$

11. $\frac{(x+4)^{2}}{2}-\frac{(y-2)^{2}}{3}=1$;

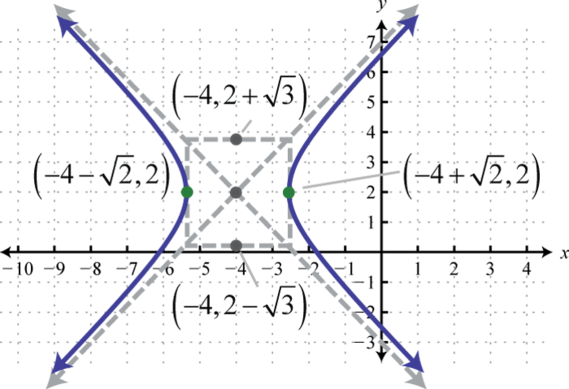
Figura$\PageIndex{37}$

13. $\frac{(y-1)^{2}}{6}-\frac{(x+1)^{2}}{18}=1$;

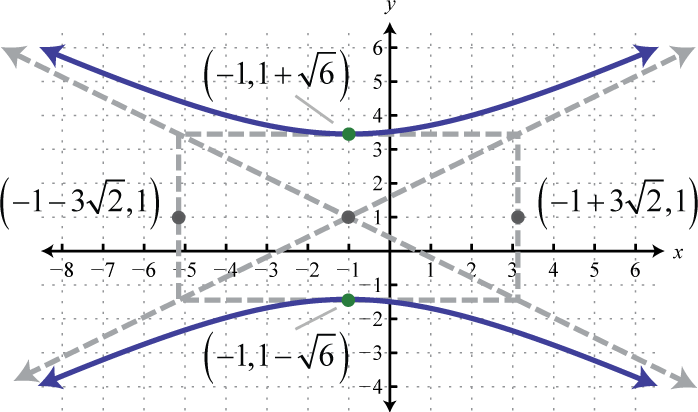
Figura$\PageIndex{38}$

15. $\frac{\left(x+\frac{3}{2}\right)^{2}}{4}-\frac{\left(y-\frac{1}{2}\right)^{2}}{1}=1$

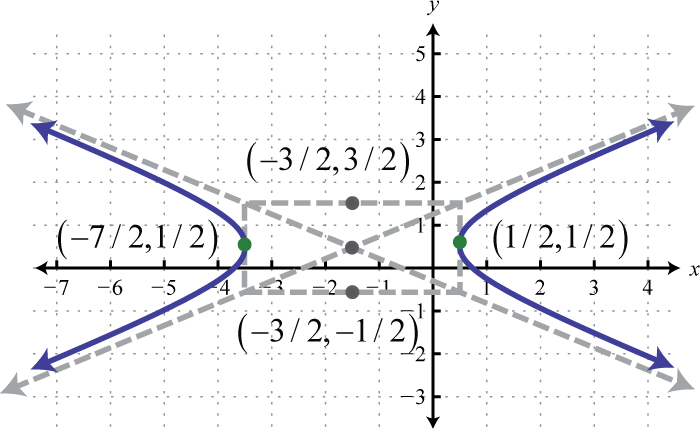
Figura$\PageIndex{39}$

17. $\frac{y^{2}}{9}-\left(x-\frac{3}{2}\right)^{2}=1$;

Figura$\PageIndex{40}$

Ejercicio$\PageIndex{8}$

Dada la forma general, determinar las intercepciones.

1. $3 x^{2}-y^{2}-11 x-8 y-4=0$
2. $4 y^{2}-8 x^{2}+2 x+9 y-9=0$
3. $x^{2}-y^{2}+2 x+2 y-4=0$
4. $y^{2}-x^{2}+6 y-8 x-16=0$
5. $5 x^{2}-2 y^{2}-4 x-3 y=0$
6. $2 x^{2}-3 y^{2}-4 x-5 y+1=0$

Contestar

1. $x$-intercepta:$\left(-\frac{1}{3}, 0\right),(4,0) ; y$ -intercepta:$(0,-4 \pm 2 \sqrt{3})$

3. $x$-intercepta:$(-1 \pm \sqrt{5}, 0) ; y$ -intercepta: ninguna

5. $x$-intercepta:$(0,0),\left(\frac{4}{5}, 0\right) ; y$ -intercepta:$(0,0),\left(0,-\frac{3}{2}\right)$

Ejercicio$\PageIndex{9}$

Encuentra las ecuaciones de las asíntotas a la hipérbola dada.

1. $\frac{(y-5)^{2}}{9}-\frac{(x+8)^{2}}{16}=1$
2. $\frac{(x+9)^{2}}{36}-\frac{(y-4)^{2}}{4}=1$
3. $16 x^{2}-4 y^{2}-24 y-96 x+44=0$
4. $4 y^{2}-x^{2}-8 y-4 x-4=0$

Contestar

1. $y=-\frac{3}{4} x-1, y=\frac{3}{4} x+11$

3. $y=-2 x+3, y=2 x-9$

Ejercicio$\PageIndex{10}$

Dada la gráfica de una hipérbola, determinar su ecuación en forma general.

1.

Figura$\PageIndex{41}$

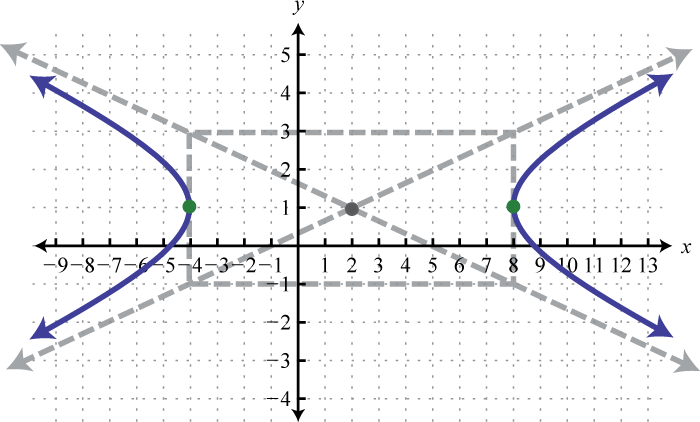
2.

Figura$\PageIndex{42}$

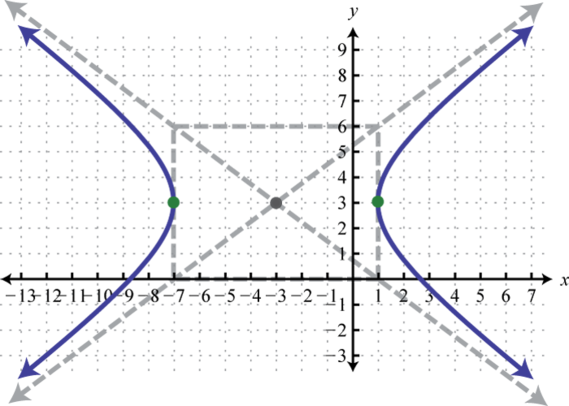
3.

Figura$\PageIndex{43}$

4.

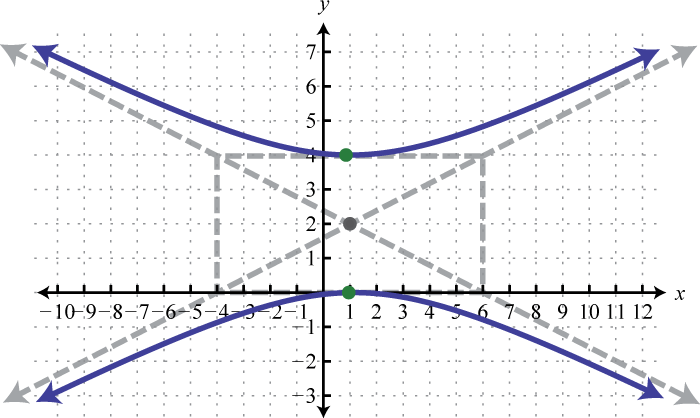
Figura$\PageIndex{44}$

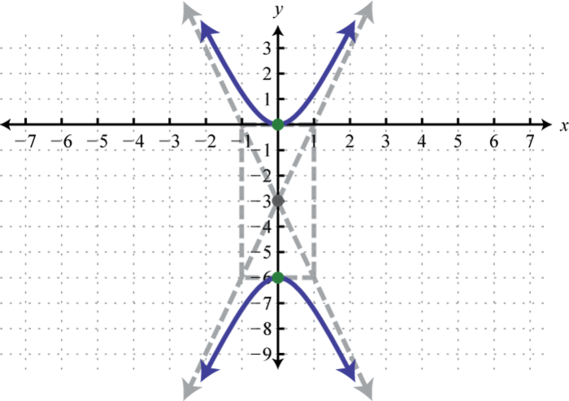
Contestar

1. $x^{2}-9 y^{2}-4 x+18 y-41=0$

3. $25 y^{2}-4 x^{2}-100 y+8 x-4=0$

Ejercicio$\PageIndex{11}$

Identificar lo siguiente como la ecuación de una línea, parábola, círculo, elipse o hipérbola.

1. $x^{2}+y^{2}+10 x-2 y+23=0$
2. $x^{2}+y+2 x-3=0$
3. $2 x^{2}+y^{2}-12 x+14=0$
4. $3 x-2 y=24$
5. $x^{2}-y^{2}+36=0$
6. $4 x^{2}+4 y^{2}-32=0$
7. $x^{2}-y^{2}-2 x+2 y-1=0$
8. $x-y^{2}+2 y+1=0$
9. $3 x+3 y+5=0$
10. $8 x^{2}+4 y^{2}-144 x-12 y+641=0$

Contestar

1. Círculo

3. Elipse

5. Hipérbola

7. Hipérbola

9. Línea

Ejercicio$\PageIndex{12}$

Identificar las secciones cónicas y reescribir en forma estándar.

1. $x^{2}-y-6 x+11=0$
2. $x^{2}+y^{2}-12 x-6 y+44=0$
3. $x^{2}-2 y^{2}-4 x-12 y-18=0$
4. $25 y^{2}-2 x^{2}+36 x-50 y-187=0$
5. $7 x^{2}+4 y^{2}-84 x+16 y+240=0$
6. $4 x^{2}+4 y^{2}-80 x+399=0$
7. $4 x^{2}+4 y^{2}+4 x-32 y+29=0$
8. $16 x^{2}-4 y^{2}-32 x+20 y-25=0$
9. $9 x-18 y^{2}+12 y+7=0$
10. $16 x^{2}+12 y^{2}-24 x-48 y+9=0$

Contestar

1. Parábola;$y=(x-3)^{2}+2$

3. hipérbola;$\frac{(x-2)^{2}}{4}-\frac{(y+3)^{2}}{2}=1$

5. Elipse;$\frac{(x-6)^{2}}{4}+\frac{(y+2)^{2}}{7}=1$

7. Círculo;$\left(x+\frac{1}{2}\right)^{2}+(y-4)^{2}=9$

9. Parábola;$x=2\left(y-\frac{1}{3}\right)^{2}-1$

Ejercicio$\PageIndex{13}$

1. Desarrollar una fórmula para las ecuaciones de las asíntotas de una hipérbola. Compártelo junto con un ejemplo en el panel de discusión.
2. Haz tu propia ecuación de una hipérbola, escríbela en forma general y graficala.
3. ¿Todas las hipérbolas tienen intercepciones? ¿Cuáles son los posibles números de intercepciones para una hipérbola? Explique.
4. Investigar y discutir ejemplos del mundo real de hipérbolas.

Contestar

1. La respuesta puede variar

3. La respuesta puede variar

Notas al pie

²³ El conjunto de puntos en un plano cuyas distancias desde dos puntos fijos, llamados focos, tiene una diferencia absoluta que es igual a una constante positiva.

²⁴ Las dos curvas separadas de una hipérbola.

²⁵ Puntos en las ramas separadas de una hipérbola donde la distancia es mínima.

²⁶ La ecuación de una hipérbola escrita en la$\frac{(x-h)^{2}}{a^{2}}-\frac{(y-k)^{2}}{b^{2}}=1$ forma.El centro es$(h, k)$,$a$ define el eje transversal, y$b$ define el eje conjugado.

²⁷ La ecuación de una hipérbola escrita en la forma$\frac{(y-k)^{2}}{b^{2}}-\frac{(x-h)^{2}}{a^{2}}=1$. El centro es$(h, k)$,$b$ define el eje transversal y$a$ define el eje conjugado.

²⁸ El segmento lineal formado por los vértices de una hipérbola.

²⁹ Un segmento lineal a través del centro de una hipérbola que es perpendicular al eje transversal.

³⁰ El rectángulo se formó utilizando los extremos de una hipérbola, ejes transversales y conjugados.

³¹ La ecuación de una hipérbola escrita en la forma$px^{2} − qy^{2} + cx +dy + e = 0$ o$qy^{2} − px^{2} − cx +dy + e = 0$ dónde$p, q > 0$.