5.E: Funciones polinómicas (Ejercicios)

5.1: Funciones

En los Ejercicios 1-6, indicar el dominio y el rango de la relación dada.

1)$R=\{(7,4),(2,4),(4,2),(8,5)\}$

Contestar

Dominio$=\{2,4,7,8\}$ y Rango$=\{2,4,5\}$

2)$S=\{(6,4),(3,3),(2,5),(8,7)\}$

3)$T=\{(7,2),(3,1),(9,4),(8,1)\}$

Contestar

Dominio$=\{3,7,8,9\}$ y Rango$=\{1,2,4\}$

4)$R=\{(0,1),(8,2),(6,8),(9,3)\}$

5)$T=\{(4,7),(4,8),(5,0),(0,7)\}$

Contestar

Dominio$=\{0,4,5\}$ y Rango$=\{0,7,8\}$

6)$T=\{(9,0),(3,6),(8,0),(3,8)\}$

En los Ejercicios 7-10, indicar el dominio y el rango de la relación dada.

7)

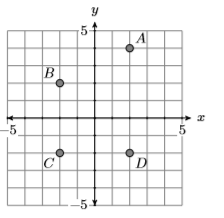
Contestar

Dominio$=\{-2,2\}$ y Rango$=\{-2,2,4\}$

8)

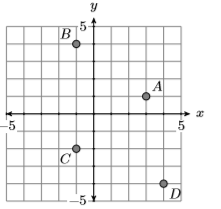
9)

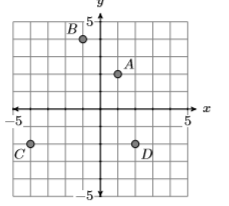
Contestar

Dominio$=\{-4,-1,1,2\}$ y Rango$=\{-2,2,4\}$

10)

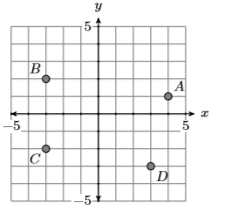
En los Ejercicios 11-18, determinar si la relación dada es una función.

11)$R=\{(-6,-4),(-4,-4),(1,-4)\}$

Contestar

Función

12)$T=\{(-8,-3),(-4,-3),(2,-3)\}$

13)$T=\{(-1,-7),(2,-5),(4,-2)\}$

Contestar

Función

14)$S=\{(-6,-6),(-4,0),(9,1)\}$

15)$T=\{(-9,1),(1,6),(1,8)\}$

Contestar

No es una función

16)$S=\{(-7,0),(1,1),(1,2)\}$

17)$R=\{(-7,-8),(-7,-6),(-5,0)\}$

Contestar

No es una función

18)$T=\{(-8,-9),(-8,-4),(-5,9)\}$

En los Ejercicios 19-22, determinar si la relación dada es una función.

19)

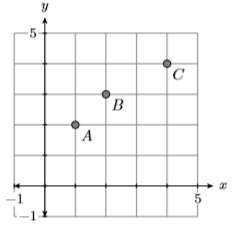
Contestar

Función

20)

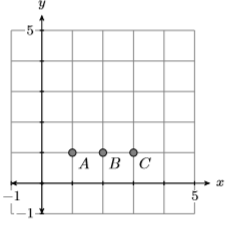
21)

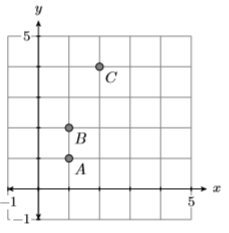
Contestar

No es una función

22)

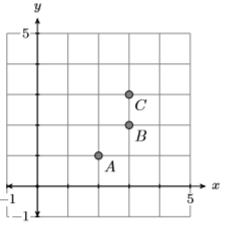
23) Dado$f(x)=|6 x-9|$, evaluar$f(8)$.

Contestar

$39$

24) Dado$f(x)=|8 x-3|$, evaluar$f(5)$.

25) Dado$f(x)=-2 x^{2}+8$, evaluar$f(3)$.

Contestar

$-10$

26) Dado$f(x)=3 x^{2}+x+6$, evaluar$f(-3)$.

27) Dado$f(x)=-3 x^{2}+4 x+1$, evaluar$f(2)$.

Contestar

$-3$

28) Dado$f(x)=-3 x^{2}+4 x-2$, evaluar$f(2)$.

29) Dado$f(x)=|5 x+9|$, evaluar$f(-8)$.

Contestar

$31$

30) Dado$f(x)=|9 x-6|$, evaluar$f(4)$.

31) Dado$f(x)=\sqrt{x-6}$, evaluar$f(42)$.

Contestar

$6$

32) Dado$f(x)=\sqrt{x+8}$, evaluar$f(41)$.

33) Dado$f(x)=\sqrt{x-7}$, evaluar$f(88)$.

Contestar

$9$

34) Dado$f(x)=\sqrt{x+9}$, evaluar$f(16)$.

35) Dado$f(x)=-4 x+6$, evaluar$f(8)$.

Contestar

$-26$

36) Dado$f(x)=-9 x+2$, evaluar$f(-6)$.

37) Dado$f(x)=-6 x+7$, evaluar$f(8)$.

Contestar

$-41$

38) Dado$f(x)=-6 x-2$, evaluar$f(5)$.

39) Dado$f(x)=-2 x^{2}+3 x+2$ y$g(x)=3 x^{2}+5 x-5$, evaluar$f(3)$ y$g(3)$.

Contestar

$f(3)=-7$y$g(3)=37$

40) Dado$f(x)=3 x^{2}-3 x-5$ y$g(x)=2 x^{2}-5 x-8$, evaluar$f(-2)$ y$g(-2)$.

41) Dado$f(x)=6 x-2$ y$g(x)=-8 x+9$, evaluar$f(-7)$ y$g(-7)$.

Contestar

$f(-7)=-44$y$g(-7)=65$

42) Dado$f(x)=5 x-3$ y$g(x)=9 x-9$, evaluar$f(-2)$ y$g(-2)$.

43) Dado$f(x)=4 x-3$ y$g(x)=-3 x+8$, evaluar$f(-3)$ y$g(-3)$.

Contestar

$f(-3)=-15$y$g(-3)=17$

44) Dado$f(x)=8 x+7$ y$g(x)=2 x-7$, evaluar$f(-9)$ y$g(-9)$.

45) Dado$f(x)=-2 x^{2}+5 x-9$ y$g(x)=-2 x^{2}+3 x-4$, evaluar$f(-2)$ y$g(-2)$.

Contestar

$f(-2)=-27$y$g(-2)=-18$

46) Dado$f(x)=-3 x^{2}+5 x-2$ y$g(x)=3 x^{2}-4 x+2$, evaluar$f(-1)$ y$g(-1)$.

5.2: Polinomios

En los Ejercicios 1-6, indicar el coeciente y el grado de cada uno de los siguientes términos.

1)$3 v^{5} u^{6}$

Contestar

$=3,$Grado de Coeficiente$=11$

2)$-3 b^{5} z^{8}$

3)$-5 v^{6}$

Contestar

$=-5,$Grado de Coeficiente$=6$

4)$-5 c^{3}$

5)$2 u^{7} x^{4} d^{5}$

Contestar

$=2,$Grado de Coeficiente$=16$

6)$9 w^{4} c^{5} u^{7}$

En los Ejercicios 7-16, indique si cada una de las siguientes expresiones es un monomio, binomio o trinomio.

7)$-7 b^{9} c^{3}$

Contestar

Monomio

8)$7 b^{6} c^{2}$

9)$4 u+7 v$

Contestar

Binomial

10)$-3 b+5 c$

11)$3 b^{4}-9 b c+9 c^{2}$

Contestar

Trinomio

12)$8 u^{4}+5 u v+3 v^{4}$

13)$5 s^{2}+9 t^{7}$

Contestar

Binomial

14)$-8 x^{6}-6 y^{7}$

15)$2 u^{3}-5 u v-4 v^{4}$

Contestar

Trinomio

16)$6 y^{3}-4 y z+7 z^{3}$

En los Ejercicios 17-20, ordenar cada uno de los polinomios dados en potencias descendentes de$x$.

17)$-2 x^{7}-9 x^{13}-6 x^{12}-7 x^{17}$

Contestar

$-7 x^{17}-9 x^{13}-6 x^{12}-2 x^{7}$

18)$2 x^{4}-8 x^{19}+3 x^{10}-4 x^{2}$

19)$8 x^{6}+2 x^{15}-3 x^{11}-2 x^{2}$

Contestar

$2 x^{15}-3 x^{11}+8 x^{6}-2 x^{2}$

20)$2 x^{6}-6 x^{7}-7 x^{15}-9 x^{18}$

En los Ejercicios 21-24, ordenar cada uno de los polinomios dados en poderes ascendentes de$x$.

21)$7 x^{17}+3 x^{4}-2 x^{12}+8 x^{14}$

Contestar

$3 x^{4}-2 x^{12}+8 x^{14}+7 x^{17}$

22)$6 x^{18}-6 x^{4}-2 x^{19}-7 x^{14}$

23)$2 x^{13}+3 x^{18}+8 x^{7}+5 x^{4}$

Contestar

$5 x^{4}+8 x^{7}+2 x^{13}+3 x^{18}$

24)$-6 x^{18}-8 x^{11}-9 x^{15}+5 x^{12}$

En Ejercicios 25-32, simplifica el polinomio dado, combinando términos similares, luego arreglando tu respuesta en potencias descendentes de$x$.

25)$-5 x+3-6 x^{3}+5 x^{2}-9 x+3-3 x^{2}+6 x^{3}$

Contestar

$2 x^{2}-14 x+6$

26)$-2 x^{3}+8 x-x^{2}+5+7+6 x^{2}+4 x^{3}-9 x$

27)$4 x^{3}+6 x^{2}-8 x+1+8 x^{3}-7 x^{2}+5 x-8$

Contestar

$12 x^{3}-x^{2}-3 x-7$

28)$-8 x^{3}-2 x^{2}-7 x-3+7 x^{3}-9 x^{2}-8 x+9$

29)$x^{2}+9 x-3+7 x^{2}-3 x-8$

Contestar

$8 x^{2}+6 x-11$

30)$-4 x^{2}-6 x+3-3 x^{2}+3 x-6$

31)$8 x+7+2 x^{2}-8 x-3 x^{3}-x^{2}$

Contestar

$-3 x^{3}+x^{2}+7$

32)$-x^{2}+8-7 x+8 x-5 x^{2}+4 x^{3}$

En los Ejercicios 33-44, simplifica el polinomio dado, combinando términos similares, luego arreglando tu respuesta en un orden razonable, quizás en potencias descendentes de cualquiera de las variables. Nota: Las respuestas pueden variar, dependiendo de la variable que elijas para dictar el orden.

33)$-8 x^{2}-4 x z-2 z^{2}-3 x^{2}-8 x z+2 z^{2}$

Contestar

$-11 x^{2}-12 x z$

34)$-5 x^{2}+9 x z-4 z^{2}-6 x^{2}-7 x z+7 z^{2}$

35)$-6 u^{3}+4 u v^{2}-2 v^{3}-u^{3}+6 u^{2} v-5 u v^{2}$

Contestar

$-7 u^{3}+6 u^{2} v-u v^{2}-2 v^{3}$

36)$7 a^{3}+6 a^{2} b-5 a b^{2}+4 a^{3}+6 a^{2} b+6 b^{3}$

37)$-4 b^{2} c-3 b c^{2}-5 c^{3}+9 b^{3}-3 b^{2} c+5 b c^{2}$

Contestar

$9 b^{3}-7 b^{2} c+2 b c^{2}-5 c^{3}$

38)$4 b^{3}-6 b^{2} c+9 b c^{2}-9 b^{3}-8 b c^{2}+3 c^{3}$

39)$-8 y^{2}+6 y z-7 z^{2}-2 y^{2}-3 y z-9 z^{2}$

Contestar

$-10 y^{2}+3 y z-16 z^{2}$

40)$8 x^{2}+x y+3 y^{2}-x^{2}+7 x y+y^{2}$

41)$7 b^{2} c+8 b c^{2}-6 c^{3}-4 b^{3}+9 b c^{2}-6 c^{3}$

Contestar

$-4 b^{3}+7 b^{2} c+17 b c^{2}-12 c^{3}$

42)$7 x^{3}-9 x^{2} y+3 y^{3}+7 x^{3}+3 x y^{2}-7 y^{3}$

43)$9 a^{2}+a c-9 c^{2}-5 a^{2}-2 a c+2 c^{2}$

Contestar

$4 a^{2}-a c-7 c^{2}$

44)$7 u^{2}+3 u v-6 v^{2}-6 u^{2}+7 u v+6 v^{2}$

En Ejercicios 45-50, indicar el grado del polinomio dado.

45)$3 x^{15}+4+8 x^{3}-8 x^{19}$

Contestar

$19$

46)$-4 x^{6}-7 x^{16}-5+3 x^{18}$

47)$7 x^{10}-3 x^{18}+9 x^{4}-6$

Contestar

$18$

48)$3 x^{16}-8 x^{5}+x^{8}+7$

49)$-2-x^{7}-5 x^{5}+x^{10}$

Contestar

$10$

50)$x^{11}+7 x^{16}+8-7 x^{10}$

51) Dado$f(x)=5 x^{3}+4 x^{2}-6$, evaluar$f(-1)$.

Contestar

$-7$

52) Dado$f(x)=-3 x^{3}+3 x^{2}-9$, evaluar$f(-1)$.

53) Dado$f(x)=5 x^{4}-4 x-6$, evaluar$f(-2)$.

Contestar

$82$

54) Dado$f(x)=-2 x^{4}-4 x-9$, evaluar$f(2)$.

55) Dado$f(x)=3 x^{4}+5 x^{3}-9$, evaluar$f(-2)$.

Contestar

$-1$

56) Dado$f(x)=-3 x^{4}+2 x^{3}-6$, evaluar$f(-1)$.

57) Dado$f(x)=3 x^{4}-5 x^{2}+8$, evaluar$f(-1)$.

Contestar

$6$

58) Dado$f(x)=-4 x^{4}-5 x^{2}-3$, evaluar$f(3)$.

59) Dado$f(x)=-2 x^{3}+4 x-9$, evaluar$f(2)$.

Contestar

$-17$

60) Dado$f(x)=4 x^{3}+3 x+7$, evaluar$f(-2)$.

En los Ejercicios 61-64, usa tu calculadora gráfica para bosquejar el polinomio cuadrático dado. En cada caso la gráfica es una parábola, así que ajusta los parámetros de VENTANA hasta que el vértice esté visible en la ventana de visualización, luego siga las Directrices de envío de la calculadora al reportar su solución en su tarea.

61)$p(x)=-2 x^{2}+8 x+32$

Contestar

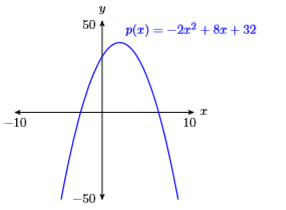
62)$p(x)=2 x^{2}+6 x-18$

63)$p(x)=3 x^{2}-8 x-35$

Contestar

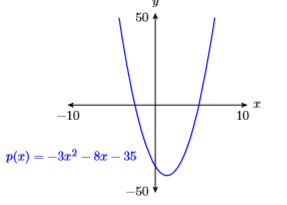
64)$p(x)=-4 x^{2}-9 x+50$

En los Ejercicios 65-68, usa tu calculadora gráfica para bosquejar el polinomio usando los parámetros VENTANA dados. Siga las pautas de envío de la calculadora al informar su solución en su tarea.

65)$p(x)=x^{3}-4 x^{2}-11 x+30$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50$

Contestar

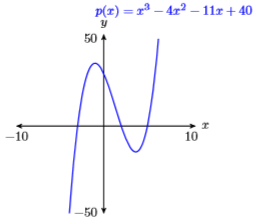
66)$p(x)=-x^{3}+4 x^{2}+27 x-90$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-150 \quad \mathbf{Y} \max =50$

67)$p(x)=x^{4}-10 x^{3}-4 x^{2}+250 x-525$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-1000 \quad \mathbf{Y} \max =500$

Contestar

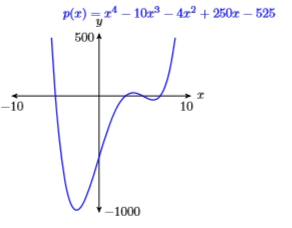
68)$p(x)=-x^{4}+2 x^{3}+35 x^{2}-36 x-180$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50$

5.3: Aplicaciones de polinomios

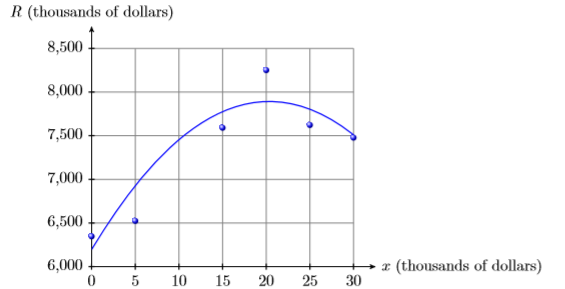
1) Un firm recoge datos sobre la cantidad que gasta en publicidad y los ingresos resultantes recaudados por el firm. Ambos datos están en miles de dólares.

$x$(costos de publicidad)	0	5	15	20	25	30
$R$(ingresos)	6347	6524	7591	8251	7623	7478

Los datos se trazan luego fitados con el siguiente polinomio de segundo grado, donde$x$ está la cantidad invertida en miles de dólares y$R(x)$ es la cantidad de ingresos obtenidos por el firm (también en miles de dólares).

$R(x)=−4.1x^2 + 166.8x+ 6196$

Usa la gráfica y luego el polinomio para estimar los ingresos del firm cuando el firm invierte$\$10,000$ en publicidad.

Contestar

Aproximadamente$\$7,454,000$

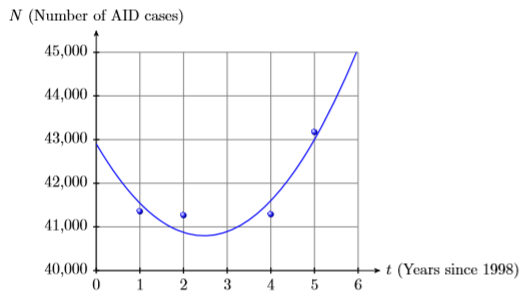
2) La siguiente tabla enumera el número estimado de casos de ayudas en Estados Unidos para los años 1999-2003.

Año	1999	2000	2002	2003
Casos de SIDA	41,356	41,267	41,289	43,171

Los datos se trazan luego con el siguiente polinomio de segundo grado, donde$t$ está el número de años que han pasado desde 1998 y$N(t)$ es el número de casos de ayudas reportados$t$ años después de 1998.

$N(t) = 345.14t^2−1705.7t+ 42904$

Utilice la gráfica y luego el polinomio para estimar el número de casos de SIDA en el año 2001.

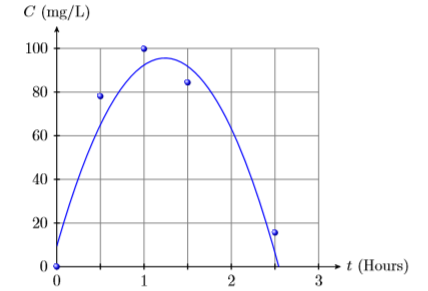
3) La siguiente tabla registra la concentración (en miligramos por litro) de medicamento en la sangre de un paciente después de que hayan pasado los tiempos indicados.

Tiempo (Horas)	0	0.5	1	0.5	2.5
Concentración (mg/L)	0	78.1	99.8	84.4	15.6

Los datos se trazan luego con el siguiente polinomio de segundo grado, donde$t$ está el número de horas que han pasado desde que tomó el medicamento y$C(t)$ es la concentración (en miligramos por litro) del medicamento en la sangre del paciente después de que hayan pasado$t$ las horas.

$C(t)=−56.214t^2 + 139.31t+9.35$

Use la gráfica y luego el polinomio para estimar la concentración de medicamento en la sangre del paciente$2$ horas después de tomar el medicamento.

Contestar

Aproximadamente$63 \mathrm{mg} / \mathrm{L}$

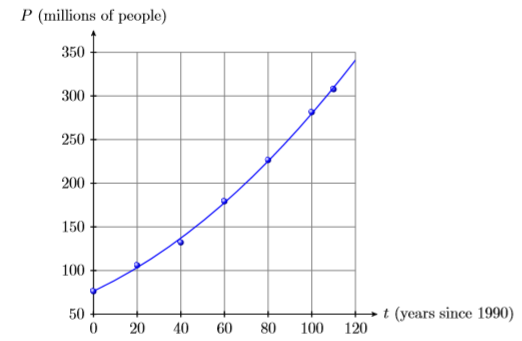
4) La siguiente tabla registra la población (en millones de personas) de Estados Unidos para el año dado.

Año	1900	1920	1940	1960	1980	2000	2010
Población (millones)	76.2	106.0	132.2	179.3	226.5	281.4	307.7

Los datos se trazan luego con el siguiente polinomio de segundo grado, donde$t$ está el número de años que han pasado desde 1990 y$P(t)$ es la población (en millones)$t$ años después de 1990.

$P(t)=0 .008597t^2 +1,1738t+ 76 .41$

Utilice la gráfica y luego el polinomio para estimar la población de Estados Unidos en el año 1970.

5) Si un proyectil es lanzado con una velocidad inicial de$457$ metros por segundo ($457 \mathrm{m/s}$) desde un techo$75$ metros ($75 \mathrm{m}$) sobre el nivel del suelo, ¿en qué momento el proyectil alcanzará primero una altura de$6592$ metros ($6592 \mathrm{m}$)? Redondee su respuesta al segundo más cercano.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Contestar

$17.6$segundos

6) Si un proyectil es lanzado con una velocidad inicial de$236$ metros por segundo ($236 \mathrm{m/s}$) desde un techo$15$ metros ($15\mathrm{m}$) sobre el nivel del suelo, ¿en qué momento el proyectil alcanzará primero una altura de$1838$ metros ($1838\mathrm{m}$)? Redondee su respuesta al segundo más cercano.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

7) Si un proyectil es lanzado con una velocidad inicial de$229$ metros por segundo ($229 \mathrm{m/s}$) desde un techo$58$ metros ($58\mathrm{m}$) sobre el nivel del suelo, ¿en qué momento el proyectil alcanzará primero una altura de$1374$ metros ($1374\mathrm{m}$)? Redondee su respuesta al segundo más cercano.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de 9.8 metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Contestar

$6.7$segundos

8) Si un proyectil es lanzado con una velocidad inicial de$234$ metros por segundo ($234 \mathrm{m/s}$) desde un techo$16$ metros ($16\mathrm{m}$) sobre el nivel del suelo, ¿en qué momento el proyectil alcanzará primero una altura de$1882$ metros ($1882\mathrm{m}$)? Redondee su respuesta al segundo más cercano.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

En los Ejercicios 9-12, primero usa una técnica algebraica para encontrar el cero de la función dada, luego usa la utilidad 2:zero en tu calculadora gráfica para localizar el cero de la función. Utilice las Directrices de envío de la calculadora al informar el cero encontrado usando su calculadora gráfica.

9)$f(x)=3.25 x-4.875$

Contestar

Cero:$1.5$

10)$f(x)=3.125-2.5 x$

11)$f(x)=3.9-1.5 x$

Contestar

Cero:$2.6$

12)$f(x)=0.75 x+2.4$

13) Si se lanza un proyectil con una velocidad inicial de$203$ metros por segundo ($203 \mathrm{m/s}$) desde una azotea a$52$ metros ($52\mathrm{m}$) sobre el nivel del suelo, ¿a qué hora volverá el proyectil al nivel del suelo? Redondee su respuesta a la décima de segundo más cercana.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Contestar

$41.7$segundos

14) Si se lanza un proyectil con una velocidad inicial de$484$ metros por segundo ($484 \mathrm{m/s}$) desde una azotea a$17$ metros ($17\mathrm{m}$) sobre el nivel del suelo, ¿a qué hora volverá el proyectil al nivel del suelo? Redondee su respuesta a la décima de segundo más cercana.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

15) Si se lanza un proyectil con una velocidad inicial de$276$ metros por segundo ($276 \mathrm{m/s}$) desde una azotea a$52$ metros ($52\mathrm{m}$) sobre el nivel del suelo, ¿a qué hora volverá el proyectil al nivel del suelo? Redondee su respuesta a la décima de segundo más cercana.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Contestar

$56.5$segundos

16) Si se lanza un proyectil con una velocidad inicial de$204$ metros por segundo ($204 \mathrm{m/s}$) desde una azotea a$92$ metros ($92\mathrm{m}$) sobre el nivel del suelo, ¿a qué hora volverá el proyectil al nivel del suelo? Redondee su respuesta a la décima de segundo más cercana.

Nota: La aceleración debida a la gravedad cerca de la superficie terrestre es de$9.8$ metros por segundo por segundo ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

5.4: Sumando y restando polinomios

En los Ejercicios 1-8, simplificar la expresión dada. Organice su respuesta en algún tipo de orden razonable.

1)$\left(-8 r^{2} t+7 r t^{2}+3 t^{3}\right)+\left(9 r^{3}+2 r t^{2}+4 t^{3}\right)$

Contestar

$9 r^{3}-8 r^{2} t+9 r t^{2}+7 t^{3}$

2)$\left(-a^{3}-8 a c^{2}-7 c^{3}\right)+\left(-7 a^{3}-8 a^{2} c+8 a c^{2}\right)$

3)$\left(7 x^{2}-6 x-9\right)+\left(8 x^{2}+10 x+9\right)$

Contestar

$15 x^{2}+4 x$

4)$\left(-7 x^{2}+5 x-6\right)+\left(-10 x^{2}-1\right)$

5)$\left(-2 r^{2}+7 r s+4 s^{2}\right)+\left(-9 r^{2}+7 r s-2 s^{2}\right)$

Contestar

$-11 r^{2}+14 r s+2 s^{2}$

6)$\left(-2 r^{2}+3 r t-4 t^{2}\right)+\left(7 r^{2}+4 r t-7 t^{2}\right)$

7)$\left(-8 y^{3}-3 y^{2} z-6 z^{3}\right)+\left(-3 y^{3}+7 y^{2} z-9 y z^{2}\right)$

Contestar

$-11 y^{3}+4 y^{2} z-9 y z^{2}-6 z^{3}$

8)$\left(7 y^{2} z+8 y z^{2}+2 z^{3}\right)+\left(8 y^{3}-8 y^{2} z+9 y z^{2}\right)$

En los Ejercicios 9-14, simplifique la expresión dada distribuyendo el signo menos.

9)$-\left(5 x^{2}-4\right)$

Contestar

$-5 x^{2}+4$

10)$-\left(-8 x^{2}-5\right)$

11)$-\left(9 r^{3}-4 r^{2} t-3 r t^{2}+4 t^{3}\right)$

Contestar

$-9 r^{3}+4 r^{2} t+3 r t^{2}-4 t^{3}$

12)$-\left(7 u^{3}-8 u^{2} v+6 u v^{2}+5 v^{3}\right)$

13)$-\left(-5 x^{2}+9 x y+6 y^{2}\right)$

Contestar

$5 x^{2}-9 x y-6 y^{2}$

14)$-\left(-4 u^{2}-6 u v+5 v^{2}\right)$

En los Ejercicios 15-22, simplificar la expresión dada. Organice su respuesta en algún tipo de orden razonable.

15)$\left(-u^{3}-4 u^{2} w+7 w^{3}\right)-\left(u^{2} w+u w^{2}+3 w^{3}\right)$

Contestar

$-u^{3}-5 u^{2} w-u w^{2}+4 w^{3}$

16)$\left(-b^{2} c+8 b c^{2}+8 c^{3}\right)-\left(6 b^{3}+b^{2} c-4 b c^{2}\right)$

17)$\left(2 y^{3}-2 y^{2} z+3 z^{3}\right)-\left(-8 y^{3}+5 y z^{2}-3 z^{3}\right)$

Contestar

$10 y^{3}-2 y^{2} z-5 y z^{2}+6 z^{3}$

18)$\left(4 a^{3}+6 a c^{2}+5 c^{3}\right)-\left(2 a^{3}+8 a^{2} c-7 a c^{2}\right)$

19)$\left(-7 r^{2}-9 r s-2 s^{2}\right)-\left(-8 r^{2}-7 r s+9 s^{2}\right)$

Contestar

$r^{2}-2 r s-11 s^{2}$

20)$\left(-4 a^{2}+5 a b-2 b^{2}\right)-\left(-8 a^{2}+7 a b+2 b^{2}\right)$

21)$\left(10 x^{2}+2 x-6\right)-\left(-8 x^{2}+14 x+17\right)$

Contestar

$18 x^{2}-12 x-23$

22)$\left(-5 x^{2}+19 x-5\right)-\left(-15 x^{2}+19 x+8\right)$

En Ejercicios 23-28, para las funciones polinómicas dadas$f(x)$ y$g(x)$, simplificar$f(x)+g(x)$. Organice su respuesta en poderes descendentes de$x$.

23)$\begin{aligned}f(x)&=-2 x^{2}+9 x+7 \\ g(x)&=8 x^{3}-7 x^{2}+5\end{aligned}$

Contestar

$8 x^{3}-9 x^{2}+9 x+12$

24)$\begin{aligned}f(x)&=-8 x^{3}+6 x-9 \\ g(x)&=x^{3}-x^{2}+3 x\end{aligned}$

25)$\begin{aligned}f(x)&=5 x^{3}-5 x^{2}+8 x \\ g(x)&=7 x^{2}-2 x-9\end{aligned}$

Contestar

$5 x^{3}+2 x^{2}+6 x-9$

26)$\begin{aligned}f(x)&=-x^{2}+8 x+1 \\ g(x)&=-7 x^{3}+8 x-9\end{aligned}$

27)$\begin{aligned}f(x)&=-3 x^{2}-8 x-9 \\ g(x)&=5 x^{2}-4 x+4\end{aligned}$

Contestar

$2 x^{2}-12 x-5$

28)$\begin{aligned}f(x)&=-3 x^{2}+x-8 \\ g(x)&=7 x^{2}-9\end{aligned}$

En los Ejercicios 29-34, para las funciones polinómicas dadas$f(x)$ y$g(x)$, simplificar$f(x)−g(x)$. Organice su respuesta en poderes descendentes de$x$.

29)$\begin{aligned}f(x)&=-6 x^{3}-7 x+7 \\ g(x)&=-3 x^{3}-3 x^{2}-8 x\end{aligned}$

Contestar

$-3 x^{3}+3 x^{2}+x+7$

30)$\begin{aligned}f(x)&=5 x^{3}-5 x+4 \\ g(x)&=-8 x^{3}-2 x^{2}-3 x\end{aligned}$

31)$\begin{aligned}f(x)&=12 x^{2}-5 x+4 \\ g(x)&=8 x^{2}-16 x-7\end{aligned}$

Contestar

$4 x^{2}+11 x+11$

32)$\begin{aligned}f(x)&=-7 x^{2}+12 x+17 \\ g(x)&=-10 x^{2}-17\end{aligned}$

33)$\begin{aligned}f(x)&=-3 x^{3}-4 x+2 \\ g(x)&=-4 x^{3}-7 x^{2}+6\end{aligned}$

Contestar

$x^{3}+7 x^{2}-4 x-4$

34)$\begin{aligned}f(x)&=-9 x^{2}+9 x+3 \\ g(x)&=7 x^{3}+7 x^{2}+5\end{aligned}$

En los Ejercicios 35-36, encontrar el área del cuadrado dado sumando las áreas de sus cuatro partes.

35)

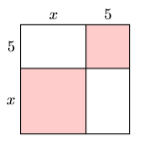
Contestar

$x^{2}+10 x+25$

36)

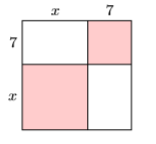
37) Rachel dirige un pequeño negocio vendiendo canastas de mimbre. Sus costos comerciales para producir y vender x cestas de mimbre están dados por la función polinómica$C(x) = 232+ 7x−0.0085x^2$. El ingreso que obtiene al vender x cestas de mimbre viene dado por la función polinómica$R(x) = 33.45x$. Encuentra una fórmula para$P(x)$, el profit hecho a partir de la venta de cestas$x$ de mimbre. Usa tu fórmula para determinar el perfil de Rachel si vende canastas$233$ de mimbre. Redondee su respuesta al centavo más cercano.

Contestar

$\$6,392.31$

38) Eloise dirige un pequeño negocio que vende cunas para bebés. Sus costos comerciales para producir y vender$x$ cunas están dados por la función polinómica$C(x) = 122 + 8x − 0.0055x^2$. El ingreso que obtiene$x$ al vender cunas viene dado por la función polinómica$R(x) = 33.45x$. Encuentra una fórmula para$P(x)$, el profit hecho a partir de la venta de cunas$x$ para bebés. Usa tu fórmula para determinar el perfil de Eloise si vende cunas$182$ para bebés. Redondee su respuesta al centavo más cercano.

5.5: Leyes de los Exponentes

En los Ejercicios 1-8, simplifica cada una de las expresiones exponenciales dadas.

1)$(-4)^{3}$

Contestar

$-64$

2)$(-9)^{2}$

3)$\left(-\dfrac{5}{7}\right)^{0}$

Contestar

$1$

4)$\left(-\dfrac{2}{5}\right)^{0}$

5)$\left(-\dfrac{4}{3}\right)^{2}$

Contestar

$\dfrac{16}{9}$

6)$\left(-\dfrac{2}{3}\right)^{2}$

7)$(-19)^{0}$

Contestar

$1$

8)$(-17)^{0}$

En los Ejercicios 9-18, simplifique cada una de las expresiones exponenciales dadas.

9)$(7 v-6 w)^{18} \cdot(7 v-6 w)^{17}$

Contestar

$(7 v-6 w)^{35}$

10)$(8 a+7 c)^{3} \cdot(8 a+7 c)^{19}$

11)$3^{4} \cdot 3^{0}$

Contestar

$3^{4}$

12)$5^{7} \cdot 5^{0}$

13)$4^{n} \cdot 4^{8 n+3}$

Contestar

$4^{9 n+3}$

14)$4^{6 m+5} \cdot 4^{m-5}$

15)$x^{8} \cdot x^{3}$

Contestar

$x^{11}$

16)$a^{9} \cdot a^{15}$

17)$2^{5} \cdot 2^{3}$

Contestar

$2^{8}$

18)$2^{10} \cdot 2^{3}$

En los Ejercicios 19-28, simplifique cada una de las expresiones exponenciales dadas.

19)$\dfrac{4^{16}}{4^{16}}$

Contestar

$1$

20)$\dfrac{3^{12}}{3^{12}}$

21)$\dfrac{w^{11}}{w^{7}}$

Contestar

$w^{4}$

22)$\dfrac{c^{10}}{c^{8}}$

23)$\dfrac{(9 a-8 c)^{15}}{(9 a-8 c)^{8}}$

Contestar

$(9 a-8 c)^{7}$

24)$\dfrac{(4 b+7 c)^{15}}{(4 b+7 c)^{5}}$

25)$\dfrac{2^{9 n+5}}{2^{3 n-4}}$

Contestar

$2^{6 n+9}$

26)$\dfrac{2^{4 k-9}}{2^{3 k-8}}$

27)$\dfrac{4^{17}}{4^{9}}$

Contestar

$4^{8}$

28)$\dfrac{2^{17}}{2^{6}}$

En los Ejercicios 29-38, simplificar cada una de las expresiones exponenciales dadas.

29)$\left(4^{8 m-6}\right)^{7}$

Contestar

$4^{56 m-42}$

30)$\left(2^{2 m-9}\right)^{3}$

31)$\left[(9 x+5 y)^{3}\right]^{7}$

Contestar

$(9 x+5 y)^{21}$

32)$\left[(4 u-v)^{8}\right]^{9}$

33)$\left(4^{3}\right)^{2}$

Contestar

$4^{6}$

34)$\left(3^{4}\right)^{2}$

35)$\left(c^{4}\right)^{7}$

Contestar

$c^{28}$

36)$\left(w^{9}\right)^{5}$

37)$\left(6^{2}\right)^{0}$

Contestar

$1$

38)$\left(8^{9}\right)^{0}$

En los Ejercicios 39-48, simplificar cada una de las expresiones exponenciales dadas.

39)$(u w)^{5}$

Contestar

$u^{5} w^{5}$

40)$(a c)^{4}$

41)$(-2 y)^{3}$

Contestar

$-8 y^{3}$

42)$(-2 b)^{3}$

43)$\left(3 w^{9}\right)^{4}$

Contestar

$81 w^{36}$

44)$\left(-3 u^{9}\right)^{4}$

45)$\left(-3 x^{8} y^{2}\right)^{4}$

Contestar

$81 x^{32} y^{8}$

46)$\left(2 x^{8} z^{6}\right)^{4}$

47)$\left(7 s^{6 n}\right)^{3}$

Contestar

$343 s^{18 n}$

48)$\left(9 b^{6 n}\right)^{3}$

En los Ejercicios 49-56, simplifique cada una de las expresiones exponenciales dadas.

49)$\left(\dfrac{v}{2}\right)^{3}$

Contestar

$\dfrac{v^{3}}{8}$

50)$\left(\dfrac{t}{9}\right)^{2}$

51)$\left(-\dfrac{2}{u}\right)^{2}$

Contestar

$\dfrac{4}{u^{2}}$

52)$\left(-\dfrac{3}{w}\right)^{3}$

53)$\left(-\dfrac{r^{8}}{5}\right)^{4}$

Contestar

$\dfrac{r^{32}}{625}$

54)$\left(-\dfrac{x^{11}}{5}\right)^{5}$

55)$\left(\dfrac{5}{c^{9}}\right)^{4}$

Contestar

$\dfrac{625}{c^{36}}$

56)$\left(\dfrac{5}{u^{12}}\right)^{2}$

57) Completar cada una de las leyes de exponentes presentadas en la primera columna, luego utilizar los resultados para simplificar las expresiones de la segunda columna.

$a^{m} a^{n}=?$	$a^{3} a^{5}=?$
$\dfrac{a^{m}}{a^{n}}=?$	$\dfrac{a^{6}}{a^{2}}=?$
$\left(a^{m}\right)^{n}=?$	$\left(a^{5}\right)^{7}=?$
$(a b)^{m}=?$	$(a b)^{9}=?$
$\left(\dfrac{a}{b}\right)^{m}=?$	$\left(\dfrac{a}{b}\right)^{3}=?$

Contestar

Las respuestas generales son:$a^{m+n}, a^{m-n}, a^{m n}, a^{m} b^{m}, \dfrac{a^m}{b^m}$.

Las respuestas especificas son:$a^{8}, a^{4}, a^{35}, a^{9} b^{9}, \dfrac{a^3}{b^3}$.

5.6: Multiplicar polinomios

En los Ejercicios 1-10, simplifique la expresión dada.

1)$-3(7 r)$

Contestar

$-21 r$

2)$7(3 a)$

3)$\left(-9 b^{3}\right)\left(-8 b^{6}\right)$

Contestar

$72b^{9}$

4)$\left(8 s^{3}\right)\left(-7 s^{4}\right)$

5)$\left(-7 r^{2} t^{4}\right)\left(7 r^{5} t^{2}\right)$

Contestar

$-49 r^{7} t^{6}$

6)$\left(-10 s^{2} t^{8}\right)\left(-7 s^{4} t^{3}\right)$

7)$\left(-5 b^{2} c^{9}\right)\left(-8 b^{4} c^{4}\right)$

Contestar

$40 b^{6} c^{13}$

8)$\left(-9 s^{2} t^{8}\right)\left(7 s^{5} t^{4}\right)$

9)$\left(-8 v^{3}\right)\left(4 v^{4}\right)$

Contestar

$-32 v^{7}$

10)$\left(-9 y^{3}\right)\left(3 y^{5}\right)$

En los Ejercicios 11-22, utilice la propiedad distributiva para expandir la expresión dada.

11)$9\left(-2 b^{2}+2 b+9\right)$

Contestar

$-18 b^{2}+18 b+81$

12)$9\left(-4 b^{2}+7 b-8\right)$

13)$-4\left(10 t^{2}-7 t-6\right)$

Contestar

$-40 t^{2}+28 t+24$

14)$-5\left(-7 u^{2}-7 u+2\right)$

15)$-8 u^{2}\left(-7 u^{3}-8 u^{2}-2 u+10\right)$

Contestar

$56 u^{5}+64 u^{4}+16 u^{3}-80 u^{2}$

16)$-3 s^{2}\left(-7 s^{3}-9 s^{2}+6 s+3\right)$

17)$10 s^{2}\left(-10 s^{3}+2 s^{2}+2 s+8\right)$

Contestar

$-100 s^{5}+20 s^{4}+20 s^{3}+80 s^{2}$

18)$8 u^{2}\left(9 u^{3}-5 u^{2}-2 u+5\right)$

19)$2 s t\left(-4 s^{2}+8 s t-10 t^{2}\right)$

Contestar

$-8 s^{3} t+16 s^{2} t^{2}-20 s t^{3}$

20)$7 u v\left(-9 u^{2}-3 u v+4 v^{2}\right)$

21)$-2 u w\left(10 u^{2}-7 u w-2 w^{2}\right)$

Contestar

$-20 u^{3} w+14 u^{2} w^{2}+4 u w^{3}$

22)$-6 v w\left(-5 v^{2}+9 v w+5 w^{2}\right)$

En los Ejercicios 23-30, utilice la técnica demostrada en el Ejemplo 5.6.8 y Ejemplo 5.6.9 para expandir cada una de las siguientes expresiones utilizando la propiedad distributiva.

23)$(-9 x-4)(-3 x+2)$

Contestar

$27 x^{2}-6 x-8$

24)$(4 x-10)(-2 x-6)$

25)$(3 x+8)(3 x-2)$

Contestar

$9 x^{2}+18 x-16$

26)$(-6 x+8)(-x+1)$

27)$-12 x^{3}+14 x^{2}+6 x-5$

Contestar

$-\dfrac{930}{289}$

28)$(4 x-6)\left(-7 x^{2}-10 x+10\right)$

29)$(x-6)\left(-2 x^{2}-4 x-4\right)$

Contestar

$-2 x^{3}+8 x^{2}+20 x+24$

30)$(5 x-10)\left(-3 x^{2}+7 x-8\right)$

En Ejercicios 31-50, utilice la técnica de atajo demostrada en el Ejemplo 5.6.10, Ejemplo 5.6.11 y Ejemplo 5.6.12 para expandir cada una de las siguientes expresiones usando la propiedad distributiva.

31)$(8 u-9 w)(8 u-9 w)$

Contestar

$64 u^{2}-144 u w+81 w^{2}$

32)$(3 b+4 c)(-8 b+10 c)$

33)$(9 r-7 t)(3 r-9 t)$

Contestar

$27 r^{2}-102 r t+63 t^{2}$

34)$(-6 x-3 y)(-6 x+9 y)$

35)$(4 r-10 s)\left(-10 r^{2}+10 r s-7 s^{2}\right)$

Contestar

$-40 r^{3}+140 r^{2} s-128 r s^{2}+70 s^{3}$

36)$(5 s-9 t)\left(-3 s^{2}+4 s t-9 t^{2}\right)$

37)$(9 x-2 z)\left(4 x^{2}-4 x z-10 z^{2}\right)$

Contestar

$36 x^{3}-44 x^{2} z-82 x z^{2}+20 z^{3}$

38)$(r-4 t)\left(7 r^{2}+4 r t-2 t^{2}\right)$

39)$(9 r+3 t)^{2}$

Contestar

$81 r^{2}+54 r t+9 t^{2}$

40)$(4 x+8 z)^{2}$

41)$(4 y+5 z)(4 y-5 z)$

Contestar

$16 y^{2}-25 z^{2}$

42)$(7 v+2 w)(7 v-2 w)$

43)$(7 u+8 v)(7 u-8 v)$

Contestar

$49 u^{2}-64 v^{2}$

44)$(6 b+8 c)(6 b-8 c)$

45)$(7 b+8 c)^{2}$

Contestar

$49 b^{2}+112 b c+64 c^{2}$

46)$(2 b+9 c)^{2}$

47)$\left(2 t^{2}+9 t+4\right)\left(2 t^{2}+9 t+4\right)$

Contestar

$4 t^{4}+36 t^{3}+97 t^{2}+72 t+16$

48)$\left(3 a^{2}-9 a+4\right)\left(3 a^{2}-9 a+2\right)$

49)$\left(4 w^{2}+3 w+5\right)\left(3 w^{2}-6 w+8\right)$

Contestar

$12 w^{4}-15 w^{3}+29 w^{2}-6 w+40$

50)$\left(4 s^{2}+3 s+8\right)\left(2 s^{2}+4 s-9\right)$

51) La demanda de widgets viene dada por la función$x = 320−0.95p$, donde$x$ está la demanda y$p$ es el precio unitario. ¿Qué precio unitario debe cobrar un minorista por los widgets para que sus ingresos por ventas sean iguales$\$7,804$? Redondee sus respuestas al centavo más cercano.

Contestar

$\$ 26.47$,$\$ 310.37$

52) La demanda de widgets viene dada por la función$x = 289−0.91p$, donde$x$ está la demanda y$p$ es el precio unitario. ¿Qué precio unitario debe cobrar un minorista por los widgets para que sus ingresos por ventas sean iguales$\$7,257$? Redondee sus respuestas al centavo más cercano.

53) En la imagen que sigue, el borde del cuadrado exterior es$6$ pulgadas más largo que$3$ veces el borde del cuadrado interior.

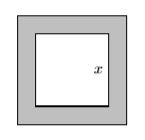
1. Expresar el área de la región sombreada como polinomio en términos de$x$, el borde del cuadrado interior. Su respuesta final debe presentarse como un polinomio de segundo grado en la forma$A(x)=ax^2 + bx + c$.
2. Dado que el borde del cuadrado interior es$5$ pulgadas, use el polinomio en la parte (a) para determinar el área de la región sombreada.

Contestar

$A(x)=8 x^{2}+36 x+36$, pulgadas$A(5)=416$ cuadradas

54) En la imagen que sigue, el borde del cuadrado exterior es$3$ pulgadas más largo que$2$ veces el borde del cuadrado interior.

1. Expresar el área de la región sombreada como polinomio en términos de$x$, el borde del cuadrado interior. Su respuesta final debe presentarse como un polinomio de segundo grado en la forma$A(x)=ax^2 + bx + c$.
2. Dado que el borde del cuadrado interior es$4$ pulgadas, use el polinomio en la parte (a) para determinar el área de la región sombreada.

55) Un jardín rectangular está rodeado por un borde uniforme de$x$ unidades de medición de césped de ancho. Toda la parcela rectangular mide$31$ por$29$ pies.

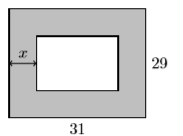
1. Encontrar el área del jardín rectangular interior como polinomio en términos de$x$. Su respuesta final debe presentarse como un polinomio de segundo grado en la forma$A(x)=ax^2 + bx + c$.
2. Dado que el ancho del borde es$9.3$ pies, utilice el polinomio en la parte (a) para determinar el área del jardín rectangular interior.

Contestar

$899-120 x+4 x^{2}$, pies$128.96$ cuadrados

56) Un jardín rectangular está rodeado por un borde uniforme de$x$ unidades de medición de césped de ancho. Toda la parcela rectangular mide$35$ por$24$ pies.

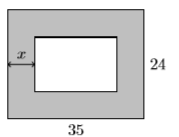
1. Encontrar el área del jardín rectangular interior como polinomio en términos de$x$. Su respuesta final debe presentarse como un polinomio de segundo grado en la forma$A(x)=ax^2 + bx + c$.
2. Dado que el ancho del borde es$1.5$ pies, utilice el polinomio en la parte (a) para determinar el área del jardín rectangular interior.

5.7: Productos especiales

En los Ejercicios 1-12, utilice el atajo FOIL como en el Ejemplo 5.7.3 y Ejemplo 5.7.4 para multiplicar los binomios dados.

1)$(5 x+2)(3 x+4)$

Contestar

$15 x^{2}+26 x+8$

2)$(5 x+2)(4 x+3)$

3)$(6 x-3)(5 x+4)$

Contestar

$30 x^{2}+9 x-12$

4)$(6 x-2)(4 x+5)$

5)$(5 x-6)(3 x-4)$

Contestar

$15 x^{2}-38 x+24$

6)$(6 x-4)(3 x-2)$

7)$(6 x-2)(3 x-5)$

Contestar

$18 x^{2}-36 x+10$

8)$(2 x-3)(6 x-4)$

9)$(6 x+4)(3 x+5)$

Contestar

$18 x^{2}+42 x+20$

10)$(3 x+2)(4 x+6)$

11)$(4 x-5)(6 x+3)$

Contestar

$24 x^{2}-18 x-15$

12)$(3 x-5)(2 x+6)$

En los Ejercicios 13-20, utilice el atajo de diferencias de cuadrados como en el Ejemplo 5.7.5 para multiplicar los binomios dados.

13)$(10 x-12)(10 x+12)$

Contestar

$100 x^{2}-144$

14)$(10 x-11)(10 x+11)$

15)$(6 x+9)(6 x-9)$

Contestar

$36 x^{2}-81$

16)$(9 x+2)(9 x-2)$

17)$(3 x+10)(3 x-10)$

Contestar

$9 x^{2}-100$

18)$(12 x+12)(12 x-12)$

19)$(10 x-9)(10 x+9)$

Contestar

$100 x^{2}-81$

20)$(4 x-6)(4 x+6)$

En los Ejercicios 21-28, utilice la cuadratura de un atajo binomial como en el Ejemplo 5.7.8 para expandir la expresión dada.

21)$(2 x+3)^{2}$

Contestar

$4 x^{2}+12 x+9$

22)$(8 x+9)^{2}$

23)$(9 x-8)^{2}$

Contestar

$81 x^{2}-144 x+64$

24)$(4 x-5)^{2}$

25)$(7 x+2)^{2}$

Contestar

$49 x^{2}+28 x+4$

26)$(4 x+2)^{2}$

27)$(6 x-5)^{2}$

Contestar

$36 x^{2}-60 x+25$

28)$(4 x-3)^{2}$

En los Ejercicios 29-76, utilice el atajo apropiado para multiplicar los binomios dados.

29)$(11 x-2)(11 x+2)$

Contestar

$121 x^{2}-4$

30)$(6 x-7)(6 x+7)$

31)$(7 r-5 t)^{2}$

Contestar

$49 r^{2}-70 r t+25 t^{2}$

32)$(11 u-9 w)^{2}$

33)$(5 b+6 c)(3 b-2 c)$

Contestar

$15 b^{2}+8 b c-12 c^{2}$

34)$(3 r+2 t)(5 r-3 t)$

35)$(3 u+5 v)(3 v-5 v)$

Contestar

$9 u^{2}-25 v^{2}$

36)$(11 a+4 c)(11 a-4 c)$

37)$\left(9 b^{3}+10 c^{5}\right)\left(9 b^{3}-10 c^{5}\right)$

Contestar

$81 b^{6}-100 c^{10}$

38)$\left(9 r^{5}+7 t^{2}\right)\left(9 r^{5}-7 t^{2}\right)$

39)$(9 s-4 t)(9 s+4 t)$

Contestar

$81 s^{2}-16 t^{2}$

40)$(12 x-7 y)(12 x+7 y)$

41)$(7 x-9 y)(7 x+9 y)$

Contestar

$49 x^{2}-81 y^{2}$

42)$(10 r-11 t)(10 r+11 t)$

43)$(6 a-6 b)(2 a+3 b)$

Contestar

$12 a^{2}+6 a b-18 b^{2}$

44)$(6 r-5 t)(2 r+3 t)$

45)$(10 x-10)(10 x+10)$

Contestar

$100 x^{2}-100$

46)$(12 x-8)(12 x+8)$

47)$(4 a+2 b)(6 a-3 b)$

Contestar

$24 a^{2}-6 b^{2}$

48)$(3 b+6 c)(2 b-4 c)$

49)$(5 b-4 c)(3 b+2 c)$

Contestar

$15 b^{2}-2 b c-8 c^{2}$

50)$(3 b-2 c)(4 b+5 c)$

51)$(4 b-6 c)(6 b-2 c)$

Contestar

$24 b^{2}-44 b c+12 c^{2}$

52)$(4 y-4 z)(5 y-3 z)$

53)$\left(11 r^{5}+9 t^{2}\right)^{2}$

Contestar

$121 r^{10}+198 r^{5} t^{2}+81 t^{4}$

54)$\left(11 x^{3}+10 z^{5}\right)^{2}$

55)$(4 u-4 v)(2 u-6 v)$

Contestar

$8 u^{2}-32 u v+24 v^{2}$

56)$(4 u-5 w)(5 u-6 w)$

57)$\left(8 r^{4}+7 t^{5}\right)^{2}$

Contestar

$64 r^{8}+112 r^{4} t^{5}+49 t^{10}$

58)$\left(2 x^{5}+5 y^{2}\right)^{2}$

59)$(4 r+3 t)(4 r-3 t)$

Contestar

$16 r^{2}-9 t^{2}$

60)$(3 r+4 s)(3 r-4 s)$

61)$(5 r+6 t)^{2}$

Contestar

$25 r^{2}+60 r t+36 t^{2}$

62)$(12 v+5 w)^{2}$

63)$(3 x-4)(2 x+5)$

Contestar

$6 x^{2}+7 x-20$

64)$(5 x-6)(4 x+2)$

65)$(6 b+4 c)(2 b+3 c)$

Contestar

$12 b^{2}+26 b c+12 c^{2}$

66)$(3 v+6 w)(2 v+4 w)$

67)$\left(11 u^{2}+8 w^{3}\right)\left(11 u^{2}-8 w^{3}\right)$

Contestar

$121 u^{4}-64 w^{6}$

68)$\left(3 u^{3}+11 w^{4}\right)\left(3 u^{3}-11 w^{4}\right)$

69)$(4 y+3 z)^{2}$

Contestar

$16 y^{2}+24 y z+9 z^{2}$

70)$(11 b+3 c)^{2}$

71)$(7 u-2 v)^{2}$

Contestar

$49 u^{2}-28 u v+4 v^{2}$

72)$(4 b-5 c)^{2}$

73)$(3 v+2 w)(5 v+6 w)$

Contestar

$15 v^{2}+28 v w+12 w^{2}$

74)$(5 y+3 z)(4 y+2 z)$

75)$(5 x-3)(6 x+2)$

Contestar

$30 x^{2}-8 x-6$

76)$(6 x-5)(3 x+2)$

Para cada una de las siguientes figuras, calcule el área del cuadrado usando dos métodos.

1. Encuentra el área sumando las áreas de sus partes (ver Ejemplo 5.5.7).
2. Encuentra el área al cuadrar el lado del cuadrado usando el cuadratura de un atajo binomial.

77)

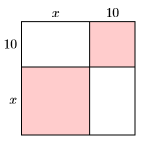
Contestar

$A=x^{2}+20 x+100$

78)

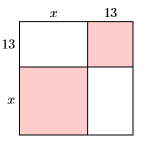
79) Una pieza cuadrada de cartón mide$12$ pulgadas en cada lado. Cuatro cuadrados, cada uno con un lado de$x$ pulgadas, se cortan y se retiran de cada una de las cuatro esquinas de la pieza cuadrada de cartón. Luego se pliegan los lados a lo largo de las líneas discontinuas para formar una caja sin parte superior.

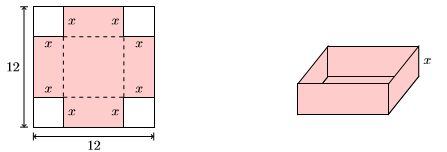
1. Encuentra el volumen de la caja en función de$x$, la medida del lado de cada cuadrado cortado a partir de las cuatro esquinas de la pieza de cartón original. Multiplica para colocar tu respuesta en forma polinómica estándar, simplificando tu respuesta tanto como sea posible.
2. Utilice el polinomio resultante para determinar el volumen de la caja si se cortan cuadrados de$1.25$ pulgadas de longitud de cada esquina de la pieza de cartón original. Redondee su respuesta a la pulgada cúbica más cercana.

Contestar

1. $V(x)=144 x-48 x^{2}+4 x^{3}$
2. $V(1.25) \approx 113$pulgadas cúbicas

80) Consideremos nuevamente la caja formada en el Ejercicio 79.

1. Encuentra el área de superficie de la caja en función de$x$, la medida del lado de cada cuadrado cortado a partir de las cuatro esquinas de la pieza de cartón original. Multiplica para colocar tu respuesta en forma polinómica estándar, simplificando tu respuesta tanto como sea posible.
2. Use el polinomio resultante para determinar el área de superficie de la caja si se cortan cuadrados de$1.25$ pulgadas de longitud de cada esquina de la pieza de cartón original. Redondee su respuesta a la pulgada cuadrada más cercana.