Saltar al contenido principal
LibreTexts Español

1.8: Decimales

  1. Última actualización
  2. Guardar como PDF
  • Page ID
    110483

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

    ( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\id}{\mathrm{id}}\)

    \( \newcommand{\Span}{\mathrm{span}}\)

    \( \newcommand{\kernel}{\mathrm{null}\,}\)

    \( \newcommand{\range}{\mathrm{range}\,}\)

    \( \newcommand{\RealPart}{\mathrm{Re}}\)

    \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

    \( \newcommand{\Argument}{\mathrm{Arg}}\)

    \( \newcommand{\norm}[1]{\| #1 \|}\)

    \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

    \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

    \( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

    \( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

    \( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vectorC}[1]{\textbf{#1}} \)

    \( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

    \( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

    \( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

    \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

    \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

    \(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
    Objetivos de aprendizaje

    Al final de esta sección, podrás:

    • Nombrar y escribir decimales
    • Decimales redondos
    • Sumar y restar decimales
    • Multiplicar y dividir decimales
    • Convertir decimales, fracciones y porcentajes
    Nota

    Una introducción más completa a los temas tratados en esta sección se puede encontrar en el capítulo Preálgebra, Decimales.

    Nombrar y escribir decimales

    Los decimales son otra forma de escribir fracciones cuyos denominadores son poderes de 10.

    \[\begin{array} {ll} {0.1 = \frac { 1 } { 10 }} &{0.1 \text { is "one tenth" }} \\ {0.01 = \frac { 1 } { 100 }} &{0.01 \text { is "one hundredth }} \\ {0.001 = \frac { 1 } { 1,000 }} &{0.001 \text { is "one thousandth }} \\ {0.0001 = \frac { 1 } { 10,000 }} &{0.0001 \text { is "one ten-thousandth" }} \end{array}\]

    Observe que “diez mil” es un número mayor que uno, pero “uno diez mil th” es un número menor que uno. El “th” al final del nombre te dice que el número es menor que uno.

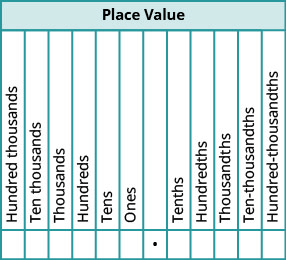
    Cuando nombramos un número entero, el nombre corresponde al valor posicional basado en las potencias de diez. Leemos 10 mil como “diez mil” y 10 millones como “diez millones”. De igual manera, los nombres de los decimales corresponden a sus valores de fracción. La figura\(\PageIndex{1}\) muestra los nombres de los valores posicionales a la izquierda y derecha del punto decimal.

    Se muestra una tabla con el título Valor posicional. De izquierda a derecha la fila dice “Cien miles”, “Diez miles”, “Miles”, “Cientos”, “Decenas” y “unos”. Después hay una celda en blanco y debajo de ella hay un punto decimal. A la derecha de esto, las celdas dicen “Décimas”, “Centésimas”, “Milésimas”, “Diez milésimas” y “Cientos milésimas”.
    Figura\(\PageIndex{1}\): El valor posicional de los números decimales se muestran a la izquierda y derecha del punto decimal.
    Ejercicio\(\PageIndex{1}\)

    Nombra el decimal\(4.3\).

    Responder

    Se da una tabla con cuatro pasos. Adicionalmente, se da el número 4.3. El primer paso dice “Paso 1. Nombra el número a la izquierda del punto decimal”. A la derecha de ésta, se observa que “4 está a la izquierda del punto decimal”. A la derecha de esto, se lee “cuatro” seguido de un gran espacio en blanco.El segundo paso dice “Paso 2. Escribe 'y' para el punto decimal”. A la derecha de esto se lee “cuatro y” seguido de un espacio en blanco.El tercer paso dice “Paso 3. Nombra la parte del 'número' a la derecha del punto decimal como si se tratara de un número entero”. A la derecha de esto, dice “3 está a la derecha del punto decimal”. A la derecha de esto, se lee “cuatro y tres” seguido de un espacio en blanco.Por último, el último paso dice “Paso 4. Nombrar el lugar decimal”. A la derecha de esto, se lee “cuatro y tres décimas”.

    Ejercicio\(\PageIndex{2}\)

    Nombra el decimal\(6.7\).

    Responder

    seis y siete décimas

    Ejercicio\(\PageIndex{3}\)

    Nombra el decimal\(5.8\).

    Responder

    cinco y ocho décimas

    A continuación resumimos los pasos necesarios para nombrar un decimal.

    NOMBRE DECIMAL.
    1. Nombra el número a la izquierda del punto decimal.
    2. Escriba “y” para el punto decimal.
    3. Nombra la parte “número” a la derecha del punto decimal como si se tratara de un número entero.
    4. Nombra el lugar decimal del último dígito.
    Ejercicio\(\PageIndex{4}\)

    Nombra el decimal:\(−15.571\).

    Responder
      \(−15.571\)
    Nombra el número a la izquierda del punto decimal. menos quince __________________________________
    Escriba “y” para el punto decimal. menos quince y ______________________________
    Nombra el número a la derecha del punto decimal. menos quince quinientos setenta y uno __________
    El\(1\) está en el lugar milésimas. menos quince quinientos setenta y una milésimas
    Ejercicio\(\PageIndex{5}\)

    Nombra el decimal:\(−13.461\).

    Responder

    menos trece cuatrocientos sesenta y una milésimas

    Ejercicio\(\PageIndex{6}\)

    Nombra el decimal:\(−2.053\).

    Responder

    menos dos y cincuenta y tres milésimas

    Cuando escribimos un cheque escribimos tanto los números como el nombre del número. Veamos cómo escribir el decimal a partir del nombre.

    Ejercicio\(\PageIndex{7}\): How to Write decimals

    Escribe “catorce y veinticuatro milésimas” como decimal.

    Responder

    Se da una tabla con cuatro pasos. El primer paso dice “Paso 1. Busque la obra 'y' — localiza el punto decimal. Coloque un punto decimal debajo de la palabra 'y'. Traduzca las palabras antes de 'y' al número entero y colóquelo a la izquierda del punto decimal”. A la derecha de esto, tenemos las palabras “catorce y veinticuatro milésimas”. Debajo de esta palabra, tenemos “catorce y veinticuatro milésimas” con la palabra “y” subrayada. Debajo de esta palabra, tenemos un pequeño espacio en blanco separado de un espacio en blanco más grande por un punto decimal. Debajo de esto, tenemos 14 en el pequeño espacio en blanco seguido del punto decimal y el espacio en blanco más grande.El segundo paso dice “Paso 2. Marcar el número de decimales necesarios a la derecha del punto decimal anotando el valor posicional indicado por la última palabra.” A la derecha de esto se lee “La última palabra es milésimas”. A la derecha de ésta se encuentra el número 14 seguido de un punto decimal y tres pequeños espacios en blanco. Bajo los espacios en blanco, se escriben las palabras “décimas”, “centésimas” y “milésimas”.El tercer paso dice “Paso 3. Traducir las palabras después de 'y' en el número a la derecha del punto decimal. Escribe el número en los espacios — poniendo el último dígito en el último lugar”. A la derecha de esto, tenemos 14 seguidos de un decimal seguido de un espacio en blanco seguido de 2 y 4 en los otros dos espacios previamente en blanco.Por último, el último paso dice “Paso 4. Rellene los ceros para los portapacios vacíos según sea necesario”. A la derecha de esto, dice “Se necesitan ceros en el décimo lugar”. A la derecha de esto, tenemos 14 seguidos de un punto decimal seguido de 0, 2 y 4, respectivamente, en los espacios en blanco. Debajo de esto, tenemos “catorce y veinticuatro milésimas está escrito 14.024”.

    Ejercicio\(\PageIndex{8}\)

    Escribir como decimal: trece y sesenta y ocho milésimas.

    Responder

    13.068

    Ejercicio\(\PageIndex{9}\)

    Escribir como decimal: cinco y noventa y cuatro milésimas.

    Responder

    5.094

    Resumimos los pasos para escribir un decimal.

    Escribe un DECIMAL.
    1. Busque la palabra “y” —localiza el punto decimal.
      • Coloque un punto decimal debajo de la palabra “y”. Traduzca las palabras antes de “y” al número entero y colóquelo a la izquierda del punto decimal.
      • Si no hay “y”, escribe un “0” con un punto decimal a su derecha.
    2. Marque el número de decimales necesarios a la derecha del punto decimal anotando el valor posicional indicado por la última palabra.
    3. Traducir las palabras después de “y” en el número a la derecha del punto decimal. Escribe el número en los espacios, poniendo el último dígito en el último lugar.
    4. Rellene ceros para los portalugares según sea necesario.

    Decimales Redondos

    Redondear decimales es muy parecido a redondear números enteros. Redondearemos decimales con un método basado en el que usamos para redondear números enteros.

    Ejercicio\(\PageIndex{10}\)

    Vuelta 18.379 a la centésima más cercana.

    Responder

    Se da una tabla con cuatro pasos. El primer paso dice “Paso 1: Localiza el valor posicional dado y márcalo con una flecha”. A la derecha de esto, tenemos el número 18.379; encima de él, están las palabras cientos lugar, que tiene una flecha apuntando a la 7.El segundo paso dice “Paso 2. Subrayar el dígito a la derecha del valor posicional dado”. A la derecha de esto, tenemos 18.379 con los 9 subrayados.El tercer paso dice “Paso 3. ¿Este dígito es mayor o igual a 5? Debajo de esto se lee: “Sí: suma 1 al dígito en el valor posicional dado”. Debajo de esto se lee: “No: no cambies el dígito en el valor posicional dado”. A la derecha de esto, dice “Porque 9 es mayor o igual que” A la derecha de esto, tenemos el número 18.379 con el 9 marcado como “eliminar” y el 7 marcado como “agregar 1”.Por último, el último paso dice “Paso 4. Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo”. A la derecha de esto, tenemos 18.38 seguido de “18.38 es 18.379 redondeado a la centésima más cercana”.

    Ejercicio\(\PageIndex{11}\)

    Vuelta a la centésima más cercana: 1.047.

    Responder

    1.05

    Ejercicio\(\PageIndex{12}\)

    Vuelta a la centésima más cercana: 9.173.

    Responder

    9.17

    Resumimos aquí los pasos para redondear un decimal.

    DECIALES REDONDOS.
    1. Localice el valor posicional dado y márquelo con una flecha.
    2. Subrayar el dígito a la derecha del valor posicional.
    3. ¿Este dígito es mayor o igual a 5?
      • sí: agregue 1 al dígito en el valor posicional dado.
      • no: no cambie el dígito en el valor posicional dado.
    4. Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo.
    Ejercicio\(\PageIndex{13}\)

    Vuelta 18.379 al más cercano

    1. décimo
    2. número entero.
    Responder

    Redonda 18.379

    1. al décimo más cercano

    Localiza el décimo lugar con una flecha. .
    Subrayar el dígito a la derecha del valor posicional dado. .
    Debido a que 7 es mayor o igual a 5, agregue 1 al 3. .
    Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo. .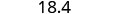
    Observe que los dígitos eliminados NO fueron reemplazados por ceros. Entonces, 18.379 redondeado a la décima más cercana es 18.4.


    2. al número entero más cercano
    Localiza el lugar con una flecha. .
    Subrayar el dígito a la derecha del valor posicional dado. .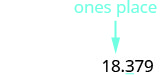
    Dado que 3 no es mayor ni igual a 5, no agregue 1 al 8. .
    Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo. .
      Entonces, 18.379 redondeado al número entero más cercano es 18.
    Ejercicio\(\PageIndex{14}\)

    Redondea 6.582 al más cercano

    1. centésima
    2. décimo
    3. número entero.
    Responder
    1. 6.58
    2. 6.6
    3. 7
    Ejercicio\(\PageIndex{15}\)

    Vuelta 15.2175 al más cercano

    1. milésima
    2. centésima
    3. décima.
    Responder
    1. 15.218
    2. 15.22
    3. 15.2

    Sumar y restar decimales

    Para sumar o restar decimales, alineamos los puntos decimales. Al alinear los puntos decimales de esta manera, podemos sumar o restar los valores posicionales correspondientes. Luego sumamos o restamos los números como si fueran números enteros y luego colocamos el punto decimal en la suma.

    SUMA O RESTAR DECIMALES.
    1. Escribe los números para que los decimales se alineen verticalmente.
    2. Use ceros como portaobjetos, según sea necesario.
    3. Sumar o restar los números como si fueran números enteros. Luego coloque el punto decimal en la respuesta debajo de los puntos decimales en los números dados.
    Ejercicio\(\PageIndex{16}\)

    Agregar:\(23.5+41.38\).

    Responder

    \[\text{Write the numbers so that the decimal points line up vertically.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Put 0 as a placeholder after the 5 in 23.5. Remember, } \frac{5}{10} = \frac{50}{100}, \text{ so } 0.5 = 0.50 \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline \end{array}\]
    \[\text{Add the numbers as if they were whole numbers . Then place the decimal point in the sum.} \quad \begin{array} {r} { 23.50 } \\ { + 41.38 } \\ \hline 64.88 \end{array}\]

    Ejercicio\(\PageIndex{17}\)

    Agregar:\(4.8+11.69\).

    Responder

    \(16.49\)

    Ejercicio\(\PageIndex{18}\)

    Agregar:\(5.123+18.47\).

    Responder

    \(23.593\)

    Ejercicio\(\PageIndex{19}\)

    Restar:\(20−14.65\).

    Responder

    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {20 - 14.65} \\ {20.} \\ {-14.65} \\ \hline \end{align}} \\ {\text{Remember, 20 is a whole number, so place the decimal point after the 0.}} &{} \end{array}\]
    \[\begin{array} {ll} {\text{Put zeros to the right as placeholders.}} &{ \begin{align} {20.00} \\ {-14.65} \\ \hline \end{align}} \end{array}\]
    \[\begin{array} {ll} {\text{Write the numbers so that the decimal points line up vertically.}} &{ \begin{align} {\tiny{9} \quad \tiny{9}\qquad} \\ {\small{1} \not{\small{10}} \not{\small10}\not{\small10}}\\ {\not{2}\not{0.}\not{0}\not{0}} \\ {-14.65} \\ \hline \\{5.35} \end{align}} \end{array}\]

    Ejercicio\(\PageIndex{20}\)

    Restar:\(10−9.58\).

    Responder

    0.42

    Ejercicio\(\PageIndex{21}\)

    Restar:\(50−37.42\).

    Responder

    12.58

    Multiplicar y dividir decimales

    Multiplicar decimales es muy parecido a multiplicar números enteros, solo tenemos que determinar dónde colocar el punto decimal. El procedimiento para multiplicar decimales tendrá sentido si primero los convertimos a fracciones y luego multiplicamos.

    Entonces veamos qué obtendríamos como producto de los decimales al convertirlos primero en fracciones. Haremos dos ejemplos uno al lado del otro. ¡Busca un patrón!

      .

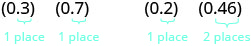    Convertir a fracciones.    		 .
    Multiplicar. .
    Convertir a decimales. .
    Mesa\(\PageIndex{1}\)

    Observe, en el primer ejemplo, multiplicamos dos números que cada uno tenía un dígito después del punto decimal y el producto tenía dos decimales. En el segundo ejemplo, multiplicamos un número con un decimal por un número con dos decimales y el producto tenía tres decimales.

    Multiplicamos los números así como hacemos números enteros, ignorando temporalmente el punto decimal. Luego contamos el número de puntos decimales en los factores y esa suma nos dice el número de decimales en el producto.

    Las reglas para multiplicar números positivos y negativos también se aplican a los decimales, ¡claro!

    Al multiplicar dos números,

    • si sus signos son los mismos el producto es positivo.
    • si sus signos son diferentes el producto es negativo.

    Cuando multiplicamos decimales firmados, primero determinamos el signo del producto y luego multiplicamos como si los números fueran ambos positivos. Por último, escribimos el producto con el letrero correspondiente.

    Multiplicar decimales.
    1. Determinar el signo del producto.
    2. Escribe en formato vertical, alineando los números de la derecha. Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales.
    3. Coloque el punto decimal. El número de decimales en el producto es la suma del número de decimales en los factores.
    4. Escriba el producto con el letrero correspondiente.
    Ejercicio\(\PageIndex{22}\)

    Multiplicar:\((−3.9)(4.075)\).

    Responder
      \((−3.9)(4.075)\)
    Los signos son diferentes. El producto será negativo.  
    Escribe en formato vertical, alineando los números de la derecha. .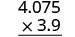
    Multiplicar. .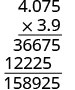
    Suma el número de decimales en los factores\((1 + 3)\).

    .
    Coloque el punto decimal a 4 lugares de la derecha.    		 .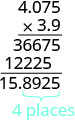
    Los signos son diferentes, por lo que el producto es negativo. \((−3.9)(4.075) = −15.8925\)
    Ejercicio\(\PageIndex{23}\)

    Multiplicar:\(−4.5(6.107)\).

    Responder

    \(−27.4815\)

    Ejercicio\(\PageIndex{24}\)

    Multiplicar: −10.79 (8.12).

    Responder

    \(−87.6148\)

    En muchas de tus otras clases, especialmente en las ciencias, multiplicarás decimales por potencias de 10 (10, 100, 1000, etc.). Si multiplica algunos productos en papel, puede notar un patrón que relaciona el número de ceros en la potencia de 10 al número de decimales movemos el punto decimal a la derecha para obtener el producto.

    MULTIPLICA UN DECIMAL POR UN PODER DE
    1. Mueve el punto decimal hacia la derecha el mismo número de lugares que el número de ceros en la potencia de 10.
    2. Agrega ceros al final del número según sea necesario.
    Ejercicio\(\PageIndex{25}\)

    Multiplicar 5.63

    1. por 10
    2. por 100
    3. por 1,000.
    Responder

    Al observar el número de ceros en el múltiplo de diez, vemos el número de lugares que necesitamos para mover el decimal a la derecha.

    ⓐ

      \(5.63(10)\)
    Hay 1 cero en 10, así que mueve el punto decimal 1 lugar a la derecha. .

    ⓑ

      \(5.63(100)\)
    Hay 2 ceros en 100, así que mueve el punto decimal 2 lugares hacia la derecha. .

    ⓒ

       
    Hay 3 ceros en 1,000, así que mueve el punto decimal 3 lugares a la derecha. .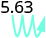
    Se debe agregar un cero al final. .
    Ejercicio\(\PageIndex{26}\)

    Multiplicar 2.58

    1. por 10
    2. por 100
    3. por 1,000.
    Responder
    1. 25.8
    2. 258
    3. 2,580
    Ejercicio\(\PageIndex{27}\)

    Multiplicar 14.2

    1. por 10
    2. por 100
    3. por 1,000.
    Responder
    1. 142
    2. 1,420
    3. 14,200

    Al igual que con la multiplicación, la división de decimales es muy parecida a dividir números enteros. Sólo tenemos que averiguar dónde se debe colocar el punto decimal.

    Para dividir decimales, determinar por qué poder de 10 multiplicar el denominador para convertirlo en un número entero. Después multiplica el numerador por esa misma potencia de 10. Debido a la propiedad de fracciones equivalentes, ¡no hemos cambiado el valor de la fracción! El efecto es mover los puntos decimales en el numerador y denominador el mismo número de lugares a la derecha. Por ejemplo:

    \[\begin{array} { c } { \frac { 0.8 } { 0.4 } } \\ { \frac { 0.8 ( 10 ) } { 0.4 ( 10 ) } } \\ { \frac { 8 } { 4 } } \end{array}\]

    También usamos las reglas para dividir números positivos y negativos con decimales. Al dividir decimales firmados, primero determinar el signo del cociente y luego dividir como si los números fueran ambos positivos. Por último, escribir el cociente con el signo correspondiente.

    Revisamos la notación y vocabulario para la división:

    \[\begin{array} {ll} {} &{\underset{\text{quotient}}{c}} \\ {\underset{\text{dividend}}{a} \div \underset{\text{divisor}}{b} = \underset{\text{quotient}}{c}} & {\underset{\text{divisor}}{b})\overline{\underset{\text{dividend}}{a}}} \end{array}\]

    Escribiremos los pasos a seguir al dividir decimales, para facilitar la referencia.

    Divide decimales.
    1. Determinar el signo del cociente.
    2. Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. “Mueve” el punto decimal en el dividendo el mismo número de lugares, agregando ceros según sea necesario.
    3. Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.
    4. Escriba el cociente con el signo correspondiente.
    Ejercicio\(\PageIndex{28}\)

    Dividir:\(−25.65\div (−0.06)\).

    Responder

    Recuerda, puedes “mover” los decimales en el divisor y dividendo debido a la Propiedad de Fracciones Equivalentes.

      \(−25.65\div (−0.06)\)
    Los signos son los mismos. El cociente es positivo.
    Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha.  
    “Mover” el punto decimal en el dividendo el mismo número de lugares. .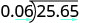
    Dividir.
    Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.    		 .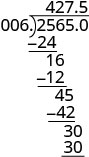
    Escriba el cociente con el signo correspondiente. \(−25.65\div (−0.06) = 427.5\)
    Ejercicio\(\PageIndex{29}\)

    Dividir:\(−23.492\div (−0.04)\).

    Responder

    687.3

    Ejercicio\(\PageIndex{30}\)

    Dividir:\(−4.11\div(−0.12)\).

    Responder

    34.25

    Una aplicación común de dividir números enteros en decimales es cuando queremos encontrar el precio de un artículo que se vende como parte de un paquete múltiple. Por ejemplo, supongamos que un caso de 24 botellas de agua cuesta\($3.99\). Para encontrar el precio de una botella de agua, dividiríamos\($3.99\) por 24. Mostramos esta división en Ejercicio\(\PageIndex{31}\). En los cálculos con dinero, redondearemos la respuesta al centavo más cercano (centésima).

    Ejercicio\(\PageIndex{31}\)

    Dividir:\($3.99\div 24\).

    Responder
    Se da .99 dividido por 24. Un problema de división larga se configura con 24 dividiendo 3.99. Se da una tabla con indicaciones a la izquierda y los pasos matemáticos a la derecha. El primer paso dice “Colocar el punto decimal en el cociente por encima del punto decimal en el dividendo. Dividir como de costumbre. ¿Cuándo paramos? Dado que esta división involucra dinero, lo redondeamos al centavo más cercano (centésima). Para ello, debemos llevar la división al lugar milésimas”. A la derecha de esto, tenemos un problema de división larga configurado con 24 dividiendo 3.990. El cociente se da como 0.166. Para mostrar la obra, por debajo de 3.990 se lee 24, línea horizontal continua, 159, 144, línea horizontal continua, 150, 144, línea horizontal continua, y finalmente 6. El quinto paso dice “Redondear al centavo más cercano”. A la derecha de esto, tenemos $0.166 es aproximadamente igual a $0.17 y por lo tanto >.99 dividido por 24 es $0.17”. >
      \($3.99\div 24\)
    Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.  
    Dividir como de costumbre.
    ¿Cuándo paramos? Dado que esta división involucra dinero, lo redondeamos al centavo más cercano (centésima.) Para ello, debemos llevar la división al lugar milésimas.    		 .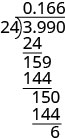
    Redondear al centavo más cercano. \($0.166\approx $0.17\)
    \($3.99\div 2\approx $0.17\)
    Ejercicio\(\PageIndex{32}\)

    Dividir:\($6.99\div 36\).

    Responder

    \($0.19\)

    Ejercicio\(\PageIndex{33}\)

    Dividir:\($4.99\div 12\).

    Responder

    \($0.42\)

    Convertir decimales, fracciones y porcentajes

    Convertimos decimales en fracciones identificando el valor posicional del último dígito (más a la derecha). En el decimal 0.03 el 3 está en el lugar centésimas, por lo que 100 es el denominador de la fracción equivalente a 0.03.

    \[00.03 = \frac { 3 } { 100 }\]

    Observe, cuando el número a la izquierda del decimal es cero, obtenemos una fracción cuyo numerador es menor que su denominador. Fracciones como esta se llaman fracciones propias.

    Los pasos a seguir para convertir un decimal a una fracción se resumen en el cuadro de procedimiento.

    CONVERTIR UN DECIMAL A UNA FRAC
    1. Determinar el valor posicional del dígito final.
    2. Escribe la fracción.
      • numerador—los “números” a la derecha del punto decimal
      • denominador—el valor posicional correspondiente al dígito final
    Ejercicio\(\PageIndex{34}\)

    Escribe 0.374 como fracción.

    Responder
      0.374
    Determinar el valor posicional del dígito final. .

    Escribe la fracción para 0.374:

    • El numerador es 374.
    • El denominador es 1,000.
    		 \(\dfrac{374}{1000}\)
    Simplifica la fracción. \(\dfrac{2\cdot 187}{2\cdot 500}\)
    Dividir los factores comunes. \(\dfrac{187}{500}\)
    entonces,\(0.374=\dfrac{187}{500}\)

    ¿Notó que el número de ceros en el denominador de\(\dfrac{374}{1000}\) es el mismo que el número de decimales en 0.374?

    Ejercicio\(\PageIndex{35}\)

    Escribe 0.234 como fracción.

    Responder

    \(\dfrac{117}{500}\)

    Ejercicio\(\PageIndex{36}\)

    Escribe 0.024 como fracción.

    Responder

    \(\dfrac{3}{125}\)

    Hemos aprendido a convertir decimales en fracciones. Ahora haremos lo contrario: convertir fracciones a decimales. Recuerda que la barra de fracción significa división. Entonces\(\dfrac{4}{5}\) se puede escribir\(4\div 5\) o\(5)\overline{4}\). Esto lleva al siguiente método para convertir una fracción a un decimal.

    CONVERTIR UNA FRACCIÓN A DECI

    Para convertir una fracción a decimal, divida el numerador de la fracción por el denominador de la fracción.

    Ejercicio\(\PageIndex{37}\)

    Escribir\(-\dfrac{5}{8}\) como decimal.

    Responder

    Dado que una barra de fracción significa división, comenzamos por escribir\(\dfrac{5}{8}\) como\(8)\overline{5}\). Ahora divide.

    Este es un problema de división larga con 8 dividiendo 5.000 y 0.625 como cociente. Por debajo de 5.000 tenemos 48, una línea horizontal sólida, 20, 16, una línea horizontal sólida, 40, y una línea horizontal final. Entonces cinco octavos equivale a 0.625.

    Ejercicio\(\PageIndex{38}\)

    Escribir\(-\dfrac{7}{8}\) como decimal.

    Responder

    −0.875

    Ejercicio\(\PageIndex{39}\)

    Escribir\(-\dfrac{3}{8}\) como decimal.

    Responder

    −0.375

    Cuando dividimos, no siempre obtendremos un resto cero. A veces el cociente termina con un decimal que se repite. Un decimal repetido es un decimal en el que el último dígito o grupo de dígitos se repite sin cesar. Se coloca una barra sobre el bloque repetido de dígitos para indicar que se repite.

    DECIMAL

    Un decimal repetido es un decimal en el que el último dígito o grupo de dígitos se repite sin cesar.

    Se coloca una barra sobre el bloque repetido de dígitos para indicar que se repite.

    Ejercicio\(\PageIndex{40}\)

    Escribir\(\dfrac{43}{22}\) como decimal.

    Responder

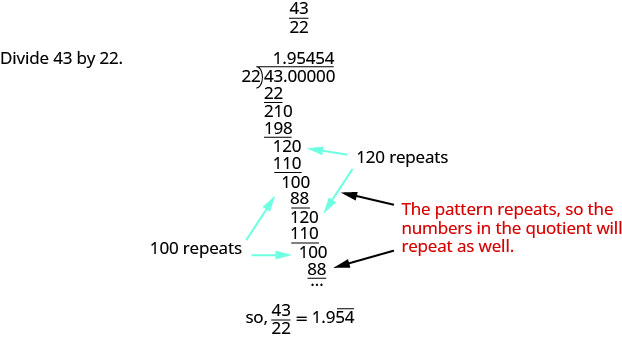
    Se da el número 43/22. Se le da la dirección a “Dividir 43 por 22”. Se da un problema de división larga con 22 dividiendo 43.00000 con 1.95454 como cociente. Por debajo de 43.00000 tenemos 22, una línea horizontal sólida, 210, 198, una línea horizontal continua, 120, 110, una línea horizontal, 100, 88, una línea horizontal continua, 120, 110, una línea horizontal continua, 100, 88, una línea horizontal sólida, y luego tres puntos. Se observa que las 120 repeticiones y que las 100 repeticiones. Esto se explica con más detalle como “El patrón se repite, por lo que los números en el cociente también se repetirán. Al final, se nos da la afirmación de que 43/22 equivale a 1.954 con una pequeña línea horizontal sobre la 54.

    Ejercicio\(\PageIndex{41}\)

    Escribir\(\dfrac{27}{11}\) como decimal.

    Responder

    \(2.\overline{45}\)

    Ejercicio\(\PageIndex{42}\)

    Escribir\(\dfrac{51}{22}\) como decimal.

    Responder

    \(2.3\overline{18}\)

    A veces podemos tener que simplificar expresiones con fracciones y decimales juntos.

    Ejercicio\(\PageIndex{43}\)

    Simplificar:\(\dfrac{7}{8}+6.4\).

    Responder

    Primero debemos cambiar un número para que ambos números estén en la misma forma. Podemos cambiar la fracción a un decimal, o cambiar el decimal a una fracción. Por lo general, es más fácil cambiar la fracción a un decimal.

        \(\dfrac{7}{8}+6.4\)
    Cambiar\(\dfrac{7}{8}\) a un decimal. .  
    Agregar.   \(0.875+6.4\)
        \(7.275\)
        Entonces,\(\dfrac{7}{8}+6.4 = 7.275\)
    Ejercicio\(\PageIndex{44}\)

    Simplificar:\(\dfrac{3}{8}+4.9\).

    Responder

    \(5.275\)

    Ejercicio\(\PageIndex{45}\)

    Simplificar:\(5.7 + \dfrac{13}{20}\).

    Responder

    \(6.35\)

    Un por ciento es una relación cuyo denominador es 100. Porcentaje de medias por cien. Utilizamos el símbolo de porcentaje,%, para mostrar el porcentaje.

    POR CIENTO

    Un por ciento es una relación cuyo denominador es 100.

    Dado que un porcentaje es una relación, se puede expresar fácilmente como una fracción. Porcentaje de medias por 100, por lo que el denominador de la fracción es 100. Luego cambiamos la fracción a un decimal dividiendo el numerador por el denominador.

    \[\begin{array} {llll} {} &{\text{6%}} &{\text{78%}} &{\text{135%}} \\ {\text { Write as a ratio with denominator } 100. } &{\dfrac{6}{100}} &{\dfrac{78}{100}} &{\dfrac{135}{100}} \\ { \text { Change the fraction to a decimal by dividing}} &{0.06} &{0.78} &{1.35}\\ {\text{the numerator by the denominator.}} &{} &{} &{} \end{array}\]

    ¿Ves el patrón? Para convertir un número porcentual a un número decimal, movemos el punto decimal dos lugares hacia la izquierda.

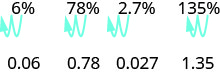
    La primera parte de esta figura muestra 6% con una flecha dibujada entre el 6 y el signo porcentual al espacio a la izquierda de 6 y luego al espacio más a la izquierda de ese espacio. Debajo de esto, se da el número 0.06. La segunda parte de esta figura muestra 78% con una flecha dibujada de entre el 8 y el signo porcentual al espacio entre el 7 y el 8 y luego al espacio a la izquierda del 7. Debajo de esto, se da el número 0.78. La tercera parte de esta figura muestra 2.7% con una flecha dibujada desde el punto decimal hasta el espacio a la izquierda del 2 y luego al espacio más a la izquierda de ese espacio. Debajo de esto, se da el número 0.027. La cuarta parte de esta figura muestra 135% con una flecha dibujada de entre el 5 y el signo porcentual al espacio entre 3 y 5 y luego al espacio entre 1 y 3. Debajo de esto, se da el número 1.35.
    Figura\(\PageIndex{2}\)
    Ejercicio\(\PageIndex{46}\)

    Convertir cada porcentaje a un decimal:

    1. 62%
    2. 135%
    3. 35.7%.
    Responder
    1.  
      .
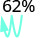
    Mueve el punto decimal dos lugares hacia la izquierda. 0.62
    2.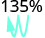  
      .
    Mueve el punto decimal dos lugares hacia la izquierda. 1.35
    3.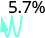  
      .
    Mueve el punto decimal dos lugares hacia la izquierda. 0.057
    Ejercicio\(\PageIndex{47}\)

    Convertir cada porcentaje a un decimal:

    1. 9%
    2. 87%
    3. 3.9%.
    Responder
    1. 0.09
    2. 0.87
    3. 0.039
    Ejercicio\(\PageIndex{48}\)

    Convertir cada porcentaje a un decimal:

    1. 3%
    2. 91%
    3. 8.3%.
    Responder
    1. 0.03
    2. 0.91
    3. 0.083

    Convertir un decimal a un porcentaje tiene sentido si recordamos la definición de porcentaje y tenemos en mente el valor posicional.

    Para convertir un decimal a un por ciento, recuerde que por ciento significa por cien. Si cambiamos el decimal a una fracción cuyo denominador es 100, es fácil cambiar esa fracción a un porcentaje.

    \[\begin{array} {llll} {} &{0.83} &{1.05} &{0.075} \\ {\text {Write as a fraction }} &{\frac{83}{100}} &{\small{1}\frac{5}{100}} &{\frac{75}{1000}} \\ { \text {The denominator is 100.}} &{} &{\frac{105}{100}} &{\frac{7.5}{100}}\\ {\text{Write the ratio as a percent.}} &{\text{83%}} &{\text{105%}} &{\text{7.5%}} \end{array}\]

    ¿Reconoces el patrón? Para convertir un decimal a un porcentaje, movemos el punto decimal dos lugares a la derecha y luego agregamos el signo de porcentaje.

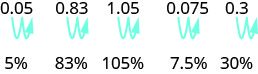
    La primera parte de esta figura muestra 0.05 con una flecha dibujada desde el punto decimal hasta el espacio entre 0 y 5 y luego al espacio posterior al 5. Debajo de esto, se da el número 5%. La segunda parte de esta figura muestra 0.83 con una flecha dibujada desde el punto decimal hasta el espacio entre 8 y 3 y luego al espacio posterior al 3. Debajo de esto, se da el número 83%. La tercera parte de esta figura muestra 1.05 con una flecha dibujada desde el punto decimal hasta el espacio entre 0 y 5 y luego al espacio posterior al 5. Debajo de esto, se da el número 105%. La cuarta parte de esta figura muestra 0.075 con una flecha dibujada desde el punto decimal hasta el espacio entre 0 y 7 y luego al espacio entre 7 y 5. Debajo de esto, se da el número 7.5%. La quinta parte de esta figura muestra 0.3 con una flecha dibujada desde el punto decimal hasta el espacio después de 3 y luego al espacio más a la derecha de ese 3. Debajo de esto, se da el número 30%.
    Figura\(\PageIndex{3}\)
    Ejercicio\(\PageIndex{49}\)

    Convertir cada decimal a un porcentaje:

    1. 0.51
    2. 1.25
    3. 0.093.
    Responder
    1.  
      .
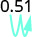
    Mueve el punto decimal dos lugares a la derecha. \(51%\)
    2.  
      .
    Mueve el punto decimal dos lugares a la derecha. \(125%\)
    3.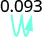  
      .
    Mueve el punto decimal dos lugares a la derecha. \(9.3%\)
    Ejercicio\(\PageIndex{50}\)

    Convertir cada decimal a un porcentaje:

    1. 0.17
    2. 1.75
    3. 0.0825
    Responder
    1. 17%
    2. 175%
    3. 8.25%
    Ejercicio\(\PageIndex{51}\)

    Convertir cada decimal a un porcentaje:

    1. 0.41
    2. 2.25
    3. 0.0925.
    Responder
    1. 41%
    2. 225%
    3. 9.25%

    Conceptos clave

    • Nombrar un decimal
      1. Nombra el número a la izquierda del punto decimal.
      2. Escribe” y” para el punto decimal.
      3. Nombra la parte “número” a la derecha del punto decimal como si se tratara de un número entero.
      4. Nombra el lugar decimal del último dígito.
    • Escribir un decimal
      1. Busque la palabra 'y', localiza el punto decimal. Coloque un punto decimal debajo de la palabra 'y'. Traduzca las palabras antes de 'y' al número entero y colóquelo a la izquierda del punto decimal. Si no hay “y”, escribe un “0” con un punto decimal a su derecha.
      2. Marque el número de decimales necesarios a la derecha del punto decimal anotando el valor posicional indicado por la última palabra.
      3. Traducir las palabras después de 'y' en el número a la derecha del punto decimal. Escribe el número en los espacios, poniendo el último dígito en el último lugar.
      4. Rellene ceros para los portalugares según sea necesario.
    • Redondear un decimal
      1. Localice el valor posicional dado y márquelo con una flecha.
      2. Subrayar el dígito a la derecha del valor posicional.
      3. ¿Este dígito es mayor o igual a 5? sí: agregue 1 al dígito en el valor posicional dado. no: no cambie el dígito en el valor posicional dado.
      4. Reescribe el número, eliminando todos los dígitos a la derecha del dígito de redondeo.
    • Suma o resta decimales
      1. Escribe los números para que los decimales se alineen verticalmente.
      2. Use ceros como portaobjetos, según sea necesario.
      3. Sumar o restar los números como si fueran números enteros. Luego coloque el decimal en la respuesta debajo de los puntos decimales en los números dados.
    • Multiplicar decimales
      1. Determinar el signo del producto.
      2. Escribe en formato vertical, alineando los números de la derecha. Multiplique los números como si fueran números enteros, ignorando temporalmente los decimales.
      3. Coloque el punto decimal. El número de decimales en el producto es la suma de los decimales en los factores.
      4. Escriba el producto con el letrero correspondiente.
    • Multiplicar un decimal por una potencia de diez
      1. Mueve el punto decimal hacia la derecha el mismo número de lugares que el número de ceros en la potencia de 10.
      2. Agrega ceros al final del número según sea necesario.
    • Dividir decimales
      1. Determinar el signo del cociente.
      2. Haz del divisor un número entero “moviendo” el punto decimal todo el camino hacia la derecha. “Mover” el punto decimal en el dividendo el mismo número de lugares - agregando ceros según sea necesario.
      3. Dividir. Coloque el punto decimal en el cociente por encima del punto decimal en el dividendo.
      4. Escriba el cociente con el signo correspondiente.
    • Convertir un decimal a una fracción apropiada
      1. Determinar el valor posicional del dígito final.
      2. Escribe la fracción: numerador—los 'números' a la derecha del punto decimal; denominador—el valor posicional correspondiente al dígito final.
    • Convertir una Fracción a Decimal Divide el numerador de la fracción por el denominador.

    This page titled 1.8: Decimales is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform.