5.6: Decimales y Fracciones (Parte 2)
- Page ID
- 114297
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Encuentra la Circunferencia y el Área de Círculos
Las propiedades de los círculos han sido estudiadas desde hace más de 2 mil años. Todos los círculos tienen exactamente la misma forma, pero sus tamaños se ven afectados por la longitud del radio, un segmento de línea desde el centro hasta cualquier punto del círculo. Un segmento de línea que pasa por el centro de un círculo conectando dos puntos en el círculo se llama diámetro. El diámetro es el doble de largo que el radio. Ver Figura\(\PageIndex{1}\).
El tamaño de un círculo se puede medir de dos maneras. La distancia alrededor de un círculo se llama su circunferencia.

Figura\(\PageIndex{1}\)
Arquímedes descubrió que para círculos de todos los tamaños diferentes, dividir la circunferencia por el diámetro siempre da el mismo número. El valor de este número es pi, simbolizado por letra griega\(\pi\) (pastel pronunciado). Sin embargo, el valor exacto de\(\pi\) no se puede calcular ya que el decimal nunca termina ni se repite (aprenderemos más sobre números como este en Las propiedades de los números reales).
Si queremos la circunferencia exacta o área de un círculo, dejamos el símbolo\(\pi\) en la respuesta. Podemos obtener una respuesta aproximada sustituyendo 3.14 como valor de\(\pi\). Utilizamos el símbolo ≈ para mostrar que el resultado es aproximado, no exacto.
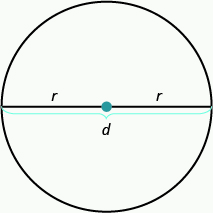
r es la longitud del radio.
d es la longitud del diámetro.
La circunferencia es de 2\(\pi\) r.\[C = 2 \pi r\]
El área es\(\pi\) r 2. \[A = \pi r^{2}\]
Dado que el diámetro es el doble del radio, otra forma de encontrar la circunferencia es usar la fórmula C =\(\pi\) d.
Supongamos que queremos encontrar el área exacta de un círculo de radio 10 pulgadas. Para calcular el área, evaluaríamos la fórmula para el área cuando r = 10 pulgadas y dejaríamos la respuesta en términos de\(\pi\).
\[\begin{split} A & = \pi r^{2} \\ A & = \pi (10^{2}) \\ A & = \pi \cdot 100 \end{split}\]
Escribimos\(\pi\) después de los 100. Entonces el valor exacto del área es A = 100 pulgadas\(\pi\) cuadradas. Para aproximar el área, sustituiríamos\(\pi\) ≈ 3.14.
\[\begin{split} A & = 100 \pi \\ & \approx 100 \cdot 3.14 \\ & \approx 314\; square\; inches \end{split}\]
Recuerde usar unidades cuadradas, como pulgadas cuadradas, cuando calcule el área.
Un círculo tiene un radio de 10 centímetros. Aproximar su (a) circunferencia y (b) área.
Solución
(a) Encuentra la circunferencia cuando r = 10.
| Escribe la fórmula para la circunferencia. | C = 2\(\pi\) r |
| Sustituto 3.14 para\(\pi\) y 10 para r. | C ≈ 2 (3.14) (10) |
| Multiplicar. | C ≈ 62.8 centímetros |
(b) Encontrar el área cuando r = 10.
| Escribe la fórmula para el área. | A =\(\pi\) r 2 |
| Sustituto 3.14 para\(\pi\) y 10 para r. | A ≈ (3.14) (10) 2 |
| Multiplicar. | A ≈ 314 centímetros cuadrados |
Un círculo tiene un radio de 50 pulgadas. Aproximar su (a) circunferencia y (b) área.
- Contestar a
-
314 in.
- Respuesta b
-
7850 sq. in.
Un círculo tiene un radio de 100 pies. Aproximar su (a) circunferencia y (b) área.
- Contestar a
-
628 pies
- Respuesta b
-
31,400 pies cuadrados
Un círculo tiene un radio de 42.5 centímetros. Aproximar su (a) circunferencia y (b) área.
Solución
(a) Encuentra la circunferencia cuando r = 42.5.
| Escribe la fórmula para la circunferencia. | C = 2\(\pi\) r |
| Sustituir 3.14 para\(\pi\) y 42.5 por r. | C ≈ 2 (3.14) (42.5) |
| Multiplicar. | C ≈ 266.9 centímetros |
(b) Encontrar el área cuando r = 42.5.
| Escribe la fórmula para el área. | A =\(\pi\) r 2 |
| Sustituir 3.14 para\(\pi\) y 42.5 por r. | A ≈ (3.14) (42.5) 2 |
| Multiplicar. | A ≈ 5671.625 centímetros cuadrados |
Un círculo tiene un radio de 51.8 centímetros. Aproximar su (a) circunferencia y (b) área.
- Contestar a
-
325.304 cm
- Respuesta b
-
8425.3736 cm cuadrados
Un círculo tiene un radio de 26.4 metros. Aproximar su (a) circunferencia y (b) área.
- Contestar a
-
165.792 m
- Respuesta b
-
2188.4544 Metros cuadrados
Aproximado\(\pi\) con una Fracción
Convierte la fracción\(\dfrac{22}{7}\) a un decimal. Si usas tu calculadora, el número decimal llenará la pantalla y mostrará 3.14285714. Pero si redondeamos ese número a dos decimales, obtenemos 3.14, la aproximación decimal de\(\pi\). Cuando tenemos un círculo con radio dado como fracción, podemos sustituir\(\dfrac{22}{7}\) a 3.14.\(\pi\) Y, dado que también\(\dfrac{22}{7}\) es una aproximación de π, usaremos el símbolo ≈ para mostrar que tenemos un valor aproximado.
Un círculo tiene radio\(\dfrac{14}{15}\) metro. Aproximar su (a) circunferencia y (b) área.
Solución
(a) Encontrar la circunferencia cuando r =\(\dfrac{14}{15}\)
| Escribe la fórmula para la circunferencia. | C = 2\(\pi\) r |
| Sustituto\(\pi\) y\(\dfrac{22}{7}\)\(\dfrac{14}{15}\) para r. | $$C\ aprox 2\ izquierda (\ dfrac {22} {7}\ derecha)\ izquierda (\ dfrac {14} {15}\ derecha) $$ |
| Multiplicar. | C ≈\(\dfrac{88}{15}\) metros |
. (b) Encontrar el área cuando r =\(\dfrac{14}{15}\).
| Escribe la fórmula para el área. | A =\(\pi\) r 2 |
| Sustituto\(\pi\) y\(\dfrac{22}{7}\)\(\dfrac{14}{15}\) para r. | $$A\ aprox\ izquierda (\ dfrac {22} {7}\ derecha)\ izquierda (\ dfrac {14} {15}\ derecha) ^ {2} $$ |
| Multiplicar. | A ≈ metros\(\dfrac{616}{225}\) cuadrados |
Un círculo tiene\(\dfrac{5}{21}\) metros de radio. Aproximar su (a) circunferencia y (b) área.
- Contestar a
-
\(\frac{220}{147}\)m
- Respuesta b
- \(\frac{550}{3087}\)metros cuadrados
Un círculo tiene\(\dfrac{10}{33}\) pulgadas de radio. Aproximar su (a) circunferencia y (b) área.
- Contestar a
-
\(\frac{40}{21}\)en.
- Respuesta b
- \(\frac{200}{693}\)sq. in.
La práctica hace la perfección
Convertir fracciones a decimales
En los siguientes ejercicios, convierte cada fracción a un decimal.
- \(\dfrac{2}{5}\)
- \(\dfrac{4}{5}\)
- \(- \dfrac{3}{8}\)
- \(- \dfrac{5}{8}\)
- \(\dfrac{17}{20}\)
- \(\dfrac{13}{20}\)
- \(\dfrac{11}{4}\)
- \(\dfrac{17}{4}\)
- \(- \dfrac{310}{25}\)
- \(- \dfrac{284}{25}\)
- \(\dfrac{5}{9}\)
- \(\dfrac{2}{9}\)
- \(\dfrac{15}{11}\)
- \(\dfrac{18}{11}\)
- \(\dfrac{15}{111}\)
- \(\dfrac{25}{111}\)
En los siguientes ejercicios, simplificar la expresión.
- \(\dfrac{1}{2}\)+ 6.5
- \(\dfrac{1}{4}\)+ 10.75
- 2.4 +\(\dfrac{5}{8}\)
- 3.9 +\(\dfrac{9}{20}\)
- 9.73 +\(\dfrac{17}{20}\)
- 6.29 +\(\dfrac{21}{40}\)
Ordene Decimales y Fracciones
En los siguientes ejercicios, ordene cada par de números, utilizando < or >.
- \(\dfrac{1}{8}\)___0.8
- \(\dfrac{1}{4}\)___0.4
- \(\dfrac{2}{5}\)___0.25
- \(\dfrac{3}{5}\)___0.35
- 0.725___\(\dfrac{3}{4}\)
- 0.92___\(\dfrac{7}{8}\)
- 0.66___\(\dfrac{2}{3}\)
- 0.83___\(\dfrac{5}{6}\)
- −0.75___\(- \dfrac{4}{5}\)
- −0.44___\(- \dfrac{9}{20}\)
- \(- \dfrac{3}{4}\)___−0.925
- \(- \dfrac{2}{3}\)___−0.632
En los siguientes ejercicios, escribe cada conjunto de números en orden de menor a mayor.
- \(\dfrac{3}{5}, \dfrac{9}{16}\), 0.55
- \(\dfrac{3}{8}, \dfrac{7}{20}\), 0.36
- 0.702,\(\dfrac{13}{20}, \dfrac{5}{8}\)
- 0.15,\(\dfrac{3}{16}, \dfrac{1}{5}\)
- −0.3,\(- \dfrac{1}{3}, - \dfrac{7}{20}\)
- −0.2,\(- \dfrac{3}{20}, - \dfrac{1}{6}\)
- \(- \dfrac{3}{4}, - \dfrac{7}{9}\), −0.7
- \(- \dfrac{8}{9}, - \dfrac{4}{5}\), −0.9
Simplificar las expresiones usando el orden de las operaciones
En los siguientes ejercicios, simplifique.
- 10 (25.1 − 43.8)
- 30 (18.1 − 32.5)
- 62 (9.75 − 4.99)
- 42 (8.45 − 5.97)
- \(\dfrac{3}{4}\)(12.4 − 4.2)
- \(\dfrac{4}{5}\)(8.6 + 3.9)
- \(\dfrac{5}{12}\)(30.58 + 17.9)
- \(\dfrac{9}{16}\)(21.96 − 9.8)
- 10 ÷ 0.1 + (1.8) 4 − (0.3) 2
- 5 ÷ 0.5 + (3.9) 6 − (0.7) 2
- (37.1 + 52.7) ÷ (12.5 ÷ 62.5)
- (11.4 + 16.2) ÷ (18 ÷ 60)
- \(\left(\dfrac{1}{5}\right)^{2}\)+ (1.4) (6.5)
- \(\left(\dfrac{1}{2}\right)^{2}\)+ (2.1) (8.3)
- \(− \dfrac{9}{10} \cdot \dfrac{8}{15}\)+ 0.25
- \(− \dfrac{3}{8} \cdot \dfrac{14}{15}\)+ 0.72
Práctica Mixta
En los siguientes ejercicios, simplifique. Dar la respuesta como decimal.
- \(3 \dfrac{1}{4}\)− 6.5
- \(5 \dfrac{2}{5}\)− 8.75
- 10.86 ÷\(\dfrac{2}{3}\)
- 5.79 ÷\(\dfrac{3}{4}\)
- \(\dfrac{7}{8}\)(103.48) +\(1 \dfrac{1}{2}\) (361)
- \(\dfrac{5}{16}\)(117.6) +\(2 \dfrac{1}{3}\) (699)
- 3.6\(\left(\dfrac{9}{8} − 2.72\right)\)
- 5.1\(\left(\dfrac{12}{5} − 3.91\right)\)
Encuentra la Circunferencia y el Área de Círculos
En los siguientes ejercicios, aproximar la (a) circunferencia y (b) área de cada círculo. Si las mediciones se dan en fracciones, deje las respuestas en forma de fracción.
- radio = 5 in.
- radio = 20 pulg.
- radio = 9 ft.
- radio = 4 ft.
- radio = 46 cm
- radio = 38 cm
- radio = 18.6 m
- radio = 57.3 m
- radio =\(\dfrac{7}{10}\) milla
- radio =\(\dfrac{7}{11}\) milla
- radio =\(\dfrac{3}{8}\) yarda
- radio =\(\dfrac{5}{12}\) yarda
- diámetro =\(\dfrac{5}{6}\) m
- diámetro =\(\dfrac{3}{4}\) m
Matemáticas cotidianas
- Kelly quiere comprar un par de botas que están a la venta por\(\dfrac{2}{3}\) del precio original. El precio original de las botas es de $84.99. ¿Cuál es el precio de venta de los zapatos?
- Un arquitecto planea poner un mosaico circular en la entrada de un nuevo edificio. El mosaico tendrá la forma de un círculo con un radio de 6 pies. ¿Cuántos pies cuadrados de azulejo se necesitarán para el mosaico? (Redondea tu respuesta hasta el siguiente número entero.)
Ejercicios de escritura
- ¿Te resulta más fácil convertir un decimal a una fracción o una fracción a un decimal? Explique.
- Describe una situación en tu vida en la que podrías necesitar encontrar el área o circunferencia de un círculo.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección

(b) ¿Qué te dice esta lista de verificación sobre tu dominio de esta sección? ¿Qué pasos tomarás para mejorar?


