5.7: Resolver ecuaciones con decimales
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Determinar si un decimal es una solución de una ecuación
- Resolver ecuaciones con decimales
- Traducir a una ecuación y resolver
Antes de comenzar, toma este cuestionario de preparación.
- Evaluar x +23 cuando x =−14. Si te perdiste este problema, revisa el Ejemplo 4.9.15.
- Evaluar 15 − y cuando y = −5. Si te perdiste este problema, revisa el Ejemplo 3.6.12.
- Resolvern−7 = 42. Si te perdiste este problema, revisa el Ejemplo 4.12.5.
Determinar si un decimal es una solución de una ecuación
Resolver ecuaciones con decimales es importante en nuestra vida cotidiana porque el dinero suele escribirse con decimales. Cuando las aplicaciones involucran dinero, como comprar para ti mismo, hacer el presupuesto de tu familia o planificar para el futuro de tu negocio, estarás resolviendo ecuaciones con decimales.
Ahora que hemos trabajado con decimales, estamos listos para encontrar soluciones a ecuaciones que involucren decimales. Los pasos que tomamos para determinar si un número es una solución a una ecuación son los mismos si la solución es un número entero, un entero, una fracción o un decimal. Volveremos a enumerar estos pasos aquí para una fácil referencia.
- Paso 1. Sustituir el número por la variable en la ecuación.
- Paso 2. Simplifica las expresiones en ambos lados de la ecuación.
- Paso 3. Determinar si la ecuación resultante es verdadera.
- Si es así, el número es una solución.
- Si no, el número no es una solución.
Determinar si cada uno de los siguientes es una solución de x − 0.7 = 1.5: (a) x = 1 (b) x = −0.8 (c) x = 2.2
Solución
(a) x - 0.7 = 1.5
| Sustituto1 por x. | textcolorrojo1−0.7 stackrel?=1.5 |
| Restar. | $0.3\ neq 1.5$$ |
Dado que x = 1 no da como resultado una ecuación verdadera, 1 no es una solución a la ecuación.
(b) x - 0.7 = 1.5
| Sustituto−0.8 por x. | textcolorrojo−0.8−0.7 stackrel?=1.5 |
| Restar. | −1.5 neq1.5 |
Dado que x = −0.8 no da como resultado una ecuación verdadera, −0.8 no es una solución a la ecuación.
(c) x - 0.7 = 1.5
| Sustituto2.2 por x. | textcolorrojo2.2−0.7 stackrel?=1.5 |
| Restar. | $1.5 = 1.5\;\ checkmark$$ |
Dado que x = 2.2 da como resultado una ecuación verdadera, 2.2 es una solución a la ecuación.
Determine si cada valor es una solución de la ecuación dada. x − 0.6 = 1.3: (a) x = 0.7 (b) x = 1.9 (c) x = −0.7
- Responder a
-
no
- Respuesta b
-
si
- Respuesta c
-
no
Determinar si cada valor es una solución de la ecuación dada. y − 0.4 = 1.7: (a) y = 2.1 (b) y = 1.3 (c) −1.3
- Responder a
-
si
- Respuesta b
-
no
- Respuesta c
- no
Resolver ecuaciones con decimales
En capítulos anteriores, resolvimos ecuaciones utilizando las Propiedades de la Igualdad. Utilizaremos estas mismas propiedades para resolver ecuaciones con decimales.
|
Resta Propiedad de Igualdad Para cualquier número a, b y c, Si a = b, entonces a − c = b − c. |
Adición Propiedad de Igualdad Para cualquier número a, b y c, Si a = b, entonces a + c = b + c. |
|
La División Propiedad de Igualdad Para cualquier número a, b y c, y c ≠ 0 Si a = b, entoncesac=bc |
La multiplicación de la propiedad de la igualdad Para cualquier número a, b y c, Si a = b, entonces ac = bc |
Cuando sumas, restas, multiplicas o divides la misma cantidad de ambos lados de una ecuación, aún tienes igualdad.
Resolver: y + 2.3 = −4.7.
Solución
Utilizaremos la Propiedad de Sustracción de Igualdad para aislar la variable.
| Restar2.3 de cada lado, para deshacer la suma. | y+2.3 textcolorrojo−2.3=−4.7 textcolorrojo−2.3 |
| Simplificar. | y=−7 |
Comprobar:
| Sustituto y =−7. | textcolorrojo−7+2.3 stackrel?=−4.7 |
| Simplificar. | −4.7=−4.7 checkmark |
Dado que y = −7 hace que y + 2.3 = −4.7 sea una declaración verdadera, sabemos que hemos encontrado una solución a esta ecuación.
Resolver: y + 2.7 = −5.3.
- Responder
-
y=−8
Resolver: y + 3.6 = −4.8.
- Responder
-
y=−8.4
Resolver: a − 4.75 = −1.39.
Solución
Utilizaremos la Propiedad de Adición de Igualdad.
| Agrega 4.75 a cada lado, para deshacer la resta. | a−4.75 textcolorrojo+4.75=−1.39 textcolorrojo+4.75 |
| Simplificar. | a=3.36 |
Comprobar:
| Sustituir a =3.36. | textcolorrojo3.36−4.75 stackrel?=−1.39 |
| −1.39=−1.39 checkmark |
Dado que el resultado es una afirmación verdadera, a = 3.36 es una solución a la ecuación.
Resolver: a − 3.93 = −2.86.
- Responder
-
a=1.07
Resolver: n − 3.47 = −2.64.
- Responder
-
n=0.83
Resolver: −4.8 = 0.8n.
Solución
Utilizaremos la División Propiedad de Igualdad. Utilice las Propiedades de Igualdad para encontrar un valor para n.
| Debemos dividir ambos lados por 0.8 para aislar n. | dfrac−4.8 textcolorrojo0.8= dfrac0.8n textcolorrojo08 |
| Simplificar. | −6=n |
Comprobar:
| Sustituto n =−6. | −4.8 stackrel?=0.8( textcolorrojo−6) |
| −4.8=−4.8 checkmark |
Dado que n = −6 hace que −4.8 = 0.8n sea una declaración verdadera, sabemos que tenemos una solución.
Resolver: −8.4 = 0.7b.
- Responder
-
b=−12
Resolver: −5.6 = 0.7c.
- Responder
-
c=−8
Resolver:p−1.8 = −6.5.
Solución
Utilizaremos la Propiedad de la Multiplicación de la Igualdad.
| Aquí, p se divide por −1.8. Debemos multiplicar por −1.8 para aislar p. | textcolorrojo−1.8 izquierda( dfracp−1.8 derecha)= textcolorrojo−1.8(−6.5) |
| Multiplicar. | p=11.7 |
Comprobar:
| Sustituto p =11.7. | dfrac textcolorrojo11.7−1.8 stackrel?=−6.5 |
| −6.5=−6.5 checkmark |
Una solución ap−1.8 = −6.5 es p = 11.7.
Resolver:c−2.6 = −4.5.
- Responder
-
c=−11.7
Resolver:b−1.2 = −5.4.
- Responder
-
b=6.48
Traducir a una ecuación y resolver
Ahora que hemos resuelto ecuaciones con decimales, estamos listos para traducir frases de palabras a ecuaciones y resolver. Recuerda buscar palabras y frases que indiquen las operaciones a utilizar.
Traducir y resolver: La diferencia de n y 4.3 es 2.1.
Solución
| Traducir. | 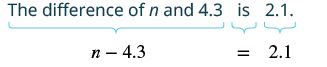 |
| Agregar 4.3 a ambos lados de la ecuación. | n−4.3 textcolorrojo+4.3=2.1 textcolorrojo+4.3 |
| Simplificar. | n=6.4 |
Comprobar:
| Dejar n = 6.4. | ¿La diferencia de 6.4 y 4.3 es igual a 2.1? |
| Traducir. | 6.4−4.3 stackrel?=2.1 |
| Simplificar. | $2.1 = 2.1\;\ checkmark$$ |
Traducir y resolver: La diferencia de y y 4.9 es 2.8.
- Responder
-
y−4.9=2.8;y=7.7
Traducir y resolver: La diferencia de z y 5.7 es 3.4.
- Responder
-
z−5.7=3.4;z=9.1
Traducir y resolver: El producto de −3.1 y x es 5.27.
Solución
| Traducir. |  |
| Divide ambos lados por −3.1. | dfrac−3.1x textcolorrojo−3.1= dfrac5.27 textcolorrojo−3.1 |
| Simplificar. | x=−1.7 |
Comprobar:
| Dejar x = −1.7. | ¿El producto de −3.1 y −1.7 es igual a 5.27? |
| Traducir. | −3.1(−1.7) stackrel?=5.27 |
| Simplificar. | 5.27=5.27 checkmark |
Traducir y resolver: El producto de −4.3 y x es 12.04.
- Responder
-
−4.3x=12.04;x=−2.8
Traducir y resolver: El producto de −3.1 y m es 26.66.
- Responder
-
−3.1m=26.66;m=−8.6
Traducir y resolver: El cociente de p y −2.4 es 6.5.
Solución
| Traducir. |  |
| Multiplica ambos lados por −2.4. | textcolorrojo−2.4 izquierda( dfracp−2.4 derecha)= textcolorrojo−2.4(6.5) |
| Simplificar. | p=−15.6 |
Comprobar:
| Dejar p = −15.6. | ¿El cociente de −15.6 y −2.4 es igual a 6.5? |
| Traducir. | dfrac textcolorrojo−15.6−2.4 stackrel?=6.5 |
| Simplificar. | 6.5=6.5 checkmark |
Traducir y resolver: El cociente de q y −3.4 es 4.5.
- Responder
-
1−3.4=4.5;q=−15.3
Traducir y resolver: El cociente de r y −2.6 es 2.5.
- Responder
-
r−2.6=2.5;r=−6.5
Traducir y resolver: La suma de n y 2.9 es 1.7.
Solución
| Traducir. |  |
| Restar 2.9 de cada lado. | n+2.9 textcolorrojo−2.9=1.7 textcolorrojo−2.9 |
| Simplificar. | n=−1.2 |
Comprobar:
| Dejar n = −1.2. | ¿La suma −1.2 y 2.9 es igual a 1.7? |
| Traducir. | $$-1.2 + 2.9\ stackrel {?} {=} 1.79$ |
| Simplificar. | 1.7=1.7 checkmark |
Traducir y resolver: La suma de j y 3.8 es 2.6.
- Responder
-
j+3.8=2.6;j=−1.2
Traducir y resolver: La suma de k y 4.7 es 0.3.
- Responder
-
k+4.7=0.3;k=−4.4
La práctica hace la perfección
Determinar si un decimal es una solución de una ecuación
En los siguientes ejercicios, determinar si cada número es una solución de la ecuación dada.
- x − 0.8 = 2.3
- x = 2
- x = −1.5
- x = 3.1
- y + 0.6 = −3.4
- y = −4
- y = −2.8
- y = 2.6
- h1.5= −4.3
- h = 6.45
- h = −6.45
- h = −2.1
- 0.75k = −3.6
- k = −0.48
- k = −4.8
- k = −2.7
Resolver ecuaciones con decimales
En los siguientes ejercicios, resuelve la ecuación.
- y + 2.9 = 5.7
- m + 4.6 = 6.5
- f + 3.45 = 2.6
- h + 4.37 = 3.5
- a + 6.2 = −1.7
- b + 5.8 = −2.3
- c + 1.15 = −3.5
- d + 2.35 = −4.8
- n − 2.6 = 1.8
- p − 3.6 = 1.7
- x − 0.4 = −3.9
- y − 0.6 = −4.5
- j − 1.82 = −6.5
- k − 3.19 = −4.6
- m − 0.25 = −1.67
- q − 0.47 = −1.53
- 0.5x = 3.5
- 0.4p = 9.2
- −1.7c = 8.5
- −2.9x = 5.8
- −1.4p = −4.2
- −2.8m = −8.4
- −120 = 1.5q
- −75 = 1.5y
- 0.24x = 4.8
- 0.18n = 5.4
- −3.4z = −9.18
- −2.7u = −9.72
- a0.4= −20
- b0.3= −9
- x0.7= −0.4
- y0.8= −0.7
- p−5= −1.65
- q−4= −5.92
- r−1.2= −6
- s−1.5= −3
Práctica Mixta
En los siguientes ejercicios, resuelve la ecuación. Entonces revisa tu solución.
- x − 5 = −11
- −25= x + (\ dfrac {3} {4}\)
- p + 8 = −2
- p +23=112
- −4.2m = −33.6
- q + 9.5 = −14
- q +56=112
- 8.615= − d
- 78m=110
- j−6.2= −3
- −23= y +38
- s − 1.75 = −3.2
- 1120= − f
- −3.6b = 2.52
- −4.2a = 3.36
- −9.1n = −63.7
- r − 1.25 = −2.7
- 14n=710
- h−3= −8
- y − 7.82 = −16
Traducir a una ecuación y resolver
En los siguientes ejercicios, traduzca y resuelva.
- La diferencia de n y 1.9 es 3.4.
- La diferencia n y 1.5 es 0.8.
- El producto de −6.2 y x es −4.96.
- El producto de −4.6 y x es −3.22.
- El cociente de y y −1.7 es −5.
- El cociente de z y −3.6 es 3.
- La suma de n y −7.3 es 2.4.
- La suma de n y −5.1 es 3.8.
Matemáticas cotidianas
- Shawn compró un par de zapatos a la venta por 78 dólares. Resuelve la ecuación 0.75p = 78 para encontrar el precio original de los zapatos, p.
- Mary compró un refrigerador nuevo. El precio total incluyendo el impuesto a las ventas fue de $1,350. Encuentra el precio al por menor, r, del refrigerador antes de impuestos resolviendo la ecuación 1.08r = 1,350.
Ejercicios de escritura
- Piensa en resolver la ecuación 1.2y = 60, pero en realidad no la resuelvas. ¿Crees que la solución debería ser mayor a 60 o menor a 60? Explica tu razonamiento. Entonces resuelve la ecuación para ver si tu pensamiento era correcto.
- Piensa en resolver la ecuación 0.8x = 200, pero en realidad no la resuelvas. ¿Crees que la solución debería ser mayor a 200 o menor a 200? Explica tu razonamiento. Entonces resuelve la ecuación para ver si tu pensamiento era correcto.
Autocomprobación
(a) Después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.

b) En una escala del 1 al 10, ¿cómo calificaría su dominio de esta sección a la luz de sus respuestas en la lista de verificación? ¿Cómo se puede mejorar esto?


