9.4: Decimales
- Page ID
- 113279
El significado de los decimales se entiende mejor una vez que se tiene una comprensión real del valor posicional y las fracciones. La notación decimal que comúnmente usamos es una extensión del valor posicional en base diez. El punto decimal indica que los dígitos sucesivos representan décimas, centésimas, milésimas, etc. Así que una persona debe entender lo que significan estas fracciones para poder entender y hacer la conexión con los decimales.
La clave para entender la relación entre decimales y fracciones (o números mixtos) comienza con LEER el decimal correctamente. La mayoría de la gente lee 5.3 como “cinco punto tres”, lo que no ayuda a entender su significado. Debe leerse “cinco y tres décimas”. Al hacerlo, la conexión entre el decimal 5.3 y el número mixto\(5 \frac{3}{10}\) es clara. De igual manera, 18.035 debe leerse “Dieciocho y treinta y cinco milésimas” y corresponde al número mixto\(18\frac{35}{1000}\). Aquí hay algunos más:
- 0.309 y ambos\(\frac{309}{1000}\) se leen correctamente “trescientos nueve milésimas”
- 10.04 y ambos\(10\frac{4}{100}\) se leen correctamente “diez y cuatro centésimas”
Tenga en cuenta que el punto decimal se lee como “y”. El punto decimal (y la palabra “y”) separa toda la parte de la parte fraccionaria de un número mixto. Este es el único uso correcto de la palabra “y” al leer números. 760 se lee “setecientos sesenta”. Un error común es leer 760 como “setecientos sesenta”. Si no hay punto decimal, no digas la palabra “y”.
La gente que acaba de aprender sobre los decimales (como los niños de primaria) NO debe leer el número 5.4 como “cinco punto cuatro”. Esta es una forma abreviada de leer el número que solo es apropiado usar una vez que uno realmente entiende la conexión entre decimales y fracciones. ¡Recuerda que un número escrito en forma decimal es realmente solo una forma diferente de escribir un número mixto donde el denominador de la parte fraccionaria es una potencia de diez! El nombre de la parte fraccionaria (décimas, centésimas, milésimas, etc.) es el valor posicional del último dígito del número después del punto decimal, que también pasa a ser el denominador del número escrito en forma fraccionaria.
Mirar de nuevo a 0.309 y\(\frac{309}{1000}\). En el decimal, hay tres dígitos (o valores posicionados) después del punto decimal. En la fracción, hay tres ceros después del 1 (que es el número 1000 en el denominador). Lo mismo se aplica a 18.035 y\(18\frac{35}{1000}\). Para 5.3 y\(5\frac{3}{10}\), el decimal tiene un dígito después del punto decimal, y la fracción tiene un cero después del 1. Lo mejor es que a los estudiantes se les permita descubrir este hecho por sí mismos. Siempre es más significativo descubrir las relaciones (que a menudo se convierten en reglas) por tu cuenta. Los estudiantes a quienes regularmente se les pide que lean decimales, fracciones y números mixtos de la manera correcta tienen más probabilidades de hacer este descubrimiento particular por sí mismos.
Los números mixtos como 5.3 y 18.035 también se pueden escribir inmediatamente como fracciones impropias. El denominador de la fracción seguirá siendo el mismo que si estuviera escrito como un número mixto. El numerador es el número sin punto decimal en absoluto. Por ejemplo, 5.3 puede escribirse como\(5\frac{3}{10}\) o\(\frac{53}{10}\); y 18.035 puede escribirse como\(18\frac{35}{1000}\) o\(\frac{18035}{1000}\).
Tenga en cuenta que cuando escribe por primera vez un decimal como fracción, no es necesariamente en forma más simple (o reducida).
En la línea, escribe con palabras cómo leer cada uno de los siguientes decimales. No utilice la palabra “punto”. Después, debajo, escribe cada decimal como una fracción. Si el número es mayor o igual a 1, primero escribe la fracción como un número mixto y luego escríbela como una fracción impropia. Simplifica cualquier fracción que no esté en la forma más simple. Mostrar todos los pasos (incluidas las fracciones originales antes de simplificar).
a. 0.4 _________________________________________________________________
0.4 =
b. 0.26 _________________________________________________________________
0.26 =
c. 3.08 _________________________________________________________________
3.08 =
d. 9.85 _________________________________________________________________
9.85 =
e. 17.305 _____________________________________________________________
17.305 =
Escribe cada fracción propiamente dicha como decimal. Escribe cada fracción impropia primero como un número mixto (no reducir), y luego también como decimal. No use su calculadora.
a.\(\frac{14}{100}\) = __________
b.\(\frac{8}{1000}\) = __________
c.\(\frac{435}{100}\) = _______________ = _______________
d.\(\frac{5638}{10}\) = _______________ = _______________
e.\(\frac{305}{100}\) = _______________ = _______________
La regla que quizás recuerdes para multiplicar fracciones es multiplicar los números juntos como si no hubiera un punto decimal, y luego mover el punto decimal desde la derecha el número total de lugares en los que se encuentra para ambos números. Por ejemplo, (8) (0.4) se realiza multiplicando 8 por 4 y luego moviendo el punto decimal en un lugar para obtener 3.2. De igual manera, (0.06) (0.7) se realiza multiplicando 6 por 7 y moviendo el punto decimal en tres lugares (dos para 0.06 y uno más para 0.7 para un total de tres) para obtener 0.042. Muchas personas hacen esto más difícil de lo que realmente es y no se dan cuenta de que pueden multiplicar fácilmente 0.3 y 0.4 en su cabeza. Es tan simple como 3\(\cdot\) 4 y mover el decimal en dos lugares para obtener 0.12. Ahora bien, ¿qué tal 1.1 veces 1.2? Es simplemente 11 veces 12 con el decimal movido en dos lugares: 1.32.
Observemos por qué esta regla para multiplicar decimales funciona reescribiendo los números como fracciones primero. La clave aquí es escribir números mayores o iguales a uno como fracciones impropias. Después multiplica (sin cancelar ni reducir) las fracciones. Por último, reescribir la fracción como decimal.
(8) (0.4) =\(\frac{8}{1} \cdot \frac{4}{10} = \frac{32}{10}\) = 3.2 (observe que el punto decimal es un lugar para .4)
(1.2) (1.01) =\(\frac{12}{10} \cdot \frac{101}{100} = \frac{1212}{1000}\) = 1.212
(observe que el punto decimal es de tres lugares en, uno para 1.2 más dos más para 1.01)
Multiplica mentalmente los siguientes decimales y escribe la respuesta en el espacio en blanco. Luego hazlo nuevamente mostrando los mismos pasos que se muestran en los dos ejemplos anteriores donde cada decimal se escribe primero como una fracción, luego multiplica los numeradores y denominadores, y luego convierte esa respuesta (no simplifique) a un decimal. No use su calculadora.
a. (0.4) (.07) = ______________
(0.4) (.07) =
b. (1.6) (0.2) = ______________
(1.6) (0.2) =
c. (0.25) (0.3) = ______________
(0.25) (0.3) =
d. (2.2) (0.3) = ______________
(2.2) (0.3) =
Reconocer decimales equivalentes y comparar decimales
Los ceros, que están detrás del último dígito distinto de cero de un decimal, se pueden sumar o eliminar sin cambiar el valor del decimal. Si miras alguna fracción equivalente, verás por qué esto debería ser cierto. Por ejemplo,
\[\dfrac{14}{10} = \dfrac{140}{1000} = \dfrac{1400}{10000} = \dfrac{14000}{100000}. \nonumber \]
Estos son todos equivalentes a\(\frac{14}{100}\) porque el numerador y denominador se multiplicaron por alguna potencia de 10 (10, 100 o 1000) para obtener una de las otras fracciones equivalentes. Si reemplazamos cada una de las cuatro fracciones anteriores con sus equivalentes decimales, obtenemos 0.14 = 0.140 = 0.1400 = 0.14000. Llamemos a cualquier cero al final del último dígito distinto de cero de un decimal "ceros finales”. Entonces, podríamos concluir que cualquier número que comience con .14 que tenga ceros finales también es equivalente, como 0.1400000.
Dos decimales son iguales solo si se puede hacer que uno se vea idéntico al otro agregando o eliminando ceros finales. También puede determinar si son equivalentes eliminando cualquier exceso de ceros finales de cada uno para ver si son idénticos.
Para el primer decimal dado, circule cualquiera de los siguientes cuatro decimales que sean iguales a él.
| a. | 1.900; | 1.0900 | 1.9 | 1.90000 | 0.190 |
| b. | 4.034; | 4.0340 | 4.0334 | 4.0034 | 4.3040 |
Para comparar dos o más decimales que no sean iguales, pero que tengan el mismo número de dígitos después del punto decimal, puede escribir cada uno como una fracción con el mismo denominador y luego comparar el numerador. Por ejemplo 0.14 es menor que 0.21 ya que catorce centésimas es menos de veintiuna centésimas. Básicamente, en este caso, es como comparar números enteros. Podrás determinar cuál es más grande comparando cada número como si no hubiera un punto decimal. Pero, ten en cuenta que esto solo tiene sentido si los números que estás viendo tienen el mismo número de dígitos después del punto decimal.
Compara cada uno de los siguientes decimales usando <, = or >.
| a. | 3.5 | 0.9 |
| b. | 35.06 | 35.0600 |
| c. | 0.089 | 0.098 |
Para comparar dos o más decimales que no sean iguales que no todos tengan el mismo número de dígitos después del punto decimal, primero escriba cada decimal con el mismo número de dígitos después del punto decimal (agregando ceros finales a uno o más si es necesario). Al hacer eso, estás comparando décimas con décimas, o centésimas con centésimas, etc., como hiciste en el ejercicio 5.
Compara cada uno de los siguientes decimales usando <, = or >.
| a. | 3.51 | 3.488 |
| b. | 35.061 | 35.35 |
| c. | 0.08933 | 0.0894 |
Si se escribe una fracción con una potencia de diez en el denominador, es básico escribir el mismo número en forma decimal. Eso lo hiciste en el Ejercicio 2. Cualquier fracción que se escriba con una potencia de 10 en el denominador puede escribirse como un decimal terminal. Esto significa que es posible escribir el número con ceros al final. Pero ¿y si la fracción no tiene una potencia de 10 (como 10, 100, 1000, etc.) en el denominador? ¡A veces esos pueden ser complicados!
Si una fracción SIN una potencia de diez en el denominador PUEDE escribirse como una fracción equivalente CON una potencia de diez en el denominador, entonces se puede escribir como un decimal de terminación.
Por ejemplo, se\(\frac{1}{2}\) puede escribir como\(\frac{5}{10}\) (multiplicando el numerador y el denominador por 5)
Por lo tanto,\(\frac{1}{2}\)\(\frac{5}{10}\) = = 0.5 (recuerde leer esto como cinco décimas)
Bueno, esa no fue muy dura, pero ¿y qué pasa\(\frac{7}{80}\)? La pregunta es si puedes multiplicar el denominador, 80, por algo para obtener 10, 100, 1000, 10000, etc. no hay un número entero por el que puedas multiplicar 80 para obtener 10, 100 o 1000. Pero, si multiplicas 80 por 125, equivale a 100000. Entonces, al multiplicar tanto 7 como 80 por 125, obtenemos la fracción equivalente\(\frac{875}{10000}\) para la\(\frac{7}{80}\) cual ahora se puede escribir como el decimal 0.0875.
¿Qué\(\frac{5}{6}\) tal escribir como decimal de terminación? Bueno, no hay nada por lo que puedas multiplicar 6 para obtener 10 o 100 o 1000 o 10000. ¿Hay tal vez algún número por el que podríamos multiplicar 6 para obtener algún poder superior de diez? Bueno, ¡esa es una buena pregunta! En realidad, no la hay, pero ¿cómo podrías estar seguro? Desde luego no se puede probar cada potencia de diez ya que hay un número infinito de ellos para probar.
Sería bueno si hubiera una manera fácil de determinar si alguna fracción dada podría escribirse como un decimal de terminación. La clave es considerar los factores del denominador de una fracción que puede escribirse como decimal de terminación. Si una fracción se puede escribir como decimal de terminación, entonces hay alguna fracción equivalente donde el denominador debe ser una potencia de diez: 10 o 100 o 1000, etc.
Escribe la factorización prima de cada uno de los siguientes:
a. 10 = _______________
b. 100 = _______________
c. 1000 = _______________
d. 10000 = _______________
e. 100000 = _______________
¿Cuáles son los únicos factores primos de poderes de 10? ______________
Si una potencia de diez tiene tres factores de 5, ¿cuántos factores de 2 tiene? ______
Si una potencia de diez tiene dos factores de 2, ¿cuántos factores de 5 tiene? _____
Poderes de diez sólo tienen 2s y 5s como sus factores primos y nada más.
Volvamos a nuestros tres números,,\(\frac{1}{2}\)\(\frac{7}{80}\), y\(\frac{5}{6}\), que estábamos tratando de escribir como decimales terminadores y analizar la situación.
\(\frac{1}{2}\)se simplifica, y en su forma factorizada prima, hay exactamente un 2 en el denominador. Para escribir como fracción equivalente con un denominador que sea una potencia de diez, debe tener solo 2s y 5s como factores primos en el denominador, ¡y el mismo número de cada uno! Por lo tanto, multiplicar por uno más 5 en el numerador y denominador ¡hizo el truco!
Factor primo el numerador y denominador de esta fracción reducida:\(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5}\)
Debemos determinar si es posible multiplicar el denominador por algo para que el denominador resultante se componga de sólo 2s y 5s y el mismo número de cada uno. Bueno, hay cuatro factores de 2 y un factor de 5. Ya que necesitamos el mismo número de cada factor, hacer una fracción equivalente multiplicando el numerador y denominador por tres factores más de 5 hará el truco.
\(\frac{7}{80} = \frac{7}{2 \cdot 2 \cdot 2 \cdot 2 \cdot 5} \cdot \frac{5 \cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.0875\)
En ambos ejemplos, tenga en cuenta que o bien multiplicamos por factores extra de 2 o 5, ¡pero no ambos!
¿Y qué pasa\(\frac{5}{6}\)? Bueno, se reduce, y la desfactorización del denominador es 2\(\cdot\) 3. No importa por qué se multiplica el denominador, nos quedaremos atascados con un factor de 3 en el denominador. Dado que los únicos factores primos de potencias de 10 son 2 y 5, no puede haber un factor primo de 3 en el denominador si queremos terminar con solo una potencia de 10 en el denominador. Por lo tanto, al ser imposible escribir\(\frac{5}{6}\) como fracción equivalente con una potencia de diez en el denominador, no puede escribirse como decimal terminante.
¿Qué tal\(\frac{63}{72}\)? Si hacemos factor primo el denominador, obtenemos 2\(\cdot\) 2\(\cdot\) 2\(\cdot\) 3\(\cdot\) 3.
Bueno, ¿qué opinas? ¿\(\frac{63}{72}\)Se puede escribir como un decimal de terminación? ________
Explique por qué o por qué no.
Una forma de verificar que estás obteniendo los resultados correctos es usar una calculadora. Para\(\frac{1}{2}\), obtuvimos 0.5, que puedes verificar haciendo la división 1\(\div\) 2 en tu calculadora.
Usa tu calculadora para encontrar el equivalente decimal para cada uno de los siguientes:
a.\(\frac{7}{80}\) = _____________
b.\(\frac{63}{72}\) = _____________
Hmmm, ¿obtuviste 0.0875 por la parte a? _________
Si hiciste la parte b en tu calculadora, ¿obtuviste un decimal terminador de 0.875?
¿Eso es lo que esperabas? ¿Por qué o por qué no?
La razón que se\(\frac{63}{72}\) puede escribir como decimal de terminación es porque en su forma simplificada, solo tiene 2 y/o 5 como factores primos. Aquí es cómo terminar este problema simplificando primero, y luego multiplicando por cualquier factor necesario de 2 o 5 para obtener el mismo número de cada uno:
\(\frac{63}{72} = \frac{3 \cdot 3 \cdot 7}{2 \cdot 2 \cdot 2 \cdot 3 \cdot 3} = \frac{7}{2 \cdot 2 \cdot 2} \cdot \frac{5\cdot 5 \cdot 5}{5 \cdot 5 \cdot 5} = \frac{875}{10000} = 0.875\)
Para cada fracción, determinar si se puede escribir como una fracción equivalente con una potencia de diez en el denominador. Si una fracción no puede escribirse como decimal terminal, explique por qué no. De lo contrario, mostrar TODOS los pasos (como se muestra en los ejemplos anteriores) para escribirlo como decimal terminal. Los pasos se enumeran a continuación.
- Simplificar si es posible
- Factor primo el denominador
- Multiplique el numerador y denominador por un número apropiado de factores de 2 o 5 para que el denominador sea una potencia de 10
- Simplificar el numerador y denominador
- Escribir como un decimal de terminación
Después, verifica tu respuesta con una calculadora tomando la fracción original y dividiendo el numerador por el denominador. Debe obtener el mismo decimal obtenido haciendo los cinco pasos descritos anteriormente.
a.\(\frac{3}{4}\)
b.\(\frac{9}{20}\)
c.\(\frac{9}{15}\)
d.\(\frac{18}{25}\)
e.\(\frac{5}{14}\)
Bien, ahora tenemos que lidiar con esas fracciones que no se pueden escribir como decimales terminadores. Cualquier fracción simplificada que tenga al menos un factor primo que no sea 2 o 5 está en esta categoría. Veamos de\(\frac{5}{6}\) nuevo. Una forma de escribir esto como decimal es dividir 5 por 6.
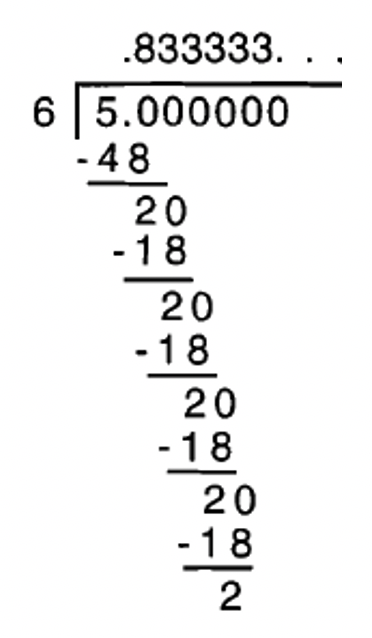
Como se puede ver, sigo dividiendo 6 en 20, escribo 3, multiplico para obtener 18, restar de 20, obtener 2, bajar el 0, y empezar todo de nuevo. Esto puede durar para siempre y para siempre. Entonces, los 3 al final seguirán para siempre. Esto NO es un decimal de terminación ya que el número no se puede escribir con ceros finales. En este caso, hay trailing 3s. Los tres puntos al final (llamados elipses) del número son para mostrar que los 3s se repiten para siempre. La respuesta se puede escribir como 0.8333333... o\(0.8\bar{3}\). ¡Recuerda poner las elipses (tres puntos) al final del número! El listón sobre el 3 indica que el 3 se repite para siempre y para siempre. Aquí hay otras formas de representar lo mismo:\(0.8\overline{33}\) o\(0.8333\bar{3}\). En el primer caso, dice 33 repeticiones para siempre. En el segundo caso, dice después de los tres primeros 3, los 3 se repiten para siempre. En ambos casos, cuando lo escribes en forma larga, se ve como 0.8333333... así que es el mismo número. Por lo general, escribiremos 0.8333333... o\(0.8\bar{3}\).
Escribe 0.8333333... o\(0.8\bar{3}\) de tres formas más, diferentes a\(0.8\overline{33}\) o\(0.8333\bar{3}\).
____________________, ____________________ y ____________________
Una cosa a notar de lo que pasó cuando dividimos 5 por 6 es que seguí recibiendo 2 después de cada resta en la división, esto es como el resto. También recuerda que cuando divides, cada resto debe ser menor o igual que lo que estás dividiendo.
Escribe los posibles restos para cada número.
a. 6: _________________________________
b. 7: _________________________________
c. 9: _________________________________
d. 11: _________________________________
e. 3: _________________________________
Veamos ahora qué sucede cuando haces cómputos de división larga\(\frac{4}{11}\) y\(\frac{2}{7}\).
 |
 |
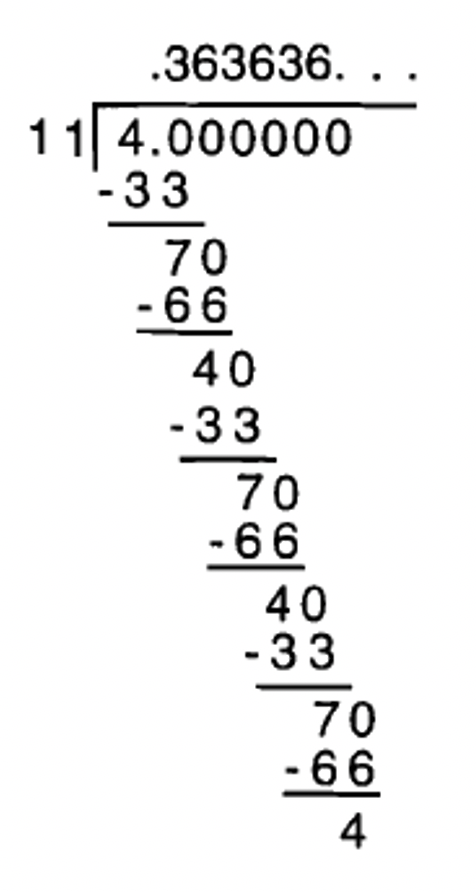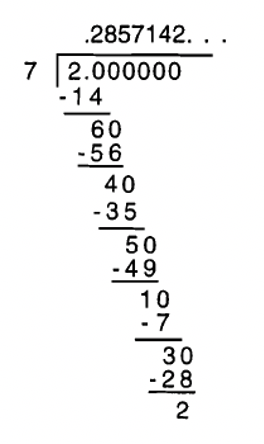En ambos casos, eventualmente, obtienes un resto que obtuviste previamente, por lo que el cómputo se repite. En el caso de dividir 4 por 11, aparecen dos restos antes de que haya alguna repetición 4 y 7. A partir del 16d, deberías haberte dado cuenta que los únicos restos posibles para 11 son 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y 10. Ahora bien, si tienes un resto de 0 al dividir, tendrías un decimal de terminación. Entonces, al dividir por 11, la mayor cantidad de restos que podrías obtener en fila antes de que uno se repita es de 10 seguidos. Pero en el caso de\(\frac{4}{11}\), los restos se repiten después del 4 y 7. Esto significa que sigues dividiendo en 40 o 70 (ya que bajas el cero) y es por eso que en el cociente los dígitos empiezan a repetirse. Recuerda poner las elipses (tres puntos) al final del número si hay un patrón de dígitos repetitivos.
Ahora en el caso de dividir 2 por 7, los restos que obtienes a medida que avanzas son 6, luego 4, luego 5, luego 1, luego 3, y luego 2. Cuando bajas el 0, estás dividiendo 7 en 20 nuevamente, y de ahí se repiten los restos. Observe que la secuencia de restos (6, 4, 5, 1, 3 y 2) es diferente a la secuencia de dígitos que se repiten en el cociente. Los dígitos que se repiten en el cociente son 285714, así\(\frac{2}{7}\) = 0.285714285714... o\(0.\overline{285714}\).
Dado que solo hay seis restos posibles distintos de cero al dividir por 7, solo una secuencia de 6 dígitos posiblemente podría repetirse. En este caso, los seis posibles restos de 7 aparecieron en la división larga.
Hay muchas maneras de expresar el infinito o repetido decimal 0.285714285714... o\(0.\overline{285714}\). En primer lugar, para establecer lo que se está repitiendo, se querría ver la secuencia de dígitos repitiéndose al menos dos veces a través. Por lo tanto, 0.285714285714... es la forma más corta posible de mostrarlo cuando se utilizan las elipses (tres puntos). Si simplemente escribiste 0.285714..., no quedaría claro si los 4 repetidos o los 14 repetidos o los 14 repetidos, etc.
Aquí hay algunas otras formas de escribir 0.285714285714... además\(0.\overline{285714}\).
0.285714285714285714285714...
0.2857142857142857142...
(en este caso, usted lo ve como el 857142 repitiendo a partir de este punto)
0.2857142857142857...
(en este caso, usted lo ve como el 142857 que se repite a partir de este punto)
\(0.28\overline{571428}\)
(en este caso, usted lo ve como el 571428 repitiendo a partir de este punto)
Escribe 0.285714285714... dos formas más usando elipses (los tres puntos) y dos formas más usando una barra sobre una secuencia repetida de dígitos.
Determinar cuál de los siguientes equivale a 0.383432432432...
Una forma de hacerlo es escribir el número en forma larga continuando cuidadosamente el patrón y luego verificar los dígitos un valor posicional a la vez.
- 0.3834324324...
- 0.383432432...
- 0.3834323432...
- \(0.38343\overline{243}\)
- \(0.38\overline{34324}\)
Ten en cuenta que si estás encontrando un equivalente decimal para una fracción con 17 en el denominador, puede haber hasta dieciséis dígitos seguidos antes de que veas alguna repetición. Ahora, obviamente, sólo hay 10 dígitos (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) en la base diez. Tenga en cuenta que la secuencia de dígitos que se repiten en el cociente es totalmente diferente a los posibles restos que podría obtener al dividir por 17 ya que un resto puede ser más que un número de un solo dígito.
a. ¿Cuántos restos posibles podría haber si se divide un número por 33?
b. Hacer división larga para escribir\(\frac{31}{33}\) como decimal repetido usando elipses y luego usando la barra sobre los dígitos repetidos en esta línea: ______________________________
Mostrar trabajo aquí:
c. En la división larga, ¿cuántos dígitos se repiten? ______
d. En la división larga, ¿cuáles eran los restos que seguirías obteniendo si continuaras la división para siempre y para siempre? _________________
Usa tu calculadora para escribir cada uno como un decimal repetido. Escribe la respuesta de dos maneras, primero con una barra sobre los dígitos repetidos, y luego en forma larga, usando elipses. Tenga en cuenta que su calculadora puede o no redondear el último dígito mostrado. No puede mostrar dígitos repitiéndose para siempre, así que hay que ser lo suficientemente inteligente para saber si el decimal que se muestra en la pantalla es terminal o si es una aproximación.
a.\(\frac{5}{9}\) = ________________ = _______________________________
b.\(\frac{5}{7}\) = ________________ = _______________________________
c.\(\frac{1}{6}\) = ________________ = _______________________________
d.\(\frac{2}{3}\) = ________________ = _______________________________
e.\(\frac{7}{11}\) = ________________ = _______________________________
f.\(\frac{5}{12}\) = ________________ = _______________________________
g.\(\frac{8}{15}\) = ________________ = _______________________________
h.\(\frac{16}{45}\) = ________________ = _______________________________
i.\(\frac{5}{66}\) = ________________ = _______________________________
Si estás cambiando una fracción simplificada a un decimal donde el denominador es x, ¿cuántos dígitos como máximo se pueden repetir en el cociente? _________
Bueno, has aprendido a escribir decimales terminadores como fracciones, y a escribir fracciones como decimales. Debe poder determinar si una fracción se puede escribir como decimal de terminación o repetición antes de hacer la división real.
Los números racionales se definen como números que se pueden expresar como la relación de dos enteros. Las fracciones como solemos referirles (sin puntos decimales ni raíces cuadradas, etc. en el numerador o denominador) son números racionales. Dado que todas las fracciones se pueden escribir como decimales terminantes o no terminantes (infinitos, repetitivos), entonces todos los decimales terminantes y repetitivos también son números racionales. En el Ejercicio 1, escribiste algunos decimales terminadores como fracciones. Como todos los decimales no terminadores vinieron de una fracción, ahora queremos poder ir al revés y escribir un decimal repetido como fracción. ¡Tenemos un truco genial para hacer precisamente eso!
Digamos que queríamos escribir\(0.\overline{72}\) o 0.727272727272... como fracción.
Primero, fíjese que este es un número muy diferente de 0.72, ya que 0.72 es setenta y dos centésimas, o\(\frac{72}{100}\). Esto simplifica a\(\frac{18}{25}\). Así, 0 .72 y\(\frac{18}{25}\) son el mismo número. Puede verificar para asegurarse de que\(\frac{18}{25}\) es la fracción correcta usando una calculadora y dividiendo 18 por 25. La calculadora debería leer 0.72, que es donde empezamos.
Bien, entonces, ¿cómo escribimos\(0.\overline{72}\) como fracción? Dado que se trata de un decimal repetido que tiene infinitamente muchos dígitos, no hay una sola potencia de diez que podamos poner en el denominador. El truco es usar álgebra para escribir un número de una manera que elimine la parte infinitamente repetitiva del decimal. Primero, escribamos\(0.\overline{72}\) el largo camino:
\(0.\overline{72}\)= .727272727272... y llámalo el número x. Así x = 0.727272727272...
Recuerda que si multiplicas un decimal por 10, el punto decimal se mueve un lugar a la derecha, y cuando multiplicas un decimal por 100, el punto decimal se mueve dos lugares hacia la derecha, etc.
Si x = 0.727272727272..., entonces escribe lo que equivale a 10x, 100x y 1000x. Escríbelo sin usar la barra sobre los dígitos repetidos. Usa las elipses (tres puntos).
10x = _______________________________
100x = _______________________________
1000x = _______________________________
Bien, vamos a trabajar con x = 0.7272727272... y 100x = 72.727272727272...
a. en álgebra, ¿qué es 100x - x? _________ (Pista: Restar coeficientes.)
b. computar 100x - x de otra manera: Alinea los puntos decimales y resta 0.727272727272... de 72.727272727272... Observe que si los decimales están alineados, las “colas” al final de ambos decimales repetidos son exactamente las mismas por lo que debería ser fácil restar. Muestra el trabajo a continuación.
c. Escribe una ecuación para que la respuesta a la parte a sea igual a la respuesta a la parte b. Luego usa álgebra para resolver para x. Mostrar trabajo.
d. Simplifica la fracción que obtuviste para x en la parte c. Mostrar trabajo.
e. Usa una calculadora para reescribir la fracción que obtuviste en la parte c como decimal:
¿Es igual a\(0.\overline{72}\)? __________
Si es así, ¡debes haber escrito\(0.\overline{72}\) como la fracción correcta!
Aquí está el truco para cambiar decimales repetidos a fracciones simplificadas:
Llama al número que estás tratando de escribir como decimal una variable, like\(n\) o x.
Si hay un dígito repetido, computa 10x; si hay dos dígitos repetitivos, computa 100x; si hay tres dígitos repetitivos, calcula 1000x, etc. Esto alinea los decimales repetidos entre sí para que la cola de x y el otro número (10x, 100x, 1000x, etc.) sean los mismos.
Luego resta x del otro número (10x, 100x, 1000x, etc.) Las colas de ambos números se desprenderán y deberías tener un problema algebraico que resolver en este punto. Asegúrate de escribir tu respuesta como una fracción reducida con solo números enteros en el numerador y denominador.
Aquí hay dos ejemplos. Si escribes el número en forma decimal sin la barra sobre el número, ¡recuerda poner las elipses (tres puntos) al final!
|
Escribir\(0.\bar{2}\) como una fracción simplificada. Dejar x =\(0.\bar{2}\) = .222222... Dado que solo se repite un dígito, multiplica x por 10. Entonces 10x = 2.222222... \[\begin{aligned} 10x = & 2.22222.... \\ - x = & .2222..... \\ \hline 9x = & 2 \end{aligned} \nonumber \] \[x = \frac{2}{9}\nonumber \] Usa una calculadora para verificar eso\(\frac{2}{9} = 0.\bar{2}\) |
Escribir\(0.\overline{54}\) como una fracción simplificada. Dejar x =\(0.\overline{54}\) = .545454... Dado que dos dígitos se repiten, multiplique x por 100. Entonces 100x = 54.545454... \[\begin{aligned} 100x = & 54.545454... \\ - x = & .545454... \\ \hline 99x = & 54 \end{aligned} \nonumber \] \[x = \frac{54}{99} = \frac{6}{11}\nonumber \] Usa una calculadora para verificar eso\(\frac{6}{11} = 0.\overline{54}\) |
Reescribe cada uno de los siguientes decimales como fracciones simplificadas. Para repetir decimales, utilice la técnica mostrada en los ejemplos anteriores. Luego, verifica tu respuesta usando una calculadora dividiendo el numerador por el denominador para ver si el resultado coincide con el problema original.
a. 0.4
b.\(0.\bar{4}\) comience por dejar x =\(0.\bar{4}\) o x = 0.44444...
c. 0.06 =
d.\(0.\overline{06}\) comience por dejar x =\(0.\overline{06}\) o x = 0.060606...
e. 0.9
f.\(0.\bar{9}\) Comience por dejar x =\(0.\bar{9}\) o x = 0.9999... (esta respuesta podría sorprenderte)
g. 0.45
h.\(0.\overline{45}\) Comience por dejar x =\(0.\overline{45}\) o x = 0.454545...
i. 0.084
j.\(0.\overline{084}\) Comience por dejar x =\(0.\overline{084}\) o 0.084084084...
A veces, la aritmética se vuelve un poco más desafiante. Considera escribir 0.14444... como fracción. Las 4 repeticiones iniciando dos lugares después del punto decimal. Nos sumergimos hacia adelante como antes, pero hay una pequeña falla al final porque un lado de la ecuación tendrá un punto decimal en él. Si tuviéramos que dividir por 9, la fracción tendrá un punto decimal en el numerador por lo que no es un número racional reducido; tanto el numerador como el denominador tienen que ser enteros. Aquí están los pasos básicos hasta ese punto.
\(10n = 1.444444...\)y\(n = 0.144444\)
Restando, obtenemos\(9n = 1.3\)
Una forma de remediar esta situación es multiplicar ambos lados de la ecuación por 10 (o 100 o 1000 según sea necesario) para eliminar el decimal. Esto es como borrar fracciones multiplicando ambos lados de una ecuación por el mínimo denominador común.
Así que multiplica ambos lados de\(9n = 1.3\) por 10 para conseguir\(90n = 13\). Después divide por 90 para conseguir\(\frac{13}{90}\).
Otra forma de remediar esta situación es escribir el lado derecho de la ecuación como una fracción. Recuerda que 1.3 es\(\frac{13}{10}\). Entonces la ecuación es\(9n=\frac{13}{10}\).
Puedes cruzar multiplicar para obtener\(90n = 13\) y luego dividir por 90 para obtener\(n = \frac{13}{90}\)
En cualquier caso, recuerde que una fracción reducida es la relación de dos enteros que son relativamente primos.
Reescribe cada decimal repetido, usa la técnica mostrada en el ejemplo anterior, como fracción simplificada. Después, usando tu calculadora, divide el numerador por el denominador y ve si el resultado coincide con el problema original.
a. 0.02828...
b. 0.2888...
c. 0.00666...
d. 0.1011011...
e. 0.3999...
Entonces, ¿qué opinas de la respuesta a 24f y 25e? Ambos son poco alucinantes. Es un poco difícil de aceptar, pero 0.999999... es realmente el mismo número que 1. No es menos de 1 ¡es exactamente 1! Para 24f, si dejas\(10n = 9.999...\) y\(n =0 .999...\), luego restando\(n\) de\(10n\) rendimientos\(9n = 9\), entonces\(n = 1\). Eso es difícil de tragar, ¡pero es la verdad! Otra forma de ver esto es darse cuenta de que 1/3 + 2/3 = 1. Pero 1/3 = 0.333333... y 2/3 = 0.666666... Entonces, 1/3 + 2/3 = 0.33333... + 0.66666... = 0.99999... Sabemos 1/4 + 2/3 = 1, así que 0.99999... también debe ser igual a 1, también. ¡Oh, estas cosas son demasiado geniales!
Para 0.39999..., el resultado de repetir 9s después de un decimal hace 0.39999... = 0.4 =\(\frac{4}{10} = \frac{2}{5}\).
Entonces, básicamente, cualquier número con un montón de 9 finales termina siendo un decimal de terminación.
Todos los números con los que hemos estado tratando hasta ahora fracciones, terminando decimales y repitiendo decimales conforman los números racionales. Cada número racional se puede escribir como la relación de dos números enteros relativamente primos, y también se puede escribir como un decimal de terminación o repetición. Por el contrario, cada decimal de terminación y repetición es un número racional.
Oh, pero hay más... ¡mucho más!
Los racionales constituyen una parte muy pequeña de los números reales. Para completar el sistema de números reales, tenemos que hablar de los números irracionales. Cada número real es racional o irracional. Aquellos números que no se pueden escribir como la relación de dos números enteros primos relativamente son irracionales. Esos números decimales que ni terminan ni repiten son irracionales. Entonces, ¿cómo se ven?
Uno de los números irracionales más comúnmente conocidos es\(\pi\). Es el número que es la relación de la circunferencia de un círculo a su diámetro. Parece que es una proporción de dos enteros, ¡pero no lo es! \(\pi\)sólo se puede aproximar. La aproximación más común es 3.14 o 22/7. Ninguno de estos es igual\(\pi\) porque ambos son números racionales, ¡y no lo\(\pi\) es!
Otros números irracionales son raíces cuadradas de números que no son cuadrados perfectos, o raíces cubo de números que no son cubos perfectos, etc.
Por ejemplo, estos números son irracionales:\( \sqrt{5}, \sqrt{3}, \sqrt{12}, \sqrt{20}, \sqrt[3]{35}, \sqrt[4]{72}\)
Escribe cinco números irracionales que no estén ya listados arriba ________________________
¿Es\(\sqrt{9}\) irracional? _____ ¿Por qué o por qué no? ________________________________
Otra forma de expresar un número irracional en forma decimal es componer un decimal que quizás tenga algún patrón al mismo, pero nunca termina ni se repite. Dos ejemplos de este tipo son 2.12112111211112... y 5.010203040506070809010011012...
Escribe cuatro números irracionales en forma decimal que muestre un patrón claro.
Escribe tanto un número racional como un número irracional en forma decimal que esté entre 0.53 y 0.54.
Escribe tanto un número racional como un número irracional en forma decimal que esté entre 0.53333... y 0.54444...
Racional ______________________
Irracional ______________________
Clasificar cada uno de los siguientes números como racionales o irracionales.
a. 0.428222... ___________________
b. 0.283848... ___________________
c.\(\frac{5}{13}\) ___________________
d.\(\sqrt{80}\) ___________________
e.\(\sqrt{100}\) ___________________
f.\(\pi\) ___________________