1.3: Decimales
- Page ID
- 110884
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)
La notación decimal se basa en potencias de\(10\):\(0.1\) es una décima,\(0.01\) es una centésima,\(0.001\) es una milésima, y así sucesivamente.
| miles | cientos | decenas | ones/unidades | . | décimas | centésimas | milésimas |
Escribe cada número.
1. noventa y veintitrés centésimas
2. siete y cincuenta y seis milésimas
- Contestar
-
1. 90.23
2. 7.056
Sumando y restando decimales
Antes de sumar o restar decimales, debes alinear los decimales.
Sumar cada par de números.
3. \(3.75+12.8\)
4. \(71.085+112.93\)
- Contestar
-
3. \(16.55\)
4. \(184.015\)
Al restar, es posible que deba agregar ceros al primer número para que pueda pedir prestado correctamente.
Restar cada par de números.
5. \(46.57-38.29\)
6. \(82.78-67.024\)
- Contestar
-
5. \(8.28\)
6. \(15.756\)
Multiplicar decimales
Para multiplicar números decimales:
- Ignorar temporalmente los decimales.
- Multiplique los números como si fueran números enteros.
- Suma el número total de dígitos decimales en los dos números multiplicados. El resultado tendrá ese número de dígitos a la derecha del punto decimal.
Nota: NO es necesario alinear los puntos decimales cuando se está multiplicando.
Multiplica cada par de números.
7. \(13.5\cdot2.9\)
8. \(4.18\cdot3.7\)
9. Evie trabajó\(37.5\) horas a una tasa de pago de $\(17.50\) por hora. ¿Cuánto ganó en total?
- Contestar
-
7. \(39.15\)
8. \(15.466\)
9. $\(656.25\)
Dividiendo decimales
Repasemos el tema favorito de todos, la división larga. Las tres partes de una división se nombran de la siguiente manera: dividendo\(\div\) divisor = cociente. Cuando esto se escribe con un símbolo de división larga, el dividendo está dentro del símbolo, el divisor está a la izquierda y el cociente es la respuesta que creamos en la parte superior.
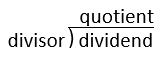
Para dividir por un decimal:
- Escribir en forma de división larga.
- Mueve el punto decimal del divisor hasta que sea un número entero.
- Mueve el punto decimal del dividendo el mismo número de lugares a la derecha.
- Coloque el punto decimal en el cociente directamente por encima del punto decimal en el dividendo. Divide los números como si fueran números enteros.
- Si es necesario, añadir ceros a la derecha del último dígito del dividendo para continuar.
Divide cada par de números.
10. \(97.4\div0.4\)
11. \(9.74\div0.04\)
- Contestar
-
10. \(243.5\)
11. \(2,435\)
Redondeo de números
A menudo es necesario redondear un número a un valor positorio especificado. Discutiremos esto con mucha más profundidad en un módulo futuro, pero practiquemos el redondeo ahora.
Redondeo de un número:
- Localice el dígito de redondeo en el lugar al que esté redondeando.
- Mire el dígito de prueba directamente a la derecha del dígito de redondeo.
- Si el dígito de prueba es 5 o mayor, aumente el dígito de redondeo en 1 y deje caer todos los dígitos a su derecha. Si el dígito de prueba es menor que 5, mantenga el dígito de redondeo igual y baje todos los dígitos a su derecha.
Redondear cada número al valor posicionar indicado.
12. \(6,473\)(miles)
13. \(6,473\)(cientos)
14. \(6,473\)(decenas)
15. \(0.7049\)(décimas)
16. \(0.7049\)(centésimas)
17. \(0.7049\)(milésimas)
- Contestar
-
12. \(6,000\)
13. \(6,500\)
14. \(6,470\)
15. \(0.7\)
16. \(0.70\)
17. \(0.705\)
Si una respuesta decimal sigue y sigue, puede ser práctico redondearla.
18. Jerry condujo\(257\) millas usando\(11\) galones de gasolina. ¿Cuántas millas por galón obtuvo su auto? Redondee su resultado a la décima más cercana.
- Contestar
-
18. \(23.4\)millas por galón