2.6: Resolver una fórmula para una variable específica
( \newcommand{\kernel}{\mathrm{null}\,}\)
Al final de esta sección, podrás:
- Usa la fórmula Distancia, Velocidad y Tiempo
- Resolver una fórmula para una variable específica
Antes de comenzar, toma este cuestionario de preparación.
- Resolver:15t=120.
Si te perdiste este problema, revisa el Ejercicio 2.2.1. - Resolver:6x+24=96.
Si te perdiste este problema, revisa el Ejercicio 2.3.1.
Utilice la fórmula de distancia, tasa y tiempo
Una fórmula que usarás a menudo en álgebra y en la vida cotidiana es la fórmula para la distancia recorrida por un objeto que se mueve a un ritmo constante. Tasa es una palabra equivalente para “velocidad”. La idea básica de tarifa puede que ya te sea familiar. ¿Sabes qué distancia recorres si conduces a una tasa constante de 60 millas por hora durante 2 horas? (Esto podría suceder si usas el control de crucero de tu auto mientras conduces por la carretera). Si dijiste 120 millas, ¡ya sabes cómo usar esta fórmula!
Para un objeto que se mueve a una velocidad uniforme (constante), la distancia recorrida, el tiempo transcurrido y la velocidad están relacionados por la fórmula:
\begin{array} {lllll}{ d = r t} &{\text { where }} &{ d} &{=} &{\text{distance}} \\ {} &{} &{ r} &{=} &{\text{rate}} \\{} &{} &{ t} &{=} &{\text{time}} \end{array}
Utilizaremos la Estrategia para la Resolución de Aplicaciones que usamos anteriormente en este capítulo. Cuando nuestro problema requiere una fórmula, cambiamos el Paso 4. En lugar de escribir una oración, escribimos la fórmula apropiada. Escribimos los pasos revisados aquí para referencia.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Escribir la fórmula apropiada para la situación. Sustituir en la información dada.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
Es posible que desee crear un mini-gráfico para resumir la información en el problema. Ver el gráfico en este primer ejemplo.
Jamal monta su bicicleta a una tarifa uniforme de 12 millas por hora durante3\frac{1}{2} horas. ¿Qué distancia ha recorrido?
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identifica lo que buscas. distancia recorrida Paso 3. Nombre. Elija una variable para representarla. Dejar d = distancia. Paso 4. Traducir: Escribe la fórmula apropiada. d=rt 
Sustituir en la información dada. d = 12\cdot 3\frac{1}{2} Paso 5. Resuelve la ecuación. d=42\text{ miles} Paso 6. Cheque ¿Tiene sentido 42 millas? Paseos en Jamal: 
Paso 7. Contesta la pregunta con una oración completa. Jamal cabalgó 42 millas.
Lindsay manejó durante5\frac{1}{2} horas a 60 millas por hora. ¿Cuánta distancia recorrió?
- Contestar
-
330 millas
Trinh caminó durante2\frac{1}{3} horas a 3 millas por hora. ¿Qué tan lejos caminó?
- Contestar
-
7 millas
Rey planea conducir desde su casa en San Diego para visitar a su abuela en Sacramento, a una distancia de 520 millas. Si puede conducir a un ritmo constante de 65 millas por hora, ¿cuántas horas tomará el viaje?
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identifica lo que buscas. Cuántas horas (tiempo) Paso 3. Nombre.
Elija una variable para representarla.Dejar t = tiempo. 
Paso 4. Traducir.
Escriba la fórmula apropiada.d=rt Sustituir en la información dada. 520 = 65t Paso 5. Resuelve la ecuación. t = 8 Paso 6. Cheque. Sustituye los números en
la fórmula y asegúrate de que el resultado sea una declaración
verdadera.\begin{array}{lll} {d} &{=} &{rt} \\ {520} &{\stackrel{?}{=}} &{65\cdot 8}\\ {520} &{=} &{520\checkmark} \end{array} Paso 7. Contesta la pregunta con una oración completa. El viaje de Rey tomará 8 horas.
Lee quiere conducir desde Phoenix hasta el departamento de su hermano en San Francisco, a una distancia de 770 millas. Si conduce a un ritmo constante de 70 millas por hora, ¿cuántas horas tomará el viaje?
- Contestar
-
11 horas
Yesenia está a 168 millas de Chicago. Si necesita estar en Chicago en 3 horas, ¿a qué ritmo necesita conducir?
- Contestar
-
56 mph
Resolver una fórmula para una variable específica
Probablemente estés familiarizado con algunas fórmulas de geometría. Una fórmula es una descripción matemática de la relación entre variables. Las fórmulas también se utilizan en las ciencias, como la química, la física y la biología. En medicina se utilizan para cálculos para dispensar medicamentos o determinar el índice de masa corporal. Los programas de hojas de cálculo se basan en fórmulas para hacer cálculos. Es importante estar familiarizado con las fórmulas y poder manipularlas fácilmente.
En Ejercicio\PageIndex{1} y Ejercicio\PageIndex{4}, utilizamos la fórmulad=rt. Esta fórmula da el valor de d, distancia, cuando se sustituye en los valores de r y t, la tasa y el tiempo. Pero en Ejercicio\PageIndex{4}, tuvimos que encontrar el valor de t. Sustituimos en valores de d y r y luego usamos álgebra para resolver por tt. Si tuvieras que hacer esto a menudo, tal vez te preguntes por qué no existe una fórmula que dé el valor de t cuando sustituyas en los valores de d y r. Podemos hacer una fórmula como esta resolviendo la fórmulad=rt para t.
Resolver una fórmula para una variable específica significa aislar esa variable en un lado del signo igual con un coeficiente de 1. Todas las demás variables y constantes están en el otro lado del signo igual. Para ver cómo resolver una fórmula para una variable específica, comenzaremos con la fórmula de distancia, tasa y tiempo.
Resuelve la fórmula d=rt para t:
- cuando d=520 y r=65
- en general
- Contestar
-
Escribiremos las soluciones lado a lado para demostrar que resolver una fórmula en general usa los mismos pasos que cuando tenemos números para sustituir.
1. cuando d=520 y r=65 2. en general Escribe la fórmula. d=rt Escribe la fórmula. d=rt Sustituto. 520=65t Dividir, para aislar t. \frac{520}{65} = \frac{65t}{65} Dividir, para aislar tt. \frac{d}{r} = \frac{rt}{t} Simplificar. 8 = t Simplificar. \frac{d}{r}=t Decimos que la fórmulat = \frac{d}{r} está resuelta para t.
Resuelve la fórmulad=rt para r:
- cuando d=180 y t=4
- en general
- Contestar
-
- r = 45
- r = \frac{d}{t}
Resuelve la fórmulad=rt para r:
- cuando d=780 y t=12
- en general
- Contestar
-
- r = 65
- r = \frac{d}{rt
Resuelve la fórmulaA = \frac{1}{2}bh para h:
- cuándoA = 90 yb = 15
- en general
- Contestar
-
Ahora podemos encontrar la altura de un triángulo, si conocemos el área y la base, usando la fórmulah = \frac{2A}{b}1. cuándoA = 90 yb = 15 2. en general Escribe la fórmula. 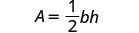
Escribe la fórmula. 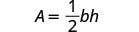
Sustituto. 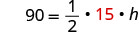
Despeja las fracciones. 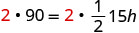
Despeja las fracciones. 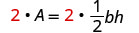
Simplificar. 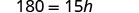
Simplificar. 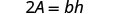
Resolver por h. 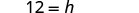
Resolver para hh. 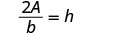
Resuelve la fórmulaA = \frac{1}{2}bh para h:
- cuándoA = 170 yb = 17
- en general
- Contestar
-
- h = 20
- h = \frac{2A}{b}
Resuelve la fórmulaA = \frac{1}{2}bh para h:
- cuándoA = 62 yh = 31
- en general
- Contestar
-
- b = 4
- b = \frac{2A}{h}
La fórmulaI=Prt se utiliza para calcular el interés simple, I, para un principal, P, invertido a tasa, r, para t años.
Resuelve la fórmula I=Prt para encontrar el principal, P:
- cuando I=$5,600, r= 4%, t=7años
- en general
- Contestar
-
1. I=$5,600, r= 4%, t=7años 2. en general Escribe la fórmula. 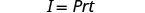
Escribe la fórmula. 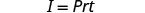
Sustituto. 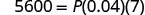
Simplificar. 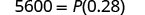
Simplificar. 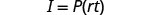
Dividir, para aislar P. 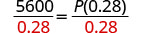
Dividir, para aislar P. 
Simplificar. 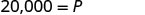
Simplificar. 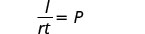
El principal es 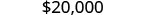
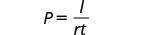
Resuelve la fórmula I=Prt para encontrar el principal, P:
- cuando I=$2160, r= 6%, t=3 años
- en general
- Contestar
-
- $12000
- P = \frac{1}{rt}
Resuelve la fórmula I=Prt para encontrar el principal, P:
- cuando I=$5400, r= 12%, t=5 años
- en general
- Contestar
-
- $9000
- P = \frac{1}{rt}
Resuelve la fórmula 3x+2y=18 para y:
- cuando x=4
- en general
- Contestar
-
1. cuando x=4 2. en general 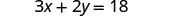
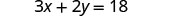
Sustituto. 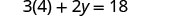
Restar para aislar el
término y.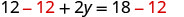
Restar para aislar el
término y.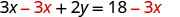
Dividir. 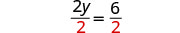
Dividir. 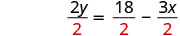
Simplificar. 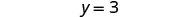
Simplificar. 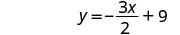
Resuelve la fórmula 3x+4y=10 para y:
- cuandox = \frac{14}{3}
- en general
- Contestar
-
- y = -1
- y = \frac{10 - 3x}{4}
Resuelve la fórmula 5x+2y=18 para y:
- cuandox = 4
- en general
- Contestar
-
- y = -1
- y = \frac{18 - 5x}{2}
Resuelve la fórmula P=A+B+C para a.
- Contestar
-
Aislaremos aa en un lado de la ecuación. 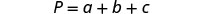
Tanto b como c se suman a a, por lo que los restamos de ambos lados de la ecuación. 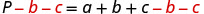
Simplificar. 
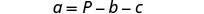
Resolver la fórmula P=a+B+C para b.
- Contestar
-
b=p−a−c
Resolver la fórmula P=A+B+C para c.
- Contestar
-
C=p−a−b
Resuelve la fórmula 6x+5y=13 para y.
- Contestar
-
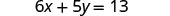
Restar 6x de ambos lados para aislar el término con y. 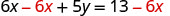
Simplificar. 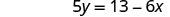
Dividir por 5 para hacer el coeficiente 1. 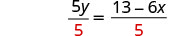
Simplificar. 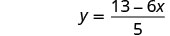
La fracción se simplifica. No podemos dividir 13−6x por 5.
Resuelve la fórmula 4x+7y=9 para y.
- Contestar
-
y = \frac{9 - 4x}{7}
Resuelve la fórmula 5x+8y=1 para y.
- Contestar
-
y = \frac{1 - 5x}{8}
Conceptos clave
- Para resolver una aplicación (con una fórmula)
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Escribir la fórmula apropiada para la situación. Sustituir en la información dada.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
- Distancia, Velocidad y Tiempo
Para un objeto que se mueve a una velocidad uniforme (constante), la distancia recorrida, el tiempo transcurrido y la velocidad se relacionan por la fórmula: d=rt donde d = distancia, r = velocidad, t = tiempo. - Resolver una fórmula para una variable específica significa obtener esa variable por sí misma con un coeficiente de 1 en un lado de la ecuación y todas las demás variables y constantes en el otro lado.


