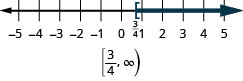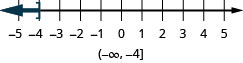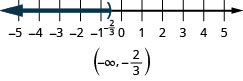2.7: Resolver desigualdades lineales
( \newcommand{\kernel}{\mathrm{null}\,}\)
Al final de esta sección, podrás:
- Graficar desigualdades en la recta numérica
- Resolver desigualdades usando las Propiedades de Suma y Suma de la desigualdad
- Resolver desigualdades utilizando las Propiedades de División y Multiplicación de la desigualdad
- Resolver desigualdades que requieren simplificación
- Traducir a una desigualdad y resolver
Antes de comenzar, toma este cuestionario de preparación.
- Traducir del álgebra al inglés:15>x.
Si te perdiste este problema, revisa el Ejercicio 1.3.1. - Resolver:n−9=−42.
Si te perdiste este problema, revisa el Ejercicio 2.1.7. - Resolver:−5p=−23.
Si te perdiste este problema, revisa el Ejercicio 2.2.1. - Resolver:3a−12=7a−20.
Si te perdiste este problema, revisa el Ejercicio 2.3.22.
Graficar desigualdades en la recta numérica
¿Recuerdas lo que significa que un número sea una solución a una ecuación? Una solución de una ecuación es un valor de una variable que hace una declaración verdadera cuando se sustituye en la ecuación.
¿Qué pasa con la solución de una desigualdad? ¿Qué número haríax>3 verdadera la desigualdad? ¿Estás pensando, 'x podría ser 4'? Eso es correcto, pero x podría ser 5 también, o 20, o incluso 3.001. Cualquier número mayor a 3 es una solución a la desigualdadx>3.
Mostramos las soluciones a la desigualdadx>3 en la recta numérica sombreando todos los números a la derecha de 3, para mostrar que todos los números mayores que 3 son soluciones. Debido a que el número 3 en sí no es una solución, ponemos un paréntesis abierto en 3. La gráfica dex>3 se muestra en la Figura2.7.1. Tenga en cuenta que se utiliza la siguiente convención: las flechas azul claro apuntan en la dirección positiva y las flechas azul oscuro apuntan en la dirección negativa.
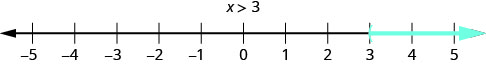
La gráfica de la desigualdadx≥3 es muy parecida a la gráfica dex>3, pero ahora necesitamos demostrar que 3 es una solución, también. Lo hacemos poniendo un corchete enx=3, como se muestra en la Figura2.7.2.
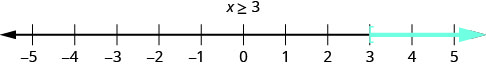
Observe que el símbolo de paréntesis abiertos, (, muestra que no se incluye el punto final de la desigualdad. El símbolo de corchete abierto, [, muestra que el punto final está incluido.
Gráfica en la recta del número:
- x≤1
- x<5
- x>−1
- Contestar
-
1. x≤1Esto significa que todos los números menores o iguales a 1. Sombreamos en todos los números de la línea numérica a la izquierda de 1 y ponemos un corchete en x=1 para mostrar que está incluido.
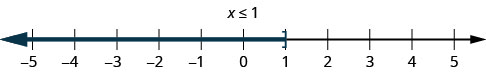
2. x<5Esto significa todos los números menores que 5, pero sin incluir 5. Sombreamos todos los números en la recta numérica a la izquierda de 5 y ponemos un paréntesis en x=5 para mostrar que no está incluido.
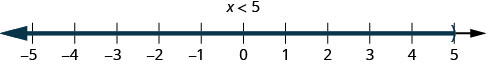
3. x>−1Esto significa todos los números mayores que −1, pero sin incluir −1. Sombreamos todos los números en la línea numérica a la derecha de −1, luego ponemos un paréntesis en x=−1 para mostrar que no está incluido.
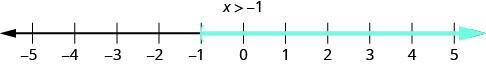
Gráfica en la recta numérica:
- x≤−1
- x>2
- x<3
- Contestar
-
Gráfica en la recta numérica:
- x>−2
- x<−3
- x≥−1
- Contestar
-
También podemos representar desigualdades usando notación de intervalos. Como vimos anteriormente, la desigualdadx>3 significa todos los números mayores que 3. No hay un extremo superior para la solución a esta desigualdad. En notación de intervalos, expresamosx>3 como(3,∞). El símbolo∞ se lee como 'infinito'. No es un número real. La figura2.7.3 muestra tanto la línea numérica como la notación de intervalo.

La desigualdadx≤1 significa todos los números menores o iguales a 1. No hay un extremo inferior para esos números. Escribimosx≤1 en notación de intervalos como(−∞,1]. El símbolo−∞ se lee como 'infinito negativo'. La figura2.7.4 muestra tanto la línea numérica como la notación de intervalo.


¿Se dio cuenta de cómo el paréntesis o paréntesis en la notación de intervalo coincide con el símbolo en el punto final de la flecha? Estas relaciones se muestran en la Figura2.7.5.

Gráfica en la recta numérica y escribe en notación de intervalos.
- x≥−3
- x<2.5
- x≤35
- Contestar
-
1.
2.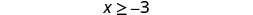
Sombra a la derecha de −3 y coloque un soporte en −3. 
Escribir en notación de intervalos. 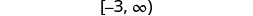
3.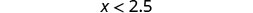
Sombra a la izquierda de 2.5, y ponga un paréntesis en 2.5. 
Escribir en notación de intervalos. 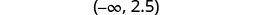
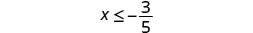
Sombra a la izquierda de−35, y poner un soporte en−35. 
Escribir en notación de intervalos. 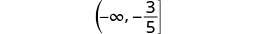
Gráfica en la recta numérica y escribe en notación de intervalo:
- x>2
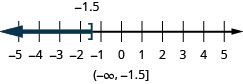
- x≤−1.5
- x≥34
- Contestar
-
Gráfica en la recta numérica y escribe en notación de intervalo:
- x≤−4
- x≥0.5
- x<−23
- Contestar
-
Resolver desigualdades usando las propiedades de resta y suma de la desigualdad
Las Propiedades de Suma y Suma de Igualdad establecen que si dos cantidades son iguales, cuando sumamos o restamos la misma cantidad de ambas cantidades, los resultados serán iguales.
Subtraction Property of Equality Addition Property of Equality For any numbers a,b, and c, For any numbers a,b, and c if a=b, if a=b then a−c=b−c. then a+c=b+c
Propiedades similares son ciertas para las desigualdades.
| Por ejemplo, sabemos que −4 es menor que 2. | 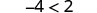 |
| Si restamos 5 de ambas cantidades, ¿el lado izquierdo sigue siendo menor que el lado derecho? | 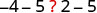 |
| Obtenemos −9 a la izquierda y −3 a la derecha. |  |
| Y sabemos que −9 es menor que −3. |  |
|
El signo de desigualdad se mantuvo igual. |
De igual manera podríamos demostrar que la desigualdad también se mantiene igual para la suma.
Esto nos lleva a las Propiedades de Suma y Suma de la Desigualdad.
Subtraction Property of Inequality Addition Property of Inequality For any numbers a,b, and c, For any numbers a,b, and c if a<b if a<b then a−c<b−c. then a+c<b+c if a>b if a>b then a−c>b−c. then a+c>b+c
Utilizamos estas propiedades para resolver desigualdades, dando los mismos pasos que usamos para resolver ecuaciones. Resolviendo la desigualdadx+5>9, los pasos se verían así:
x+5>9Subtract 5 from both sides to isolate x.x+5−5>9−5x>4
Cualquier número mayor a 4 es una solución a esta desigualdad.
Resuelva la desigualdadn−12≤58, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
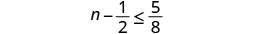
Agregar12 a ambos lados de la desigualdad. 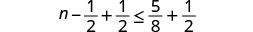
Simplificar. 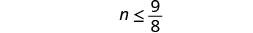
Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos.
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
p−34≥16
- Contestar
-
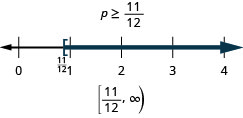
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
r−13≤712
- Contestar
-
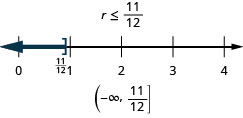
Resolver desigualdades utilizando las propiedades de división y multiplicación de la desigualdad
Las Propiedades de División y Multiplicación de Igualdad establecen que si dos cantidades son iguales, cuando dividimos o multiplicamos ambas cantidades por la misma cantidad, los resultados también serán iguales (siempre que no dividamos por 0).
Division Property of EqualityMUltiplication Property of EqualityFor any numbers a, b, c, and c≠0For any numbers a, b, cif a=bifa=bthen ac=bcthen ac=bc
¿Existen propiedades similares para las desigualdades? ¿Qué pasa con una desigualdad cuando dividimos o multiplicamos ambos lados por una constante?
Considera algunos ejemplos numéricos.
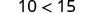 |
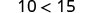 |
||
| Divide ambos lados por 5. | 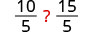 |
Multiplica ambos lados por 5. |  |
| Simplificar. |  |
 |
|
| Rellenar los signos de desigualdad. |  |
 |
Los signos de desigualdad permanecieron igual.
¿La desigualdad permanece igual cuando dividimos o multiplicamos por un número negativo?
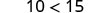 |
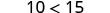 |
||
| Divide ambos lados por -5. | 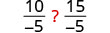 |
Multiplica ambos lados por -5. |  |
| Simplificar. |  |
 |
|
| Rellenar los signos de desigualdad. |  |
 |
Los signos de desigualdad invirtieron su rumbo.
Cuando dividimos o multiplicamos una desigualdad por un número positivo, el signo de desigualdad permanece igual. Cuando dividimos o multiplicamos una desigualdad por un número negativo, el signo de desigualdad se invierte.
Aquí están las Propiedades de División y Multiplicación de la Desigualdad para una fácil referencia.
Para cualquier número real a, b, c
if a<b and c>0, thenac<bc and ac<bcif a>b and c>0, thenac>bc and ac>bcif a<b and c<0, thenac>bc and ac>bcif a>b and c<0, thenac<bc and ac<bc
Cuando dividimos o multiplicamos una desigualdad por un:
- número positivo, la desigualdad se mantiene igual.
- número negativo, la desigualdad se invierte.
Resuelva la desigualdad7y<42, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
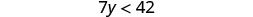
Dividir ambos lados de la desigualdad entre 7.
Ya que7>0, la desigualdad se mantiene igual.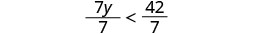
Simplificar. 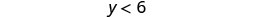
Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. 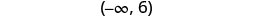
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
9c>72
- Contestar
-
c>8

(8, \infty)
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
12d\leq 60
- Contestar
-
d\leq 5

(-\infty, 5]
Resuelva la desigualdad−10a\geq 50, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
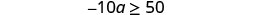
Dividir ambos lados de la desigualdad entre −10.
Ya que−10<0, la desigualdad revierte.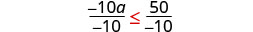
Simplificar. 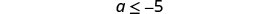
Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. 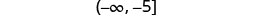
Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.
−8q<32
- Contestar
-
q>−4
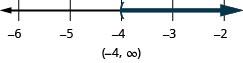
Resuelve cada desigualdad, grafica la solución en la recta numérica y escribe la solución en notación de intervalos.
−7r\leq −70
- Contestar
-
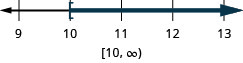
A veces al resolver una desigualdad, la variable termina por la derecha. Podemos reescribir la desigualdad a la inversa para obtener la variable a la izquierda.
\begin{array}{l} x > a\text{ has the same meaning as } a < x \end{array}
Piénsalo como “Si Xavier es más alto que Alex, entonces Alex es más bajo que Xavier”.
Resuelva la desigualdad-20 < \frac{4}{5}u, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
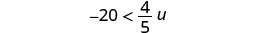
Multiplicar ambos lados de la desigualdad por\frac{5}{4}.
Ya que\frac{5}{4} > 0, la desigualdad se mantiene igual.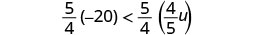
Simplificar. 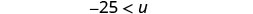
Reescribe la variable de la izquierda. 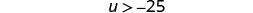
Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. 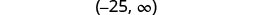
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
24 \leq \frac{3}{8}m
- Contestar
-
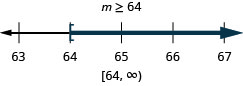
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
-24 < \frac{4}{3}n
- Contestar
-
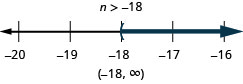
Resuelva la desigualdad\frac{t}{-2} \geq 8, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
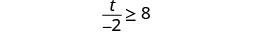
Multiplique ambos lados de la desigualdad por −2.
Ya que−2<0, la desigualdad revierte.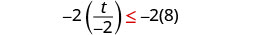
Simplificar. 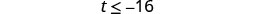
Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. 
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
\frac{k}{-12}\leq 15
- Contestar
-
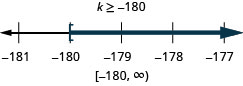
Resuelva la desigualdad, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
\frac{u}{-4}\geq -16
- Contestar
-
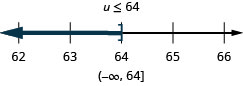
Resolver desigualdades que requieren simplificación
La mayoría de las desigualdades tardarán más de un paso en resolverse. Seguimos los mismos pasos que usamos en la estrategia general para resolver ecuaciones lineales, pero asegúrese de prestar mucha atención durante la multiplicación o división.
Resuelva la desigualdad4m\leq 9m+17, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
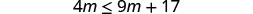
Restar 9m de ambos lados para recoger las variables de la izquierda. 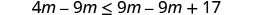
Simplificar. 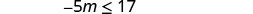
Dividir ambos lados de la desigualdad por −5 e invertir la desigualdad. 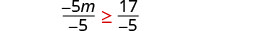
Simplificar. 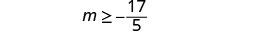
Grafique la solución en la recta numérica. 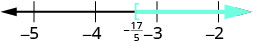
Escribe la solución en notación de intervalos. 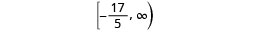
Resuelva la desigualdad3q\geq 7q−23, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
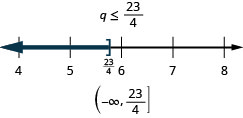
Resuelva la desigualdad6x<10x+19, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
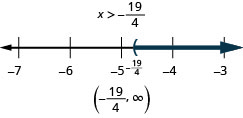
Resolver la desigualdad8p+3(p−12)>7p−28 grafica la solución en la recta numérica, y escribe la solución en notación de intervalos.
- Contestar
-
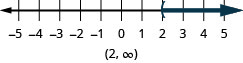
Simplifica cada lado tanto como sea posible. 8p+3 (p−12) >7p−28 Distribuir. 8p+3p−36>7p−28 Combina términos similares. 11p−36>7p−28 Restar 7p de ambos lados para recoger las variables de la izquierda. 11p−36−7p>7p−28−7p Simplificar. 4p−36>−28 Agrega 36 a ambos lados para recoger las constantes de la derecha. 4p−36+36>−28+36 Simplificar. 4p>8 Dividir ambos lados de la desigualdad por 4; la desigualdad permanece igual. \frac{4p}{4}>84 Simplificar. p>2 Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. (2, \infty)
Resuelva la desigualdad9y+2(y+6)>5y−24, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
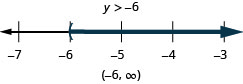
Resuelva la desigualdad6u+8(u−1)>10u+32, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
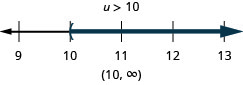
Así como algunas ecuaciones son identidades y otras son contradicciones, las desigualdades pueden ser identidades o contradicciones, también. Reconocemos estas formas cuando solo nos quedan constantes a medida que resolvemos la desigualdad. Si el resultado es una declaración verdadera, tenemos una identidad. Si el resultado es una declaración falsa, tenemos una contradicción.
Resuelva la desigualdad8x−2(5−x)<4(x+9)+6x, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
Simplifica cada lado tanto como sea posible. 8x−2 (5−x) <4 (x+9) +6x Distribuir. 8x−10+2x<4x+36+6x Combina términos similares. 10x−10<10x+36 Restar 10x de ambos lados para recoger las variables de la izquierda. 10x−10−10x<10x+36−10x Simplificar. −10<36 Los xx se han ido, y tenemos una declaración verdadera. La desigualdad es una identidad.
La solución son todos los números reales.Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. (-\infty, \infty)
Resuelva la desigualdad4b−3(3−b)>5(b−6)+2b, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
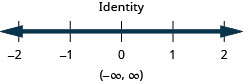
Resuelva la desigualdad9h−7(2−h)<8(h+11)+8h, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
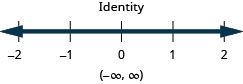
Resuelva la desigualdad\frac{1}{3}a - \frac{1}{8}a > \frac{5}{24}a + \frac{3}{4}, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
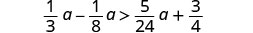
Multiplica ambos lados por la LCD, 24, para borrar las fracciones. 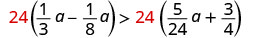
Simplificar. 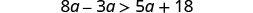
Combina términos similares. 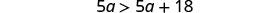
Restar 5a de ambos lados para recoger las variables de la izquierda. 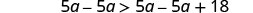
Simplificar. 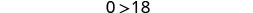
¡El enunciado es falso! La desigualdad es una contradicción. No hay solución. Grafique la solución en la recta numérica. 
Escribe la solución en notación de intervalos. No hay solución.
Resuelva la desigualdad\frac{1}{4}x - \frac{1}{12}x > \frac{1}{6}x + \frac{7}{8}, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
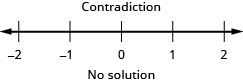
Resuelva la desigualdad\frac{2}{5}z - \frac{1}{3}z < \frac{1}{15}z - \frac{3}{5}, grafique la solución en la recta numérica y escriba la solución en notación de intervalos.
- Contestar
-
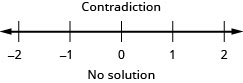
Traducir a una Desigualdad y Resolver
Para traducir frases en inglés en desigualdades, necesitamos reconocer las frases que indican la desigualdad. Algunas palabras son fáciles, como 'más que' y 'menos que'. Pero otros no son tan obvios.
Piensa en la frase 'al menos' — ¿qué significa tener 'al menos 21 años'? Significa 21 o más. La frase 'al menos' es la misma que 'mayor o igual a'.
\PageIndex{4}[1]La tabla muestra algunas frases comunes que indican desigualdades.
| > | \geq | < | \leq |
|---|---|---|---|
| “data-valign="middle” class="lt-math-15134">es mayor que | \ (\ geq\)” data-valign="middle” class="lt-math-15134">es mayor o igual a | es menor que | \ (\ leq\)” data-valign="middle” class="lt-math-15134">es menor o igual a |
| “data-valign="middle” class="lt-math-15134">es más que | \ (\ geq\)” data-valign="middle” class="lt-math-15134">es al menos | es menor que | \ (\ leq\)” data-valign="middle” class="lt-math-15134">es como máximo |
| “data-valign="middle” class="lt-math-15134">es mayor que | \ (\ geq\)” data-valign="middle” class="lt-math-15134">no es menor que | tiene menos de | \ (\ leq\)” data-valign="middle” class="lt-math-15134">no es más que |
| “data-valign="middle” class="lt-math-15134">supera | \ (\ geq\)” data-valign="middle” class="lt-math-15134">es el mínimo | es menor que | \ (\ leq\)” data-valign="middle” class="lt-math-15134">es el máximo |
Traducir y resolver. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Doce veces c no es más de 96.
- Contestar
-
Traducir. 
Solucionar: divide ambos lados por 12. 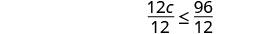
Simplificar. 
Escribir en notación de intervalos. 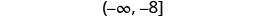
Gráfica en la recta numérica. 
Traducir y resolver. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Veinte veces y es como máximo 100
- Contestar
-
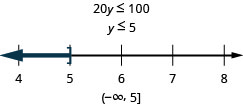
Traducir y resolver. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Nueve veces z no es menos de 135
- Contestar
-
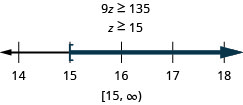
Traducir y resolver. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Treinta menos que x es al menos 45.
- Contestar
-
Traducir. 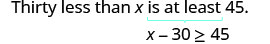
Solve: agregue 30 a ambos lados. 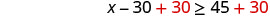
Simplificar. 
Escribir en notación de intervalos. 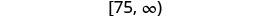
Gráfica en la recta numérica. 
Traducir y resolver. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Diecinueve menos que p no es menor que 47
- Contestar
-
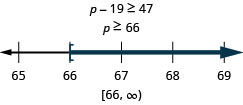
Traducir y resolver. Después escribe la solución en notación de intervalos y grafica en la recta numérica.
Cuatro más que un es como máximo 15.
- Contestar
-
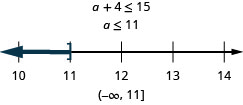
Conceptos clave
- Propiedad de resta de desigualdad
Para cualquier número a, b y c,
si a<b entonces a−c<b−c y
si a>b entonces a−c>b−c. - Adición Propiedad de Desigualdad
Para cualquier número a, b y c,
si a<b entonces a+c<b+c y
si a>b entonces a+c>b+c. - División y Multiplicación Propiedades de Inequalit y
Para cualquier número a, b, y c,
si a <b and c>0, entonces ac <bc and ac>bc.
si a>b y c>0, entonces ac>bc y ac>bc.
si a<b y cbc<0, then ac> y ac>bc.
si a>b y c<0, entonces ac<bc y ac<bc. - Cuando dividimos o multiplicamos una desigualdad por un:
- número positivo, la desigualdad se mantiene igual.
- número negativo, la desigualdad se invierte.