6.1: Sumar y restar polinomios
- Page ID
- 110382
Al final de esta sección, podrás:
- Identificar polinomios, monomios, binomios y trinomios
- Determinar el grado de polinomios
- Sumar y restar monomios
- Sumar y restar polinomios
- Evaluar un polinomio para un valor dado
Antes de comenzar, toma este cuestionario de preparación.
- Simplificar:\(8x+3x\).
Si te perdiste este problema, revisa Ejercicio 1.3.37. - Restar:\((5n+8)−(2n−1)\).
Si te perdiste este problema, revisa Ejercicio 1.10.52. - Escribir en forma expandida:\(a^{5}\).
Si te perdiste este problema, revisa el Ejercicio 1.3.7.
Identificar polinomios, monomios, binomios y trinomios
Has aprendido que un término es una constante o producto de una constante y una o más variables. Cuando es de la forma\(ax^{m}\), donde\(a\) es una constante y\(m\) es un número entero, se le llama monomio. Algunos ejemplos de monomio son\(8,−2x^{2},4y^{3}\), y\(11z^{7}\).
Un monomio es un término de la forma\(ax^{m}\), donde\(a\) es una constante y\(m\) es un número entero positivo.
Un monomio, o dos o más monomios combinados por suma o resta, es un polinomio. Algunos polinomios tienen nombres especiales, basados en el número de términos. Un monomio es un polinomio con exactamente un término. Un binomio tiene exactamente dos términos, y un trinomio tiene exactamente tres términos. No hay nombres especiales para polinomios con más de tres términos.
- polinomio —Un monomio, o dos o más monomios combinados por suma o resta, es un polinomio.
- monomial —Un polinomio con exactamente un término se llama monomio.
- binomio —Un polinomio con exactamente dos términos se llama binomio.
- trinomio —Un polinomio con exactamente tres términos se llama trinomio.
Aquí algunos ejemplos de polinomios.
\[\begin{array}{lllll}{\text { Polynomial }} & {b+1} &{4 y^{2}-7 y+2} & {4 x^{4}+x^{3}+8 x^{2}-9 x+1} \\ {\text { Monomial }} & {14} & {8 y^{2}} & {-9 x^{3} y^{5}} & {-13}\\ {\text { Binomial }} & {a+7}&{4 b-5} & {y^{2}-16}& {3 x^{3}-9 x^{2}} \\ {\text { Trinomial }} & {x^{2}-7 x+12} & {9 y^{2}+2 y-8} & {6 m^{4}-m^{3}+8 m}&{z^{4}+3 z^{2}-1} \end{array} \nonumber\]
Observe que cada monomio, binomio y trinomio es también un polinomio. Solo son miembros especiales de la “familia” de polinomios y así tienen nombres especiales. Usamos las palabras monomio, binomio y trinomio cuando nos referimos a estos polinomios especiales y simplemente llamamos a todos los polinomios restantes.
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio.
- \(4y^{2}−8y−6\)
- \(−5a^{4}b^{2}\)
- \(2x^{5}−5x^{3}−3x + 4\)
- \(13−5m^{3}\)
- q
- Contestar
-
\(\begin{array}{lll}&{\text { Polynomial }} & {\text { Number of terms }} & {\text { Type }} \\ {\text { (a) }} & {4 y^{2}-8 y-6} & {3} & {\text { Trinomial }} \\ {\text { (b) }} & {-5 a^{4} b^{2}} & {1} & {\text { Monomial }} \\ {\text { (c) }} & {2 x^{5}-5 x^{3}-9 x^{2}+3 x+4} & {5} & {\text { Ponomial }} \\ {\text { (d) }} & {13-5 m^{3}} & {2} & {\text { Binomial }} \\ {\text { (e) }} & {q} & {1} & {\text { Monomial }}\end{array}\)
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio:
- 5b
- \(8 y^{3}-7 y^{2}-y-3\)
- \(-3 x^{2}-5 x+9\)
- \(81-4 a^{2}\)
- \(-5 x^{6}\)
- Contestar
-
- monomial
- polinomio
- trinomio
- binomio
- monomial
Determinar si cada polinomio es un polinomio, binomio, trinomio u otro polinomio:
- \(27 z^{3}-8\)
- \(12 m^{3}-5 m^{2}-2 m\)
- \(\frac{5}{6}\)
- \(8 x^{4}-7 x^{2}-6 x-5\)
- \(-n^{4}\)
- Contestar
-
- binomio
- trinomio
- monomial
- polinomio
- monomial
Determinar el grado de polinomios
El grado de un polinomio y el grado de sus términos están determinados por los exponentes de la variable. Un monomio que no tiene variable, solo una constante, es un caso especial. El grado de una constante es 0, es decir, no tiene variable.
- El grado de un término es la suma de los exponentes de sus variables.
- El grado de una constante es 0.
- El grado de un polinomio es el grado más alto de todos sus términos.
Veamos cómo funciona esto al observar varios polinomios. Lo llevaremos paso a paso, comenzando por monomios, y luego progresando a polinomios con más términos.
Un polinomio está en forma estándar cuando los términos de un polinomio se escriben en orden descendente de grados. Acostúmbrese a escribir el término con el grado más alto primero.
Encuentra el grado de los siguientes polinomios.
- 10y
- \(4 x^{3}-7 x+5\)
- −15
- \(-8 b^{2}+9 b-2\)
- \(8 x y^{2}+2 y\)
- Contestar
-
- \(\begin{array}{ll} & 10y\\ \text{The exponent of y is one. } y=y^1 & \text{The degree is 1.}\end{array}\)
- \(\begin{array}{ll} & 4 x^{3}-7 x+5\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
- \(\begin{array}{ll} & -15\\ \text{The degree of a constant is 0.} & \text{The degree is 0.}\end{array}\)
- \(\begin{array}{ll} & -8 b^{2}+9 b-2\\ \text{The highest degree of all the terms is 2.} & \text{The degree is 2.}\end{array}\)
- \(\begin{array}{ll} & 8 x y^{2}+2 y\\ \text{The highest degree of all the terms is 3.} & \text{The degree is 3.}\end{array}\)
Encuentra el grado de los siguientes polinomios:
- −15b
- \(10 z^{4}+4 z^{2}-5\)
- \(12 c^{5} d^{4}+9 c^{3} d^{9}-7\)
- \(3 x^{2} y-4 x\)
- −9
- Contestar
-
- 1
- 4
- 12
- 3
- 0
Encuentra el grado de los siguientes polinomios:
- 52
- \(a^{4} b-17 a^{4}\)
- \(5 x+6 y+2 z\)
- \(3 x^{2}-5 x+7\)
- \(-a^{3}\)
- Contestar
-
- 0
- 5
- 1
- 2
- 3
Sumar y restar monomios
Has aprendido a simplificar expresiones combinando términos similares. Recuerde, los términos similares deben tener las mismas variables con el mismo exponente. Dado que los monomios son términos, sumar y restar monomios es lo mismo que combinar términos similares. Si los monomios son como términos, simplemente los combinamos sumando o restando el coeficiente.
Agregar:\(25 y^{2}+15 y^{2}\)
- Contestar
-
\(\begin{array}{ll} & 25 y^{2}+15 y^{2}\\ \text{Combine like terms.} & 40y^{2}\end{array}\)
Agregar:\(12 q^{2}+9 q^{2}\)
- Responder
-
21\(q^{2}\)
Agregar:\(-15 c^{2}+8 c^{2}\)
- Responder
-
\(-7 c^{2}\)
Restar: 16p− (−7p)
- Responder
-
\(\begin{array}{ll} & 16p−(−7p) \\ \text{Combine like terms.} & 23p\end{array}\)
Restar: 8m− (−5m).
- Responder
-
13m
Restar:\(-15 z^{3}-\left(-5 z^{3}\right)\)
- Responder
-
\(-10 z^{3}\)
Recuerda que términos similares deben tener las mismas variables con los mismos exponentes.
Simplificar:\(c^{2}+7 d^{2}-6 c^{2}\)
- Responder
-
\(\begin{array}{ll} & c^{2}+7 d^{2}-6 c^{2} \\ \text{Combine like terms.} & -5 c^{2}+7 d^{2} \end{array}\)
Agregar:\(8 y^{2}+3 z^{2}-3 y^{2}\)
- Responder
-
\(5 y^{2}+3 z^{2}\)
Agregar:\(3 m^{2}+n^{2}-7 m^{2}\)
- Responder
-
\(-4 m^{2}+n^{2}\)
Simplificar:\(u^{2} v+5 u^{2}-3 v^{2}\)
- Responder
-
\ (\ begin {array} {ll} &u^ {2} v+5 u^ {2} -3 v^ {2}
\\ text {No hay términos similares para combinar.} & u^ {2} v+5 u^ {2} -3 v^ {2}\ end {array}\)
Simplificar:\(m^{2} n^{2}-8 m^{2}+4 n^{2}\)
- Responder
-
No hay términos similares para combinar.
Simplificar:\(p q^{2}-6 p-5 q^{2}\)
- Responder
-
No hay términos similares para combinar.
Sumar y restar polinomios
Podemos pensar en sumar y restar polinomios como simplemente sumar y restar una serie de monomios. Busque los términos similares, aquellos con las mismas variables y el mismo exponente. La propiedad conmutativa nos permite reorganizar los términos para armar términos similares.
Encuentra la suma:\(\left(5 y^{2}-3 y+15\right)+\left(3 y^{2}-4 y-11\right)\)
- Responder
-
Identificar términos similares.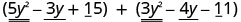 
Reorganízalo para reunir los términos similares.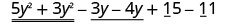 
Combina términos similares.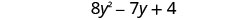 
Encuentra la suma:\(\left(7 x^{2}-4 x+5\right)+\left(x^{2}-7 x+3\right)\)
- Responder
-
\(8 x^{2}-11 x+1\)
Encuentra la suma:\(\left(14 y^{2}+6 y-4\right)+\left(3 y^{2}+8 y+5\right)\)
- Responder
-
\(17 y^{2}+14 y+1\)
Encuentra la diferencia:\(\left(9 w^{2}-7 w+5\right)-\left(2 w^{2}-4\right)\)
- Responder
-
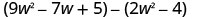
Distribuir e identificar términos similares.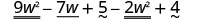 
Reorganizar los términos.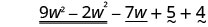 
Combina términos similares.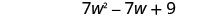 
Encuentra la diferencia:\(\left(8 x^{2}+3 x-19\right)-\left(7 x^{2}-14\right)\)
- Responder
-
\(15 x^{2}+3 x-5\)
Encuentra la diferencia:\(\left(9 b^{2}-5 b-4\right)-\left(3 b^{2}-5 b-7\right)\)
- Responder
-
\(6 b^{2}+3\)
Restar:\(\left(c^{2}-4 c+7\right)\) de\(\left(7 c^{2}-5 c+3\right)\)
- Responder
-
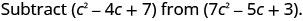
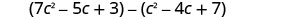
Distribuir e identificar términos similares.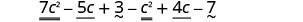 
Reorganizar los términos.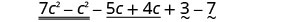 
Combina términos similares.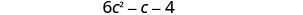 
Restar:\(\left(5 z^{2}-6 z-2\right)\) de\(\left(7 z^{2}+6 z-4\right)\)
- Responder
-
\(2 z^{2}+12 z-2\)
Restar:\(\left(x^{2}-5 x-8\right)\) de\(\left(6 x^{2}+9 x-1\right)\)
- Responder
-
\(5 x^{2}+14 x+7\)
Encuentra la suma:\(\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)\)
- Responder
-
\(\begin{array} {ll} & {\left(u^{2}-6 u v+5 v^{2}\right)+\left(3 u^{2}+2 u v\right)} \\\text{Distribute.} & {u^{2}-6 u v+5 v^{2}+3 u^{2}+2 u v} \\ \text{Rearrange the terms, to put like terms together} & {u^{2}+3 u^{2}-6 u v+2 u v+5 v^{2}} \\ \text{Combine like terms.} & {4 u^{2}-4 u v+5 v^{2}}\end{array}\)
Encuentra la suma:\(\left(3 x^{2}-4 x y+5 y^{2}\right)+\left(2 x^{2}-x y\right)\)
- Responder
-
\(5 x^{2}-5 x y+5 y^{2}\)
Encuentra la suma:\(\left(2 x^{2}-3 x y-2 y^{2}\right)+\left(5 x^{2}-3 x y\right)\)
- Responder
-
\(7 x^{2}-6 x y-2 y^{2}\)
Encuentra la diferencia:\(\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)\)
- Responder
-
\(\begin{array}{ll} & {\left(p^{2}+q^{2}\right)-\left(p^{2}+10 p q-2 q^{2}\right)} \\ \text{Distribute.} &{p^{2}+q^{2}-p^{2}-10 p q+2 q^{2}} \\\text{Rearrange the terms, to put like terms together} & {p^{2}-p^{2}-10 p q+q^{2}+2 q^{2}} \\\text{Combine like terms.} & {-10 p q+3 q^{2}}\end{array}\)
Encuentra la diferencia:\(\left(a^{2}+b^{2}\right)-\left(a^{2}+5 a b-6 b^{2}\right)\)
- Responder
-
\(-5 a b-5 b^{2}\)
Encuentra la diferencia:\(\left(m^{2}+n^{2}\right)-\left(m^{2}-7 m n-3 n^{2}\right)\)
- Responder
-
\(4 n^{2}+7 m n\)
Simplificar:\(\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)\)
- Responder
-
\(\begin{array}{ll } & {\left(a^{3}-a^{2} b\right)-\left(a b^{2}+b^{3}\right)+\left(a^{2} b+a b^{2}\right)} \\ \text{Distribute.} &{a^{3}-a^{2} b-a b^{2}-b^{3}+a^{2} b+a b^{2}} \\ \text{Rearrange the terms, to put like terms together} & {a^{3}-a^{2} b+a^{2} b-a b^{2}+a b^{2}-b^{3}} \\ \text{Combine like terms.} &{a^{3}-b^{3}}\end{array}\)
Simplificar:\(\left(x^{3}-x^{2} y\right)-\left(x y^{2}+y^{3}\right)+\left(x^{2} y+x y^{2}\right)\)
- Responder
-
\(x^{3}-y^{3}\)
Simplificar:\(\left(p^{3}-p^{2} q\right)+\left(p q^{2}+q^{3}\right)-\left(p^{2} q+p q^{2}\right)\)
- Responder
-
\(p^{3}-2 p^{2} q+q^{3}\)
Evaluar un polinomio para un valor dado
Ya aprendimos a evaluar expresiones. Dado que los polinomios son expresiones, seguiremos los mismos procedimientos para evaluar un polinomio. Sustituiremos el valor dado por la variable y luego simplificaremos usando el orden de las operaciones.
Evaluar\(5x^{2}−8x+4\) cuándo
- x=4
- x=−2
- x=0
- Responder
-
1. x=4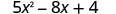 
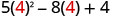
Simplifica los exponentes.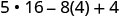 
Multiplicar.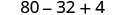 
Simplificar.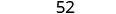 
2. x=−2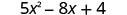 
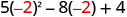
Simplifica los exponentes.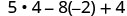 
Multiplicar.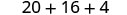 
Simplificar.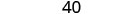 
3. x=0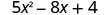 
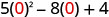
Simplifica los exponentes.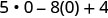 
Multiplicar.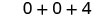 
Simplificar.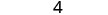 
Evaluar:\(3x^{2}+2x−15\) cuando
- x=3
- x=−5
- x=0
- Responder
-
- 18
- 50
- −15
Evaluar:\(5z^{2}−z−4\) cuando
- z=−2
- z=0
- z=2
- Responder
-
- 18
- −4
- 14
El polinomio\(−16t^{2}+250\) da la altura de una bola tt segundos después de que se cae de un edificio de 250 pies de altura. Encuentra la altura después de t=2 segundos.
- Responder
-
\(\begin{array}{ll } & −16t^{2}+250 \\ \text{Substitute t = 2.} & -16(2)^{2} + 250 \\ \text{Simplify }& −16\cdot 4+250 \\ \text{Simplify }& -64 + 250\\ \text{Simplify }& 186 \\& \text{After 2 seconds the height of the ball is 186 feet. } \end{array}\)
El polinomio\(−16t^{2}+250\) da la altura de una bola tt segundos después de que se cae de un edificio de 250 pies de altura. Encuentra la altura después de t=0 segundos.
- Responder
-
250
El polinomio\(−16t^{2}+250\) da la altura de una bola tt segundos después de que se cae de un edificio de 250 pies de altura. Encuentra la altura después de t=3 segundos.
- Responder
-
106
El polinomio\(6x^{2}+15xy\) da el costo, en dólares, de producir un contenedor rectangular cuya parte superior e inferior son cuadrados con lado x pies y lados de altura y pies. Encuentre el costo de producir una caja con x=4 pies e y=6y=6 pies.
- Responder
-
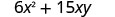
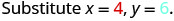
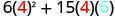
Simplificar.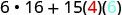 
Simplificar.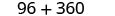 
Simplificar.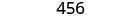 
El costo de producir la caja es de 456 dólares.
El polinomio\(6x^{2}+15xy\) da el costo, en dólares, de producir un contenedor rectangular cuya parte superior e inferior son cuadrados con lado x pies y lados de altura y pies. Encuentre el costo de producir una caja con x=6 pies e y=4 pies.
- Responder
-
$576
El polinomio\(6x^{2}+15xy\) da el costo, en dólares, de producir un contenedor rectangular cuya parte superior e inferior son cuadrados con lado x pies y lados de altura y pies. Encuentre el costo de producir una caja con x=5 pies e y=8 pies.
- Responder
-
$750
Conceptos clave
- Monomios
- Un monomio es un término de la forma\(ax^{m}\), donde aa es una constante y mm es un número entero
- Un monomio es un término de la forma\(ax^{m}\), donde aa es una constante y mm es un número entero
- Polinomios
- polinomio —Un monomio, o dos o más monomios combinados por suma o resta es un polinomio.
- monomial —Un polinomio con exactamente un término se llama monomio.
- binomio —Un polinomio con exactamente dos términos se llama binomio.
- trinomio —Un polinomio con exactamente tres términos se llama trinomio.
- Grado de un polinomio
- El grado de un término es la suma de los exponentes de sus variables.
- El grado de una constante es 0.
- El grado de un polinomio es el grado más alto de todos sus términos.
Glosario
- binomio
- Un binomio es un polinomio con exactamente dos términos.
- grado de una constante
- El grado de cualquier constante es 0.
- grado de un polinomio
- El grado de un polinomio es el grado más alto de todos sus términos.
- grado de un término
- El grado de un término es el exponente de su variable.
- monomial
- Un monomio es un término de la forma\(ax^m\), donde a es una constante y m es un número entero; un monomio tiene exactamente un término.
- polinomio
- Un polinomio es un monomio, o dos o más monomios combinados por suma o resta.
- forma estándar
- Un polinomio está en forma estándar cuando los términos de un polinomio se escriben en orden descendente de grados.
- trinomio
- Un trinomio es un polinomio con exactamente tres términos.