6.7: Exponentes enteros y notación científica
- Page ID
- 110346
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Usar la definición de un exponente negativo
- Simplificar expresiones con exponentes enteros
- Convertir de notación decimal a notación científica
- Convertir notación científica en forma decimal
- Multiplicar y dividir usando notación científica
Antes de comenzar, toma este cuestionario de preparación.
- ¿Cuál es el valor posicional del 6 en el número 64891?
Si te perdiste este problema, revisa el Ejercicio 1.2.1. - Nombrar el decimal: 0.0012.
Si te perdiste este problema, revisa el Ejercicio 1.8.1. - Restar: 5− (−3).
Si te perdiste este problema, revisa el Ejercicio 1.4.33.
Usar la definición de un exponente negativo
Vimos que la Propiedad de Cociente para Exponentes introducida anteriormente en este capítulo, tiene dos formas dependiendo de si el exponente es mayor en el numerador o en el denominador.
Si a es un número real\(a\neq0\), y m y n son números enteros, entonces
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \quad\]
y
\[\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
¿Y si simplemente restamos exponentes independientemente de cuál sea más grande?
Consideremos\(\dfrac{x^{2}}{x^{5}}\).
Restamos el exponente en el denominador del exponente en el numerador.
\[\begin{array}{c}{\dfrac{x^{2}}{x^{5}}} \\ {x^{2-5}} \\ {x^{-3}}\end{array}\]
También podemos simplificar\(\dfrac{x^{2}}{x^{5}}\) dividiendo factores comunes:
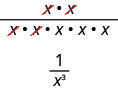
su implica eso\(x^{-3}=\dfrac{1}{x^{3}}\) y nos lleva a la definición de un exponente negativo.
Si n es un número entero y\(a\neq 0\), entonces\(a^{-n}=\dfrac{1}{a^{n}}\)
El exponente negativo nos dice que podemos reescribir la expresión tomando el recíproco de la base y luego cambiando el signo del exponente.
Cualquier expresión que tenga exponentes negativos no se considera en la forma más simple. Utilizaremos la definición de un exponente negativo y otras propiedades de exponentes para escribir la expresión solo con exponentes positivos.
Por ejemplo, si después de simplificar una expresión terminamos con la expresión\(x^{-3}\), daremos un paso más y escribiremos\(\dfrac{1}{x^{3}}\). La respuesta se considera en forma más simple cuando solo tiene exponentes positivos.
Simplificar:
- \(4^{-2}\)
- \(10^{-3}\)
- Contestar
-
- \(\begin{array}{ll}& 4^{-2} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & {\dfrac{1}{4^{2}}} \\ {\text { Simplify. }} & \dfrac{1}{16} \end{array}\)
- \(\begin{array}{ll}& 10^{-3} \\{\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}},} & \dfrac{1}{10^{3}} \\ {\text { Simplify. }} & \dfrac{1}{1000}\end{array}\)
Simplificar:
- \(2^{-3}\)
- \(10^{-7}\)
- Contestar
-
- \(\dfrac{1}{8}\)
- \(\dfrac{1}{10^{7}}\)
Simplificar:
- \(3^{-2}\)
- \(10^{-4}\)
- Contestar
-
- \(\dfrac{1}{9}\)
- \(\dfrac{1}{10,000}\)
En Ejercicio\(\PageIndex{1}\) elevamos un entero a un exponente negativo. ¿Qué sucede cuando elevamos una fracción a un exponente negativo? Empezaremos por mirar qué le sucede a una fracción cuyo numerador es uno y cuyo denominador es un entero elevado a un exponente negativo.
\(\begin{array}{ll}& \dfrac{1}{a^{-n}}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\dfrac{1}{a^{n}}} \\ {\text { Simplify the complex fraction. }} & 1 \cdot \dfrac{a^{n}}{1}\\ {\text { Multiply. }} & a^{n}\end{array}\)
Esto lleva a la Propiedad de los Exponentes Negativos.
Si n es un número entero y\(a\neq 0\), entonces\(\dfrac{1}{a^{-n}}=a^{n}\).
Simplificar:
- \(\dfrac{1}{y^{-4}}\)
- \(\dfrac{1}{3^{-2}}\)
- Contestar
-
- \(\begin{array} { ll } & \dfrac{1}{y^{-4}}\\ \text { Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & y^{4}\end{array}\)
- \(\begin{array} { ll } & \dfrac{1}{3^{-2}}\\ \text {Use the property of a negative exponent, } \dfrac{1}{a^{-n}}=a^{n} . & 3^{2} \\ \text{Simplify.}& 9\end{array}\)
Simplificar:
- \(\dfrac{1}{p^{-8}}\)
- \(\dfrac{1}{4^{-3}}\)
- Contestar
-
- \(p^{8}\)
- 64
Simplificar:
- \(\dfrac{1}{q^{-7}}\)
- \(\dfrac{1}{2^{-4}}\)
- Contestar
-
- \(q^{7}\)
- 16
Supongamos ahora que tenemos una fracción elevada a un exponente negativo. Usemos nuestra definición de exponentes negativos para conducirnos a una nueva propiedad.
\(\begin{array}{ll}& \left(\dfrac{3}{4}\right)^{-2}\\ {\text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} } & \dfrac{1}{\left(\dfrac{3}{4}\right)^{2}} \\ {\text { Simplify the denominator. }} & \dfrac{1}{\dfrac{9}{16}}\\ {\text { Simplify the complex fraction.}} &\dfrac{16}{9}\\ \text { But we know that } \dfrac{16}{9} \text { is }\left(\dfrac{4}{3}\right)^{2} & \\ \text { This tells us that: } & \left(\dfrac{3}{4}\right)^{-2}=\left(\dfrac{4}{3}\right)^{2}\end{array}\)
Para pasar de la fracción original elevada a un exponente negativo al resultado final, tomamos el recíproco de la base —la fracción— y cambiamos el signo del exponente.
Esto nos lleva al Cociente a una Propiedad de Poder Negativo.
Si\(a\) y\(b\) son números reales,\(a \neq 0, b \neq 0,\) y\(n\) es un número entero, entonces\(\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}\)
Simplificar:
- \(\left(\dfrac{5}{7}\right)^{-2}\)
- \(\left(-\dfrac{2 x}{y}\right)^{-3}\)
- Contestar
-
- \(\begin{array}{ll}& \left(\dfrac{5}{7}\right)^{-2}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(\dfrac{7}{5}\right)^{2}\\ \text { Simplify. } & \dfrac{49}{25}\end{array}\)
- \(\begin{array}{ll}& \left(-\dfrac{2 x}{y}\right)^{-3}\\ \text { Use the Quotient to a Negative Exponent Property, }\left(\dfrac{a}{b}\right)^{-n}=\left(\dfrac{b}{a}\right)^{n}& \\ \text { Take the reciprocal of the fraction and change the sign of the exponent. }&\left(-\dfrac{y}{2 x}\right)^{3}\\ \text { Simplify. } & -\dfrac{y^{3}}{8 x^{3}}\end{array}\)
Simplificar:
- \(\left(\dfrac{2}{3}\right)^{-4}\)
- \(\left(-\dfrac{6 m}{n}\right)^{-2}\)
- Contestar
-
- \(\dfrac{81}{16} \)
- \(\dfrac{n^{2}}{36 m^{2}}\)
Simplificar:
- \(\left(\dfrac{3}{5}\right)^{-3}\)
- \(\left(-\dfrac{a}{2 b}\right)^{-4}\)
- Contestar
-
- \(\dfrac{125}{27}\)
- \(\dfrac{16 b^{4}}{a^{4}}\)
Al simplificar una expresión con exponentes, debemos tener cuidado de identificar correctamente la base.
Simplificar:
- \((-3)^{-2}\)
- \(-3^{-2}\)
- \(\left(-\dfrac{1}{3}\right)^{-2}\)
- \(-\left(\dfrac{1}{3}\right)^{-2}\)
- Contestar
-
- Aquí el exponente aplica a la base −3. \(\begin{array}{ll} & (-3)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \dfrac{1}{(-3)^{-2}} \\ {\text { Simplify. }} & \dfrac{1}{9}\end{array}\)
- La expresión\(-3^{-2}\) significa “encontrar lo contrario de\(3^{-2}\)”. Aquí el exponente aplica a la base 3. \(\begin{array}{ll} &-3^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot 3^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot \dfrac{1}{3^{2}}\\ {\text { Simplify. }} & -\dfrac{1}{9}\end{array}\)
- Aquí el exponente aplica a la base\(\left(-\dfrac{1}{3}\right)\). \(\begin{array}{ll} &\left(-\dfrac{1}{3}\right)^{-2}\\ {\text { Take the reciprocal of the base and change the sign of the exponent. }}& \left(-\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & 9\end{array}\)
- La expresión\(-\left(\dfrac{1}{3}\right)^{-2}\) significa “encontrar lo contrario de\(\left(\dfrac{1}{3}\right)^{-2}\)”. Aquí el exponente aplica a la base\(\left(\dfrac{1}{3}\right)\). \(\begin{array}{ll} &-\left(\dfrac{1}{3}\right)^{-2}\\ \text { Rewrite as a product with }-1&-1 \cdot\left(\dfrac{1}{3}\right)^{-2}\\\text { Take the reciprocal of the base and change the sign of the exponent. } & -1 \cdot\left(\dfrac{3}{1}\right)^{2}\\ {\text { Simplify. }} & -9 \end{array}\)
Simplificar:
- \((-5)^{-2}\)
- \(-5^{-2}\)
- \(\left(-\dfrac{1}{5}\right)^{-2}\)
- \(-\left(\dfrac{1}{5}\right)^{-2}\)
- Contestar
-
- \(\dfrac{1}{25}\)
- \(-\dfrac{1}{25}\)
- 25
- −25
Simplificar:
- \((-7)^{-2}\)
- \(-7^{-2}\)
- \(\left(-\dfrac{1}{7}\right)^{-2}\)
- \(-\left(\dfrac{1}{7}\right)^{-2}\)
- Contestar
-
- \(\dfrac{1}{49}\)
- \(-\dfrac{1}{49}\)
- 49
- −49
Debemos tener cuidado de seguir el Orden de Operaciones. En el siguiente ejemplo, las partes (a) y (b) se ven similares, pero los resultados son diferentes.
Simplificar:
- 4\(\cdot 2^{-1}\)
- \((4 \cdot 2)^{-1}\)
- Contestar
-
- \(\begin{array}{ll} \text { Do exponents before multiplication. }&4 \cdot 2^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}}&4 \cdot \dfrac{1}{2^{1}}\\ {\text { Simplify. }} & 2 \end{array}\)
- \(\begin{array}{ll} &(4 \cdot 2)^{-1}\\ \text { Simplify inside the parentheses first. }&(8)^{-1}\\ \text { Use } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{8^{1}}\\{\text { Simplify. }} & \dfrac{1}{8} \end{array}\)
Simplificar:
- 6\(\cdot 3^{-1}\)
- \((6 \cdot 3)^{-1}\)
- Contestar
-
- 2
- \(\dfrac{1}{18}\)
Simplificar:
- 8\(\cdot 2^{-2}\)
- \((8 \cdot 2)^{-2}\)
- Contestar
-
- 2
- \(\dfrac{1}{256}\)
Cuando una variable se eleva a un exponente negativo, aplicamos la definición de la misma manera que lo hicimos con los números. Asumiremos que todas las variables son distintas de cero.
Simplificar:
- \(x^{-6}\)
- \(\left(u^{4}\right)^{-3}\)
- Contestar
-
- \(\begin{array}{ll} &x^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{x^{6}}\end{array}\)
- \(\begin{array}{ll} &\left(u^{4}\right)^{-3}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{\left(u^{4}\right)^{3}} \\ \text{ Simplify.} & \dfrac{1}{u^{12}}\end{array}\)
Simplificar:
- \(y^{-7}\)
- \(\left(z^{3}\right)^{-5}\)
- Contestar
-
- \(\dfrac{1}{y^{7}}\)
- \(\dfrac{1}{z^{15}}\)
Simplificar:
- \(p^{-9}\)
- \(\left(q^{4}\right)^{-6}\)
- Contestar
-
- \(\dfrac{1}{p^{9}}\)
- \(\dfrac{1}{q^{24}}\)
Cuando hay un producto y un exponente tenemos que tener cuidado para aplicar el exponente a la cantidad correcta. De acuerdo con el Orden de Operaciones, simplificamos las expresiones entre paréntesis antes de aplicar exponentes. Veremos cómo funciona esto en el siguiente ejemplo.
Simplificar:
- 5\(y^{-1}\)
- \((5 y)^{-1}\)
- \((-5 y)^{-1}\)
- Contestar
-
- \(\begin{array}{ll} &5 y^{-1}\\ \text { Notice the exponent applies to just the base y. }& \\ \text { Take the reciprocal of } y \text { and change the sign of the exponent. }&5 \cdot \dfrac{1}{y^{1}} \\ \text { Simplify. } & \dfrac{5}{y}\end{array}\)
- \(\begin{array}{ll} &(5 y)^{-1}\\\text { Here the parentheses make the exponent apply to the base } 5 y .& \\ \text { Take the reciprocal of } 5 y \text { and change the sign of the exponent. }&\dfrac{1}{(5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{5 y}\end{array}\)
- \(\begin{array}{ll} &(-5 y)^{-1}\\\text { The base here is }-5 y& \\ \text { Take the reciprocal of }-5 y \text { and change the sign of the exponent. }&\dfrac{1}{(-5 y)^{1}}\\ \text { Simplify. } &\dfrac{1}{-5 y}\\ \text { Use } \dfrac{a}{-b}=-\dfrac{a}{b} & -\dfrac{1}{5 y}\end{array}\)
Simplificar:
- 8\(p^{-1}\)
- \((8 p)^{-1}\)
- \((-8 p)^{-1}\)
- Contestar
-
- \(\dfrac{8}{p}\)
- \(\dfrac{1}{8 p}\)
- \(-\dfrac{1}{8 p}\)
Simplificar:
- 11\(q^{-1}\)
- \((11 q)^{-1}-(11 q)^{-1}\)
- \((-11 q)^{-1}\)
- Contestar
-
- \(\dfrac{11}{1 q}\)
- \(\dfrac{1}{11 q}-\dfrac{1}{11 q}\)
- \(-\dfrac{1}{11 q}\)
Con exponentes negativos, la Regla del Cociente necesita sólo una forma\(\dfrac{a^{m}}{a^{n}}=a^{m-n},\) para\(a \neq 0\) 0. Cuando el exponente en el denominador es mayor que el exponente en el numerador, el exponente del cociente será negativo.
Simplificar expresiones con exponentes enteros
Todas las propiedades de exponentes que desarrollamos anteriormente en el capítulo con exponentes de número entero también se aplican a exponentes enteros. Los reafirmamos aquí para referencia.
Si\(a\) y\(b\) son números reales, y\(m\) y\(n\) son números enteros, entonces
\(\begin{array}{lrll}{\textbf { Product Property }}& a^{m} \cdot a^{n} &=&a^{m+n} \\ {\textbf { Power Property }} &\left(a^{m}\right)^{n} &=&a^{m \cdot n} \\ {\textbf { Product to a Power }} &(a b)^{m} &=&a^{m} b^{m} \\ {\textbf { Quotient Property }} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0 \\ {\textbf { Zero Exponent Property }}& a^{0} &= & 1, a \neq 0 \\ {\textbf { Quotient to a Power Property }} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \\ {\textbf { Properties of Negative Exponents }} & a^{-n} &=&\dfrac{1}{a^{n}} \text { and } \dfrac{1}{a^{-n}}=a^{n}\\ {\textbf { Quotient to a Negative Exponents }}& \left(\dfrac{a}{b}\right)^{-n} &=&\left(\dfrac{b}{a}\right)^{n} \\\end{array}\)
Simplificar:
- \(x^{-4} \cdot x^{6}\)
- \(y^{-6} \cdot y^{4}\)
- \(z^{-5} \cdot z^{-3}\)
- Contestar
-
- \(\begin{array}{ll}& x^{-4} \cdot x^{6} \\ \text { Use the Product Property, } a^{m} \cdot a^{n}=a^{m+n} & x^{-4+6} \\ \text { Simplify. } & x^{2} \end{array}\)
- \(\begin{array}{ll}& y^{-6} \cdot y^{4} \\ \text { Notice the same bases, so add the exponents. }& y^{-6+4}\\ \text { Simplify. } & y^{-2} \\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}} & \dfrac{1}{y^{2}}\end{array}\)
- \(\begin{array}{ll}& z^{-5} \cdot z^{-3} \\ \text { Add the exponents, since the bases are the same. }& z^{-5-3}\\ \text { Simplify. } & z^{-8}\\ \text { Take the reciprocal and change the sign of the exponent, }& \dfrac{1}{z^{8}} \\ \text { using the definition of a negative exponent. }\end{array}\)
Simplificar:
- \(x^{-3} \cdot x^{7}\)
- \(y^{-7} \cdot y^{2}\)
- \(z^{-4} \cdot z^{-5}\)
- Contestar
-
- \(x^{4}\)
- \(\dfrac{1}{y^{5}}\)
- \(\dfrac{1}{z^{9}}\)
Simplificar:
- \(a^{-1} \cdot a^{6}\)
- \(b^{-8} \cdot b^{4}\)
- \(c^{-8} \cdot c^{-7}\)
- Contestar
-
- \(a^{5}\)
- \(\dfrac{1}{b^{4}}\)
- \(\dfrac{1}{c^{15}}\)
En los siguientes dos ejemplos, comenzaremos usando la Propiedad Conmutativa para agrupar las mismas variables juntas. Esto facilita la identificación de las bases similares antes de usar la Propiedad del Producto.
Simplificar:\(\left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right)\)
- Contestar
-
\(\begin{array}{ll}& \left(m^{4} n^{-3}\right)\left(m^{-5} n^{-2}\right) \\ \text { Use the Commutative Property to get like bases together. }& m^{4} m^{-5} \cdot n^{-2} n^{-3}\\ \text { Add the exponents for each base. }&m^{-1} \cdot n^{-5}\\ \text { Take reciprocals and change the signs of the exponents. }& \dfrac{1}{m^{1}} \cdot \dfrac{1}{n^{5}} \\ \text { Simplify. } & \dfrac{1}{m n^{5}}\end{array}\)
Simplificar:\(\left(p^{6} q^{-2}\right)\left(p^{-9} q^{-1}\right)\)
- Contestar
-
\(\frac{1}{p^3 q^3}\)
Simplificar:\(\left(r^{5} s^{-3}\right)\left(r^{-7} s^{-5}\right)\)
- Contestar
-
\(\frac{1}{r^2 s^8}\)
Si los monomios tienen coeficientes numéricos, multiplicamos los coeficientes, tal como lo hicimos antes.
Simplificar:\(\left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right)\)
- Contestar
-
\(\begin{array}{ll}& \left(2 x^{-6} y^{8}\right)\left(-5 x^{5} y^{-3}\right) \\ \text { Rewrite with the like bases together. }& 2(-5) \cdot\left(x^{-6} x^{5}\right) \cdot\left(y^{8} y^{-3}\right)\\ \text { Multiply the coefficients and add the exponents of each variable. }&-10 \cdot x^{-1} \cdot y^{5}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&-10 \cdot \dfrac{1}{x^{1}} \cdot y^{5} \\ \text { Simplify. } & \dfrac{-10 y^{5}}{x}\end{array}\)
Simplificar:\(\left(3 u^{-5} v^{7}\right)\left(-4 u^{4} v^{-2}\right)\)
- Contestar
-
\(-\frac{12v^5}{u}\)
Simplificar:\(\left(-6 c^{-6} d^{4}\right)\left(-5 c^{-2} d^{-1}\right)\)
- Contestar
-
\(\frac{30d^3}{c^8}\)
En los siguientes dos ejemplos, usaremos la propiedad de energía y el producto para una propiedad de energía.
Simplificar:\(\left(6 k^{3}\right)^{-2}\)
- Contestar
-
\(\begin{array}{ll}&\left(6 k^{3}\right)^{-2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&(6)^{-2}\left(k^{3}\right)^{-2}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&6^{-2} k^{-6}\\ \text { Use the definition of a negative exponent, } a^{-n}=\dfrac{1}{a^{n}}&\dfrac{1}{6^{2}} \cdot \dfrac{1}{k^{6}} \\ \text { Simplify. } & \dfrac{1}{36 k^{6}}\end{array}\)
Simplificar:\(\left(-4 x^{4}\right)^{-2}\)
- Contestar
-
\(\frac{1}{16x^8}\)
Simplificar:\(\left(2 b^{3}\right)^{-4}\)
- Contestar
-
\(\frac{1}{16b^{12}}\)
Simplificar:\(\left(5 x^{-3}\right)^{2}\)
- Contestar
-
\(\begin{array}{ll}&\left(5 x^{-3}\right)^{2}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{n} b^{m}&5^{2}\left(x^{-3}\right)^{2}\\ \begin{array}{l}{\text { Simplify } 5^{2} \text { and multiply the exponents of } x \text { using the Power }} \\ {\text { Property, }\left(a^{m}\right)^{n}=a^{m \cdot n} .}\end{array}&25 \cdot x^{-6}\\ \begin{array}{l}{\text { Rewrite } x^{-6} \text { by using the Definition of a Negative Exponent, }} \\ {\space a^{-n}=\dfrac{1}{a^{n}}}\end{array}&25 \cdot \dfrac{1}{x^{6}}\\ \text { Simplify. } & \dfrac{25}{x^{6}}\end{array}\)
Simplificar:\(\left(8 a^{-4}\right)^{2}\)
- Contestar
-
\(\frac{64}{a^8}\)
Simplificar:\(\left(2 c^{-4}\right)^{3}\)
- Contestar
-
\(\frac{8}{c^{12}}\)
Para simplificar una fracción, utilizamos la Propiedad Cociente y restamos los exponentes.
Simplificar:\(\dfrac{r^{5}}{r^{-4}}\)
- Contestar
-
\(\begin{array}{l} & \dfrac{r^{5}}{r^{-4}}\\ {\text { Use the Quotient Property, } \dfrac{a^{n}}{a^{n}}=a^{m-n}} & r^{5-(-4)}\\ {\text { Simplify. }} & r^{9}\end{array}\)
Simplificar:\(\dfrac{x^{8}}{x^{-3}}\)
- Contestar
-
\(x^{11}\)
Simplificar:\(\dfrac{y^{8}}{y^{-6}}\)
- Contestar
-
\(y^{14}\)
Convertir de notación decimal a notación científica
¿Recuerdas trabajar con valor posicional para números enteros y decimales? Nuestro sistema de números se basa en potencias de 10. Usamos decenas, cientos, miles, y así sucesivamente. Nuestros números decimales también se basan en potencias de diez, décimas, centésimas, milésimas, etc. Considera los números 4,000 y 0.004. Sabemos que 4,000 medias\(4 \times 1,000\) y 0.004 medias\(4 \times \dfrac{1}{1,000}\).
Si escribimos el 1000 como una potencia de diez en forma exponencial, podemos reescribir estos números de esta manera:
\[\begin{array}{ll}{4,000} & {0.004} \\ {4 \times 1,000} & {4 \times \dfrac{1}{1,000}} \\ {4 \times 10^{3}} & {4 \times \dfrac{1}{10^{3}}} \\ & {4 \times 10^{-3}}\end{array}\]
Cuando un número se escribe como producto de dos números, donde el primer factor es un número mayor o igual a uno pero menor que 10, y el segundo factor es una potencia de 10 escrita en forma exponencial, se dice que está en notación científica.
Un número se expresa en notación científica cuando es de la forma
\[a \times 10^{n} \text { where } 1 \leq a<10 \text { and } n \text { is an integer }\]
Es habitual en la notación científica utilizar como signo de\(\times\) multiplicación, aunque evitemos usar este signo en otra parte del álgebra.
Si miramos lo que pasó con el punto decimal, podemos ver un método para convertir fácilmente de la notación decimal a la notación científica.
En ambos casos, el decimal se movió 3 lugares para obtener el primer factor entre 1 y 10.
\(\begin{array}{ll}{\text { The power of } 10 \text { is positive when the number is larger than } 1 :} & {4,000=4 \times 10^{3}} \\ {\text { The power of } 10 \text { is negative when the number is between } 0 \text { and } 1 :} & {0.004=4 \times 10^{-3}} \end{array}\)
Escribir en notación científica: 37000.
- Contestar
-
Escribir en notación científica: 96000.
- Contestar
-
\(9.6 \times 10^{4}\)
Escribir en notación científica: 48300.
- Contestar
-
\(4.83 \times 10^{4}\)
- Paso 1. Mueva el punto decimal para que el primer factor sea mayor o igual a 1 pero menor que 10.
- Paso 2. Contar el número de decimales, n, que se movió el punto decimal.
- Paso 3. Escribe el número como un producto con una potencia de 10.
Si el número original es:- mayor que 1, la potencia de 10 será de 10 n.
- entre 0 y 1, la potencia de 10 será de 10 −n.
- Paso 4. Cheque.
Escribir en notación científica: 0.0052.
- Contestar
-
El número original, 0.0052, está entre 0 y 1 por lo que tendremos una potencia negativa de 10.
Mueve el punto decimal para obtener 5.2, un número entre 1 y 10. Contar el número de decimales que se movió el punto. Escribir como un producto con una potencia de 10. Cheque. \(\begin{array}{l}{5.2 \times 10^{-3}} \\ {5.2 \times \dfrac{1}{10^{3}}} \\ {5.2 \times \dfrac{1}{1000}} \\ {5.2 \times 0.001}\end{array}\) 0.0052
Escribir en notación científica: 0.0078
- Contestar
-
\(7.8 \times 10^{-3}\)
Escribir en notación científica: 0.0129
- Contestar
-
\(1.29 \times 10^{-2}\)
Convertir Notación Científica a Forma Decimal
¿Cómo podemos convertir de notación científica a forma decimal? Veamos dos números escritos en notación científica y veamos.
\[\begin{array}{cc}{9.12 \times 10^{4}} & {9.12 \times 10^{-4}} \\ {9.12 \times 10,000} & {9.12 \times 0.0001} \\ {91,200} & {0.000912}\end{array}\]
Si miramos la ubicación del punto decimal, podemos ver un método fácil para convertir un número de notación científica a forma decimal.
\[9.12 \times 10^{4}=91,200 \quad 9.12 \times 10^{-4}=0.000912\]
En ambos casos el punto decimal se movió 4 lugares. Cuando el exponente era positivo, el decimal se movía hacia la derecha. Cuando el exponente era negativo, el punto decimal se movía hacia la izquierda.
Convertir a forma decimal:\(6.2 \times 10^{3}\)
- Contestar
-
Convertir a forma decimal:\(1.3 \times 10^{3}\)
- Contestar
-
\(1,300\)
Convertir a forma decimal:\(9.25 \times 10^{4}\)
- Contestar
-
\(92,500\)
A continuación se resumen los pasos.
Convertir notación científica a forma decimal.
Para convertir la notación científica a forma decimal:
- Paso 1. Determinar el exponente,\(n\), sobre el factor\(10\).
- Paso 2. Mueva los\(n\) decimales, agregando ceros si es necesario.
- Si el exponente es positivo, mueva los\(n\) lugares decimales hacia la derecha.
- Si el exponente es negativo, mueva los\(|n|\) lugares decimales hacia la izquierda.
- Paso 3. Cheque.
Convertir a forma decimal:\(8.9\times 10^{-2}\)
- Contestar
-
Determinar el exponente,\(n\), sobre el factor\(10\). Dado que el exponente es negativo, mueva el punto decimal 2 lugares hacia la izquierda. Agregue ceros según sea necesario para los marcadores de posición.
Convertir a forma decimal:\(1.2 \times 10^{-4}\)
- Contestar
-
\(0.00012\)
Convertir a forma decimal:\(7.5 \times 10^{-2}\)
- Contestar
-
\(0.075\)
Multiplicar y dividir usando notación científica
Los astrónomos utilizan números muy grandes para describir las distancias en el universo y las edades de las estrellas y los planetas. Los químicos utilizan números muy pequeños para describir el tamaño de un átomo o la carga sobre un electrón. Cuando los científicos realizan cálculos con números muy grandes o muy pequeños, utilizan notación científica. La notación científica proporciona una forma para que los cálculos se hagan sin escribir muchos ceros. Veremos cómo se utilizan las Propiedades de los Exponentes para multiplicar y dividir números en notación científica.
Multiplicar. Escribe las respuestas en forma decimal:\(\left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\)
- Contestar
-
\(\begin{array}{ll} & \left(4 \times 10^{5}\right)\left(2 \times 10^{-7}\right)\\\text { Use the Commutative Property to rearrange the factors. }& 4 \cdot 2 \cdot 10^{5} \cdot 10^{-7} \\ \text{ Multiply.} & 8 \times 10^{-2} \\ \text { Change to decimal form by moving the decimal two places left. } & 0.08\end{array}\)
Multiplicar\((3\times 10^{6})(2\times 10^{-8})\). Escribe las respuestas en forma decimal.
- Contestar
-
\(0.06\)
Multiplicar\(\left(3 \times 10^{-2}\right)\left(3 \times 10^{-1}\right)\). Escribe las respuestas en forma decimal.
- Contestar
-
\(0.009\)
Dividir. Escribe las respuestas en forma decimal:\(\dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\)
- Contestar
-
\(\begin{array}{ll} & \dfrac{9 \times 10^{3}}{3 \times 10^{-2}}\\\text { Separate the factors, rewriting as the product of two fractions. }& \dfrac{9}{3} \times \dfrac{10^{3}}{10^{-2}}\\ \text{ Divide.} & 3 \times 10^{5} \\ \text { Change to decimal form by moving the decimal five places right. } & 300000\end{array}\)
Dividir\(\dfrac{8 \times 10^{4}}{2 \times 10^{-1}} .\) Escribe las respuestas en forma decimal.
- Contestar
-
\(400,000\)
Dividir\(\dfrac{8 \times 10^{2}}{4 \times 10^{-2}} .\) Escribe las respuestas en forma decimal.
- Contestar
-
\(20,000\)
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con exponentes enteros y notación científica:
- Exponentes negativos
- Notación Científica
- Notación científica 2
Conceptos clave
- Propiedad de los Exponentes Negativos
- Si\(n\) es un número entero positivo y\(a \ne 0\), entonces\(\dfrac{1}{a^{−n}}=a^n\)
- Si\(n\) es un número entero positivo y\(a \ne 0\), entonces\(\dfrac{1}{a^{−n}}=a^n\)
- Cociente a un exponente negativo
- Si\(a\) y\(b\) son números reales,\(b \ne 0\) y\(n\) es un número entero, entonces\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- Si\(a\) y\(b\) son números reales,\(b \ne 0\) y\(n\) es un número entero, entonces\(\left(\dfrac{a}{b}\right)^{−n}=\left(\dfrac{b}{a}\right)^n\)
- Para convertir la notación científica a forma decimal:
- Determinar el exponente,\(n\) sobre el factor\(10\).
- Mueva los\(n\) decimales, agregando ceros si es necesario.
- Si el exponente es positivo, mueva los\(n\) lugares decimales hacia la derecha.
- Si el exponente es negativo, mueva los\(|n|\) lugares decimales hacia la izquierda.
- Cheque.
- Para convertir un decimal a notación científica:
- Mueva el punto decimal para que el primer factor sea mayor o igual a\(1\) pero menor que\(10\).
- Contar el número de decimales,\(n\) que se movió el punto decimal.
- Escribe el número como un producto con una potencia de\(10\). Si el número original es:
- mayor que\(1\), el poder de la\(10\) voluntad\(10^n\)
- entre\(0\) y\(1\), el poder de la\(10\) voluntad\(10^{−n}\)
- Cheque.
Glosario
- exponente negativo
- Si\(n\) es un número entero positivo y\(a \neq 0\), entonces\(a^{-n}=\dfrac{1}{a^{n}}\).
- notación científica
- Un número se expresa en notación científica cuando es de la forma\(a \times 10^{n}\) donde\(a \geq 1\) y a<10 y\(n\) es un entero.


