6.6: Dividir polinomios

Última actualización
Guardar como PDF

Page ID: 110347

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Al final de esta sección, podrás:

Dividir un polinomio por un monomio
Dividir un polinomio por un binomio

Nota

Antes de comenzar, toma este cuestionario de preparación.

Agregar:$\dfrac{3}{d}+\dfrac{x}{d}$
Si te perdiste este problema, revisa Ejercicio 1.7.1.
Simplifica:$\dfrac{30 x y^{3}}{5 x y}$
Si te perdiste este problema, revisa Ejercicio 6.5.37.
Combina términos similares:$8 a^{2}+12 a+1+3 a^{2}-5 a+4$
Si te perdiste este problema, revisa Ejercicio 1.3.37.

Dividir un polinomio por un monomio

En la última sección aprendiste a dividir un monomio por un monomio. A medida que continúas construyendo tu conocimiento de polinomios el siguiente procedimiento es dividir un polinomio de dos o más términos por un monomio.

El método que usaremos para dividir un polinomio por un monomio se basa en las propiedades de adición de fracciones. Entonces comenzaremos con un ejemplo para revisar la adición de fracciones.

$\begin{array}{ll}{\text { The sum, }} & {\dfrac{y}{5}+\dfrac{2}{5}} \\ {\text { simplifies to }} & {\dfrac{y+2}{5}}\end{array}$

Ahora haremos esto a la inversa para dividir una sola fracción en fracciones separadas.

Indicaremos la propiedad de adición de fracción aquí tal como la aprendió y a la inversa.

Adición de fracciones

Si a, b y c son números donde$c\neq 0$, entonces

\[\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c} \quad \text { and } \quad \dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}\]

Usamos la forma de la izquierda para agregar fracciones y usamos la forma de la derecha para dividir un polinomio por un monomio.

$\begin{array}{ll}{\text { For example, }} & {\dfrac{y+2}{5}} \\ {\text { can be written }} & {\dfrac{y}{5}+\dfrac{2}{5}}\end{array}$

Utilizamos esta forma de adición de fracciones para dividir polinomios por monomios.

DIVISIÓN DE UN POLINOMIO POR UN MONOMIO

Para dividir un polinomio por un monomio, dividir cada término del polinomio por el monomio.

Ejercicio$\PageIndex{1}$

Encuentra el cociente:$\dfrac{7 y^{2}+21}{7}$

Contestar: $\begin{array}{ll} & \dfrac{7 y^{2}+21}{7}\\\text{Divide each term of the numerator by the denominator.} & \dfrac{7 y^{2}}{7}+\dfrac{21}{7} \\ \text {Simplify each fraction. } & y^{2}+3 \end{array}$

Ejercicio$\PageIndex{2}$

Encuentra el cociente:$\dfrac{8 z^{2}+24}{4}$

Contestar: $2 z^{2}+6$

Ejercicio$\PageIndex{3}$

Encuentra el cociente:$\dfrac{18 z^{2}-27}{9}$

Contestar: $2 z^{2}-3$

Recuerda que la división se puede representar como una fracción. Cuando se te pida dividir un polinomio por un monomio y no está ya en forma de fracción, escribe una fracción con el polinomio en el numerador y el monomio en el denominador.

Ejercicio$\PageIndex{4}$

Encuentra el cociente:$\left(18 x^{3}-36 x^{2}\right) \div 6 x$

Contestar: $\begin{array}{ll} & \left(18 x^{3}-36 x^{2}\right) \div 6 x\\\text { Rewrite as a fraction. } & \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}}{6 x}-\dfrac{36 x^{2}}{6 x}\\ \text { Simplify. } &3 x^{2}-6 x\end{array}$

Ejercicio$\PageIndex{5}$

Encuentra el cociente:$\left(27 b^{3}-33 b^{2}\right) \div 3 b$

Contestar: $9 b^{2}-11 b$

Ejercicio$\PageIndex{6}$

Encuentra el cociente:$\left(25 y^{3}-55 y^{2}\right) \div 5 y$

Contestar: $5 y^{2}-11 y$

Cuando dividimos por un negativo, debemos tener mucho cuidado con las señales.

Ejercicio$\PageIndex{7}$

Encuentra el cociente:$\dfrac{12 d^{2}-16 d}{-4}$

Contestar: $\begin{array}{ll} &\dfrac{12 d^{2}-16 d}{-4}\\ \text { Divide each term of the numerator by the denominator. }& \dfrac{18 x^{3}-36 x^{2}}{6 x} \\ \text { Simplify. Remember, subtracting a negative is like adding a positive! }& -3 d^{2}+4 d\end{array}$

Ejercicio$\PageIndex{8}$

Encuentra el cociente:$\dfrac{25 y^{2}-15 y}{-5}$

Contestar: $-5 y^{2}+3 y$

Ejercicio$\PageIndex{9}$

Encuentra el cociente:$\dfrac{42 b^{2}-18 b}{-6}$

Contestar: $-7 b^{2}+3 b$

Ejercicio$\PageIndex{10}$

Encuentra el cociente:$\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}$

Contestar: $\begin{array}{ll} &\dfrac{105 y^{5}+75 y^{3}}{5 y^{2}}\\ \text { Separate the terms. }& \dfrac{105 y^{5}}{5 y^{2}}+\dfrac{75 y^{3}}{5 y^{2}}\\ \text { Simplify. }& 21 y^{3}+15 y\end{array}$

Ejercicio$\PageIndex{11}$

Encuentra el cociente:$\dfrac{60 d^{7}+24 d^{5}}{4 d^{3}}$

Contestar: $15 d^{4}+6 d^{2}$

Ejercicio$\PageIndex{12}$

Encuentra el cociente:$\dfrac{216 p^{7}-48 p^{5}}{6 p^{3}}$

Contestar: $36 p^{4}-8 p^{2}$

Ejercicio$\PageIndex{13}$

Encuentra el cociente:$\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)$

Contestar: $\begin{array}{ll} &\left(15 x^{3} y-35 x y^{2}\right) \div(-5 x y)\\ \text { Rewrite as a fraction. }& \dfrac{15 x^{3} y-35 x y^{2}}{-5 x y}\\\text { Separate the terms. Be careful with the signs! }& \dfrac{15 x^{3} y}{-5 x y}-\dfrac{35 x y^{2}}{-5 x y}\\ \text { Simplify. } & -3 x^{2}+7 y\end{array}$

Ejercicio$\PageIndex{14}$

Encuentra el cociente:$\left(32 a^{2} b-16 a b^{2}\right) \div(-8 a b)$

Contestar: $-4 a+2 b$

Ejercicio$\PageIndex{15}$

Encuentra el cociente:$\left(-48 a^{8} b^{4}-36 a^{6} b^{5}\right) \div\left(-6 a^{3} b^{3}\right)$

Contestar: $8 a^{5} b+6 a^{3} b^{2}$

Ejercicio$\PageIndex{13}$

Encuentra el cociente:$\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}$

Contestar: $\begin{array}{ll} &\dfrac{36 x^{3} y^{2}+27 x^{2} y^{2}-9 x^{2} y^{3}}{9 x^{2} y}\\\text { Separate the terms. }& \dfrac{36 x^{3} y^{2}}{9 x^{2} y}+\dfrac{27 x^{2} y^{2}}{9 x^{2} y}-\dfrac{9 x^{2} y^{3}}{9 x^{2} y}\\ \text { Simplify. } & 4 x y+3 y-y^{2}\end{array}$

Ejercicio$\PageIndex{14}$

Encuentra el cociente:$\dfrac{40 x^{3} y^{2}+24 x^{2} y^{2}-16 x^{2} y^{3}}{8 x^{2} y}$

Contestar: $5 x y+3 y-2 y^{2}$

Ejercicio$\PageIndex{15}$

Encuentra el cociente:$\dfrac{35 a^{4} b^{2}+14 a^{4} b^{3}-42 a^{2} b^{4}}{7 a^{2} b^{2}}$

Contestar: $5 a^{2}+2 a^{2} b-6 b^{2}$

Ejercicio$\PageIndex{16}$

Encuentra el cociente:$\dfrac{10 x^{2}+5 x-20}{5 x}$

Contestar: $\begin{array}{ll}&\dfrac{10 x^{2}+5 x-20}{5x}\\\text { Separate the terms. }& \dfrac{10 x^{2}}{5 x}+\dfrac{5 x}{5 x}-\dfrac{20}{5 x}\\ \text { Simplify. } &2 x+1-\dfrac{4}{x}\end{array}$

Ejercicio$\PageIndex{17}$

Encuentra el cociente:$\dfrac{18 c^{2}+6 c-9}{6 c}$

Contestar: $3 c+1-\dfrac{3}{2 c}$

Ejercicio$\PageIndex{18}$

Encuentra el cociente:$\dfrac{10 d^{2}-5 d-2}{5 d}$

Contestar: $2 d-1-\dfrac{2}{5 d}$

Dividir un polinomio por un binomio

Para dividir un polinomio por un binomio, seguimos un procedimiento muy similar a la división larga de números. Entonces, veamos cuidadosamente los pasos que damos cuando dividimos un número de 3 dígitos, 875, por un número de 2 dígitos, 25.

Escribimos la división larga	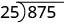$La división larga de 875 por 25.$
Dividimos los dos primeros dígitos, 87, por 25.	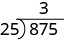$25 encaja en 87 tres veces. 3 está escrito por encima del segundo dígito de 875 en el paréntesis de división larga.$
Multiplicamos 3 por 25 y escribimos el producto bajo el 87.	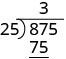$El producto de 3 y 25 es 75, que se escribe debajo de los dos primeros dígitos de 875 en el paréntesis de división larga.$
Ahora restamos 75 de 87.	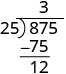$87 menos 75 es 12, que está escrito bajo 75.$
Después bajamos el tercer dígito del dividendo, 5.	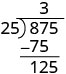$El 5 en 875 es derribado al lado del 12, haciendo 125.$
Repita el proceso, dividiendo 25 en 125.	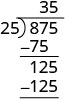$25 encaja en 125 cinco veces. 5 está escrito a la derecha del 3 en la parte superior del soporte de división larga. 5 veces 25 es 125. 125 menos 125 es cero. Hay cero resto, por lo que 25 encaja en 125 exactamente cinco veces. 875 dividido por 25 equivale a 35.$

Verificamos la división multiplicando el cociente por el divisor.

Si hicimos la división correctamente, el producto debería ser igual al dividendo.

\[\begin{array}{l}{35 \cdot 25} \\ {875}\checkmark\end{array}\]

Ahora vamos a dividir un trinomio por un binomio. Al leer el ejemplo, observe lo similares que son los pasos al ejemplo numérico anterior.

Ejercicio$\PageIndex{19}$

Encuentra el cociente:$\left(x^{2}+9 x+20\right) \div(x+5)$

Contestar

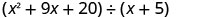
	$Un trinomio, x cuadrado más 9 x más 20, dividido por un binomio, x más 5.$
Escríbelo como un problema de división larga.
Asegúrese de que el dividendo esté en forma estándar.	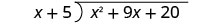$La división larga de x al cuadrado más 9 x más 20 por x más 5$
Divide x ² por x. Puede ser útil preguntarse: “¿Qué necesito multiplicar x por para obtener x ²?”
Poner la respuesta, x, en el cociente sobre el término x.	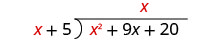$x encaja en x cuadrado x veces. x está escrito por encima del segundo término de x cuadrado más 9 x más 20 en el paréntesis de división larga.$
Multiplicar x veces x + 5. Alinee los términos similares bajo el dividendo.	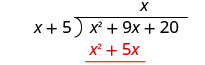$El producto de x y x más 5 es x cuadrado más 5 x, que se escribe debajo de los dos primeros términos de x al cuadrado más 9x más 20 en el soporte de división larga.$
Restar x ² + 5 x de x ² + 9 x.
$Puede que le resulte más fácil cambiar las señales y luego agregarlas.$ Después derribar el último término, 20.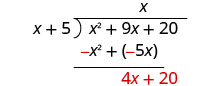	$La suma de x al cuadrado más 9 x y negativo x cuadrado más negativo 5 x es 4 x, que se escribe debajo del negativo 5 x El tercer término en x al cuadrado más 9 x más 20 se baja junto a 4 x, haciendo 4 x más 20.$
Divide 4 x por x. Puede ser útil preguntarse: “¿Qué necesito multiplicar x por para obtener 4 x?”
Poner la respuesta, 4, en el cociente sobre el término constante.	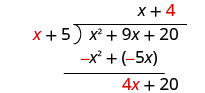$4 x dividido por x es 4. Más 4 está escrito en la parte superior del soporte de división larga, junto a x y por encima del 20 en x al cuadrado más 9 x más 20.$
Multiplica 4 veces x + 5.	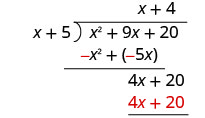$x más 5 veces 4 es 4 x más 20, que se escribe debajo de los primeros 4 x más 20.$
Restar 4 x + 20 de 4 x + 20.	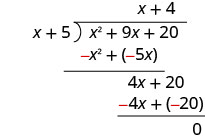$4 x más 20 menos 4 x más 20 es 0. El resto es 0. x cuadrado más 9 x más 20 dividido por x más 5 es igual a x más 4.$
Comprobar:
Multiplique el cociente por el divisor.
(x + 4) (x + 5)
Deberías obtener el dividendo.
x ² + 9 x + 20 ✓

Ejercicio$\PageIndex{20}$

Encuentra el cociente:$\left(y^{2}+10 y+21\right) \div(y+3)$

Contestar: y+7

Ejercicio$\PageIndex{21}$

Encuentra el cociente:$\left(m^{2}+9 m+20\right) \div(m+4)$

Contestar: m+5

Cuando el divisor tiene signo de resta, debemos tener mucho cuidado cuando multiplicamos el cociente parcial y luego restamos. Puede ser más seguro demostrar que cambiamos las señales y luego agregamos.

Ejercicio$\PageIndex{22}$

Encuentra el cociente:$\left(2 x^{2}-5 x-3\right) \div(x-3)$

Contestar

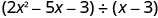
	$Un trinomio, 2 x al cuadrado menos 5 x menos 3, dividido por un binomio, x menos 3.$
Escríbelo como un problema de división larga.
Asegúrese de que el dividendo esté en forma estándar.	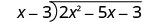$La división larga de 2 x al cuadrado menos 5 x menos 3 por x menos 3.$
Divide 2 x ² por x. Ponga la respuesta, 2 x, en el cociente sobre el término x.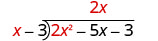	$x encaja en 2 x al cuadrado 2 x veces. 2 x está escrito por encima del segundo término de 2 x al cuadrado menos 5 x menos 3 en el paréntesis de división larga.$
Multiplicar 2 x veces x − 3. Alinee los términos similares bajo el dividendo.	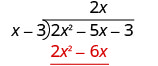$El producto de 2 x y x menos 3 es 2 x al cuadrado menos 6 x, el cual se escribe debajo de los dos primeros términos de 2 x al cuadrado menos 5 x menos 3 en el parchete de división larga.$
Restar 2 x ² − 6 x de 2 x ² − 5 x. Cambia los signos y luego agrega. Después derribar el último término.	$La suma de 2 x al cuadrado menos 5 x y negativo 2 x al cuadrado más 6 x es x, que se escribe debajo del 6 x El tercer término en 2 x al cuadrado menos 5 x menos 3 se baja junto a x, haciendo x menos 3.$
Divide x por x. Poner la respuesta, 1, en el cociente sobre el término constante.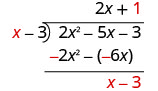	$Más 1 está escrito en la parte superior del soporte de división larga, junto a 2 x y por encima del menos 3 en 2 x al cuadrado menos 5 x menos 3.$
Multiplicar 1 veces x − 3.	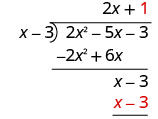$x menos 3 veces 1 es x menos 3, que se escribe debajo de la primera x menos 3.$
Restar x − 3 de x − 3 cambiando los signos y sumando.	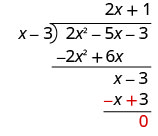$El binomio x menos 3 menos el binomio negativo x más 3 es 0. El resto es 0. 2 x cuadrado menos 5 x menos 3 dividido por x menos 3 es igual a 2 x más 1.$
Para verificar, multiplique (x − 3) (2 x + 1).
El resultado debe ser 2 x ² − 5 x − 3.

Ejercicio$\PageIndex{23}$

Encuentra el cociente:$\left(2 x^{2}-3 x-20\right) \div(x-4)$

Contestar: 2x+5

Ejercicio$\PageIndex{24}$

Encuentra el cociente:$\left(3 x^{2}-16 x-12\right) \div(x-6)$

Contestar: 3x+2

Cuando dividimos 875 por 25, no teníamos resto. Pero a veces la división de números sí deja un resto. Lo mismo ocurre cuando dividimos polinomios. En Ejercicio$\PageIndex{25}$, tendremos una división que deja un resto. Escribimos el resto como una fracción con el divisor como denominador.

Ejercicio$\PageIndex{25}$

Encuentra el cociente:$\left(x^{3}-x^{2}+x+4\right) \div(x+1)$

Contestar

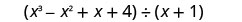
	$Un polinomio, x cubo menos x cuadrado más x más 4, dividido por otro polinomio, x más 1.$
Escríbelo como un problema de división larga.
Asegúrese de que el dividendo esté en forma estándar.	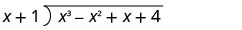$La división larga de x cubos menos x cuadrado más x más 4 por x más 1.$
Divide x ³ por x. Poner la respuesta, x ², en el cociente sobre el término x ². Multiplicar x ² veces x + 1. Alinee los términos similares bajo el dividendo.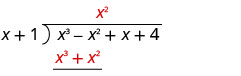	$x encaja en x cuadrado x veces. x está escrito por encima del segundo término de x cubo menos x cuadrado más x más 4 en el paréntesis de división larga.$
Restar x ³ + x ² de x ³ − x ² cambiando los signos y sumando. Después, derribar el siguiente término.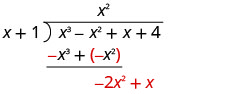	$La suma de x cubicado menos x cuadrado y negativo x cúbico más negativo x cuadrado es negativo 2 x cuadrado, que se escribe debajo del negativo x cuadrado. El siguiente término en x cubos menos x cuadrado más x más 4 se baja junto a negativo 2 x cuadrado, haciendo negativo 2 x cuadrado más x.$
Divide −2 x ² por x. Ponga la respuesta, −2 x, en el cociente sobre el término x. Multiplica −2 x veces x + 1. Alinee los términos similares bajo el dividendo.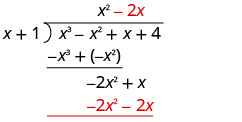	$Menos 2 x está escrito en la parte superior del soporte de división larga, junto a x al cuadrado y por encima de la x en x en cubos menos x al cuadrado más x más 4. Negativo 2 x cuadrado menos 2 x está escrito bajo negativo 2 x cuadrado más x.$
Restar −2 x ² − 2 x de −2 x ² + x cambiando los signos y sumando. Después derribar el último término.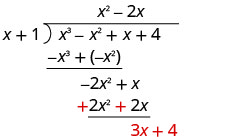	$La suma de 2 x al cuadrado negativo más x y 2 x al cuadrado más 2 x se encuentra que es 3 x El último término en x cubos menos x cuadrado más x más 4 se baja, haciendo 3 x más 4.$
Divide 3 x por x. Poner la respuesta, 3, en el cociente sobre el término constante. Multiplica 3 veces x + 1. Alinee los términos similares bajo el dividendo.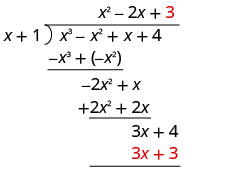	$Más 3 está escrito en la parte superior del corchete de división larga, por encima del 4 en x en cubos menos x al cuadrado más x más 4. 3 x más 3 está escrito bajo 3 x más 4.$
Restar 3 x + 3 de 3 x + 4 cambiando los signos y sumando. Escribe el resto como una fracción con el divisor como denominador.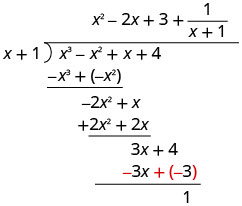	$La suma de 3 x más 4 y negativo 3 x más negativo 3 es 1. Por lo tanto, el polinomio x al cubo menos x al cuadrado más x más 4, dividido por el binomio x más 1, es igual a x al cuadrado menos 2 x más la fracción 1 sobre x más 1.$
Para verificar, multiplicar$(x+1)\left(x^{2}-2 x+3+\dfrac{1}{x+1}\right)$ El resultado debe ser$x^{3}-x^{2}+x+4$

Ejercicio$\PageIndex{26}$

Encuentra el cociente:$\left(x^{3}+5 x^{2}+8 x+6\right) \div(x+2)$

Contestar: $x^{2}+3 x+2+\dfrac{2}{x+2}$

Ejercicio$\PageIndex{27}$

Encuentra el cociente:$\left(2 x^{3}+8 x^{2}+x-8\right) \div(x+1)$

Contestar: $2 x^{2}+6 x-5-\dfrac{3}{x+1}$

Mira hacia atrás en los dividendos en Ejemplo, Ejemplo y Ejemplo. Los términos fueron escritos en orden descendente de grados, y no faltaron grados. El dividendo en Ejemplo será$x^{4}-x^{2}+5 x-2$. Le falta un$x^{3}$ término. Vamos a añadir en$0x^{3}$ como marcador de posición.

Ejercicio$\PageIndex{28}$

Encuentra el cociente:$\left(x^{4}-x^{2}+5 x-2\right) \div(x+2)$

Contestar

Observe que no hay$x^{3}$ término en el dividendo. Vamos a añadir$0x^{3}$ como marcador de posición.

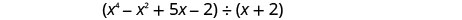
	$Un polinomio, x a la cuarta potencia menos x cuadrado menos 5 x menos 2, dividido por otro polinomio, x más 2.$
Escríbelo como un problema de división larga. Asegúrese de que el dividendo esté en forma estándar con marcadores de posición para términos faltantes.	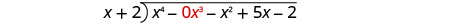$La división larga de x a la cuarta potencia más 0 x cubos menos x cuadrados menos 5 x menos 2 por x más 2.$
Divide x ⁴ por x. Poner la respuesta, x ³, en el cociente sobre el término x ³. Multiplicar x ³ veces x + 2. Alinee los términos similares. Restar y luego bajar el siguiente término.	$x en cubos se escribe encima del paréntesis de división larga por encima del término x en cubos en el dividendo. Por debajo de los dos primeros términos del dividendo x a la cuarta potencia más 2 x en cubos se resta para dar negativo 2 x cubo menos x cuadrado. Una nota al lado de la división dice “Puede ser útil cambiar las señales y agregar”.$
Divide −2 x ³ por x. Ponga la respuesta, −2 x ², en el cociente sobre el término x ². Multiplica −2 x ² veces x + 1. Alinee los términos similares. Restar y derribar el siguiente término.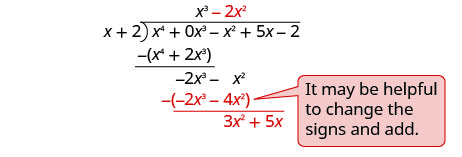	$x cubicado menos 2 x cuadrado está escrito en la parte superior del soporte de división larga. En la parte inferior de la división larga negativo 2 x al cubo menos 4 x al cuadrado se resta para dar 3 x al cuadrado más 5 x Una nota dice “Puede ser útil cambiar los signos y agregar”.$
Divide 3 x ² por x. Ponga la respuesta, 3 x, en el cociente sobre el término x. Multiplica 3 x veces x + 1. Alinee los términos similares. Restar y derribar el siguiente término.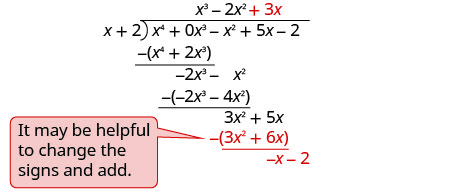	$x en cubos menos 2 x al cuadrado más 3 x está escrito en la parte superior del soporte de división larga. En la parte inferior de la división larga se resta 3 x al cuadrado más 6 x para dar negativo x menos 2. Una nota dice “Puede ser útil cambiar los signos y agregar”.$
Dividir − x por x. Poner la respuesta, −1, en el cociente sobre el término constante. Multiplica −1 veces x + 1. Alinee los términos similares. Cambia las señales, agrega.	$x cubicado menos 2 x cuadrado más 3 x menos 1 está escrito encima del soporte de división larga. En la parte inferior de la división larga negativo x menos 2 se resta para dar 0. Una nota dice “Puede ser útil cambiar los signos y agregar”. El polinomio x a la cuarta potencia menos x al cuadrado más 5 x menos 2, dividido por el binomio x más 2 es igual al polinomio x al cubo menos 2 x al cuadrado más 3 x menos 1.$
Para verificar, multiplicar$(x+2)\left(x^{3}-2 x^{2}+3 x-1\right)$
El resultado debe ser$x^{4}-x^{2}+5 x-2$

Ejercicio$\PageIndex{29}$

Encuentra el cociente:$\left(x^{3}+3 x+14\right) \div(x+2)$

Contestar: $x^{2}-2 x+7$

Ejercicio$\PageIndex{30}$

Encuentra el cociente:$\left(x^{4}-3 x^{3}-1000\right) \div(x+5)$

Contestar: $x^{3}-8 x^{2}+40 x-200$

En Ejercicio$\PageIndex{31}$, dividiremos por$2a−3$. A medida que dividamos tendremos que considerar tanto las constantes como las variables.

Ejercicio$\PageIndex{31}$

Encuentra el cociente:$\left(8 a^{3}+27\right) \div(2 a+3)$

Contestar

Esta vez vamos a mostrar la división todo en un solo paso. Necesitamos agregar dos marcadores de posición para poder dividir.

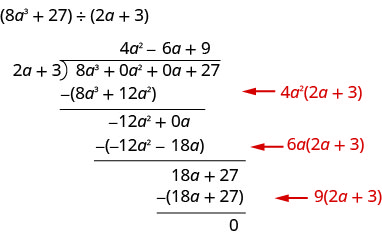
$La figura muestra la división larga de 8 a cubos más 27 por 2 a más 3. En el paréntesis de división larga, los marcadores de posición 0 a cuadrado y 0 a se agregan al polinomio. En la primera línea bajo el dividendo 8 se resta un cubo más 12 un cuadrado. A la derecha, una flecha indica que este valor vino de multiplicar 4 a al cuadrado por 2 a más 3. La resta da negativo 12 un cuadrado más 0 a. de este negativo 12 se resta un cuadrado menos 18 a. A la derecha, una flecha indica que este valor vino de multiplicar 6 a por 2 a más 3. La resta da 18 a más 27. De este 18 se resta un más 27. A la derecha, una flecha indica que este valor vino de multiplicar 9 por 2 a más 3. El resultado es 0.$

Para verificar, multiplicar$(2 a+3)\left(4 a^{2}-6 a+9\right)$

El resultado debe ser$8 a^{3}+27$

Ejercicio$\PageIndex{32}$

Encuentra el cociente:$\left(x^{3}-64\right) \div(x-4)$

Contestar: $x^{2}+4 x+16$

Ejercicio$\PageIndex{33}$

Encuentra el cociente:$\left(125 x^{3}-8\right) \div(5 x-2)$

Contestar: $25 x^{2}+10 x+4$

Nota

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con polinomios divididos:

Dividir un polinomio por un monomio
Dividir un polinomio por un monomio 2
Dividir polinomio por binomio

Conceptos clave

Adición de Fracciones
- Si a, b y c son números donde$c\neq 0$, entonces
  $\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{a+b}{c}$ y$\dfrac{a+b}{c}=\dfrac{a}{c}+\dfrac{b}{c}$
División de un polinomio por un monomio
- Para dividir un polinomio por un monomio, dividir cada término del polinomio por el monomio.

Objetivos de aprendizaje

Nota

Dividir un polinomio por un monomio

Adición de fracciones

DIVISIÓN DE UN POLINOMIO POR UN MONOMIO

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)

Ejercicio\(\PageIndex{11}\)

Ejercicio\(\PageIndex{12}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{13}\)

Ejercicio\(\PageIndex{14}\)

Ejercicio\(\PageIndex{15}\)

Ejercicio\(\PageIndex{16}\)

Ejercicio\(\PageIndex{17}\)

Ejercicio\(\PageIndex{18}\)

Dividir un polinomio por un binomio

Ejercicio\(\PageIndex{19}\)

Ejercicio\(\PageIndex{20}\)

Ejercicio\(\PageIndex{21}\)

Ejercicio\(\PageIndex{22}\)

Ejercicio\(\PageIndex{23}\)

Ejercicio\(\PageIndex{24}\)

Ejercicio\(\PageIndex{25}\)

Ejercicio\(\PageIndex{26}\)

Ejercicio\(\PageIndex{27}\)

Ejercicio\(\PageIndex{28}\)

Ejercicio\(\PageIndex{29}\)

Ejercicio\(\PageIndex{30}\)

Ejercicio\(\PageIndex{31}\)

Ejercicio\(\PageIndex{32}\)

Ejercicio\(\PageIndex{33}\)

Nota

Conceptos clave