7.6E: Ejercicios
- Page ID
- 110204
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La práctica hace la perfección
Usar la propiedad Zero Product
En los siguientes ejercicios, resuelve.
\((x−3)(x+7)=0\)
- Responder
-
\(x=3\),\(x=−7\) por lo que el conjunto de soluciones es:\(\{3, -7\}\)
\((y−11)(y+1)=0\)
\((3a−10)(2a−7)=0\)
- Responder
-
\(a=\frac{10}{3}\),\(a=\frac{7}{2}\) por lo que el conjunto de soluciones es:\(\Big\{\tfrac{10}{3}, \tfrac{7}{2}\Big\}\)
\((5b+1)(6b+1)=0\)
\(6m(12m−5)=0\)
- Responder
-
\(m=0\),\(m=\frac{5}{12}\) por lo que el conjunto de soluciones es:\(\Big\{0, \tfrac{5}{12}\Big\}\)
\(2x(6x−3)=0\)
\((y−3)^2=0\)
- Responder
-
\(y=3\)por lo que el conjunto de soluciones es:\(\{3\}\)
\((b+10)^2=0\)
\((2x−1)^2=0\)
- Responder
-
\(x=\frac{1}{2}\)por lo que el conjunto de soluciones es:\(\Big\{\tfrac{1}{2}\Big\}\)
\((3y+5)^2=0\)
Resolver ecuaciones cuadráticas por factorización
En los siguientes ejercicios, resuelve.
\(x^2+7x+12=0\)
- Responder
-
\(x=−3\),\(x=−4\) por lo que el conjunto de soluciones es:\(\{-3, -4\}\)
\(y^2−8y+15=0\)
\(5a^2−26a=24\)
- Responder
-
\(a=−\tfrac{4}{5}\),\(a=6\) por lo que el conjunto de soluciones es:\(\Big\{−\tfrac{4}{5}, 6\Big\}\)
\(4b^2+7b=−3\)
\(4m^2=17m−15\)
- Responder
-
\(m=\frac{5}{4}\),\(m=3\) por lo que el conjunto de soluciones es:\(\Big\{\tfrac{5}{4}, 3\Big\}\)
\(n^2=5−6n\)
\(7a^2+14a=7a\)
- Responder
-
\(a=−1\),\(a=0\) por lo que el conjunto de soluciones es:\(\{-1, 0\}\)
\(12b^2−15b=−9b\)
\(49m^2=144\)
- Responder
-
\(m=\frac{12}{7}\),\(m=−\frac{12}{7}\) por lo que el conjunto de soluciones es:\(\Big\{−\tfrac{12}{7}, \tfrac{12}{7}\Big\}\)
\(625=x^2\)
\((y−3)(y+2)=4y\)
- Responder
-
\(y=−1\),\(y=6\) por lo que el conjunto de soluciones es:\(\{-1, 6\}\)
\((p−5)(p+3)=−7\)
\((2x+1)(x−3)=−4x\)
- Responder
-
\(x=\frac{3}{2}\),\(x=−1\) por lo que el conjunto de soluciones es:\(\Big\{-1,\tfrac{3}{2}\Big\}\)
\((x+6)(x−3)=−8\)
\(16p^3=24p^2−9p\)
- Responder
-
\(p=0\),\(p=\frac{3}{4}\) por lo que el conjunto de soluciones es:\(\Big\{0,\tfrac{3}{4}\Big\}\)
\(m^3−2m^2=−m\)
\(20x^2−60x=−45\)
- Responder
-
\(x=\frac{3}{2}\)por lo que el conjunto de soluciones es:\(\Big\{\tfrac{3}{2}\Big\}\)
\(3y^2−18y=−27\)
Resolver aplicaciones modeladas por ecuaciones cuadráticas
En los siguientes ejercicios, resuelve.
El producto de dos enteros consecutivos es 56. Encuentra los enteros.
- Responder
-
7 y 8; −8 y −7
El producto de dos enteros consecutivos es 42. Encuentra los enteros.
El área de una alfombra rectangular es de 28 pies cuadrados. El largo es tres pies más que el ancho. Encuentra el largo y el ancho de la alfombra.
- Responder
-
4 pies y 7 pies
Un muro de contención rectangular tiene un área de 15 pies cuadrados. La altura de la pared es dos pies menos que su longitud. Encuentra la altura y la longitud de la pared.
Un banderín tiene forma de triángulo rectángulo, con hipotenusa de 10 pies. La longitud de un lado del banderín es dos pies más larga que la longitud del otro lado. Encuentra la longitud de los dos lados del banderín.
- Responder
-
6 pies y 8 pies
Una piscina reflectante tiene forma de triángulo rectángulo, con una pata a lo largo de la pared de un edificio. La hipotenusa es 9 pies más larga que el costado a lo largo del edificio. El tercer lado es 7 pies más largo que el lado a lo largo del edificio. Encuentra las longitudes de los tres lados de la piscina reflectante.
Práctica Mixta
En los siguientes ejercicios, resuelve.
(x+8) (x−3) =0
- Responder
-
\(x=−8, \; x=3\)por lo que el conjunto de soluciones es:\(\{-8, 3\}\)
(3y−5) (y+7) =0
\(p^2+12p+11=0\)
- Responder
-
\(p=−1, \;p=−11\)por lo que el conjunto de soluciones es:\(\{-11, -1\}\)
\(q^2−12q−13=0\)
\(m^2=6m+16\)
- Responder
-
\(m=−2, \; m=8\)por lo que el conjunto de soluciones es:\(\{-2, 8\}\)
\(4n^2+19n=5\)
\(a^3−a^2−42a=0\)
- Responder
-
\(a=0, \;a=−6, \;a=7\)por lo que el conjunto de soluciones es:\(\{-6, 0, 7\}\)
\(4b^2−60b+224=0\)
El producto de dos enteros consecutivos es 110. Encuentra los enteros.
- Responder
-
10 y 11; −11 y −10
La longitud de una pata de un triángulo rectángulo es tres más que la otra pierna. Si la hipotenusa es de 15, encuentra las longitudes de las dos patas.
Matemáticas cotidianas
Área de un patio Si cada lado de un patio cuadrado se incrementa en 4 pies, el área del patio sería de 196 pies cuadrados. Resuelve la ecuación (s+4) 2=196 (s+4) 2=196 para s para encontrar la longitud de un lado del patio.
- Responder
-
10 pies
Gota de sandía Se deja caer una sandía del décimo piso de un edificio. Resuelve la ecuación −16t2+144=0−16t2+144=0 para que tt encuentre el número de segundos que tarda la sandía en llegar al suelo.
Ejercicios de escritura
Explica cómo resuelves una ecuación cuadrática. ¿Cuántas respuestas esperas obtener para una ecuación cuadrática?
- Responder
-
Las respuestas pueden variar para la explicación. No debe esperar más de 2 soluciones para una ecuación cuadrática. A menudo tiene dos soluciones, pero a veces, puede tener una solución repetida o incluso ninguna solución.
Dar un ejemplo de una ecuación cuadrática que tiene un GCF y ninguna de las soluciones a la ecuación es cero.
Autocomprobación
a. después de completar los ejercicios, utilice esta lista de verificación para evaluar su dominio de los objetivos de esta sección.
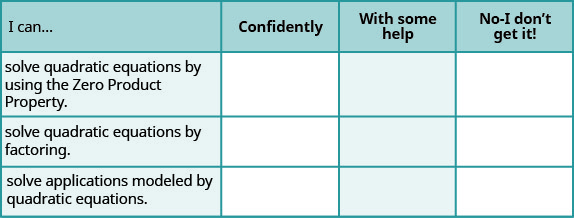
b. en general, después de mirar la lista de verificación, ¿cree que está bien preparado para la siguiente sección? ¿Por qué o por qué no?


