7.6: Ecuaciones cuadráticas
- Page ID
- 110200
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Al final de esta sección, podrás:
- Resolver ecuaciones cuadráticas usando la propiedad Zero Product
- Resolver ecuaciones cuadráticas
- Resolver aplicaciones modeladas por ecuaciones cuadráticas
Antes de comenzar, toma este cuestionario de preparación.
- Resolver:\(5y−3=0\).
Si te perdiste este problema, revisa el Ejercicio 2.3.1. - Resolver:\(10a=0\).
Si te perdiste este problema, revisa el Ejercicio 2.2.1. - Combina términos similares:\(12 x^{2}-6 x+4 x\).
Si te perdiste este problema, revisa Ejercicio 1.3.37. - Factorar\(n^{3}-9 n^{2}-22 n\) completamente.
Si te perdiste este problema, revisa el Ejercicio 7.3.10.
Ya hemos resuelto ecuaciones lineales, ecuaciones de la forma\(a x+b y=c\). En las ecuaciones lineales, las variables no tienen exponentes. Las ecuaciones cuadráticas son ecuaciones en las que la variable es cuadrada. A continuación se enumeran algunos ejemplos de ecuaciones cuadráticas:
\[x^{2}+5 x+6=0 \quad 3 y^{2}+4 y=10 \quad 64 u^{2}-81=0 \quad n(n+1)=42\]
La última ecuación no parece tener la variable al cuadrado, pero cuando simplifiquemos la expresión de la izquierda obtendremos\(n^{2}+n\).
La forma general de una ecuación cuadrática es\(a x^{2}+b x+c=0\), con\(a \neq 0\).
Una ecuación de la forma\(a x^{2}+b x+c=0\) se llama ecuación cuadrática.
\[a, b, \text { and } c \text { are real numbers and } a \neq 0\]
Para resolver ecuaciones cuadráticas necesitamos métodos diferentes a los que usamos para resolver ecuaciones lineales. Vamos a ver un método aquí y luego varios otros en un capítulo posterior.
Resolver ecuaciones cuadráticas usando la propiedad Zero Product
Primero resolveremos algunas ecuaciones cuadráticas mediante el uso de la Propiedad de Producto Cero. La Propiedad de Producto Cero dice que si el producto de dos cantidades es cero, debe ser que al menos una de las cantidades sea cero. La única manera de obtener un producto igual a cero es multiplicar por cero mismo.
\(\text { If } a \cdot b=0, \text { then either } a=0 \text { or } b=0 \text { or both. }\)
Ahora usaremos la Propiedad de Producto Cero, para resolver una ecuación cuadrática.
Resolver:\((x+1)(x-4)=0\)
- Contestar
-



Resolver:\((x-3)(x+5)=0\)
- Contestar
-
\(x=3, x=-5\)
Resolver:\((y-6)(y+9)=0\)
- Contestar
-
\(y=6, y=-9\)
Normalmente haremos un poco más de trabajo que en este último ejemplo para resolver las ecuaciones lineales que resultan del uso de la propiedad Zero Product.
Resolver:\((5 n-2)(6 n-1)=0\)
- Contestar
-
\((5 n-2)(6 n-1)=0\) Utilice la Propiedad de Producto Cero para establecer
cada factor en 0.\(5 n-2=0 \)
\(6 n-1=0\) Resuelve las ecuaciones. \(n=\frac{2}{5}\) \(n = \frac{1}{6}\) Consulta tus respuestas. 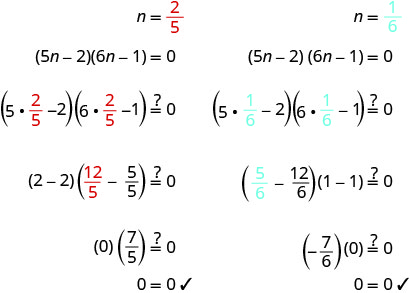
Resolver:\((3 m-2)(2 m+1)=0\)
- Contestar
-
\(m=\frac{2}{3}, m=-\frac{1}{2}\)
Resolver:\((4 p+3)(4 p-3)=0\)
- Contestar
-
\(p=-\frac{3}{4}, p=\frac{3}{4}\)
Observe cuando comprobamos las soluciones que cada una de ellas hizo solo un factor igual a cero. Pero el producto era cero para ambas soluciones.
Resolver:\(3 p(10 p+7)=0\)
- Contestar
-
\(3p(10p+7)=0\) Utilice la Propiedad de Producto Cero para establecer
cada factor en 0.3p=0 10p+7=0 Resuelve las ecuaciones. p=0 10p=−7 \(p=-\frac{7}{10}\) Consulta tus respuestas. 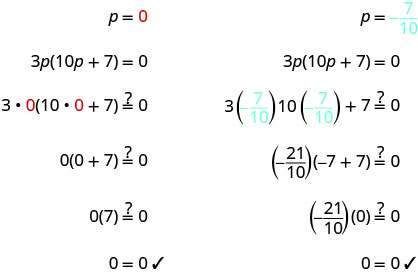
Resolver:\(2 u(5 u-1)=0\)
- Contestar
-
\(u=0, u=\frac{1}{5}\)
Resolver:\(w(2 w+3)=0\)
- Contestar
-
\(w=0, w=-\frac{3}{2}\)
Puede parecer que sólo hay un factor en el siguiente ejemplo. Recuerda, sin embargo, eso\((y-8)^{2}\) significa\((y-8)(y-8)\).
Resolver:\((y-8)^{2}=0\)
- Contestar
-
\((y−8)^{2}=0\) Reescribe el lado izquierdo como un producto. (y−8) (y−8) =0 Utilice la Propiedad de Producto Cero y
establezca cada factor en 0.y−8=0 y−8=0 Resuelve las ecuaciones. y=8 y=8 Cuando una solución se repite, la llamamos
doble raíz.Comprueba tu respuesta. 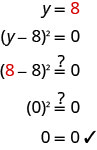
Resolver:\((x+1)^{2}=0\)
- Contestar
-
\(x=1\)
Resolver:\((v-2)^{2}=0\)
- Contestar
-
\(v=2\)
Resolver ecuaciones cuadráticas por factorización
Cada una de las ecuaciones que hemos resuelto en esta sección hasta ahora tenía un lado en forma factorizada. Para utilizar la Propiedad de Producto Cero, se debe factorizar la ecuación cuadrática, con cero en un lado. Así que nos aseguramos de comenzar con la ecuación cuadrática en forma estándar,\(a x^{2}+b x+c=0\). Después factorizamos la expresión de la izquierda.
Resolver:\(x^{2}+2 x-8=0\)
- Contestar
-

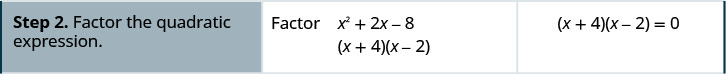



Resolver:\(x^{2}-x-12=0\)
- Contestar
-
\(x=4, x=-3\)
Resolver:\(b^{2}+9 b+14=0\)
- Contestar
-
\(b=-2, b=-7\)
- Escribir la ecuación cuadrática en forma estándar,\(a x^{2}+b x+c=0\).
- Factorar la expresión cuadrática.
- Utilice la Propiedad de Producto Cero.
- Resolver las ecuaciones lineales.
- Cheque.
Antes de factorizar, debemos asegurarnos de que la ecuación cuadrática esté en forma estándar.
Resolver:\(2 y^{2}=13 y+45\)
- Contestar
-
\(2 y^{2}=13 y+45\) Escribe la ecuación cuadrática en forma estándar. \(2 y^{2}-13 y-45=0\) Factorar la expresión cuadrática. \((2 y+5)(y-9)=0\) Utilice la Propiedad de Producto Cero
para establecer cada factor en 0.\(2 y+5=0\) \(y-9=0\) Resuelve cada ecuación. \(y=-\frac{5}{2}\) \(y=9\) Consulta tus respuestas. 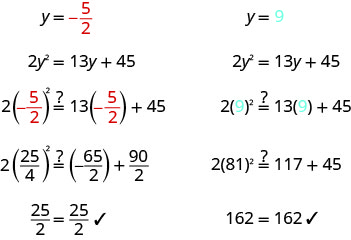
Resolver:\(3 c^{2}=10 c-8\)
- Contestar
-
\(c=0, c=\frac{4}{3}\)
Resolver:\(2 d^{2}-5 d=3\)
- Contestar
-
\(d=3, d=-\frac{1}{2}\)
Resolver:\(5 x^{2}-13 x=7 x\)
- Contestar
-
\(5 x^{2}-13 x=7 x\) Escribe la ecuación cuadrática en forma estándar. \(5 x^{2}-20 x=0\) Factorizar el lado izquierdo de la ecuación. \(5 x(x-4)=0\) Utilice la Propiedad de Producto Cero
para establecer cada factor en 0.\(5x=0\) \(x−4=0\) Resuelve cada ecuación. \(x=0\) \(x=4\) Consulta tus respuestas. 
Resolver:\(6 a^{2}+9 a=3 a\)
- Contestar
-
\(a=0, a=-1\)
Resolver:\(45 b^{2}-2 b=-17 b\)
- Contestar
-
\(b=0, b=-\frac{1}{3}\)
¡Resolver ecuaciones cuadráticas por factorización hará uso de todas las técnicas de factorización que has aprendido en este capítulo! ¿Reconoces el patrón especial del producto en el siguiente ejemplo?
Resolver:\(144 q^{2}=25\)
- Contestar
-
\(\begin{array}{lrllrl} & 144 q^{2}&=&25 \\ \text { Write the quadratic equation in standard form. }& 144 q^{2}-25&=& 0 \\ \text { Factor. It is a difference of squares. } & (12 q-5)(12 q+5) & = & 0 \\ \text { Use the Zero Product Property to set each factor to } 0 . & 12 q-5&=&0 & 12 q+5&=&0 \\\text { Solve each equation. } & 12 q & = & 5 & 12 q&=&-5 \\ & q&=&\frac{5}{12} & q & =&-\frac{5}{12} \\ \text { Check your answers. }\end{array}\)
Resolver:\(25 p^{2}=49\)
- Contestar
-
\(p=\frac{7}{5}, p=-\frac{7}{5}\)
Resolver:\(36 x^{2}=121\)
- Contestar
-
\(x=\frac{11}{6}, x=-\frac{11}{6}\)
El lado izquierdo en el siguiente ejemplo está factorizado, pero el lado derecho no es cero. Para utilizar la Propiedad de Producto Cero, un lado de la ecuación debe ser cero. Multiplicaremos los factores y luego escribiremos la ecuación en forma estándar.
Resolver:\((3 x-8)(x-1)=3 x\)
- Contestar
-
\(\begin{array}{ll} & (3 x-8)(x-1)=3 x \\ \text { Multiply the binomials. }& 3 x^{2}-11 x+8=3 x \\ \text { Write the quadratic equation in standard form. }& 3 x^{2}-14 x+8=0\\ \text { Factor the trinomial. }& (3 x-2)(x-4)=0\\\text { Use the Zero Product Property to set each factor to } 0 . & 3 x-2=0 \quad x-4=0 \\ \text { Solve each equation. } & 3 x=2 \quad x=4 \\ & x=\frac{2}{3} \\ \text { Check your answers. } & \text {The check is left to you! } \end{array}\)
Resolver:\((2 m+1)(m+3)=12 m\)
- Contestar
-
\(m=1, m=\frac{3}{2}\)
Resolver:\((k+1)(k-1)=8\)
- Contestar
-
\(k=3, k=-3\)
La Propiedad de Producto Cero también se aplica al producto de tres o más factores. Si el producto es cero, al menos uno de los factores debe ser cero. Podemos resolver algunas ecuaciones de grado más de dos usando la Propiedad Zero Product, al igual que resolvimos ecuaciones cuadráticas.
Resolver:\(9 m^{3}+100 m=60 m^{2}\)
- Contestar
-
\(\begin{array}{lrllrl} & 9 m^{3}+100 m&=&60 m^{2}\\ \text { Bring all the terms to one side so that the other side is zero. } & 9 m^{3}-60 m^{2}+100 m&=&0 \\ \text { Factor the greatest common factor first. } & m\left(9 m^{2}-60 m+100\right)&=&0 \\ \text { Factor the trinomial. } & m(3 m-10)(3 m-10)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & m&=&0 & 3 m-10&=&0 & 3 m-10&=&0 \\ \text { Solve each equation. } & m&=&0 & m&=&\frac{10}{3}& m&=&\frac{10}{3} \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Resolver:\(8 x^{3}=24 x^{2}-18 x\)
- Contestar
-
\(x=0, x=\frac{3}{2}\)
Resolver:\(16 y^{2}=32 y^{3}+2 y\)
- Contestar
-
\(y=0, y=\frac{1}{4}\)
Cuando factorizamos la ecuación cuadrática en el siguiente ejemplo obtendremos tres factores. Sin embargo, el primer factor es una constante. Sabemos que el factor no puede ser igual a 0.
Resolver:\(4 x^{2}=16 x+84\)
- Contestar
-
\(\begin{array}{lrllrl} & 4 x^{2}&=&16 x+84\\ \text { Write the quadratic equation in standard form. }& 4 x^{2}-16 x-84&=&0 \\ \text { Factor the greatest common factor first. }& 4\left(x^{2}-4 x-21\right)&=&0 \\ \text { Factor the trinomial. } & 4(x-7)(x+3)&=&0 \\ \text { Use the Zero Product Property to set each factor to 0. } & 4&\neq&0 & x-7&=&0 & x +3&=&0 \\ \text { Solve each equation. } & 4&\neq&0 & x&=&7& x&=&-3 \\ \text { Check your answers. } & \text { The check is left to you. } \end{array}\)
Resolver:\(18 a^{2}-30=-33 a\)
- Contestar
-
\(a=-\frac{5}{2}, a=\frac{2}{3}\)
Resolver:\(123 b=-6-60 b^{2}\)
- Contestar
-
\(b=2, b=\frac{1}{20}\)
Resolver aplicaciones modeladas por ecuaciones cuadráticas
La estrategia de resolución de problemas que usamos anteriormente para aplicaciones que se traducen en ecuaciones lineales funcionará igual de bien para aplicaciones que se traducen en ecuaciones cuadráticas. Copiaremos la estrategia de resolución de problemas aquí para que podamos usarla como referencia.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traducir la oración en inglés a una ecuación álgebra.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
Comenzaremos con un problema numérico para conseguir practicar la traducción de palabras en una ecuación cuadrática.
El producto de dos enteros consecutivos es\(132 .\) Buscar los enteros.
- Contestar
-
\(\begin{array}{ll} \textbf { Step 1. Read} \text { the problem. } \\ \textbf { Step 2. Identify} \text { what we are looking for. } & \text { We are looking for two consecutive integers. } \\ \textbf { Step 3. Name} \text{ what we are looking for. } & \begin{array}{l}{\text { Let } n=\text { the first integer }} \\ {\space n+1=\text { the next consecutive integer }}\end{array} \\\textbf { Step 4. Translate} \text { into an equation. Restate the } & \text { The product of the two consecutive integers is } 132 . \\ \text { problem in a sentence. } \\ \text { Translate to an equation. } & \begin{array}{c}{\text { The first integer times the next integer is } 132 .} \\ {n(n+1)=132}\end{array} \\ \textbf { Step 5. Solve}\text { the equation. } & n^{2}+n=132 \\ \text { Bring all the terms to one side. } & n^{2}+n-132=0 \\ \text { Factor the trinomial. } & (n-11)(n+12)=0 \\ \text { Use the zero product property. } & n-11=0 \quad n+12=0 \\ \text { Solve the equations. } & n=11 \quad n=-12 \end{array}\)
El producto de dos enteros consecutivos es\(240 .\) Buscar los enteros.
- Contestar
-
\(-15,-16\)y\(15,16\)
El producto de dos enteros consecutivos es\(420 .\) Buscar los enteros.
- Contestar
-
\(-21,-20\)y\(20,21\)
¿Te sorprendió el par de enteros negativos que es una de las soluciones al ejemplo anterior? El producto de los dos enteros positivos y el producto de los dos enteros negativos dan 132.
En algunas aplicaciones, las soluciones negativas resultarán del álgebra, pero no serán realistas para la situación.
Un jardín rectangular tiene una superficie de 15 pies cuadrados. La longitud del jardín es dos pies más que el ancho. Encuentra el largo y ancho del jardín.
- Contestar
-
Paso 1. Lee el problema. En problemas que involucran figuras geométricas, un boceto puede ayudarte a visualizar la situación. 
Paso 2. Identifica lo que buscas. Estamos buscando el largo y ancho. Paso 3. Nombra lo que buscas.
La longitud es dos pies más que la anchura.Dejar W = el ancho del jardín.
W + 2 = la longitud del jardínPaso 4. Traducir en una ecuación.
Reafirmar la información importante en una oración.
El área del jardín rectangular es de 15 pies cuadrados.Usa la fórmula para el área de un rectángulo. \(A=L \cdot W\) Sustituto en las variables. \(15=(W+2) W\) Paso 5. Resuelve la ecuación. Distribuir primero. \(15=W^{2}+2 W\) Consigue cero en un lado. \(0=W^{2}+2 W-15\) Factorar el trinomio. \(0=(W+5)(W-3)\) Utilice la Propiedad de Producto Cero. \(0=W+5\) \(0=W−3\) Resuelve cada ecuación. \(−5=W\) \(3=W\) Dado que W es el ancho del jardín,
no tiene sentido que sea
negativo. Eliminamos ese valor para W.\(W=−5\) cannot be the width, since it's negative.
\(W=3\)\(3=W\)
El ancho es de 3 pies.Encuentra el valor de la longitud. \(\text{length}=W+2\) \(\text{length}=3+2\) \(\text{length}=5\) La longitud es de 5 pies. Paso 6. Consulta la respuesta.
¿Tiene sentido la respuesta?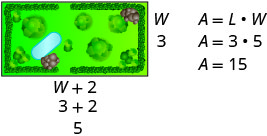
Sí, esto tiene sentido. Paso 7. Contesta la pregunta. El ancho del jardín es de 3 pies
y el largo es de 5 pies.
Un letrero rectangular tiene una superficie de 30 pies cuadrados. El largo del letrero es un pie más que el ancho. Encuentra el largo y ancho del letrero.
- Contestar
-
55 pies y 66 pies
Un patio rectangular tiene una superficie de 180 pies cuadrados. El ancho del patio es de tres pies menos que la longitud. Encuentra el largo y ancho del patio.
- Contestar
-
12 pies y 15 pies
En un capítulo anterior, se utilizó el Teorema de Pitágoras\(\left(a^{2}+b^{2}=c^{2}\right)\). Dio la relación entre las piernas y la hipotenusa de un triángulo rectángulo.
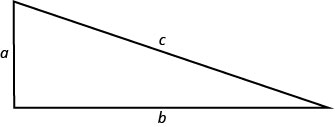
Usaremos esta fórmula para en el siguiente ejemplo.
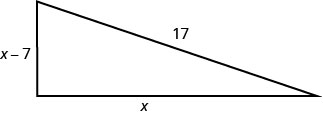
Justine quiere poner una cubierta en la esquina de su patio trasero en forma de triángulo rectángulo, como se muestra a continuación. La hipotenusa tendrá 17 pies de largo. La longitud de un lado será 7 pies menos que la longitud del otro lado. Encuentra las longitudes de los lados de la cubierta.
- Contestar
-
Paso 1. Lee el problema. Paso 2. Identifica lo que buscas. Estamos buscando las longitudes de los lados
de la cubierta.Paso 3. Nombra lo que buscas.
Un lado es 7 menos que el otro.Let x = longitud de un lado de la cubierta
x − 7 = longitud del otro ladoPaso 4. Traducir en una ecuación.
Dado que este es un triángulo rectángulo podemos usar el Teorema de
Pitágoras.\(a^{2}+b^{2}=c^{2}\) Sustituto en las variables. \(x^{2}+(x-7)^{2}=17^{2}\) Paso 5. Resuelve la ecuación. \(x^{2}+x^{2}-14 x+49=289\) Simplificar. \(2 x^{2}-14 x+49=289\) Es una ecuación cuadrática, así que consigue cero en un lado. \(2 x^{2}-14 x-240=0\) Factor el mayor factor común. \(2\left(x^{2}-7 x-120\right)=0\) Factorar el trinomio. \(2(x-15)(x+8)=0\) Utilice la Propiedad de Producto Cero. \(2\neq 0\) \(x−15=0\) \(x+8=0\) Resolver. \(2\neq 0\) \(x=15\) \(x=-8\) Ya que\(x\) es un lado del triángulo,\(x=−8\) no tiene
sentido.\(2\neq 0\) \(x=15\) \(\cancel{x=−8}\) Encuentra la longitud del otro lado. Si la longitud de un lado es \(x=15\) entonces la longitud del otro lado es \(x-7\) \(15 - 7 = 8\) 8 es la longitud del otro lado. Paso 6. Consulta la respuesta.
¿Tienen sentido estos números?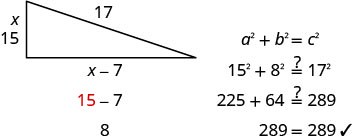
Paso 7. Contesta la pregunta. Los lados de la cubierta son de 8, 15 y 17 pies.
La vela de un barco es un triángulo rectángulo. La longitud de un lado de la vela es de 7 pies más que el otro lado. La hipotenusa es de 13. Encuentra las longitudes de los dos lados de la vela.
- Contestar
-
5 pies y 12 pies
Un jardín de meditación tiene la forma de un triángulo rectángulo, con una pierna de 7 pies. La longitud de la hipotenusa es una más que la longitud de una de las otras piernas. Encuentra las longitudes de la hipotenusa y la otra pierna.
- Contestar
-
24 pies y 25 pies
Conceptos clave
- Zero Product Property Si\(a \cdot b=0\), entonces ya sea a=0 o b=0 o ambos. Ver Ejemplo.
- Resolver una ecuación cuadrática factorizando Para resolver una ecuación cuadrática por factorización: Ver Ejemplo.
- Escribir la ecuación cuadrática en forma estándar,\(a x^{2}+b x+c=0\).
- Factorar la expresión cuadrática.
- Utilice la Propiedad de Producto Cero.
- Resolver las ecuaciones lineales.
- Cheque.
- Utilice una estrategia de resolución de problemas para resolver problemas de palabras Ver Ejemplo.
- Lee el problema. Asegúrate de que todas las palabras e ideas sean entendidas.
- Identificar lo que estamos buscando.
- Nombra lo que estamos buscando. Elija una variable para representar esa cantidad.
- Traducir en una ecuación. Puede ser útil reafirmar el problema en una oración con toda la información importante. Después, traducir la oración en inglés a una ecuación álgebra.
- Resolver la ecuación usando buenas técnicas de álgebra.
- Comprueba la respuesta en el problema y asegúrate de que tenga sentido.
- Contesta la pregunta con una oración completa.
Glosario
- ecuaciones cuadráticas
- son ecuaciones en las que la variable es cuadrada.
- Propiedad de Producto Cero
- La Propiedad de Producto Cero establece que, si el producto de dos cantidades es cero, al menos una de las cantidades es cero.


