10.5: Forma polar de números complejos
- Page ID
- 112075
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Trazar números complejos en el plano complejo.
- Encuentra el valor absoluto de un número complejo.
- Escribe números complejos en forma polar.
- Convierte un número complejo de forma polar a rectangular.
- Encuentra productos de números complejos en forma polar.
- Encuentra cocientes de números complejos en forma polar.
- Encuentra potencias de números complejos en forma polar.
- Encuentra raíces de números complejos en forma polar.
“Dios hizo los enteros; todo lo demás es obra del hombre”. Esta cita bastante famosa del matemático alemán del siglo XIX Leopold Kronecker prepara el escenario para esta sección sobre la forma polar de un número complejo. Los números complejos fueron inventados por la gente y representan más de mil años de continua investigación y lucha de matemáticos como Pitágoras, Descartes, De Moivre, Euler, Gauss, y otros. Los números complejos respondieron preguntas que durante siglos habían desconcertado a las mentes más grandes de la ciencia.
Primero encontramos números complejos en la sección de Números Complejos. En esta sección, nos centraremos en la mecánica de trabajar con números complejos: traducción de números complejos de forma polar a forma rectangular y viceversa, interpretación de números complejos en el esquema de aplicaciones y aplicación del Teorema de De Moivre.
Trazado de números complejos en el plano complejo
Trazar un número complejo\(a+bi\) es similar a trazar un número real, excepto que el eje horizontal representa la parte real del número\(a\), y el eje vertical representa la parte imaginaria del número,\(bi\).
- Etiquetar el eje horizontal como el eje real y el eje vertical como el eje imaginario.
- Trace el punto en el plano complejo moviendo\(a\) las unidades en la dirección horizontal y\(b\) las unidades en la dirección vertical.
Trazar el número complejo\(2−3i\) en el plano complejo.
Solución
Desde el origen, mover dos unidades en la dirección horizontal positiva y tres unidades en la dirección vertical negativa. Ver Figura\(\PageIndex{1}\).
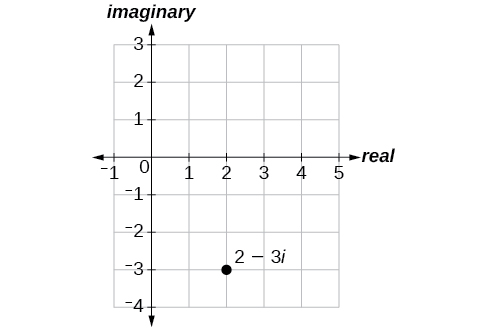
Trazar el punto\(1+5i\) en el plano complejo.
- Contestar
-
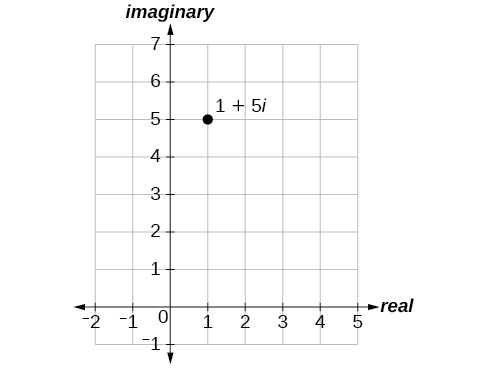
Figura\(\PageIndex{2}\)
Encontrar el valor absoluto de un número complejo
El primer paso para trabajar con un número complejo en forma polar es encontrar el valor absoluto. El valor absoluto de un número complejo es el mismo que su magnitud, o\(| z |\). Mide la distancia desde el origen hasta un punto en el plano. Por ejemplo, la gráfica de\(z=2+4i\), en la Figura\(\PageIndex{3}\), muestra\(| z |\).
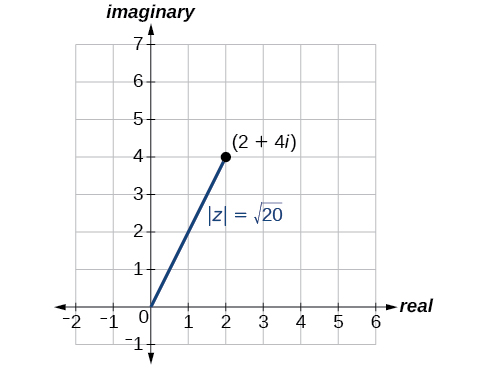
Dado\(z=x+yi\), un número complejo, el valor absoluto de\(z\) se define como
\[| z |=\sqrt{x^2+y^2}\]
Es la distancia desde el origen hasta el punto\((x,y)\).
Observe que el valor absoluto de un número real da la distancia del número desde\(0\), mientras que el valor absoluto de un número complejo da la distancia del número desde el origen,\((0, 0)\).
Encuentra el valor absoluto de\(z=\sqrt{5}−i\).
Solución
Usando la fórmula, tenemos
\[\begin{align*} |z| &= \sqrt{x^2+y^2} \\ |z| &= \sqrt{{(\sqrt{5})}^2+{(-1)}^2} \\ |z| &= \sqrt{5+1} \\ |z| &= \sqrt{6} \end{align*}\]
Ver Figura\(\PageIndex{4}\).
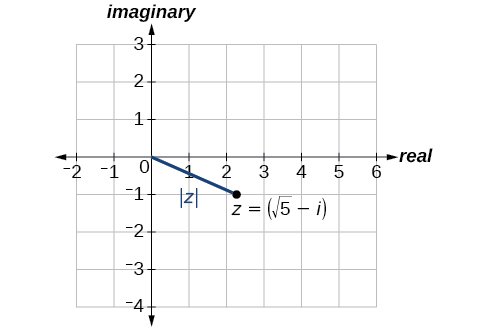
Encuentra el valor absoluto del número complejo\(z=12−5i\).
- Contestar
-
\(13\)
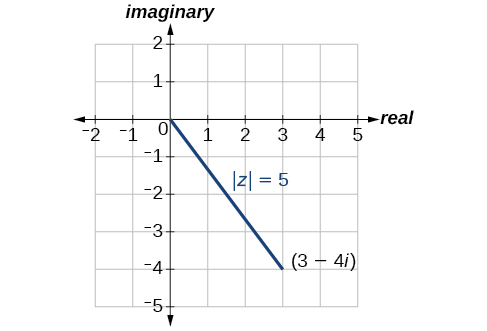
Dado\(z=3−4i\), encuentra\(| z |\).
Solución
Usando la fórmula, tenemos
\[\begin{align*} | z | &= \sqrt{x^2+y^2} \\ | z | &= \sqrt{{(3)}^2+{(-4)}^2} \\ | z | &= \sqrt{9+16} \\ | z | &= \sqrt{25} \\ | z | &= 5 \end{align*}\]
El valor absoluto\(z\) es\(5\). Ver Figura\(\PageIndex{5}\).
Dado\(z=1−7i\), encuentra\(| z |\).
- Contestar
-
\(| z |=\sqrt{50}=5\sqrt{2}\)
Escribir números complejos en forma polar
La forma polar de un número complejo expresa un número en términos de un ángulo\(\theta\) y su distancia desde el origen\(r\). Dado un número complejo en forma rectangular expresado como\(z=x+yi\), utilizamos las mismas fórmulas de conversión que hacemos para escribir el número en forma trigonométrica:
\[\begin{align*} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align*}\]
Revisamos estas relaciones en la Figura\(\PageIndex{6}\).
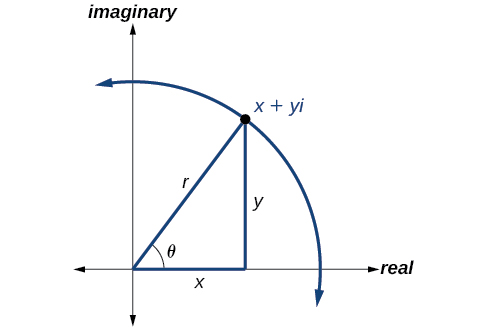
Utilizamos el término módulo para representar el valor absoluto de un número complejo, o la distancia desde el origen hasta el punto\((x,y)\). El módulo, entonces, es el mismo que\(r\), el radio en forma polar. Usamos\(\theta\) para indicar el ángulo de dirección (al igual que con las coordenadas polares). Sustituyendo, tenemos
\[\begin{align*} z &= x+yi \\ z &= r \cos \theta+(r \sin \theta)i \\ z &= r(\cos \theta+i \sin \theta) \end{align*}\]
Escribir un número complejo en forma polar implica las siguientes fórmulas de conversión:
\[\begin{align} x &= r \cos \theta \\ y &= r \sin \theta \\ r &= \sqrt{x^2+y^2} \end{align}\]
Haciendo una sustitución directa, tenemos
\[\begin{align} z &= x+yi \\ z &= (r \cos \theta)+i(r \sin \theta) \\ z &= r(\cos \theta+i \sin \theta) \end{align}\]
donde\(r\) está el módulo y\(\theta\) es el argumento. A menudo usamos la abreviatura\(r\; cis \theta\) para representar\(r(\cos \theta+i \sin \theta)\).
Exprese el número complejo\(4i\) usando coordenadas polares.
Solución
En el plano complejo, el número\(z=4i\) es el mismo que\(z=0+4i\). Escribiéndolo en forma polar, tenemos que calcular\(r\) primero.
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{0^2+4^2} \\ r &= \sqrt{16} \\ r &= 4 \end{align*}\]
A continuación, nos fijamos en\(x\). Si\(x=r \cos \theta\), y\(x=0\), entonces\(\theta=\dfrac{\pi}{2}\). En coordenadas polares, el número complejo se\(z=0+4i\) puede escribir como\(z=4\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right) \text{ or } 4\; cis\left( \dfrac{\pi}{2}\right)\). Ver Figura\(\PageIndex{7}\).
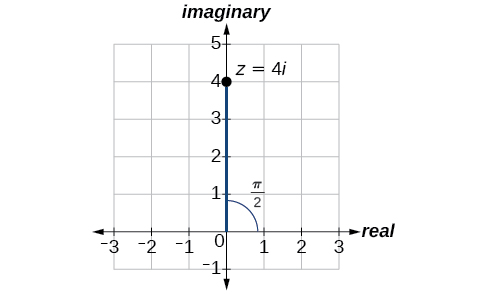
Expreso\(z=3i\) como\(r\space cis \theta\) en forma polar.
- Contestar
-
\(z=3\left(\cos\left(\dfrac{\pi}{2}\right)+i \sin\left(\dfrac{\pi}{2}\right)\right)\)
Encuentra la forma polar de\(−4+4i\).
Solución
Primero, encuentra el valor de\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(−4)}^2+(4^2)} \\ r &= \sqrt{32} \\ r &= 4\sqrt{2} \end{align*}\]
Encuentra el ángulo\(\theta\) usando la fórmula:
\[\begin{align*} \cos \theta &= \dfrac{x}{r} \\ \cos \theta &= \dfrac{−4}{4\sqrt{2}} \\ \cos \theta &= −\dfrac{1}{\sqrt{2}} \\ \theta &= {\cos}^{−1} \left(−\dfrac{1}{\sqrt{2}}\right)\\ &= \dfrac{3\pi}{4} \end{align*}\]
Así, la solución es\(4\sqrt{2}\space cis \left(\dfrac{3\pi}{4}\right)\).
Escribir\(z=\sqrt{3}+i\) en forma polar.
- Contestar
-
\(z=2\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Conversión de un número complejo de forma polar a rectangular
Convertir un número complejo de forma polar a forma rectangular es una cuestión de evaluar lo que se da y usar la propiedad distributiva. En otras palabras, dado\(z=r(\cos \theta+i \sin \theta)\), primero evaluar las funciones trigonométricas\(\cos \theta\) y\(\sin \theta\). Entonces, multiplicar por\(r\).
Convertir la forma polar del número complejo dado a forma rectangular:
\(z=12\left(\cos\left(\dfrac{\pi}{6}\right)+i \sin\left(\dfrac{\pi}{6}\right)\right)\)
Solución
Comenzamos evaluando las expresiones trigonométricas.
\[\begin{align*} \cos\left(\dfrac{\pi}{6}\right)&= \dfrac{\sqrt{3}}{2} \text{ and } \sin(\dfrac{\pi}{6})=\dfrac{1}{2}\\ \text {After substitution, the complex number is}\\ z&= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \end{align*}\]
Aplicamos la propiedad distributiva:
\[\begin{align*} z &= 12\left(\dfrac{\sqrt{3}}{2}+\dfrac{1}{2}i\right) \\ &= (12)\dfrac{\sqrt{3}}{2}+(12)\dfrac{1}{2}i \\ &= 6\sqrt{3}+6i \end{align*}\]
La forma rectangular del punto dado en forma compleja es\(6\sqrt{3}+6i\).
Encuentra la forma rectangular del número complejo dado\(r=13\) y\(\tan \theta=\dfrac{5}{12}\).
Solución
Si\(\tan \theta=\dfrac{5}{12}\), y\(\tan \theta=\dfrac{y}{x}\), primero determinamos\(r=\sqrt{x^2+y^2}=\sqrt{122+52}=13\). Luego encontramos\(\cos \theta=\dfrac{x}{r}\) y\(\sin \theta=\dfrac{y}{r}\).
\[\begin{align*} z &= 13\left(\cos \theta+i \sin \theta\right) \\ &= 13\left(\dfrac{12}{13}+\dfrac{5}{13}i\right) \\ &=12+5i \end{align*}\]
La forma rectangular del número dado en forma compleja es\(12+5i\).
Convertir el número complejo a forma rectangular:
\(z=4\left(\cos \dfrac{11\pi}{6}+i \sin \dfrac{11\pi}{6}\right)\)
- Contestar
-
\(z=2\sqrt{3}−2i\)
Encontrar productos de números complejos en forma polar
Ahora que podemos convertir números complejos a forma polar aprenderemos a realizar operaciones en números complejos en forma polar. Para el resto de esta sección, trabajaremos con fórmulas desarrolladas por el matemático francés Abraham de Moivre (1667-1754). Estas fórmulas han hecho que trabajar con productos, cocientes, poderes y raíces de números complejos sea mucho más sencillo de lo que parecen. Las reglas se basan en multiplicar los módulos y agregar los argumentos.
Si\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) y\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), entonces el producto de estos números se da como:
\[\begin{align} z_1z_2 &= r_1r_2[ \cos(\theta_1+\theta_2)+i \sin(\theta_1+\theta_2) ] \\ z_1z_2 &= r_1r_2\space cis(\theta_1+\theta_2) \end{align}\]
Observe que el producto requiere multiplicar los módulos y sumar los ángulos.
Encuentra el producto de\(z_1z_2\), dado\(z_1=4(\cos(80°)+i \sin(80°))\) y\(z_2=2(\cos(145°)+i \sin(145°))\).
Solución
Sigue la fórmula
\[\begin{align*} z_1z_2 &= 4⋅2[\cos(80°+145°)+i \sin(80°+145°)] \\ z_1z_2 &= 8[\cos(225°)+i \sin(225°)] \\ z_1z_2 &= 8\left[\cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ z_1z_2 &= 8\left[−\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ z_1z_2 &= −4\sqrt{2}−4i\sqrt{2} \end{align*}\]
Encontrar cocientes de números complejos en forma polar
El cociente de dos números complejos en forma polar es el cociente de los dos módulos y la diferencia de los dos argumentos.
Si\(z_1=r_1(\cos \theta_1+i \sin \theta_1)\) y\(z_2=r_2(\cos \theta_2+i \sin \theta_2)\), entonces el cociente de estos números es
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}[\cos(\theta_1−\theta_2)+i \sin(\theta_1−\theta_2) ],\space z_2≠0\]
\[\dfrac{z_1}{z_2}=\dfrac{r_1}{r_2}\space cis(\theta_1−\theta_2),\space z_2≠0\]
Observe que los módulos están divididos, y se restan los ángulos.
- Dividir\(\dfrac{r_1}{r_2}\).
- Encuentra\(\theta_1−\theta_2\).
- Sustituir los resultados por la fórmula:\(z=r(\cos \theta+i \sin \theta)\). Reemplazar\(r\) con\(\dfrac{r_1}{r_2}\), y reemplazar\(\theta\) con\(\theta_1−\theta_2\).
- Calcular las nuevas expresiones trigonométricas y multiplicar por\(r\).
Encuentra el cociente de\(z_1=2(\cos(213°)+i \sin(213°))\) y\(z_2=4(\cos(33°)+i \sin(33°))\).
Solución
Usando la fórmula, tenemos
\[\begin{align*} \dfrac{z_1}{z_2} &= \dfrac{2}{4}[\cos(213°−33°)+i \sin(213°−33°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[\cos(180°)+i \sin(180°)] \\ \dfrac{z_1}{z_2} &= \dfrac{1}{2}[−1+0i] \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2}+0i \\ \dfrac{z_1}{z_2} &= −\dfrac{1}{2} \end{align*}\]
Encuentra el producto y el cociente de\(z_1=2\sqrt{3}(\cos(150°)+i \sin(150°))\) y\(z_2=2(\cos(30°)+i \sin(30°))\).
- Contestar
-
\(z_1z_2=−4\sqrt{3}\);\(\dfrac{z_1}{z_2}=−\dfrac{\sqrt{3}}{2}+\dfrac{3}{2}i\)
Encontrar poderes de números complejos en forma polar
Encontrar poderes de números complejos se simplifica enormemente usando el teorema de De Moivre. Afirma que, para un entero positivo\(n\),\(z^n\) se encuentra elevando el módulo a la\(n^{th}\) potencia y multiplicando el argumento por\(n\). Es el método estándar utilizado en las matemáticas modernas.
Si\(z=r(\cos \theta+i \sin \theta)\) es un número complejo, entonces
\[\begin{align} z^n &= r^n[\cos(n\theta)+i \sin(n\theta) ] \\ z^n &= r^n\space cis(n\theta) \end{align}\]
donde\(n\) es un entero positivo.
Evaluar la expresión\({(1+i)}^5\) usando el Teorema de De Moivre.
Solución
Dado que el Teorema de De Moivre se aplica a números complejos escritos en forma polar, primero debemos escribir\((1+i)\) en forma polar. Vamos a encontrar\(r\).
\[\begin{align*} r &= \sqrt{x^2+y^2} \\ r &= \sqrt{{(1)}^2+{(1)}^2} \\ r &= \sqrt{2} \end{align*}\]
Entonces nos encontramos\(\theta\). El uso de la fórmula\(\tan \theta=\dfrac{y}{x}\) da
\[\begin{align*} \tan \theta &= \dfrac{1}{1} \\ \tan \theta &= 1 \\ \theta &= \dfrac{\pi}{4} \end{align*}\]
Utilice el Teorema de De Moivre para evaluar la expresión.
\[\begin{align*} {(a+bi)}^n &= r^n[\cos(n\theta)+i \sin(n\theta)] \\ {(1+i)}^5 &= {(\sqrt{2})}^5\left[ \cos\left(5⋅\dfrac{\pi}{4}\right)+i \sin\left(5⋅\dfrac{\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ \cos\left(\dfrac{5\pi}{4}\right)+i \sin\left(\dfrac{5\pi}{4}\right) \right] \\ {(1+i)}^5 &= 4\sqrt{2}\left[ −\dfrac{\sqrt{2}}{2}+i\left(−\dfrac{\sqrt{2}}{2}\right) \right] \\ {(1+i)}^5 &= −4−4i \end{align*}\]
Encontrar raíces de números complejos en forma polar
Para encontrar la\(n^{th}\) raíz de un número complejo en forma polar, utilizamos el Teorema de la\(n^{th}\) Raíz o Teorema de De Moivre y elevamos el número complejo a una potencia con un exponente racional. Existen varias formas de representar una fórmula para encontrar\(n^{th}\) raíces de números complejos en forma polar.
Para encontrar la\(n^{th}\) raíz de un número complejo en forma polar, utilice la fórmula dada como
\[z^{\tfrac{1}{n}}=r^{\tfrac{1}{n}}\left[ \cos\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right)+i \sin\left(\dfrac{\theta}{n}+\dfrac{2k\pi}{n}\right) \right]\]
donde\(k=0, 1, 2, 3, . . . , n−1\). Agregamos\(\dfrac{2k\pi}{n}\)\(\dfrac{\theta}{n}\) a para obtener las raíces periódicas.
Evaluar las raíces cubicas de\(z=8\left(\cos\left(\frac{2\pi}{3}\right)+i\sin\left(\frac{2\pi}{3}\right)\right)\).
Solución
Tenemos
\[\begin{align*} z^{\frac{1}{3}} &= 8^{\frac{1}{3}}\left[ \cos\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{\frac{2\pi}{3}}{3}+\frac{2k\pi}{3}\right) \right] \\ z^{\frac{1}{3}} &= 2\left[ \cos\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right)+i \sin\left(\frac{2\pi}{9}+\frac{2k\pi}{3}\right) \right] \end{align*}\]
Habrá tres raíces:\(k=0, 1, 2\). Cuando\(k=0\), tenemos
\(z^{\frac{1}{3}}=2\left(\cos\left(\dfrac{2\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}\right)\right)\)
Cuando\(k=1\), tenemos
\[\begin{align*} z^{\frac{1}{3}} &=2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{6\pi}{9}\right) \right] \;\;\;\;\;\;\;\;\; \text{Add }\dfrac{2(1)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{8\pi}{9}\right)+i \sin\left(\dfrac{8\pi}{9}\right)\right) \end{align*}\]
Cuando\(k=2\), tenemos
\[\begin{align*} z^{\frac{1}{3}} &= 2\left[ \cos\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right)+i \sin\left(\dfrac{2\pi}{9}+\dfrac{12\pi}{9}\right) \right] \;\;\;\;\;\;\; \text{Add }\dfrac{2(2)\pi}{3} \text{ to each angle.} \\ z^{\frac{1}{3}} &= 2\left(\cos\left(\dfrac{14\pi}{9}\right)+i \sin\left(\dfrac{14\pi}{9}\right)\right) \end{align*}\]
Recuerda encontrar el denominador común para simplificar fracciones en situaciones como esta. Para\(k=1\), la simplificación del ángulo es
\[\begin{align*} \dfrac{\dfrac{2\pi}{3}}{3}+\dfrac{2(1)\pi}{3} &= \dfrac{2\pi}{3}(\dfrac{1}{3})+\dfrac{2(1)\pi}{3}\left(\dfrac{3}{3}\right) \\ &=\dfrac{2\pi}{9}+\dfrac{6\pi}{9} \\ &=\dfrac{8\pi}{9} \end{align*}\]
Encuentra las cuatro cuartas raíces de\(16(\cos(120°)+i \sin(120°))\).
- Contestar
-
\(z_0=2(\cos(30°)+i \sin(30°))\)
\(z_1=2(\cos(120°)+i \sin(120°))\)
\(z_2=2(\cos(210°)+i \sin(210°))\)
\(z_3=2(\cos(300°)+i \sin(300°))\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con formas polares de números complejos.
- El producto y cociente de números complejos en forma trigonométrica
- Teorema de De Moivre
Conceptos clave
- Los números complejos en la forma\(a+bi\) se trazan en el plano complejo de manera similar a la forma en que se trazan las coordenadas rectangulares en el plano rectangular. Etiquetar el\(x\) eje -como el eje real y el eje\(y\) - como el eje imaginario. Ver Ejemplo\(\PageIndex{1}\).
- El valor absoluto de un número complejo es el mismo que su magnitud. Es la distancia desde el origen hasta el punto:\(| z |=\sqrt{a^2+b^2}\). Ver Ejemplo\(\PageIndex{2}\) y Ejemplo\(\PageIndex{3}\).
- Para escribir números complejos en forma polar, utilizamos las fórmulas\(x=r \cos \theta\),\(y=r \sin \theta\), y\(r=\sqrt{x^2+y^2}\). Entonces,\(z=r(\cos \theta+i \sin \theta)\). Ver Ejemplo\(\PageIndex{4}\) y Ejemplo\(\PageIndex{5}\).
- Para convertir de forma polar a forma rectangular, primero evalúe las funciones trigonométricas. Entonces, multiplicar por\(r\). Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
- Para encontrar el producto de dos números complejos, multiplique los dos módulos y sume los dos ángulos. Evaluar las funciones trigonométricas y multiplicar usando la propiedad distributiva. Ver Ejemplo\(\PageIndex{8}\).
- Para encontrar el cociente de dos números complejos en forma polar, encuentre el cociente de los dos módulos y la diferencia de los dos ángulos. Ver Ejemplo\(\PageIndex{9}\).
- Para encontrar el poder de un número complejo\(z^n\), elevar\(r\) al poder\(n\), y multiplicar\(\theta\) por\(n\). Ver Ejemplo\(\PageIndex{10}\).
- Encontrar las raíces de un número complejo es lo mismo que elevar un número complejo a una potencia, pero utilizando un exponente racional. Ver Ejemplo\(\PageIndex{11}\).