16.3: Anillos

Un conjunto no vacío\(R\) es un anillo si tiene dos operaciones binarias cerradas, suma y multiplicación, cumpliendo las siguientes condiciones.

1. \(a + b = b + a\)para\(a, b \in R\text{.}\)
2. \((a + b) + c = a + ( b + c)\)para\(a, b, c \in R\text{.}\)
3. Hay un elemento\(0\) en\(R\) tal que\(a + 0 = a\) para todos\(a \in R\text{.}\)
4. Por cada elemento\(a \in R\text{,}\) existe un elemento\(-a\) en\(R\) tal que\(a + (-a) = 0\text{.}\)
5. \((ab) c = a ( b c)\)para\(a, b, c \in R\text{.}\)
6. Para\(a, b, c \in R\text{,}\)

   \ begin {align*} a (b + c) &= ab +ac\\ (a + b) c & = ac + bc\ text {.} \ end {alinear*}

Esta última condición, el axioma distributivo, relaciona las operaciones binarias de suma y multiplicación. Observe que los primeros cuatro axiomas simplemente requieren que un anillo sea un grupo abeliano en adición, por lo que también podríamos haber definido un anillo para ser un grupo abeliano\((R, +)\) junto con una segunda operación binaria que satisfaga las condiciones quinta y sexta dadas anteriormente.

Si hay un elemento\(1 \in R\) tal que\(1 \neq 0\) y\(1a = a1 = a\) para cada elemento\(a \in R\text{,}\) decimos que\(R\) es un anillo con unidad o identidad. Un anillo\(R\) para\(ab = ba\) el que para todos\(a, b\) en\(R\) se llama anillo conmutativo. Un anillo conmutativo\(R\) con identidad se denomina dominio integral si, para cada uno\(a, b \in R\) de ellos,\(ab = 0\text{,}\)\(a = 0\) o\(b = 0\text{.}\) Un anillo de división es un anillo\(R\text{,}\) con una identidad, en el que cada elemento distinto de cero en \(R\)es una unidad; es decir, para cada uno\(a \in R\) con\(a \neq 0\text{,}\) existe un elemento único\(a^{-1}\) tal que\(a^{-1} a = a a^{-1} = 1\text{.}\) A un anillo de división conmutativa se le llama campo. La relación entre anillos, dominios integrales, anillos de división y campos se muestra en la Figura\(16.1\).

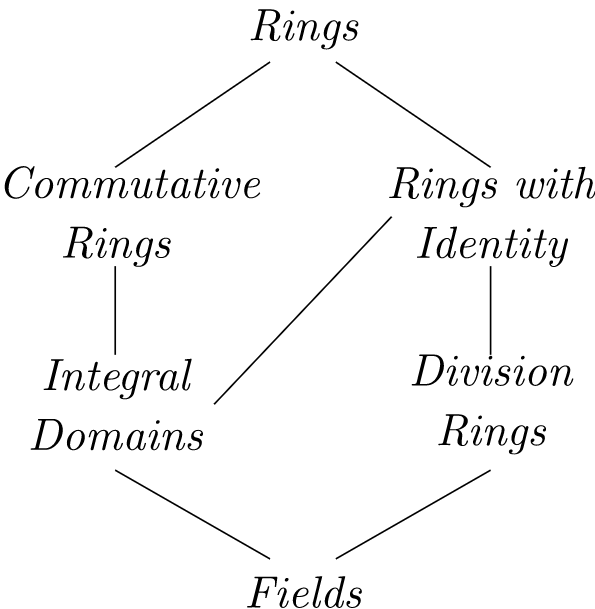
\(Figure \text { } 16.1.\)Tipos de anillos

Ejemplo\(16.2\)

Como hemos mencionado anteriormente, los enteros forman un anillo. De hecho,\({\mathbb Z}\) es un dominio integral. Ciertamente si\(a b = 0\) para dos enteros\(a\) y\(b\text{,}\) cualquiera\(a=0\) o\(b=0\text{.}\)

Solución

Sin embargo, no\({\mathbb Z}\) es un campo. No hay entero que sea el inverso multiplicativo de\(2\text{,}\) ya que no\(1/2\) es un entero. Los únicos enteros con inversos multiplicativos son\(1\) y\(-1\text{.}\)

Ejemplo\(16.3\)

Bajo las operaciones ordinarias de suma y multiplicación, todos los sistemas numéricos familiares son anillos:

Solución

los racionales,\({\mathbb Q}\text{;}\) los números reales,\({\mathbb R}\text{;}\) y los números complejos,\({\mathbb C}\text{.}\) Cada uno de estos anillos es un campo.

Ejemplo\(16.4\)

Podemos definir el producto de dos elementos\(a\) y\(b\) en\({\mathbb Z}_n\) por\(ab \pmod{n}\text{.}\)

Solución

Por ejemplo, en\({\mathbb Z}_{12}\text{,}\)\(5 \cdot 7 \equiv 11 \pmod{12}\text{.}\) Este producto convierte al grupo abeliano\({\mathbb Z}_n\) en un anillo. Ciertamente\({\mathbb Z}_n\) es un anillo conmutativo; sin embargo, puede no ser un dominio integral. Si consideramos\(3 \cdot 4 \equiv 0 \pmod{12}\) en\({\mathbb Z}_{12}\text{,}\) ella es fácil ver que un producto de dos elementos distintos de cero en el anillo puede ser igual a cero.

Un elemento distinto de cero\(a\) en un anillo conmutativo\(R\) se denomina divisor cero si hay un elemento distinto de cero\(b\) en\(R\) tal que\(ab = 0\text{.}\) En el ejemplo anterior,\(3\) y\(4\) son divisores cero en\({\mathbb Z}_{12}\text{.}\)

Ejemplo\(16.5\)

En el cálculo las funciones continuas de valor real en un intervalo\([a,b]\) forman un anillo conmutativo. Agregamos o multiplicamos dos funciones sumando o multiplicando los valores de las funciones. Si\(f(x) = x^2\) y\(g(x) = \cos x\text{,}\)

Solución

entonces\((f+g)(x) = f(x) + g(x) = x^2 + \cos x\) y\((fg)(x) = f(x) g(x) = x^2 \cos x\text{.}\)

Ejemplo\(16.6\)

Las\(2 \times 2\) matrices con entradas\({\mathbb R}\) forman un anillo bajo las operaciones habituales de adición y multiplicación de matrices.

Solución

Este anillo es no conmutativo, ya que suele darse el caso que\(AB \neq BA\text{.}\) también, note que podemos tener\(AB = 0\) cuando ni\(A\) ni\(B\) es cero.

Ejemplo\(16.7\)

Para un ejemplo de un anillo de división no conmutativo, vamos

\[ 1 = \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}, \quad {\mathbf i} = \begin{pmatrix} 0 & 1 \\ -1 & 0 \end{pmatrix}, \quad {\mathbf j} = \begin{pmatrix} 0 & i \\ i & 0 \end{pmatrix}, \quad {\mathbf k} = \begin{pmatrix} i & 0 \\ 0 & -i \end{pmatrix}\text{,} \nonumber \]

donde\(i^2 = -1\text{.}\) Estos elementos satisfacen las siguientes relaciones:

\ begin {alinear*} {\ mathbf i} ^2 = {\ mathbf j} ^2 & = {\ mathbf k} ^2 = -1\\ {\ mathbf i} {\ mathbf j} & = {\ mathbf k}\\ {\ mathbf j} {\ mathbf k} & = {\ mathbf i}\\ {\ mathbf k} {\ mathbf i} & = {\ mathbf j}\\ {\ mathbf j} {\ mathbf i} & = - {\ mathbf k}\\ {\ mathbf k} {\ mathbf j} & = - {\ mathbf i}\\ {\ mathbf i} {\ mathbf k} & = - {\ mathbf j}\ texto {.} \ end {alinear*}

Dejar\({\mathbb H}\) consistir en elementos de la forma\(a + b {\mathbf i} + c {\mathbf j} +d {\mathbf k}\text{,}\) donde\(a, b , c, d\) están los números reales. Equivalentemente, se\({\mathbb H}\) puede considerar como el conjunto de todas las\(2 \times 2\) matrices de la forma

\[ \begin{pmatrix} \alpha & \beta \\ -\overline{\beta} & \overline{\alpha } \end{pmatrix}\text{,} \nonumber \]

donde\(\alpha = a + di\) y\(\beta = b + ci\) son números complejos. Podemos definir suma y multiplicación\({\mathbb H}\) ya sea por las operaciones habituales de matriz o en términos de los generadores\(1\text{,}\)\({\mathbf i}\text{,}\)\({\mathbf j}\text{,}\) y\({\mathbf k}\text{:}\)

\ begin {reunir*} (a_1 + b_1 {\ mathbf i} + c_1 {\ mathbf j} +d_1 {\ mathbf k}) + (a_2 + b_2 {\ mathbf i} + c_2 {\ mathbf j} +d_2 {\ mathbf k})\\ = (a_1 + a_2) + (b_1 + b_2) {\ mathbf i} + (c_1 + c_2)\ mathbf j + (d_1 + d_2)\ mathbf k\ end {reunir*}

y

\[ (a_1 + b_1 {\mathbf i} + c_1 {\mathbf j} +d_1 {\mathbf k} ) ( a_2 + b_2 {\mathbf i} + c_2 {\mathbf j} +d_2 {\mathbf k} ) = \alpha + \beta {\mathbf i} + \gamma {\mathbf j} + \delta {\mathbf k}\text{,} \nonumber \]

donde

\ begin {alinear*}\ alfa & = a_1 a_2 - b_1 b_2 - c_1 c_2 -d_1 d_2\\\ beta & = a_1 b_2 + a_2 b_1 + c_1 d_2 - d_1 c_2\\\ gamma & = a_1 c_2 - b_1 d_2 + c_1 a_2 + d_1 b_2\\\ delta & = a_1 d_2 _2 + b_1 c_2 - c_1 b_2 + d_1 a_2\ texto {.} \ end {alinear*}

Solución

Aunque la multiplicación parece complicada, en realidad es un cálculo sencillo si recordamos que solo agregamos y multiplicamos elementos en polinomios\({\mathbb H}\) similares y tenemos en cuenta las relaciones entre los generadores\({\mathbf i}\text{,}\)\({\mathbf j}\text{,}\) y\({\mathbf k}\text{.}\) El anillo\({\mathbb H}\) se llama el anillo de cuaterniones.

Para demostrar que los cuaterniones son un anillo de división, debemos poder encontrar una inversa para cada elemento distinto de cero. Observe que

\[ ( a + b {\mathbf i} + c {\mathbf j} + d {\mathbf k} )( a - b {\mathbf i} - c {\mathbf j} - d {\mathbf k} ) = a^2 + b^2 + c^2 + d^2\text{.} \nonumber \]

Este elemento puede ser cero sólo si\(a\text{,}\)\(b\text{,}\)\(c\text{,}\) y\(d\) son todos cero. Así que si\(a + b {\mathbf i} + c {\mathbf j} +d {\mathbf k} \neq 0\text{,}\)

\[ (a + b {\mathbf i} + c {\mathbf j} + d {\mathbf k})\left( \frac{a - b {\mathbf i} - c {\mathbf j} - d {\mathbf k} }{a^2 + b^2 + c^2 + d^2} \right) = 1\text{.} \nonumber \]

Proposición\(16.8\)

Deja\(R\) ser un anillo con\(a, b \in R\text{.}\) Entonces

1. \(a0 = 0a = 0\text{;}\)
2. \(a(-b) = (-a)b = -ab\text{;}\)
3. \((-a)(-b) =ab\text{.}\)

Prueba

Para probar (1), observar que

\[ a0 = a(0+0)= a0+ a0; \nonumber \]

por lo tanto,\(a0=0\text{.}\) Similarmente,\(0a = 0\text{.}\) Para (2), tenemos\(ab + a(-b) = a(b-b) = a0 = 0\text{;}\) consecuentemente,\(-ab = a(-b)\text{.}\) De igual manera, la\(-ab = (-a)b\text{.}\) Parte (3) se desprende directamente de (2) ya que\((-a)(-b) = -(a(- b)) = -(-ab) = ab\text{.}\)

Así como tenemos subgrupos de grupos, tenemos una clase análoga de subestructuras para anillos. Un subring\(S\) de un anillo\(R\) es un subconjunto\(S\) de\(R\) tal que también\(S\) es un anillo bajo las operaciones heredadas de\(R\text{.}\)

Ejemplo\(16.9\)

El anillo\(n {\mathbb Z}\) es un subring de\({\mathbb Z}\text{.}\)

Solución

Observe que aunque el anillo original pueda tener una identidad, no requerimos que su subring tenga una identidad. Contamos con la siguiente cadena de subring:

\[ {\mathbb Z} \subset {\mathbb Q} \subset {\mathbb R} \subset {\mathbb C}\text{.} \nonumber \]

La siguiente proposición nos da algunos criterios fáciles para determinar si un subconjunto de un anillo es efectivamente un subring o no. (Dejaremos como ejercicio la prueba de esta proposición.)

Proposición\(16.10\)

Dejar\(R\) ser un anillo y\(S\) un subconjunto de\(R\text{.}\) Entonces\(S\) es un subring de\(R\) si y solo si se cumplen las siguientes condiciones.

1. \(S \neq \emptyset\text{.}\)
2. \(rs \in S\)para todos\(r, s \in S\text{.}\)
3. \(r-s \in S\)para todos\(r, s \in S\text{.}\)

Ejemplo\(16.11\)

Dejar\(R ={\mathbb M}_2( {\mathbb R} )\) ser el anillo de\(2 \times 2\) matrices con entradas en\({\mathbb R}\text{.}\) If\(T\) es el conjunto de matrices triangulares superiores en\(R\text{;}\) i.e.,

\[ T = \left\{ \begin{pmatrix} a & b \\ 0 & c \end{pmatrix} : a, b, c \in {\mathbb R} \right\}\text{,} \nonumber \]

Solución

entonces\(T\) es un subring de\(R\text{.}\) Si

\[ A = \begin{pmatrix} a & b \\ 0 & c \end{pmatrix} \quad \text{and} \quad B = \begin{pmatrix} a' & b' \\ 0 & c' \end{pmatrix} \nonumber \]

están en\(T\text{,}\) entonces claramente\(A-B\) también en\(T\text{.}\) También,

\[ AB = \begin{pmatrix} a a' & ab' + bc' \\ 0 & cc' \end{pmatrix} \nonumber \]

está en\(T\text{.}\)